Introduction

The non-linear configuration of the partial differential equations plays significant role within the numerous disciplines of sciences and engineering. There are numerous modern scientific disciplines in which PDEs have pivotal rule and many researchers work on it1,2,3,4,5. The optimal non-linear partial differential equations regulate problems with control and to solve this, Pesch proposed two different strategies6. After optimization, the first approach for dispersion was indirect. The second approach, the direct methodology, was optimized after being reduced to a fine level of detail. The ordinary differential equations have been used to study the models of the non-linear systems. An algorithm for computing the generalized frequency response to the family of non-linear differential equations was developed by Peyton and Billings7. Victor’s research8 provided a comprehensive description of the existence, stability, modeling, importance, and uniqueness of ordinary differential equations. Ahmed proposed an ODE-PDE system in his paper in which both ordinary differential equations and partial differential equations systems are explained9. The researchers and analysts are trying to introduce a midway track to connect both ODE-PDE system10. Now, partial differential equations are seeking significantly attention of researchers because of numerous applications in multiple disciplines of modern study11,12,13,14,15.

The astounding path to the scientific world was made possible by the integration of the fractional theory of calculus, a well-liked technique for resolving partial differential equations. Compared to classical order fractional derivatives, the fractional partial differential equations revealed some shocking as well as deep knowledge of actual physical phenomena. Many fractional order derivatives and operators have been formulated as a result of the interest in fractional theory. Some of them are presented here, Caputo fractional derivative16, conformal fractional differential operator17, \(\beta\)-fractional differential operator18, truncated M-fractional derivative19, Riemann–Liouville fractional operator20, Caputo–Fabrizio fractional derivative21, and the Atangana–Baleanu fractional derivative22. A numerous variety of applications with these fractional operators has been done in diverse fields of sciences. The analysis of local fractional Klein–Gordon equation conducted by Jagdeve and Baleanu23. Jagdeve provided the solution of differential difference and examined24. Baleanu examined a new fractional operator in the logistic equation25. Atangana analyzed the Cauchy problem as well revealed a fresh understanding of changing rate26. When studying the applications of such types of the fractional theory then obviously, a question arises why we use fractional theory, and what are the advantages of fractional theory.

Instead of asking the question of why to utilize the fractional theory of derivative, we should ask why to prefer the classical theory of differentiation. The response to, what are reasons behind the preference of fractional theory. The integer-order derivative (classical theory of differentiation) is the local operator. Thus, the integer-order differential operator is ill-suited in the situation, where heavy tails (infinity variations) are anticipated because the influence of the bigger neighborhood can’t be ignored anymore. On the contrary, the fractional derivative is the global operator, therefore it contrives to examine these influences.

The extended rational sine–cosine/sinh–cosh, and modified direct algebraic methods are utilized to examine the nonlinear differential model and their soliton solution28. Bilal et al.29,30,31 analytically discussed the Wazwaz–Benjamin–Bona–Mahony, Improved Boussinesq and nonlinear Zakharov–Kuznetsov modified equal-width equation and demonstrated their propagation. Arefin et al.32,33 investigated the Benjamin–Bona–Mahony, Calogero–Degasperis (CD) and fractional potential Kadomstev–Petviashvili via analytical approaches to understanded different phenomenon. Zaman et al.34,35 developed kink soliton, periodic, bright, dark and many solitons solutions for different dynamical system. Ayesha et al.36 applied fractional operator on Schrödinger and obtained fractional analytical exact solutions.

Analysis of fractional partial differential equations in sort of solitons is one of the remarkable studies in non-linear optics. For the study in sort of solitons, a proficient class of schemes, approaches, and method has been formulated such as extended trial equation method37, the symmetry strategy38, Lie and Buckland transformation approach39, exp-function method40, and tanh-coth trigonometric function technique41 etc. A lot of research work has been conducted by various scientists and researchers in the discipline of solitons42,43,44. Mostafa and Behzad discuss the Riemann wave propagating and examined the fractional Bogoyavlensky Konopelchenko equation and also the propagation of long-wave45. Qin and Mostafa examined the fractional Broer–Kaup system which simulates the bidirectional propagation of long-wave in shallow water46. The flow of shallow water discussed by Mostafa47. Abdel investigated the physical phenomenon of water waves propagation48. The fractional Klein–Gordon equations have investigated by Inc and Baleanu as well as the fractional Cahn–Allen equation49. The varicella-zoster virus is modeled and investigated by Qureshi50. This field has multiple applications in diverse areas of physical sciences.

This study is about the real phenomenon of ion sound and Langmuir waves. The non-linear complex system of the partial differential equation for ion sound wave and Langmuir waves is considered here that is within influence ponderomotive force can be quite important avenue one of several kinds of research and scientist, prominently in the field of high-frequency51. The system presented is52:

$$\begin{aligned} {\left\{ \begin{array}{ll} i \Xi _{t}+\frac{1}{2} \Xi _{xx}-\Delta \Xi =0, & \, \\ \Delta _{tt}-\Delta _{xx}-2(|\Xi |^{2})_{xx}=0, & \, \end{array}\right. } \end{aligned}$$
(1)

where, \(\Xi e^{i\phi pt}\) is presenting the normalized electric field (NEF) and R is normalized density perturbation (NDP) of the Langmuir oscillation. In the last decades, many scientists have found various types of outcomes of the system of partial differential equations for the ion sound and Langmuir waves51. Two basic oscillations of plasma are ion sound waves and Langmuir waves, which have different geometrical and physical meanings. Whereas Langmuir waves are high-frequency electron oscillations driven by electric fields, ion sound waves are low-frequency oscillations caused by ion inertia and electron pressure. Both kinds of waves offer profound insights into the behavior of plasmas and their interactions with electromagnetic fields, and they are essential for research on fusion, space plasmas, diagnostics of plasmas, and communication technologies. Demiray obtained the exact solution by utilizing the extended trial function method of the system for ion sound and Langmuir waves53. Vidojevic examined the effects of Langmuir waves electric fields on the shape of spectral line54. Manafian has obtained the solitonic buildings from the non-linear Schrödinger evolution equation with the prosecution of \(\tan (\frac{\phi }{2})\)-expansion method55. Mohyud-Din has been obtained the numerical soliton solutions of improved Boussinesq equation56. A lot of work has been done on it but the analysis of the framework to generate the Langmuir oscillation as well as ion sound in influence for fractional theory is not done yet. On this inspiration, we are investigating this complex system using fractional theory in sort of solitons.

This study is systemized as, section “Preliminaries” is devoted for necessary prerequisites, section “The fractional appearance with three different operators” is presenting the fractional appearance of the model as well as some useful transformations, description of scheme and applications are in section “Construction of soliton solution for ion sound and Langmuir wave equation”, section “Graphical analysis” is an explanation of graphics, and rest of the paper is conclusion and references.

Preliminaries

Here, certain pertinent contributions and notations are highlighted, which are then used to condense novel and anarchistic ideas.

Definition

The RL operator is defined as, assume  \(h:x \rightarrow h(x)\) is a continues mapping but not exceptionally differentiable. The differential operator comprises fractional-order \(\alpha\) is explicated as in20:

$$\begin{aligned} ^{RL}D^{\alpha }_{x}h(x)= {\left\{ \begin{array}{ll} \frac{1}{\Gamma (\alpha )}\int ^{x}_{o}(x-\zeta )^{-\alpha -1}(h(\zeta )-h(0))d\zeta ,& \alpha<0\\ \frac{1}{\Gamma (\alpha )}\frac{d}{dx}\int ^{x}_{o}(x-\zeta )^{-\alpha }(h(\zeta )-h(0))d\zeta ,& 0<alpha<1\\ (h^{n}(\alpha ))^{\alpha -n},& n\le \alpha \le n+1, n\ge 1 \end{array}\right. } \end{aligned}$$
(2)

Definition

The beta fractional differential operator is defined as18:

$$\begin{aligned} _{0}^{B}D^{\alpha }_{x}(h(x))=\lim _{\varepsilon \rightarrow 0}\frac{h(x+\varepsilon (x+\frac{1}{\Gamma (\alpha )}))-h(x)}{\varepsilon }. \end{aligned}$$
(3)

Definition

The Atangana–Baleanu in the sense of Riemann–Liouville fractional differential operator is defined as in22:

$$\begin{aligned} _{0}^{ABR} D^{\alpha }_{a^{+}}(h(t))=\frac{AB(\alpha )}{(1-\alpha )}\frac{d}{dt}\int ^{t}_{a}h(\tau )E_{\alpha }(\frac{-\alpha (t-\tau )^{\alpha }}{1-\alpha })d\tau , \end{aligned}$$
(4)

where \(E_{\alpha }\) is the Mittag–Leffer function and \(AB(\alpha )\) is the normalization. Thus:

$$\begin{aligned} _{0}^{ABR} D^{\alpha }_{a^{+}}(h(t))=\frac{AB(\alpha )}{(1-\alpha )}\sum ^{\infty }_{n=0}(\frac{-\alpha }{1-\alpha })^{n RL}I^{\alpha n}_{a} h(t). \end{aligned}$$
(5)

The fractional appearance with three different operators

Here we outline three unique fractional operators covering the singular of non-singular kernel that drive the fractional configuration that produces ion sound and Langmuir waves.

(1): The fractional appearance with modified Riemann–Liouville operator:

$$\begin{aligned} {\left\{ \begin{array}{ll} i ^{RL}D^{\alpha }_{t}\Xi +\frac{1}{2} ^{RL}D^{2\alpha }_{xx}\Xi -\Delta \Xi =0, & \, \\ ^{RL}D^{2\alpha }_{tt}\Delta - ^{RL}D^{2\alpha }_{xx}\Delta -2 ^{RL}D^{2\alpha }_{xx}(|\Xi |^{2})=0. & \, \end{array}\right. } \end{aligned}$$
(6)

(2): The fractional appearance with \(\beta\)-operator :

$$\begin{aligned} {\left\{ \begin{array}{ll} i _{0}^{B}D^{\alpha }_{t}\Xi +\frac{1}{2} _{0}^{B}D^{2\alpha }_{xx}\Xi -\Delta \Xi =0, & \, \\ _{0}^{B}D^{2\alpha }_{tt}\Delta - _{0}^{B}D^{2\alpha }_{xx}\Delta -2 _{0}^{B}D^{2\alpha }_{xx}(|\Xi |^{2})=0. & \, \end{array}\right. } \end{aligned}$$
(7)

(3): The fractional appearance with Atangana–Baleanu operator:

$$\begin{aligned} {\left\{ \begin{array}{ll} i _{0}^{ABR}D^{\alpha }_{t}\Xi +\frac{1}{2} _{0}^{ABR}D^{2\alpha }_{xx}\Xi -\Xi \Delta =0, & \, \\ _{0}^{ABR}D^{2\alpha }_{tt}\Delta - _{0}^{ABR}D^{2\alpha }_{xx}\Delta -2 _{0}^{ABR}D^{2\alpha }_{xx}(|\Xi |^{2})=0. & \, \end{array}\right. } \end{aligned}$$
(8)

The fractional transformation

Let’s begin by do certain negotiable changes with respect to these fractional operators that are in operation:

$$\begin{aligned} \Xi (x,t)=\mathfrak {V}(\mathfrak {L})e^{i\vartheta (x,t)}, ~~ \Delta (x,t)=\mathfrak {U}(\mathfrak {L}) \end{aligned}$$
(9)

We will pursued \(\mathfrak {L}\) and \(\vartheta\) as per concerning fractional derivative.

(1): We delegate \(\mathfrak {L}\) and \(\vartheta\) as for the Riemann–Liouville fractional differential operator:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathfrak {L}=\frac{1}{\alpha }\left( \varpi x^{\alpha }+\varsigma t^{\alpha }\right) , & \, \\ \vartheta =\frac{1}{\alpha }\left( k x^{\alpha }+\mu t^{\alpha }\right) +\gamma _{0} . & \, \end{array}\right. } \end{aligned}$$
(10)

(2): We induct \(\mathfrak {L}\) and \(\vartheta\) as for the \(\beta\)-operator:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathfrak {L}=\frac{1}{\alpha }\left( \varpi (x+\frac{1}{\Gamma {(\alpha )}})^{\alpha }+\varsigma (t+\frac{1}{\Gamma {(\alpha )}})^{\alpha }\right) , & \, \\ \vartheta =\frac{1}{\alpha }\left( k(x+\frac{1}{\Gamma {(\alpha )}})^{\alpha }+\mu (t+\frac{1}{\Gamma {(\alpha )}})^{\alpha }\right) +\gamma _{0}. & \, \end{array}\right. } \end{aligned}$$
(11)

(3): We ordain \(\mathfrak {L}\) and \(\vartheta\) as for the Atangana–Baleanu in sense of Riemann–Liouville fractional operator:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathfrak {L}=\varpi x+\frac{\varsigma (1-\alpha ) t^{-\alpha n}}{AB(\alpha )\Sigma ^{\infty }_{n=0}(-\frac{\alpha }{1-\alpha })\Gamma (1-\alpha n)} , & \, \\ \vartheta =k x+\frac{\mu (1-\alpha )t^{-\alpha n})+\gamma _{0}}{AB(\alpha )\Sigma ^{\infty }_{n=0}(-\frac{\alpha }{1-\alpha })\Gamma (1-\alpha n)}. & \, \end{array}\right. } \end{aligned}$$
(12)

Construction of soliton solution for ion sound and Langmuir wave equation

Description of proposed technique

We shall adhere to steps57.

Take a look on a general partial differential equation:

$$\begin{aligned} H( \Xi , \Xi _{t}, \Xi _{x}, \Xi _{tt}, \Xi _{xx},\ldots ) = 0. \end{aligned}$$
(13)

A non-linear ordinary differential equation may be created from it:

$$\begin{aligned} R(\mathfrak {V},\mathfrak {V}',\mathfrak {V}'',\ldots ) = 0. \end{aligned}$$
(14)

Through pushing the transition forward:

$$\begin{aligned} \Xi (x,t)=\mathfrak {V}(\mathfrak {L})e^{i\vartheta (x,t)}, \end{aligned}$$
(15)

where, \(\mathfrak {L}=k_{1}x+k_{2}t\). Let us take the solution,

$$\begin{aligned} \mathfrak {V}(\mathfrak {L})=a_{0}+\sum _{i=-j}^{j} \bigg [a_{i}(\mathfrak {F}(\mathfrak {L}))^{i}\bigg ], \end{aligned}$$
(16)

where,

$$\begin{aligned} \mathfrak {F}'(\mathfrak {L})=\ln (\ell )\left( \varrho +\upsilon \mathfrak {F}(\mathfrak {L}) + \sigma \mathfrak {F}^2 (\mathfrak {L})\right) ,~~~ \ell \ne 0,1, \end{aligned}$$
(17)

where, \(\sigma\), \(\varrho\) and \(\upsilon\) real.

(Case 1): Since \(\upsilon ^2 - 4\varrho \sigma < 0\) as well as \(\sigma \ne 0,\)

$$\begin{aligned} \mathfrak {F}_{1}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{-\beth }}{2\sigma }\tan _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) , \end{aligned}$$
(18)
$$\begin{aligned} \mathfrak {F}_{2}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }-\frac{\sqrt{-\beth }}{2\sigma }\cot _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) , \end{aligned}$$
(19)
$$\begin{aligned} \mathfrak {F}_{3}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{-\beth }}{2\sigma }\left( \tan _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) , \end{aligned}$$
(20)
$$\begin{aligned} \mathfrak {F}_{4}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{-\beth }}{2\sigma }\left( \cot _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) , \end{aligned}$$
(21)
$$\begin{aligned} \mathfrak {F}_{5}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{-\beth }}{4\sigma }\left( \tan _{\ell } \left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) - \cot _{\ell }\left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) \right) . \end{aligned}$$
(22)

(Case 2): Since \(\upsilon ^2 - 4\varrho \sigma > 0\) as well as \(\sigma \ne 0,\)

$$\begin{aligned} \mathfrak {F}_{6}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }-\frac{\sqrt{\beth }}{2\sigma }\tanh _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) , \end{aligned}$$
(23)
$$\begin{aligned} \mathfrak {F}_{7}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }-\frac{\sqrt{\beth }}{2\sigma }\coth _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) , \end{aligned}$$
(24)
$$\begin{aligned} \mathfrak {F}_{8}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{\beth }}{2\sigma }\left( -\tanh _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm i\sqrt{mn}\ sech_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) , \end{aligned}$$
(25)
$$\begin{aligned} \mathfrak {F}_{9}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }+\frac{\sqrt{\beth }}{2\sigma }\left( -\coth _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm \sqrt{mn} {{\,\textrm{csch}\,}}_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) , \end{aligned}$$
(26)
$$\begin{aligned} \mathfrak {F}_{10}(\mathfrak {L})= & -\frac{\upsilon }{2\sigma }-\frac{\sqrt{\beth }}{4\sigma }\left( \ tanh_{\ell }\left( \frac{\sqrt{\beth }}{4}\mathfrak {L} \right) +\ coth_{\ell }\left( \frac{\sqrt{\beth }}{4}\mathfrak {L} \right) \right) . \end{aligned}$$
(27)

(Case 3): Since \(\varrho \sigma > 0\) as well as \(\upsilon =0,\)

$$\begin{aligned} \mathfrak {F}_{11}(\mathfrak {L})= & \sqrt{\frac{\varrho }{\sigma }}\ tan_{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) , \end{aligned}$$
(28)
$$\begin{aligned} \mathfrak {F}_{12}(\mathfrak {L})= & -\sqrt{\frac{\varrho }{\sigma }}\ cot_{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) , \end{aligned}$$
(29)
$$\begin{aligned} \mathfrak {F}_{13}(\mathfrak {L})= & \sqrt{\frac{\varrho }{\sigma }}\left( \tan _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\ sec_{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) , \end{aligned}$$
(30)
$$\begin{aligned} \mathfrak {F}_{14}(\mathfrak {L})= & \sqrt{\frac{\varrho }{\sigma }}\left( -\ cot_{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\ csc_{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) , \end{aligned}$$
(31)
$$\begin{aligned} \mathfrak {F}_{15}(\mathfrak {L})= & \frac{1}{2}\sqrt{\frac{\varrho }{\sigma }}\left( \tan _{\ell }\left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) -\cot _{\ell }\left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) \right) . \end{aligned}$$
(32)

(Case 4): Since \(\varrho \sigma < 0\) as well as \(\upsilon =0,\)

$$\begin{aligned} \mathfrak {F}_{16}(\mathfrak {L})= & - \sqrt{-\frac{\varrho }{\sigma }}\tanh _{\ell } \left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) , \end{aligned}$$
(33)
$$\begin{aligned} \mathfrak {F}_{17}(\mathfrak {L})= & - \sqrt{-\frac{\varrho }{\sigma }}\coth _{\ell } \left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) , \end{aligned}$$
(34)
$$\begin{aligned} \mathfrak {F}_{18}(\mathfrak {L})= & \sqrt{-\frac{\varrho }{\sigma }}\left( -\tanh _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm i \sqrt{mn}\ sech_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) , \end{aligned}$$
(35)
$$\begin{aligned} \mathfrak {F}_{19}(\mathfrak {L})= & \sqrt{-\frac{\varrho }{\sigma }}\left( -\coth _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\ csch_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) , \end{aligned}$$
(36)
$$\begin{aligned} \mathfrak {F}_{20}(\mathfrak {L})= & -\frac{1}{2} \sqrt{-\frac{\varrho }{\sigma }} \left( \tanh _{\ell } \left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L} \right) +\ coth_{\ell } \left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L} \right) \right) . \end{aligned}$$
(37)

(Case 5): Since \(\upsilon = 0\) as well as \(\varrho =\sigma ,\)

$$\begin{aligned} \mathfrak {F}_{21}(\mathfrak {L})= & \tan _{\ell }\left( \varrho \mathfrak {L}\right) , \end{aligned}$$
(38)
$$\begin{aligned} \mathfrak {F}_{22}(\mathfrak {L})= & -\cot _{\ell }\left( \varrho \mathfrak {L}\right) , \end{aligned}$$
(39)
$$\begin{aligned} \mathfrak {F}_{23}(\mathfrak {L})= & \tan _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( 2\varrho \mathfrak {L}\right) , \end{aligned}$$
(40)
$$\begin{aligned} \mathfrak {F}_{24}(\mathfrak {L})= & -\cot _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( 2\varrho \mathfrak {L}\right) , \end{aligned}$$
(41)
$$\begin{aligned} \mathfrak {F}_{25}(\mathfrak {L})= & \frac{1}{2}\left( \tan _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) -\cot _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) \right) . \end{aligned}$$
(42)

(Case 6): Since \(\upsilon = 0\) as well as \(\sigma =-\varrho ,\)

$$\begin{aligned} \mathfrak {F}_{26}(\mathfrak {L})= & -\tanh _{\ell }\left( \varrho \mathfrak {L}\right) , \end{aligned}$$
(43)
$$\begin{aligned} \mathfrak {F}_{27}(\mathfrak {L})= & -\coth _{\ell }\left( \varrho \mathfrak {L}\right) , \end{aligned}$$
(44)
$$\begin{aligned} \mathfrak {F}_{28}(\mathfrak {L})= & -\tanh _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm i \sqrt{mn}\ sech_{\ell }\left( 2\varrho \mathfrak {L}\right) , \end{aligned}$$
(45)
$$\begin{aligned} \mathfrak {F}_{29}(\mathfrak {L})= & -\coth _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\ csch_{\ell }\left( 2\varrho \mathfrak {L}\right) , \end{aligned}$$
(46)
$$\begin{aligned} \mathfrak {F}_{30}(\mathfrak {L})= & -\frac{1}{2}\bigg (\tanh _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) +\coth _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) \bigg ). \end{aligned}$$
(47)

(Case 7): Since \(\upsilon ^2 = 4\varrho \sigma\),

$$\begin{aligned} \mathfrak {F}_{31}(\mathfrak {L})= \frac{-2\varrho (\upsilon \mathfrak {L} \ln \ell +2) }{\upsilon ^2 \mathfrak {L} \ln \ell }. \end{aligned}$$
(48)

(Case 8): Since \(\upsilon = p,\varrho = pq, (q\ne 0)\) as well as \(\sigma =0\),

$$\begin{aligned} \mathfrak {F}_{32}(\mathfrak {L})=\ell ^{p\mathfrak {L}} -q. \end{aligned}$$
(49)

(Case 9): Since \(\upsilon = \sigma = 0\),

$$\begin{aligned} \mathfrak {F}_{33}(\mathfrak {L})=\varrho \mathfrak {L}\ln \ell . \end{aligned}$$
(50)

(Case 10): Since \(\upsilon = \varrho = 0\),

$$\begin{aligned} \mathfrak {F}_{34}(\mathfrak {L})=\frac{-1}{\sigma \mathfrak {L} \ln \ell }. \end{aligned}$$
(51)

(Case 11): Since \(\varrho = 0\) as well as \(\upsilon \ne 0\),

$$\begin{aligned} \mathfrak {F}_{35}(\mathfrak {L})= & -\frac{m\upsilon }{\sigma \left( \cosh _{\ell }\left( \upsilon \mathfrak {L}\right) -\sinh _{\ell }\left( \upsilon \mathfrak {L}\right) + m \right) }, \end{aligned}$$
(52)
$$\begin{aligned} \mathfrak {F}_{36}(\mathfrak {L})= & -\frac{\upsilon \left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) \right) }{\sigma \left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) + n \right) }. \end{aligned}$$
(53)

(Case 12): Since \(\upsilon = p, \sigma =pq,~(q\ne 0\) as well as \(\varrho =0)\),

$$\begin{aligned} \mathfrak {F}_{37}(\mathfrak {L}) =-\frac{m\ell ^{p\mathfrak {L}}}{m-qn\ell ^{p\mathfrak {L}}}. \end{aligned}$$
(54)
$$\begin{aligned} \sinh _{\ell }(\mathfrak {L})=\frac{m\ell ^\mathfrak {L} - n\ell ^{-\mathfrak {L}}}{2},~ \cosh _{\ell }(\mathfrak {L})=\frac{m\ell ^\mathfrak {L} + n\ell ^{-\mathfrak {L}}}{2}, \\ \tanh _{\ell }(\mathfrak {L})=\frac{m\ell ^\mathfrak {L} - n\ell ^{-\mathfrak {L}}}{m\ell ^\mathfrak {L} + n\ell ^{-\mathfrak {L}}}, ~ \coth _{\ell }(\mathfrak {L})=\frac{m\ell ^\mathfrak {L} + n\ell ^{-\mathfrak {L}}}{m\ell ^\mathfrak {L} - n\ell ^{-\mathfrak {L}}}, \\ \ sech_{\ell }(\mathfrak {L})=\frac{2}{m\ell ^\mathfrak {L} + n\ell ^{-\mathfrak {L}}},~\ csch_{\ell }(\mathfrak {L})=\frac{2}{m\ell ^\mathfrak {L} - n\ell ^{-\mathfrak {L}}}, \\ \ sin_{\ell }(\mathfrak {L})=\frac{m\ell ^{i\mathfrak {L}} - n\ell ^{-i\mathfrak {L}}}{2i},~ \ cos_{\ell }(\mathfrak {L})=\frac{m\ell ^{i\mathfrak {L}} + n\ell ^{-i\mathfrak {L}}}{2}, \\ \tan _{\ell }(\mathfrak {L})=-i\frac{m\ell ^{i\mathfrak {L}} - n\ell ^{-i\mathfrak {L}}}{m\ell ^{i\mathfrak {L}} + n\ell ^{-i\mathfrak {L}}}, ~~ \cot _{\ell }(\mathfrak {L})=i\frac{m\ell ^{i\mathfrak {L}} + n\ell ^{-i\mathfrak {L}}}{m\ell ^{i\mathfrak {L}} - n\ell ^{-i\mathfrak {L}}}, \\ \sec _{\ell }(\mathfrak {L})=\frac{2}{m\ell ^\mathfrak {L} + n\ell ^{-\mathfrak {L}}},~~ \csc _{\ell }(\mathfrak {L})=\frac{2i}{m\ell ^\mathfrak {L} - n\ell ^{-\mathfrak {L}}}, \end{aligned}$$

The random variables m and n that determine the deformation’s parameters are larger then zero.

The implementation of new extended direct algebraic method

The solution to Eq. (1) will be obtained by applying a travelling wave transformation on the Eq. (1) using Eq. (9):

$$\begin{aligned} & i(\varsigma +\varpi t)\mathfrak {V}'=0. \end{aligned}$$
(55)
$$\begin{aligned} & k \mathfrak {V}''-(2\mu +k^{2})\mathfrak {V}-2\mathfrak {V}\mathfrak {U}=0. \end{aligned}$$
(56)
$$\begin{aligned} & (\varsigma ^{2}-\varpi ^{2})\mathfrak {U}''-2\varpi ^{2}(\mathfrak {V}^{2})''=0. \end{aligned}$$
(57)

Integrating twice the Eq. (57) with zero constant of integration:

$$\begin{aligned} \mathfrak {V}(\mathfrak {L})=\frac{2}{k^{2}-1}\mathfrak {V}^{2}(\mathfrak {L}),~~~~\varsigma =-\varpi k. \end{aligned}$$
(58)

Plugging Eq. (58) into Eq. (56), we will get:

$$\begin{aligned} \varpi ^{2}(k^{2}-1)\mathfrak {V}''-(2\mu ^{2}+k^{2})(k^{2}-1)\mathfrak {V}-4\mathfrak {V}^{3}=0. \end{aligned}$$
(59)

The homogeneous balancing constant N=1 of Eq. (59), therefore the answer is thought of to,

$$\begin{aligned} \mathfrak {V}(\mathfrak {L})=a_{0}+ a_{1}(\mathfrak {F}(\mathfrak {L})), \end{aligned}$$
(60)

where,

$$\begin{aligned} \mathfrak {F}'(\mathfrak {L})=\ln (\ell )\left( \varrho +\upsilon \mathfrak {F}(\mathfrak {L}) + \sigma \mathfrak {F}^2 (\mathfrak {L})\right) ,~~~ \ell \ne 0,1. \end{aligned}$$
(61)

After plugging Eq. (60) into Eq. (59) and gathering quantities for \(Q(\mathfrak {L})\) with varying powers, an algebraic set of equations is produced. Mathematica is then used to solve this framework, and the result is:

$$\begin{aligned} \bigg [a_{0}=\pm \frac{\upsilon \sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}},~~a_{1}=\pm \frac{2\sigma \sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}},~~ \mu =\pm \frac{\sqrt{-2k^{2}-\beth \varpi ^{2}\log [\ell ]^{2}}}{2}. \bigg ] \end{aligned}$$
(62)

By replacing, the whole answer is obtained Eq. (62) into Eq. (60):

$$\begin{aligned} {\left\{ \begin{array}{ll} \Xi (x,t)=\bigg (\pm \upsilon \varsigma \pm 2 \sigma \varsigma (\mathfrak {F}_{i}(\mathfrak {L}))\bigg )\times e^{i\vartheta (x,t)}, & \,\\ \Delta (x,t)=\frac{2}{k^{2}-1}\bigg (\pm \upsilon \varsigma \pm 2 \sigma \varsigma (\mathfrak {F}_{i}(\mathfrak {L}))\bigg ). & \, \end{array}\right. } \end{aligned}$$
(63)

Here \(\varsigma =\pm \frac{\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\) and \(\beth =\upsilon ^{2}-4\varrho \sigma\). It should be noted that we will obtain multiple different answers from (18)-(54) correspondingly when we use \(\mathfrak {F}_{i}\).

(Family 1): Since \(\upsilon ^2 - 4\varrho \sigma < 0\) as well as \(\sigma \ne 0,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{1}(x,t)=\pm \frac{\sqrt{-\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\tan _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{1}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \tan _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(64)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{2}(x,t)=\pm \frac{\sqrt{-\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\cot _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{2}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \cot _{\ell }\left( \frac{\sqrt{-\beth }}{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(65)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{3}(x,t)=\pm \frac{\sqrt{-\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\left( \tan _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{3}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \tan _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(66)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{4}(x,t)=\pm \frac{\sqrt{-\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\left( \cot _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{4}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \cot _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( \sqrt{-\beth }\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(67)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{5}(x,t)=\pm \frac{\sqrt{-\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{4\sqrt{2}}\left( \tan _{\ell } \left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) - \cot _{\ell }\left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{5}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{16}\left( \tan _{\ell } \left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) - \cot _{\ell }\left( \frac{\sqrt{-\beth }}{4}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(68)

(Family 2): Since \(\upsilon ^2 - 4\varrho \sigma > 0\) as well as \(\sigma \ne 0,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{6}(x,t)=\mp \frac{\sqrt{\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\tanh _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) e^{i\vartheta (x,t)}, \,\\ \Delta _{6}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \tanh _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(69)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{7}(x,t)=\mp \frac{\sqrt{\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\coth _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{7}(x,t)=\mp \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( \coth _{\ell }\left( \frac{\sqrt{\beth }}{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(70)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{8}(x,t)=\pm \frac{\sqrt{\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\left( -\tanh _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm i\sqrt{mn}\ sech_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{8}(x,t)=\pm \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( -\tanh _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm i\sqrt{mn}\ sech_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(71)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{9}(x,t)=\pm \frac{\sqrt{\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{2\sqrt{2}}\left( -\coth _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm \sqrt{mn} {{\,\textrm{csch}\,}}_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{9}(x,t)=\pm \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{4}\left( -\coth _{\ell }\left( \sqrt{\beth }\mathfrak {L} \right) \pm \sqrt{mn} {{\,\textrm{csch}\,}}_{\ell }\left( \sqrt{\beth }\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(72)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{10}(x,t)=\pm \frac{\sqrt{\beth }\sqrt{k^{2}-1}\varpi \log [\ell ]}{4\sqrt{2}}\left( \tanh _{\ell }\left( \frac{\sqrt{\beth }}{4}\mathfrak {L} \right) +\ coth_{\ell }\left( \frac{\sqrt{\beth }}{4}\mathfrak {L} \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{10}(x,t)=\pm \frac{{\beth }\varpi ^{2}\log [\ell ]^{2}}{16}\left( \tan _{\ell } \left( \frac{\sqrt{\beth }}{4}\mathfrak {L}\right) + \cot _{\ell }\left( \frac{\sqrt{\beth }}{4}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(73)

(Family 3): Since \(\varrho \sigma > 0\) as well as \(\upsilon =0,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{11}(x,t)=\varsigma \left( \pm \upsilon \pm 2 \sqrt{\varrho \sigma }\left( \tan _{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{11}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm 2 \sqrt{\varrho \sigma }\left( \tan _{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(74)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{12}(x,t)=\varsigma \left( \pm \upsilon \mp 2 \sqrt{\varrho \sigma }\left( \cot _{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{12}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2 \sqrt{\varrho \sigma }\left( \cot _{\ell }\left( \sqrt{\varrho \sigma }\mathfrak {L} \right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(75)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{13}(x,t)=\varsigma \left( \pm \upsilon \pm 2\sqrt{\varrho \sigma }\left( \tan _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\ sec_{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{13}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm 2\sqrt{\varrho \sigma }\left( \tan _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\ sec_{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(76)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{14}(x,t)=\varsigma \left( \pm \upsilon \pm 2\sqrt{\varrho \sigma }\left( -\cot _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\csc _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{14}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm 2\sqrt{\varrho \sigma }\left( -\cot _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}\csc _{\ell }\left( 2\sqrt{\varrho \sigma }\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(77)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{15}(x,t)=\varsigma \left( \pm \upsilon \pm \sqrt{\varrho \sigma }\left( \tan _{\ell }\left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) -\cot _{\ell } \left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{15}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm \sqrt{\varrho \sigma }\left( \tan _{\ell }\left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) -\cot _{\ell } \left( \frac{\sqrt{\varrho \sigma }}{2}\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(78)

(Family 4): Since \(\varrho \sigma < 0\) as well as \(\upsilon =0,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{16}(x,t)=\varsigma \left( \pm \upsilon \mp 2 \sqrt{-\varrho \sigma }\left( \tanh _{\ell }\left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{16}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2 \sqrt{-\varrho \sigma }\left( \tanh _{\ell }\left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(79)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{17}(x,t)=\varsigma \left( \pm \upsilon \mp 2 \sqrt{-\varrho \sigma }\left( \coth _{\ell }\left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{17}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2 \sqrt{-\varrho \sigma }\left( \coth _{\ell }\left( \sqrt{-\varrho \sigma }\mathfrak {L} \right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(80)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{18}(x,t)=\varsigma \left( \pm \upsilon \pm 2\sqrt{-\varrho \sigma }\left( -\tanh _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm i\sqrt{mn}{{\,\textrm{sech}\,}}_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{18}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm 2\sqrt{-\varrho \sigma }\left( -\tanh _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm i\sqrt{mn}{{\,\textrm{sech}\,}}_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(81)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{19}(x,t)=\varsigma \left( \pm \upsilon \pm 2\sqrt{-\varrho \sigma }\left( -\coth _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}{{\,\textrm{csch}\,}}_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{19}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm 2\sqrt{-\varrho \sigma }\left( -\coth _{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L} \right) \pm \sqrt{mn}{{\,\textrm{csch}\,}}_{\ell }\left( 2\sqrt{-\varrho \sigma }\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(82)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{20}(x,t)=\varsigma \left( \pm \upsilon \mp \sqrt{-\varrho \sigma }\left( \tanh _{\ell }\left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L}\right) +\coth _{\ell } \left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L}\right) \right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{20}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \pm \sqrt{-\varrho \sigma }\left( \tanh _{\ell }\left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L}\right) +\coth _{\ell } \left( \frac{\sqrt{-\varrho \sigma }}{2}\mathfrak {L}\right) \right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(83)

(Family 5): Since \(\upsilon = 0\) as well as \(\varrho =\sigma ,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{21}(x,t)=\pm 2 \sigma \varsigma \left( \tan _{\ell }\left( \varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{21}(x,t)=\pm {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( \tan _{\ell }\left( \varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(84)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{22}(x,t)=\mp 2 \sigma \varsigma \left( \cot _{\ell }\left( \varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{22}(x,t)=\mp {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( \cot _{\ell }\left( \varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(85)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{23}(x,t)=\pm 2 \sigma \varsigma \left( \tan _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( 2\varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{23}(x,t)=\pm {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( \tan _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\sec _{\ell }\left( 2\varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(86)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{24}(x,t)=\pm 2 \sigma \varsigma \left( -\cot _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( 2\varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{24}(x,t)=\pm {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( -\cot _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\csc _{\ell }\left( 2\varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(87)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{25}(x,t)=\pm \sigma \varsigma \left( \tan _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) -\cot _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{25}(x,t)=\pm \frac{\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}{4} \left( \tan _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) -\cot _{\ell }\left( \frac{\varrho }{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(88)

(Family 6): Since \(\upsilon = 0\) as well as \(\sigma =-\varrho ,\)

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{26}(x,t)=\mp 2 \sigma \varsigma \left( \tanh _{\ell }\left( \varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{26}(x,t)=\mp {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( \tanh _{\ell }\left( \varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(89)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{27}(x,t)=\mp 2 \sigma \varsigma \left( \coth _{\ell }\left( \varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{27}(x,t)=\mp {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( \coth _{\ell }\left( \varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(90)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{28}(x,t)=\pm 2 \sigma \varsigma \left( -\tanh _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm i \sqrt{mn}\ sech_{\ell }\left( 2\varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{28}(x,t)=\pm {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( -\tanh _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm i \sqrt{mn}\ sech_{\ell }\left( 2\varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(91)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{29}(x,t)=\pm 2 \sigma \varsigma \left( -\coth _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\ csch_{\ell }\left( 2\varrho \mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, & \,\\ \Delta _{29}(x,t)=\pm {\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}\left( -\coth _{\ell }\left( 2\varrho \mathfrak {L}\right) \pm \sqrt{mn}\ csch_{\ell }\left( 2\varrho \mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(92)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{30}(x,t)=\mp \sigma \varsigma \left( \tanh _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) +\coth _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) \right) e^{i\vartheta (x,t)}, \,\\ \Delta _{30}(x,t)=\mp \frac{\varpi ^{2}\sigma ^{2}\log [\ell ]^{2}}{4} \left( \tanh _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) +\coth _{\ell }\left( \frac{ \varrho }{2}\mathfrak {L}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(93)

(Family 7): Since \(\upsilon ^2 = 4\varrho \sigma\),

$$\begin{aligned} {\left\{ \begin{array}{ll} \Xi _{31}(x,t)=\varsigma \left( \pm \upsilon \mp 4 \sigma \left( \frac{\varrho (\upsilon \mathfrak {L} \ln \ell +2) }{\upsilon ^2 \mathfrak {L} \ln \ell }\right) \right) e^{i\vartheta (x,t)}, \,\\ \Delta _{31}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4} \left( \pm \upsilon \mp 4 \sigma \left( \frac{\varrho (\upsilon \mathfrak {L} \ln \ell +2) }{\upsilon ^2 \mathfrak {L} \ln \ell }\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(94)

(Family 8): Since \(\upsilon = p,\varrho = pq, (q\ne 0)\) as well as \(\sigma =0\),

$$\begin{aligned} \Xi _{32}(x,t)=Constant~ Solution. \end{aligned}$$
(95)

(Family 9): Since \(\upsilon = \sigma = 0\),

$$\begin{aligned} \Xi _{33}(x,t)=0. \end{aligned}$$
(96)

(Family 10): Since \(\upsilon = \varrho = 0\),

$$\begin{aligned} {\left\{ \begin{array}{ll} \Xi _{34}(x,t)=\mp \frac{2\varsigma }{ \mathfrak {L} \ln \ell }\times e^{i\vartheta (x,t)}, \,\\ \Delta _{34}(x,t)=\frac{\varpi ^{2}}{\mathfrak {L}^{2}}. & \, \end{array}\right. } \end{aligned}$$
(97)

(Family 11): Since \(\varrho = 0\) as well as \(\upsilon \ne 0\),

$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{35}(x,t)=\varsigma \left( \pm \upsilon \mp 2\left( \frac{m\upsilon }{\left( \cosh _{\ell }\left( \upsilon \mathfrak {L}\right) -\sinh _{\ell }\left( \upsilon \mathfrak {L}\right) + m \right) }\right) \right) e^{i\vartheta (x,t)}, \,\\ \Delta _{35}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2 \left( \frac{m\upsilon }{\left( \cosh _{\ell }\left( \upsilon \mathfrak {L}\right) -\sinh _{\ell }\left( \upsilon \mathfrak {L}\right) + m \right) }\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(98)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \Xi _{36}(x,t) =\varsigma \left( \pm \upsilon \mp 2 \left( \frac{\upsilon \left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) \right) }{\left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) + n \right) }\right) \right) e^{i\vartheta (x,t)}, \,\\ \Delta _{36}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2 \left( \frac{\upsilon \left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) \right) }{\left( \sinh _{\ell }\left( \upsilon \mathfrak {L}\right) +\cosh _{\ell }\left( \upsilon \mathfrak {L}\right) + n \right) }\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(99)

(Family 12): Since \(\upsilon = p, \sigma =pq,~(q\ne 0\) as well as \(\varrho =0)\),

$$\begin{aligned} {\left\{ \begin{array}{ll} \Xi _{37}(x,t) =\varsigma \left( \pm \upsilon \mp 2\left( \frac{m\ell ^{p\mathfrak {L}}}{m-qn\ell ^{p\mathfrak {L}}}\right) \right) e^{i\vartheta (x,t)}, \,\\ \Delta _{37}(x,t)=\pm \frac{\varpi ^{2}\log [\ell ]^{2}}{4}\left( \pm \upsilon \mp 2\left( \frac{m\ell ^{p\mathfrak {L}}}{m-qn\ell ^{p\mathfrak {L}}}\right) \right) ^{2}. & \, \end{array}\right. } \end{aligned}$$
(100)

In reference to the fractional model, we will use \(\mathfrak {L}\), as stated in Eqs. (10), (11), and (12), which correspond to the Riemann–Liouville fractional derivative, \(\beta\)-fractional differential operator, and the Atangana–Baleanue operator within the Riemann–Liouville.

Fig. 1
figure 1

3D pictorial anatomization of \(\Xi _{1}(x,t)\) and \(\Delta _{1}(x,t)\) at at \(\alpha =0.1\). (a) 3-D characterization of NEF along-with RL. (b) 3-D characterization of NDP anlog-with RL. (c) 3-D characterization of NEF along-with β (d) 3D characterization of NDP along-with β. (e) 3D characterization of NEF along-with AB (f) 3D characterization of NDP along-withAB.

Full size image
Fig. 2
figure 2

3D pictorial anatomization of \(\Xi _{1}(x,t)\) and \(\Delta _{1}(x,t)\) at \(\alpha =0.5\). (a) 3-D characterization of NEF along-with RL. (b) 3-D characterization of NDP along-with RL. (c) 3-D characterization of NEF along-with β (d) 3-D characterization of NDP along-with β. (e) 3-D characterization of NEF along-with AB. (f) 3-D characterization of NDP along-with AB.

Full size image
Fig. 3
figure 3

3-D pictorial anatomization for \(\Xi _{1}(x,t)\) and \(\Delta _{1}(x,t)\) at \(\alpha =0.7\). (a) 3-D characterization of NEF along-with RL. (b) 3-D characterization of NDP along-with RL. (c) 3-D characterization of NEF along-with β. (d) 3-D characterization of NDP along-with β. (e) 3-D characterization of NEF along-with AB. (f) 3-D characterization of NDP along-with AB.

Full size image
Fig. 4
figure 4

2-D pictorial comparison for RL, \(\beta\) as well as AB operator of \(\Xi _{1}(x,t)\) as along \(\Delta _{1}(x,t)\). (a) 2-D comparision of NEF upon α = 0.1. (b) 2-D comparision of NDP upon α = 0.1. (c) 2-D comparision of NEF upon α = 0.5. (d) 2-D comparision of NDP upon α = 0.5. (e) 2-D comparision of NEF upon α = 0.7. (f) 2-D comparision of NDP upon α = 0.7. (g) 2-D comparision of NEF upon α = 1. (h) 2-D comparision of NDP upon α = 1.

Full size image
Fig. 5
figure 5

2-D pictorial comparision of operators as well as influence of fractional order on derivative also compared with classic order for \(\Xi _{1}(x,t)\) and \(\Delta _{1}(x,t)\). (a) 2D comparision for NEF with RL. (b) 2D comparision for NDP with RL. (c) 2D comparision for NEF with β. (d) 2D comparision for NDP with β. (e) 2D comparision for NEF with AB. (f) 2D comparision for NDP with AB.

Full size image
Fig. 6
figure 6

3-D pictorial anatomization of \(\Xi _{35}(x,t)\) as well as \(\Delta _{35}(x,t)\) at at \(\alpha =0.1\). (a) 3-D of NEF with RL. (b) 3-D overview for NDP along-with RL. (c) 3-D overview for NEF along-with β. (d) 3-D overview for NDP along-with β. (e) 3-D overview for NEF along-with AB. (f) 3-D overview for NDP along-with AB.

Full size image
Fig. 7
figure 7

3-D pictorial anatomization for \(\Xi _{35}(x,t)\) and \(\Delta _{35}(x,t)\) at \(\alpha =0.5\). (a) 3-D overview for NEF along-with RL. (b) 3-D overview for NDP along-with RL. (c) 3-D overview for NEF along-with β. (d) 3-D overview for NDP along-with β. (e) 3-D overview for NEF along-with AB. (f) 3-D overview for NDP along-with AB.

Full size image
Fig. 8
figure 8

3D pictorial anatomization of \(\Xi _{35}(x,t)\) and \(\Delta _{35}(x,t)\) at \(\alpha =0.7\). (a) 3-D characterization for NEF along-with RL. (b) 3-D characterization for NDP along-with RL. (c) 3-D characterization for NEF along-with β. (d) 3-D characterization for NDP along-with β. (e) 3-D characterization for NEF along-with AB. (f) 3-D characterization for NEF along-with AB.

Full size image
Fig. 9
figure 9

2-D pictorial comparision for RL, \(\beta\) as well as AB operator for \(\Xi _{35}(x,t)\) along with \(\Delta _{35}(x,t)\). (a) 2-D comparision of NEF on α = 0.1.(b) 2-D comparision of NDP on α = 0.1. (c) 2-D comparision of NEF on α = 0.5. (d) 2-D comparision of NDP on α = 0.5. (e) 2-D comparision of NEF on α = 0.7. (f) 2-D comparision of NDP on α = 0.7. (g) 2-D comparision of NEF on α = 1. (h) 2-D comparision for NDP on α = 1.

Full size image
Fig. 10
figure 10

2D pictorial comparision of operators, as well as the impact from fractional-order on derivative also compared with classic order for \(\Xi _{35}(x,t)\) and \(\Delta _{35}(x,t)\). (a) 2D comparision for NEF with RL. (b) 2D comparision for NDP with RL. (c) 2D comparision for NEF with β. (d) 2D comparision for NDP with β. (e) 2D comparision for NEF with AB. (f) 2D comparision for NDP with AB.

Full size image

Graphical analysis

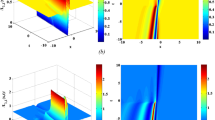
Figure 1 is illustrating the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,~\upsilon =1,~\varrho =1,~\sigma =1\) and \(\gamma _{0}=1\) at \(\alpha =0.1\) for the normalized electric field \(\Xi _{1}(x,t)\) and normalized density perturbation \(\Delta _{1}(x,t)\).

Figure 1a,c, as well as Fig. 1e have been 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 1b,d, as well as Fig. 1f have been 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative respectively.

Remark

The Atangana–Baleanu operator is describing the different pattern from the Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of the Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 2 is depicting 3D graphical compare and contrast three different fractional operators considering parametric values, \(\ell =0.5,~k=0.2,~\varpi =0.6,~\upsilon =1,~\varrho =1,~\sigma =1\) and \(\gamma _{0}=1\) at \(\alpha =0.5\) for the normalized electric field \(\Xi _{1}(x,t)\) and normalized density perturbation \(\Delta _{1}(x,t)\).

Figure 2a,c, as well as Fig. 2e have been 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 2b,d,f are 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Remark

The Atangana–Baleanu operator is describing the different pattern from the Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of the Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 3 is depicting the 3D graphical comparision between three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,~\upsilon =1,~\varrho =1,~\sigma =1\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{1}(x,t)\) and normalized density perturbation \(\Delta _{1}(x,t)\).

Figure 3a,c, as well as Fig. 3e are 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 3b,d, as well as Fig. 3f are 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative respectively.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 4 is depicting the 3D graphical comparision between three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,~\upsilon =1,~\varrho =1,~\sigma =1\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{1}(x,t)\) and normalized density perturbation \(\Delta _{1}(x,t)\).

Figure 4a,c, as well as Fig. 4e are 2D comparision of normalized electric field of three different used derivatives at \(\alpha =0.1,~\alpha =0,3\) and \(\alpha =0.7\) accordingly.

Figure 4b,d, as wll as Fig. 4f are 2D comparision of normalized electric field of three different used derivatives at \(\alpha =0.1,~\alpha =0,3\) and \(\alpha =0.7\) accordingly.

Figure 4g,h is presenting the 2D graphical comparision of operators at classic order for NEF and NDP.

Remark

The Atangana–Baleanu operator is describing the different pattern from the Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of the Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 5 is depicting the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,~\upsilon =1,~\varrho =1,~\sigma =1\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{1}(x,t)\) and normalized density perturbation \(\Delta _{1}(x,t)\).

Figure 5a,c, as well as Fig. 5e are 2D compare and contrast of normalized electric field and influences of fractional order on Riemann–Liouville operator \(\beta\)-derivative and Atangan–Baleanu derivative accordingly.

Figure 5b,d, as well as Fig. 5f are 2D compare and contrast of normalized density perturbation and influences of fractional order on Riemann–Liouville operator \(\beta\)-derivative and Atangan–Baleanu derivative accordingly.

Figure 4g,h is presenting the 2D graphical compare and contrast of operators at classic order for NEF and NDP.

Remark

The Atangana–Baleanu operator is describing the different pattern from the Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of the Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 6 is depicting the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,\) and \(\gamma _{0}=1\) at \(\alpha =0.1\) for the normalized electric field \(\Xi _{35}(x,t)\) and normalized density perturbation \(\Delta _{35}(x,t)\).

Figure 6a,c, as well as Fig. 6e are 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 6b,d, as well as Fig. 6f are 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 7 is depicting the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,\) and \(\gamma _{0}=1\) at \(\alpha =0.5\) for the normalized electric field \(\Xi _{35}(x,t)\) and normalized density perturbation \(\Delta _{35}(x,t)\).

Figure 7a,c, as well as Fig. 7e are 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 7b,d, as well as Fig. 7f are 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP. Figure 8 is depicting the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{35}(x,t)\) and normalized density perturbation \(\Delta _{35}(x,t)\).

Figure 8a,c, as well as Fig. 8e are 3D anatomization of normalized electric field with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Figure 8b,d, as well as Fig. 8f are 3D anatomization of normalized density perturbation with Riemann–Liouville operator, \(\beta\)-derivative, and Atangana–Baleanu derivative accordingly.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 9 is depicting the 3D graphical compare and contrast three different fractional operators using the parametric numbers, \(\ell =0.5,~k=0.2,~\varpi =0.6,\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{35}(x,t)\) and normalized density perturbation \(\Delta _{35}(x,t)\).

Figure 9a,c, as well as Fig. 9e are 2D comparision of normalized electric field of three different used derivatives at \(\alpha =0.1,~\alpha =0,3\) and \(\alpha =0.7\) accordingly.

Figure 9b,d, as well as Fig. 9f are 2D comparision of normalized electric field of three different used derivatives at \(\alpha =0.1,~\alpha =0,3\) and \(\alpha =0.7\) accordingly.

Figure 9g,h is presenting the 2D graphical comparision of operators at classic order for NEF and NDP.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Figure 10 is depicting the 3D graphical compare and contrast three different fractional operators considering parameters and their values, \(\ell =0.5,~k=0.2,~\varpi =0.6,\) and \(\gamma _{0}=1\) at \(\alpha =0.7\) for the normalized electric field \(\Xi _{35}(x,t)\) and normalized density perturbation \(\Delta _{35}(x,t)\).

Figure 10a,c,e are 2D compare and contrast of normalized electric field and influences of fractional order on Riemann–Liouville operator \(\beta\)-derivative and Atangan–Baleanu derivative accordingly.

Figure 10b,d,f are 2D compare and contrast of normalized density perturbation and influences of fractional order on Riemann–Liouville operator \(\beta\)-derivative and Atangan–Baleanu derivative accordingly.

Figure 9g,h is presenting the 2D graphical comparision of operators at classic order for NEF and NDP.

Remark

The Atangana–Baleanu operator is describing the different pattern from Riemann–Liouville operator and \(\beta\)-derivative for NEF. The behavior of Atangana–Baleanu derivative is on both positive as well as negative axis and not similar to Riemann–Liouville operator and \(\beta\)-derivative for NDP.

Conclusion

The ponderomotive force model-influenced dynamical system of ion sound, which arises from the non-linear force experienced by charged particles in the inhomogenous electromagnetic oscillating region owing to the high-frequency effect, has been the subject of this study. The dynamical system is analyzed using the fractional operators \(\beta\), Atangana–Baleanu, and Riemann–Liouville. To obtain the fractional analytical exact soliton solutions, a novel extended direct algebraic method was utilized. The obtained solitonic structures contain various classes of solutions: dark, bright, dark-singular, bright-singular, and periodic solitons. The effects of the fractional-order and fractional operators on the physics of the system are shown graphically.

Future direction

The researchers can explore and use this study further to visualize other dynamical aspects of the physical phenomena. The power spectrum and return map tools can be utilized for further analysis of the model in future studies. The breathers, rogue waves, multiple solitons and their interaction can be discussed by using the different mechanism like Hirota bilinear approach etc.