Introduction

HSI captures hundreds of continuous and segmented spectral signals simultaneously imaging the target area through a spectrometer1. The surface information is obtained at the same time as its spectral information, which is a true spectral–spatial combination. It can accurately characterize the physical properties of an object. HSI classification is the task of classifying image pixel labels. As a core technology for Earth observation missions2,3, it has been applied in various fields, including food industry4, ship detection5, precision agriculture6, and other diverse fields7. Early phase, HSI classification primarily used machine learning methods, such as Principal Component Analysis (PCA)8 and Support Vector Machines (SVM)9. PCA can reduce the data dimensions of HSI and retain the main feature information to avoid redundant information affecting the classification performance. SVM can effectively deal with the nonlinear problem in the high-dimensional space of HSI, and determine the decision boundary through the support vectors to identify the key samples in the feature information. Fu et al.10 proposed a novel principal component analysis (PCA) and segmented-PCA (SPCA)-based multi-scale 2-D-singular spectrum analysis (2-D-SSA) fusion method, which uses the PCA and SPCA to reduce spectral dimension. Shao et al.11 proposed a hierarchical semisupervised support vector machine (SVM), which learns a suitable framework for classifying cluster features by a semisupervised SVM and thus makes use of the advantages of classification. Chen et al.8 proposed a new multi-scale filter-based PCA and SVM algorithm, which uses PCA to reduce the dimension and SVM to classify every pixel. To better exploit the inherent nonlinear features of HSI12, Fauvel et al.13 proposed a nonlinear parsimonious feature selection algorithm, which used Gaussian mixture model (GMM) to selects iteratively nonlinear features of spectrum. Zhang et al.14 proposed a spatial–spectral graph-based non-linear embedding (SSGNE) method, which extends the general graph embedding framework to nonlinear space by constraining the sparsity and low rank of the graph training data set. However, the feature extraction capability of machine learning limits the scenario applicability of different HSI.

Over the past few decades, deep learning technology has been widely used in different HSI scenes15,16,17. Compared to traditional classification methods, the deep learning model can better capture the nonlinear relationships between bands through the nonlinear mapping of multilevel neural networks. It also learns high-level features of the data and automatically discovers patterns and regularities in the data. Its end-to-end approach reduces the complexity of manual intervention and trimming. The features of the deep model better match the requirements of the hyperspectral image classification task, which leads to better realization of the classification task. Chen et al.18 proposed a spatially dominant information-based classification method, which designs 2D CNN stacked self-encoders to obtain deepth features by compressing the latent space. Li et al.19 proposed a central vector oriented self-similarity network (CVSSN), which designs an adaptive weight addition and a Euclidean distance self-similarity module to explore the feature correlation between the center vector and the neighborhood vectors. Since 2D convolution networks ignore spectral features, 3D convolution operations were introduced to the HSI classification task. To further obtain discriminant information from more scales20, Yin et al.21 proposed a multi-branch 3D-densely connected network by using the 3D convolutional kernels of different sizes to extract multi-scale spatial–spectral features. Roy et al.22 extracted more robust spatial–spectral features by using a hybrid network of 3D convolution and 2D convolution networks.

Recently, many studies have begun to introduce attention mechanism (AM) into HSI classification tasks and have achieved remarkable results. The attention mechanism can help the model effectively capture key information and integrate spatial information of the image to better understand the correlation and continuity between bands. Zhu et al.23 proposed a residual spectral–spatial attention network (RSSAN) for fine-grained spectral–spatial feature learning by introducing spectral attention and spatial attention modules in spectral–spatial residual network (SSRN). Hang et al.24 proposed a dual-branching attention-assist CNN model, which consists of a spectral attention module and a spatial attention module to fully explore information on different spectral bands and spatial locations. Roy et al.25 proposed an attention-based adaptive spectral–spatial kernel improved residual network (A2S2K-ResNet) model, which uses improved 3D-ResBlocks and an efficient feature recalibration (EFR) attention mechanism26 to improve classification performance. Xue et al.27 proposed a novel local transformer with a spatial partition restore network (SPRLT-Net) to realize remote context modeling and dynamic inference. While all of the above models achieve good performance on HSI classification, the fixed convolution kernel limits the learning weight of the model. The CNN is not flexible enough and unable to capture fine-grained structures when dealing with irregular patterns. Therefore, it ignores potential relationships between pixels.

To alleviate above problem, we propose a novel adaptive pixel attention network (APAN) for HSI classification. First, we propose a spectral–spatial superposition enhancement (SSSE) module, which fuses two mirrored 1D spectral vectors and 3D spatial–spectral patches via pixel addition. It can not only ensure the rich and continuous spectral information, but also enhance the spatial information. In addition, we propose an adaptive pixel attention (APA) mechanism. This mechanism extracts spatial spectral features by constructing a pixel self-attention mechanism through cosine and Euclidean similarity based on auto-adaptive neuron RF. It extracts fine-grained image information by optimize the learning weights. The feature correlation between average pooled pixels and adaptive spectral space is fully explored. Finally, to prevent the omission of effective information and better extract different semantic and geometric attribute features, the cross-layer information complement (CLIC) module is proposed as a deep feature extraction module by fusing the output information from different convolution layers.

The main contributions of this paper are summarized as follows.

  1. (1)

    We propose a novel adaptive pixel attention network (APAN). The adaptive pixel attention (APA) mechanism is introduced for the first time to explore the potential relationships among the output feature pixels of the adaptive convolution kernel.

  2. (2)

    A spectral–spatial superposition enhancement (SSSE) is designed to enhance the spatial feature information and efficiently learn spectral–spatial features in a 2D Conv pattern.

  3. (3)

    A cross-layer information complement (CLIC) is proposed to prevent the omission of useful information and further improve the network performance.

The remainder of the paper is structured as follows. The proposed APAN is thoroughly explained in “Related work”section. The experimental parameter settings, outcomes, and accompanying analyses are reported in Section III. In Section IV, conclusions and recommendations for future research are offered.

Related work

In this section, we review two topics most relevant to our work: Deep Learning- Based Methods and HSI Classification With Attention Mechanism.

Deep learning-based methods

Depending on the network model used, current deep learning-based HSI classification methods include CNN, graph convolution network (GCN)28,29,30, transformer model, etc.

GCN network is super-pixel level inferring the information of other nodes through the information of that node. Ding et al.28 proposed a graph convolution with an adaptive filters network (AF2GNN) to deal with the problems of land cover discrimination and noise impaction. Kong et al.29 developed multi-branch super-pixel GNN (MBGNN) to take into account the multi-scale spatial information. However, pixels in the hyper-pixel of GNN are described as having the same features, and the local spectral–spatial information of individual pixels may not be captured by the graph nodes. The GNN network needs to take the whole image as an input, and the number of parameters is large. The Transformer model is essentially an Encoder-Decoder architecture that handles contextual features at a distance. Zhong et al.31 proposed a spectral–spatial transformer network (SSTN), which overcomes the limitations of the convolutional kernel by enabling long-distance interaction between distant features through the Transformer. Zhang et al.32 designed a dual-dimension spectral–spatial bottleneck transformer (D2S2BoT) framework to effectively capture spatial–spectral correlations. However, the Transformer’s ability to acquire local information is not strong. The gradient vanishing problem will easily occur when the number of layers of the Transformer is large. The most popular deep learning network in HSI classification method is CNN. Lee et al.33 proposed a contextual deep CNN, which can optimally explore local contextual interactions by jointly exploiting local spatial–spectral relationships of neighboring individual pixel vectors. Iyer et al.34 and Shen et al.35 use 2D CNNs and 3D CNNs to better extract spectral–spatial learning features. Li et al.36 use 3D CNNs and attention mechanisms to better extract spectral–spatial learning features. Ma et al.37 used 3D dilated convolution to improve the quality of spatial features. Esmaeili et al.38 designed residual-injection morphological features and 3DCNN layers to extract structural information, shapes, and interregional interactions. Farhan et al.39 proposed a deep smooth wavelet CNN shots ensemble to extract spectral features and employ a cyclic annealing schedule to converge to several local minima along its optimization path. However, the fixed convolution kernel of CNN networks ignores the connections between image pixels and does not allow for better feature extraction.

HSI classification with attention mechanism

Recently, some works23,40,41,42 have attempted to introduce attention mechanism methods to the HSI classification task. Zhang et al.43 proposed a self-attention network for agriculture, which combines the spatial–spectral non-local block structure and the multi-scale spectral self-attention (SSA) structure to integrate spectral and contextual information while emphasizing self-correlation within the HSI. Zheng et al.44 proposed a kind of deep clustering model, which designs a three-dimensional attention convolutional autoencoder (3D-ACAE) to extract essential spatial–spectral features and enhance captured features. Li et al.45 proposed an adaptive mask sampling and manifold to the Euclidean subspace learning (AMS-M2ESL) framework, which designs a dual-channel distance covariance representation (DC-DCR) module to explore linear and nonlinear interdependence in the spectral ___domain. Zhang et al.46 proposed a 3D-2D hybrid convolution and a graph attention mechanism (3D-2D-GAT) model, which uses a graph attention mechanism to learn long-range spatial relationships to distinguish between intraclass variation and interclass similarity across samples. Xue et al.41 proposed a novel attention-based second-order pooling network (A-SPN), which designs an attention-based second-order pooling (A-SOP) operator to obtain second-order statistical features and reduce hyper-parameters. However, the underlying structure of these attention mechanisms remains a convolutional network. The similarity between pixels and their surrounding pixels is still ignored in the feature extraction phase. In addition, Sun et al.47 proposed a spectral–spatial attention network (SSAN) to capture discriminative spectral–spatial features from attention areas of HSI cubes. Zhang et al.40 proposed a spectral–spatial self-attention network (SSSAN), which contains a spectral self-attention module and a spatial self-attentive module for adaptively integrating local features with long-range dependencies related to the pixel to be classified. However, SSAN and SSSAN models consist of two branches, and this two-branch structure model is complex in terms of parameters and computation.

Proposed method

In formal, the original HSI \({X}_{{o}}\epsilon \Re ^{{h}\times {w}\times {b}}\) is a spectral-space 3D cube with height h, width w, and spectral channel b. \({X}_{{o}}\) consists of \({z}={h}\times {w}\) pixels, which is divided all the pixels into two sets \({z}={p}\times {q}\), \({X}_{{o}}={X}_{{p}}\cup {X}_{{q}}\). \({X}_{{p}}\) denotes the set of labeled pixels, which is p in total, and \({X}_{{q}}\) denotes the set of unlabeled pixels, which is q in total. All \({X}_{{i,j}}\epsilon {X}_{{o}}\), where \({i} = 1,2,\ldots ,{w}\), and \({j} = 1,2,\ldots ,{h}\). The two parameters together denote the position of a pixel in \({X}_{{o}}\). All pixels are classified into land cover classes of type C. Each pixel \({x}_{{i,j}}\epsilon {R}_{{{{b}}}}\) in \({X}_{\{p\}}\) corresponds to one of the classes of semantic labels \({y}_{{i,j}} ={c}\). It belongs to the corresponding labeled pixel set \({Y}_{{\{p\}}}=\{{y}_{1},{y}_{2},\ldots ,{y}_{{p}}\}\), where \({c} = 1,2,\ldots ,{C}\). The purpose of the HSI classification task is to assign a semantic label \({y}_{{i,j}}\) to each of pixel \({x}_{{i,j}}\) of the HSI original \({X}_{{o}}\) based on the labeled pixel set \({X}_{\{p\}}\) and the labeled pixel set \({Y}_{\{p\}}\). To better utilize the spectral and spatial information of the HSI, many models divide \({X}_{{o}}\) into 3D blocks of size \({P}\epsilon \Re ^{{s}\times {s}\times {B}}\), where each cube is centered on a \({P}_{{i,j}}\) pixel and \({s}\times {s}\) is the spatial size.

Figure 1
figure 1

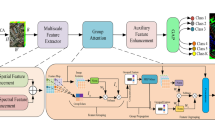
The framework of APAN model, which includes the SSSE module, the APA module, the CLIC module, and finally the softmax-based connected module. We visualize the input in python-3.8.16. URL: https://www.python.org/downloads/.

Full size image

The flowchart of the proposed APAN is shown in Fig. 1, which contains four components, SSSE module, APA module, CLIC module and final classification module. First, the SSSE module fuses two populated 1D spectral vectors \({{{{\varvec{P}}}}}_{{{{{\varvec{Z}}}}}_{{{{\varvec{i,j}}}}}}\) and \({{{{\varvec{P}}}}}_{{{{{\varvec{r}}}}}_{{{{\varvec{i,j}}}}}}\), then it is connected with the 3D cube’s input data \({P}_{{i,j}}\) to enhance spatial information and efficiently learn spectral–spatial features in the 2D Conv pattern. Next, the APA mechanism utilizes adaptive kernel \(1\times 1\) and \(3\times 3\) to extract information \({P}_{{spa}}\) and \({P}_{{spe}}\), then uses cosine similarity CosSim and euclidean similarity EDSim operations to explore pixel potential relationships. It includes the distance and angle relationships of pixels. Thirdly, the CLIC module ensures the information integrity and extracts deep feature by fusing the output features \({X}_{{i,j}}\) and \({X}_{{i,j}}^{{l+2}}\)of different convolution layers. Finally, classification is performed via a softmax-based classifier.

SSSE module

To enhance spatial information and efficiently learn spectral–spatial feature in 2D Conv pattern, we propose a new information fusion module SSSE, which superimposes 1D spectral vectors by two operational fills, zeropad and reflectionpad. The fusion of 1D superimposed spectra and 3D input modules enhances features while ensuring dimensional and spectral continuity. At the same time, SSSE enables the model to use a 2D convolution kernel in the feature extraction phase, which can reduce the number of parameters and computation of the network. Therefore, we design the SSSE module for the fusion enhancement of spectral spatial features. It ensures the effectiveness and efficiency of the subsequent use of 2D convolution.

As shown in Fig. 1, the filling method is to fill the one-dimensional spectral vectors according to the size of the set patch. Zero filling fills with zero data, and reflection filling mirrors the fill centered on the last data. SSSE first passes the central spectral vectors through zero padding and reflection padding. It ensures that each channel window of the shaped 3D spectral patch is filled with elements. Zeropad can control the spatial dimension of the output data. Reflection padding ensures the continuity of the spectrum and prevents the edge shading problem caused by zero filling. The fill vector length depends on the spectral bands of the different HSI datasets and on the spatial window size of the 3D sectioned patches. It eliminates the need to manually set the fill vector length. The shaping direction of the center 1D spectral vector is the horizontal row direction48. The zero-filled mirror-filled shaped spectral patches are superimposed to enhance the real feature information while maintaining the original continuity of the spectral vectors. The operation of the SSSE module can be expressed as:

$$\begin{aligned} & {{{{\varvec{P}}}}}_{{{{{\varvec{Z}}}}}_{{{{\varvec{i,j}}}}}}={Reshape}({ZeroPad}({{{{\varvec{x}}}}}_{{{{\varvec{i,j}}}}})) \end{aligned}$$
(1)
$$\begin{aligned} & {{{\varvec{P}}}}_{{{{\varvec{r}}}}_{{{\varvec{i,j}}}}}={Reshape}({ReflectionoPad}({{{\varvec{x}}}}_{{{\varvec{i,j}}}})) \end{aligned}$$
(2)
$$\begin{aligned} & {P}_{{i,j}}^{'}={Concat}({P}_{{i,j}},({{{\varvec{P}}}}_{{{{\varvec{Z}}}}_{{{\varvec{i,j}}}}}\oplus {{{\varvec{P}}}}_{{{{\varvec{r}}}}_{{{\varvec{i,j}}}}})) \end{aligned}$$
(3)

where \(\oplus\) denotes the elements are summing operations and \({P}_{{i,j}}\) denotes the original input patch. \({{{\varvec{P}}}}_{{{{\varvec{Z}}}}_{{{\varvec{i,j}}}}}\) and \({{{\varvec{P}}}}_{{{{\varvec{r}}}}_{{{\varvec{i,j}}}}}\) represent two kinds of patches after filling and shaping respectively. \({P}_{{i,j}}^{'}\) denotes the spectral–spatial patch after superposition and fusion. Through the spectral–spatial feature fusion of the SSSE module, the spatial features can be enhanced, which is helpful to improve the effectiveness of the subsequent use of 2D convolution patterns.

APA mechanism

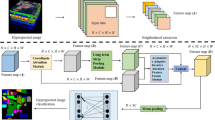
Due to atmospheric interference, light angle49, and other factors during the imaging process, the mixed-category problem leads to similarity among various ground objects in HSI. That is the same type exhibits different spectral characteristics, or different categories appear with similar spectral characteristics50. However, most studies51,52 use a fixed convolution kernel, which leads to the problem of model-constrained learning weights that capture fine-grained structures or eliminate coarse-grained image structures. So it fails to accurately capture the structural features of the image and explore the pixel’s relationships. To solve this problem, we propose the APA mechanism. The module consists of two main parts: the adaptive spatial–spectral kernel and the pixel attention. The adaptive spatial–spectral kernel focuses on the adaptive extraction of spatial–spectral features using convolution kernels of different scales. The pixel attention part utilizes cosine and Euclidean similarity calculations to adaptively explore the distance and angle relationship properties between pixels in two different scales of convolution patch features. As shown in Fig. 2, the APA mechanism is designed in the proposed APAN.

Figure 2
figure 2

Framework of the proposed APA.

Full size image

Adaptive spatial–spectral kernel

The adaptive spatial–spectral kernel module mainly uses convolutional kernels of different sizes for shallow information extraction from the input feature blocks. It can realize information fusion between multiple regions. As shown in Fig. 2, the input is the spectral–spatial patch fused by SSSE. \({X}\epsilon \Re ^{{s}\times {s}\times {b'}}\) is the input HSI cube, where \({s}\times {s}\) denotes the selected spatial size, \({b'}\) denotes the fused spectral band. X is subjected to a convolution operation with two convolution kernels of sizes \(1\times 1\) and \(3\times 3\) respectively. They are used to extract the spectral and spatial feature maps.

$$\begin{aligned} {P}_{{spe}}^{{l+1}}= & {F}_{{spectral}}^{{l+1}}({X}^{{l}})={X}^{{l}}*{W}_{(1\times 1)}^{{l+1}}+{b}^{{l+1}} \end{aligned}$$
(4)
$$\begin{aligned} {P}_{{spa}}^{{l+1}}= & {F}_{{spatial}}^{{l+1}}({X}^{{l}})={X}^{{l}}*{W}_{(3\times 3)}^{{l+1}}+{b}^{{l+1}} \end{aligned}$$
(5)

where \({X}^{{l}}\) is the input of layer l and \({P}_{{spe}}^{{l+1}}\) , \({P}_{{spa}}^{{l+1}}\) are the outputs of the spectral and spatial spectra of layer l after convolution operation. \({X}^{{l}}\rightarrow {P}_{{spe}}^{{l+1}}\epsilon \Re ^{{s}\times {s}\times {b'}}\), \({X}^{{l}}\rightarrow {P}_{{spa}}^{{l+1}}\epsilon \Re ^{{s}\times {s}\times {b'}}\). \({F}_{{spectral}}^{{l+1}}\), \({F}_{{spatial}}^{{l+1}}\) denote spectral feature extraction and spatial feature extraction operation respectively. \(*\) denotes three-dimensional convolution operation. \({W}^{{l+1}}\) and \({b}^{{l+1}}\) denote the weights and bias parameters of the \({l+1}\) layer respectively. If the input is a feature map of size \({s}^{{l}}\times {s}^{{l}}\) including \({n}^{{l}}\) features, the convolution layer contains \({m}^{{l+1}}\) convolution kernels of size \({k}^{{l+1}}\times {k}^{{l+1}}\), and generates \({n}^{{l+1}}\) output features of size \({s}^{{l+1}}\times {s}^{{l+1}}\). The distribution of input data in each layer of the network is relatively stable by batch normalization (BN). The output characteristics of the feature map after the convolution operation in layer l can be mathematically defined as:

$$\begin{aligned} & {X}_{{i}}^{{l+1}}={R}(\sum \limits _{j=1}^{x^{l}}{\mathscr {F}}_{{{bn}}}({X}_{{j}}^{{l}})*{W}_{{i}}^{{l+1}}+{b}^{{l+1}}) \end{aligned}$$
(6)
$$\begin{aligned} & {\mathscr {F}}_{{{bn}}}({X}_{{j}}^{{l}})=\dfrac{{X}_{{j}}^{{l}}-{E}({X}_{{j}}^{{l}})}{\sqrt{Var^{2}({X}_{{j}}^{{l}})+\epsilon }}\times \gamma +\beta \end{aligned}$$
(7)

where R is a nonlinear activation function54 that introduces nonlinear features. \({\mathscr {F}}_{{{bn}}}({X}_{{j}}^{{l}})\) is the BN of the l th layer of the j th feature \({X}^{l}\). \({E}({X}_{{j}}^{{l}})\) and \(Var^{2}({X}_{{j}}^{{l}})\) are the batch mean and variance of the input feature mappings respectively. \(\epsilon\) is a small constant used for numerical stabilization. \({W}_{{i}}^{{l+1}}\) and \({b}^{{l+1}}\) are the weights and bias parameters of the j th filter bank of the \(l+1\) th layer. \(\gamma\) is the scaling factor and \(\beta\) is the offset.

The features extracted from the two kernels are fused to obtain a new feature mapping, which can be defined as:

$$\begin{aligned} {G}^{{l+1}}={P}_{{spe}}^{{l+1}}\odot {P}_{{spa}}^{{l+1}} \end{aligned}$$
(8)

Adaptive average pooling (AAP) layer operation is performed on the obtained fused feature mappings. It adaptively computes the kernel size and the step size of each move, which can better explore the feature dependencies obtained from RFs of different sizes. This will compress the spatial dimension of \({G}^{{l+1}}\) to \({{{{\varvec{S}}}}}^{{{{\varvec{l+1}}}}}\epsilon \Re ^{{1}\times {1}\times {B}}\) along the band direction. To better achieve convergence of the model, the parameter r is introduced to compress the dimension to \({{{{\varvec{Z}}}}}^{{{{\varvec{l+1}}}}}\epsilon \Re ^{{1}\times {1}\times {B/r}}\) by convolution. In conducting the experiments, we set r to 2 to compress the band to 1/2 of the original. It can be mathematically described as:

$$\begin{aligned} & {{{\varvec{S}}}}^{{{{\varvec{l+1}}}}}={AAP}({G}^{{l+1}}) \end{aligned}$$
(9)
$$\begin{aligned} & {{{{\varvec{Z}}}}}^{{{{\varvec{l+1}}}}}={\mathscr {F}}^{{l+1}}({{{\varvec{S}}}}^{{{{\varvec{l+1}}}}})={{{{\varvec{S}}}}}^{{{{\varvec{l+1}}}}}*{W}^{{l+1}}+{b}^{{l+1}} \end{aligned}$$
(10)

Pixel attention

The pixel attention module explores the relationship between distance and angle between different convolutionally fast pixel features by employing cosine and Euclidean similarity adaptively. It can efficiently extract features between pixels. As shown in Fig. 2, the dimensions of the feature compression extracted from the adaptive spatial kernel in the previous section are extended to extract the similarity between neighbors through euclidean distance and cosine similarity. Among them, the Euclidean distance is concerned with the difference between values inside the same dimension. It is mathematically described as:

$$\begin{aligned} {dist(X,Y})= & \sqrt{\sum \limits _{i=1}^{n}{({x}_{i}-{y}_{i})^{2}}} \end{aligned}$$
(11)
$$\begin{aligned} { EDSim}= & \frac{1}{1+{dist(X,Y)}} \end{aligned}$$
(12)

Cosine similarity is concerned with relative differences in direction. It is mathematically described as:

$$\begin{aligned} {cos}\theta =\frac{\sum \limits _{i=1}^{n}({A}_{i}\times {{B}}_{i})}{\sqrt{\sum \limits _{i=1}^{n}(A_{i})^{2}\times \sum \limits _{i=1}^{n}({B}_{i})^{2}}}=\dfrac{A^{T}\cdot {{B}}}{\parallel {{A}}\parallel \times \parallel {{B}}\parallel } \end{aligned}$$
(13)

After adaptive spatial kernel operation and adaptive pooling operation, a one-dimensional vector is obtained which reflects the average pixels of the extracted image features. The vector \({{{{\varvec{u}}}}}^{{{{{\varvec{l+1}}}}}}\epsilon \Re ^{{1}\times {1}\times {B}}\) and the fused \({G}^{{l+1}}\epsilon \Re ^{{s}\times {s}\times {B}}\) are subjected to the euclidean distance similarity metric and the cosine angle similarity metric respectively. It compute the self-similarity representations oriented to the corresponding averaged pooled spectral vectors.

$$\begin{aligned} {E}_{i,j}= & {EDSim}(u_{i,j},{G}_{i,j}) \end{aligned}$$
(14)
$$\begin{aligned} e_{i,j}= & {EDSimV}(u_{i,j},x_{i,j})=\frac{1}{1+\sqrt{\sum \limits _{i=1}^{n}(u_{i,j}-x_{i,j})^{2}}} \end{aligned}$$
(15)

where EDSim denotes the similarity matrix \(E_{i,j}\) for computing the average pooled spectral vectors \(u_{i,j}\) and the fused feature mapped spectral space patch G. \(e_{i,j}\) denotes the euclidean distance similarity value for the \(u_{i,j}\) vector and \(x_{i,j}\). \(x_{i,j}\) is one of the vectors of G. Note that the similarity values are represented by the normalized unity. The higher the similarity, the closer the similarity value is to 1. Similarly, the cosine similarity matrix and cosine similarity value are calculated as follows:

$$\begin{aligned} C_{i,j}= & {CosSim}(u_{i,j},G_{i,j}) \end{aligned}$$
(16)
$$\begin{aligned} c_{i,j}= & {CosSimV}(u_{i,j},x_{i,j})=\dfrac{u^{T}_{i,j}\cdot {x_{i,j}}}{\parallel {u_{i,j}}\parallel \times \parallel {x_{i,j}}\parallel } \end{aligned}$$
(17)

where CosSim computes the cosine angle similarity matrix of u and G by calculating the cosine angle similarity value between \(u_{i,j}\) and \(x_{i,j}\). In addition, the Softmax function can be further normalized. The corresponding self-similarity note maps \({EDS}_{i,j}\epsilon \Re ^{{s}\times {s}}\), \({CosS}_{i,j}\epsilon \Re ^{{s}\times {s}}\) are obtained via euclidean distance similarity matrices and cosine angle similarity matrices respectively. The Softmax function guarantees that the sum of all element values of the target self-similarity attention graph is 1 and the non-negativity of the self-similarity attention graph values.

$$\begin{aligned} {EDS}_{i,j}= & {Softmax}(E_{i,j})=\dfrac{exp(e_{i,j})}{\sum \limits _{i=1}^{s}\sum \limits _{j=1}^{s}exp(e_{i,j})} \end{aligned}$$
(18)
$$\begin{aligned} {CosS}_{i,j}= & {Softmax}(C_{i,j})=\dfrac{exp(c_{i,j})}{\sum \limits _{i=1}^{s}\sum \limits _{j=1}^{s}exp(c_{i,j})} \end{aligned}$$
(19)

On this basis, the spatial information representation is enhanced by introducing the parameter \(\lambda\). Adaptive weight summation mode is used to fuse two self-similar attention maps, which enhances the spatial information representation.

$$\begin{aligned} {ECS}_{i,j}^{\lambda }=\lambda \times {{EDS}_{i,j}+(1-\lambda )\times {{CosS}_{i,j}}} \end{aligned}$$
(20)

where \({ECS}_{i,j}^{\lambda }\epsilon \Re ^{{s}\times {s}}\) is the fusion self-similarity attention map. \(\lambda\) is a weighted parameter with an initial value of 0.5, which can be adaptively optimized during model optimization. The recalibrated spectral space patch \({P}_{i,j}^{l}\epsilon \Re ^{{s}\times {s}\times {b'}}\) is mathematically described as:

$$\begin{aligned} {P}_{i,j}^{l}={ECS}_{i,j}^{\lambda }\otimes {{G}_{i,j}^{l}}+{G}_{i,j}^{l} \end{aligned}$$
(21)

where \(\otimes\) denotes the element-by-element multiplication along the spectral channel dimension. In particular, the element-wise addition operation \(P_{i,j}^{l}\) is performed to avoid gradient vanishing and network degradation. More effective information can be extracted by calculating the average spectral vector and the pixel similarity of the feature module.

CLIC module

We designed the CLIC module as a deep feature extraction module in Part III. It mainly constitutes a contextual interaction structure by integrating the output features of different convolution layers. This module makes full use of the features by complementing the information across layers, which can prevent discriminative information from one floor and further improve the performance of the network.

As shown in Fig. 1, the input of this module is \({X}_{i}\epsilon \Re ^{{s}\times {s}\times {b'}}\). \({X}_{i}\) is extracted spectral–spatial features through a convolution scale consisting of \(1\times {1}\) convolution layer, batch normalization (BN) layer, LeakyRelu function and a convolution scale consisting of \(1\times {1}\) convolution layer, BN layer respectively. Element-by-element additive operation is used to fuse the different features of the two scale branches to achieve the complementary information of the same layer. The total transform can be expressed as follows:

$$\begin{aligned} X_{i,j}^{l+1}={LR}({B}(W_{1\times {1}}^{l+1}*{X_{i,j}^{l}}))+{R}(W_{1\times {1}}^{l+1}*{X_{i,j}^{l}}+b_{1\times {1}}^{l+1}) \end{aligned}$$
(22)

where \({X}_{{i,j}}^{{l+1}}\epsilon \Re ^{{s}\times {s}\times {b'}}\) is the feature map generated in the \(l+1\) th layer. \({W}_{1\times {1}}^{{l+1}}\) table corresponds to the weights of the \(l+1\) th layer and \({b}_{{i}}^{{l+1}}\) is the bias. Since the first \(1\times {1}\) convolution has a BN operation, no bias is used.

Similarly, the spectral–spatial features are extracted by passing \({X}_{{i,j}}^{l+1}\) through a convolution scale consisting of a \(3\times {3}\) convolution layer, a BN layer, a LeakyRelu function and a convolution scale consisting of a \(1\times {1}\) convolution layer, a BN layer. The element-by-element addition operation is applied to both branches as well as to the inputs of this module. It realizes cross-layer information complementarity. It mathematically expressed as follows:

$$\begin{aligned} & {X}_{{i,j}}^{{l+2}}={R}({LR}({B}({W}_{3\times {3}}^{l+2}*{{X}_{{i,j}}^{l}})))+{R}(({W}_{1\times {1}}^{l+1}*{X_{{i,j}}^{l}}+{b}_{1\times {1}}^{l+1})+{X}_{{i,j}}^{l}) \end{aligned}$$
(23)
$$\begin{aligned} & {X}_{{i,j}}^{{out}}={X}_{{i,j}}^{{l+1}}+{X}_{{i,j}}^{{l+2}} \end{aligned}$$
(24)

\({X}_{{i,j}}^{{out}}\) is the final output of the CLIC module. The CLIC module has the advantage of a narrower network with fewer parameters. Gradient vanishing is a problem caused by the transfer of input and gradient information between many layers. This connection is equivalent to directly connecting input and loss in each layer, which makes the transfer of features and gradients more efficient. In addition, due to the reduction of parameters, there is some inhibition of overfitting.

Final classification of APAN

Finally, a fully-connected network is used for the HSI classification. The proposed APAN network is trained and optimized using the cross-entropy loss function. It is mathematically described as:

$$\begin{aligned} {\mathscr {L}}=-\frac{1}{{M}}\sum \limits _{m=1}^{{M}}\sum \limits _{k=1}^{{K}}{ln}({y}^{{m}}_{{K}}){log}(\hat{{y}}^{{m}}_{{K}}) \end{aligned}$$
(25)

where M is the number of samples in the small sample set. K is the total number of categories. \({y}^{{m}}_{{K}}\) and \(\hat{{y}}^{{m}}_{{K}}\) represent the actual and predicted sample labels respectively.

Experimental results

Data sets description and assessment means

To demonstrate the efficiency and effectiveness of our proposed model, we conducted classification experiments on four well-known public datasets. They are Indian Pines (IP), University of Pavia (UP), Kennedy Space Center (KSC), and University of Houston 13 (HU).

The IP data set contains 145 \(\times\) 145 pixels with a spatial resolution of 20 m/pixel. After removing 20 bands with water absorption and low signal-to-noise ratios, 200 bands of 10,249 labeled pixels in the 400–2500 nm wavelength range were used for analysis. The ground truth was assigned to 16 classes, and the number of samples in some classes was highly unbalanced.

The UP data set contains 610 \(\times\) 340 pixels with a spatial resolution of 1.3 m/pixel, covering 103 spectral bands from 430 to 860 nm after the removal of 12 noise bands. The UP data set contains 42,776 labeled pixels for 9 urban classes.

The KSC data set contains 512 \(\times\) 614 pixels with a spatial resolution of 18 m/pixel and a wavelength range of 400–2500 nm. After removing the absorbing and low signal-to-noise bands, 176 bands were used for the analyses. The KSC data set is comprised of 13 upland and wetland classes with 5211 labeled pixels.

The HU data set consists of 349 \(\times\) 1905 pixels with 144 spectral channels ranging from 364 to 1046 nm and a spatial resolution of 2.5 m/pixel. In addition, the ground truth reference was subdivided into spatially disjoint subsets for training and testing, including 15 mutually exclusive urban land cover classes with 15,029 labeled pixels.

In addition, detailed class information for each data set is uniformly reported in Tables 1 and 2. Approximately 1%, 0.1%, and 98.99% of the total labeled pixels from each class are randomly selected as the training, validation, and test sets for the IP, UP, KSC, and HU scenes.

Table 1 Details of the land-cover types and the number of training, validation, and testing samples for IP and KSC data sets.
Full size table
Table 2 Details of the land-cover types and the number of training, validation, and testing samples for UP and HU data sets.
Full size table

To quantitatively compare the classification performance of different methods and modules from various aspects, in the following experiments, we adopt four commonly used evaluation metrics, namely, Overall Accuracy (OA), Average Accuracy (AA), Kappa Coefficient (Kap) and Accuracy per Class (AEC).

OA is the ratio of the number of correctly classified labeled samples to the total number of samples in the test set. AA is the average of the accuracy of all land cover classes. Kappa integrally measures the agreement between the classification results and the base truth. AEC is the accuracy per class, which is particularly useful for unbalanced data. In addition, to quantify the efficiency of the analyses, we use training time \(({T}_{{train}})\) and testing time \(({T}_{{test}})\) to jointly evaluate the running time of each method.

Experimental setup and parameter evaluation

All experiments are performed on a computer with a CPU graphics processing unit. The software environment is Windows 11 64-bit operating system, implemented using Python-3.8.16 and pytorch-1.10.2 frameworks. For model training, an adaptive moment estimation (Adam) optimizer is used with the batch size, learning rate, and number of training epochs set to 32, 0.001, and 100, respectively. In addition, the whole process is repeated ten times. The average accuracy and standard deviation are recorded. To better compare the strengths and weaknesses of different networks, the best results are labeled using bold.

Space window size parameter

In the HSI classification model, the size of the selection has a direct indirect effect on how much content of spatially neighboring pixel information is selected. The larger spatial dimension size means that feature extraction will mine more complex hybrid image elements. It may also bring the problem of limited resources such as arithmetic power, which will affect the performance and efficiency of the model. To better explore the spatial dimension size needed in the model for different datasets, corresponding experiments need to be conducted to determine it. Experiments are conducted on four selected datasets, UP, IP, KSC, and HU, from a set of spatial window sizes set from 3 \(\times\) 3 to 1 7 \(\times\) 17 intervals 2-pixel sizes. About 1%, 0.1%, and 98.9% of the total labeled pixels from each class are randomly selected as the training, validation, and test sets for the IP, UP, KSC, and HU scenes. The final classification results of the four datasets are evaluated for OA, AA, and Kappa. In this case, the length of the original spectral band is less than the length of the vector that needs to be mapped and filled. Using the triangulation principle, that is, filling in two parts. As shown in Fig. 3.

Figure 3
figure 3

Window parameter experiments on IP, KSC, UP and HU data sets.

Full size image

The general trend of performance on both UP and HU datasets is to first increase and then decrease as the spatial window increases. When the spatial size is smaller than 9 \(\times\) 9, the evaluation results increase and reach an optimum of 9 \(\times\) 9, after which the accuracy curve grows slowly or even decreases. For the other three datasets, different optimal results occur. However, the larger the spatial window, the higher the computational cost of the model. Considering multiple aspects of the experiment, for the UP and HU datasets considered in all subsequent experiments, we set the spatial window size to 9 \(\times\) 9. For the other two, we set the spatial selection size to 11 \(\times\) 11.

Activation function nonlinearity experiments

The network introduces nonlinear features through the activation function. The Relu function makes the deep network trainable, improves the computational speed, and alleviates certain overfitting problems. But there exists the Dead Relu Problem, which means certain neurons may never be activated due to problems such as parameter initialization. It leads to the corresponding parameter not being updated all the time, and the gradient explosion occurs. LeakyRelu expands the range of Relu function and also alleviates the Dead Relu Problem well. Therefore, we experiment with the CLIC module with different activation functions.

Table 3 Classification results using different combinations of Relu and LeakyRelu on four datasets.
Full size table

Table 3 records the parametric results of OA, AA and Kap for the two convolution kernels in the CLIC module using different activation functions to introduce nonlinear features. The experiments are performed on four datasets. The combination of the three evaluated parameters is optimal using the “ \({LR+LR}\) ”activation function on the IP, KSC, and HU datasets. On the HU data set, the “\({LR+R}\)” is best for OA,AA and Kap. Summarizing the overall performance on the four datasets, we choose “ \({LR+LR}\) ” as the activation function combination for introducing nonlinear features in the third panel.

Comparison of classification performance

To more significantly evaluate the overall performance and efficiency of the proposed model. We conduct a comprehensive comparison of the proposed APAN with two classical machine learning methods, RF53 and SVM9, as well as eight other representative state-of-the-art deep learning models. Deep learning models include the three-dimensional CNN model ContextNet33, residual learning method RSSAN23, spectral-space double-branch model SSTN31, two-seed network architecture method SSSAN40, various attention mechanism SSAtt24, A2S2K-ResNet25, and spatial–spectral feature fusion pixel processing model CVSSN19. These models provide a comprehensive coverage of the methods currently popular in the HSI classification field. For a fair comparison, all methods use the same experimental setup as mentioned above. Ten experiments are performed for all models, and the average accuracy and standard deviation are recorded. The datasets are public. The False-color composite images in qualitative accuracy analysis are drawn by python-3.8.16 selecting the dataset bands.

Table 4 Classification results of different methods on IP data set trained with 1% labeled data.
Full size table
Table 5 Classification results of different methods on KSC data set trained with 1% labeled data.
Full size table
Table 6 Classification results of different methods on UP data set trained with 1% labeled data.
Full size table
Table 7 Classification results of different methods on HU data set trained with 1% labeled data.
Full size table

Quantitative accuracy analysis

Tables 4, 5, 6, and 7 show the results of the quantitative evaluation of the four evaluation parameters on the four datasets and the corresponding standard deviations calculated by realizing 10 times. For the traditional classification that can only utilize simple spectral information, it is obvious that RF and SVM are very limited. Deep learning methods, ContextNet and RSSAN, improve the effect on the traditional classification methods to some extent. However, the effect is not obvious for the small sample training classification. Subsequently, SSTN and SSSAN explore feature overlay extraction of similarity through global spatial correlation mining by transformer, and two-branch exploration of similarity, respectively. SSAtt hopes to further improve the model performance through the introduction of a two-channel spectral spatial attention module. Through experiments, it can be seen that the effectiveness of these models make a further breakthrough compared to other deep learning models. However, IP, KSC and HU still fail to break the 60, 70 and 80 mark when using 1% of the training samples. Recently, A2S2K-ResNet and CVSSN have made breakthroughs on three datasets using adaptive kernel and spatial and center-vector relation exploration, respectively. But there are still limitations.

The performance of our proposed model is significantly improved for OA, AA, and Kappa on both IP and KSC datasets. On IP, it improves 6.18%, 5.45%, and 7.15% in OA, AA, and Kappa, respectively. Compared to CVSSN, it improves 9.54%, 9.6%, and 10.92% respectively. It achieves the highest classification accuracy in the experimental model for 10 out of the total 16 feature classes compared to A2S2K-ResNet. In the KSC data set, it improved by 6.22%, 7.63%, and 6.93% in OA, AA, and Kappa, respectively. It achieved the highest accuracy in 8 out of the total of 13 feature categories. For both UP and HU datasets, corresponding improvements were also obtained in all three evaluation parameters. The highest was achieved for 5 out of 9 and 6 out of 15 categories for the UP and HU datasets, respectively.

In summary, our proposed model breaks through again on both IP and KSC datasets. The results are improved on UP and HU datasets. Thus, the classification comparison results implicitly show that mining center vector-oriented spatial relationships in the input space and high-level feature space are valuable and important.

Qualitative accuracy analysis

Figure 4
figure 4

Classification maps for IP data set. (a) False-color composite image. (b) Ground truth. (c–i) Classification maps produced by the RF, the SVM, the ContextNet, the RSSAN, the SSTN, the SSSAN, the SSAtt, the A2S2K-ResNet, the CVSSN, and the Proposed. We visualize all in python-3.8.16. URL: https://www.python.org/downloads/.

Full size image

For qualitative evaluation, the classification diagrams of the visualization results of the four datasets classified by different models are shown in Figs. 4, 5, 6, and 7. To judge the classification performance of the models more easily and intuitively, we also show the three-band false-color synthetic plots of the datasets as well as the real legend. Among them, the visualization results correspond to the data counted in the table respectively, and the results remain consistent.

As shown in Figs. 4, 5, 6, and 7, for the IP data set, there is a problem with many feature categories and unbalanced sample distribution. The KSC data set samples are scattered. The traditional machine learning methods will cause a lot of noise on the final visualized display map. Other machine learning methods are ineffective in classifying categories with small distribution areas and mixed categories. Our proposed model achieves a significant improvement in classification on datasets with scattered and unbalanced categories. The processing of edge information outperforms other deep learning networks. The generated visualization results correspond more closely to the pseudo-color composites and real images corresponding to the four datasets.

Efficiency analysis

To consider the performance of the model holistically, we experiment with the proposed model with other different methods in both training time, testing time, parameters and FLOPs of the neural network to discuss the efficiency of the model.

Table 8 Comparisons on model time of different methods on IP, KSC, UP, and HU datasets.
Full size table

Table 8 records the training and testing time of different classification methods on four datasets IP, KSC, UP, and HU. It is worth noting that when 1% and 0.1% are selected as the training and validation sets, the two models, RSSAN and SSAtt, require a short time. However, there are flaws in combining their categorization effects. A2S2K-Res makes a breakthrough in classification results by combining the 3D convolution network and residual network, which improves the accuracy. However, the required runtime will be significantly increased. The CVSSN and the proposed method both consume little time with fewer samples. They both fuse spectral and spatial information and use 2D convolution networks for feature extraction to reduce time consumption. The proposed model explores the relationship between pooled vectors and adaptive spatial features, which has good classification results for datasets with small sample imbalances and scattered distribution.

Figure 5
figure 5

Classification maps for KSC data set. (a) False-color composite image. (b) Ground truth. (c–i) Classification maps produced by the RF, the SVM, the ContextNet, the RSSAN, the SSTN, the SSSAN, the SSAtt, the A2S2K-ResNet, the CVSSN, and the Proposed. We visualize all in python-3.8.16. URL: https://www.python.org/downloads/.

Full size image
Table 9 Comparisons on model Params and FLOPs of different methods on IP, KSC, UP, and HU datasets.
Full size table

Table 9 records some experimental results of classification networks using a 3D convolution kernel with the proposed method in terms of the number of parameters and FLOPs of the neural network. 3D-CNN has the least FLOPs, but the network has more parameters. Since A2S2K’s network main body uses a residual network, it has the smallest number of parameters and a high computational amount. The results show that the proposed method is in second place in terms of the number of network parameters and FLOPs. Therefore, our proposed SSSE module fuses spatial and spectral information. The network uses 2D convolution for feature extraction. Compared to 3D convolution, the network reduces the number of parameters and FLOPs while ensuring the validity of the model.

Ablation Study

To further explore the contribution of different modules in the proposed APAN model. The ablation experiments were conducted on four datasets.

Figure 6
figure 6

Classification maps for UP data set. (a) False-color composite image. (b) Ground truth. (c–i) Classification maps produced by the RF, the SVM, the ContextNet, the RSSAN, the SSTN, the SSSAN, the SSAtt, the A2S2K-ResNet, the CVSSN, and the Proposed. We visualize all in python-3.8.16. URL: https://www.python.org/downloads/.

Full size image

The validation of filling operation

Table 10 The ablation experiments on four data sets.
Full size table

The Filling Operation column in Table 10 records the validation of the SSSE module using the operations of zero filling, mirror filling, and superimposition of the two fillings respectively. The operation using zero fill alone performs better on the UP data set. However, the classification of the other three datasets is poor. To better control the spatial dimension of the output data and ensure the continuity of the spectra, combined with the experimental results, we choose the two-filling superposition operation.

Figure 7
figure 7

Classification maps for HU data set. (a) False-color composite image. (b) Ground truth. (c–i) Classification maps produced by the RF, the SVM, the ContextNet, the RSSAN, the SSTN, the SSSAN, the SSAtt, the A2S2K-ResNet, the CVSSN, and the Proposed. We visualize all in python-3.8.16. URL: https://www.python.org/downloads/.

Full size image

The validation of attention mechanisms

The column of attention mechanism in Table 10 records the classification results of the model paired with different attention mechanisms on the four datasets. The results show that the classification results of our proposed attention mechanism are improved on all four datasets compared to the classical Squeeze-and-Excitation Module (SE) and Convolution Block Attention Module (CBAM). Compared with the recently published attention mechanisms, our proposed APA mechanism has superior results.

The validation of CLIC module

Figure 8
figure 8

Feature extraction module experiments on IP, KSC, UP and HU data sets. (a) OA. (b) AA. (c) Kap.

Full size image

In the part of the model feature extraction, to effectively prevent information omission, we propose two deep feature extraction modules: Dual-core information complement (DCIC) and Cross-layer information complement (CLIC). The DCIC module has two layers of four different sizes while convolution kernels to achieve feature extraction.

Figure 8a–c show the classification results of the model after information fusion using DCIC and CLIC modules on the four datasets UP, IP, HU, and KSC respectively. The experimental results show that different information fusion modules are adopted to achieve different final classification effects. For UP and SA, since these two datasets contain rich sample information and the distribution of data set categories is centralized, their performance will be relatively more stable. In contrast, the datasets of IP and KSC have imbalanced categories, loose distribution of categories, and large differences in the number of samples selected between categories. They will have better classification results for samples of large categories. It is worth noting that by experimenting with the four main datasets. It is not difficult to conclude that the CLIC module performs better results for information fusion to prevent information omission. This feature is more obvious in the IP and KSC datasets. Figure 8a–c demonstrates the comparison of the experimental results of DCIC and CLIC. The results show that the CLIC module is better than the DCIC.

The validation of different modules

Table 11 The ablation experiments on four data sets.
Full size table
Figure 9
figure 9

OA and AA accuracies obtained by IP, KSC, UP, and HU with different training sample sizes for different methods. (a) IP-OA. (b) KSC-OA. (c) UP-OA. (d) HU-OA. (e) IP-AA. (f) KSC-AA. (g) UP-OA. (h) HU-AA.

Full size image

Table 11 documents the accuracy of the four datasets for OA, AA, and Kappa with different combinations of modules. The SSSE module is to enhance spatial information and efficiently learn spectral–spatial features in 2D Conv pattern. APA and CLIC are used as the feather extract alone, and the classification results are average. The accuracy of the three evaluated parameters of the combination of the two modules, APA and CLIC, is only second to that of the model proposed in this paper. Both modules are used in combination with SSSE respectively, and the classification performance is degraded to different degrees. Among them, different combinations show different phenomena on different datasets. “SSSE+APA” performs better on the KSC data set and “SSSE+CLIC” performs better on the UP data set. We can reasonably infer that the APA module is mainly used to extract features and performs more prominently on datasets with fewer samples. The CLIC module is mainly used for complementary information. When there are many training samples and sufficient information, CLIC fuses the information of different convolution layers to reduce the omission of useful information. Different modules and combination tests verify the different roles played by each module and further validating the effectiveness of the proposed model.

Effect of the proportion of training samples

To verify the robustness of the proposed model, we investigate the classification performance of different methods on three datasets using different proportions of labeled samples for model training.

As shown in Fig. 9a–h, the overall curve trend of each method shows an upward trend as the percentage of training samples increases. Specifically, on the four datasets, the two machine learning classification models show some limitations with different training samples. The deep learning approach can effectively improve the classification performance of the models. The two approaches, A2S2K-ResNet and CVSSN, show more satisfactory classification results in most cases. Among them, A2S2K-ResNet shows better performance on UP data set. CVSSN has better classification effect on HU data set. However, the effect of our proposed model is slightly better. APAN is slightly less effective than CVSSN in the 5% training sample condition, but more effective than all other methods on other percentage scenarios, especially on both IP and KSC data. Our proposed model is far ahead on both OA and AA, both of which are significantly enhanced. Combining the different training sample percentage experiments on the four datasets, our proposed has superior performance compared to other models.

Conclusion

In this paper, we present a novel self-attentive pixel adaptive network for HSI classification tasks. First, the SSSE module superimposes spectral and spatial information, thus enhancing the effective information and efficiently learning the spectral–spatial features in 2D Conv mode. More importantly, the APA mechanism mines the potential relationship between pixel distances and angles by adaptively computing the similarity between pixels of different scale convolution blocks. Finally, CLIC is designed as a deep feature extraction module to avoid information omission by fusing the output characteristics of different convolution layers to form a remote contextual information interaction. We compare the proposed method with typical machine learning and different modes of deep learning in various aspects. Experiments are conducted on four datasets (IP, UP, HU, and KSC), and the experimental results and analyses show that the proposed APAN network can effectively solve the problem that a fixed convolution kernel will limit the learning weights of the channels. The adaptive pixel attention mechanism we designed can effectively explore the potential relationship between pixels. In addition, the complexity of the proposed APAN model is lower. Future work includes further optimizing the training and testing time of the network, as well as achieving the general applicability of the model in more scenarios with different types of datasets.