Introduction

Engineering blasting technology is one of the economical and efficient means of rock breaking1,2. However, some secondary harmful effects of blasting are inevitably produced, such as blasting vibration (BV)3, flying stones4,5, shock waves5, blasting noise and poisonous gas eruption6. Moreover, some studies have shown that BV is one of the most serious secondary harmful effects during the blasting process7,8. It may cause the instability and damage to the surrounding structures9, even leading to serious accident.

When BV propagating in the rock gets a sufficient intensity10, a variety of damage phenomena of rock can come into being11,12. As far as slope blasting is concerned, more and more attention has been paid to the elevation effect of BV of rock mass13,14,15. For instance, Yu et al.13. obtained better numerical results of BV of the rock mass by adjusting the micro-parameters. Tang et al.14. experimentally presented the empirical formula of BV, which could reflect the elevation amplification effect. In addition, many relevant studies have shown that it is related with the elevation and terrain conditions10,16,17,18. For instance, Zhang and his coworkers10 presented that the elevation has both amplification and attenuation effects on BV of rock. Recently, Graizer18 found that the main reasons for the vibration effect are the low-velocity region and geological landform. In conclusion, the elevation effect and its mechanism of the rock slope were extensively studied by many researchers15,19,20.

Besides causing the damage of rock, BV can also result in the destructiveness of the surrounding engineering structures, such as pipes21,22, subway structures23, and building structures24. As a consequence, it has been one of the most important issues to investigate the destructiveness of BV to engineering structures. As far as the pipe is concerned, it has been one of the important ways of long-distance transportation of oil and gas. However, with the increase of blasting operation and the complexity of blasting environment, it is easy for BV to cause the damage to the existing buried pipes around the blasting field25,26,27,28,29,30,31. At present, many researchers have carried out the studies on the dynamic performance and damage modes of buried pipes under blasting loads. For instance, Qu et al.22. numerically studied the dynamic performance of buried polyethylene (PE) pipes under subsurface localized explosion. Cao and his coworkers25 investigated the failure mode of glass fiber-reinforced composite tubes subjected to explosion load. He et al.26. numerically analyzed the influence of explosive mass and pipe parameters on the damage of the pipes under blast loading. Song et al.27. studied the influence of explosion mass, contact area and wall thickness of pipes on the failure mechanism of X70 pipes. Qu et al.28. found that the interaction between pipe and soil could support the back burst surface of the X70 steel pipe and effectively reduce the displacement of the pipe. Li and his coworkers29 firstly pointed out that, compared with the weld type, blasting height plays a major role in the peak vibration velocity (PVV) of the X70 pipe under blasting load. Recently, Qu and his coworkers firstly investigated the dynamic buckling response of the steel pipe with bolted flange connection subjected to two-charge explosion loads31.

It is well known that the Sadovsky’s empirical formula is commonly used to study the attenuation law of PVV of rock particle. Data have also shown that the larger deviation of calculation results from the Sadovsky’s empirical formula under different terrain conditions with the practical measurement results10,14,15,16. This means that the Sadovsky’s empirical formula fails to predict the attenuation of the blasting vibration velocity of pipes during the slope blasting process. As a consequence, the elevation effect of slope blasting on the BV of steel pipes was numerically investigated according to finite element model, Ma et al.32. improved the Sadovsky’s empirical formula, which could reflect the elevation effect of slope blasting to predict PVV of the gas pipe through experimental research.

Obviously, the elevation effect and the vibration attenuation law of the existing buried pipes under different elevations are different from that of surrounding rock mass due to different transmission mediums and landforms. However, scarce information is available on the influence of the elevation effect of slope blasting on the BV of surrounding structures, especially existing buried pipes. Consequently, the elevation effect of slope blasting on the BV of steel pipes was numerically investigated according to finite element model, which was verified against the experimental result. The present study could provide a certain technical reference to evaluate the influence of the elevation effect of slope blasting on the existing buried steel pipes.

The remainder of this paper is organized as follows. The calculation formula to predict the PVV of rock mass are presented in “Analytical method” section. “Calculation formulas to predict vibration velocity” section presents finite element (FE) modeling and material models used to study the elevation effect of steel pipes under the three different terrain conditions. The FE model was verified against the experimental results. In “FE modeling and material models” section regression analysis is conducted for predicting PVV of the steel pipe by using the Sadovsky’s empirical formula and the modified Sadovsky’s empirical formula. In “Results and discussion” section the elevation effect of the steel pipes under different terrain conditions is discussed according to numerical results. Finally, a summary and main conclusions are presented in “Summary and conclusions” section.

Analytical method

An analysis is carried out to investigate vibration velocity attenuation law of the buried steel pipes under different terrain conditions including positive elevation, negative elevation, and flat terrain. Regression analysis is also carried out by using the Sadovsky’s empirical formula and the modified Sadovsky’s empirical formula. The scheme of analytical study is shown in Fig. 1.

Fig. 1
figure 1

Scheme of analytical study procedure.

Full size image

Calculation formulas to predict vibration velocity

Sadovsky’s empirical formula

Many researchers have paid most attention to the blasting vibration velocity, which directly reflects the energy of the blast wave reaching the position28,33. Moreover, the Sadovsky’s empirical formula has been extensively used to predict the PVV of rock mass under flat terrain condition with a high accuracy by engineering experiments32,33.

$$v=K{\left( {\frac{{\sqrt[3]{Q}}}{R}} \right)^\alpha }$$
(1)

Where v is PVV of the particle, Q is the explosive charge, R is the blasting distance from blasting source to the measuring point, K and α is the two attenuation coefficients.

Modified Sadovsky’s empirical formula

Some previous studies have showed that the elevation is an important factor, which has direction with the propagation attenuation law of BV. Equation (1) does not take the influence of the elevation effect into consideration, however. Considering the influence of the elevation effect, the modified formula of Eq. (1) is expressed as follows in Eq. (2)32:

$$v=K{\left( {\frac{{\sqrt[3]{Q}}}{R}} \right)^\alpha }{\left( {\frac{{\sqrt[3]{Q}}}{H}} \right)^\beta }$$
(2)

Where H is the elevation difference, β is the elevation influence coefficient.

As can be seen from Eq. (2), the propagation of BV in terrain with elevation difference is affected by the amount of explosive, the distance between blasting center and elevation difference.

For the convenience of regression analysis, the following equation is obtained as shown in Eq. (3):

$$y={\beta _1}{x_1}+{\beta _2}{x_2}+b$$
(3)

Where \(y=\lg v\),\({x_{\text{1}}}{\text{=lg}}\left( {\frac{{\sqrt[3]{Q}}}{R}} \right)\),\({x_{\text{2}}}{\text{=lg}}\left( {\frac{H}{R}} \right)\),\(b{\text{=}}\lg k\).

Other empirical formula

Ma et al.32. presented the formula shown in Eq. (4) by introducing the concept of pipe explosion equivalent:

$$v=K \cdot \eta {M_0} \cdot {R^{ - \alpha }}$$
(4)

Where M0 is the pipe explosion equivalent (kg); η is the conversion coefficient of vibration energy; K and α is the two attenuation coefficients.

FE modeling and material models

FE modeling

In the present study, positive elevation and negative elevation conditions were introduced to study the elevation effect of steel pipes under slope blasting load. Positive elevation means the elevation of the monitoring point of the pipe is higher than that of the blasting source. Contrarily, negative elevation means the elevation of the monitoring point of the pipe is lower than that of the blasting source. ANSYS/LS-DYNA package was used to establish the numerical model based on the actual blasting engineering. The length × width × height of the FE model is 1300 cm ×500 cm × H1 (See Fig. 2). The slope angle is 75º shown in Fig. 2. The steel pipe with external diameter of 1016 mm and wall thickness of 20.3 mm was selected according to the current national specification of China34. Moreover, No. 2 rock emulsion explosive was adopted in the present study.

Fig. 2
figure 2

Calculation models: (a) negative elevation difference model; (b) positive elevation difference model.

Full size image

The depth of the blast hole is 300 cm shown in Fig. 2. The length of the cylindrical explosive charge is 120 cm, and the length of blasting mud is 180 cm. The distance from the charge center to the rock surface is fixed to 240 cm. The model mainly includes the following five materials: explosive, rock, filling material, steel pipe and blasting mud. The Lagrange mesh was used for rock, filling material and steel pipes, and the Euler mesh was used for explosive and blasting mud. ALE (Arbitrary Lagrange-Euler) algorithm summarized in Ref35. was used to simulate the interaction between detonation product gas, rock and steel pipe for coupling calculation.

Material models

Material model for explosive

In the simulation, 2# rock emulsion explosive was described by ∗MAT_HIGH_EXPLOSIVE_BURN model. The corresponding JWL equation of state was applied to describe the relationship between detonation pressure, relative volume and internal energy of explosive36. The JWL equation of state is defined as follows36,37:

$$P=A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){{\text{e}}^{ - {R_1}V}}+B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){{\text{e}}^{ - {R_2}V}}+\frac{{\omega {E_0}}}{V}$$
(5)

Where P is the detonation pressure; V is the relative volume of explosion products; R1, R2, ω, A and B are the five material parameters of explosive; E0 is the initial specific internal energy. The material parameters of the explosive are shown in Table 138.

Table 1 Material parameters of the explosive38.
Full size table

Material models for rock and pipe

Rock is usually looked on as a continuous, isotropic elastoplastic material during the simulation process39. ∗MAT_PLASTIC_KINEMATIC model was applied to describe the performance of the rock material. The yield condition expression is as follows40:

$$\left\{ {\begin{array}{*{20}{c}} {\phi =\frac{1}{2}\xi _{{\operatorname{ij} }}^{2} - \frac{1}{3}\sigma _{{\text{y}}}^{2}=0} \\ {{\sigma _{\text{y}}}=\left[ {1+{{\left( {\frac{\varepsilon }{c}} \right)}^{\frac{1}{{\text{\varvec{\uprho}}}}}}} \right]\left( {{\sigma _0}+\beta {E_{\text{p}}}\varepsilon _{{{\text{eff}}}}^{{\text{p}}}} \right)} \\ {\xi _{{\operatorname{ij} }}^{2}={s_{{\text{ij}}}} - {a_{{\text{ij}}}}} \end{array}} \right.$$
(6)

Where \({s_{\text{i}\text{j}}}\) is Cauchy stress tensor; p and c are the two input constants; β is the hardening parameter; σ0 is the yield stress; Ep is the plastic hardening modulus; ε and\(\varepsilon _{{{\text{eff}}}}^{{\text{p}}}\)are the strain rate and effective plastic strain, respectively.

In addition, the plastic deformation of steel pipe material conforms to the power hardening law. The constitutive equation of steel material also uses the isotropic follow-up and mixed hardening elastoplastic model. All of the material parameters of rock and steel pipe are shown in Table 2.

Table 2 Material parameters of rock, steel pipe, and filling material29,39.
Full size table

Material model for filling material

Material model named * MAT_PLASTIC_KINEMATIC was also used as the model of the filling material. The relevant parameters of the filling material is shown in Table 229,39.

Material model for blasting mud

*MAT_SOIL_AND_FORM is used to define the performance of blasting mud. The stress yield constant of the material model is defined as follows38.

$$f{\text{ }}={\text{ }}{S_{{\text{ij}}}}{\delta _{{\text{ij}}}}/2 - \left( {{a_0}+{a_1}{\text{ }}{p_{\text{t}}}+{a_2}{\text{ }}{p_{\text{t}}}^{2}{\text{ }}} \right)$$
(7)

Where Sij is the Cauchy deviatoric stress tensor of soil material; δij is the Kronecker coefficient of soil material; a0, a1 and a2 are the three influence coefficients of the soil friction angle; pt is the soil pressure; soil cohesion and dynamic load effect of soil explosion, respectively. The material parameters of the blasting mud are shown in Table 340.

Table 3 Material parameters of blasting mud40.
Full size table

Meshing and general settings

The model adopts an eight-node SOLID164 element and uses a sweeping method to divide the mesh. The meshing of the model is shown in Fig. 3a–e. The grid size of the rock and filling material is 12 cm, and the grid size of the steel pipe is 4 cm shown in Fig. 3b. The grid size is 2 cm in the circumferential direction of explosive charge (See Fig. 3e). The grid size is 12 cm in the axial direction of explosive charge (See Fig. 3e). The grid size of the blasting mud is the same as that of the explosive. Moreover, local grid refinement was used to get the meshing of the filling media around the explosive and pipe (See Fig. 3).

Fig. 3
figure 3

FE model: (a) meshing of negative elevation difference model; (b) meshing of steel pipe; (c) meshing of positive elevation difference; (d) meshing of rock around the blast hole; (e) meshing of explosive charge.

Full size image

The surrounding and bottom surfaces of the rock were set as non-reflecting boundaries, and the top and sloping surfaces were set as free boundaries (see Fig. 2) to eliminate the reflection impact of explosion shock waves. The coupling region between the pipe and the fill media adopted the automatic contact searching algorithm, which could realize the force transferring between the steel pipe and the soil.

Rationality of numerical simulation

Background experiment

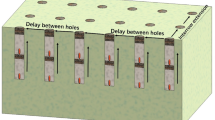
The simulated slope blasting process of the model was generated according to the actual blasting engineering. Test site was located in the construction new limestone mine of Fuxin city in China41. The TC-4850 type vibrometer was used to measure the PVV of the surface rock in the vertical direction (Y-direction). The layout of the measuring points is shown in Fig. 4. The horizontal distances to the explosion center were fixed to 10 m, 12 m, 14 m, 16 m, 18 m and 20 m (See Fig. 4), respectively.

Fig. 4
figure 4

Layout of the measuring points41.

Full size image

Rationality analysis

Taking the single hole blasting test as an example, simulation results were used to verify the rationality of FE model. The explosive charge was 7 kg41. Figure 5 shows the comparison between experimental and simulation results. The field experimental data is slightly larger than the simulation results (See Fig. 5). The changing trend of data was basically the same. The maximum error of the PVV occurred at the blasting distance of 18 m. As for the reason, it may be associated with the complex rock structures in the field experiment, which affected the propagation of BV. The definition of pipe-soil contact could refer to the our previous studies22. It was proved to be reasonable. As a result, it is concluded that the simulation results are basically consistent with the experimental results in the permissible error range.

Fig. 5
figure 5

Comparison between experimental and simulation results.

Full size image

Calculation cases

Table 4 shows the calculation cases to investigate the elevation effect of slope blasting on the buried steel pipe under three different terrain conditions.

Table 4 Calculation cases.
Full size table

Results and discussion

The elevation amplification effect analysis

Based on previous reports15,42,43, it is found that the elevation amplification effect is dominated in the vertical direction. Accordingly, the vertical direction representing elevation difference (H) marked as Y-direction is mainly used to show the influence of positive/negative elevation difference of slope blasting (H) on the existing pipes. Moreover, the BV of the horizontal direction (lateral) marked as X-direction is used to conduct a comparative analysis. The BV of the steel pipe along the second horizontal direction (longitudinal) marked as Z-direction is not discussed due to the relatively weak elevation amplification effect. The monitoring point facing the explosion center was arranged to show the influence of the elevation effect of slope blasting due to the local effect of explosion22,36.

Figure 6 shows the time-history curves of vibration velocity of the typical unit on the steel pipe under the slope blasting with H = 3.6 m and L = 6.3 m. The X-direction velocity of the typical unit on the steel pipe firstly increased to the maximum in the positive direction, and then lowered down quickly and got the maximum in the opposite direction (See Fig. 6a). The X-direction velocity of the typical unit showed a tendency to decrease gradually with the propagation time increasing. The similar changes occurred in Y-direction velocity of the typical unit (See Fig. 6b). Moreover, it is obvious that PVV of the typical unit in the Y-direction is more than that in the X-direction. As a results, the velocity of the steel pipe in the Y-direction had the manifest elevation effect.

Fig. 6
figure 6

Time-history curves of velocity of the typical unit on the steel pipe under the slope blasting with H = 3.6 m and L = 6.3 m: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

Figure 7 shows the time-history curves of velocity of the typical unit on the steel pipe under the slope blasting with H = -3.6 m and L = 6.3 m. Similar changes occurred in X-direction velocity and Y-direction velocity of the typical unit (See Fig. 7). Moreover, X-direction velocity of the pipe had the manifest elevation effect than that of Y-direction velocity of the pipe.

Fig. 7
figure 7

Time-history curves of velocity of the typical unit on the steel pipe under the slope blasting with H = -3.6 m and L = 6.3 m: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

Figure 8 shows PVV of the typical unit of the steel pipe with L changing. The X-direction PVV of the pipes tends to gradually decrease with L increasing (See Fig. 8a). For the same H and L, it is found that the amplification phenomenon of the velocity of the pipe occurred only at some individual points of the steel pipe (see Fig. 8) under the terrain with positive elevation difference.

Fig. 8
figure 8

PVV of the typical unit of the steel pipe with L changing: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

As for the reason, it may be associated with the smaller distance between explosion center and the steel pipe. Under the terrain conditions of positive/negative elevation difference, the blasting distance between the explosion center and the pipe increases due to the elevation difference increasing. The X-direction PVVs of the steel pipe under positive/negative elevation difference are relatively close. Moreover, X-direction PVV of the pipe under negative elevation difference is slightly larger (see Fig. 8a). With the increase of L, the attenuation trend of the Y-direction PVV of the pipe in the flat terrain is relatively gentle. It is also slower than that of the pipe under the terrain with positive and negative elevation difference (see Fig. 8b). In the case of the same elevation difference and horizontal distance, the topographic velocity of the steel pipe in the terrain with positive elevation difference is greater than that of the terrain with negative elevation difference (see Fig. 8b). The numerical results are consistent with the previous reports15,42,43. In conclusion, the vertical direction is the dominated showing a significant elevation amplification effect.

The amplification coefficient, which is the ratio of PVV of the steel pipe under the terrain with positive (or negative) elevation difference to that of the pipe in the flat terrain is introduced to further discuss the elevation effect of slope blasting. The variation curves of the amplification factor with the elevation difference increasing are shown in Fig. 9. Under the terrain with positive elevation difference, the amplification factor increases firstly, and then decreases with the elevation difference increasing(See Fig. 9). When the elevation difference is 3.1 m, the amplification factor is the largest, 1.998. Under the terrain with negative elevation difference, the amplification generally shows a gradual decline trend. When the initial elevation difference is 2.1 m, the amplification factor is the largest, 1.441. When the elevation difference is the same, the amplification factor of the pipe in positive elevation difference terrain is always greater than that in negative elevation difference terrain. This means that the amplification effect is more obvious in the terrain with positive elevation difference.

Fig. 9
figure 9

Variation curve of the amplification factor with elevation differences.

Full size image

Regression analysis

Seven groups of simulation tests were conducted to further analyze the PVV of the steel pipe under the terrain with positive and negative elevation difference. The explosive quantity was fixed in the model, and the horizontal distances and elevation differences were changed. Figure 10 shows the regression line of PVV of the steel pipe under the conditions of flat terrain by using the Sadovsky’s empirical formula.

Fig. 10
figure 10

Regression line of PVV of the steel pipe under the flat terrain by using the Sadovsky’s empirical formula: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

The following empirical formula of PVV is obtained by sorting out the fitting results shown in Fig. 10.

Horizontal direction (R2 = 0.9279):

$${v_{\text{v}}}=19.17{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{1.66}}$$
(8a)

Vertical direction (R2 = 0.9247):

$${v_{\text{H}}}=1.73{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{0.93}}$$
(8b)

Regression analysis is carried out by using the Sadovsky’s empirical formula, and the fitting results are shown in Figs. 11 and 12, respectively.

Fig. 11
figure 11

Regression line of PVV of steel pipe under the conditions of positive elevation difference terrain by using the Sadovsky’s empirical formula: (a) X-direction velocity; (b) Y-direction velocity.

Full size image
Fig. 12
figure 12

Regression line of PVV of the steel pipe under the conditions of negative elevation difference terrain by using the modified Sadovsky’s empirical formula: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

As a sequence, one can obtain the following the empirical formula to predict the PVV of the steel pipe under the conditions of positive elevation difference terrain shown in Fig. 11.

Horizontal direction (R2 = 0.7595):

$${v_{\text{v}}}=18.04{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.597}}$$
(9a)

Vertical direction (R2 = 0.8290):

$${v_{\text{H}}}=9.97{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{1.805}}$$
(9b)

As a sequence, one can obtain the following the empirical formula to predict the PVV of the steel pipe under the conditions of negative elevation difference terrain shown in Fig. 12.

Horizontal direction (R2 = 0.99961):

$${v_{\text{v}}}=18.92{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.30}}$$
(10a)

Vertical direction (R2 = 0.9183):

$${v_{\text{H}}}=18.13{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.96}}$$
(10b)

In order to obtain a more suitable formula to predict PVV of the existing pipes and analyzing the elevation amplification effect of slope blasting with different elevations, regression analysis is also carried out by using the modified Sadovsky’s formula. The ratio of proportional charge and elevation difference to distance between blasting sources is taken as independent variable, and the PVV of the steel pipe is taken as dependent variable. The fitting results are shown in Figs. 13 and 14, respectively.

Fig. 13
figure 13

Fitting diagram of velocity of the steel pipe under terrain with positive elevation difference by using the modified Sadovsky’s empirical formula: (a) X-direction velocity; (b) Y-direction velocity.

Full size image
Fig. 14
figure 14

Fitting diagram of PVV of the steel pipe under terrain with negative elevation difference based on the modified Sadovsky’s empirical formula: (a) X-direction velocity; (b) Y-direction velocity.

Full size image

The fitting results are sorted out in Fig. 13 and the corresponding empirical formula is obtained:

Horizontal direction (R2 = 0.7721):

$${v_{\text{v}}}=9.2{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.2}}{\left( {\frac{H}{R}} \right)^{ - 0.2916}}$$
(11a)

Vertical direction (R2 = 0.843):

$${v_{\text{H}}}=14.55{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.017}}{\left( {\frac{H}{R}} \right)^{0.1767}}$$
(11b)

The fitting results are sorted out in Fig. 14 and the corresponding empirical formula is obtained:

Horizontal direction (R2 = 0.99965):

$${v_{\text{v}}}=14.29{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.125}}{\left( {\frac{H}{R}} \right)^{ - 0.1101}}$$
(12a)

Vertical direction (R2 = 0.9243):

$${v_{\text{H}}}=12.08{\left( {\frac{{{Q^{1/3}}}}{R}} \right)^{2.725}}{\left( {\frac{H}{R}} \right)^{ - 0.1848}}$$
(12b)

Prediction effect analysis

Table 5 illustrated the relative error of vibration velocity of the steel pipe in terrain with positive elevation difference. The average relative error of PVV in the horizontal direction of the pipes by using the modified Sadovsky’s empirical formula is 12.536%, which is less 13.218% than that by using the Sadovsky’s empirical formula (see Table 5). Moreover, the average relative error of PVV in the vertical direction of the pipes by using the modified Sadovsky’s empirical formula is 7.593%, which is less 8.174% than that by using the Sadovsky’s empirical formula (see Table 5).

Table 6 illustrated the relative error of vibration velocity of the steel pipe in terrain with negative elevation difference. The average relative error of PVV in the horizontal direction of the pipes by using the modified Sadovsky’s empirical formula is 1.151%, which is less 1.165% than that by using the Sadovsky’s empirical formula (see Table 6). Moreover, the average relative error of PVV in the vertical direction of the pipes by using the modified Sadovsky’s empirical formula is 8.509%, which is less 8.539% than that by using the Sadovsky’s empirical formula (see Table 6).

In conclusion, the modified Sadovsky’s empirical formula is more suitable for analyzing the influence of the elevation effect of slope blasting and predicting the PVV of the buried steel pipes under slope blasting load.

Table 5 Relative error of vibration velocity of the steel pipe in terrain with positive elevation difference.
Full size table
Table 6 Relative error of vibration velocity of the steel pipes in terrain with negative elevation difference.
Full size table

Summary and conclusions

  1. 1.

    Compared with the flat terrain, PVV of the steel pipe had the manifest elevation effect during slope blasting process. The elevation has both amplification and attenuation effect on the BV of the steel pipe. The elevation amplification effect is significant in the vertical direction of the steel pipe.

  2. 2.

    Increasing the horizontal distance (or elevation) difference, PVV of the steel pipe decreases faster than that under the flat terrain. Under the same elevation difference, PVV of the steel pipe in positive elevation difference terrain is greater than that in negative elevation difference terrain.

  3. 3.

    The amplification factor of the steel pipe increases firstly and then decreases with the elevation difference increasing under the terrain with positive elevation difference. The amplification factor of the steel pipe under the terrain with positive elevation difference is always greater than that of the same negative elevation difference, and the elevation effect is more significant.

  4. 4.

    Compared with the fitting results, the modified Sadovsky’s empirical formula is more suitable for analyzing and predicting the influence of the elevation effect of slope blasting on the buried steel pipes.

It is pointed out that the present study firstly investigated the influence of the elevation effect of slope blasting on the PVV of the buried steel pipes. In view of the complexity of the dynamic flow in the pipes, the limitation of blasting construction conditions, the present study does not consider the influence of the dynamic flow and blasting construction conditions such as slope angle. In follow-up research, it is necessary to carry out the relevant research to meet the diversity of the actual situation.