Introduction

Based on the physical characteristics of the ore body itself and artificial induction, the technical activity of the block caving method mining process creates a pull-down space through rock drilling and blasting at the bottom of the ore block, causing changes in the geological structure1, resulting in the collapse of the ore rock above it and the formation of a surface subsidence. The increase in the mining airspace leads to the expansion of the collapse area. The surface subsidence problem induced by large-scale mining is bound to have a series of negative impacts on the environment and society2. As the largest mine with block caving method in China, Pulang Copper Mine in the north-east of Shangri-La County, Yunnan Province, China, has serious surface subsidence problems, with the largest block caving height of the ore body in the middle section of the first mining up to 370 m, and the average block caving height of 280 m. In recent years, with the advancement of the mining, the subsidence area has been expanding, which has led to the destabilisation of the surrounding buildings, and the depletion of the ore has been elevated, the bottom structure is seriously deformed by stress concentration, and the risk of underground mud and rock mass disaster is increasing. Therefore, how to achieve effective prediction of mining-induced surface subsidence will be an urgent problem to be solved3,4.

This paper focuses on the prediction of surface collapse by subsidence variables under block caving method mining conditions. Among the common variables are maximum subsidence height and subsidence area. The maximum subsidence height delineates the utmost vertical alteration during ore body collapse, while the subsidence area delineates the progressive stage-by-stage extent of surface subsidence. Currently, surface subsidence prediction methods can be broadly classified into four categories: empirical, experimental, functional and computational. Where the empirical method is based on measured data and empirical formulas for similar scenarios for estimation5. The experimental method predicts surface subsidence by acquiring a range of complex physical parameters, such as lithological characteristics and force conditions, followed by numerical simulation to elucidate the mechanism of surface subsidence6. Functional methods use mathematical probability to explain real engineering geological events, e.g. probability integral method7,8, Knothe function9, etc. The above three methods depend on the geological structure of the study area, and there is a gap between the predicted and actual values obtained, which is not easy to promote. The computational method collects data through mapping and uses it to predict surface subsidence using the scientific method10. mapping technology, new surveying and mapping technology gradually replace the conventional measurement methods to extract the information of surface settlement variables, such as INSAR11, LIDAR12, GNSS13 and UAV aerial surveying methods14, etc., and the above monitoring methods have different defects in the process of monitoring the mining area, which are not adapted to the research scenario of this paper. Among them, although INSAR technology has the characteristics of large scene and all-weather monitoring, the subsidence displacement in the measurement area is too large, the method relies on the SAR wavelength to monitor the subsidence displacement, and some of the monitoring points are unable to detect the displacement change between the two imaging events15, which makes the method more suitable for tracking the settlement which is relatively slow and with small deformation16. LIDAR needs to have a clear line of sight between the sensor and the ground, and scanning in collapsed areas is “blacked out”17. Individual GNSS monitoring points are expensive and complex to install, and a progressively expanding subsidence zone may destroy established GNSS monitoring points18. Based on the instability of the geological formations in the survey area and the lag in surface settlement that makes the collapse zone inaccessible19, traditional UAV aerial surveying methods will not be able to perform aerial triangulation calculations through the ground control point (GCP)20. Moreover, these methods are susceptible to errors induced by factors like seasonal variations and lighting conditions21,22, leading to inadequate data alignment precision23. Therefore, based on real-world scenarios, how to monitor the surface subsidence characteristics for each time period without travelling to the site, while ensuring a high level of accuracy, is an important part of predicting surface subsidence. Nowadays, computer technology is developing rapidly, and computational methods using machine learning algorithms for data mining have become the most widely used for surface collapse prediction, such as Random Forests (RF)24,25, Support Vector Machines (SVM)26, Convolutional Neural Networks (CNN)27, Long- and Short-Term Memory Networks (LSTM)28,29, etc. The above algorithms have different application scenarios, using a single model to deal with the scenarios in this paper is not applicable, for example, RF is not suitable for classification and regression problems of low-dimensional data (data with few features), and it cannot provide continuous output values, and is not suitable for solving time series problems30. SVM is sensitive to missing values and is not effective in sample imbalance problems31. CNN is not good at dealing with complex long term sequence prediction problems32. LSTM can capture the dependency of long-term sequences but is not good at dealing with the key information of spatial patterns33.

Accordingly, this paper utilises a computational method for surface subsidence prediction. we propose a two-stage network structure based on the UAV oblique photography method, integrating the Prediction Integral Method (PIM) with a multilayer recurrent neural network (RNN). In terms of data acquisition, in order to solve the problem of surface collapse issues that make the survey area unavailable, we used a geo-alignment method that does not require GCP instead of the traditional UAV aerial survey method34, but the systematic error and accuracy control of this alternative is still a problem for this technology, so we performed checkpoint verification and quantitative analysis of the aerial survey model to ensure its reliability. In terms of data mining, in order to overcome the problem of lack of consideration of the physical mechanism of surface subsidence in the computational method, we use PIM fusion neural network to establish the basic model, and to solve the problem of long time series prediction and data length inconsistency, this paper outputs the subsidence variables through “graph model + RNN”. The network structure considers the impact of reducing special cover composition on surface subsidence features in the PIM and enhances the multivariate RNN to achieve precise monthly predictions of maximum subsidence height and subsidence area. Initially, we introduce the factors influencing surface subsidence and data collection process. Subsequently, we present the prediction method of FIMF-RNN, outlining its basic model and network structure. Finally, we conduct comprehensive validation and analysis using surface data from the Pulang copper mine spanning 2018–2020.

Surface subsidence analyses

This paper concentrates on surface subsidence within block caving method mining environments. This subsection outlines the mining process and factors influencing surface subsidence resulting from this mining method.

Mining process

In the block caving method of mining, the ore body, under the influence of gravity and stress, collapses naturally, relying on either natural nodal fissures or fractures induced by artificial fracturing. The primary mining process involves four steps: opening, mining preparation, undercutting, and ore drawing. Over time, as the undercut workings are excavated, the overlying ore body continuously subsides until it reaches the surface, resulting in the formation of an extensive mining area resembling an open-pit mine. Figure 1 illustrates the division of surface subsidence in block caving method mining into several zones: caved rock zone, fracture zone, and continuous subsidence zone.

Fig. 1
figure 1

Schematic diagram of the block caving method. It demonstrated the natural disintegration method of mining and modelled a multiple funnel ore drawing.

Full size image

Factors affecting

The evolutionary mechanism of surface subsidence induced by the block caving method is highly complex and necessitates multifactorial analysis utilizing multi-scale monitoring data, such as surface elevation monitoring35, micro-seismic monitoring36, TDR37, and borehole monitoring38. These influencing factors can be broadly categorized into internal and external factors. Internal factors primarily relate to the collapsible coefficient of the ore rock in the study area and the flow of the ore rock during breakage. These issues can be addressed through simulation of the collapse process using mathematical models to determine correlation coefficients, including the subsidence coefficient, angle of break, radius of influence, angle of propagation of mining influence, and the size of the ore column. External factors mainly examine the impact of artificial mining progress and weather on collapse during the ore drawing process. Consequently, subsidence prediction based on internal collapse causes and simulated ore drawing experiments involves introducing stochastic medium theory to construct a multi-funnel model of ore drawing, as depicted in Fig. 1. Furthermore, we investigate the influence of external factors on surface subsidence by varying ore drawing quantity and undercut area.

Analysis of internal factors

Based on the block caving method, surface subsidence arises from undercutting and ore extraction. As the hydraulic radius of the exposed surface increases, it initiates the gradual collapse of ore rock in non-caving-through areas. The block caving process typically comprises four phases: preliminary undercutting, initial caving, caving development, and caving through the surface. These phases directly influence surface subsidence evolution. Surface subsidence, primarily influenced by fault fracture zones, follows a distinct process. As undercutting progresses, fault fracture zones disintegrate, leading to upward subsidence pits. This process may induce faulting, resulting in secondary tectonic fissures and additional subsidence pits. Moreover, geological conditions significantly impact surface subsidence, which can be quantified through regional cavability analysis of ore rock and fracture angle assessment. In the first mining area of the Pulang copper mine, ore rock cavability falls within the middle to upper range. Ore rock cavability predominantly corresponds to III and IV avalanche zones (according to the Laubscher cavability classification)39, comprising 77.14% and 21.96%, respectively40. The ore rock fragmentation is medium to fine. Empirical estimations suggest a chipping angle ranging from 67° to 85°41.

Analysis of external factors

The external factors influencing subsidence can be classified as follows: (1) Undercut area. Undercutting involves creating an underground void to facilitate block caving and ore extraction42. The extent of the undercut area influences the rate of caving. Monthly data on the undercut and subsidence areas at the Pulang copper mine from 2018 to 2020 were analyzed, as illustrated in Fig. 2a. Generally, the subsidence area exceeds the undercut area, indicating a positive correlation. (2) Underground ore drawing quantity. This metric is pivotal in mining operations. Figure 2b demonstrates a lag in the subsidence area’s response to changes in ore drawing quantity. (3) Rainfall. The Pulang copper mine’s surface comprises a significant portion of the fourth series moraine layer, with a thickness ranging from 10 to 40 m. Intense rainfall during the wet season mobilizes the moraine layer and weathered rock debris into the subsidence pit, exacerbating collapse. Consequently, subsidence during the rainy season surpasses that in the dry season, even with consistent ore drawing quantities. During the 3-year period of 2018–2020, the annual precipitation in the mining area is 680.6 mm, 524.2 mm and 657.9 mm respectively, of which the rainfall from May to October occupies 87.1% of the whole year. Figure 2c indicates the relationship between monthly rainfall and subsidence area, from which it can be seen that the dry and rainy seasons are obvious in the mining area, but the subsidence area does not change abruptly with rainfall, but only increases slowly with increasing rainfall, and is slowly less with less rainfall. (4) Surface backfilling quantity. Backfilling, a surface management measure, mitigates subsidence by filling voids created by collapse43. This explains instances where subsidence values register negatively in statistical analyses. In Fig. 2d, it can be seen that from June to October each year, the amount of backfill is 0. This is because the amount of rainfall increases during this period, and the amount of mud increases, ranging from 300 to 9500 m3 during the period, in which the northwest ore chute of the survey area is prone to mudslides, and the safety hazard is huge. At the beginning of each year, there is a clear negative correlation between the amount of backfill and subsidence area, but this relationship is not prominent during the mid-year period. This is due to the fact that during the middle of the year, the surface of the mine area is washed with rainwater, and the mine area is protected by appropriate drainage, which affects the subsidence of the surface. During the end of the year, the negative correlation is visible due to the relative dryness of the surface and the increased ore drawing amount.

Fig. 2
figure 2

Influence of external factors on subsidence, (a) Correlation analysis between undercut and subsidence area, (b) Correlation analysis between ore drawing quantity and subsidence area, (c) Correlation analysis between rainfall and subsidence area, (d) Correlation analysis between backfilling amount and subsidence area.

Full size image

Materials and methods

Study area

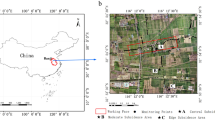
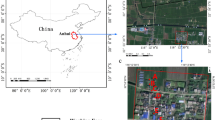
As shown in Fig. 3, this study focuses on the Pulang copper mine area in Yunnan Province, which is currently the largest mine in China utilizing the block caving mining method. Located in the northeast of Shangri-La County, Diqing Tibetan Autonomous Prefecture, northwest Yunnan Province, the mine area is situated 72 km from the city of Shangri-La, under the jurisdiction of Gezanxiang, Shangri-La County. The altitude of the mining area ranges from 3520 to 4569.6 m. This research specifically examines the initial mining area of the mine, characterized by steep terrain and the propensity for collapse pits to trigger mudslides and other disasters. Manual monitoring in such conditions poses significant safety risks, underscoring the importance of developing an accurate and operationally convenient surface subsidence prediction method for this region.

Fig. 3
figure 3

Study area and ___location of the mine. The mine area can be divided into mining site, ore-processing plant, and tailings reservoir, which ponds to Gerzanxiang. This map was created using Arcmap (version 10.7), a desktop component of Esri’s ArcGIS product family. The raw data of this map is the 2023 map of Yunnan Province, China. URL: https://yunnan.tianditu.gov.cn/MapResource.

Full size image

Remote sensing data

Data collection

Nowadays, the mainstream strategy of UAV oblique photography is to ensure model accuracy by RTK44, PPK45 and GNSS + PPK46,47. Study shows that GCP deployment seriously affects the accuracy of UAV aerial surveys48. When there are no conditions to establish GCPs, people usually calculate the compensation error values or use combined positioning methods instead of direct geographic alignment, for example, literature49 uses multiple GNSS base stations to reduce the systematic error of elevation data to meet the accuracy requirements of aerial surveys. Literature50 conducted two flights to establish a dual grid to eliminate the system elevation error and improve the accuracy of aerial surveys without image control points. Literature51 used a GCP with the NRTK signal disconnected and performed post-process kinematics (PPK). We use a kind of NRTK + PPK method for acquisition, which can be corrected in real time and solved better compared to the PPK method. Its basic process is shown in Fig. 4, which is the process of getting Point of Sale (POS) data by NRTK, getting a brand-new POS by PPK, and performing 3D modelling.

Fig. 4
figure 4

Flowchart of the telematic low-altitude remote sensing methodology (NRTK + PPK).

Full size image

The network RTK system, depicted in Fig. 4, involves a UAV obtaining real-time dynamic differential POS information from the network carrier phase via multiple Continuously Operating Reference Stations (CORS) established regionally. However, this localization technique is susceptible to exposure point delay errors52. The exposure delay adjustment model is typically defined as follows:

$$\left. {\left. {\left[ {\begin{array}{*{20}c} x \\ y \\ { - f} \\ \end{array} } \right] = \lambda R^{T} \left( {\left[ {\begin{array}{*{20}c} X \\ Y \\ Z \\ \end{array} } \right]} \right. - \left( {\left[ {\begin{array}{*{20}c} X \\ Y \\ Z \\ \end{array} } \right]} \right._{GPS} + \left[ {\begin{array}{*{20}c} X \\ Y \\ Z \\ \end{array} } \right]_{V} * \Delta t - R\left[ {\begin{array}{*{20}c} {x_{0} } \\ {y_{0} } \\ {z_{0} } \\ \end{array} } \right]_{GPS} } \right)} \right)$$
(1)

where the matrices \(\left[ {\begin{array}{*{20}c} x & y & { - f} \\ \end{array} } \right]^{T}\), \(\left[ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right]^{T}\), \(\left[ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right]_{GPS}^{T}\), \(\left[ {\begin{array}{*{20}c} {x_{0} } & {y_{0} } & {z_{0} } \\ \end{array} } \right]^{T}\) and \(\left[ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right]_{V}^{T}\) represent the coordinates in the image spatial coordinate system, coordinate value of the image point in the auxiliary coordinates of the image space, the GPS coordinates of the camera position at the moment of exposure, the coordinates of the GPS antenna phase center, and the velocity vector of the UAV, respectively. λ is the offset parameter of the projection coefficients in the solution process, RT is the transpose matrix, and Δt denotes the exposure delay time. According to Eq. (1), shorter exposure times lead to higher accuracy when the orthogonal transformation matrix R of the outer orientation elements remains constant. In cases where there is no ground control point (GCP) available for correction, connecting the camera shutter to a flash trigger can enhance synchronization accuracy between the GPS differential module and the camera. In Fig. 4, the typical process for updating POS data using PPK involves calculating the ambiguity of the entire week using the initialized OTF (On The Fly) and establishing the relative position relationship by linearly combining the GNSS signals from the UAV with the ground reference receiver information. This forms a virtual carrier phase observation. At any given time, the observation equations for the reference station \(a\) and UAV \(b\) for a satellite are as follows:

$$\sigma_{a}^{i} = \frac{f}{c}\left( {\sqrt {\left( {X^{i} - X_{a} } \right)^{2} + \left( {Y^{i} - Y_{a} } \right)^{2} + \left( {Z^{i} - Z_{a} } \right)^{2} } - \left( {V_{ion} } \right)_{a}^{i} - \left( {V_{trop} } \right)_{a}^{i} } \right) + fV_{ti} - fV_{ta} - N_{a}^{i}$$
(2)
$$\sigma_{b}^{i} = \frac{f}{c}\left( {\sqrt {\left( {X^{i} - X_{b} } \right)^{2} + \left( {Y^{i} - Y_{b} } \right)^{2} + \left( {Z^{i} - Z_{b} } \right)^{2} } - \left( {V_{ion} } \right)_{b}^{i} - \left( {V_{trop} } \right)_{b}^{i} } \right) + fV_{ti} - fV_{tb} - N_{b}^{i}$$
(3)

where \(\sigma_{a}^{i}\) and \(\sigma_{b}^{i}\) denotes respectively the carrier phase observation of a and b for satellite \(i.\)\(\left( {V_{ion} } \right)_{a}^{i}\) and \(\left( {V_{trop} } \right)_{a}^{i}\) denote the ionospheric delay and tropospheric delay of the path from \(a\) to satellite \(i\); \(\left( {V_{ion} } \right)_{b}^{i}\) and \(\left( {V_{trop} } \right)_{b}^{i}\) denote the ionospheric delay and tropospheric delay of the path from \(b\) to satellite \(i\). \(V_{ta}\), \(V_{tb}\) and \(V_{ti}\) is the clock difference of \(a\), \(b\) and \(i\). \(N_{a}^{i}\) and \(N_{b}^{i}\) is the whole-week ambiguity of the carrier phase observation of \(a\) and \(b\) for satellite \(i.\)\(\left( {\begin{array}{*{20}c} {X^{i} } & {Y^{i} } & {Z^{i} } \\ \end{array} } \right),\)\(\left( {\begin{array}{*{20}c} {X_{a} } & {Y_{a} } & {Z_{a} } \\ \end{array} } \right)\) and \(\left( {\begin{array}{*{20}c} {X_{b} } & {Y_{b} } & {Z_{b} } \\ \end{array} } \right)\) denote the spatial position of satellite \(i\) as well as \(a\) and \(b,\) respectively, at that moment in time. Also, \(f\) is the carrier frequency and \(c\) is the speed of light. Subtracting from Eqs. (2) and (3) yields the single-difference observation \(\sigma_{ab}^{i}\), which represents the difference between \(a\) and \(b\)'s observations of satellite \(i\). Similarly, the value of the single-difference observation \(\sigma_{ab}^{j}\), which is expressed as the difference between \(a\) and \(b\)'s observations of satellite \(j\), can be obtained. Subtracting the two single-difference observations yields Eq. (4):

$${\Delta }\sigma_{ab}^{ij} = \frac{f}{c}(\rho_{ab}^{ij} - (V_{ion} )_{ab}^{ij} - (V_{trop} )_{ab}^{ij} ) - N_{ab}^{ij}$$
(4)

where \(\Delta \sigma_{ab}^{ij}\) denotes the double-difference observation of satellite \(i\) and \(j\) for \(a\) and \(b\).\(\rho_{ab}^{ij}\) denotes the difference between the spatial distances of \(b\) and \(a\) to satellite \(j\), respectively, minus the difference between the spatial distances of \(b\) and \(a\) to satellite \(i\), respectively. \((V_{ion} )_{ab}^{ij}\), \((V_{trop} )_{ab}^{ij}\) and \(N_{ab}^{ij}\) represent the difference between the ionospheric delay, tropospheric delay and whole-week ambiguity of the carrier phase observation of \(b\) and \(a\) to satellite \(j\), respectively, minus the difference between the ionospheric delay, tropospheric delay and whole-week ambiguity of the carrier phase observation of \(b\) and \(a\) to satellite \(i\), respectively. According to Eq. (4), the simultaneous observation of 5 satellites by \(a\) and \(b\) gives 10 double-difference observation equations for 2 calendar elements, exceeding the number of unknowns. Therefore, completing the solution requires the simultaneous observation of at least 2 calendar elements or 4 or more satellites.

Data processing

This study employed a Pegasus multi-rotor E2000S UAV equipped with a sensor size of 23.5 × 15.6 mm (aps-c), operating at an average flight speed of 14 m/s. The UAV utilized a fixed-focus single lens of 25 mm without image control points. The flight path extended approximately 50 m from the ranging line, designed to prevent flight phenomena leakage. Aligning with the north–south measurement area, the flight path ran parallel to map contour lines, with an east–west direction layout. Take-off occurred near the office area at an altitude of 3720 m, with a reference station set adjacent for simultaneous GNSS static observations during aerial survey. The take-off point was positioned 1.5 km from the farthest survey area point, with a flight altitude of 500 m, based on a maximum altitude of 4100 m in the surface collapse area. Two sorties were conducted, totaling a flight time of 25 min. For instance, on December 17, 2019, 1326 aerial photographs were captured, yielding 1325 valid image datasets. A one-time aerial triangulation pass rate of 71.8% was achieved (952 fixed solutions and 373 single-point solutions). Figure 5 illustrates aerial triangulation survey views, indicating a maximum position uncertainty of 5.54 m and an average of 0.08 m. The minimum and maximum number of photographs per connection point were 3 and 136, respectively, with an average of 6 tie points per photograph. The average reprojection error stood at 0.37 pixels, while the average resolution was 0.03 m/pixel. As depicted in Fig. 6, the southwest edge of the model exhibits high positional uncertainty, warranting manual exclusion of this region.

Fig. 5
figure 5

Visualization of the quality of aerial triangulation, which illustrates various metrics involved in the aerial triangulation calculation. In this picture, a represents the distribution of the degree of uncertainty in the position of the connection point; b denotes the number of photos taken of the observed connection point; c indicates the distribution of reprojection error; and d signifies the resolution of the connection points.

Full size image
Fig. 6
figure 6

Map of inspection points. We set up 12 GTPs and analysed the accuracy of the model by evaluating the metrics.

Full size image

Evaluation metrics of the model

To address the challenge of observing inaccessible areas, the model is constructed using the aforementioned positioning technology. Additionally, it must adhere to geographic information engineering specifications and undergo accuracy evaluation. Evaluation can be performed using orthophotos or ground test points (GTPs) collected from the model. The error calculation formula is provided below:

$$R = \sqrt {\frac{1}{n}\mathop \sum \limits_{n}^{i = 1} \left| {D_{{i{\text{mage}}}}^{i} - D^{i} } \right|^{2} }$$
(5)

where \(D_{image}^{i}\) denotes the orthophoto of the No. \(i\) GTP or the measured value in the model, \(D^{i}\) denotes the measured value of the No. \(i\) GTP. \(R\) stands for root mean square error (RMSE), \(n\) is the number of GTPs.

As depicted in Fig. 6, we selected 12 ground test points (K1–K12) within the Yunnan Pulang Copper Mine’s collapse area. These points are relatively stable and resistant to collapse, ensuring the accuracy of our long-term detection model. Figure 7 illustrates the error of these ground test points. The error for DX, DY and DZ are carefully controlled, ranging from − 6.25 to 5.93 cm. Specifically, the error values for \(R_{x}\), \(R_{y}\) and \(R_{z}\) are 2.493 cm, 2.732 cm and 3.448 cm, respectively, satisfying the specifications of geographic information engineering.

Fig. 7
figure 7

Error map based on X, Y, Z direction, denoted by DX, DY and DZ respectively.

Full size image

Methodology

This paper employs a prediction method based on FIMF-RNN for UAV oblique photography. This subsection outlines the fundamental model of FIMF-RNN and its network architecture. FIMF-RNN is a novel network structure created by merging the traditional PIM prediction model with the multi-module RNN model. The network structure of FIMF-RNN comprises three sections: the acquisition layer, the maximum subsidence height output layer, and the subsidence area output layer.

Predictive modelling

This paper utilizes the FIMF-RNN network architecture to predict the maximum subsidence height through multiple feature superposition, followed by determining the subsidence area. Specifically, we employ the PIM to simulate surface subsidence in the mine, calculating the released height and fitting to obtain the surface features post-subsidence. These features are then inputted into various modules of the RNN for feature fusion, with the RNN subsequently predicting the maximum subsidence height and subsidence area through different modules. The ensuing section elaborates on the PIM model and the graph model within this structure.

  1. (1)

    PIM model

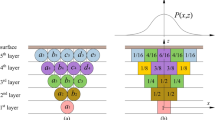
Mining subsidence prediction involves quantitatively studying the distribution pattern of rock and surface movement influenced by mining over time and space. In this study, parameters of the ore drawing-induced surface subsidence prediction model (such as subsidence coefficient, maximum influence angle tangent, depth, mining influence propagation angle, pillar size, etc.) are selected. A numerical model based on the probability integral method and stochastic medium theory is employed for subsidence prediction, as depicted schematically in Fig. 8.

Fig. 8
figure 8

Probabilistic integral method subsidence prediction model diagram.

Full size image

Where \(W_{0}\) denotes the maximum subsidence, \(m\) denotes the thickness of the formation,\(q\) denotes the subsidence factor, \(\cos \alpha\) denotes the cosine of the dip of the formation, where \(\alpha\) is the dip angle of the formation. \(W\) denotes the settlement value. \(D_{1}\) and \(D_{2}\) are the dimensions of the extent of the mining workings. \(r\) is the radius of the main influence, where \(\tan \beta\) is the tangent of the maximum influence angle. \(H\) is the height difference in elevation between an arbitrary point \(A(x,y)\) on the surface to be calculated and a micro-element \(B(s,t)\) on the ore layer. The equation for calculating the subsidence of \(A(x,y)\) is:

$$W_{0} = mq\cos \alpha$$
(6)
$$r = H/\tan \beta$$
(7)
$$W(x,y) = W_{0} \int\nolimits_{0}^{{D_{1} }} \int\nolimits_{0}^{{D_{2} }} \frac{1}{{r^{2} }}e^{{ - \pi \frac{{(x - s)^{2} + (y - t)^{2} }}{{r^{2} }}}} dtds$$
(8)

In addition, the angle of propagation of mining influence \(\theta = 90^{^\circ } - k\alpha\), \(k\) is taken as 0.6–0.8. The inflection point offset \(S_{0}\) indicates the offset distance of the inflection point due to the cantilevering effect of the ore rock layer above the ore stratum, which is not reflected in Eq. (8) and needs to be considered in the calculation. The superscript "°" in the upper right corner of the relevant parameter indicates the value of movement and deformation of limited mining, and the parameter \(b\) is the coefficient of horizontal movement.\(A(x,y)\) in the tilt \(i(x,y,\varphi )\) and curvature \(k(x,y,\varphi )\) along the direction of \(\alpha\), the horizontal movement \(u(x,y,\varphi )\) as well as the horizontal deformation \(\varepsilon (x,y,\varphi )\) are respectively:

$$i(x,y,\varphi ) = \frac{1}{{W_{0} }}[i^{^\circ } (x)W^{^\circ } (y)\cos \varphi + W^{^\circ } (x)i^{^\circ } (y)\sin \varphi ]$$
(9)
$$k(x,y,\varphi ) = \frac{\partial i(x,y,\varphi )}{{\partial x}}\cos \varphi + \frac{\partial i(x,y,\varphi )}{{\partial y}}\sin \varphi$$
(10)
$${\mathcal{U}}(x,y,\varphi ) = bri(x,y,\varphi )$$
(11)
$$\varepsilon (x,y,\varphi ) = brk(x,y,\varphi )$$
(12)

The proposed method forecasts surface subsidence cycles using a 3.2 oblique photography model, termed the initial surface, as input. The height of released ore pillars is determined through calculations involving the number of drawpoints and ore drawing quantity for each cycle. Subsequently, after conducting subsidence prediction calculations based on these parameters, the model outputs the corresponding subsidence value for the surface, referred to as the resultant surface. For subsequent predictions, the model takes as input the resultant surface from the previous iteration, along with the planned ore drawing quantity and drawpoints, until reaching the planned drawing quantity cycle. This process yields the final subsidence after the surface model and the maximum subsidence height.

  1. (2)

    Graph model

The graph model is a predictive model that utilizes graph neural networks to handle time series data53. Due to the complexity of the mine environment and work plans, the records for undercut area and ore drawing quantity exhibit discontinuity. The graph model excels at handling such heterogeneous data54. Additionally, it can predict cave-ins under varying ore drawing quantities, fully learn the characteristics of different cave-in moments, and explore the nonlinear correlation between ore drawing quantity and cave-in quantity55. Unlike traditional neural networks, this model emphasizes the attention mechanism of the graph unit structure, making the features more prominent56. It also incorporates recurrent neural networks for feature iteration to accomplish comprehensive feature extraction. Each drawpoint can be viewed as an independent graph structure, with each feature acting as a node unit. It aggregates neighborhood information of the nodes57 through graph convolution operations to obtain the feature of a point, as depicted in Eq. (13):

$$Z = f(X,A) = {\text{SoftMax(}}\hat{A}{\text{Re}} LU(\hat{A}XW^{(0)} )W^{(1)} )$$
(13)
$$\hat{A} = \tilde{D}^{ - 1/2} \tilde{A}\tilde{D}^{ - 1/2}$$
(14)

where \(X\) denotes the feature matrix, \(W^{(0)}\) denotes the number of weights in the first layer convolution,\(W^{(1)}\) denotes the number of weights in the second layer convolution, and ReLU and SoftMax are the activation functions. Equation (14) represents the process of normalizing the adjacency matrix by left and right multiplication and updating the adjacency matrix which is used to balance the contribution of nodes with different degrees to the information aggregation. Where \(\hat{A}\) denotes a variant of the adjacency matrix, which can be understood as its updated value.\(\widetilde{A}\) denotes the adjacency matrix and \(\widetilde{D}\) denotes the degree matrix. Combined with the self-attention mechanism to weight the adjacency matrix, to get no longer in the form of a matrix whose matrix elements are 0 or 1, a brand adjacency matrix is obtained by the calculation of the attention weight of each neighboring node to that node. The formula for calculating the attention factor \(e_{ij}\) is shown in Eq. (15):

$$e_{ij} = a(Wh_{i} ,Wh_{j} )$$
(15)

where \(h_{i}\) and \(h_{j}\) represents the feature vectors of node \(i\) and \(j\) respectively, \(W\) is the node weight parameter.\(a\) is the attention parameter. Substituting Eqs. (15), (16) is obtained:

$$\alpha_{ij} = soft\max_{j} (e_{ij} ) = \frac{{\exp (e_{ij} )}}{{\mathop \sum \limits_{kV(i)} \exp (e_{ik} )}} = \frac{{\exp (a(Wh_{i} ,Wh_{j} ))}}{{\mathop \sum \limits_{{k{ \ncong }N(i)}} \exp (a(Wh_{i} ,Wh_{j} ))}}$$
(16)

\(\alpha_{ij}\) is the attention weight between node \(i\) and \(j\),\(\sum\nolimits_{k\varepsilon N(i)} {\exp (e_{ik} )}\) denotes the set of neighboring nodes of node \(i\).

Network architecture

The network architecture, depicted in Fig. 9 below, comprises several layers. The acquisition layer involves generating a 3D model from image data collected via UAV aerial surveys. Subsequently, a specific detection point is selected on the model or digital surface model (DSM), and both its detection point and the mining data gathered from each detection are utilized to establish the time-series dataset, serving as the input values for the subsequent two layers. The maximum subsidence height output layer, a result of the acquisition layer fused with PIM, employs the graph model to forecast the collapse value of each detection point’s subsidence. Finally, the subsidence area output layer, utilizing information from the collection layer as its input, predicts the subsidence area for each month using the LSTM network.

Fig. 9
figure 9

Three-layer network architecture of FIMF-RNN prediction methods. (a) Acquisition layer, (b) Maximum subsidence height output layer, (c) Subsidence area output layer.

Full size image
  1. (1)

    Acquisition layer

This study achieves comprehensive data collection and integration through the acquisition layer. Figure 9a illustrates this process. Firstly, utilizing the telematic low-altitude remote sensing method described earlier, a 3D model is constructed, followed by accuracy evaluation. Subsequently, information extraction is conducted on the subsidence zone, with the extracted data serving as ground truth for evaluating the accuracy of predicted values. Concurrently, time-series datasets concerning ore drawing points are established within the acquisition layer. For maximum subsidence height prediction, these datasets encompass ore drawing quantity, subsidence coefficient, column size, maximum impact angle, and release height of each drawpoint throughout the observation period. Regarding subsidence area prediction, the integration involves factors such as the number of drawpoints, maximum subsidence height, undercut area, and backfill volume per month, with the input for maximum subsidence height being derived from the output of the second layer.

  1. (2)

    Maximum subsidence height output layer

The collapse exogenous analysis reveals a significant influence of underground ore rock collapse and movement on subsidence, indicated by a generally positive correlation between ore drawing quantity and subsidence. Consequently, the maximum subsidence height predicted by the surface subsidence model for each cycle is positioned above the center of the released column model for that cycle. To achieve this, the ground point directly above the drawpoints serves as the detection point in each cycle. By assessing the subsidence height of each detection point, the extraction of the maximum subsidence height of the subsidence surface in each cycle is facilitated.

The input data for this layer comprises three components: the subsidence height of each detection point, the time-series dataset of drawpoints, and the drawpoint height derived from the PIM. While the first two components are comprehensively covered in the preceding discussion on the acquisition layer, the third component, representing the released height from the PIM, must be integrated into the graph structure as an eigenvector for each point within the recurrent network.

As depicted in Fig. 9b, the graph structure comprises nodes and edges. Node features are updated via the adjacency matrix, incorporating moment information into the input embedding, applying position embedding, and reinforcing the temporal sequence of nodes through position encoding. Edges update weight parameters through self-attention mechanisms between nodes, facilitating directional information transfer between connected nodes58. These edges can be linked to a fully connected network, mapping through cross-attention, effectively suppressing lower attention to derive weights between the nodes.

Within a single graph structure, feature information from individual time points is extracted, inter-moment data features are constructed using an RNN network structure, iterated through two layers of RNN network, and further enhanced through multi-head attention mechanisms. This process updates the overall weights of the graph structure’s features. The resultant output vector is then passed through a point-to-point feed-forward network for initial processing, followed by connection to a residual network for normalization. This process mirrors the encoder processing in transformers, aiming to provide a continuous representation of the input with attentional information, contributing to enhanced feature learning. The final output is computed by connecting to a fully connected network and conducting SoftMax regression, enabling accuracy evaluation against model values, with the maximum value selected as the output of the layer.

  1. (3)

    Subsidence area output layer

The SE (Squeeze-and-Excitation) attention mechanism processes this layer, followed by integration into the LSTM network structure for iterative computation. Subsequently, the subsidence area value obtained from the joint probability integration method undergoes normalization via the ResNet residual network. Finally, accuracy is assessed against real values to generate the output. The flowchart detailing this process is illustrated in Fig. 9c.

The SE attention mechanism is a module designed to perform an attention operation on the channel dimension, aimed at emphasizing the attention weight of features between channels while suppressing unimportant features. Its implementation typically comprises three steps: first, the Squeeze operation compresses each channel feature, maintaining the number of feature channels; next, global pooling converts each channel feature to a real value. Second, the Excitation activation calculates attention weights by mapping global features from two fully connected layers into a weight vector, normalized using the sigmoid function. Finally, the attention weights are multiplied with the original features to generate new features, which are then fed into the LSTM network for time-series data feature extraction.

Following the LSTM network, the data undergoes convolutional processing to extract additional feature information and is then combined with the PIM output value. Subsequently, the PIM residual network, built upon the RNN output value, performs ResNet residual network normalization computation on the RNN output value and the combined output value. This process aims to filter the feature values, addressing the inherent error resulting from the two layers of regression operations on the RNN output value. The resulting set of subsidence area values is derived by fitting the PIM output value, which is integrated with the RNN output value, into the residual network calculation. This approach enhances feature extraction, mitigates errors stemming from multi-layer regression, and approximates the real value more accurately.

Results and analyses

This subsection presents the experimental results of our study. The workstation specifications include an Intel(R) Core i9-9900KF CPU @ 3.60 GHz, Interl64 Family 6 Model 158 Stepping 12, and an NVIDIA GeForce RTK 2070 SUPER GPU. The system is equipped with 64 GB of RAM. The PIM prediction model was developed using C++ on the Dimine platform, while the RNN implementation was carried out in Python.

Data sources

We compiled complete surface subsidence data spanning 35 months from February 2018 to January 2021, alongside corresponding mine release data. According to the data segment of the oblique photography survey, we can get the overall topography of the survey area. As can be seen in Table 1, the mine area is located in the alpine canyon area at an altitude of 3600–4500 m. The Pulang River Canyon on the west side of the mine area is at an elevation of 3200–3300 m, with a relative elevation difference of 1300 m. Above 4200 m is the Tibetan Plateau surface, where there are more gently sloping platforms with relatively gentle ground slopes. Below 4200 m there is strong cutting, with steep terrain slopes and large relative elevation differences. The gradient of the mountain slopes is generally 25°–35°, and the local sections form steep cliffs. The ground slope in most sections around the mine is close to the natural angle of repose of broken rocks (36.5°). The collapse area is distributed with collapse funnels and high and steep slopes with uneven slopes, and the slopes in the north and east have larger slopes, locally up to 50°–65°.

Table 1 Table of surface slopes in the survey area.
Full size table

As illustrated in Fig. 10, panels a, b, and c depict surface information on January 17, 2019, 2020, and 2021, respectively. To ensure the reliability of the extraction of subsidence variables using aerial survey methods, this paper uses 3D laser scanning and oblique photography methods to quantify the subsidence variables for each of the three months, which can be seen in Table 2. Figure 10-(1) presents a digital surface model (DSM), offering insight into basic survey area changes. Figure 10-(2) displays mesh data, revealing alterations in collapse pit distribution. Figure 10-(3) showcases an oblique photography model used for subsidence area measurement. Figure 10-(4) shows the surface point cloud model of 3D laser scanning.

Fig. 10
figure 10

Surface information extraction from February 2018 to January 2021, which allows monitoring of the actual surface, the size of the skylight groups, the subsidence area respectively and Laser-scanned surface model.

Full size image
Table 2 Values of subsidence variables in the survey area during some months, comparing the errors between the oblique photography measurement method and the LS method.
Full size table

Preprocessing

The outcrop level of the collapse area stands at 3720 m above sea level, marking the initiation of surface collapse at Pulang copper mine in the 12th month of production, specifically on February 16, 2018. Consequently, surface subsidence prediction by mine release commenced from February 17, 2018, with 121 active drawpoints at the onset, progressively increasing daily. Surface subsidence prediction intervals were set at one month. Initially, the actual number and volume of drawpoints for the month were inputted based on the collapse prediction cycle, with subsequent calculations fed into the following month’s projections. The size of the released pillar body was inputted to generate the model for the current cycle, with released height values obtained through simulation. Four time periods of the release column body model were chosen, as depicted in Fig. 11, illustrating the column body’s evolution.

Fig. 11
figure 11

Probabilistic Integration Method Based Modeling of Ore Release Pillars, this figure shows the column model for some months.

Full size image

Figure 11 shows the model of the released columns for each time period between 2 February 2018 and January 2021. From Fig. 11, it can be seen that in October 2018, the amount of ore released from the southwest corner of the survey area increased significantly; in June 2019, the amount of ore released from some columns in the western part of the survey area was zero, and the query of the release plan, at this time, the release points in this area were in the state of closure due to optimization problems; in October 2019, the east–west release plan of the survey area increased, and at this time, the height of the model’s east and west side of the columns increased; in June 2020, the number of the release points in the west corner of the survey area gradually increased number of drawpoints in the south-east corner of the survey area, and in August 2020 the number of drawpoints in the north-west corner is increased, which is reflected in the model as an expansion of the column in the north-west and south-east. Overall, the modelled extent of the released columns has been gradually extended in an east–west direction, which is consistent with the plan to increase the east–west deployment of the drawpoints at a later stage.

Unifying sequence length is necessary to determine matrix dimensions for predicting subsidence at each observation point. As of January 17, 2021, the maximum number of drawpoints is 473. Data spans from February 2018 to January 2021, observed monthly, totaling 35 time points. Eigenvalues represent drawpoint quantities, drainage, backfill, discharge grade, and discharge height (output from the discharge column model) at each drawpoint. This constitutes a matrix of dimensions [35,473,5]. Non-participating drawpoints were set to 0. Eigenvalues were iterated through the network, and regression operations were conducted to obtain maximum subsidence height values for each participating drawpoint corresponding to the detected points. The maximum subsidence height value per cycle was output through maximum pooling. This value, along with drawpoint count, undercut area, total drawdown, rainfall, and backfill, forms input features of dimensions 6,35 for subsidence area prediction in the output cycle.

Projections and analyses

The model prediction comprises three steps. Firstly, we compute the release height of each column using PIM. Next, we derive the subsidence value of each detection point by fitting the release height at each point. This prediction is determined by the PIM subsidence prediction model based on stochastic medium theory. It is known that \(m\), \(\alpha\) is known, \(W_{0}\) = 2.0, according to Eq. (6), it is derived that \(q\) is 0.76; when fully extracted, \(r\) is 1.25 times the point spacing of 0.16 \(W_{0}\) cm–\(W_{0}\) cm. According to Eq. (7), \(\tan \beta\) can be calculated and the value is 2.1; according to literature 59, the mineral rock relaxation coefficient \(K_{s}\) is 1.25. Figures 12, 13 and 14 display the subsidence cloud generated by this prediction result, illustrating the vertex subsidence situation in each cycle after simulation and plotting the contour lines. The vertex subsidence can be interpreted as the subsidence height of the detection point.

Fig. 12
figure 12

Surface subsidence values and modeling of subsidence surface from Feb 2018 to Mar 2019.

Full size image
Fig. 13
figure 13

Surface subsidence values and modeling of subsidence surface from Jan 2019 to Jan 2020.

Full size image
Fig. 14
figure 14

Surface subsidence values and modeling of subsidence surface from Jan 2020 to Jan 2021.

Full size image

Figure 12 depicts the monthly subsidence cloud maps from February 2018 to January 2019. Vertex subsidence gradually decreases from the central collapse area in all directions. Notably, the central area of Fig. 12-d and e showing a surge in the vertex subsidence with respect to Fig. 12-a, b, and c, the central area of Fig. 12-f showing a decrease in the vertex subsidence, and an expansion of the collapse area to the north, and the central areas of Fig. 12-h to k showing an Vertex subsidence value increases with the value of 4–5 m, and the degree of collapse gradually increases from the central region to the surrounding area; Fig. 13 represents the monthly subsidence cloud map from January 2019 to January 2020, in which the degree of subsidence is lower in Fig. 13-b and I, and the maximum vertex subsidence is maintained in the range of 3.9–6.3 m in the other months, and it can be seen in Fig. 13-f that, from June 2019 onwards, the maximum vertex subsidence gradually shifted to the north from the southern part of the central region; Fig. 14 represents the monthly subsidence cloud maps from January 2019 to January 2020, with the maximum vertex subsidence shifted to the east from Fig. 14-a to c, the subsidence is not significant in Fig. 14-d, the maximum vertex subsidence maintained at 4.8–6.3 m from Fig. 14-e to h, and the maximum vertex subsidence from Fig. 14-I to L shifted to the north-west with gradually decreasing values, but the overall extent of subsidence increased.

The maximum subsidence height values for each cycle and the distribution of subsidence locations for that cycle are depicted in Figs. 12, 13 and 14. However, the accuracy of these prediction results is insufficient, as they do not account for external factors such as weather rainfall and artificial backfilling, which influence surface subsidence. Therefore, these results are input into the RNN network for the second step of prediction. The training dataset and test dataset are divided in a ratio of 7:3. The training progress, illustrated by the variation of loss, is depicted in Fig. 15 below. It is crucial to ensure adequate training data to avoid uneven samples and insufficient model training, while also considering the potential noise from excessive training. Figure 15 indicates that the model converges between epochs 105 and 140. Hence, we choose to set the training epoch to 140, with a batch size of 35 per epoch. The training utilizes the Adam gradient descent algorithm, with an initial learning rate of 0.01, segmented scheduling.

Fig. 15
figure 15

Training loss variation. This process represents the prediction of collapse height values and subsidence area.

Full size image

Based on the fact that the aim of the second prediction step is to generate the value of the maximum subsidence height of the ground surface in each cycle, it is obvious that the error analysis of the resulting predicted values in sequence is not only a huge amount of work but also of little significance. We uniformly select six points to be analysed one by one, and select the maximum value of the obtained prediction value in each cycle as the maximum subsidence height value of the ground surface. Drawpoints are named using the “direction + number” convention. The specific steps are as follows: The data is divided into three batches for testing: from February 2018 to February 2019, from February 2019 to March 2020, and from March 2020 to January 2021. In each batch, two drawpoints are selected as new drawpoints. A comparative analysis of predicted subsidence values at detection points, PIM simulated subsidence values, and original values are plotted as time series graphs, as shown in Fig. 16. Integrating these points provides the cycle maximum subsidence height values, as shown in Fig. 18.

Fig. 16
figure 16

Time-series plot of detection points above the mine put-out site, where the drawpoints are N1-E10, S2-E9, S4-E4, S4-W2, S5-W4 and N4-E28.

Full size image

From February 2018 to February 2019, the subsidence height of N1-E10 is smaller than that of S2-E9, consistent with the distribution of apex subsidence in Fig. 12. From February 2019 to March 2020, S4-E4 and S4-W2, situated on the same horizontal penetrating vein and relatively close, exhibit similar changes in subsidence heights. From March 2020 to January 2021, N4-E28 demonstrates a continuous decrease in subsidence heights from September 2020 to December 2020, while S5-W4 shows a slow increase in subsidence heights during the same period, consistent with backfilling in the northeastern portion of the collapse area. Overall, the second-step prediction aligns more closely with real values relative to the first-step prediction. As shown in Fig. 17, the errors of six points are tabulated, and the prediction errors in this period range between − 0.6 and 0.5 m. Samples 1–12 represent the monthly settlement data in the corresponding time period, while samples 5–10 pertain to the rainy season, with slightly larger errors than samples 1–5. However, the overall error performance is satisfactory.

Fig. 17
figure 17

Plot of errors for each time period at the predicted detection point. Using monthly samples as records, we recorded 12, 13 and 10 continuous months in each of the three time periods.

Full size image

Figure 18 reveals that the PIM prediction results generally underestimate the original settlement values, particularly evident during the July–December period, coinciding with the region’s rainy season. In October–November 2018, the PIM + RNN algorithm and the PIM method existed with a maximum error of 1.328 m, and in June–July 2019, they existed with a minimum error of 0.02 m. The PIM + RNN algorithm’s accuracy in predicting the maximum subsidence height was 91.47%.

Fig. 18
figure 18

Maximum subsidence height prediction under fusion-based algorithm, compared with PIM prediction and original values.

Full size image

These obtained predictions of the maximum subsidence height for each cycle are then continued to the third prediction step, where the samples are the surface subsidence surfaces per month, yielding the prediction value of subsidence area per cycle. Comparative analysis is conducted between these predictions, PIM prediction values, and the real values, as depicted in Fig. 19. Notably, Fig. 19 illustrates a significant gap between the PIM prediction method and the real values from February 2018 to April 2019, a period characterized by artificial backfilling to decelerate surface collapse. The PIM + RNN prediction method, accounting for external factors, achieves an accuracy of 87.52%, demonstrating predictions more closely aligned with actual subsidence values.

Fig. 19
figure 19

Prediction of subsidence area based on fusion algorithm, compared with PIM prediction and original values.

Full size image

Comparison

We evaluated the fusion algorithm using three metrics: the coefficient of determination (R2), the root mean square error (RMSE), and the mean absolute percentage error (MAPE). The coefficient of determination assesses the model’s ability to explain the dependent variable, with values ranging from 0 to 1; higher values indicate better fit. RMSE measures the disparity between predicted and actual values, with smaller values indicating greater accuracy. MAPE indicates the overall performance of the model, with 0 representing a perfect fit and values exceeding 1 indicating poor quality. Table 3 presents a comparative analysis of these metrics across different model predictions.

Table 3 Comparison of experimental results of different prediction models.
Full size table

The three traditional machine learning algorithms in the table do not incorporate the putative height eigenvalues computed by the PIM simulation. Across all metrics, LSTM outperforms both the traditional model (ARIMA) and the random forest algorithm (RF). However, the FIM-RNN fusion algorithm demonstrates a 9.7% improvement in accuracy compared to LSTM, yielding an RMSE and a MAPE of 0.2282 and 0.0730, respectively.

Conclusion

In this paper, we propose a method that utilizes UAV oblique photography surveying to collect surface data from mines and employs the PIMF-RNN model for predicting surface subsidence. This approach offers effective data support for mitigating surface subsidence hazards associated with block caving mining methods. Moreover, our study explores additional applications of UAV oblique photography surveying techniques in mining operations, while also establishing a cost-effective and efficient process for surface subsidence prediction in mines. To evaluate the accuracy of our predictions, we analyze data from the Pulang copper mine in Yunnan. The main conclusions drawn from our study are outlined below.

  1. (1)

    We improved the RTK/PPK method to complete the measurement task when the study area is inaccessible. Using this method, the measurement error of oblique photography can be controlled within the range of − 6.25 to 5.93 cm, which is fully compliant with engineering specifications.

  2. (2)

    Traditional methods for predicting mine surface subsidence often overlook the combined influence of internal and external factors on surface collapse. In response, we propose a prediction model (PIM + RNN) that combines the probability integral method with deep learning. This model leverages daily drawpoints and learns from the results of PIM predictions. Compared to traditional PIM prediction methods, our approach demonstrates significant improvement in predicting surface subsidence at the Pulang copper mine. Specifically, we achieve a prediction accuracy of up to 91.42% for maximum subsidence height and up to 87.52% for subsidence area.

  3. (3)

    We converted the surface subsidence data and drawpoints data into graph data, encoded global information using graph neural networks, and integrated local information for analysis. This method effectively identifies and corrects heterogeneity within long time series datasets.

  4. (4)

    In the traditional LSTM framework for processing time series data, we incorporate a local attention mechanism and integrate the computational module with PIM results by introducing a residual network. This multi-module RNN structure effectively addresses the limitations of LSTM, such as insufficient memory for long sequence prediction and distortion in predictions caused by multi-layer regression.

  5. (5)

    There exists a correlation between the ore drawing quantity and the undercut area and the surface subsidence area. The average monthly ore drawing quantity varies in accordance with the fluctuation in the number of active drawpoints per month. However, there is a certain delay in the change of subsidence area concerning.

In addition, this paper is not scientific and systematic enough for the determination of the relevant parameters in the PIM, and its determination and optimisation is what needs to be researched in the next step, which is also a direction to improve the overall accuracy of the model.