Introduction

With the increasing development of society, the demand for energy is gradually growing. Solar energy, as an inexhaustible and sustainable green energy source, has been widely applied in various industries. Photovoltaic power generation, as an important application of solar energy, is influenced by the quality of photovoltaic panels, which plays a crucial role in its energy conversion efficiency. However, during the production process of photovoltaic (PV) panels, various defects inevitably occur due to equipment or human factors. As an essential component of the development of the PV industry, the defect detection of PV panels holds significant importance in promoting the advancement of PV energy1,2,3,4,5. Therefore, facing the huge market demand and strict quality requirements, the issue of photovoltaic panel defect detection in intelligent manufacturing becomes particularly important.

The task of PV panel defect detection is to identify the category and ___location of defects in EL images. As illustrated in Fig. 1, the common types of defects in PV panels include crack, finger interruption, black core, thick line, star crack, corner, horizontal dislocation, vertical dislocation, and short circuit often accompanied by complex background interference. However, defect detection in EL images requires highly specialized knowledge. For instance, misalignment or printing issues can lead to EL images that closely resemble vertical dislocation and horizontal dislocation defects. Similarly, disconnection or cell failure may result in appearances similar to short circuit defects. Generally, areas in the image with high brightness typically represent crystalline silicon regions with high conversion efficiency, while darker areas indicate defective regions with inactive and non-emitting light6. In addition to the actual defects, the busbars can also manifest as dark areas due to color influences, sometimes overlapping with the defects, further increasing the complexity of automatic defect detection in EL images of PV panels.

Fig. 1
figure 1

The most common types of PV pannel defect.

Full size image

Traditional methods have played an important role in surface defect detection. An improved anisotropic diffusion filter is presented in previous work7, which enhances the efficiency of the filtering strategy by employing an sigmoid transformation function for adaptive threshold processing. By filtering, significant edges are preserved while other less significant edges and areas are smoothed to achieve the purpose of image enhancement. Afterwards, a shape-based descriptor is used to establish a supervised learning strategy with Support Vector Machine (SVM). Dhimish et al.8 conducted a study that focused on using the Discrete Fourier Transform (DFT) for two-dimensional spectral analysis of EL images of solar cells. To improve the detection capability of cracks in solar cells, they adjusted the Fourier transform components in the intermediate frequency ___domain. They accomplished this by analyzing the geometric features of these binary images, being able to identify specific patterns or shapes associated with cracks in solar cells.

In recent years, convolutional neural networks (CNNs) have indeed achieved remarkable success in various fields leaning on their hierarchical structure and ability to capture local and global patterns. CNNs have demonstrated the capability to automatically learn relevant features from raw image data, unlike traditional computer vision algorithms that rely on handcrafted features requiring ___domain knowledge and manual engineering. This advantage has led to their widespread adoption in the photovoltaic (PV) production industry9,10,11,12.

However, existing methods face challenges in achieving a good balance between detection accuracy and efficiency, particularly when dealing with defects that have low contrast and are subject to noisy background interference. Moreover, the complex nature of PV cell defects, including their varied shapes, sizes, and distributions, poses additional challenges for automatic detection systems.

Recent studies have attempted to address these issues through various approaches2,13,14. Despite these advancements, there remains a need for a more adaptive and efficient approach that can handle the multi-scale nature of PV cell defects while maintaining real-time detection capabilities. To address this gap, we propose a novel detection method based on adaptive complementary fusion. Our approach, YOLO-ACF, aims to enhance detection performance, achieve model lightweighting, and accelerate detection speed.

In summary, the major contributions of this work is provided as following:

  • To eliminate redundancy among feature embeddings and acquire effective representations of defects in photovoltaic panels, we propose a YOLO-ACF network model equipped with an Adaptive Complementary Fusion (ACF) module. This aims to enhance detection performance, achieve model lightweighting, and accelerate detection speed.

  • We propose an Adaptive Complementary Fusion (ACF) module, which adaptively condenses embedded information from two distinct dimensions: channels and spatial aspects. Subsequently, it complements and fuses these two dimensions, facilitating efficient extraction of representative embeddings.

  • We conducted extensive ablation experiments as well as comparative experiments with other methods on the dataset of electroluminescence images of photovoltaic panels, showcasing the superiority of our proposed YOLO-ACF model from both quantitative and qualitative perspectives.

Related works

Defect detection of PV panel

Machine vision-based approaches have become an important direction in the field of defect detection. Many researchers have proposed different algorithms11,15,16 for photovoltaic panel defect detection by creating their own datasets. Buerhop et al.17 constructed a publicly available dataset using EL images for optical inspection of photovoltaic panels. Based on this dataset, researchers have developed numerous algorithms9,10,12 for photovoltaic panel defect detection. Deep learning, compared to traditional machine learning, has powerful feature extraction capabilities, thus exhibiting better robustness and generalization. To meet the data requirements, Su et al.18 proposed PVEL-AD dataset for photovoltaic panel defect detection and conducted several subsequent studies19,20,21 based on this dataset.

In recent years, the PVEL-AD dataset has become a benchmark for photovoltaic (PV) cell defect detection research using electroluminescence (EL) images. This dataset has facilitated the development of various deep learning-based approaches, particularly those utilizing convolutional neural networks (CNNs), to address the challenges in PV cell defect detection. The key challenges identified in this field include complex backgrounds, small-sized defects, and irregular defect shapes. To tackle these issues, researchers have proposed several innovative techniques, including image preprocessing methods like Contrast Limited Adaptive Histogram Equalization (CLAHE)2, lightweight network architectures based on efficient backbones such as EfficientNet-B02, and novel feature enhancement modules like Graph Channel Attention Modules (GCAM)2 and Global Feature Enhancement Modules (GFEM)13. Additionally, advanced architectures such as the Adaptive Space to Depth (ASDD-Net)14 has been developed to address multi-scale defect detection challenges. These approaches incorporate strategies like downsampling adjustment, feature fusion optimization, and detection head improvement to enhance the model’s ability to detect defects of various sizes and shapes.

These advanced methods have shown promising results on the PVEL-AD dataset, demonstrating high reliability in defect detection. Efforts have been made to develop models capable of real-time defect detection, with some achieving impressive accuracy and processing speeds. However, existing approaches often struggle with feature redundancy and inefficient representations of defects in photovoltaic panels. To address these limitations, there is a need for more sophisticated feature fusion techniques and lightweight model architectures. Such improvements could potentially enhance detection performance, especially for extremely small defects, while also increasing robustness to various defect types. Furthermore, developing more efficient models is crucial for large-scale industrial applications, where both accuracy and speed are of paramount importance.

Defect detection based on YOLO

Since its inception, each version of the YOLO family iterate based on the previous version, aiming to overcome shortcomings and enhance performance. Through multiple iterations and continuous development, the YOLO family has now evolved to its 8th version.

In the myriad of YOLO versions, YOLOv5, with its compact size and user-friendly nature, has been extensively leveraged for a multitude of industry inspection tasks. Due to the unsatisfactory recognition effect of a series of feature fusion techniques on low contrast and defects of different sizes in industry surface. Chen et al.1 refined the original Spatial Pyramid Pooling (SPPF) within the framework of YOLOv5 by introducing the SPPFKCSPC module. This enhancement amplifies the network’s ability to extract features from targets at various scales and more effectively integrates multiscale features. Consequently, it results in an enhanced detection performance for industrial components. Zhou et al.22 combined the advantages of the CSPlayer module based on the YOLOv5s model and a global attention enhancement mechanism to address various complex defects on the surface of metal materials, along with the abundance of background texture information, which can lead to false or missed detections during the process of detecting small defects. Furthermore, Gao et al.23 proposed a novel method for steel surface defect recognition, termed YOLOv5-KBS, to address background interference and variations in defect size in images. Tang et al.24 proposed the YOLOv5-C3CA-SPPF network architecture for detecting defects on the surface and inside of the lens. Because of their ambiguous form and diminutive size, optical lens defects often present a challenge for detection - particularly with low-resolution images where the recognition is poor. This results in subpar detection outcomes with conventional methods. To address these issues, Yang et al.25 have proposed a deep-learning algorithm known as ISE-YOLO. Additionally, the use of YOLOv5 for PCB defect detection26 and surface defects in hot-rolled steel strips27 has also achieved favorable detection results.

The excellent performance of YOLOv5 in the field of visual detection, along with its successful application in industry defect detection, proves that it would be a good choice as the baseline network for photovoltaic panel defect detection.

Attention mechanism

The attention mechanism proves to be highly effective in capturing subtle features in tasks related to machine vision and has found extensive application in object recognition, which efficiently filters the embedding information of the detected objects, placing greater emphasis on small and inconspicuous targets, in order to enhance their expressive capability focusing on relevant information, ultimately achieving precise detection28.

Spatial attention focuses on identifying important spatial regions within an image. Jaderberg et al.29 introduced a spatial transformer module that uses attention to learn affine transformations on input images. This allows the model to align and manipulate the input data adaptively, leading to improved geometric invariance and better recognition results. Wang et al.30 introduced a non-local operation that captures long-range dependencies across pixels in an image, enabling the model to attend to distant regions and improve object recognition accuracy. Channel attention aims to emphasize essential channels or feature maps while suppressing irrelevant ones. Hu et al.31 proposed a network module that explicitly models channel dependencies and recalibrates feature maps adaptively. This approach significantly enhances the representational power of the model and improves object recognition accuracy. Woo et al.32 proposed a module that incorporates both spatial and channel attention mechanisms into convolutional neural networks, leading to improved feature representation and higher recognition performance. Fu et al.33 introduced a dual attention mechanism that simultaneously models spatial and channel dependencies, achieving state-of-the-art results in scene segmentation tasks. Dosovitskiy et al.34 presented a vision transformer model that replaces convolutional layers with self-attention mechanisms, demonstrating competitive performance in image classification tasks. This work showcases the potential of attention-based transformers in object recognition. These recent achievements highlight the diverse applications of attention mechanisms in object recognition. By selectively attending to relevant spatial regions, channels, or capturing global dependencies, attention-based methods have significantly improved the performance of object recognition models. Ongoing research in the field continues to explore new variations and combinations of attention mechanisms, paving the way for further advancements in object recognition tasks.

While these attention mechanisms can enhance the baseline network’s performance, the introduced convolutional operations tend to escalate parameter count, expand the model size, and decreases model speed. Consequently, there arises a necessity to minimize parameters while preserving detection performance, ultimately reducing model’s size and boosting detection speed. In order to tackle the challenges posed by these attention mechanisms, we developed the ACF module to realize this objective.

Methods

Given the outstanding performance of YOLOv5 in the field of object detection and its successful application in industry defect detection through improved versions, we introduce YOLOv5 into defect detection for photovoltaic panels. Furthermore, we propose enhancing it with an adaptive complementary fusion module to further improve detection performance.

Baseline with ACF

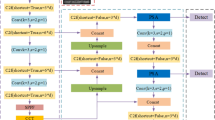
YOLOv5s v6.0 is chosen as the baseline network. This framework consists of four components: the input side (Input), backbone network (Backbone), neck network (Neck), and prediction head (Head). The structure of the network is illustrated in Fig. 2.

Fig. 2
figure 2

The network architecture of YOLO-ACF.

Full size image

Among them, the Input uses Mosaic data augmentation operations to enhance the training speed of the model and the accuracy of the network. The Backbone consists of Conv2d+BN2d+SiLU (Conv) structure , CSP Layer (C3) and Adaptive Complementary Fusion (ACF) module, which can adaptively calculate anchor boxes and adaptively resize images. The primary role of it is to extract features and progressively decrease the size of feature maps. The Neck consists of a series of network layers that mix and combine image features, and can perform fusion for relatively shallow features from the backbone with deep semantic features and pass it to the prediction layer. The Prediction achieves predictions on image features, generates bounding boxes, and predicts categories.

In the Backbone, feature extraction is performed. C3 leverages the processing philosophy from CSPNet, employing n Bottleneck structures, 3 convolutional modules, and 1 Concat operation for its realization. By minimizing the redundancy of gradient information, C3 substantially reduces the computational burden while simultaneously boosting accuracy. In essence, it bolsters the learning capability of the backbone, eradicates computational bottlenecks, and curtails memory overheads. When compared to CSPNet, C3 stands out with its simplicity, superior integration, and essentially equivalent enhancement of CNN’s learning ability. It holds the potential to augment the learning capacity of a CNN, simultaneously achieving network light-weighting and an improvement in precision.

Adaptive complementary fusion module

Due to the significant redundancy among embedding information, we attempt to exploit spatial and channel dimensions separately for collaborative fusion. This approach is designed to refine representative embedding, thereby enhancing detection performance, reducing model complexity, and speeding up the detection process.

Fig. 3
figure 3

Adaptive complementary fusion module.

Full size image

As shown in Fig. 3, the Adaptive Complementary Fusion (ACF) module is a technology that refines the input embedding information by sequentially passing it through a spatial adaptive fusion unit and a channel adaptive fusion unit. Specifically, the embedding information E is initially fed into the spatial adaptive fusion unit \(AF_s\) to obtain the refined spatial embedding information \(E_s\), as shown in equation (1). Subsequently, \(E_s\) is passed through the channel adaptive fusion unit \(AF_c\) to further refine the channel information, ultimately yielding the refined embedding information \(E_c\), as indicated in equation (2).

$$\begin{aligned} E_s= & AF_s ( E ) \end{aligned}$$
(1)
$$\begin{aligned} E_c= & AF_c (E_s) \end{aligned}$$
(2)

Here, \(E \in R^{N{\times }{C}{\times }{H}{\times }{W}}\), N denotes the batch size, indicating the number of samples processed simultaneously in each step. C refers to the number of channels in the tensor of input feature embedding. H and W respectively refer to the height and width of the input feature map containing embedding information .

Spatial adaptive fusion

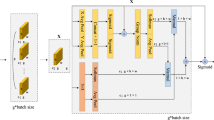
To better refine spatial embedding information, we have employed a spatial adaptive fusion unit, as depicted in Fig. 4. Its function is to adaptively allocate weights to the embedding information between different spatial positions based on their importance. Then, through the cross-fusion of information, the adaptive fusion of spatial embedding information is ultimately achieved.

Fig. 4
figure 4

Spatial adaptive fusion.

Full size image

The first stage involves adaptively weighting the embedding information between different spatial positions. To balance the embedding information from different feature maps, we utilize the scaling factors from the Group Normalization (GN)35 layer. Specifically, the input embedding information E is normalized by subtracting the mean value m and dividing it by the standard deviation d, as expressed in Eq. (3):

$$\begin{aligned} GN(E)= \gamma \frac{E-m}{\sqrt{d^2+\varepsilon }} + \beta \end{aligned}$$
(3)

Where E is the input feature embedding , m and d correspond to the mean and standard deviation of it, respectively. \(\varepsilon\) is a very small positive number introduced to ensure normal division operation. \(\gamma\) and \(\beta\) represent the learnable scale and shift of affine transformation.

In the GN layer, we utilize the learnable parameter \(\gamma\) to balance the spatial pixel variances within each batch and channel. As higher pixel variance signifies more prominent spatial pixel variations and richer spatial information, the value of \(\gamma\) increases accordingly. Therefore, we employ \(\gamma\) as the foundation for adaptive weighting. The normalized weights \(W_\gamma\) are acquired as equation (4):

$$\begin{aligned} W_\gamma =\{ \omega _i \} = \frac{\gamma _i}{\sum _{j=1}^{C} \gamma _j}, i,j=1,2,...,C \end{aligned}$$
(4)

In order to further refine the embedding information, thus obtaining strong information embedding and weak information embedding, we firstly pass the group-normalized embedding information GN(E) weighted by \(W_\gamma\) through a sigmoid activation function S and then through a gate function G to obtain it, as described in Eq. (5). When the value after the sigmoid is greater than or equal to the threshold T (where T is 0.5), we get the weight \(W_1\) of the strong embedding information. Otherwise, we get the weight \(W_2\) of weak embedding information.

$$\begin{aligned} W_s=G(S(GN(E)*W_\gamma ))=\left\{ \begin{aligned} W_1&, S(GN(E)*W_\gamma ) \ge T\\ W_2&,S(GN(E)*W_\gamma ) < T \end{aligned} \right. \end{aligned}$$
(5)

Next, we use the obtained \(W_1\) and \(W_2\) to adaptively weight the input embedding information E, where \(\otimes\) denotes element-wise multiplication, thus obtaining the strong embedding information \(E^w_1\) and the weak embedding information \(E^w_2\), as depicted in Eqs. (6) and (7).

$$\begin{aligned} E^w_1= & W_1 \otimes E \end{aligned}$$
(6)
$$\begin{aligned} E^w_2= & W_2 \otimes E \end{aligned}$$
(7)

The second stage is the cross-fusion of embedding information. The adaptively weighted embedding information from the two branches is fused in a cross manner to enhance the information flow between them, as denoted by Eqs. (8) and (9), where \(\oplus\) represents element-wise summation. Here, the \(E_{11}^w\) and \(E_{12}^w\) represent two segments split from \(E^w_1\), while \(E_{21}^w\) and \(E_{22}^w\) denote two segments split from \(E^w_2\).

$$\begin{aligned} E^{w1}= & E_{11}^w \oplus E^w_{22} \end{aligned}$$
(8)
$$\begin{aligned} E^{w2}= & E_{12}^w \oplus E^w_{21} \end{aligned}$$
(9)

In the end, the embedding information, after adaptive weighting and cross fusion, is merged together through concatenation function CT, as illustrated by Eq. (10) .

$$\begin{aligned} E_s=CT(E^{w1},E^{w2}) \end{aligned}$$
(10)

Channel adaptive fusion

To further refine the spatially-adapted fused embedding information in the channel dimension, we employ the unit of channel adaptive fusion, as illustrated in Fig. 5.

Fig. 5
figure 5

Channel Adaptive Fusion.

Full size image

Due to the sparse connections between Group Convolution (GC), the parameter and computational overhead of GC is significantly reduced compared to standard convolutions when extracting high-level embeddings. Therefore, we initially process the embedding information obtained through spatial refinement using a GC (with a group number of 2), but this is at the expense of losing inter-group information flow. To further refine channel embedding information without increasing parameter and computational overhead, we perform additional GC on the results of the initial GC. However, this may further reduce the interaction of information between channels. Pointwise Convolution (PC) can precisely compensate for this loss, enabling information to flow across channels. Therefore, for one of the group (G1) mentioned above, we add together the results of GC and PC to acquire complementary fusion \({E_{c1}}\) of rich representative embedding captured in different ways, outlined by Eq. (11).

$$\begin{aligned} E_{c1}= GC(G_1) \oplus PC(G_1) \end{aligned}$$
(11)

To ensure diversity in the captured information, for another group (G2), we concatenate the results with a cheap 1 \(\times\) 1 convolution and the original output to obtain complementary fusion of supplementary detailed embedding \({E_{c2}}\) in accordance with Eq. (12).

$$\begin{aligned} E_{c2}= CT(G2,Conv(G2)) \end{aligned}$$
(12)

We employ the simplified SKNet36 approach to adaptively integrate the output embeddings \(E_{c1}\) and \(E_{c2}\). In conformity with the formula (13), we first concatenate (CT) the refined embeddings of the two groups, then we employ global average pooling (GP) to gather global information corresponding to each channel. Subsequently, we apply the soft attention operation, softmax (SM), to each channel to derive weights \(W_c\).

$$\begin{aligned} W_c= SM(GP(CT(E_{c1},E_{c2}))) \end{aligned}$$
(13)

Next, in line with Eq. (14), the refined embeddings are adaptively weighted using the weights \(W_c\) to yield the weighted embeddings \(E^w\).

$$\begin{aligned} E^w= W_c*CT(E_{c1},E_{c2}) \end{aligned}$$
(14)

Lastly, in keeping with the formula (15) and (16), the weighted embeddings are segregated into the weighted embeddings of the two groups, \(E^w_{c1}\) and \(E^w_{c2}\), followed by element-wise addition to achieve complementary fusion between the two groups.

$$\begin{aligned} & {E_{c1}^w,E_{c2}^w}= ST(E^w) \end{aligned}$$
(15)
$$\begin{aligned} & E_c= E_{c1}^w \oplus E_{c2}^w \end{aligned}$$
(16)

Loss

The loss function employed in YOLO-ACF which includes regression box loss \(Loss_{box}\) (18) for localization, confidence loss \(Loss_{conf}\) (21) for regression box, and classification loss \(Loss_{cls}\) (22) . The overall expression of the loss function is defined as formula (17).

$$\begin{aligned} Loss = Loss_{box} + Loss_{conf} + Loss_{cls} \end{aligned}$$
(17)

The regression box loss \(Loss_{box}\) employs CIoU, as represented by formula (18), which amalgamates three strengths: area loss from IoU, central point loss from DIoU, and aspect ratio loss based on its own dimensions.

$$\begin{aligned} Loss_{box} = 1 - CIoU = 1-IoU + \frac{\rho ^2(p,p^{gt})}{c^2} + \alpha v \end{aligned}$$
(18)

where CIoU stands for Complete Intersection over Union, which measures the similarity between predicted and ground truth bounding boxes. IoU is the Intersection over Union, a metric for evaluating the overlap between predicted and ground truth bounding boxes. \(\rho\) is a term related to the distance between box centers and the diagonal of their enclosing bounding box. p and \(p^{gt}\) are variables representing the predicted bounding box and the ground truth bounding box, respectively. c represents the diagonal length of the smallest enclosing box covering both predicted and ground truth bounding boxes. \(\alpha\) is a coefficient used in the loss function calculation. v is a parameter related to the aspect ratios of the predicted and ground truth bounding boxes. The definitions of \(\alpha\) and v are shown in formulas (19) and (20), respectively.

$$\begin{aligned} \alpha= & \frac{v}{(1-IoU)+v} \end{aligned}$$
(19)
$$\begin{aligned} v= & \frac{4}{\pi ^2}(acrtan \frac{w^{gt}}{h^{gt}} - arctan\frac{w}{h})^2 \end{aligned}$$
(20)

where \(w^{gt}\) and \(h^{gt}\) represent the width and height of the ground truth bounding box, respectively. w and h represent the width and height of the predicted bounding box, respectively. arctan denotes the arctangent function. \(\pi\) represents the mathematical constant pi.

The confidence loss, \(L_{conf}\) (21), and the classification loss, \(L_{cls}\) (22), both utilize the BCEWithLogitsLoss function. This function effectively combines binary cross-entropy loss with the sigmoid activation function, providing a seamless integration for efficient computation.

$$\begin{aligned} L_{conf}(p_o, p_{IoU}) = -w_{conf} ( p_{IoU} \log (\sigma (p_o)) + (1 - p_{IoU}) \log (1 - \sigma (p_o))) \end{aligned}$$
(21)

where \(p_o\) is the predicted probability that an object is present in a given bounding box. \(p_{IoU}\) represents the actual target presence label. \(w_{conf}\) represents the weight parameter of the target presence loss. \(\sigma\) represents the sigmoid function.

$$\begin{aligned} L_{cls}(c_p, c_{gt}) = -w_{cls} ( c_{gt} \log (\sigma (c_p)) + (1 - c_{gt}) \log (1 - \sigma (c_p)) ) \end{aligned}$$
(22)

where \(c_p\) represents the model’s predicted class probability, \(c_{gt}\) represents the ground truth class label, \(w_{cls}\) represents the weight parameter for the classification loss.

Experiments

Dataset

The PVEL-AD dataset was jointly released by Hebei University of Technology and Beihang University18. The publicly accessible portion of this dataset comprises 4500 near-infrared images of electroluminescence, featuring one normal class and twelve types of defects. We opted for 9 defect classes and one normal class for our experiments, considering the insufficient samples of certain classes and aligning with recent published works2,13. The selected classes are: crack, finger, black_core, thick line, star_crack, corner, horizontal dislocation, vertical dislocation, and short_circuit, along with the normal class. The training set, validation set, and test set are divided into a ratio of 8:1:1 based on the number of images. Given that certain images may contain multiple instances, the distribution of instances across the three subsets varies. Table 1 provides a comprehensive summary of the number of instances across the different categories in the dataset. The table showcases the distribution of instances in the training, validation, and test sets for each category, along with the total number of instances per category. Additionally, the total number of images across all categories is 4488. The number of images and instances utilized for training, validation, and testing within this dataset are visually depicted in Fig. 6.

Table 1 Summary of instances and images across categories.
Full size table
Fig. 6
figure 6

The number of images and instances utilized for training, validation, and testing.

Full size image

Metric

To perform a objective and comprehensive evaluation of the proposed algorithm, we thoroughly examine three key aspects: detection performance, model complexity and speed. For evaluating detection performance, we employ essential metrics like Precision (P), Recall (R) and mean Average Precision (mAP). And model complexity is assessed using three key metrics: parameter count (Params), Floating-point Operations (FLOPs) and weight file size (Weight). Additionally, the model’s speed, including both time required to process one image (Time) and Frames Per Second (FPS), is also taken into consideration.

Implementation details

The experiments were conducted on a server with an Intel Xeon CPU E5-2678 v3 and an NVIDIA GeForce GTX 1080 Ti GPU. For training and evaluating the YOLO-ACF model on the PVEL-AD dataset, we used the following parameters: a batch size of 16, 100 epochs, and an input image size of \(640\times 640\) pixels. We employed the SGD optimizer with an initial learning rate of 0.001, momentum of 0.937, and weight decay of 0.0005.

Ablation studies

To demonstrate the effectiveness of our proposed ACF module, we conducted ablation experiments as presented in Tables 2, 3, 4 and Fig. 7, respectively. The results comparing the detection of networks without or with different attention mechanisms are shown in Table 2. The “Without” signifies the absence of attention mechanisms. “C3ACF” and “ACF” utilize the ACF module proposed in this paper, albeit in different ways. C3ACF integrates the ACF within the C3 module, whereas ACF replaces the C3 module with the ACF module. Similarly, CBAM32 and CA37 adopt a analogous approach.

Fig. 7
figure 7

Comparison of PR curves between the baseline network without attention mechanism and the YOLO-ACF network.

Full size image
Table 2 Ablation study without or with different attention mechanisms.
Full size table
Table 3 Ablation study on varying numbers of ACF modules.
Full size table
Table 4 Ablation study on different loss functions.
Full size table

From Table 2, it’s evident across the “Without,” “C3ACF,” and “ACF” rows that incorporating both C3ACF and ACF modules significantly boosted detection performance, resulting in improvements in key performance metrics like P, R, and mAP. Moreover, integrating the ACF module notably streamlined model complexity while enhancing model speed. This is clearly demonstrated by the significant decrease in metrics indicating model complexity, namely Params, FLOPs, and Weight, as well as the decrease in processing time per image (Time) and the increase in FPS, representing model speed.

In addition, our ACF module, relative to other attention mechanisms, not only demonstrates superior detection performance and faster detection speed but also achieves greater lightweighting, making it more practical for industrial defect detection.

When comparing the PR curves in Fig. 7, the effectiveness of our approach becomes more pronounced. Specifically, our YOLO-ACF model, relative to the baseline network, not only achieves similar or better results in most categories but also shows a remarkable improvement of 33.2 percentage points in the detection precision of “corner” type defects. Overall, the detection precision across the entire test set is boosted by 3.5 percentage points.

To further refine detection performance, we conducted an ablation study on the quantity of ACF modules. In Table 3, “Without” denotes results without using ACF, while “ACF” and “2*ACF” respectively display results using one and two ACF modules. We found that several performance metrics are superior when using a single ACF module compared to using two ACF modules. This can be attributed to the fact that a single ACF module already effectively removes redundant information, rendering further increases unnecessary.

Furthermore, we conducted ablation experiments on the loss function utilized for regression boxes. The results, as depicted in Table 4, indicate that employing CIoU leads to superior overall performance.

Comparison with other detection methods

To objectively assess the effectiveness of our proposed method for photovoltaic panel defect detection, we conducted both quantitative and qualitative comparisons against established techniques like Faster R-CNN38, RetinaNet39, YOLOv340, YOLOv541, YOLOv642, YOLOv841. The quantitative results of these experiments are presented in Table 5, while Fig. 10 illustrates the qualitative outcomes.

Quantitative comparisons. As can be gleaned from the all metrics in Table 5, it’s evident that the proposed YOLO-ACF method nearly delivers either top-tier or second-best performance across all metrics. When benchmarked against the top-performing YOLOv8 in terms of detection prowess, our method shows enhancements of 5.2, 0.8 and 2.3 percentage points in R, mAP50, and mAP50-95, respectively. Compared to the most lightweight and fastest YOLOv5, we achieve reductions of 12.9%, 12.4%, and 4.2% in Params, Weight, and Time, respectively, while experiencing a 5% increase in FPS. Furthermore, analysis of the confusion matrices in Fig. 8 reveals that YOLO-ACF demonstrates improved classification accuracy for several defect types compared to YOLOv8. Notably, YOLO-ACF achieves higher accuracy for ’crack’ (84% vs 80%), ’thick_line’ (83% vs 77%), and ’black_core’ (100% vs 99%) defects. Additionally, YOLO-ACF shows reduced misclassification of defects as background, particularly for ’crack’ (15% vs 19%) and ’horizontal_dislocation’ (0 vs 7%) categories, indicating enhanced ability to distinguish defects from the background.

Table 5 Quantitative comparisons with other methods.
Full size table
Fig. 8
figure 8

Comparison of confusion matrixs between the YOLOv8 and the YOLO-ACF network.

Full size image

Taken together, our proposed YOLO-ACF outshines Faster R-CNN, RetinaNet, YOLOv3, YOLOv5, and YOLOv8 in terms of detection performance, model lightweighting and detection speed. As illustrated in Fig. 9, our YOLO-ACF has successfully struck a fine balance between performance and model speed. The amalgamation of these three advantages renders YOLO-ACF of substantial practical significance for the application of defect detection in photovoltaic panels.

Fig. 9
figure 9

Comparison of performance and speed.

Full size image

Qualitative comparisons. The qualitative comparison results of different methods are presented in Fig. 10. Each row exhibits the ground truth (GT) manually annotated alongside the detection results of various methods for the same image. The first column denotes the ground truth (GT), while the second to the seventh columns respectively portray the outcomes of Faster R-CNN, RetinaNet, YOLOv3, YOLOv5, YOLOv6 and YOLOv8 methods. The last column showcases the results of the method proposed in this paper.

Fig. 10
figure 10

Qualitative comparison with other methods.

Full size image

The first row showcases an instance of the crack defect. Faster R-CNN and RetinaNet show false positives, while YOLOv3 and YOLOv5 exhibit missed detections. In contrast, YOLO-ACF, YOLOv6, and YOLOv8 can accurately detect and locate the defect. The second row presents the detection results of the finger defect. YOLOv3, YOLOv5, YOLOv6, and YOLOv8 all have missed detections, while RetinaNet shows a higher number of false positives. In comparison, our YOLO-ACF and Faster R-CNN can accurately detect and locate this type of defect. The third row demonstrates a detection example of the black_core defect, where all methods can detect the defect. The fourth row showcases a detection instance of the thick_line defect, where YOLOv3 misses the detection, and RetinaNet, YOLOv5, YOLOv6, and YOLOv8 have false detections. However, the proposed YOLO-ACF and Faster R-CNN can accurately detect and locate the defect. The fifth row presents the star_crack type, and the image also contains crack and finger type defects. RetinaNet shows a higher number of false positives, and YOLOv3, YOLOv5, and YOLOv6 also have false positive cases. Our YOLO-ACF, Faster R-CNN, and YOLOv8 can better detect and recognize the three different types of defects present in the image. The sixth row demonstrates the corner defect type. In addition to the two corner defects, the image also contains a crack type defect. RetinaNet has a higher number of false positives, YOLOv6 has false detections, and the other methods have missed detections. The seventh row showcases the horizontal_dislocation defect type. RetinaNet shows a higher number of false positives, and the detections by YOLOv3, YOLOv5, and YOLOv8 are incomplete. Our YOLO-ACF, Faster R-CNN, and YOLOv6 can accurately detect and recognize this type of defect. The eighth row presents an example of the vertical_dislocation defect, where Faster R-CNN, RetinaNet, YOLOv3, YOLOv5, and YOLOv8 methods show false positives, while YOLOv6’s detection is incomplete. However, our YOLO-ACF can accurately identify and locate the defect. The last row demonstrates an instance of the short_circuit defect. YOLOv3 fails to detect the defect, RetinaNet exhibits false positives, while YOLO-ACF and the other four methods can accurately detect and identify the defect.

Through qualitative comparison, we can observe that our proposed YOLO-ACF demonstrates a certain level of versatility in identifying diverse types of defects in photovoltaic panels of different sizes and appearances. It exhibits particular effectiveness in detecting both single and multiple types of defects present in photovoltaic panels.

Conclusions

To address the frequent challenges of missed detections and false alarms in photovoltaic panel defect detection due to the high similarity between embedded defect features and complex background information, we propose a method aimed at synergistically integrating spatial and channel dimensions. This approach aims to condense representative embeddings and reduce parameter computation, thereby enhancing detection performance, achieving model lightweighting, and speeding up detection. To achieve this, we introduce an Adaptive Complementary Fusion (ACF) module, which adaptively integrates spatial and channel information and incorporates it into YOLOv5 to obtain the YOLO-ACF model. We partitioned a dataset comprising defective photovoltaic panel electroluminescence images into training, validation, and test sets, and then carried out ablation and comparative experiments. Our evaluation includes both quantitative and qualitative analyses. Quantitatively, our YOLO-ACF method exhibits improvements of 5.2, 0.8, and 2.3 percentage points in R, mAP50, and mAP50-95, respectively, compared to the state-of-the-art YOLOv8 in terms of detection capability. Regarding model size and detection speed, our method outperforms even the lightest and fastest YOLOv5, achieving reductions in parameters, weight, and time by 12.9%, 12.4%, and 4.2%, respectively, while boosting FPS by 5%. Furthermore, qualitative comparison underscores the effectiveness of our YOLO-ACF approach across various defect types. These findings collectively affirm the superior detection performance, reduced model size, and accelerated detection speed of the proposed YOLO-ACF model, thus validating its practical utility in production workflows.