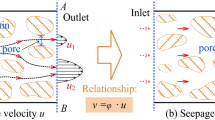
Abstract
To examine the permeability alterations in coal seams induced by liquid CO2 injection, we employed COMSOL simulations to recreate the flow, force, and temperature fields, along with the corresponding physical parameters of the geological formation. We established a mathematical model to track the evolution of the coal body’s permeability, enabling us to capture the phase distribution of CO2, the dynamics of fluid transportation, and the coal body’s mechanical responses during the liquid CO2 injection process. Our findings revealed that the coal seam undergoes significant changes due to low-temperature freezing and shrinkage, gas-liquid phase transitions, and expansion impacts from solid-liquid phase changes. These factors collectively modify the pore structure, subsequently influencing the coal seam’s permeability. Notably, the coal body’s permeability, influenced by the pore structure and the Klinkenberg effect, increases logarithmically with rising injection pressure and falling temperatures. The structural changes in the coal body are markedly impacted by seepage and phase change pressures, with the permeability enhancement from secondary phase changes being 2.28 times greater than that from primary phase changes, and five times greater than in scenarios without phase change.
Similar content being viewed by others
Introduction
Recent national statistics indicate that coal constitutes 56.2% of China’s total energy consumption. Projections suggest this figure will decrease to 45% by 2030. Despite this anticipated reduction, coal is expected to remain a pivotal component of China’s energy landscape in the foreseeable future. Given that coal seams are rich in methane—a combustible and explosive gas—the prudent management of methane not only yields economic benefits but is also crucial for ensuring the safety of coal miners. In China, the majority of coal reservoirs exist under high-pressure and low-permeability conditions. To enhance the extraction rate of coal bed methane, technologies such as hydraulic fracturing, liquid nitrogen freeze-thaw cycling1,2, and supercritical blasting have been extensively adopted. Among these enhancement strategies, the use of CO2 is particularly appealing as it aligns with the nation’s dual-carbon policy objectives. CO2’s advantageous properties, such as its low viscosity and high permeability, enable it to efficiently penetrate defects within the coal seam, hence lowering the threshold for crack initiation. When subjected to pressure, the introduction of low-temperature liquid CO2 results in the freezing and contraction of the coal matrix3,4,5. This process leads to phase change icing of the coal’s pore water, inflicting damage on the pore structure. The pressurization effect of liquid CO2 phase changes exerts a negative impact on the coal seam by facilitating pore opening and crack extension. Moreover, CO2’s interaction with CH4—competing for adsorption sites within the coal seam—fosters the desorption of methane6,7. This improves gas extraction efficiency, mitigates the risk of sudden gas outbursts, and enhances the safety of mining operations.
Scholars have conducted extensive research on CO2 pressure injection in coal bodies under various conditions. Qin X used micro-CT to study low-rank coal’s microstructure and found that gas in large pore-throat structures easily escapes8. Sampath SMSK developed a flow-adsorption-deformation model, showing that a large matrix expansion occurs before pressure equilibrium, confirming adsorption-induced expansion9. Niu Q investigated anthracite coal’s mechanical parameters under the influence of CO2 saturation pressure, saturation time, and water content, attributing coal softening to physicochemical reactions with CO210. Tan Peng’s triaxial fracturing experiments demonstrated that fracture characteristics are influenced by natural fractures, with vertical expansion following the principle of least resistance11. Men X’s seepage simulation experiments indicated that fractured fissures are the main seepage channels, with larger pressure differences increasing gas production12. Yin G studied the effect of inlet pressure on production efficiency, finding that higher injection pressure results in earlier breakthrough and that low-pressure injection has better CH4 recovery efficiency13. Wei G’s experiments on CH4 recovery using liquid CO2 showed that low-pressure injection is more efficient than high-pressure injection in maintaining CH4 concentration14.
CO2 injection into coal seams encompasses complex interplays of temperature and stress fields, prompting extensive research into the multiphysics coupling involved in this process through mathematical modelling by both domestic and international scholars. Laurent Perrier developed a model accounting for pore and effective stress under adsorption strain, based on the Gibbs adsorption isotherm. This model highlights the changes in pore volume resulting from solubilization and the matrix’s adsorption expansion, presenting a modified Gibbs formula to encapsulate these dynamics15. Hwang W.R. provided a numerical solution for flow within porous media, establishing an effective permeability equation based on equivalence theory, alongside a finite element flow solution for two-scale porous media16. Zhitao Lv conducted freezing experiments on saturated sandstones, formulating a coupled thermal-force model for porous rocks under freeze-thaw conditions. This model illustrated the impact of plastic residual strain on the mechanical structure and fluid movement through saturated sandstone, revealing an initial increase followed by a decrease in freezing expansion with temperature reduction, characterized by stages of thermal contraction, freezing expansion, and stabilization17. Shuwei Zhou introduced an elastic deformation matrix and phase field tracking process for the hydraulic fracturing of coal bodies, using the phase field method. This approach incorporates energy generalization and displacement-pressure control equations to distinguish between fractured and unfractured domains and to describe fracture propagation18. Chunguang Wang devised a coupled heat-water-force model to investigate the influence of parameter variations of supercritical CO2 on heat extraction efficiency. His findings indicate a direct correlation between heat extraction rate, pore pressure, and mass flow, and an inverse relationship with inlet temperature, pointing to mechanical compression and thermal impact deformation as driving forces behind structural changes induced by supercritical CO2 injection19. Xingwang Tian presented a convection model for porous media under the influence of viscous dissipation, invoking the Brinkman expansion equation and local thermal non-equilibrium effects. Results suggest that porous media reach local thermal equilibrium with a high interphase heat transfer coefficient, and that thermal non-equilibrium is exacerbated by increasing the modified inertia coefficient and decreasing the modification coefficient and Brinkman coefficient20. Sun X conducted repetitive hydraulic fracturing experiments under varying triaxial stress conditions to analyze fracture expansion in coal seams and the coal’s mechanical properties pre-and post-fracturing. The experiments demonstrated that hydraulic action advances along fractures, generating primary fractures parallel to the maximum horizontal stress21. Wang H developed a coal seam fracturing model and performed liquid CO2 phase change fracturing experiments to compare the gas resolution index before and after blasting. These experiments determined the extent of fracturing impact and gas influx, providing vital insights into the efficacy and consequences of liquid CO2 injection in coal seam fracturing efforts22.
To encapsulate, prevailing research into enhancing coal seam permeability via liquid injection primarily revolves around studying the patterns of cracking, expansion, and permeability alterations under varied conditions. However, these studies often overlook the intricate dynamics of coal structure modifications brought on by the heat-fluid-solid interactions during liquid CO2 injection. Additionally, the interplay between fluid movement and temperature shifts resulting from gas-liquid and solid-liquid phase transitions receives limited attention. In addressing these gaps, this study introduces a mathematical model to explore the permeability evolution of coal bodies subjected to liquid CO2 freeze-thaw cycles. It simulates the alterations in pressure, temperature, and permeability through the lens of heat-solid-fluid coupling within coal seams. Moreover, it investigates the laws governing the interdependence between fluid mass transfer and temperature shift during coal body deformation. Through meticulous tracking of CO2 phase transitions and concentration variations, this model determines the pressurization and dissemination range of liquid CO2 within the coal seam. It also accounts for the Klinkenberg effect and examines the impact of liquid CO2 on coal seam permeability under various pressurized injection scenarios. This comprehensive approach lays a solid foundation for future investigations into leveraging pressurized liquid CO2 injections to enhance gas extraction from fractured coal bodies.
Mathematical model
Coupling relation
Given the complexity of coal as an isomer, where achieving a harmonization between its structural and mechanical characteristics poses a significant challenge, simplifications are necessary to study fluid dynamics, mechanical alterations within the coal body, and temperature transfer across coal seams effectively. Hence, in constructing the model for these purposes, the following assumptions about the coal seam are made to streamline the analysis:
(1) The coal seam exhibits a uniform distribution of pore fractures, with residual strains considered negligible for the purposes of this study.
(2) Within the coal seam, fluid movement adheres to Darcy’s Law, whereas gas transport is governed by the principles of the ideal gas law, ensuring a standard framework for analyzing fluid and gas flow dynamics.
(3) Pore water within the coal is assumed to be evenly distributed throughout, with the migration of water within the seam disregarded to focus on primary processes affecting permeability and fluid flow.
(4) Gas adsorption is modeled according to Langmuir’s Law, providing a predictable framework for adsorption dynamics. Similarly, gas diffusion is conceptualized through Fick’s Law, offering a basis for understanding the movement of gas at the molecular level.
(5) Neglecting the effect of changes in gas solubility in water on coal permeability.
In the coal seam, the injection of liquid CO2 operates under Darcy flow principles, where the contact between the liquid injection port and the pore walls initially undergoes deformation due to pressure effects. This pressure-driven injection of liquid CO2 disrupts the original mechanical equilibrium of the coal seam, leading to alterations in the pore structure and the dynamics of liquid CO2 pressure injection as illustrated in Fig. 1. The interaction between liquid CO2 and the coal structure, as depicted in Fig. 2, is mutual, influencing each other significantly. The structural transformations occurring during the liquid injection process can be attributed to several factors: (1)The heat exchange gasification between the liquid CO2 and coal seam elevates the pressure.(2)The cold temperature of the liquid CO2 induces shrinkage and deformation of the coal matrix.(3)This chill prompts the condensation of coal seam water into ice, exerting an expansive pressure.(4)Thermal stress arises from the discrepancy between the coal body’s surface and internal temperatures. These structural modifications within the coal matrix impact the heat transfer characteristics23, altering the heat transfer coefficients, thermal expansion coefficients, and other related parameters. The dynamics of fluid seepage and diffusion undergo changes due to variations in pore penetration and compressibility, heralding the emergence of new pores, alongside the compression or expansion of existing ones. Liquid CO2’s gasification and absorption within the coal matrix provoke shifts in the adsorbed gas content, influencing fluid viscosity, density, and other crucial parameters. The changing adsorption-desorption dynamics of the coal matrix produce disparate expansion and contraction effects24. Moreover, ice formation from pore water acts as an impediment to subsequent fluid transfer, affecting pressure propagation across the system.
Gas equation of state
The gas present within the coal seam adheres to the principles of the ideal gas law, allowing the state parameters of the gas to be accurately established via Eq. (1).
In this context, ρ signifies the density of the fluid within the coal seam, measured in kg/m3; M denotes the molar mass in kg/mol; P represents the pressure within the coal seam, in pascals (Pa); R stands for the gas constant, expressed in joules per mole-kelvin J/(mol·K); T indicates the temperature in kelvin (K); i = 1 and i = 2 correspond to methane (CH4) and carbon dioxide (CO2), respectively; while x = 1 and x = 2 refer to the pressures of CH4 and CO2 within the coal seam, respectively.
To aid in assessing the distribution dynamics of liquid CO2 and the conditions affecting gasification pressurization, a CO2 phase diagram is provided, as depicted in Fig. 3. The empirical formula25 (2) serves as a tool for evaluating the state transitions of liquid CO2 when injected into the coal seam.
Where Tt=216.56 K, Pt=0.518MPa, a1=-14.740846, a2 = 2.432701, a3=-5.3061778.
Within the coal seam, CO2 exists in two distinct phases, leading to the formulation of a composite parameter that captures the essence of phase presence, expressed as follows:
ρc represents the integrated density of CO2, measured in kg/m3; αm denotes the mass fraction; Cp,c is the integrated specific heat of CO2 across varying contents, quantified in J/(kg·K); L12 signifies the heat of vaporization for CO2, expressed in J/kg. θ indicates the content of CO2, with 1 and 2 corresponding to the liquid and gaseous phases, respectively; kc stands for the thermal conductivity of the composite phase, measured in W/(m·K).
Fluid flow equation
Seepage equation
The flow of both CH4 and CO2 in a coal seam obeys Darcy’s law, as shown in the following equation:
Where p as the seepage pressure is affected by the injection pressure, the liquid increases with the increase in injection pressure through the seepage channel velocity increases, the fluid is subjected to gravity, pressure, the initial flow rate produces a certain amount of kinetic energy dissipation, the Darcy flow equations for the expansion of the complementary, can be expressed in the following equation:
where v is the velocity, m/s; ψ is the porosity; I is the unit vector; k is the permeability, m2; u is the hydrodynamic viscosity, Pa·s; F is the acting force; Qm is the mass source; and ▽ is the Hamilton operator.
The seepage velocity formula (sun, 2019) can be expressed as follows:
Diffusion equation
Gas flow in coal seam conforms to FICK diffusion, which can be expressed in Eq. (6)26:
According to the law of conservation of mass, the amount of gas adsorbed and resolved by the coal matrix are equal, which is expressed as (Padua et al.27):
According to the situation of gas in coal seam, it can be divided into adsorption state and free state, which can be expressed by mass concentration as follows:
The total mass can be subtracted from the original mass of coalbed methane28,29, and the adsorption conforms to Langmuir equation (Wang et al.22), then the adsorption change can be expressed as follows:
where D is the fluid diffusion coefficient, m2/s; c is the mass concentration, kg/m3; Vj is the Langmuri volume constant, m3/kg; P is the Langmuri pressure constant, 1/MPa; p is the substrate pressure, Pa; ρc is the coal density, kg/m3; ρg is the standard condition density of gas, kg/m3; K is the Langmuri constant, m3/mol; cm is the maximum adsorption capacity, mol/kg; j = 1,j = 2 denote CH4 and CO2, respectively; the diffusion model uses Millington Quik correction model.
Stress equation
In the elastic deformation assumed above, coal deformation follows generalized Hooke’s law, and the deformation form of coal body can be expressed as25:
where δij is the Cronecker function; aT is the adsorption thermal expansion coefficient, 1/K; b is the biot coefficient; K is the bulk modulus, Pa; G is the shear modulus, Pa; E is the modulus of elasticity, Pa; v is the Poisson’s ratio; and Es is the modulus of elasticity of the coal skeleton, Pa; Ks is the coal skeleton bulk modulus, Pa.
With the gas obeying the Langmuri adsorption equation, the analytically induced stresses due to gas adsorption obtained from surface physicochemical principles are given by26:
σs is the gas adsorption resolving stress; W0 is the volume of micropores, m3; Pl1 and Pl2 represent the adsorption constants for methane and carbon dioxide, respectively, Pa−1; The elasticity matrix of coal can be used in Eq. (23).
The tensor form is:
The above equations are combined to obtain the general equation of coal deformation:
Temperature equation
According to previous studies on heat transfer equation, the equation19 can be used to calculate heat conduction and saturation:
When liquid CO2 is injected into a coal seam, it traverses along the seepage channels, encountering heat convection transfer in the process. Primarily, the heat transfer mechanism for liquid CO2 entering the coal matrix involves heat conduction. However, as pore penetration and fracture development progress, the enhanced seepage effect amplifies the role of heat convection transfer. Moreover, as the liquid CO2 vaporizes within the coal matrix, the heat transfer properties of the fluid undergo alterations, incorporating the latent heat associated with the phase change during vaporization. Under these circumstances, the dynamics of heat transfer can be captured by the following equation:
Where dz is the thickness, m; ρ is the coal density, kg/m3; C is the specific heat capacity of the coal seam, J/(kg·K); ρg is the fluid density, kg/m3; Cg is the specific heat capacity of the gas, J/(kg·K); v is the velocity, m/s.
The thermal conductivity and specific heat capacity can be calculated by the following gas mixture formula:
λz is the thermal conductivity, W/(m·K); λg is the thermal conductivity of the mixed fluid, W/(m·K); λs is the thermal conductivity of the coal skeleton, W/(m·K); λq is the thermal conductivity of the water, W/(m·K); Cw is the specific heat of the water, J/(kg·K); θs is the solid matrix component; θq is the water content of the coal seam; i and j are 1 and 2 for CH4 and CO2, respectively; Cs is the specific heat of coal skeleton, J/(kg·K); Cw is the specific heat of water, J/(kg·K).
Porosity and permeability models
In order to facilitate the establishment of the pore relationship of the coal body, a unit in the coal seam is selected as the ideal model, and the coal body as a double-pore structure has a uniform distribution of pores and cracks30, as shown in Fig. 4.
Upon being subjected to various forces, a coal seam will experience three distinct phases: compression, elasticity, and damage. This behavior can be attributed to the coal’s dual-pore structure. As the coal skeleton encounters fluid pressure and thermal stress among other forces, and with the coal seam encapsulated by an impermeable boundary, it faces compression from both internal and external loads. Initially, the seams’ fractures compress under the seepage pressure introduced by the injection of liquid CO2. Subsequently, the coal body undergoes elastic deformation and progresses to a damage threshold31,32,33. The cumulative impact of seepage pressure from the liquid CO2 injection, coupled with the phase change of the liquid CO2 and other resulting pressures, causes the cracks within the coal to widen, leading to tensile damage34.
The coal seam follows the dual pore homogeneity homodirectional model, and the basic formula of pores is as follows:
Where εv is the volume strain; ΔVs is the volume change of coal skeleton. Vs0 is the initial volume of the coal skeleton. The temperature strain can be expressed as follows:
Where aT is the coefficient of thermal expansion,1/K; Tref is the volume reference temperature, generally 293.15 K;
The volumetric expansion strain of water-ice phase transition can be calculated using the difference of water concentration, and its expression can be as follows:
β is the expansion coefficient 0.09m3/kg; Mw is the molar mass of water, kg/mol; cw is the water concentration under the original stress, mol/m3; cwref is the strain reference concentration, mol/m3.
There is dynamic equilibrium in the original formation, and the compression of liquid CO2 to the coal body can be expressed as follows:
Where Ky is the volume compression coefficient, 1/MPa; P0 is the original ground stress.
The expression of porosity obtained by combining the above formula is as follows:
Ignoring the viscosity dissipation and adding the influence of slippage effect on the permeability35, the final permeability expression is:
Where bk is klinkenberg coefficient, MPa; pj is matrix pressure, Pa.
Physical calculation model
For this simulation, the model is configured as a cube measuring 10 m · 10 m · 10 m, featuring a central fluid injection hole with a radius of 0.1 m. The model’s boundary is impermeable, exposed to a formation pressure of 1 MPa. It is designed to eliminate heat exchange or fluid movement between the boundary and the surrounding coal seam. The mesh is meticulously divided into 496,607 ___domain cells and 11,054 boundary cells, as illustrated in Fig. 5.
Numerical simulation of fracturing coal seam with liquid CO2 injection
Key parameters including coal seam temperature, pressure, permeability, strain, and adsorption were in COMSOL for the purpose of simulating and analyzing the dynamics of fluid transport, heat and mass transfer, as well as stress and strain throughout the process of liquid CO2 injection.
Condition and parameter settings
To investigate the impact of liquid CO2 injection conditions on the structural transformations of coal seams, 11 distinct liquid CO2 scenarios varying in pressure and temperature were established for injecting into the coal matrix, as detailed in Table 1. The coal seams commenced with an initial permeability of 1.597 × 10−14 m2 and an initial porosity of 0.0976, with the injection period set at 120 min. These values were selected spanning from the tri-phase point to the supercritical point, reflecting the phase transition behavior of CO2.
The coal matrix was situated in a geological setting, subjected to an encasing pressure of 1 MPa, where the coalbed methane (CBM) pressure attained a dynamic balance. This setup ensured no slip deformation or backflow occurred at the boundaries. Initial conditions were set at a temperature of 293.15 K and an initial concentration denoted as C0. The physical parameters pertinent to the simulation are presented in Table 2, underlining the comprehensive approach to model the complex behavior of liquid CO2 injection in coal seams.
CO2 distribution and phase state in coal seam
Through the simulation of liquid CO2 injection under varying pressures and temperatures, the pressure and concentration distributions within the coal seam during the process were assessed utilizing the gas equation of state, Fick’s law, and Darcy’s law. Additionally, the characterization of temperature fluctuations within the coal seam was achieved through the analysis of porous heat transfer. This facilitated the delineation of the transformation rules governing the temperature, pressure, and concentration fields of the liquid CO2 subsequent to its penetration into the coal seam. The outcomes of these simulations, distinguished by differing injection pressures and temperatures, are showcased in Figs. 6 and 7.
As the injection pressure increases, both the distribution and the spread of liquid CO2 within the coal seam expand. Conversely, an increase in injection temperature causes a gradual decrease in the distribution of liquid CO2, though the overall extent of CO2 diffusion within the coal seam remains largely unchanged. This phenomenon can be attributed to the lower viscosity coefficient of gaseous CO2 compared to that of liquid CO2, facilitating easier diffusion. This implies that the phase state significantly influences the diffusion extent of CO2. Moreover, broadening the fluid’s influence range. Proximity to the injection site correlates with higher fluid pressure and cooler temperatures, whereas areas farther from the injection port experience reduced fluid pressure and elevated temperatures. Through the CO2 phase function, the extent of liquid CO2 is identified, employing red and blue colorations to denote the liquid and gaseous states of CO2, respectively. Moving away from the injection point, the presence of liquid CO2 diminishes until fully transitioning to a gaseous state. The influence of temperature prompts an expansion in both the state range and concentration of liquid CO2, whereas an increase in temperature leads to a diminished presence of liquid CO2, transitioning towards a saturated gaseous state intermediate between liquid and gaseous phases.
In line with Fick’s law, diffusion flux is proportional to the diffusion coefficient of the fluid and its concentration gradient. Additionally, the pressure gradient plays a pivotal role in shaping the concentration gradient and the rate of gas transfer, where heightened injection pressure escalates both the extent of concentration diffusion and the gas transfer rate.
The interaction of liquid CO2 with the coal matrix elevates temperatures within the coal and the CO2 itself. Phase changes of liquid CO2, accompanied by vaporization and heat absorption, lower the temperatures of both the coal matrix and the pore fluid. The domains of CO2 diffusion within the coal seam are determined by several factors, including the physical properties of CO2, the coal’s pore structure, injection pressures and temperatures, as well as phase change pressures of both CO2 and pore water ice, among others. These variables contribute to alterations in the coal’s pore structure and subsequently influence the fluid transfer rate, viscosity, and heat transfer mechanisms. Notably, injection pressures and temperatures directly impact CO2’s physical properties and the coal’s pore structure. The dynamics between fluid injection conditions and changes in coal’s physical mechanics are illustrated in Fig. 8.
Elevating the pressure of liquid injection leads to a more rapid decrease in the coal seam’s temperature over the same duration, although the impact of this temperature reduction gradually diminishes, indicating a finite effect of pressure increase on temperature alterations. Concurrently, as the temperature of liquid injection ascends, so does the pressure within the coal seam, suggesting that higher liquid injection temperatures facilitate the phase change pressurization of liquid CO2. As depicted in Fig. 9, both the pressure increase rate and the temperature decrease rate in the Y and Z directions of the coal seam outpace those in the X direction. This discrepancy arises from the lower transverse mechanical load of the coal body compared to its longitudinal counterpart, making it more susceptible to penetration by CO2. Consequently, the coal seams in the Y and Z directions experience enhanced CO2 ingress, receiving more phase change pressure and exposure to colder CO2.
Analysis of influencing factors of coal seam structure
The influence of liquid injection on coal seam permeability is manifestly observed through alterations in pore structure. As liquid CO2 circulates within the coal seam, various forces including fluid compression stress, thermal stress, phase change pressure, and adsorption dissolution collectively modify the coal seam’s architecture. The process of liquid CO2 entering and initiating heat exchange with the coal seam brings the coal directly into contact with low-temperature liquid CO2. The resultant gasification and heat absorption of liquid CO2 lowers the coal body’s temperature, causing the coal matrix to contract and deform in response to the cold. This phenomenon of freezing and shrinking strain in the coal matrix is illustrated in Fig. 10, with contractions of the coal matrix labeled as negative and expansions as positive. It is evident that both an increase in liquid injection pressure and a decrease in liquid injection temperature augment the freeze-shrink deformation of the coal matrix. The enhanced pressure expands the mass diffusion range, thereby extending the influence of freeze-shrink strain over a broader area. Conversely, the relationship between temperature and heat conduction velocity is directly proportional; hence, a reduction in temperature amplifies the temperature gradient, bolstering the freeze-shrink effect.
The increase of injection pressure makes the adsorption amount, adsorption speed and resolution speed improve, the effect of different injection pressure on the deformation of coal body adsorption and resolution is shown in Fig. 11, the left axis is the deformation of coal body caused by gas adsorption, and the right axis is the deformation of coal body caused by gas resolution. The deformation of coal body caused by gas adsorption under the pressure of 2 MPa is 4 × 10−5, and the deformation of coal body caused by gas adsorption under the pressure of 12 MPa is 3.5 × 10−4. The adsorption and desorption processes of coal bed methane adhere to the Langmuir model; with heightened CO2 pressure, the frequency of gas molecule collisions with the coal matrix per unit time rises, leading to an enhanced CO2 adsorption rate. CO2 possesses a stronger adsorption capability compared to CH4, enabling CO2 to displace CH4 from its adsorption sites, thereby accelerating CH4 desorption. Initially, the volume of CH4 released from the coal matrix surpasses the CO2 adsorption volume, causing the coal matrix to contract. As CO2 adsorption increases and CH4 adsorption lessens, CO2 adsorption volumes eventually exceed those of CH4 released, resulting in the expansion and deformation of the coal matrix21. As the liquid injection temperature decreases, the amount and rate of coal body adsorption and resolution decreases, the effect of different liquid injection temperatures on the deformation of coal body adsorption and resolution is shown in Fig. 12, and the left and right axes are the deformation of coal body caused by gas resolution and adsorption, respectively.The deformation of coal body caused by coal body adsorption is 1.88 × 10−4 at 270 K, and the deformation of coal body caused by coal body adsorption is 1.54 × 10−4 at 220 K. This phenomenon occurs because lower temperatures reduce the kinetic energy of CO2 and CH4 molecules, slowing their velocity, which in turn gradually decelerates the adsorption rate more than the desorption rate. Given that adsorption releases heat, reduced temperatures are conducive to adsorption, whereas desorption, which absorbs heat, is inhibited by temperature drops. To analyze the impact of phase changes on pore structure, scenarios without phase change, with primary phase change, and with secondary phase change were employed for comparative simulation. The primary phase change, excluding the gas-liquid phase transition of CO2 and considering only the solid-liquid transformation of coal seam pore water, is depicted in Fig. 13. The secondary phase change exerts the most significant influence on pore space, surpassing the primary phase change: it causes pore water crystallization, expanding the pore space. The porosity increased from 9.76 × 10−2 to 9.82 × 10−2, and a phase transition secondarily increased the porosity to 9.78 × 10−2. Moreover, secondary phase change not only enhances permeability significantly but also increases seepage pressure and enlarges the interface for CO2 and coal matrix heat exchange. This accelerates coal skeleton freeze shrinkage, amplifies fatigue damage surfaces, and expands the scope of pore structure alterations. Liquid CO2 pressurization and gasification from coal seam heat exchange during continual liquid injection escalate coal seam pressure, potentially impeding future pressurization from gasification, and slowing down the rate of fracture expansion and pore development, as shown in Figs. 13 and 14.
Tensile strain emerges within the coal body under liquid CO2 compression, with the duration needed for the fluid to progress the coal matrix to the point of fracture decreasing as injection pressure increases, as illustrated in Fig. 14. A temperature rise leads to a lower concentration of liquid CO2, which in turn reduces the pressurization effect owing to phase transition. Furthermore, a diminished temperature gradient corresponds to a decrease in freeze-shrinkage strain exerted on the coal matrix, accompanied by a modest increment in porosity. Notably, the most significant increase in porosity observed in the Y and Z directions can be attributed to the coal body in these directions being more susceptible to CO2 infiltration, thereby reaching the damage threshold more readily. From Figs. 10, 11, 12, 13 and 14, it becomes apparent that injection pressure is the principal determinant of changes in the coal body’s pore structure. This is followed in importance by the impact of CO2 phase transitions on pore structure and the combined effects of adsorption-desorption processes and freeze-shrinkage deformation.
Permeability change of coal seam
This study investigates the influence of the Klinkenberg coefficient on permeability, selecting a liquid CO2 injection pressure of 2 MPa for analysis. At this point the permeability with and without the Klinkenberg effect increased from 1.597 × 10−14 to 1.62 × 10−14 and 1.604 × 10−14 respectively. Under this pressure, the impact of the Klinkenberg coefficient on permeability becomes pronounced, exhibiting initial fluctuations characterized by an increase followed by a decrease, as depicted in Fig. 15. This behavior is attributed to adsorption hysteresis, with CH4 desorption occurring more swiftly than CO2 adsorption. This sequential gas exchange momentarily reduces the coal matrix pressure, enlarging the average free path of molecules, which in turn facilitates their passage through the pores and momentarily boosts permeability. As pressure rises, the gradual adsorption of CO2 elevates the coal matrix pressure to a critical threshold where the Klinkenberg effect starts to restrain the growth of permeability. With further increments in fluid pressure, compression of the coal body commences distant from the injection site, leading to a reduction in porosity and consequently, a drop in permeability. Upon pressure reaching the coal body’s damage threshold, cracking ensues, enhancing pore interconnectivity and fracture network density. This development results in an escalated seepage rate. The analysis reveals that phase changes significantly enhance coal seam porosity, with Figs. 16 and 17 showcasing the derived permeability evolution trend. As pressure mounts and temperature drops, permeability experiences a notable increment. Initial stages of fluid injection witness permeability fluctuations commencing earlier and with greater magnitude, yet the rate of permeability growth diminishes as pressure continues to escalate.
Discussion
Cracking damage mechanism of liquid CO2 pressurized coal
The Fig. 18 illustrates the fracture damage mechanism of coal bodies under the pressure injection of liquid CO2. Liquid CO2 is introduced into the coal structure through pre-existing holes in the coal wall. The ensuing fracture damage arises from several key processes: the injection pressure of liquid CO2, the phase change from heat exchange between liquid CO2 and the coal seam, and the gas pressure generated. Moreover, thermal stress stems from the uneven heating of the coal body, while phase change freezing induced by temperature transfer between pore water and the low-temperature CO2 creates an expansive force. Additionally, the differential adsorption rates of CO2 and CH4 cause uneven expansion and contraction within the substrate. Upon gasification, liquid CO2 can exert pressures up to 296 MPa. This pressure, alongside increasing temperature and decreasing pressure, facilitates the phase change gasification of liquid CO2.
During the coal seam liquid injection process, both the ice within the pores and the injection pressure restrain the flow and phase change of liquid CO2. Due to the layered structure of coal, CO2 navigates along these layers, initially completing the compression and elastic deformation of the coal body. As pressure escalates, the coal framework reaches its yield threshold, undergoing plastic damage and fissuring. In the course of tensile damage, the coal body experiences compression around the borehole, reducing the volume of micropores within the coal body and broadening pore throats. Some micropores become interconnected, subsequently enlarging fissure volumes. This adjustment enhances the seepage efficiency and ultimately improves the coal seam’s permeability.
Potential application and prospect
The study of the phase state of CO2 within the coal body, along with its influence range and deformation behavior, highlights that seepage pressure and phase change pressure of CO2 are crucial drivers for enhancing coal body permeability. Phase transition of liquid CO2 significantly contributes to the fracturing effect, making it more pronounced. By increasing the injection pressure and reducing the injection temperature, the CO2 concentration can be augmented. This allows a greater volume of liquid CO2 to permeate the coal seam, generating higher phase change pressure and thereby facilitating the fracturing of the coal seam. To maximize the interaction surface area between liquid CO2 and the coal seam, circular drilling techniques are employed, enlarging the contact area between the coal body and CO2. This approach not only increases the CO2 concentration but also ensures that the coal body is subjected to greater phase change pressure. Given the variability in geological conditions across coal seams, practical implementations can adapt injection pressures and temperatures to modulate the Klinkenberg effect’s impact on permeability. This strategy aims to enhance permeability while concurrently minimizing production costs.
Conclusion
1. With the escalating pressure of liquid CO2 injected into the coal seam and the declining injection temperature, the permeability of the coal body logarithmically increases. The impact of pressure on both the extent of fluid transfer and the permeability range surpasses that of temperature. At a constant pressure, lower temperatures yield a higher CO2 concentration. Subsequently, following the heat exchange between liquid CO2 and coal, a greater phase change pressure is achieved, and an elevated temperature gradient leads to an increase in the amount of contraction due to freezing within the coal skeleton.
2. The permeability of the coal body is influenced by the synergistic effects of pore structure and the coal seam’s original pressure, with increased porosity leading to enhanced permeability. Among primary phase changes, secondary phase changes, and conditions without phase change, the secondary phase change exerts the most pronounced effect on expanding pore space. In comparison, the increase in pore space is more substantial in the Y and Z directions than in the X direction.
3. Seepage pressure stands as the paramount factor influencing the permeability changes in coal seams, succeeded by the pressurizing effect of CO2 phase changes, the cryogenic freezing and shrinkage of the coal skeleton, and deformation due to adsorption resolution. The impact of seepage pressure on augmenting porosity was found to be 2.2, 9.1, and 110 times greater than that of phase changes, cryogenic freezing and shrinkage, and adsorption resolution effects, respectively.
4. Initially, the permeability of the coal body is influenced by the Klinkenberg effect, leading to an initial increase followed by a decrease in permeability. Tensile damage, occurring subsequent to the compression and deformation of the coal body, causes the fissures within the coal body to extend. Consequently, the permeability exhibits an overarching trend of decreasing initially, before exhibiting an increase.
Data availability
The research data can be accessed from [Zenode], the link is [https://doi.org/10.5281/zenodo.13230090]. Software - Figures were made with COMSOL Multiphysics version6.0 (Released on 14 December 2021), http://cn.comsol.com/.
References
Zhang, C. H., Zhang, H. X., Yu, Y. J., Li, H. W. & Wang, L. G. Effect of water saturation and resolubilisation on the fracturing of coal frozen in liquid nitrogen. Coal J. S2, 400–406. https://doi.org/10.13225/j.cnki.jccs.2015.1650 (2016).
Qin, L. Characteristics of Pore Structure Evolution and Mechanism of Permeability Enhancement in Coal Fractured by Liquid Nitrogen Cycle [Doctoral dissertation China University of Mining and Technology]. (2018).
Lv, Z., Luo, S., Xia, C. & Zeng, X. A thermal–mechanical Coupling Elastoplastic Model of Freeze–Thaw Deformation for Porous Rocks. Rock Mech. Rock Eng. 55(6), 3195–3212. https://doi.org/10.1007/s00603-022-02794-y (2022).
Lv, Z., Xia, C., Li, Q. & Si, Z. Empirical Frost Heave Model for Saturated Rock under Uniform and unidirectional freezing conditions. Rock Mech. Rock Eng. 52(3), 955–963. https://doi.org/10.1007/s00603-018-1666-z (2019).
Bai, G. et al. Experimental study on damage law of liquid CO2 cyclic freeze–thaw coal. Energy. 284, 128532. https://doi.org/10.1016/j.energy.2023.128532 (2023).
Sun, Z. X. et al. Molecular modelling of the effect of CO2/N2 binary gas on methane adsorption in coal. Coalf. Geol. Explor. 3, 127–136. https://doi.org/10.3969/j.issn.1001-1986.2022.03.013 (2022).
He, X. Q., Wang, E. Y., Lin & H. Y Mechanism of Pore Gas Effect on Coal Body deformation and Erosion. J. China Univ. Min. Technol. 1, 6–11 (1996).
Qin, X., Cai, J. & Wang, G. Pore-scale modeling of pore structure properties and wettability effect on permeability of low-rank coal. Int. J. Min. Sci. Technol. 33(5), 573–584. https://doi.org/10.1016/j.ijmst.2023.02.005 (2023).
Sampath, K. H. S. M., Perera, M. S. A., Matthai, S. K., Ranjith, P. G. & Dong-yin, L. Modelling of fully-coupled CO2 diffusion and adsorption-induced coal matrix swelling. Fuel. 262, 116486. https://doi.org/10.1016/j.fuel.2019.116486 (2020).
Niu, Q. et al. Experimental study on the softening effect and mechanism of anthracite with CO2 injection. Int. J. Rock Mech. Min. Sci.138, 104614. https://doi.org/10.1016/j.ijrmms.2021.104614 (2021).
Tan, P. et al. Vertical propagation behavior of hydraulic fractures in coal measure strata based on true triaxial experiment. J. Petroleum Sci. Eng.158, 398–407. https://doi.org/10.1016/j.petrol.2017.08.076 (2017).
Men, X., Tao, S., Liu, Z., Tian, W. & Chen, S. Experimental study on gas mass transfer process in a heterogeneous coal reservoir. Fuel Process. Technol.216, 106779. https://doi.org/10.1016/j.fuproc.2021.106779 (2021).
Yin, G. et al. Impact of injection pressure on CO2–enhanced coalbed methane recovery considering mass transfer between coal fracture and matrix. Fuel. 196, 288–297. https://doi.org/10.1016/j.fuel.2017.02.011 (2017).
Wei, G. et al. Liquid CO2 injection to enhance coalbed methane recovery: an experiment and in-situ application test. Fuel. 284, 119043. https://doi.org/10.1016/j.fuel.2020.119043 (2021).
Perrier, L., Pijaudier-Cabot, G. & Grégoire, D. Poromechanics of adsorption-induced swelling in microporous materials: a new poromechanical model taking into account strain effects on adsorption. Continuum Mech. Thermodyn. 27(1), 195–209. https://doi.org/10.1007/s00161-014-0359-4 (2015).
Hwang, W. R. & Advani, S. G. Numerical simulations of Stokes–Brinkman equations for permeability prediction of dual scale fibrous porous media. Phys. Fluids. 22(11). https://doi.org/10.1063/1.3484273 (2010).
Lv, Z., Xia, Caichu, L. & Qiang Experimental and numerical study on frost heave of saturated rock under uniform freezing conditions. J. Geophys. Eng. (2018).
Zhou, S., Zhuang, X. & Rabczuk, T. Phase field method for quasi-static hydro-fracture in porous media under stress boundary condition considering the effect of initial stress field. Theoret. Appl. Fract. Mech. 107. https://doi.org/10.1016/j.tafmec.2020.102523 (2020).
Wang, C. et al. Dynamic analysis of heat extraction rate by supercritical carbon dioxide in fractured rock mass based on a thermal-hydraulic-mechanics coupled model. Int. J. Min. Sci. Technol. 32(2), 225–236 (2022).
Tian, X., Zhang, K., Liu, F., Wang, P. & Xu, S. Characteristics of Convection Heat transfer in PowerLaw Fluid Saturated Porous Media Channel. J. Harbin Inst. Technology: Engl. Ed. 29(2), 52–61 (2022).
Sun, X., Zhang, S., Ma, X., Zou, Y. & Lin, G. Experimental investigation on Propagation Behavior of Hydraulic fractures in Coal Seam during Refracturing. Geofluids. 2019(1), 4278543. https://doi.org/10.1155/2019/4278543 (2019).
Wang, H. et al. Elimination of coal and gas outburst risk of an outburst-prone coal seam using controllable liquid CO2 phase transition fracturing. Fuel. 284, 119091. https://doi.org/10.1016/j.fuel.2020.119091 (2021).
Si, G., Durucan, S., Shi, J. Q., Korre, A. & Cao, W. Parametric Analysis of Slotting Operation Induced failure zones to stimulate low permeability coal seams. Rock Mech. Rock Eng. 52(1), 163–182. https://doi.org/10.1007/s00603-018-1579-x (2019).
Day, S., Fry, R., Sakurovs, R. & Weir, S. Swelling of coals by supercritical gases and its relationship to Sorption. Energy Fuels. 24(4), 2777–2783. https://doi.org/10.1021/ef901588h (2010).
Fan, S. X. Study on permeability enhancement and fracture formation mechanism of liquid CO2 fractured coal rock. J. Rock. Mech. Eng. 4, 703–712. https://doi.org/10.13722/j.cnki.jrme.2020.0228 (2021).
Yang, Y. Response Mechanism and Permeability Modelling of Gas-Containing Coal Flow-Solid Coupling under Stress Perturbation [Master’s Thesis thesis, Chongqing University]. (2022). https://doi.org/10.27670/d.cnki.gcqdu.2022.000932
Padua, A., Wakeham, W. A. & Wilhelm, J. The viscosity of liquid carbon dioxide. Int. J. Thermophys. 15(5), 767–777. https://doi.org/10.1007/bf01447093 (1994).
Cho, Y., Lo, R., Krishnan, K., Yin, X. & Kazemi, H. Measuring absolute adsorption in porous rocks using oscillatory motions of a spring-mass system. Chin. J. Chem. Eng. (English Edition). 44(4), 131–139 (2022).
Schroeder, K., Busch, A., Duffy, G., Fitzgerald, J. E. & White, C. Interlaboratory Comparison of CO2 Adsorption Isotherms on Coals. Pittsburgh Coal Conference Pittsburgh Coal Conference. (2003).
Chongbin, Z., Bruce, H. & Alison, O. Transient-state instability analysis of dissolution-timescale reactive infiltration in fluid-saturated porous rocks: purely mathematical approach. Sci. China: Technological Sci. 63(2), 10 (2020).
Yu, Y. J., Zhang, H., Zhang, C. H., Hao, Z. & Wang, L. G. Effect of temperature and stress on the permeability of moulded coal samples. Coal J. 6, 936–941. https://doi.org/10.13225/j.cnki.jccs.2013.06.029 (2013).
Xue, D. Numerical Simulation of Liquid Carbon Dioxide Flow Process and Penetration Enhancement in Coal Seams [Master’s Thesis thesis, China University of Mining and Technology]. (2021). https://doi.org/10.27623/d.cnki.gzkyu.2021.001371
Xu, J. Z. Study on Pore Structure and Damage Mechanical Characteristics of Liquid CO2 Cyclic Impact Fractured Coal Body [Master’s Thesis thesis, China University of Mining and Technology]. (2020). https://link.cnki.net/doi/10.27623/d.cnki.gzkyu.2020.000556
Hu, S. B., Cai, Y. K. & Wang, E. Y. Mechanism of phase transition cracking in high temperature and high pressure CO2 reaction flow. J. China Univ. Min. Technol. 6, 1203–1215. https://doi.org/10.13247/j.cnki.jcumt.20220621 (2023).
Li, L. G., Kang, T. H. & Li, Y. B. Coal reservoir permeability prediction model considering dynamic Klingberg coefficient. Geophys. J. 1, 304–310. https://doi.org/10.1007/s00603-018-1666-z (2018).
Author information
Authors and Affiliations
Contributions
Qixin Cheng wrote the main manuscript text, Chengyu Li.Gang Bai provided research information and supervised the review, and Xihua Zhou.Fangfang Zhang.Wenjing Zhang. collated the data. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, C., Cheng, Q., Bai, G. et al. Mathematical model of permeability evolution of liquid CO2 pressurized coal. Sci Rep 14, 26314 (2024). https://doi.org/10.1038/s41598-024-75866-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-75866-4