Introduction

Faults exist widely in strata. They are structures in which the crust is fractured by force and significant relative displacement occurs along both sides of the fracture surface1,2,3. They range in size from tens of centimeters to hundreds of kilometers and are often composed of many faults4,5,6. By causing faults, rock strata are destroyed and their stress and displacement fields are changed7,8. Under the influence of underground mining disturbance, the activation of fault surface is easy to induce various mine disasters such as rock burst9, mine water inrush10,11,12 and surface subsidence13,14,15, which seriously threatens national life and property and economic development. For example, a fault-activated rockburst accident in the Jilin Province’s Longjiapu Coal Mine killed 9 and injured 12 people on June 9, 2019. Investigation of the accident revealed that the fault slip was induced by fault tectonic stress and mining disturbances at the mining face16.

For this reason, the causes of fault slip have been studied extensively by scholars. Pan et al.17 believe that fault slip is caused by the stress reduction of vertical fault plane and the stress increase of parallel fault plane due to mining activities. On this basis, according to the fault stick-slip model, the main factor affecting the fault stick-slip behavior is the normal stress on the fault plane. From the initial stage of sliding to the later stage of sliding, the normal stress gradually tends to be stable from fluctuation18. After that, the concept of ground pressure induced by fault coal pillar appeared, which includes: fault activation, pillar failure and coupling deformation19. Sainoki et al.20,21,22 studied three potential mechanisms that may trigger fault slip, namely rough shear, stope mining and the combination of the two. Wang et al.23 established a calculation model of stress distribution of fault plane influenced by tectonic and mining stress, and obtained the stress variation rules of vertical and parallel fault planes. Cai et al.24 summarized four conceptual models of fault activation and concluded that fault-type rock burst is superimposed by fault high static load stress and fault slip load stress.

On the influence of fault slip on mining stress, Ji et al.25 conducted simulation studies on the longwall working face parallel to the fault strike and the working face perpendicular to the fault strike, respectively, and obtained the corresponding stress distribution state near the fault. Chen et al.26 studied the distribution law of supporting stress when the mining face crosses the fault through microseismic monitoring system and numerical simulation. Zhang et al.27 conducted a simulation study on the displacement, stress and plastic zone distribution of roadway near the fault. Wang et al.28 found that under the influence of faults, the stress in the stable state would increase abnormally, and the displacement of overlying rock on both sides of the fault was significantly different.

In summary, scholars’ research on faults mostly focuses on the fault slip mechanism, and the influence of fault activation on mining stress evolution is relatively small, and the relationship between fault surface activation and mining stress evolution of mining face is rarely analyzed. At the same time, there are few analyses on other factors affecting fault activation (such as fault dip angle). Therefore, in this paper, the interaction between mining stress and fault activation and the effect of fault dip are studied by theoretical, experimental and simulation methods.

Mechanical mechanism of fault activation

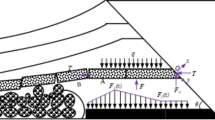
In-depth understanding of the fault slip mechanism is beneficial to underground safe mining. Therefore, the distribution model of mining stress and fault tectonic stress during vertical fault direction advance is established, and a mechanical model is established by taking a tiny unit of the fault plane (Fig. 1).

Fig. 1
figure 1

Mechanical model of fault activation.

Full size image

Base on the theory of elastic mechanics29, the relationship between normal stress σn and shear stress τn on the fault plane with respect to fault inclination α is shown in Eq. 1.

$$\left\{ {\begin{array}{*{20}l} {\sigma _{n} = p_{x} l + p_{y} m} \\ {\tau {}_{n} = p_{x} m + p_{y} l} \\ {p_{x} = \sigma _{{xx}} l + \tau _{{yx}} m} \\ {p_{y} = \sigma _{{yy}} m + \tau _{{xy}} l} \\ {l = \sin \alpha } \\ {m = \cos \alpha } \\ \end{array} } \right. \Rightarrow \begin{array}{*{20}l} {\sigma _{\alpha } = \frac{{\sigma _{{xx}} + \sigma _{{yy}} }}{2} + \frac{{\sigma _{{yy}} - \sigma _{{xx}} }}{2}\cos 2\alpha + \tau _{{xy}} \sin 2\alpha } \\ {\tau _{\alpha } = \frac{{\sigma _{{xx}} - \sigma _{{yy}} }}{2}\sin 2\alpha + \tau _{{xy}} \cos 2\alpha } \\ \end{array}$$
(1)

In the formula, px and py are the components of the total stress p on the fault plane of the element body in the coordinate axis direction, N/m2; l and m are the cosine of the angle between the normal direction outside the fault plane and the positive direction of the x and y axes. τxy = τyx is the stress component of the element body, N/m2. σxx and σyy are horizontal and vertical stresses respectively.

When the τα = 0, the total stress P on the fault plane is the main stress σ. According to the normal stress solution method, the expression can be obtained as follows:

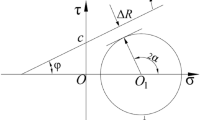
$$\left. \begin{gathered} {\sigma _{\hbox{max} }} \hfill \\ {\sigma _{\hbox{min} }} \hfill \\ \end{gathered} \right\}=\frac{{{\sigma _{xx}}+{\sigma _{yy}}}}{2} \pm \sqrt {{{\left( {\frac{{{\sigma _{xx}} - {\sigma _{yy}}}}{2}} \right)}^2}+{\tau ^2}_{{xy}}}$$
(2)

On this basis, the Mohr-Coulomb strength criterion is used to analyze the failure and instability of the fault plane. The relationship between Mohr circle and strength curve is shown in Fig. 2.

$${\tau _\alpha }={\sigma _\alpha }\tan \varphi +c$$
(3)

Where: φ and c are the fault friction angle and cohesion.

Fig. 2
figure 2

Mohr’s stress circle and its fault plane Coulomb strength criterion envelope.

Full size image

In order to make the fault whose stress state is in Mohr circle ① fail and lose stability, it is necessary to change its stress to make it intersect with the failure criterion line. The shear stress and the maximum principal stress σ1 of the fault can be increased to the Mohr circle ②, and the shear stress can be increased and the minimum principal stress σ3 can be reduced to the Mohr circle ③. If the coordinate system is established by the main plane, τxy = 0, for the normal fault, σyy = σ1, σxx = σ3, the angle between the maximum principal stress and the outer normal is the fault dip angle α; for reverse faults, σyy = σ3, σxx = σ1, and the angle between the maximum principal stress and the outer normal is π/2-α. Then, the normal stress solution principle is used to solve it and combined with Eq. 3. Finally, the criterion of normal and reverse fault activation can be obtained by simplification:

Normal fault:

$${\left( {{\sigma _1} - {\sigma _3}} \right)_{slip}}=\frac{{2\left( {{\sigma _3}\tan \varphi +c} \right)}}{{\left( {1 - \cot \alpha \tan \varphi } \right)\sin 2\alpha }}$$
(4)

Reverse fault:

$${\left( {{\sigma _1} - {\sigma _3}} \right)_{slip}}=\frac{{2\left( {{\sigma _3}\tan \varphi +c} \right)}}{{\left( {1 - \tan \alpha \tan \varphi } \right)\sin 2\alpha }}$$
(5)

Let the left (σ1-σ3) slip of Eqs. 4 and 5 be the fault slip threshold, which is obviously positive. Therefore, to make the right side of the equation positive, the fault dip α must satisfy the criterion of positive and reverse fault activation: φ < α < π/2 (normal fault), 0 < α < π/2-φ (reverse fault).

When the Mohr circle is tangent to the failure criterion (Fig. 3), the relationship between the fault inclination α and the internal friction angle φ of the fault is as follows: α = π/4 + φ/2 (normal fault), α = π/4-φ/2 (reverse fault).

Fig. 3
figure 3

Mohr stress circles and their fault plane Coulomb strength criterion envelope of positive and reverse faults.

Full size image

That is, when the fault dip angle α = π/4 + φ/2, the minimum critical value of normal fault activation occurs; when the fault dip angle α = π/4-φ/2, the minimum critical value of reverse fault activation occurs. Substituting them into Eq. 4 and Eq. 5 respectively, the minimum fault slip threshold can be obtained as follows:

Normal fault:

$${\left( {{\sigma _1} - {\sigma _3}} \right)_{slip - \hbox{min} }}=\frac{{2\left( {{\sigma _3}\tan \varphi +c} \right)}}{{\left[ {1 - \cot \left( {\frac{\pi }{4}+\frac{\varphi }{2}} \right)\tan \varphi } \right]\cos \varphi }}$$
(6)

Reverse fault:

$${\left( {{\sigma _1} - {\sigma _3}} \right)_{slip - \hbox{min} }}=\frac{{2\left( {{\sigma _3}\tan \varphi +c} \right)}}{{\left[ {1 - \tan \left( {\frac{\pi }{4} - \frac{\varphi }{2}} \right)\tan \varphi } \right]\cos \varphi }}$$
(7)

The minimum fault slip threshold (σ1-σ3) slip−min is positively correlated with fault internal friction angle φ, cohesion c and minimum principal stress σ3. The fault slip threshold with the change of fault dip angle can be obtained by numericalizing Eq. 4 and Eq. 5, as shown in Fig. 4. Where φ = 30 °, c = 6 MPa.

Fig. 4
figure 4

Evolution of critical value in fault reactivation along with the variation of fault dip.

Full size image

The fault slip threshold (σ1-σ3) slip and the fault dip angle α are symmetrical in the range of φ ~ π/2 (normal fault dip angle range) and 0 ~ π/2-φ (reverse fault dip angle range). When the fault dip angle α = π/4 + φ/2, π/4-φ/2, respectively, corresponding to the minimum fault slip threshold (σ1-σ3) slip−min, the dip angle is the minimum critical dip angle of fault activation. In the process of underground operation, the mining stress of the fault plane shows the characteristics of pressure relief and vertical loading in the horizontal goaf, that is, σ3 decreases and σ1 increases. At this time, the critical value of fault activation (σ1-σ3) slip decreases and the possibility of fault slip increases.

The smaller the normal stress σα of the fault plane is, the smaller the friction force generated by it. The greater the shear stress τα, the greater the possibility of failure slip. In this regard, relevant scholars defined the ratio of the two as the fault plane slip tendency index Ts30, namely:

$${T_s}=\frac{{{\tau _\alpha }}}{{{\sigma _\alpha }}}=\frac{{\left( {{\sigma _{xx}} - {\sigma _{yy}}} \right)\sin \alpha \cos \alpha +\left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right){\tau _{xy}}}}{{{\sigma _{xx}}{{\sin }^2}\alpha +2{\tau _{xy}}\sin \alpha \cos \alpha +{\sigma _{yy}}{{\cos }^2}\alpha }}$$
(8)

The larger the Ts is, the more easily the fault plane slips and fails. When the fault dip angle α is closer to the minimum critical dip angle of fault activation and the propulsive distance L is close enough, the fault slip will occur. The internal relationship among mining, fault activation and stress evolution of surrounding rock is shown in Fig. 5.

Fig. 5
figure 5

Relationship between mining, fault activation and stress evolution.

Full size image

On the basis of the above analysis, taking the geological structure conditions of Zhangshuanglou Coal Mine 74,104 as an example, the interaction law between mining stress and fault activation is deeply studied by physical and numerical simulation methods.

Physical model test

Geological structure of 74,104 mining face

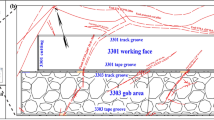
The 74,104 coal mining face of Zhangshuanglou Coal Mine starts from the protective pillar of the industrial square in the east, the west is the unmined area, the south is the 74,102 goaf, and the north is close to the boundary of the mine field. The coal is 4 m thick, located 1130 m underground, with a propulsion length of 1280 m and a mining face length of 174.6 m. During the excavation of the roadway, 8 normal faults with a drop height greater than 1.0 m were exposed, and the most influential faults were f2 and f3 faults. The dip angle of f2 fault was 22 °, and the drop height was 2.6–4.3 m. The dip angle of f3 fault is 65 °, and the drop is 4 m. The overall fault dip angle range is 22 ° ~ 65 °, with an average of about 45 °, and the fault drop range is 1.3 ~ 4.3 m, with an average of about 2 m. The ___location of the mining face and the fault and the geological columnr are shown in Fig. 6.

Fig. 6
figure 6

Longwall working face and fault relative position and column diagram.

Full size image

Physical model establishment

Principle of similarity theory

Due to the limitations of long monitoring time and high cost in field tests, physical simulation can effectively characterize the movement behavior of overlying strata caused by mining activities with short monitoring time and low cost. Therefore, physical simulation is widely used by many researchers in mining stress evolution and surface subsidence caused by mining31,32 and the fault slip process1,4.Because the actual coal mining face is different from the size of the laboratory experiment, the model material and the field conditions need to have a suitable physical ratio, so the modeling material needs to be tested for mechanical properties, and its performance should meet the principle of similarity theory33,34. The stress ratio Cσ, density ratio Cρ and geometric ratio CL should be as follows:

$$\frac{{{C_\sigma }}}{{{C_\rho } \times {C_L}}}=1$$
(9)
$${C_L}=\frac{{{L_p}}}{{{L_m}}},{C_\sigma }=\frac{{{\sigma _p}}}{{{\sigma _m}}},{C_\rho }=\frac{{{\rho _p}}}{{{\rho _m}}}$$
(10)

Where: the subscript p represents the prototype, and m represents the model; L represents length, σ represents stress, and ρ represents volume density. If the constants CL, Cρ and Cσ are determined, they can be obtained according to Eq. 1.

Physical model establishment

A physical model of 2.5 × 0.3 × 1.7 m (length × width × height) was established (Fig. 7). Considering the platform size and other factors, CL is set to 100. Cρ is generally set from 1.2 to 1.7 (Jiang et al. 2013), and Cρ is 1.7. According to Eq. 9, Cσ is 170. The material ratios of different rock formations are obtained through mechanical experiments as shown in Fig. 8, and the material ratios of different rock formations are shown in Table 1. The equivalent load on the upper part of the model is 0.151 MPa, the model’s advancing direction is from left to right, and the excavation step length is 5 cm.

Fig. 7
figure 7

Physical model and monitoring system.

Full size image
Fig. 8
figure 8

Example of material ratio experiment.

Full size image
Table 1 Experimental material ratio.
Full size table

Monitoring system

The TS3890N resistance strain gauge and the Coord Measis photogrammetry system (camera, scaleplate, photogrammetry system software) were used to monitor the stress and displacement changes during the test (Fig. 9). The resolution of the TS3890N static resistance strain gauge is ± 1µε, and the accuracy of the photogrammetry system is 10−3 mm. The specific monitoring scheme is as follows: stress monitoring adopts pressure box, and two measuring lines are arranged. One of them is located in the floor of 7# coal seam, with a total of 19 pressure boxes, and the other is located in the overlying fault surface of coal seam, with a total of 6 pressure boxes, which are used to monitor the advance abutment pressure and the stress change of fault surface in the mining process of working face. Seven displacement survey lines were arranged at a distance of 10 cm at a distance of 10 cm from 7# coal, 26 measuring points for each line, a total of 182 measuring points, which were used to monitor the evolution of overburden displacement before and after the working face advancing to the fault (Fig. 7).

Fig. 9
figure 9

Model monitoring system.

Full size image

Result analysis

Overburden rock and fault failure characteristics

Due to the large number of mining face advancing steps, some typical overlying strata movement pictures are selected for detailed description and analysis, as shown in Fig. 10; Table 2 respectively.

Fig. 10
figure 10

Failure characteristics of overlying strata at different distances from faults (“-” Representative after the fault).

Full size image
Table 2 Description of overlying strata failure characteristics.
Full size table

From Fig. 10; Table 2, it has experienced the first pressure and 7 cycles of pressure from the excavation to the fault 70 m. Under the experimental scale (model 1 cm = actual 1 m), the first basic roof caving step distance is 55 cm. Before passing through the fault, the regional periodic pressure distance affected by the fault is 10 ~ 15 cm, and the periodic pressure distance after passing through the fault is basically 20 cm. During this process, the height of fracture development increased from 32.3 cm to 83.4 cm, and the height of fracture development increased the most when the fault was first activated, which increased by 47 cm compared with the previous pressure.

For fault movement, when the mining face advances 15 cm from the fault, the initial activation occurs in the upper part of the fault, and the activation height is 63.4 cm. When advancing to the fault, the second activation occurs at the lower part of the fault, and the upper rock layer of the fault is destroyed and slipped, with a slip height of 2.9 cm. When the fault is 20 m, the hanging wall of the fault produce large longitudinal cracks. After that, the cracks in the rock strata near the fault gradually close and finally tend to be stable. In summary, when the mining face is advancing upward from the foote of the normal fault, the overburden migration around the fault is intense from 15 m away from the fault to 20 m behind the fault, the pressing step of the mining face is small, and the fault activation and fracture development are transferred from the high to the low of the fault.

Characteristic of overlying strata deformation

Fig. 11
figure 11

Contour maps of overburden displacement at different distances from faults (“-” Representative after the fault).

Full size image

As can be seen from Fig. 11, advancing from the normal fault footwall upward direction, the displacement of the fault footwall is higher than that of the upper wall, and the displacement of the upper strata of the fault is higher than that of the lower strata and gradually expands to the lower strata. When the longwall working face is from 15 m away from the fault to 20 m after the fault, the overburden displacement is greatly affected by the fault, especially when it is pushed to the fault, the overburden displacement changes sharply.

From Fig. 12 (the displacement in the figure is the actual displacement after proportional conversion), before the fault, the maximum variation of overburden displacement (the difference between the previous maximum displacement) is all above 3.18 m, while within 30 m after the fault, the maximum variation of displacement is all below 0.8 m, and the maximum variation of mining face displacement before and after the fault is very different. The position of the maximum displacement change is also closer to the fault with the increase of the advancing distance. This shows that fault activation leads to abrupt displacement of overlying rock, which releases a lot of elastic energy and is easy to strong ore pressure accidents.

Fig. 12
figure 12

Overburden displacement curves at different distances from faults (“-” Representative after the fault).

Full size image

Characteristic of stress variation

Fig. 13
figure 13

Advance abutment pressure peak and stress distribution of fault plane change curve.

Full size image

From Fig. 13a, when the fault is 15 m away from the fault and located at the fault, the dislocation slip occurs in the upper part of the fault corresponding to the above analysis and gradually expands along the fault plane, the overburden migration and failure characteristics change greatly, and the peak increases greatly. The peak value is higher within 20 m after the fault, although the reduction of stress is large. When 30 m after crossing the fault, the overburden pressure is normal, and the peak value increase is small. If the stress stabilization stage 30 m after the fault is taken as the basis, the peak stress increase area is within 20 m before and after the fault, the maximum stress is 62.68 MPa.

From Fig. 13b, when the mining face is excavated to 40 m, 55 m and 75 m, the peak stress of the fault plane is 37.06 MPa, 38.49 MPa and 39.43 MPa respectively, which are located at measuring points 21, 22 and 24 respectively. The number of measuring points of the fault plane is from the top down, as shown in Fig. 7. Therefore, the peak stress value of the fault surface gradually shifts from the top to the bottom with the increase of mining distance, indicating that the fault above the goaf first suffers damage and cracks under the influence of mining, and then gradually expands to the lower strata of the fault, which corresponds to the migration characteristics of the overburden rocks above the fault.

Combined with the experimental analysis of Table 2; Figs. 11, 12 and 13, it can be seen that with the decrease of the distance between the working face and the fault, the fault is affected by the periodic weighting and fracture development of the overlying strata in the goaf. The horizontal stress of the fault gradually decreases, the lateral limit weakens, and the vertical stress gradually increases. Combined with the theoretical analysis, it can be seen that the critical value of fault activation gradually decreases, and the tendency of fault activation increases, which eventually leads to fault activation. The experimental conclusion and the above theoretical analysis model are mutually demonstrated.

Due to the limitation of similar simulation stress monitoring, numerical simulation will be used to further study the impact of fault on mining stress evolution.

Numerical simulation and field monitoring

Numerical model

FLAC3D (Fast Lagrangian Analysis of Continua in 3Dimensions) is a three-dimensional explicit finite difference method (FDM) numerical simulation software. The explicit FDM is used to solve the constitutive model of the material. The stress and strain state of the material element is gradually updated in the Lagrangian framework to deal with complex nonlinear problems and large deformation problems. It has high computational efficiency and is suitable for numerical simulation in the field of geology and geotechnical engineering. Therefore, combined with the geological column diagram (Fig. 6), the numerical model was established by FLAC3D software (Fig. 14) (taking the fault dip angle of 45° as an example).

Fig. 14
figure 14

Numerical fault model.

Full size image

Mohr-Coulomb constitutive model is a classical soil mechanics and rock mechanics model, which is based on Mohr stress circle and Coulomb failure criterion. It is widely used in geotechnical engineering and mining engineering to simulate the strength and failure behavior of materials (such as soil and rock) under shear stress. Therefore, the numerical model of this paper adopts Mohr-Coulomb constitutive model, and adopts large strain deformation mode in order to be more in line with the actual situation35. The model size was 500 (length) ×270 (width) ×160 (height) m. The interface contact plane element was used to simulate the fault plane, and the Coulomb shear model was used for the fault plane. The main parameters were normal stiffness of 20 GPa, tangential stiffness of 10 GPa, internal friction angle of 20° and cohesion of 0.7 MPa36. The top of the model is subjected to 25.6 MPa vertical stress and 41.4 MPa horizontal stress, only the top of the model is free. Rock mechanics parameters are obtained by empirical reduction on the basis of experimental data (Table 3). The samples were sampled on site and processed into standard specimens, and the compressive, tensile and shear tests were carried out respectively (Fig. 15). The reduction formula of rock mechanics parameters is as follows37,38:

$$\frac{{E_{m} }}{{E_{r} }} = 10^{{0.0186RQD - 1.91}}$$
(11)

Where: Em and Er are the elastic modulus of rock mass and intact rock mass, GPa; RQD is the rock quality index, %.

The strength of rock mass is calculated according to the elastic modulus ratio Em/Er, as shown below.

$$\sigma _{{cm}} = \sigma _{c} \times \frac{{E_{m} }}{{E_{r} }}$$
(12)

Where: σcm and σc are the strength of rock mass and intact rock mass, MPa.

Fig. 15
figure 15

Mechanical parameter experiment of coal and rock mass.

Full size image
Table 3 Rock mechanics parameters in simulation.
Full size table

Influence of mining stress on fault activation

Fig. 16
figure 16

Stress nephogram at different distance from fault.

Full size image

As can be seen from Fig. 16a ~ f, the influence range of mining stress gradually increases with the increase of advancing distance. When 100 m away from the fault (Fig. 16c), the mining stress is connected with the static load stress field at the fault, and the stress of the surrounding rock of the fault increases. After this, the degree of stress superposition deepens and the activation risk increases. Considering that there are many times of advancing distance, the stress curve drawn according to the advancing distance in Fig. 15 will not be clear enough, and when the working face is 100 m away from the fault, mining will have a significant impact on the fault stress. Therefore, the advancing distance within 100 m from the fault is taken as an example to draw the stress curve, as shown in Fig. 17.

Fig. 17
figure 17

Advancing abutment pressure curve of mining face at different distance from fault.

Full size image

When 100 m, 70 m, 30 m, 20 m and 10 m away from the fault, the abutment pressure at the fault is 33.4 MPa, 34.8 MPa, 41.1 MPa, 46.1 MPa and 59.6 MPa, respectively. The stress concentration coefficients are 1.18, 1.23, 1.43, 1.63 and 2.1 respectively (the in-situ stress is 28.2 MPa), with an increase of 4.2%, 16.3%, 14% and 28.8%, respectively. It can be seen that the advancing distance of the working face is positively correlated with the stress of the fault surface. Especially within 30 m from the fault, the superimposed increase of mining stress and static load stress of the fault gradually increases. At this time, the advancing distance of the working face has a strong positive correlation with the fault stress.

In the simulation results, stress measurement lines are arranged on the fault plane above the floor of 7# coal seam, and σxx, σyy and τxy at different mining distances are obtained respectively. The changes of normal stress σn and shear stress τn of the fault plane during the advancing process can be obtained by substituting them into Eq. 1, as shown in Fig. 18.

Fig. 18
figure 18

σn and τn change curve of fault plane at different distance from fault.

Full size image

When the working face is 80 m away from the fault, the σn and τn of the fault plane around 80 m away from the floor of 7# coal seam begin to change significantly. After that, the normal stress position and stress value of the fault plane gradually decreased. The minimum normal stress was 25.6 MPa, 22 MPa, 15.3 MPa and 1.7 MPa, respectively, with a decrease of 14%, 30.5% and 88.9%. The positions were located at 54 m, 35 m, 25 m and 7.4 m from the floor of 7# coal seam. The maximum shear stress of the fault plane is 9.9 MPa, 11.8 MPa, 12.6 MPa and 16.7 MPa, respectively, with an increase of 19%, 6.8% and 32.5%, respectively, and its position is 80 m, 78 m, 51 m and 31.8 m from the floor of the 7# coal seam. It indicates that during the mining process, the minimum σn of the fault plane gradually decreases, the maximum τn gradually increases, and the positions of both fault planes gradually shift from the high to the low. It should be pointed out that within 40 m from the fault, the shear stress of the fault plane appears negative and the negative region also gradually moves down and increases. According to Eq. 1, the vertical stress σyy in this region is greater than the horizontal stress σxx, and the fault activation possibility is greater.

The change curve of fault activation tendency index (Ts) can be obtained by the ratio of the σn to the τn on the above fault plane, and the corresponding change curve of fault displacement can be obtained by the displacement measurement line, as shown in Fig. 19.

Fig. 19
figure 19

Fault activation tendency index (Ts) and displacement distribution curve at different distances from faults.

Full size image

According to the Coulomb shear failure criterion of contact surface in FLAC3D, the shear stress Fsmax required for contact surface nodes to slide can be given as39:

$${F_{s\hbox{max} }}={C_{if}}A+\tan {\varphi _{if}}{F_n}$$
(13)

Where: Cif represents the cohesive force on the contact surface node, MPa; A represents the area of the contact node, m2; φif represents the internal friction angle of the contact surface node, °; Fn stands for normal stress of contact surface joint, MPa. Considering that the cohesive force is small relative to the σn and τn on the node, it can be ignored, then Eq. 13 can be simplified as:

$$\tan {\varphi _{if}}=\frac{{{\tau _{\hbox{max} }}}}{{{\sigma _n}}}$$
(14)

According to Eq. 14, the fault activation risk reference line can be derived, as shown in Fig. 19a (the internal friction angle of the fault is 18°). When Ts≥tanφif (above the fault activation reference line), the fault plane can be judged to be activated; when Ts < tanφif (below the fault activation reference line), the fault plane is in the elastic stage. It can be seen from the figure that when the mining face is 20 m away from the fault, the fault plane located in the range of 25 ~ 80 m away from the floor of the 7# coal seam is activated. When pushed to the fault, all the faults above the 7# coal seam are activated. The displacement change corresponds to the fault activation, and the activation of the upper part of the fault is more serious, and the corresponding displacement is also larger, and the maximum displacement is 2 m, which is consistent with the fault drop. When the longwall working face is advanced to the fault, the lower part of the fault (within 25 m from the 7# coal seam floor) also begins to activate, and the corresponding displacement increment is larger, as shown in Fig. 19b.

In summary, during the mining process, abutment pressure at fault increases gradually, σn at fault plane decreases gradually, τn increases gradually, fault activation tendency and displacement increase and transfer from high to low fault, which is mutually verified with the physical simulation conclusions.

Evolution law of mining stress under fault influence

Fig. 20
figure 20

Variation curve of peak abutment pressure at different distance from fault.

Full size image

As shown in Fig. 20, during the period 190 ~ 150 m away from the fault, the stress increase is mainly influenced by the setup entry and the initial pressure, and then the stress increase decreases. With the gradual decrease of the distance from the fault, the fault slip tendency index (Ts) gradually increases, and the advance abutment pressure peak gradually increases. When the fault is 20 m away from the fault, the fault slip tendency index (Ts) is higher than the base line of fault activation risk, the fault is activated for the first time, the stress surges, and the peak leading abutment pressure surges from 62.3 MPa to 65.3 MPa, with an increment of 3 MPa. When 0 m away from the fault, the fault occurs secondary activation, the peak value increases from 65.3 MPa to 67.3 MPa. Because the initial activation range of fault is wider than the new addition range of fault secondary activation, the initial activation of fault has the greatest impact on the leading abutment pressure of the mining face, and the peak increment of abutment pressure is large, which is easy to induce strong ore pressure disaster. The mining stress gradually decreases after crossing the fault and finally becomes stable.

If the peak stability stage is taken as the basis (the average peak stability is 62 MPa), the peak rise area is within 20 m away from the fault to 10 m across the fault, and the maximum concentration coefficient is 2.4. The result of the numerical simulation is similar to that of the similar simulation, but the difference is that the similar simulation is a two-dimensional model and lacks a set of side limits. The collapse of the similar simulation is more serious, and the peak stress increase area after the fault is 10 m more than that of the numerical simulation.

Field monitoring demonstration

The 32-channel SOS microseismic monitoring system equipped with 74,104 working face of Zhangshuanglou Coal Mine was used to monitor the microseismic energy in the fault area, and the conclusions of the previous research were analyzed and verified. Figure 21 shows the change process of microseismic energy and vibration number recorded by the nearby microseismic monitoring probe during the process of advancing to the f5 fault.

Fig. 21
figure 21

Evolution process of microseismic energy and vibration times when advancing to f5 fault.

Full size image

With the increase of advance date, the distance from fault f5 decreases gradually, and the microseismic energy and vibration times increase gradually. When it is about 20 m away from the fault and located at the fault, the sudden increase of microseismic energy is easy to induce strong mine pressure disasters such as rock burst. When the fault is about 20 m away, the microseismic energy suddenly increases from 1.1 × 104 J to 3.4 × 104 J, with an increase of 2.3 × 104 J. When the fault is located, the microseismic energy suddenly increases from 2.8 × 104 J to 3.7 × 104 J, with an increase of 0.9 × 104 J. The microseismic energy and vibration frequency decrease gradually after about 10 m crossing the fault.

It shows that when the fault is about 20 m away, the fault may be activated for the first time, resulting in a sudden energy increase, and the increase is the largest. When the fault is located at the fault, the secondary activation occurs, and the microseismic energy and vibration times are the largest, and the increase rate is lower than the first fault activation. The monitoring results are mutually verified with the above physical and numerical simulation results.

Discussion

In order to discuss the influence of fault dip on fault slip and mining stress evolution of mining face, based on the above model, numerical models of fault dip of 20°, 30°, 45° and 60° were established according to clockwise rotation of the central part of 7# coal seam as the circular point O of the rotation change of fault dip (Fig. 22). The research results are shown in Figs. 23, 24.

Fig. 22
figure 22

Numerical model of different fault dip angles.

Full size image
Fig. 23
figure 23

Variation curve of advance abutment pressure of 7# coal seam under different fault dip angles.

Full size image

As can be seen from Fig. 23, during the advancing of the mining face, the peak abutment pressure at the fault decreases with the increase of fault inclination (except 20°). For the different distance from the fault, the peak value under different fault dip angle is different, indicating that the advance distance required for fault activation with different dip angle is different. Fault activation tendency index (Ts) under each fault dip angle is shown in Fig. 24.

Fig. 24
figure 24

Fault activation tendency index (Ts) varies with advancing distance under different fault inclination angles.

Full size image

When the fault dip angle increases from 20 ° to 60 °, the distance between the working face and the fault during fault activation decreases from 100 m to 20 m, and the fault initial activation occurs, and the fault activation range is 60 ~ 80 m, 70 ~ 80 m, 25 ~ 80 m and 28 ~ 55 m away from the 7# coal seam floor respectively. It shows that the smaller the dip angle of the fault, the advancing distance of the mining face required for the initial activation of the fault decreases gradually. The greater the fault dip, the higher fault plane will be far away from the edge of the collapse angle of the working face, and the advancing distance of the mining face required for the initial fault activation will gradually increase and the slip range of the fault will decrease.

If the peak stability stage of advanced abutment pressure under each fault dip (20 m across the fault) is taken as the basis, the peak elevation area with fault dip angles of 30°, 45° and 60° is from 20 m before the fault to 10 m after the fault. The peak elevation area of fault inclination of 20° is 20 ~ 100 m before the fault.

Conclusion

  1. (1)

    Combining the theory of elasticity and the Mohr-Coulomb criterion, the criterion of positive and negative fault activation is obtained. It is found that there is a symmetric relationship between the fault slip threshold (σ1-σ3) slip and the fault inclination α. The mechanical mechanism of fault activation is that the vertical principal stress σ1 increases, the horizontal principal stress σ3 decreases, and the fault slip threshold (σ1-σ3) slip decreases.

  2. (2)

    When advancing from the normal fault footwall upward direction, the σn of the fault plane gradually decreases, the τn gradually increases, the fault slip tendency index (Ts) and the advance abutment pressure gradually increase, and the increase of the activation position, stress and displacement peak value is transmitted from the high to the low fault plane.

  3. (3)

    When the longwall working face is mined from the footwall of the normal fault to the hanging wall, the mining distance required for fault activation gradually decreases with the decrease of the fault dip angle, and the peak rise area of the longwall working face gradually increases with the decrease of the fault dip angle.

  4. (4)

    Based on field microseismic monitoring, it is known that when the mining face is about 20 m away from the front and back of the fault, the fault will be activated, the peak of leading abutment pressure will change greatly, and the microseismic energy will increase abruptly, which is the main control area of impact disaster.