Introduction

Recent advancements in digital systems have significantly transformed transactions between individuals and businesses. The efficiency and convenience offered by digital payment systems have bolstered their popularity; however, they have also introduced serious fraud concerns. As illustrated in Fig. 1, digital banking offers numerous advantages. Nonetheless, safeguarding customers’ private information remains a formidable challenge in online commerce1. Digital payment fraud threatens the integrity of the financial ecosystem and erodes user trust and security in e-commerce2. With fraud tactics evolving in tandem with technological advancements, financial institutions, businesses, and payment service providers must adopt robust fraud detection strategies.

Fig. 1
figure 1

Benefits of digital banking.

Full size image

Threats to cyber security in digital banking are shown in Fig. 2. The protection of data networks and systems against complex, dynamic, and rapidly evolving cyber threats requires constant adaption. Proactively identifying and preventing illegal or suspicious activities within the digital payment space is essential for safeguarding these systems. Such fraudulent activities can include identity theft, account takeover, unauthorized access, and other cyberattacks that exploit vulnerabilities in payment systems3. The complex and sophisticated nature of digital payment fraud highlights the need for advanced and adaptable detection techniques. Traditional fraud prevention methods, such as rule-based systems and manual monitoring, are becoming less effective as fraud techniques grow more sophisticated.

Fig. 2
figure 2

Threats for cyber security in digital banking.

Full size image

The main areas relevant to understanding and mitigating these cyber threats are within the significant fields of data science and artificial intelligence4. AI has several opportunities to improve the protection of data and systems against cyber threats. The fast-paced advancement of information technology, which can be best demonstrated through the example of online banking, has changed the face of the banking sector in a very dramatic manner5.

These AI systems are changing the way banks protect their digital infrastructure from ever-evolving cyber threats@@6,7,8. AI, while analysing vast transaction data volumes in real-time, can identify anomalies and patterns indicative of fraudulent behaviour, thereby enhancing detection rates. For example, Danske Bank implemented an AI-based algorithm for fraud detection, which increased its fraud detection capability by 50% while reducing false positives by 60%9. Moreover, AI can also predict any kind of cyber breach in advance by analysing historical data for the visibility of vulnerabilities within the IT infrastructure. Through the scanning of IT asset inventory and user behaviours, AI platforms are in a position to identify applications susceptible to attacks so that IT teams can zero in on their responses. AI can automate threat-hunting processes and increase detection rates by more than 95%. New threats can be anticipated and detected even in their early instigating stimulation due to the capability of AI in learning, adapting, and even evolving with the patterns of previous aggressions. With the growing popularity of mobile banking and other remote devices, endpoint security has become of growing concern10. AI applications can set up behavioural baselines for devices and user activities, alerting IT teams to investigate the unusual behaviour as it arises. As digital banking continues to proliferate, AI will play an essential role in safeguarding sensitive financial data11,12.

While AI can help improve cybersecurity in digital banking, but it also has cons. Poor quality data can result in inaccurate threat detection, increasing the number of false positives and leading to a loss of trust in the AI system. Moreover, biased or incomplete data will compromise the effectiveness of AI models13. More and more, hackers are employing advanced means such as AI. This implies that banks are at greater risk of falling victim to AI-based attacks. Growing threats of this nature especially towards successive anti-virus mechanisms can lead to the development of a vicious cycle. Most even look expensive and unfeasible to implement especially on regions such as financial institutions which do not have the system or the capability already in place. For example, bridging gaps created by different AI tools may pose a challenge if the tools are not designed to work with the other security systems, thus creating additional gaps. Many AI-driven cybersecurity solutions are expensive, particularly in terms of technology, training, and upkeep14,15,16. For this reason, smaller financial institutions often lack the resources to fund AI, further exacerbating the disparities in cybersecurity between large and small banks. Addressing these concerns is critical to ensuring the rigorous and efficient application of AI to fortify systems against ever-evolving cyber threats17. Deep learning models offer promising solutions to these problems, and their impact on society will likely be significant.

The major contribution of this research work is:

  • To introduce a new FinSafeNet based on CNN, Bi-LSTM and dual-attention mechanism to enhance the security of digital banking transactions.

  • To introduce a new, I-SLOA optimization algorithm for optimal feature selection. This algorithm mimics the Hierarchical Particle Swarm Optimization (HPSO) in the attacking phase and Adaptive Differential Evolution (ADE) in the reproduction process, resulting in highly convergent and efficient feature selection.

  • To develop a new MKPCA with Nyström Approximation for a reduction in computational complexity and improvement in the model’s efficiency.

The remainder section of this article is organized as follows: Sect. 2 discusses about the existing works on digital banking and cyber-security. The proposed approach for efficient and secured digital banking is discussed in Sect. 3. The results recorded by the proposed model are discussed in Sect. 4. This article concludes with Sect. 5.

Literature review

In 2024, AL-Dosari et al.,8 assessed the impact of AI on cybersecurity at Qatar Bank. A thematic analysis of interviews was conducted with nine experts from the Qatari financial industry, using the NVIVO 12 tool. Key findings included: AI as a major tool for enhancing cybersecurity at Qatar Bank; intelligence in banks to improve cybersecurity faced challenges; and it threatened the security network of Qatar Bank. Additionally, Qatar Bank is projected to face new challenges in the future due to changes in regulatory frameworks and the increasing availability of AI-enabled malware.

In 2022, Rodrigues et al.,7 attempted to address this issue by developing a realistic decision-making model that combined knowledge-based and decision-making trial and evaluation (DEMATEL) methods. Meetings were held with a group of experts to incorporate reality into the final results using this methodology.

In 2022, Narsimha et al.,18 introduced a network security solution based on artificial intelligence (AI) and machine learning (ML), integrated with Feedzai’s existing security model for banking fraud detection. The study provided advanced training for popular machine learning and AI models using the random forest algorithm.

In 2022, Ghelani et al.,1 utilized machine learning, biometrics, and hybrid methods. These methods became functional for the system and helped protect data from unauthorized access using the best optimization techniques to obtain accurate data. The study proposed a banking system model where biometric identification and digital signatures supported all transactions. The proposal suggested increasing the security of Smart Online Banking Systems (SOBS) by using biometric printing, thereby reducing the number of threats.

In 2022, Folds16 conducted research using a Machine Learning approach for the efficient detection of fraud in the banking sector. Cybersecurity experts raised multiple concerns over the risks caused by the misuse of AI in the banking industry. Results confirmed that banks still struggle to prevent AI-driven attacks due to a lack of AI training and knowledge.

Problem statement

Most security arrangements currently in place within banks are insufficient against the intricacies of today’s cyber-attack threats. The rapid development of technology has outpaced the effectiveness of traditional security systems that were implemented years ago, leaving banks vulnerable to sophisticated attacks. This reliance on outdated systems and a reactive approach exposes financial institutions to significant financial losses, reputational damage, and erosion of customer trust. Accordingly, banks must quickly adopt proactive security processes utilizing advanced technologies to mitigate risks and counter new threats.

Traditional security strategies for detection or response typically activate after a threat has breached a network or compromised sensitive data. However, such measures often fail in cases of novel or sophisticated attacks. Many banking institutions still rely on archaic security systems and protocols that are ill-equipped to handle modern cyber threats. In particular, cybercriminals target legacy systems—which are inflexible, narrow, and non-interoperable. These systems often lack basic security features like real-time monitoring, encryption, and multi-factor authentication, making them easy targets for attackers. Furthermore, fragmented legacy IT infrastructures prevent banks from implementing comprehensive security postures, leaving gaps that attackers can exploit.

The consequences of relying on outdated and reactive security measures are grave for banking institutions. In addition to direct financial losses from cyberattacks, banks sustain enormous reputational damage and lose customer trust. Moreover, regulatory bodies are imposing stringent penalties for the inadequate protection of customer data, further adding to the financial costs of a breach. Considering these factors, banks must reorient their security strategies toward proactive approaches, incorporating advanced technologies like artificial intelligence, machine learning, behavioral analytics, and predictive modeling to improve their cybersecurity posture. Every bank can take a crucial step toward security by fostering a culture of cybersecurity awareness and vigilance, empowering employees to act as the first line of defense against cyber threats19.

Proposed methodology for digital banking cybersecurity analysis: a deep learning approach

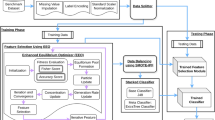
The architecture of the proposed cyber security model with AI for digital banking is shown in Fig. 3.

Fig. 3
figure 3

Detailed architecture of the FinSafeNet model for digital payment fraud detection.

Full size image

Data acquisition

The raw data \(D_{i}^{{in}},i=1,2,.n\) are gathered from the Paysim dataset \(D_{i}^{{in(p)}}\)and the Credit Card Dataset\(D_{i}^{{in(c)}}\).

Paysim dataset

A synthetic dataset created by an agent-based simulation is called PaySim. The simulation replicates the transactions made possible by Mobile Money applications, which are especially common in developing countries. The simulation trains agents to communicate with one another by using gathered information, producing a dataset of 6,362,620 transactions. A crucial component that guarantees the total privacy of the underlying data is anonymization. The dataset is noteworthy because it addresses the lack of publicly available datasets for studying fraudulent transactions20. Figure 4 shows the Pearson correlation graph of the PaySim Dataset \(D_{i}^{{in(p)}}\).

Fig. 4
figure 4

Pearson correlation graph for PaySim dataset.

Full size image

The “amount” feature has the highest correlation (0.077) with the Pearson correlation graph, and the “isFraud” attribute has the lowest correlation. Figure 5 shows the distribution of different types of transactions.

Fig. 5
figure 5

Distribution of different types of transaction.

Full size image

Credit card dataset

The Credit Card dataset \(D_{i}^{{in(c)}}\)consists of 284,807 transactions that a cardholder made over two days in September 2013 Just 492 transactions, or 0.172% of the total, have been flagged as fraudulent in this dataset. The transformed features are denoted as \(\:\text{V}1,\:\text{V}2,\:\text{V}3,.,\:\text{V}28,\:\)while the ‘time,’ ‘amount,’ and ‘class’ features remain unaltered. The response variable is the ‘class’ feature, which takes on a value of 0 in the absence of fraud and 1 in the presence of it. The characters of credit card data are shown in Table 15. After being gathered, the raw data are pre-processed in the next step.

Table 1 Characteristics of credit card dataset.
Full size table

Data pre-processing

The gathered unprocessed data \(D_{i}^{{in}}=(D_{i}^{{in(c)}},D_{i}^{{in(P)}})\)are pre-processed using improved data standardization techniques like data cleaning \(D_{i}^{{pre(dc)}}\) and min-max normalization \(D_{i}^{{pre(norm)}}\)-based data normalization.

Data cleaning

One of the most crucial steps in the data-cleaning process is filling in the missing variables of \(D_{i}^{{in}}\). Although there are several solutions to this issue, most of them will likely influence the outcomes, such as ignoring the entire tuple. Since the source file had actual transactions and no records with missing data, filling them became unproblematic. Meaningless values for the multiples were eliminated from the files because they did not produce significant data or skew the data in any way. In addition, the subsequent modifications, including splitting the date and time column into two and eliminating superfluous columns, were implemented19. The cleaned data is denoted as \(D_{i}^{{pre(dc)}}\).

Data normalization

To ensure a precise evaluation of the Paysim and Credit Card Dataset, it is imperative to normalize the values of \(D_{i}^{{pre(dc)}}\)within a predetermined range during the preparatory stage. Failure to do so can lead to unpredictable or erroneous results21. To accomplish this, apply the subsequent Eq. (1), wherein the relationships between the values of the original data are preserved through min-max normalization.

$$\:{\text{Z}}^{\text{*}}=\frac{\text{z}-\text{m}\text{i}\text{n}\left(\text{z}\right)}{\text{r}\text{a}\text{n}\text{g}\text{e}\left(\text{z}\right)}=\frac{\text{z}-\text{m}\text{i}\text{n}\left(\text{z}\right)}{\text{m}\text{a}\text{x}\left(\text{z}\right)-\text{m}\text{i}\text{n}\left(\text{z}\right)}$$
(1)

where \(\:\text{m}\text{i}\text{n}(\text{z}\)) denotes the lowest value and range(z) denotes the range between the maximum and minimum. \(\:{\text{Z}}^{\text{*}}\) has a range that is contained in the interval [0, 1], and its width is 1. The normalized data is denoted as \(D_{i}^{{pre(norm)}}\).

Feature extraction

Then, joint data integration (JMIM), which improves the correlation between the variables \(D_{i}^{{pre(norm)}}\)is extracted. Along with this, the higher features (skewness, variation) and statistical features (harmonic mean, median, standard deviation), Kernel-PCA-based features are extracted from \(D_{i}^{{pre(norm)}}\).

Statistical features

Evaluating and interpreting statistical data requires a good understanding and analysis of the underlying information in order to understand the properties of statistics.

Harmonic Mean: The Harmonic mean value of \(D_{i}^{{pre(norm)}}\)is represented in Eq. (2).

$$\:\frac{1}{{\text{r}}_{\text{M}}}=\frac{1}{\text{s}}{\sum\:}_{\text{n}=1}^{\text{s}}\frac{1}{{\text{c}}_{\text{n}}}\:\text{o}\text{r}\:{\text{r}}_{\text{M}}=\frac{\text{s}}{{\sum\:}_{\text{n}=1}^{\text{s}}\frac{1}{{\text{c}}_{\text{n}}}}$$
(2)

The reciprocal of the arithmetic mean of the reciprocals of a collection of numbers is known as the harmonic mean. When the average of rates is required, it is employed.

Median: The data \(D_{i}^{{pre(norm)}}\) is sorted, and the middle value provides information about the data’s centre and resistance to outliers.

Standard deviation: A data dispersion metric that illustrates the orbits of propagated data points of \(D_{i}^{{pre(norm)}}\), around the mean22 is said to be a standard deviation.

Higher order statistical features

Along with the basic statistics, higher-order statistical characteristics encompass a range of more intricate qualities that illuminate the complex properties inherent in the distribution of the data. These comprehensive qualities delve deeper into the intricacies and intricacies of data distribution, shedding light on the multifaceted nature of the statistical properties that extend beyond the limitations of basic statistics.

Skewness: Skewness is a measure of the data’s \(D_{i}^{{pre(norm)}}\)asymmetry around the sample mean. If the skewness is negative, the data are more distributed to the left of the mean than the right. Positive skewness signifies a larger distribution of the data to the right. The skewness equation is shown in Eq. (3).

$$\:{{\upgamma\:}}_{1}=\frac{{{\upmu\:}}_{3}}{{{\upmu\:}}_{2}^{3/2}}=\frac{\text{I}{(\text{B}-{\upmu\:})}^{3}}{{\left[\text{I}{(\text{B}-{\upmu\:})}^{3}\right]}^{3/2}},$$
(3)

where \(\:{\upmu\:}\:\)is the mean of the random variable B, \(\:{{\upmu\:}}_{\text{m}}\:\)= is the \(\:{\text{m}}^{\text{t}\text{h}}\) central moment, and \(\:\text{I}(\cdot\:)\) signifies the predicted value of the quantity in the parenthesis. It should be noted that a random variable with a normal probability distribution function or, more generally, one that is symmetric, has zero skewness23.

Variance: The mathematical expression of variance of \(D_{i}^{{pre(norm)}}\)is shown in Eq. (4),

$${{\upsigma}}^{2}=\left(1/{\text{s}}_{1}+{\text{s}}_{2}\right)\div\left[{\text{s}}_{1}\left({{{\upsigma}}_{1}}^{2}+{{\text{i}}_{1}}^{2}\right)+{\text{s}}_{2}\left({{{\upsigma}}_{2}}^{2}+{{\text{i}}_{2}}^{2}\right)\right]$$
(4)

\({\text{i}}_{1}={\underline{{\text{d}}}}_{1}-\underline{{\text{d}}}\), \({\text{i}}_{2}={\underline{\text{d}}}_{2}-\underline{{\text{d}}}\), and \(\underline{{\text{i}}}=\left({\text{s}}_{1}{\underline{{\text{d}}}}_{1}+{\text{s}}_{2}{\underline{{\text{d}}}}_{2}\right)\div\left({\text{s}}_{1}+{\text{s}}_{2}\right)\)  

Where

\({{\upsigma\:}}_{1}\)and \({{\upsigma\:}}_{2}\) are two standard deviations of two series of sizes \({\text{s}}_{1}\)and \(\:{\text{s}}_{2}\) with means \(\:{\underline{{\text{d}}}}_{1}\)and \(\:{\underline{{\text{d}}}}_{2}.\)

Joint mutual information maximisation (proposed)

JMIM practices the “maximum of the minimum” strategy and joint mutual understanding with an iterative forward greedy search technique, to select the most appropriate characteristics of \(D_{i}^{{pre(norm)}}\). The characteristics are then chosen by JMIM based on the novel standard that follows in Eq. (5)

$$\:{\text{g}}_{\text{J}\text{M}\text{I}\text{M}}=\text{a}\text{r}\text{g}\text{a}\text{r}\text{g}\:{\text{m}\text{a}\text{x}}_{{\text{g}}_{\text{j}\in\:}\text{G}-\text{T}}\left({\text{m}\text{i}\text{n}}_{{\text{g}}_{\text{t}\in\:}\text{T}}\left(\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)\right)\right)\:$$
(5)

Where, the values of \(\:\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)\) is shown in Eq. (6) and Eq. (7)

$$\:\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)=\text{J}\left({\text{g}}_{\text{t}};\text{D}\right)+\text{J}\left({\text{g}}_{\text{j}};\frac{\text{D}}{{\text{g}}_{\text{t}}}\right),$$
(6)
$$\:\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)=\text{J}\left(\text{D}\right)-\text{J}\left(\frac{\text{D}}{{{\text{g}}_{\text{j}},\:\text{g}}_{\text{t}}}\right),$$
(7)

And the final mathematical expression of the \(\:\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)\) is shown in Eq. (8)

$$\:\text{J}\left({\text{g}}_{\text{j}},{\text{g}}_{\text{t}};\text{D}\right)=\left[-{\sum\:}_{\text{d}\in\:\text{D}}^{}\text{q}\left(\text{d}\right)\text{l}\text{o}\text{g}\text{l}\text{o}\text{g}\:\left(\text{q}\left(\text{d}\right)\right)\:\right]-\left[{\sum\:}_{\text{d}\in\:\text{D}}^{}{\sum\:}_{{\text{g}}_{\text{j}}\in\:\:\text{G}-\text{T}}^{}{\sum\:}_{{\text{g}}_{\text{t}\in\:}\text{T}}^{}\text{l}\text{o}\text{g}\text{l}\text{o}\text{g}\:\left(\frac{\text{q}\left({\text{g}}_{\text{j}}{\text{g}}_{\text{t}},\frac{\text{d}}{{\text{g}}_{\text{t}}}\right)}{\text{q}\left({\text{g}}_{\text{j}}{\text{g}}_{\text{t}}\left)\:\text{q}\right(\frac{\text{d}}{{\text{g}}_{\text{t}}}\right)}\right)\:\right]$$
(8)

The iterative forward greedy search technique finds the suitable feature subset of size k inside the feature space. Algorithm 1 illustrates the forward greedy search strategy’s pseudo code. The Analysis of JMIM over Standard JM for paysim and credit card database is shown in Fig. 6.

Algorithm 1
figure 6

Pseudocode of forward greedy search strategy.

Full size image
Fig. 6
figure 7

Analysis of JMIM over Standard JM for (a) Paysim and (b) credit card database.

Full size image

For Paysim database: JMIM achieved an accuracy of 0.97, compared to JM’s 0.85. This 12% improvement demonstrates the stronger capability of JMIM to select more relevant features for classification.

For the credit card database: JMIM reaches 0.98, surpassing JM’s 0.87. This 11% increase signifies JMIM’s ability to extract more discriminative features, leading to better overall classification performance. The comparative analysis reveals that Joint Mutual Information Maximization (JMIM) provides superior performance across accuracy, precision, recall, and F1-score when applied to both the Paysim and Credit Card datasets. This suggests that JMIM is a more effective feature extraction technique than JM, particularly in applications involving imbalanced data and critical classification tasks such as fraud detection.

Improved correlation-based features (proposed)

By evaluating the association between features based on the degree of duplication, this approach defines the feature subset. Information theory based on entropy is utilized for correlation-based features. Entropy24, a unit of measurement for uncertainty, is expressed in the Eqs. (9),

$$\:\text{J}\left(\text{b}\right)=-{\Sigma\:}\text{R}\left({\text{b}}_{\text{k}}\right)\left({\text{b}}_{\text{k}}\right)),$$
(9)

After observing the values of another variable, “R,” the entropy of “Z” is defined in Eqs. (10),

$$\:\text{J}\left(\frac{\text{B}}{\text{T}}\right)=-{\Sigma\:}\text{R}\left({\text{t}}_{\text{l}}\right)\left(\text{R}\left(\frac{{\text{b}}_{\text{k}}}{{\text{t}}_{\text{l}}}\right)\right)\:,$$
(10)

In this case, \(\:\text{R}\left({\text{b}}_{\text{k}}\right)\) represents the previous probability for all values of “B,” while \(\:\text{R}\left(\frac{{\text{b}}_{\text{k}}}{{\text{t}}_{\text{l}}}\right)\) represents the posterior probability of “B” if “T” is known. The information gain, denoted by T and found in the equation below, is revealed by the reduction of the entropy value in ‘B,’ revealing more data about B. the mathematical expression of \(\:\text{K}\text{I}\left(\frac{\text{B}}{\text{T}}\right)\) is shown in Eq. (11)

$$\:\text{K}\text{I}\left(\frac{\text{B}}{\text{T}}\right)=\text{J}\left(\text{B}\right)-\text{J}\left(\frac{\text{B}}{\text{T}}\right),$$
(11)

If a feature B satisfies the following criteria shown in Eq. (12) then, it has a stronger correlation with feature T than with feature U,

$$\:\text{K}\text{I}\left(\frac{\text{T}}{\text{B}}\right)>\text{K}\text{I}\left(\frac{\text{B}}{\text{T}}\right),$$
(12)

Another metric that shows the association between features is symmetrical uncertainty (SU), which is shown in the Eq. (13) below:

$$\:\text{U}\text{W}\left(\text{B},\text{T}\right)=2\frac{\text{K}\text{I}\left(\frac{\text{B}}{\text{T}}\right)}{\text{J}\left(\text{B}\right)+\text{J}\left(\text{T}\right)},$$
(13)

SU normalizes the feature value in the interval [0, 1], where 1 represents the value of the other variables that can be predicted from knowing either of the two variables and 0 represents the independence of Z and A. The information bias of the gain toward characteristics with larger values is compensated for by this method. Feature-extracted data are moved to the feature selection stage to select the optimal feature. The Analysis of improved correlation over Standard correlation is shown in Fig. 7.

Fig. 7
figure 8

Analysis on improved correlation over Standard correlation for (a) paysim and (b) credit card database.

Full size image

  • Paysim Dataset: The improved correlation-based features show a significant improvement over the standard method, particularly in accuracy (0.95 vs. 0.85), precision (0.93 vs. 0.82), recall (0.92 vs. 0.78), and F1-score (0.93 vs. 0.79).

  • Credit Card Dataset: Similarly, the improved method outperforms the standard method across all metrics, with notable gains in accuracy (0.97 vs. 0.87), precision (0.96 vs. 0.84), recall (0.95 vs. 0.81), and F1-score (0.96 vs. 0.82).

This suggests that the proposed improved correlation-based feature extraction method offers better overall performance, particularly in complex datasets like Paysim and Credit Card, where precision and recall are critical. ​.

Feature selection

The Improved-Snow Leopard Optimization Algorithm (I-SLOA), a hybrid optimization algorithm, is utilized to choose the most appropriate features from the feature-extracted data. The I-SLOA is acquired from the Snow Leopard Optimization Algorithm with a new velocity updating mechanism with Hierarchical Particle Swarm Optimization (HPSO) in the hunting stage. In addition, the Adaptive Differential Evolution (ADE) with a modified crossover and mutation rate has been incorporated, to enhance the balance between the exploration and exploitation phases.

Improved snow leopard optimization algorithm (I-SLOA)

The Panthera uncia is a species found only in the highlands of South and Central Asia. It can be found in mountainous and alpine regions at elevations ranging from 3000 to 4500 m. A recommended strategy centres on four essential snow leopard traits. To improve search efficiency, the first behaviour involves movement and travel paths that simulate zigzag movements25. The second behaviour is hunting method, which involves imitating motions to find the best areas to seek prey. The third habit is reproduction, which is the process of mating to produce new members and enhance search power. The fourth behaviour is mortality, which simulates a weaker person’s death in order to weed out unfit individuals. This behaviour modelling allows the algorithm to maintain a steady population throughout rounds.

Mathematical modelling

Panthera uncia is a part of every Snow Leopard Optimization Algorithm. Search agents for Panthera Uncia are members of Snow Leopard Optimization Algorithm. In optimization techniques, the population members are identified by the population matrix. Members of the population are represented by the number of rows in the population matrix. The optimization variables are represented by the number of columns in the matrix. The population matrix is defined by utilizing Eq. (14).

$$\begin{aligned} & W = \left[ {\begin{array}{*{20}l} {W_{1} } & \vdots & {W_{h} } & \vdots & {W_{M} } \\ \end{array} } \right]_{{M \times l}} = \left[ {W_{{{\text{1,1}}}} \: \ldots \:W_{{1,c}} \: \vdots \:W_{{h,1}} \: \vdots \: \ddots \: \ldots \: \ddots \: \vdots \:W_{{h,c}} \: \vdots \:W_{{M,1}} \: \ldots } \right. \\ & \left. {W_{{M,c}} \: \ldots \:W_{{1,l}} \: \ddots \: \vdots \: \ldots \: \ddots \: \ldots \:W_{{h,l}} \: \vdots \:W_{{M,l}} } \right]_{{M \times l}} \\ \end{aligned}$$
(14)

Where \(\:W\) is the population of Panthera uncia \(\:{w}_{l}\) is the \(\:l-th\) Panthera uncia, \(\:{y}_{h,c}\:\)is the parameter for \(\:c-th\) problem variable suggested by \(\:h-th\) Panthera uncia, \(\:M\) is the number of Panthera uncia in the algorithm population, and \(\:l\:\)is the total number of issue variables. The problem variable values are determined by where each Panthera uncia fits into the population in the problem-solving space. As a result, for every Panthera uncia, a value for the problem’s intended purpose can be calculated. Equation (15) provides the parameters of the intended function as a vector.

$$\:E={\left[E\: \vdots \:\:{E}_{h}\: \vdots \:{E}_{M}\:\:\right]}_{M\times\:1}={\left[E\left({W}_{1}\right)\: \vdots \:\:E\left({W}_{h}\right)\: \vdots \:E\left({W}_{M}\right)\:\:\right]}_{M\times\:1}$$
(15)

In this case, E is the target function’s vector, and \(\:{E}_{h}\)is the desired value derived from the h-th Panthera uncia.

The snow leopard population is updated by the suggested SLOA by simulating their natural activities. Propagation, hunting, breeding, and mortality are the four phases. The subsections provide mathematical modelling of various stages and natural events.

Phase 1: travel routes and movement

Panthera uncia employs scent cues, just like other cats, to communicate their ___location and route of travel. The reason behind these symptoms is that the hind hooves scrape the ground prior to urinating or shitting. Indirect lines are also used by snow leopards to move in a zigzag style. As a result, they can approach or follow one another according to their innate tendency. This portion of the suggested SLOA is quantitatively modelled using Eq. (16)–Eq. (18).

$$\:{W}_{h,c}^{{O}_{1}}={W}_{h,c}+q\times\:\left({W}_{l,c}-H\times\:{W}_{h,c}\right)\times\:sign\:\left({E}_{h}-{E}_{l}\right),$$
(16)
$$\:{W}_{h}=\{{W}_{h}^{{O1}_{\:}},{C}_{h}^{O1}<{C}_{h,}\:{W}_{h},\:\:\:\:\:\:\:\:\:\:\:\:else,\:\:\:$$
(17)
$$\:H=\:round\:(1+q)$$
(18)

Here,\(\:\:{W}_{h}^{{O1}_{\:}}\) is an unknown number in the interval [0,1], l is the row number of the chosen Panthera uncia for guiding h-th snow panther in the c-th axis and is the new value for the c-th problem variable derived from h-th Panthera uncia based on phase 1. \(\:{W}_{h}^{{O1}_{\:}}\)is the updated ___location of h-th snow panther based on stages 1, and \(\:{W}_{h}^{{O1}_{\:}}\)is its intended function value.

Phase 2: hunting

When updating the population, Panthera uncia uses rocks as a means of concealment when hunting. The snow leopard stalks its victim from a distance, then bites its neck to kill it. This tendency can be mathematically modelled using Eq. (19)- Eq. (21). Equation (22), which mimics the movements of the amur leopard approaching its prey, contains a parameter called \(\:O.\) In the simulation, the observed value of parameter \(\:O\) is taken into account. The snow leopard’s post-attack ___location is simulated by Eq. (23). If the value of the objective function is bigger, an algorithm member considers the new position to be acceptable. An efficient update is used to do this. The Hierarchical Particle Swarm Optimization (HPSO) model efficiently organizes computation arising complexity and feature selection iterating the particles in the hierarchy and the search process by unitedly moving through the search space. The hierarchical structure has an impact on the velocity update in HPSO. Particles are affected by three factors: their own best position (\(\:{o}_{best}\)), the best position of their sub-swarm (\(\:{o}_{best}^{s}\)), and the best position of the overall swarm (\(\:{o}_{best}\)) which is described in the Eq. (24):

$$\:{o}_{h,c}={W}_{h,c},\:c=\text{1,2},3,\dots\:,l$$
(19)
$$\:{W}_{h,c}^{O2}={W}_{h,c}.{v}_{i}^{(t+1)}+q\times\:\left(\left({o}_{h,c}-{W}_{h,c}\right)\times\:O+\:\left({o}_{h,c}-2\times\:{W}_{h,c}\right)\times\:\left(1-O\right)\right)$$
(20)
$$\:xsign\:({E}_{h\:}-{E}_{o\:})$$
(21)
$$\:{W}_{h}=\{{W}_{h}^{O2},{E}_{h}^{O2}<{E}_{h\:};\:{W}_{h},\:\:\:\:\:\:\:\:\:\:\:\:else,\:$$
(22)
$$\:{v}_{i}^{(t+1)}={\omega\:v}_{i}^{\left(t\right)}+{c}_{1}{r}_{1}\left({p}_{i}^{\left(t\right)}-{W}_{h,c}\right)+{c}_{2}{r}_{2}\left({o}_{best}^{s}-{W}_{h,c}\right)+{c}_{3}{r}_{3}\left({o}_{best}-{W}_{h,c}\right)$$
(23)

Where:

  • ​\(\:{v}_{i}^{(t+1)}\) is the updated velocity of particle \(\:i\) at iteration \(\:t+1,\)

  • \(\:\omega\:\) is the inertia weight,

  • ​\(\:{c}_{1},{c}_{2},{c}_{3}\) are acceleration coefficients,

  • ​\(\:{r}_{1},{r}_{2},{r}_{3}\) are random values uniformly distributed in [0, 1],

Here, the prey’s c-th dimension is represented by \(\:{o}_{h,c}\), the h-th snow leopard considered it, the intended function value is based on the prey’s ___location, \(\:{W}_{h}^{O2}\) is the new value for the \(\:{e}^{th}\) problematic variable attained by the h-th snow panther based on phase 2 is represented by \(\:{E}_{h}^{O2}\), and the objective function value is \(\:{E}_{o}\).

Phase 3: reproduction

In the first stage, half of the algorithm’s population is introduced, considering the snow leopards’ natural reproductive habits. It is believed that a cub will be born when two snow leopards mate. Based on the ideas that have been mentioned, Eq. (24) models the reproductive process of snow leopards quantitatively. The purpose of Adaptive Differential Evolution (ADE) is to balance computational complexity and accuracy through dynamic adaptation and balanced exploration and exploitation.

$$\:{B}_{k}=F\left(\frac{{W}_{k}+{W}_{m-k+1}}{2}\right),\:\:\:\:\:\:\:\:\:\:k=\text{1,2},3,\dots\:,\frac{m}{2}\:\:\:\:\:\:\:\:\:\:$$
(24)

Here, \(\:{B}_{k}\) is the \(\:{k}^{th}\) cub to be born from a pair of winter leopards that mate. In ADE, the scaling factor \(\:F\) is dynamically adjusted as shown in Eq. (25):

$$\:{F}^{(t+1)}={F}_{min}+({F}_{max}-{F}_{min})\cdot\:{e}^{-kt}$$
(25)

Where:

  • \(\:{F}_{min}\) and \(\:{F}_{max}\) are the minimum and maximum values for \(\:F,\)

  • \(\:k\:\)is a decay constant,

  • \(\:t\) is the current iteration number.

The crossover probability \(\:CR\) is also dynamically adjusted as shown in Eq. (26):

$$\:{CR}^{(t+1)}={CR}_{min}+({CR}_{max}-{CR}_{min})\cdot\:\frac{1}{1+{e}^{-bt}}$$
(26)

Where:

  • \(\:{CR}_{min}\) and \(\:{CR}_{max}\) are the minimum and maximum values for the crossover probability,

  • \(\:b\) is a growth rate constant,

  • \(\:t\) is the current iteration number.

The balance between exploration and exploitation is achieved by adapting the mutation and crossover parameters as described in Eq. (27):

$$\:{u}_{i}^{\left(t\right)}=\{{v}_{i}^{\left(t\right)}\:\:\:\:\:if\:{rand}_{j}\:\le\:CR\:or\:j={j}_{rand}\:{x}_{i}^{\left(t\right)}\:\:\:\:\:\:\:otherwise\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(27)

Where:

  • \(\:{u}_{i}^{\left(t\right)}\) is the trial vector,

  • \(\:{v}_{i}^{\left(t\right)}\) is the mutant vector,

  • \(\:{x}_{i}^{\left(t\right)}\) is the target vector,

  • \(\:{rand}_{j}\) is a random number in [0,1],

  • \(\:{j}_{rand}\) is a randomly selected index to ensure at least one parameter is taken from the mutant vector.

The unique solution-solving process is to carry only the most favourable implementations over the subsequent model generation in compliance with the Eq. (28):

$$\:{x}_{i}^{(t+1)}=\{{u}_{i}^{\left(t\right)}\:\:\:if\:f\left({u}_{i}^{\left(t\right)}\right)<f\left({x}_{i}^{\left(t\right)}\right)\:{x}_{i}^{\left(t\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\:$$
(28)

Where:

  • \(\:f\left(x\right)\) is the fitness function evaluating the quality of the solution.

Phase 4: mortality

Every living thing has the potential to end. Despite reproduction brought on by deaths and losses, the population of snow leopards is still constant. According to the proposed SLOA, the number of pups produced and the death rate of snow leopards are similar. The value of the objective function determines the snow leopard’s mortality. A lower objective function raises the possibility of snow leopard death. Certain cubs can also die as a result of inadequate objective function.

The proposed SLOA comprises four phases. The first and second phases update the population of snow leopards in each iteration, while the third and fourth phases expose the algorithm’s population to natural processes of reproduction and mortality. These SLOA operations are repeated until the stop condition is satisfied. The SLOA provides the best-obtained solution, also known as the best quasi-optimal solution after the algorithm has been fully applied to an optimization problem. Algorithm 2 displays the SLOA pseudocode.

Algorithm 2
figure 9

Pseudocode of I-SLOA.

Full size image

Dimensionality reduction via MKPCA with Nyström approximation

MKPCA is an extension of traditional Kernel PCA26,27 that focuses on reducing the dimensionality of high-dimensional data while addressing some of the limitations of standard Kernel PCA. It aims to improve computational efficiency and robustness against noise. The key idea behind MKPCA is to approximate the original kernel matrix and apply dimensionality reduction to this approximation. One common technique used for approximation is the Nyström method.

The dimensions of the extracted features are optimized via the new MKPCA with the Nystron Approximation approach. Kernel Matrix: Given a set of data points \(X = \{ x_{1} ,x_{2} , \ldots ,\:x_{n} \}\), where each \(\:x_{\text{i}}\:\in\:\:R^{\text{d}},\) a kernel matrix \(\:K\) is computed using a kernel function \(\:k\) as per Eqs. (29),

$$\:K\:=\:\left[k\right(x_{\text{i}},\:x_{\text{j}}\left)\right]\:for\:i,\:j\:=\:1\:to\:n$$
(29)

Nyström Approximation: Instead of working with the entire kernel matrix \(\:K\), a subset of the data is selected. Let \(\:X_{\text{s}}\) be this subset of data points, and \(\:K_{\text{s}}\) be the sub-matrix of \(\:K\) corresponding to \(\:X_\text{s}\). The Nyström approximation of \(\:K\) is given as per Eq. (30).

$$\:K\:\approx\:\:K_{\text{s}}\:=\:\left[k\right(x_{\text{i}},\:x\text{i}\left)\right]\:for\:i,\:j\:=\:1\:to\:s$$
(30)

Here, \(\:s\:<\:n\) is the size of the subset, and s is typically much smaller than \(\:n\). The approximation is chosen to be a subset of the original data to reduce computational complexity.

Eigenvalue Decomposition: Now, the eigenvalue decomposition is performed on the approximated kernel matrix Ks to find the eigenvectors and eigenvalues and calculated as per Eq. (31).

$$\:K_{\text{s}}\:=\:\varPhi\:\:\varLambda\:\:\varPhi^{\text{T}}$$
(31)

Where \(\:\varPhi\:\) contains the eigenvectors and \(\:\varLambda\:\) is a diagonal matrix with eigenvalues.

Reduced Dimensionality: The next step is to select the top k eigenvectors associated with the largest eigenvalues to obtain a reduced-dimensional representation. These eigenvectors can be arranged in a matrix \(\:\varPhi_\text{k}.\)

Projection: To project new data points into the reduced-dimensional space, Eq. (32) is used:

$$\:\varPhi_{\text{k}}^\text{T}\:k\left(x\right)\:\approx\:\:\alpha\:$$
(32)

Where\(\:\:\alpha\:\) represents the coordinates of the data points in the reduced-dimensional space. The Analysis of MKPCA over kernel PCA and standard PCA is shown in Table 2.

Modified Kernel PCA allows for the reduction of dimensionality while retaining essential information. The Nyström approximation improves computational efficiency by working with a smaller subset of data points. This can be especially useful when dealing with large datasets. It’s important to choose the size of the subset (\(\:s\)) and the number of top eigenvectors (\(\:k\)) thoughtfully to strike a balance between computational complexity and dimensionality reduction quality.

Table 2 Analysis of MKPCA over kernel PCA and standard PCA.
Full size table

The feature-selected data moved on to the FinSafeNet Classifier model to detect digital payment fraud.

FinSafeNet-based digital payment fraud detection

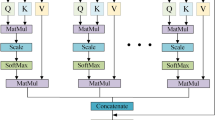
The architecture of the newly developed FinSafeNet is shown in Fig. 8. Using the selected optimal features, the Digital Payment Fraud model referred to as FinSafeNet is trained. The FinSafeNet (Hybrid Classifier model) is a combination of the optimized Bi-LSTM and Convolutional Neural Network (CNN) and dual-attention mechanism. FinSafeNet-based digital payment fraud detection begins with an input layer that receives optimal features derived from previous preprocessing steps. These features are then fed into a sequence of Bi-LSTM layers, which are designed to capture complex temporal dependencies in the data. The dual processing of Bi-LSTM allows the model to analyze both past and future contextual information, significantly enhancing its ability to detect patterns indicative of fraudulent activities. This layer is complemented by CNN components, which further process the input features by applying convolutional operations, pooling layers, and dropout to improve feature extraction while mitigating overfitting. Following the feature extraction stage, the architecture integrates dual attention mechanisms such as channel and spatial attention modules that help the model focus on the most relevant parts of the input data. These attention mechanisms enhance the model’s ability to prioritize important features and relationships, improving overall performance. The processed outputs are then fed into fully connected layers (FC1 and FC2) and concluded with a softmax layer, which generates the final predictions regarding transaction classification. This comprehensive architecture combines advanced DL techniques to achieve high accuracy and robustness in fraud detection, demonstrating its practical applicability in digital banking environments.

Fig. 8
figure 10

Architecture of FinSafeNet.

Full size image

Bi-LSTM

The statistics are composed of a sequence of sensor signals that interfere with each other. When fuzzy data is present, it has a detrimental effect on the outcome of the forecast. In order to mitigate this interference, the Bi-LSTM network is utilized to estimate and eliminate the noise. When it comes to estimating time series data in a single direction, LSTM networks are commonly employed. Conversely, Bi-LSTM networks incorporate two-way stacked LSTM networks. The basic architecture of Bi-LSTM28 is illustrated by the forward and backward LSTM networks in Fig. 9. In FinSafeNet, the Bi-LSTM architecture enhances the model’s ability to analyze sequential transaction data by processing inputs in both forward and backward directions. This dual processing allows the Bi-LSTM to capture contextual information from past and future transaction behaviors, improving the understanding of complex patterns associated with fraudulent activities. By employing the strengths of LSTM cells, which effectively retain relevant information over long sequences while mitigating issues like vanishing gradients, the proposed FinSafeNet identifies intricate temporal dependencies in transaction sequences. This capability significantly boosts the model’s performance in accurately detecting fraudulent transactions, making it a critical component in ensuring secure digital banking operations.

Fig. 9
figure 11

Basic architecture of Bi-LSTM.

Full size image

The information gathered from the two previously described hidden states is merged in the last layer. Equation (33) to (38) explain the procedure in an LSTM cell.

$$\:{\mathfrak{I}}_{t}=\sigma\:\left({\mathcal{W}}_{i}\cdot\:\left[{\mathfrak{h}}_{t-1}\right],{\mathcal{X}}_{T}+{\mathfrak{b}}_{i}\right)$$
(33)
$$\:{F}_{t}=\sigma\:\left({\mathcal{W}}_{f}\cdot\:\left[{\mathfrak{h}}_{t}-1\right],{\mathcal{X}}_{T}+{\mathfrak{b}}_{f}\right)$$
(34)
$$\:{\mathcal{D}}_{t}=\sigma\:\left({\mathcal{W}}_{o}\cdot\:\left[{\mathfrak{h}}_{t}-1\right],{\mathcal{X}}_{T}+{\mathfrak{b}}_{o}\right)$$
(35)
$$\:{\mathcal{C}}_{t}=tanh\left({\mathcal{W}}_{m}\cdot\:\left[{\mathfrak{h}}_{t}-1\right],{\mathcal{X}}_{T}+{\mathfrak{b}}_{m}\right)$$
(36)
$$\:{\widehat{\mathcal{C}}}_{t}={F}_{t}\odot{\widehat{\mathcal{C}}}_{t-1}+{\mathfrak{I}}_{t}\odot{\mathcal{C}}_{t}$$
(37)
$$\:{\mathfrak{h}}_{t}={\mathcal{D}}_{t}tanh\odot\left({\widehat{\mathcal{C}}}_{t}\right)$$
(38)

Here, the input gate\(\:\:{\mathfrak{I}}_{t},\:\)forget gate \(\:{F}_{t}\), output gate \(\:{\mathcal{D}}_{t}\) and cell state \(\:{\mathcal{C}}_{t}\) are computed based on \(\:\mathfrak{b}\), \(\:\mathcal{W},\)\(\:\mathcal{X}\), and \(\:T\) indicating bias vector, weight matrix, input vector, and time respectively. In addition, \(\:\sigma\:\) specifies the sigmoid function and \(\odot\) stands for element-wise multiplication.

Equation (39) to Eq. (41), which describe the functions performed in the bi-LSTM unit.

$$\:{g}_{s}=\sigma\:\left({v}_{1}{w}_{s}+{v}_{2}{g}_{s}-1\right)\times\:tanh\left({B}_{s}\right),$$
(39)
$$\:{g}_{s}^{{\prime\:}}=\sigma\:\left({v}_{3}{w}_{s}+{v}_{4}{{g}^{{\prime\:}}}_{s-1}-1\right)\times\:tanh\left({B}_{s}^{{\prime\:}}\right),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$
(40)
$$\:n{f}_{s}=v{g}_{s}+{v}_{6}{g{\prime\:}}_{s}\:,$$
(41)

where \(\:v{\prime\:}q\:\)are the weights of the LSTM cell’s gates and \(\:{w}_{s}\) is the input at time s. The forward and backward outputs are denoted by \(\:{g}_{s}\) and\(\:{{g}^{{\prime\:}}}_{s}\), respectively. The bi-directional step information is stored in the output gate \(\:{ME}_{t}\).

Convolutional neural network (CNN)

CNNs are a type of neural network that possess the capability to extract intricate and localized features from input data, enabling them to make accurate predictions. This was a revolutionary concept first developed in the 1980s; major improvements were made in this in 1998, really setting it as one of the top deep learning tools available.

Many hidden layers are a part of the architecture in CNNs, such as but not limited to convolutional layers, pooling layers, and all layers, which are intended for some purpose in all the functionalities of the network. The convolution technique is particularly useful because it effectively uses filters to identify and extract important features from the input, resulting in new maps that encompass important features of the ideas. To prevent overfitting and reduce dimensionality, layer pooling plays an important role by carefully reducing the complexity of extraction and ensuring that the network maintains its stability and efficiency for generalization29. In addition, functions such as smoothed linear units (ReLU) and sigmoid functions implemented in CNNs enhance the nonlinearity of the network, allowing it to capture and model the integration of factor features and desired results. Overall, the application of CNN to deep learning has revolutionized the detection and prediction of complex patterns, making it an important tool in many fields. Figure 10 illustrates the framework of CNN.

Fig. 10
figure 12

Convolutional neural networks.

Full size image

The architecture of CNN consists of three separate structures. The convolutional layer, pooling layer, and fully linked layer are the three types of layers.

  1. (1)

    Convolutional layer:

A kernel filter, which is a component of the convolutional layer, is used to pass transaction data and produce a feature map. In Eq. (42), the involvedness process is expressed.

$$\:a=\frac{p+2t-i}{w}+1$$
(42)

where the symbols \(\:q,\:s,\:i,\:and\:v\) stand for the matrix of the input data, the padding size, the matrix of the filter, and the stride, correspondingly. The size of the output matrix is \(\:c\times\:c.\) The activation function provides a nonlinear characteristic structure after the convolution layer, enabling the DNN to perform hierarchical nonlinear mapping. A rectified linear unit\(\:\:(ReLU,\:i\left(a\right)=\:max\left(0,b\right)),\) is the frequently employed activation function in CNNs, and also gives a higher performance in terms of adaption as well as developing time.

  1. (2)

    Pooling layer:

In order to minimize computing effort and prevent overfitting, the PL lowers the dimension of the characteristics map by the normal or extreme while retaining the essential qualities. The size of the output matrix is \(\:c\times\:c.\) Eq. (43) shows the value of \(\:a.\)

$$\:a=\frac{p-i}{w}+1$$
(43)

Where the input image matrix is denoted by p, the filter matrix by j, and the number of strides by w.

  1. (3)

    Fully connected layer:

A few Fully Connected layers appear after the pooling and combined convolution layers. Every neuron in the subsequent layer is connected to every other neuron in this initial stage using Eq. (44) that follows below:

$$\:{A}_{m}=\sum\:{\text{A}}_{\text{m}}\text{*}{\text{a}}_{\text{m}}+{\text{f}}_{\text{n}}$$
(44)

where \(\:\text{b},\:\text{c},\:\text{m},\:\text{a}\text{n}\text{d}\:\text{n}\) stand for the results of the previous layer, current layer, and stage, respectively, and \(\:\text{a}\:\text{a}\text{n}\text{d}\:\text{f}\) indicate the weight and variation amounts. The final FC layer’s \(\:\text{o}/\text{p}\) is fed into the SF function, which then uses this information to predict the class by determining how likely it is that each transaction data point represents a legitimate or fraudulent participant in the digital transaction system. The output from these two architectures is then combined to produce a detected result, which improves the model’s capacity to identify fraudulent activity in digital payment systems and turns it into a reliable tool for protecting financial transactions.in addition, the outcome from CNN and Bi-LSTM is fed as input to the attention model, which includes the spatial and channel-wise attention mechanism. These attention mechanisms assist in refining the feature maps thereby making the detection more accurate. Finally, two fully connected layers and a SoftMax classifier are used as classifiers (presence/absence of fraud in transactions).

Experimental setup

The recommended framework has been implemented in PYTHON. The suggested model has been evaluated utilizing the Paysim dataset (https://www.kaggle.com/datasets/ealaxi/paysim1) and the Credit Card Dataset (https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud). 70% of the collected data has been used for training and 30% for testing. A comparative analysis has been made with state-of-the-art techniques. This assessment considered various metrics like sensitivity, specificity, accuracy, precision, FPR, FNR, NPV, F-Measure MCC, and Recall.

Performance metrics

Numerical indicators known as performance metrics are used to evaluate the accuracy and quality of predictions. Machine learning tasks are inherently linked to assessment measures. This makes it more difficult to assess a model’s performance and provides important information about its advantages and disadvantages. A model’s presentation can be evaluated using three different kinds of metrics. Metrics used for classification include “F-measure, sensitivity, specificity, accuracy, precision, Matthews Correlation Coefficient, NPV, False Positive Rate, and False Negative Rate.

Comprehensive performance metrics analysis of the proposed model on paysim data

Table 3 shows the various performance measures of deep learning models using Paysim database. In this work, different models are compared, which include VGGNET, RESNET, 3DCNN, Bi-LSTM, CNN, and the proposed model. Among these, the proposed model achieved an accuracy of 97.9%, the highest among all the models evaluated in this study, far ahead of RESNET at 93.4%. Such high accuracy is indicative of the proposed model having effectively made the classification and detected relevant patterns in the dataset. In terms of precision, the proposed model recorded 96.6%, which outperformed the RESNET model at 92.3%. What is more important here is that very few false positive errors were made in the predictions by the proposed model. The sensitivity of the proposed model reached 95.5%, outperforming other models like Bi-LSTM at 93.2%. This metric reflects how good the model is at correctly classifying true positive cases. Besides that, the specificity value for the proposed model was 95.1%, showing high accuracy in correctly rejecting negative cases—very important in an application where false negatives of significant consequence are involved. The model being proposed also gave the best results on error measures: the FPR equalled 1.6% with an FNR of 1.3%, both much lower compared to other models. This further goes on to support the reliability and effectiveness of the model. The very fact that the model’s performance metrics have been thoroughly checked proves its lead over existing models in enhancing security protocols and all those applications that require a high level of accuracy and reliability.

Table 3 Comparative performance analysis of proposed FinSafeNet over existing deep learning model for paysim database.
Full size table

Comprehensive performance metrics analysis of the proposed model on credit card data

In this regard, the estimated performance of several deep learning models against Credit card databases is summarized in Table 4. The compared models are VGGNET, RESNET, 3DCNN, Bi-LSTM, CNN, and the proposed model. The proposed model is performing better in every parameter. The accuracy achieved was very good, 98.5%, way above that of other models, where the RESNET came second at 92.2%. This accuracy shows how effective the proposed model is in classifying and detecting relevant patterns in the dataset. For precision, the proposed model returned 97.9%, which is an exceedingly good value in comparison with the 87.0% obtained by the VGGNET and 85.2% obtained by the CNN. Such high precision is indicative of the proposed model providing a low false positive rate, hence reliable predictions. Besides, sensitivity for the proposed model was at 98.1%, way higher than for all other models, whether CNN-based, Bi-LSTM, or Bi-LSTMCN. This metric presents the strength of a model in correctly classifying true positive cases. The suggested model also exhibited great specificity, at 96.7%, proving itself highly relevant for the identification of negative cases in applications where false negatives could result in tremendous consequences. The proposed model also did well in error measures; an FPR of 1.3% and an FNR of 1.7%, well below other models. This again underpins the reliability and efficiency of the model. The proposed model has shown better performance on all the metrics compared to the existing models; thus, it is a strong solution where high accuracy and reliability of tasks are desirable. This suggests that the proposed model is effective in performance as well as offering quite substantial improvements over traditional approaches in the field.

Table 4 Comparative performance analysis of proposed FinSafeNet over existing deep learning model for credit card database.
Full size table

Algorithmic performance evaluation of proposed FinSafeNet model on paysim database

Figure 11 shows the overall performance analysis of the proposed model over the existing models in terms of metrics that are Accuracy, Precision, Sensitivity, Specificity, F-Measures, MCC, NPV, FPR and FNR. In light of the recorded results, the proposed model demonstrated outstanding efficiency for several performance metrics and was established as the leading solution in the subject ___domain. The proposed model is not only excellent in terms of accuracy but also improved in several key metrics. For instance, it is observed that the precision of the proposed model was 96.6% as opposed to that of the FOA model at 92.3%. Moreover, other measures of sensitivity and specificity continue to portray the effectiveness of the proposed model in correctly identifying positive and negative cases, since the values stand at 95.5% and 95.1%, respectively. Moreover, the proposed model demonstrates minimal error measures, with a False Positive Rate (FPR) of 1.56% and a False Negative Rate (FNR) of 1.34%, significantly lower than those of the other models. Overall, the proposed model is better than the existing model.

Fig. 11
figure 13

Comparative performance analysis of the proposed I-SSO algorithm against existing models for paysim database.

Full size image

Algorithmic performance evaluation of proposed FinSafeNet model on credit card database

Figure 12 summarizes the comparative performance of the proposed model against existing models. Going by the recorded results, it can be inferred that the proposed model is very efficient and effective on these performance metrics, making it one of the leading solutions in this field. The proposed model realized an accuracy of 98.5%, the highest among all the considered models. This high improvement in accuracy proves that the model effectively identifies both positive and negative instances. In terms of precision, the proposed model recorded 97.9%, outperforming the FOA model at 91.9%. This therefore means high precision, hence very few false-positive errors by the model, reliable results. Sensitivity and specificity metrics continue to indicate the strengths of the model, with values equal to 98.1% and 96.7%, respectively. The results in this section already prove that the proposed model can detect true positives while ensuring that false negatives are at a minimum, which in turn is very important in high-security applications. The proposed model also returned a very low error rating, with an FPR of 1.33% and a FNR of 1.66%. These low error rates indicate that the model is working not only effectively but also reliably. This makes the model a very valuable asset as it shows comprehensive performance metrics evaluation better than the existing models.

Fig. 12
figure 14

Comparative performance analysis of the proposed I-SSO algorithm against existing models for credit card database.

Full size image

Algorithmic performance evaluation of proposed FinSafeNet model over recent fraud detection models

In order to verify the competence of the proposed FinSafeNet model, a comparative study is carried out using several recent fraud detection methods such as Anti-fraud-Tensorlink4cheque (AFTL4C)30, Random Forest (RF)31, eXtreme Gradient Boosting (XGBoost)32, and Genetic Algorithm-Extreme Learning Machine (GA-ELM)33. Table 5 summarizes the comparative analysis of proposed FinSafeNet over Recent fraud detection models. Among all the models, the proposed FinSafeNet demonstrates the highest accuracy at 97.88%, indicating its superior capability in correctly identifying fraudulent transactions compared to the other methods, which range from 89.45 to 95.91%. Additionally, FinSafeNet achieves the highest precision (96.55%), sensitivity (95.46%), and specificity (95.12%), underscoring its effectiveness not only in detecting positive cases (fraudulent transactions) but also in minimizing false positives. This comprehensive performance suggests that FinSafeNet is a robust solution for fraud detection, outperforming traditional techniques and offering significant advancements in accuracy and reliability.

Table 5 Comparative analysis of proposed FinSafeNet over recent fraud detection models.
Full size table

Discussion

In this subsection, the discussion between the proposed model and existing models as well as the existing algorithmic model is compared in terms of accuracy, precision, sensitivity, specificity, F-Measure, MCC, NPV, and low FPR and FNR.

Performance comparison of the proposed FinSafeNet model with established deep learning models

When the suggested model is compared to well-known models like CNN, RESNET, 3DCNN, VGGNET, and Bi-LSTM, it stands out. The suggested model routinely outperforms the competition in terms of accuracy across both datasets, demonstrating its capacity to accurately categorize occurrences. In real-world applications, where accuracy, sensitivity, and specificity are critical, this proficiency is essential. The model’s excellent sensitivity, which highlights its ability to correctly identify positive cases, and high precision, which indicates a low false positive rate, further underscore its superiority. Additionally, the suggested model retains competitive specificity, demonstrating its proficiency in accurately detecting negative cases. The F-Measure, which combines sensitivity and precision, confirms that the model performs in a balanced manner. These findings are supported by the Matthews Correlation Coefficient (MCC), which shows that the suggested model is accurate and capable of managing dataset imbalances. All things considered, the suggested model proves to be a reliable and adaptable solution, surpassing previous models in a variety of crucial measures.

Comparative analysis of the proposed FinSafeNet model against traditional algorithmic approaches

Compared with algorithmic models such as SSO, AVO, GWO and FOA, the proposed model has similar performance on both datasets. The higher accuracy indicates that the proposed models are better at identifying complex patterns in the data than algorithmic methods. The improvement of the accuracy of the proposed model indicates the ability to reduce the error, thus increasing the accuracy of the prediction. At the same time, the proposed model showed good understanding, indicating the ability to analyse the situation well. The model is effective in preventing defects, as shown by its high specificity, which is a measure to correctly identify defects. The comprehensive F-Measure evaluation underscores the proposed model’s proficiency in accurately identifying both fraudulent and legitimate transactions, highlighting its balanced performance. The Matthews correlation coefficient (MCC) further validates the model’s robustness, demonstrating its ability to effectively manage inconsistent data while maintaining simplicity and reliability across various scenarios. Overall, the proposed model has proven to be a promising, reliable, and flexible solution for digital fraud detection, consistently outperforming existing algorithmic approaches in multiple metrics.

Performance and limitation of proposed FinSafeNet

FinSafeNet achieves a high accuracy level of 97.8% in fraud detection by integrating a Bi-LSTM model with a CNN and a dual-attention mechanism, which enhances its ability to capture both temporal and spatial patterns in transaction data. The use of the I-SLOA for feature selection optimizes the relevance of input features, while MKPCA with Nyström Approximation reduces dimensionality without sacrificing important information. This comprehensive approach results in robust performance validated through the Paysim database, translating to practical significance in improving fraud detection, reducing financial losses, enhancing consumer trust in digital banking, ensuring regulatory compliance, and providing a competitive advantage for financial institutions in an increasingly digital landscape.

While FinSafeNet demonstrates high accuracy in fraud detection, several limitations warrant consideration. Firstly, its performance is sensitive to the quality and diversity of the training data. If the dataset lacks representation of certain fraud patterns, the model may not generalize well to new or evolving threats. Additionally, the computational complexity associated with the dual-attention mechanism and advanced optimization techniques limits real-time application in high-volume transaction environments. Future studies could focus on enhancing the model’s adaptability to emerging fraud tactics, incorporating more diverse datasets for training, and exploring lightweight architectures for improved scalability and speed in real-time systems. Furthermore, investigating the integration of FinSafeNet with other cybersecurity measures could create a more comprehensive fraud detection framework.

Conclusion

The FinSafNet model proposed in this research for secured digital cash transactions serves as a significant advancement in the banking sector. The Bi-LSTM model with the combination of CNN and a dual-attention mechanism has achieved high effectiveness in identifying fraud activities at low transaction time. Application of an Improved Snow-lion Optimization Algorithm (I-SLOA) which combined HPSO and ADE provided a high-quality feature subset selection enhancing the model’s elements and improved accuracy as well as better convergence speed. This novel Multi Kernel PCA (MKPCA) with Nyström Approximation for feature dimensionality reduction, improved correlation as well Joint Mutual Information Maximization obtained features along contributed to a stable and efficient model The FinSafeNet model has performed quite well with a great accuracy of 97.8% in the standard Paysim database, which is way better than a traditional approach to detect fraudulent transaction. The model’s high accuracy indicates the possibility of using it in practice to increase the safety of digital banking transactions, making it a viable method for combating cyber threats within financial services. Despite excellent performances observed with the Paysim database, future work can be pursued to study real-time banking environments by deploying FinSafeNet and inferring its capacities in diverse transactional loads and conditions. Understanding the model’s scalability to work in other banking system transaction volumes would be key for broad adoption. If explored, the integration of blockchain technology in FinSafeNet could add yet another layer of protection for digital transactions. It also enables DL mechanisms like this model to work in conjunction with blockchain’s decentralized structure and its security measures, for a significantly more secure global financial system.