Introduction

As the pace of global development accelerates, the need for resources and infrastructure becomes more urgent. In recent years, the construction of high-speed rail, highway and underground space is on the rise, and there are numerous problems involved in rock engineering1,2. Due to the complexity of geological environment, a large number of cracks and tiny holes are randomly distributed in rock mass, and the instability failure of rock mass is mostly caused by the occurrence, development and penetration of these cracks3. Therefore, how to scientifically and accurately measure the internal defects of rock and the influence of its internal crack propagation mode on rock instability and failure is an urgent problem for geotechnical engineering.

In recent years, scholars have conducted long-term and effective research on different working conditions of fractured rock4,5,6,7,8. The mechanical properties of rocks under different defect geometry and different loading modes, including pre-existing defect geometry9,10,11,12,13,14, defect filling conditions15 and confining pressure16 are discussed. In addition, the cracking process was evaluated in terms of crack initiation, coalescence and failure modes17,18,19,20,21. As for the experimental loading method of fractured rocks, Chen et al.22 conducted uniaxial compression tests on sandstone samples with single round pores with double fractures to study the effects of rock bridge Angle β and fracture Angle α on rock mechanical properties and fracture evolution characteristics. Wang et al.23 conducted biaxial compression tests on specimens and found that the rock bridge coalescence patterns could be roughly divided into three categories. Li et al.24 conducted true triaxial compression tests on transverse isotropic shale samples with double fractures, focusing on the study of their mechanical properties and failure characteristics. Other experimental loading methods include conventional triaxial compression test25, Brazilian splitting test26, laboratory direct shear test27, Uniaxial cyclic loading and unloading test28,29, multistage constant amplitude frequency conversion cyclic load test30, dynamic and static coupling load test31, hydraulic-coupling test32, etc.

On the other hand, aiming at different test monitoring and analysis means, Zhang et al.33 adopted the non-contact monitoring device DIC to conduct a comprehensive test of the full-field strain of the specimen. Huang et al.34 combined with computed tomography technology, revealed the fracture behavior and ligament failure mode of the specimen, and studied the failure characteristics and mechanical properties of the specimen. Zhou et al.35 used acoustic emission and digital image correlation techniques to study the spatio-temporal evolution of crack growth in a soft-hard composite layered rock mass (SHCLRM) with double cracks under uniaxial compression. Chen et al.36 conducted an in-depth study on the infrared radiation temperature (IRT) response characteristics of precast fractured sandstone and the effects of fracture Angle on mechanical properties, failure mode and infrared radiation. Niu et al.37 used acoustic emission (AE) and digital image correlation (DIC) techniques to monitor and record the cracking process of specimens in real time, and analyzed the AE characteristics during the cracking process. through photographic monitoring of crack initiation, expansion, merging and failure modes of rock-like samples, Tian et al.38 found that V-shaped crack properties had little influence on crack initiation ___location, but had great influence on crack trajectory. In order to better understand the basic characteristics and phenomena of compressive failure of rock mass structure, a series of uniaxial compression tests on sandstone specimens were carried out by using loading equipment, acoustic emission system, computed tomography system and high-speed camera39. Chen et al.40 used uniaxial compression test, nuclear magnetic resonance (NMR), scanning electron microscopy (SEM), energy dispersive spectroscopy (EDS) and X-ray diffraction (XRD) to deeply investigate the influence of high humidity on the mechanical properties of crushed pillars. In terms of theoretical and simulation studies, Shan et al.41 established a nonlinear creep damage model of frozen fissure red sandstone based on the nonlinear creep characteristics of frozen rock. Yang et al.42 identified 9 different crack types (stretching, shearing, lateral, far-field and surface spalling) of a single crack according to its geometry and crack propagation mechanism. Sun et al.43 quantitatively analyzed the dynamic change of sandstone cracks by using box dimension, and established a fractal model of sandstone crack propagation with time based on fractal theory. Based on the numerical method of rock failure discontinuous deformation analysis (DDARF), Li et al.44 simulated the shear failure process of jointed rock mass and the stress and displacement changes at key monitoring points. Zhang et al.45 established a damage constitutive model reflecting the unique characteristics of the deformation and failure process of fractured rock mass on the basis of considering the mechanical properties and behavioral evolution of rock mass under different fracture lengths and confining pressures. Wang et al.46 used an improved rigid block spring method to discuss the effects of crack inclination and length on uniaxial compressive strength (UCS) and failure mode. Yao et al.47 and Li et al.48 used particle flow discrete element software PFC2D to reveal the failure modes of defective rocks at different angles, and studied the crack growth and stress evolution of cracked rocks at different angles. Huang et al.49 conducted a series of laboratory tests and PFC numerical simulation on rock-like material samples with two non-parallel cracks to reveal the macroscopic mechanical behavior and microscopic mechanism of pre-cracked specimens under different loading rates.

To sum up, scholars have made rich achievements on the mechanical properties of fractured rock mass under different actual working conditions, but the research on the evolution mechanism of microscopic cracks in rocks with different fracture inclination angles is not detailed. Therefore, this paper conducts uniaxial compression and acoustic emission monitoring tests for red sandstones with different fracture inclination angles. By comprehensively applying acoustic emission equipment and rock pressure test system, a joint acoustical and force monitoring method is formed to deeply explore the internal crack patterns and evolution rules of red sandstones with different fracture inclination angles, providing effective theoretical support for the stability and early warning of instability failure of engineering rock mass.

Sample preparation and scheme

Sample preparation

The red sandstone used in the test has uniform texture, no obvious joint on the surface and good integrity. According to the Standard of Test Methods for Engineering Rock Mass (GB/T 50266 − 2013), red sandstone rock samples are made into cuboid specimens of 50 mm 50 mm 100 mm through drilling and end grinding. The precast through crack size is 15 mm 2 mm 50 mm. The crack inclination angles are 0°, 30°, 45°, 60° and 90° respectively, and the specific geometric parameters are shown in Fig. 150. After measurement, the error values of length, width and height are not more than 0.1 mm, the non-parallelism of the two end faces is not more than 0.03 mm, and the end face is perpendicular to the axis of the sample, and the maximum deviation value is not more than 0.25°. All indicators are within the range of rock mechanics test standards prescribed by the state. The fractured red sandstone rock sample treated by the above operating procedures is shown in Fig. 2. The basic physical and mechanical parameters of the samples were calibrated, and rock samples with good homogeneity were selected for the following tests. The specific procedure includes that the quality of the specimen was weighed by an electronic scale, accurate to two decimal places. The volume was obtained by measuring the length, width, and height of the specimen three times at different locations using a vernier caliper, taking the average value, and then multiplying these measurements. Specific rock sample parameters and numbering are shown in Table 1.

Fig. 1
figure 1

Sample geometry parameters.

Full size image
Fig. 2
figure 2

Red sandstone sample.

Full size image
Table 1 Parameters and numbers of red sandstone.
Full size table

Test scheme

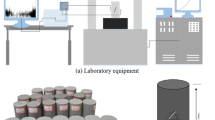
The test equipment mainly consists of two parts: uniaxial compression system and acoustic emission system. The uniaxial compression system includes a pressure testing machine, a control valve and a data acquisition host, and the acoustic emission system includes a full-information acoustic emission instrument, a signal processing host, a preamplifier and a probe. The schematic diagram of the test system is shown in Fig. 3.

Fig. 3
figure 3

Test system diagram.

Full size image

The test is mainly divided into two parts: uniaxial compression test and acoustic emission monitoring. The uniaxial compression test adopts displacement loading, and the loading rate is 0.05 mm/min. In rock testing, the generated acoustic signals typically range from a few kilohertz (kHz) to several megahertz (MHz), depending on the specific test and rock properties. The wavelength of the acoustic signal is inversely related to its frequency, meaning higher frequencies produce shorter wavelengths, which can enhance the resolution of the results. Shorter wavelengths are better at resolving finer details, such as small fractures or density variations in the rock. However, higher frequencies can be more quickly attenuated in certain materials, limiting penetration depth. Conversely, lower frequencies penetrate deeper but may overlook finer details. Therefore, selecting the optimal frequency involves balancing resolution and penetration based on the testing needs. The threshold value of acoustic emission monitoring was set at 30dB to ensure signal reliability and sensitivity, the sampling frequency was 3 MHz, and the two probes were placed at the center points of the left and right sides of the red sandstone samples respectively. In the follow-up analysis, the best experimental effect of each group was selected for analysis.

Mechanical characteristics analysis

According to the above test scheme, the stress-strain curves and peak strength changes of fractured red sandstone with different crack inclination angles are obtained, as shown in Fig. 4. As can be seen from the figure, the peak strength of intact red sandstone samples is 92.35 MPa, and the peak strength of red sandstone fractured at 0°, 30°, 45°, 60° and 90° is 58.49 MPa, 58.98 MPa, 63.04 MPa, 71.05 MPa and 84.05 MPa, respectively. Its peak strength changes in the shape of “U” with the crack inclination Angle, because when the crack inclination Angle is close to the internal friction Angle of the sample itself, its resistance to deformation will be greatly weakened, resulting in the reduction of the elastic modulus and compressive strength of the sample, but the 0° sample is significantly lower than other samples because its crack inclination is approximately parallel to its bedding direction. When the crack inclination is 30° and 45°, two stress drops occur in the stress-strain curve at the same time: the first stress occurs at 79% and 83% of the peak strength respectively, and then the slope of the curve drops significantly, which proves that irreversible damage occurs in the specimen. The second occurs near the peak strength, indicating that the sample is about to fail. The two stress drops also show that when the crack Angle is close to the internal friction Angle, the instability of the sample strength increases.

Fig. 4
figure 4

Loading mechanical characteristic curve.

Full size image

Figure 5 shows the relationship between the stress of fractured red sandstone samples and the cumulative ringing count rate during initial loading. It can be seen from Fig. 5(a) that for intact red sandstone, a small number of acoustic emission events occurred in the early loading stage, corresponding to the compaction of pores inside the rock sample. A typical “acoustic emission quiet period” appeared in the elastic stage, which proves that elastic deformation does not cause grain dislocation or crack initiation within the rock sample. When loading reached 80% of the peak stress, a large number of acoustic emission events began to occur within the specimen, indicating that the reactive red sandstone had entered the plastic stage, with large-scale damage appearing before the peak stress. As seen in Fig. 5(b) - (f), for crack samples at 30° and 45°, a significant number of acoustic emission events started in the early stage of the first stress drop, which is a symptom of large cracks in the rock. Subsequently, continuous acoustic emission events emerged, indicating that the rock had entered the stage of irreversible damage, with a sudden increase occurring again when the rock reached peak stress. This can also serve as an important precursor to rock failure. For the 60° and 90° crack specimens, there was no obvious stress drop, but the elastic modulus decreased significantly compared to the intact specimens due to the influence of the cracks. In summary, there is a significant correspondence between the acoustic emission signals during the rock loading process and the macroscopic mechanical properties.

Fig. 5
figure 5

Time-stress-cumulative ringing count rate relationship.

Full size image

Analysis of acoustic emission characteristics

Damage and rupture mode

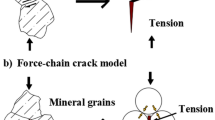
Analysis based on acoustic emission characteristic parameters is an important means to study the internal damage of rocks. RA (ratio of acoustic emission rise time to rise value) and AF (ratio of acoustic emission ringing count to duration) are often used to characterize the microscopic fracture mode of acoustic emission sources. High AF and low RA values correspond to tensile cracks, and high RA and low AF values correspond to shear cracks. The distribution of relationships is shown in Fig. 6.

Fig. 6
figure 6

RA-AF relationship distribution diagram.

Full size image

Previous studies have shown that a small number of acoustic emission events occur in the compaction stage of rocks, while almost no acoustic emission events occur in the elastic deformation stage, resulting in the so-called “acoustic emission quiet period.” Therefore, effective studies on rocks based on acoustic emission parameters should mainly focus on the period after the elastic stage and before peak failure. According to the analysis of mechanical properties, fractured red sandstone enters the stage of stable fracture development when it is loaded to about 60% of the peak strength, and it enters the stage of unstable fracture development after 80% of the peak strength. Based on this calculation, the RA and AF values of the red sandstone with different fracture inclinations at these two stages are obtained. Only complete red sandstone, 30° red sandstone, and 90° red sandstone are analyzed, as shown in Figs. 7, 8 and 9.

As can be seen from Fig. 7, when the complete red sandstone is loaded to the stage of fracture instability development, the RA value is between 0 and 10, and the AF value is basically within the range of 0-200. At this time, the internal damage failure is mainly dominated by tensile cracks, accompanied by a small number of low shear cracks. The few overall data points indicate that the internal damage, as a whole, is in the stage of low-speed and stable growth. When loaded to the unstable development stage of cracks, the number of acoustic emission events increases significantly, the tensile cracks maintain a steady growth, and the RA value range also expands to 0–50, reflecting the rapid increase in the number and size of shear cracks in the rock. Finally, the combination of tensile cracks and shear cracks leads to the decline of rock compressive capacity and even failure.

Fig. 7
figure 7

Intact RA-AF diagram of red sandstone.

Full size image

According to the analysis in Fig. 8, it can be seen that in the stage of stable fracture development, the RA and AF values of 30° fractured red sandstone are significantly higher than those of intact red sandstone, and the AF values are between 0 and 500 and evenly distributed, indicating that tensile cracks are fully developed in the rock at this stage. In addition, “shear crack groups” exist in the range of 30–40 RA values. Corresponding to the state of “stress drop” in the stress-strain curve, this proves that the stress drop is caused by the development and expansion of shear cracks in the rock. In the unstable development stage of cracks, the number of acoustic emission events inside the rock increases sharply, and the shear cracks increase significantly compared to the complete specimens. The reason is that the prefabricated cracks at 30° have a similar internal friction angle to the rock itself, and the particles near the crack tip are more prone to friction slipping during the loading process, resulting in the deterioration of the overall mechanical properties of the rock.

Fig. 8
figure 8

RA-AF relationship diagram of 30°red sandstone.

Full size image

As can be seen from Fig. 9, the number of cracks in the 90° fractured red sandstone is smaller than that in the intact and 30° fractured red sandstone. In the stable development stage of cracks, the AF value is mainly in the range of 0-200, and the RA value is in the range of 0–5. Internal damage is mainly caused by tensile cracks, with only a small amount of shear cracks occurring. In the stage of fracture instability development, the data points with high AF value and low RA value continue to rise, while the data points with high RA value and low AF value increase slowly, indicating that the damage and failure at both stages are mainly controlled by internal tensile cracks. This is because the 90° crack is aligned parallel to the principal stress, leading to a fracture failure mode dominated by tensile cracks.

Fig. 9
figure 9

RA-AF relationship diagram of 90°red sandstone.

Full size image

According to the comprehensive analysis of Figs. 7, 8 and 9, the first stage of rock loading involves internal damage mainly caused by tensile cracks, supplemented by shear cracks. At this time, the rock as a whole remains stable. As the external load increases and enters the second stage, tensile cracks increase steadily while shear cracks increase rapidly. At this point, the rock gradually transitions from the stage of stable fracture development to the stage of unstable fracture development, which can also serve as precursor information for large-scale fractures within the rock. When the rock itself has cracks aligned with the principal stress, instability failure may occur. The third stage involves the simultaneous generation of large-scale tensile and shear cracks, leading the rock to reach peak strength and destabilize.

Fracture inclination - acoustic emission fractal characteristics

Fractal theory is an effective tool to characterize the complexity and nonlinear characteristics of things. Previous studies have believed that crack propagation inside rocks also has significant nonlinear characteristics. Therefore, it is one of the effective ways to explore the damage characteristics inside rocks during loading based on rock acoustic emission signals as the carrier. The box-counting method calculates fractal dimension by covering an object with boxes of various sizes, making it simple and versatile for complex shapes. The fractal spectrum focuses on structural changes at different scales, offering a comprehensive analysis but requiring more complex calculations. Self-similarity emphasizes how objects maintain similar patterns across scales, often observed in natural phenomena like clouds and mountains. Compared with the above fractal theory, Hurst index is more focused on measuring the long-term dependence of time series data, revealing the characteristics of persistence or inversion. It provides clearer insights into dynamic systems and is particularly advantageous in analyzing time series compared to traditional fractal dimensions. Through comparison, it is found that R/S analysis method and Hurst index has significant advantages in analyzing fractal laws and memory processes of time series. Therefore, “resampler” and “rescale range” codes are compiled based on python, and the calculation principle is shown as follows.

First, the time series \(\left\{ {{x_t}} \right\}\)of an acoustic emission signal is divided into \(M\) equidistant intervals, and the time length of each sub-interval is \(n\), so each sub-interval corresponds to:

$${X_{t,n}}=\sum\limits_{{u=1}}^{t} {({x_u} - {M_n})}$$
(1)

Where \({M_n}\) represents the average of the \(n\)  interval \({x_u}\), and \({X_{t,n}}\) represents the cumulative deviation of the \(n\)  interval.

The definition of \({M_n}\) is derived from Eq. (2) :

$${M_n}=\frac{1}{n}\sum\limits_{{u=1}}^{n} {x(t)}$$
(2)

The formula for the value range \(R\)  of the subsequence is:

$$R=\hbox{max} ({X_{t,n}}) - \hbox{min} ({X_{t,n}})$$
(3)

If \(S\)  represents the standard deviation of \({x_u}\) sequence, the relation is derived from Eq. (4) :

$$S=\sqrt {\frac{1}{n}\sum\limits_{{t=1}}^{n} {{{\left[ {x(t) - {M_n}} \right]}^2}} }$$
(4)

Then the rescaled range \(R/S\) can be defined as:

$$R/S=K{(n)^H}$$
(5)

Transforming Eq. (5) yields:

$$H=d\ln (R/S)/d\ln (n)$$
(6)

In addition, the relation between Hurst index (\(H\)) and fractal dimension (\({D}\)) is:

$$D=2 - H$$
(7)

Based on the above R/S statistical method, the time series of internal crack damage evolution during rock loading was analyzed, and the R/S statistical analysis results of acoustic emission signals from red sandstone samples with different fractures were obtained, as shown in Fig. 10. As can be seen from Fig. 10, the Hurst index of the complete red sandstone is 0.745, and the Hurst index of the crack specimens ranging from 0° to 90° is 0.768, 0.707, 0.749, 0.945, and 0.994 respectively. With the increase of crack inclination, the Hurst index of the crack specimens also shows a gradual increasing trend in general. The values range from 0.7 to 1, and the correlation coefficients are all greater than 0.95, indicating that the time series of acoustic emission signals in fractured red sandstone during loading conforms to the R/S statistical distribution law. This also proves that the acoustic emission signals are positively correlated with the degree of development of internal fractures during the loading and deformation of rock.

Fig. 10
figure 10

R/S Statistical analysis results.

Full size image

Based on Eq. (7), the fractal dimensions of red sandstone with different fracture inclination angles are shown in Fig. 11. As can be seen from Fig. 11, with the increase in fracture inclination angle, the fractal dimension of the rock generally presents a downward trend, followed by an upward trend, and then a downward trend again. This pattern corresponds to the complexity and self-similarity of crack growth and development in the rock during the loading process. According to the fractal dimension, when the rock crack is close to its internal friction angle, the crack evolution in the rock always moves in a certain direction and maintains higher self-similarity under different observation scales.

Fig. 11
figure 11

Fracture dip-fractal dimension relation.

Full size image

Conclusions

  1. 1.

    The peak strength of fractured red sandstone changes in the shape of a “U” with the size of the crack inclination. Two stress drops occur during the loading of samples at 30° and 45°, and there is a good correspondence with the acoustic emission ringing count rate. The reason is that when the crack inclination is close to the internal friction angle of the sample itself, the rock’s resistance to deformation is greatly weakened. The angle of the 0° specimen is parallel to the direction of the bedding, making it much weaker than the other specimens.

  2. 2.

    Based on the acoustic emission RA and AF values in the loading process, it can be seen that the internal damage in the rock is mainly caused by tensile cracks, supplemented by shear cracks, and the rock remains stable as a whole. With the increase in external load, tensile cracks increase steadily while shear cracks increase rapidly. At this time, the rock gradually transitions from the stage of stable fracture development to the stage of unstable fracture development. This can also serve as precursor information for large-scale fractures within the rock. Following this, large-scale tensile and shear cracks lead the rock to reach peak strength, resulting in destabilized failure.

  3. 3.

    The D/S statistical analysis of the time series of rock acoustic emission signals shows that with the increase in crack inclination angle, its fractal dimension D presents a downward trend, which corresponds to the change in the complexity of crack development in the rock. When the rock crack is close to its own internal friction angle, the crack evolution in the rock always moves in a certain direction and maintains higher self-similarity at different scales.

In conclusion, the integration of acoustic emission technology and a rock pressure test system has resulted in the establishment of a joint acoustical and force monitoring methodology. This approach enables a detailed investigation of the internal crack patterns and evolution mechanisms of red sandstones with varying fracture inclination angles. The findings contribute valuable theoretical insights for assessing stability and implementing early warning systems for instability failures in engineering rock masses.