Introduction

Layered rocks, such as slate, shale and schist, are common rock types in underground engineering projects such as tunnels and mines. They are widely distributed throughout the crust of the Earth. The deformation and failure mechanism of layered rock is complex because of its bedding structure. Therefore, it is significant to study its mechanical properties to reveal the disaster mechanism of layered rock underground engineering. Laboratory tests are essential means to reveal the mechanical properties of layered rock. Zhang et al.1 studied the anisotropic mechanical properties of layered rock with different bedding angles under cyclic loading. The test results show that with the bedding dip angle of the samples from 0° to 90°, the failure type of the samples changed from splitting shear to slip shear failure, and then to splitting tensile failure. Wang et al.2 carried out uniaxial compression tests on schists, and the results show that the deformation and failure of schists have obvious anisotropy characteristics. Niandou et al.3 found that shale exhibits large anisotropic plastic deformation under conventional triaxial compression and the anisotropic behavior of failure depends largely on the confining pressure and loading direction. Li et al.4 found that the mechanical parameters and failure modes of slate show strong anisotropic characteristics by uniaxial compression and Brazilian splitting test. Zhang et al.5 studied the damage characteristics of Carboniferous slate under freeze–thaw cycles and found that it was significantly affected by bedding angle. Similar studies include Zhang6, Firdaus7, Backeberg8. According to these test results, the deformation, strength and failure of layered rocks show strong anisotropy. However, natural layered rocks have difficulties in sampling, sample preparation, and large discreteness. Especially when the sample is processed according to a specific bedding angle, the problem of sample preparation failure is often encountered. To solve these problems, some studies have been conducted based on layered rock similar samples. Xi et al.9 made layered composite rock models of sandstone and limestone, and the deformation and failure characteristics were studied. Yang et al.10 made the composite rock material with hard rock and soft rock. Then, the strength and deformation of the composite rock were studied using a triaxial compression test. Tien et al.11 prepared transversely isotropic artificial rock samples using artificial materials and studied their mechanical properties. These studies produce artificial rock samples using various methods to overcome the difficulty of sampling natural rocks. However, this method has problems such as high manufacturing costs, significant errors, and uncontrollable conditions. To solve this problem, 3D printing technology was introduced in this study to make layered rock samples.

3D printing is a rapid prototyping technology that integrates many cutting-edge technologies such as digital modeling, electromechanical control, information, material science, and chemistry12. At present, a variety of industrial-grade 3D printers have been commercialized. 3D printing technology has been widely used in industrial design, manufacturing, bioengineering, automotive engineering, aerospace engineering, and construction engineering and has been gradually introduced into rock mechanics experimental research13,14,15. 3D printing has the advantages of high precision, low discreteness, and strong reliability compared with artificial rock. The 3D printing method to make layered rocks can overcome the problems of large discreteness and the high cost of artificial construction and can be used in mechanical experiments of layered rocks. Wet material extrusion molding and powder bonding printing are commonly used printing processes in rock mechanics. Tian et al.16 developed a new method for the preparation of soft and hard interbed rocks based on 3D-printed sand core technology. Fu et al.17 printed layered rocks with different dip angles and studied their dynamic load mechanical properties, based on the powder bonding process. Tian et al.18 produced layered rock samples with various angles and sizes by powder bonding molding 3D printing technology, and carried out uniaxial compression and Brazilian splitting tests. Wang et al.19 made 3D-printed samples of sand powder and conducted dynamic impact tests on five samples with different bedding angles. Ma et al.20 printed the tunnel model based on the wet material extrusion molding process, and studied its internal damage and fracture characters. Mei et al.21 proposed a method for making marble-like rock samples based on wet material extrusion molding process. At present, the fabrication of model samples for layered rocks is mainly based on powder bonding printing process. However, this manufacturing method has the problems of high printing cost and low printing efficiency, and it is difficult to popularize and apply in large-scale physical model tests. The printing cost of wet material extrusion molding 3D printing process is low, and large-scale physical model tests can be conveniently carried out. Currently, this process is widely used in the study of mechanical properties of homogeneous and isotropic rocks, but it is rarely reported in layered rocks. Therefore, we try to establish a wet material extrusion molding 3D printing method for layered rock, aiming to fully combine the advantages of 3D printing technology and model test, and more reliably, economically and scientifically understand the mechanical properties of layered rocks.

In this study, the wet material accumulation extrusion molding 3D printing process was used, and five kinds of layered rock samples with bedding dip angles of 0°, 30°, 45°, 60°, and 90° were printed out based on the desktop-level concrete 3D printer equipment. Then uniaxial compression mechanical tests were carried out on the 3D-printed samples using digital image correlation (DIC). The stress–strain curve, strength, and failure mode of the samples were obtained, and then the mechanical properties of layered rock-like materials were studied.

Test methods for 3D printing of layered rocks

Test device

This study used a desktop concrete 3D printer, WTS material testing machine and digital image correlation (DIC) monitoring equipment to carry out the experimental research. The mechanical properties of thin layered rocks can be reflected to the greatest extent based on the wet material extrusion deposition molding process by 3D-printer. The 3D printer equipment is mainly composed of the operation system, frame work, print nozzle, extrusion system, storage bin, etc. When printing, the material is added into the storage bin to extrude it from the print nozzle. The printing requirements can be met during the printing process by adjusting the filling rate, filling angle, extrusion speed, and other parameters and changing the printing nozzles to different diameters. The WTS testing machine is used to conduct uniaxial compression tests on printed rock-like samples. It composes the control system, oil cylinder, and pressure plate. During the uniaxial compression test, the displacement rate-controlled loading mode was adopted, and the loading rate was 0.2 mm/min. DIC monitoring equipment is mainly composed of CCD camera, fill light, and image acquisition software. During the test, the collection rate was set to 1 frame per second22. The components of the test equipment are shown in Fig. 1.

Fig. 1
figure 1

Test equipment: (a) desktop-level concrete 3D printer; (b) uniaxial compression loading system.

Full size image

Test process

Based on the desktop-level concrete 3D printer equipment, the thin layer rock-like sample printing and mechanical property test process are shown in Fig. 2.

Fig. 2
figure 2

Test flow chart.

Full size image

The specific steps are as follows:

  1. (1)

    Determine the aggregate type and particle size interval. After preliminary deployment, quartz sand with particle size intervals of 70–110 mesh, 110–160 mesh, and 160–200 mesh were selected as aggregates, with a ratio of 4: 3: 3. Portland cement, sulphoaluminate cement, fly ash, and silica fume were selected as cementitious materials.

  2. (2)

    By adjusting the dosage of admixtures, the printability of the material can be controlled, so that it can meet reasonable self-sustaining force, extrudability, and appropriate initial setting time.

  3. (3)

    The three-dimensional model of the printed sample was established, and the parameters such as printing speed, filling rate, filling angle, and printing layer height were set. Five kinds of samples with bedding dip angles of 0°, 30°, 45°, 60°, and 90° were printed, with three groups of samples printed for each bedding dip angle.

  4. (4)

    The printed samples were cured in a standard curing box for 7 days, and then the samples were cut and polished to a sample with a size of 50 mm × 30 mm × 100 mm (length × width × height).

  5. (5)

    The uniaxial compression tests were conducted, supplemented by DIC monitoring of full-field strain, to analyze the deformation and failure characteristics of samples with different bedding dip angles.

The general steps of printing and testing of layered rock samples are introduced above. In this study, the material ratio of each component of the sample is shown in Table 1, and the printing parameter settings are shown in Table 2.

Table 1 The dosage of each component in 1 kg 3D printing main material and admixture, unit: g.
Full size table
Table 2 Printing parameter settings.
Full size table

Test results and analysis

Stress–strain curves

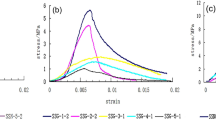
The typical stress–strain curves of 3D-printed samples with different bedding dip angles are shown in Fig. 3. When the bedding is horizontal (β = 0°), the pre-peak stress–strain curve of the sample has an obvious compaction stage, elastic stage, and pre-peak yield stage. After the peak, the stress decreases slowly with the increase of strain. Similar to β = 0°, β = 30° and 45° also have obvious compaction stage, elastic stage, and pre-peak yield stage. Compared with β = 0°, the stress–strain curves after the peak of β = 60° and 90° show a brittle drop, indicating increased brittleness. The elastic modulus of the sample is relatively low when the bedding dip angles are small. Overall, the stress–strain curve characteristics of the 3D-printed sample are similar to those reported in many related studies on the mechanical properties of layered rocks23,24.

Fig. 3
figure 3

Typical stress–strain curves of 3D-printed samples with different bedding dip angles.

Full size image

Strength characteristics

The strength characteristics of the five bedding dip angles are shown in Fig. 4. The strength of the sample with β = 0° is the highest, and the strength of the sample with β = 60° is the lowest. The strength of the 3D-printed samples exhibits a typical "U" shaped curve, which is similar to the uniaxial compressive strength test results on slate from Feng et al.25. The function y = 0.0025x2 − 0.2464x + 9.3662 can describe the change of sample strength with bedding dip angles. It can be seen that there is a significant difference in strength between samples with different bedding dip angles. For example, σβ = 0° / σβ = 60° ≈ 3.4, which shows that the bedding dip angles are an important factor affecting the strength of layered samples. The anisotropic characteristics of strength indicate that the 3D-printed layered samples are similar to natural layered rocks.

Fig. 4
figure 4

Variation of the strength of 3D-printed samples with bedding dip angles.

Full size image

Failure characteristics

Typical failure modes of samples with different bedding dip angles are shown in Fig. 5. When β = 0°, the sample presents a tensile-shear failure through bedding. When β = 30°, the sample produces shear failure along the bedding and tensile failure across the bedding. When β = 45° and 60°, the shear failure along the beddings are mainly presented. When β = 90°, the splitting failure along the bedding is mainly presented.

Fig. 5
figure 5

Typical failure modes of samples with different bedding dip angles.

Full size image

The above analysis shows that the bedding dip angles have an important impact on the failure of 3D-printed samples. With the increase of bedding dip angles, the degree of failure controlled by bedding structure increases, and the failure modes transitions from shear failure through bedding to shear and tension along the bedding. The failure modes of printed samples with different bedding dip angles are quite different, which indicates that the failure of 3D-printed samples has strong anisotropic characteristics. This is similar to the results of many reports on the mechanical properties of layered rocks26,27,28.

Characteristics of full-field strain evolution

Because the strain band concentration process of the sample can be better reflected in the transverse tensile strain field, the evolution characteristics of the tensile strain field of the samples with different bedding dip angles during the loading process are analyzed25. The strain variance can reflect the non-uniform evolution process of the strain field, so the variance of the tensile strain field is calculated and normalized (Eqs. (1)–(2)).

$$S_{\varepsilon xx} \left( t \right) = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \overline{x} } \right)^{2} } }}{n}$$
(1)
$$v_{\varepsilon xx} \left( t \right) = \frac{{s_{\varepsilon xx} \left( t \right)}}{{s_{\varepsilon xx} \left( {t_{\max } } \right)}}$$
(2)

where Sεxx(t) is the variance of the full field strain at a given time; xi is the tensile strain value at each point in the strain field; \(\overline{x}\) is the mean of tensile strain at all points in the strain field; vεxx(t) is the normalized full-field strain variance at a certain time, and Sεxx(tmax) is the variance of full-field strain at peak stress.

Figure 6 shows the normalized tensile strain variance variation and stress with loading time for β = 0° ~ 90°. The entire loading stage can be roughly divided into four stages: (a) compaction stage, (b) elastic stage, (c) inflection point stage of variance curve, (d) near-peak stress stage, as shown in Fig. 7. The tensile strain field cloud map was extracted at the corresponding stage.

Fig. 6
figure 6

Variation of tensile strain variance and stress with loading time, when the β is different: (a) β = 0°; (b) β = 30°; (c) β = 45°; (d) β = 60°; (e) β = 90°.

Full size image
Fig. 7
figure 7

Evolution of tensile strain field at different loading stages.

Full size image

As shown in Fig. 7, for the samples with β = 30°, 45°, and 60°, when the shear failure along the bedding occurs, the strain concentration zone has developed in the elastic stage. The strain concentration zone expands and runs through remarkably near the inflection point of the variance curve. When β = 30° and 45°, the shear stress along the bedding direction is relatively small, and the vertical tensile strain concentration bands appear. When β = 0°, the strain concentration zone development of the sample has a certain randomness, and the failure of the sample has little correlation with bedding.

When β = 90°, the sample develops vertical tensile strain concentration bands with an obvious elongation process. Overall, when the bedding dip angles are large, there is an obvious inflection point when the variance curve of the transverse strain field is close to the peak stress. It shows that for 3D-printed samples, the shear or tensile failure along the bedding has a certain degree of mutation, and the development, propagation, and it penetration of shear or tensile cracks along the bedding are rapid. This is consistent with the brittle failure characteristics exhibited by the stress–strain curve.

Conclusions

In this study, a wet material extrusion 3D printing process was adopted to prepare layered rock-like samples with five different bedding dip angles. This method can produce layered rock-like samples in bulk, with advantages such as low cost, convenient production, no need for molds, and small discreteness, providing a new approach and method for the study of layered rock mechanics experiments. Uniaxial compression tests were carried out on five samples with different bedding dip angles, and the mechanical properties of the samples with different bedding dip angles were studied using digital image correlation (DIC) monitoring technology. The main conclusions are as follows:

  1. (1)

    The stress–strain curves of the samples with five bedding dip angles have a compaction stage, elastic stage, and pre-peak yield stage. The samples with β = 45° ~ 90° have strong brittleness, while the samples with β = 0° and 30° show strong ductility. With the decrease of bedding dip angles, the elastic modulus of the samples decrease gradually. The strength shows a typical “-U -curve” with the change of bedding dip angles.

  2. (2)

    The sample exhibits shear failure through bedding at β = 0°. The main cracks of the sample with β = 30° develop along the bedding and are accompanied by local tensile failure across the bedding. The samples with β = 45° and 60° exhibit typical shear failure along the bedding. The sample with β = 90° mainly undergoes tensile failure along the bedding. It shows that the failure of 3D-printed samples with different bedding dip angles has strong anisotropy characteristics.

  3. (3)

    The strain field evolution characteristics of the samples with different bedding dip angles have significant differences. The strain concentration bands of β = 30°, 45°, 60° appeared earlier and distributed along the bedding. Generally, as the bedding dip angles increase, the variance curve of the transverse strain field exhibits an apparent inflection point near the peak stress. It shows that for 3D-printed samples, the shear or tensile failure along the bedding has a certain degree of mutation.

  4. (4)

    The mechanical properties of the layered specimens formed by the wet material extrusion 3D printing process are similar to those of natural layered rocks and have obvious anisotropy. This method has low cost and high accuracy in printing layered samples, which can provide a new idea for large-scale layered rock physical model test research.