Introduction

Faults are among the most common geological structures in underground coal mines1,2,3,4,5. When activated by mining activities, they can often trigger major hazards such as rock bursts6,7,8,9,10,11, coal and gas outbursts12,13,14,15, fault water inrushes16,17,18, and seismic events. Additionally, as the working face advances towards the fault, the extraction process transitions from stable primary coal to fractured tectonic coal. During this transition, the capacity of the support shield to maintain the stability of the primary coal pillar (hereafter referred to as the coal pillar for ease of description) is challenged.

As shown in Fig. 1, the spalling of coal pillar creates space for the lateral leakage of tectonic coal, which can even lead to roof collapse19,20, support skewing, and crushing injuries21.

Fig. 1
figure 1

Process of working face passing through a fault: (a) boundary between primary coal and tectonic coal; (b) spalling of coal pillar; (c) lateral leakage of tectonic coal; (d) injuries caused by overloaded support structures.

Full size image

Scholars have conducted extensive research on the issue of coal pillar spalling during the process of the working face crossing faults22,23,24. Pan et al.25 established a mechanical model for coal pillar spalling in steeply inclined coal seams, taking into account the rotational forces of main roof, and derived the deflection equation of coal pillars related to the deflection angle of main roof. Wu et al.26 proposed that the stress variations in the rock during the working face crossing a fault exhibit staged characteristics: a high-stress stage near the fault and a low-stress stage away from the fault. Wang et al.27 developed a physical model of fault displacement evolution, identifying the boundaries between unaffected zones, affected zones, and severely affected zones. Lan et al.28, through theoretical analysis and numerical simulation, studied the no danger zone, medium danger zone, and high danger zone. Chen et al.29 investigated the instability process of irregular coal pillars using theoretical analysis and numerical simulation, categorizing the internal areas of irregular coal pillars into four distinct zones: damaged zone, progressive zone, stable zone, and special zone. Yao et al.30 observed five typical failure modes of coal pillars during the mining process: (a) upper-rib spall, (b) upper-rib spall and roof caving, (c) integral spall, (d) V-shaped spall, and (e) arcuate spall.

These studies have made significant progress in understanding the conditions of fault activation, the evolution of stress distribution (vertical stress), and typical failure modes of coal pillars. However, when studying the issue of coal pillar spalling as the working face crossing faults, only a few researchers31,32,33 have focused on the changes in the micro-pore structure and coalification near the fault. Nonetheless, in coal seam mining, the differences in macroscopic manifestations caused by changes in coal quality and the large-scale lateral migration of tectonic coal deserve more attention.

This paper takes the 15,106 working face of Wangyun Coal Mine as the research object. By combining the loading characteristics of coal pillars in fault areas and using theories of soil mechanics and material mechanics34, we established a mechanical model of coal pillars in fault areas. This model considers the cohesion between coal and rock layers, pressure on the roof and floor, the support role of hydraulic shields, and horizontal tectonic stress. The stability factors affecting the coal pillar are analyzed, and techniques for safely passing through the fault are proposed.

Engineering overview

Working face overview

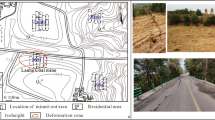
Wangyun Coal Mine is located in Gaoping City, Shanxi Province. The 15,106 working face extracts No.15 coal seam, with an average coal thickness of 4.7 m and an average coal seam dip angle of 5°. The main roof is gray-black mudstone with a thickness of 8.29 m, the immediate roof is K2 limestone with a thickness of 5.72 m, the immediate floor is bauxitic mudstone with a thickness of 7.15 m, and the main floor is sandstone with a thickness of 10.0 m. The layout of the working face and the stratigraphic column derived from the borehole are presented in Fig. 2a,b.

Fig. 2
figure 2

Layout of the working face: (a) plan view of the working face; (b) stratigraphic column from the borehole; (c) heat map of the hydraulic support working resistance; (d) on-site photographs.

Full size image

On-site damage phenomena

Fault F36 traverses the entire working face, from 254 m in the headgate to 200 m in the tailgate, oriented N3°E with a dip angle of 75° and a displacement of approximately 2.5 m. When the working face is positioned 4 to 5 m from the fault, the working resistance of the end hydraulic support (models 1 to 20) increases, as illustrated in Fig. 2c. Notably, a significant change in coal quality is observed in the downstream transportation channel (as indicated in Fig. 2d). Additionally, a substantial area of tectonic coal-roof debris mixture is leaking sideways and accumulating locally. This accumulation prevents normal progression of the working face, as shown in Fig. 3a. Figure 3b presents a statistical analysis of the hydraulic support’s tilt on site. The histogram reveals varying degrees of skewness in the hydraulic support, with some supports tilting more than 31 degrees, which poses a serious safety risk.

Fig. 3
figure 3

On-site conditions: (a) on-site photographs; (b) condition of the hydraulic supports.

Full size image

Analysis of coal pillar spalling during working face crossing faults

Failure process of coal pillar in fault areas

Under geological processes, the structure of coal body near faults is highly fragmented and loose. Based on structural differences, the coal seam near the fault can be divided into primary coal and tectonic coal. Primary coal retains its original sedimentary structure and features, while tectonic coal has undergone changes in composition and structure due to tectonic stress. Some tectonic coal is severely damaged, with well-developed fractures and extremely low strength, appearing as powdery material that can be crushed by hand, as shown in Fig. 4.

The process of the working face crossing a fault involves transitioning from primary coal to tectonic coal and then back to primary coal. As the working face advances, the width of the structurally intact coal pillar decreases continuously. The inherent stiffness of the coal pillar becomes insufficient to withstand the combined effects of mining-induced stresse and tectonic stress, leading to spalling. Subsequently, the mixture of tectonic coal and roof debris on one side of the coal pillar leakages laterally, causing roof subsidence and uneven loading and misalignment of the support structures.

Fig. 4
figure 4

Failure process of coal pillar in fault areas.

Full size image

Analysis of tectonic stress on coal pillars

Under the influence of advanced mining-induced stress, tectonic coal undergoes volumetric deformation, exerting a non-uniform horizontal load on the coal pillar. Due to the highly fragmented structure of tectonic coal, measuring the horizontal tectonic stress using conventional techniques is challenging. Considering the structure characteristics of tectonic coal, the calculation of horizontal tectonic stress is conducted using soil mechanics methods for retaining wall earth pressure35. The horizontal tectonic stress is calculated based on the deformation compatibility relationship between horizontal tectonic stress and coal pillar deformation.

As shown in Fig. 5, during the formation of fault structures, the minimum principal stress is the vertical stress, the maximum principal stress is the tectonic stress perpendicular to the fault trace, and the intermediate principal stress is the tectonic stress parallel to the fault trace. When the fault activity ceases and the strata stabilize, the stress on the fault surface reaches an equilibrium state36, expressed as:

$$\sigma _{h} \left( {{\text{sin}}\alpha - \mu {\text{cos}}\alpha ) = \sigma _{v} \left( {{\text{cos}}\alpha + \mu {\text{sin}}\alpha } \right.} \right.)$$
(1)
$$\sigma _{v} /\sigma _{h} = {\text{tan}}\left( {\alpha - \varphi } \right)$$
(2)

where, σv is vertical stress, MPa; σh is tectonic stress perpendicular to the fault trace, MPa; α is angle between the normal direction of the fault plane and the direction of the maximum principal stress, °; α is friction angle of the fault plane, °; µ is friction coefficient during sliding between the upper and lower fault blocks, µ=tan φ.

Fig. 5
figure 5

Stress state and stress equilibrium of a fault.

Full size image

Based on the coal pillar failure phenomena observed during the process of the 15,106 working face crossing the fault, it is assumed that there is an interface OE in the coal seam, representing the boundary between primary coal and tectonic coal (as shown in Fig. 6). The region ODCE is tectonic coal, while the region OABE is primary coal. As the working face approaches the fault, the mining-induced load q continuously compresses the tectonic coal, causing it to have a tendency to slide along the fault plane CD, and applies a non-uniformly distributed tectonic stress on the primary coal pillar OABE.

To analyze the distribution characteristics of tectonic stress, a right-angled trapezoidal microelement of thickness dh is taken at a height h from the roof OD. The microelement is subjected to vertical stress σv on its upper side, upward vertical stress σv + dv on its bottom side, σh and τhv on its left side, and σα and τα on its right side, along with the body force df.

Fig. 6
figure 6

Schematic diagram of tectonic coal and primary coal near the fault.

Full size image

Based on the force balance conditions of the right-angled trapezoidal microelement in the horizontal and vertical directions, we obtain:

$$\sigma _{h} \;dh + \tau _{\alpha } \;dh\;{\text{cot}}\alpha - \sigma _{\alpha } \;dh = 0$$
(3)
$$\left( {H - h} \right)\sigma _{v} {\text{cot}}\alpha + df - \left( {H - h - dh} \right)\left( {\sigma _{v} + d\sigma _{v} } \right){\text{cot}}\alpha - \tau _{{hv}} dh - \tau _{\alpha } dh - \sigma _{\alpha } dh\;{\text{cot}}\alpha = 0$$
(4)
$$df = dh\left( {H - h} \right){\text{cot}}\alpha \;\rho \;g - \frac{{dh^{2} {\text{cot}}\alpha }}{2}\rho \;g$$
(5)
$$\left\{ {\begin{array}{*{20}l} {\tau _{{hv}} = \sigma _{h} {\text{tan}}\phi } \hfill \\ {\tau _{\alpha } = \sigma _{\alpha } {\text{tan}}\varphi } \hfill \\ \end{array} } \right.$$
(6)

Substituting Eq. (6) into Eq. (3), we get:

$$\sigma _{\alpha } = \sigma _{v} \frac{{{\text{cot}}\left( {\alpha - \varphi } \right){\text{tan}}\phi }}{{\left( {1 - {\text{tan}}\varphi\;{\text{cot}}\alpha } \right)}}$$
(7)

By combining and simplifying Eq. (2) through (7), and neglecting higher-order small quantities, we obtain:

$$\frac{{d\sigma _{v} }}{{dh}} = \frac{{\sigma _{v} \left[ {1 - {\text{tan}}\alpha\;{\text{cot}}\left( {\alpha - \phi } \right)\left( {{\text{tan}}\varphi + {\text{cot}}\left( {\alpha - \phi } \right)} \right)} \right]}}{{\left( {H - h} \right)}} + \rho g$$
(8)

where, ϕ is the friction angle of coal body, °. α is the dip angle of fault, °. φ is the friction angle of fault plane, °. ρg is the unit weight of coal body, N/m³.

In Eq. (8), we make the following substitution: \(k=1-{k}_{0}\), \(k_{0} = {\text{tan}}\;\alpha\;{\text{cot}}\left( {\alpha - \varphi } \right)\left( {{\text{tan}}\phi + {\text{cot}}\left( {\alpha - \varphi } \right)} \right)\). Here, k0 is a parameter related to the friction angle of the coal body, the dip angle of fault, and the friction angle of fault plane, which we can call the “angle factor.” Thus, we have:

$$\frac{{d\sigma _{v} }}{{dh}} - \frac{k}{{\left( {H - h} \right)}}\sigma _{v} = \rho g$$
(9)

Equation (9) is a first-order non-homogeneous linear equation, which can be solved using the method of variation of parameters to find its general solution:

$$\sigma _{v} = \left( { - \frac{1}{{k + 1}}\rho g\left( {H - h} \right)^{{k + 1}} + C} \right)\left( {H - h} \right)^{{ - k}}$$
(10)

Using the boundary condition on the OD boundary: when h = 0, σv = q, we can solve for the undetermined coefficient C in the general solution (10) and simplify it to obtain:

$$\sigma _{v} = \left( {q - \frac{{\rho gH}}{{\left( {2 - k_{0} } \right)}}} \right)\left( {1 - \frac{h}{H}} \right)^{{k_{0} - 1}} - \frac{{\rho gH}}{{2 - k_{0} }}\left( {1 - \frac{h}{H}} \right)$$
(11)

By combining Eqs. (2), (6), and (11), we get:

$$\sigma _{h} = {\text{cot}}\left( {\alpha - \varphi } \right)\left[ {\left( {q - \frac{{\rho gH}}{{\left( {2 - k_{0} } \right)}}} \right)\left( {1 - \frac{h}{H}} \right)^{{k_{0} - 1}} - \frac{{\rho gH}}{{2 - k_{0} }}\left( {1 - \frac{h}{H}} \right)} \right]$$
(12)
$$\tau _{{hv}} = {\text{tan}}\phi\;{\text{cot}}\left( {\alpha - \varphi } \right)\left[ {\left( {q - \frac{{\rho gH}}{{\left( {2 - k_{0} } \right)}}} \right)\left( {1 - \frac{h}{H}} \right)^{{k_{0} - 1}} - \frac{{\rho gH}}{{2 - k_{0} }}\left( {1 - \frac{h}{H}} \right)} \right]$$
(13)

Equations (12) and (13) represent the tectonic stress and shear stress on the OE plane of primary coal, respectively.

Distribution pattern of tectonic stress

From the stress distribution function expressions (12) and (13) at the interface between primary coal and tectonic coal, it is evident that the angle factor k0 is the key parameter determining the functional form. To further analyze the tectonic stress on the primary coal pillar OABE, the parameters for the 15,106 working face of Wangyun Coal Mine are used as an example, with values listed in Table 1.

Table 1 Parameter value.
Full size table

As previously defined, the value of the angle factor k0 varies with the friction angle of fault plane, the dip angle of fault, and the friction angle of coal body. As shown in Fig. 7a, when the dip angle of fault is 75°, the angle factor k0 approaches infinity as the friction angle of fault plane approaches 75° (indicating a singularity at this point), determined by the fault stability condition. Figure 7b–d show the values of the angle factor k0 for fault with dip angles of 75°, 50°, and 25°, respectively, where the gray area indicates k0<1 and the colored area indicates k0 ≥ 1.

Fig. 7
figure 7

Variation pattern of the parameter k0.

Full size image

From Eq. (12), when the angle factor k0 < 1, the tectonic stress σh distribution function is a negative exponential function. The distribution characteristics of tectonic stress when k0 < 1 are shown in Fig. 8. The tectonic stress first increases and then decreases from the top to the bottom of the coal pillar, with the peak value located in the lower middle part of the coal pillar. The smaller the dip angle of fault, the greater the tectonic stress on the coal pillar, which is consistent with the numerical simulation results in the literature37.

Fig. 8
figure 8

Distribution characteristics of tectonic stress when the angle factor k0 < 1.

Full size image

When the angle factor k0 ≥ 1, the tectonic stress σh distribution function becomes a positive exponential function. Similarly, the smaller the dip angle of fault, the greater the horizontal tectonic stress on the coal pillar, resulting in different value ranges of the tectonic stress distribution function for different dip angles of fault.

To facilitate analysis, the function values of the tectonic stress distribution function are normalized, as shown in Fig. 9. The normalized results indicate that within 0 to 4 m from the roof of the coal seam, the tectonic stress function is a monotonic function, decreasing monotonically when the dip angle of coal seam α < π/2-ϕ and increasing monotonically otherwise.

Fig. 9
figure 9

Distribution characteristics of horizontal tectonic stress when the angle factor k0 ≥ 1.

Full size image

Mechanical model of coal pillar in fault areas

In terms of establishing a coal pillar stability analysis model, some scholars have treated the coal pillar as a compression member with one end elastically supported and the other end fixed, to address the instability problem of high-cut coal walls. Other scholars argue that the rotational pressure of the roof during the instability process of high-cut coal walls cannot be ignored and suggest that the “coal strips” near the coal wall should be regarded as a compressed “column strip” with a fixed lower end and a hinged upper end. Additionally, for the instability problem of coal walls where fractures extend through as a plate, some scholars simplify it as the bending problem of a rectangular thin plate under uniformly distributed pressure. For the stability analysis of coal pillars in fault zones, a beam-column mechanical model subjected to axial pressure and lateral loads is particularly suitable. Given that the ends of the beam-column model are fixed, this configuration more accurately reflects the cementation between the primary coal pillar and the top and bottom plates, thereby facilitating a more precise calculation of load distribution and mechanical response.

Basic assumptions

The loading on coal pillars in fault areas is complex, influenced by roof and floor pressures, cohesion between coal and rock layers, hydraulic support protection, and horizontal tectonic stress. To facilitate analysis, the following basic assumptions are made when establishing the mechanical model:

  1. (1)

    The tectonic stress σh on the OE section of the coal pillar is analyzed using its maximum value. For safety considerations, the value of σh used in calculations is the maximum value σhmax from Eq. (12) within the height range of the coal pillar to analyze its stability.

  2. (2)

    The effect of the shear stress τhv on the OE section of the coal pillar is neglected. As shown in Eq. (13), the shear stress on the OE section is minimal and perpendicular to the direction of the coal pillar’s bending deformation, thus its influence on the horizontal deflection of the coal pillar can be ignored.

  3. (3)

    The influence of the volume force of the coal pillar is neglected. In situations with small mining heights, the volume force of the coal pillar has a negligible impact on its horizontal deflection.

Establishment of the mechanical model

Taking a unit length of the coal pillar along the advancing direction of the working face, the roof and floor pressures are equivalent to a pair of symmetrically distributed loads . Under the influence of horizontal tectonic stress, the cohesion between the coal pillar and the roof and floor resists the relative movement of the coal pillar. According to Saint-Venant’s principle38,39, the cohesion between the roof and floor and the coal pillar is equivalent to a pair of equal and opposite moments.

Based on the above analysis, a mechanical analysis model of coal pillar fixed at both ends and subjected to uniformly distributed horizontal tectonic stress and multiple concentrated loads is established, as shown in Fig. 10a. Figure 10b illustrates the support force of the hydraulic support side guard plate on the coal pillar, Fig. 10c shows the uniformly distributed load applied by the tectonic coal on the coal pillar in the horizontal direction, and Fig. 10d depicts the cohesion between the coal pillar and the roof and floor.

Fig. 10
figure 10

Mechanical model of coal pillar.

Full size image

Fundamental differential equation

As shown in Fig. 11, the coal pillar is subjected to vertical roof and floor pressures q and horizontal tectonic stress σhmax, where σhmax is a function of x. To derive the basic equation for the deflection of the coal pillar, a differential segment of length dx is considered from Fig. 11. Within the differential segment, the intensity of the tectonic stress σhmax can be considered constant, with its direction being the same as the positive y-axis (to the left), and assuming the shear force FS and bending moment M acting on the two sides of the segment as shown in the Fig. 11 are positive.

Fig. 11
figure 11

Relationship between tectonic stress, shear force, and bending moment in the coal pillar.

Full size image

From the equilibrium relationship in the y-axis direction of the differential segment, we have:

$$\sigma _{{hmax}} dx + \left( {F_{S} + dF_{S} } \right) = F_{S} \quad {\text{or}}\quad \sigma _{{hmax}} = - \frac{{dF_{S} }}{{dx}}$$
(14)

Assuming the angle between the coal pillar axis and the vertical line is small, taking the moment about point G, neglecting higher-order infinitesimals and simplifying, we get:

$$F_{S} = \frac{{dM}}{{dx}} - q\frac{{dy}}{{dx}}$$
(15)

In the absence of shear deformation and axis shortening, the curvature expression of the axis is:

$$EI\frac{{d^{2} y}}{{dx^{2} }} = - M$$
(16)

Combining Eqs. (14), (15), and (16), we obtain the differential equation in the axial direction:

$$F_{S} = - EI\frac{{d^{3} y}}{{dx^{3} }} - q\frac{{dy}}{{dx}}\quad {\text{or}}\quad \sigma _{{hmax}} = EI\frac{{d^{4} y}}{{dx^{4} }} + q\frac{{d^{2} y}}{{dx^{2} }}$$
(17)

where, EI is the bending stiffness of the coal pillar in the xoy plane; E is the elastic modulus of the coal pillar; I = L3/12 is the moment of inertia of the coal pillar; and L is the width of the coal pillar.

Analysis of factors affecting the stability of coal pillar

Influence of support force of side guard plate

Under the roof and floor pressures, the influence of the support force of side guard plate on the deflection of the coal pillar is a statically indeterminate problem. The bending moment generated by the roof and floor pressures needs to be solved under certain boundary conditions. The process is as follows:

As shown in Fig. 10b, the distance from the concentrated load P to the origin O is h. The bending moments in the upper and lower segments of the coal pillar are:

$$\left\{ {\begin{array}{*{20}l} {M = \frac{{Ph}}{H}x + Py,\quad \left( {0 \le x \le H - h} \right)} \hfill \\ {M = \frac{{P\left( {H - h} \right)}}{H}\left( {H - x} \right) + Py,\quad \left( {H - h \le x \le H} \right)} \hfill \\ \end{array} } \right.$$
(18)

Combining Eqs. (16) and (18) and solving the resulting differential equation, the general solution is:

$$\left\{ {\begin{array}{*{20}l} {w_{P} \left( x \right) = A_{1} {\text{cos}}\lambda x + B_{1} {\text{sin}}\lambda x - \frac{{Ph}}{{qH}}x} \hfill \\ {w_{P} \left( x \right) = A_{2} {\text{cos}}\lambda x + B_{2} {\text{sin}}\lambda x - \frac{{P\left( {H - h} \right)\left( {H - x} \right)}}{{qH}}} \hfill \\ \end{array} } \right.$$
(19)

where, \(\lambda = \sqrt {q/EI}\), and A1, A2, B1, B2 are integration constants.

Based on the boundary conditions: The deflection at the upper and lower ends of the coal pillar is zero. The deflection curve is continuous at the point of application of the support force P, meaning the deflection curves of the upper and lower segments are identical and have a common tangent at this point. Determining the integration constants and substituting into Eq. (19), we obtain the deflection curve equations for the upper and lower segments:

$$\left\{ {\begin{array}{*{20}l} {w_{P} \left( x \right) = \frac{{P{\text{sin}}\lambda h}}{{q\lambda {\text{sin}}\lambda H}}{\text{sin}}\lambda x - \frac{{Ph}}{{qH}}x,\quad \left( {0 \le x \le H - h} \right))} \hfill \\ {w_{P} \left( x \right) = \frac{{P{\text{sin}}\lambda \left( {H - h} \right){\text{sin}}\lambda \left( {H - x} \right)}}{{q\lambda {\text{sin}}\lambda H}} - \frac{{P(H - h)(H - x)}}{{qH}},\quad \left( {H - h \le x \le H} \right)} \hfill \\ \end{array} } \right.$$
(20)

When the point of action of the side guard plate is at the middle of the coal pillar, the angles of rotation at the roof and floor can be derived by differentiating Eq. (20) and substituting h = H/2, x = 0:

$$\theta _{{Po}} = - \theta _{{PE}} = \left( {\frac{{dw_{P} \left( x \right)}}{{dx}}} \right)_{{h = H/2,x = 0}} = \frac{{PH^{2} \left( {{\text{sec}}\;u - 1} \right)}}{{8EI\;u^{2} }}$$
(21)

where, u = λH/2.

From Eq. (20), it can be seen that the support force of side guard plate is most effective in resisting the bending deformation of the coal pillar when the point of action is at the middle of the coal pillar. The deflection at this point is:

$$\left. {w_{{Pmax}} = w_{P} \left( x \right)} \right|_{{x = h = \frac{H}{2}}} = \frac{{PH^{3} }}{{48EI}}\frac{{3\left( {{\text{tan}}\;u - u} \right)}}{{u^{3} }}$$
(22)

Influence of maximum horizontal tectonic stress

As shown in Fig. 10c, the tectonic stress σh is a function of h. In the height range of the coal pillar, the maximum value of σh, denoted as σhmax, is considered. The deflection curve under the action of tectonic stress can be viewed as the cumulative effect of infinitesimal load elements σhmaxdh at distance h from point O. From Eq. (20), the deflection curve under the maximum horizontal tectonic stress is:

$$\begin{aligned} w_{{\sigma _{{h{\text{max}}}} }} \left( x \right) & = \frac{{{\text{sin}}\lambda x}}{{q\lambda {\text{sin}}\lambda H}}\smallint _{0}^{{H - x}} \sigma _{{h{\text{max}}}} {\text{sin}}\lambda hdh - \frac{x}{{qH}}\smallint _{0}^{{H - x}} \sigma _{{h{\text{max}}}} hdh \\ & \quad + \frac{{{\text{sin}}\lambda \left( {H - x} \right)}}{{q\lambda {\text{sin}}\lambda {\mkern 1mu} H}}\smallint _{{H - x}}^{H} \sigma _{{h{\text{max}}}} {\text{sin}}\lambda \left( {H - h} \right)dh \\ & \quad - \frac{{(H - x)}}{{qH}}\smallint _{{H - x}}^{H} \sigma _{{h{\text{max}}}} (H - h)dh \\ \end{aligned}$$
(23)

Integrating and simplifying:

$$w_{{\sigma _{{h{\text{max}}}} }} \left( x \right) = \frac{{\sigma _{{h{\text{max}}}} H^{4} }}{{16EIu^{4} }}\left[ {\frac{{{\text{cos}}\left( {2ux/H - u} \right)}}{{{\text{cos}}u}} - 1} \right] - \frac{{x\left( {H - x} \right)H^{2} \sigma _{{h{\text{max}}}} }}{{8EIu^{2} }}$$
(24)

The angles of rotation at points O and E can be obtained by differentiating the deflection curve equation:

$$\theta _{{\sigma _{{h{\text{max}}}} O}} = - \theta _{{\sigma _{{h{\text{max}}}} E}} = \left( {\frac{{dw_{{M_{0} }} \left( x \right)}}{{dx}}} \right)_{{x = 0}} = \frac{{H^{3} \sigma _{{h{\text{max}}}} }}{{8EI}}\left( {\frac{{{\text{tan}}\;u - u}}{{u^{3} }}} \right)$$
(25)

The deflection at the middle of the coal pillar under the maximum horizontal tectonic stress is:

$$\left. {w_{{\sigma _{{h{\text{max}}}} {\text{max}}}} = w_{{\sigma _{{h{\text{max}}}} }} \left( x \right)} \right|_{{x = \frac{H}{2}}} = \frac{{5\sigma _{{h{\text{max}}}} H^{4} }}{{384EI}}\left[ {\frac{{12\left( { - u^{2} + 2{\text{sec}}\;u - 2} \right)}}{{5u^{4} }}} \right]$$
(26)

Influence of cohesion

To analyze the effect of the equivalent moment of cohesion on the deflection of the coal pillar, the deflection curve under the action of one side moment can be solved first, then the deflection curve under the action of the other side moment can be solved based on symmetry, and the two curves can be superimposed. As shown in Fig. 10b, the closer the point of action of the concentrated load is to the origin O, the smaller the moment h and the larger the concentrated load P. When the moment h approaches zero, there exists a concentrated load P such that the product of P and h equals the moment M0. At this point, sin λh is equivalent to λh, and substituting sin λh = λh, Ph = M0 into Eq. (20), the deflection curve equation under the action of symmetrical moments can be obtained based on symmetry:

$$w_{{M_{0} }} \left( x \right) = \frac{{M_{0} H^{2} }}{{4EIu^{2} }}\left[ {{\text{cos}}\left( {\frac{{2u}}{H}x - u} \right){\text{sec}}\;u - 1} \right]$$
(27)

The rotational angles at points O and E can be derived from Eq. (22) of the deflection curve equation as follows:

$$\theta _{{M_{0} o}} = - \theta _{{M_{0} E}} = \left( {\frac{{dw_{{M_{0} }} \left( x \right)}}{{dx}}} \right)_{{x = 0}} = \frac{{M_{0} H}}{{2EI}}\left( {\frac{{{\text{tan}}\;u}}{u}} \right)$$
(28)

Thus, the deflection of the middle part of coal pillar under the effect of cohesion is:

$$\left. {w_{{M_{0} {\text{max}}}} = w_{{M_{0} }} \left( x \right)} \right|_{{x = H/2}} = \frac{{M_{0} H^{2} }}{{8EI}}\frac{{2\left( {{\text{sec}}\;u - 1} \right)}}{{u^{2} }}$$
(29)

Stability criterion of coal pillars

From Eqs. (22), (26), and (29), it can be seen that the support force of side guard plate, the maximum horizontal tectonic stress, and the cohesion are all positively correlated with the deflection of the coal pillar. By substituting the data from Table 1 into these equations, the impact of different factors on the deflection of the coal pillar can be obtained.

Due to the different dimensions of the three influencing factors, the values of the three influencing factors are normalized. The results are shown in Fig. 12. The support force of side guard plate, the maximum horizontal tectonic stress, and the cohesion of roof and floor are all positively proportional to the deflection of the coal pillar. The curve slope corresponding to the maximum horizontal tectonic stress is the largest, followed by the curve slope corresponding to the cohesion of roof and floor, and the curve slope corresponding to the support force of side guard plate is the smallest.

Fig. 12
figure 12

Influence of different factors on the deflection of the coal pillar.

Full size image

Due to the bending deformation of the coal pillar under the combined effect of the tectonic stress σhmax and the roof and floor pressure q. The side guard plate provides a concentrated load P to resist the bending deformation of the coal pillar, while the cohesion of roof and floor provides a pair of symmetrical moments to resist the bending deformation of the coal pillar. According to the superposition principle, the deflection at the middle part of the coal pillar when stable should satisfy the following equilibrium relationship:

$$w_{{\sigma _{{h{\text{max}}}} {\text{max}}}} = w_{{M_{0} {\text{max}}}} + w_{{P{\text{max}}}}$$
(30)

Substituting Eqs. (22), (26), and (29) into Eq. (30), we get:

$$\frac{{5\sigma _{{h{\text{max}}}} H^{4} }}{{384EI}}\left[ {\frac{{12\left( { - u^{2} + 2{\text{sec}}\;u - 2} \right)}}{{5u^{4} }}} \right] = \frac{{M_{0} H^{2} }}{{8EI}}\frac{{2\left( {{\text{sec}}\;u - 1} \right)}}{{u^{2} }} + \frac{{PH^{3} }}{{48EI}}\frac{{3\left( {{\text{tan}}\;u - u} \right)}}{{u^{3} }}$$
(31)

According to the boundary conditions:

$$\theta _{{\sigma _{{h{\text{max}}}} o}} = \theta _{{Po}} + \theta _{{M_{0} o}}$$
(32)

We get:

$$M_{0} = \frac{{H^{2} \sigma _{{h{\text{max}}}} }}{4}\left( {\frac{{{\text{tan}}\;u - u}}{{u^{2} {\text{tan}}\;u}}} \right) - \frac{{PH}}{{4u\;{\text{tan}}\;u}}\left( {{\text{sec}}\;u - 1} \right)$$
(33)

Substituting Eq. (33) into Eq. (31), we get:

$$\sigma _{{h{\text{max}}}} H\left[ {\left( {\frac{{ - u^{2} + 2\left( {{\text{sec}}\;u - 1} \right)}}{{\left( {{\text{sec}}\;u - 1} \right)}}} \right) - \left( {\frac{{{\text{tan}}\;u - u}}{{{\text{tan}}\;u}}} \right)} \right] = 2P\left[ {\left( {\frac{{{\text{tan}}\;u - u}}{{\left( {{\text{sec}}\;u - 1} \right)}}} \right) - \frac{{\left( {{\text{sec}}\;u - 1} \right)u}}{{{\text{tan}}\;u}}} \right]$$
(34)

To analyze the influencing factors of the stability of coal pillar, the elastic modulus of the coal pillar E = 1.23 × 109 Pa, the moment of inertia I = L3/12, and other parameters involved in Table 1 are substituted into Eq. (34). Using MATLAB, the variation curves of different parameters are plotted as shown in Fig. 13.

Fig. 13
figure 13

Influencing factors of the stability of coal pillar: (a) different mining heights; (b) different roof and floor pressures; (c) different coal pillar integrities.

Full size image

Figure 13a illustrates the relationship between coal pillar width and side guard support force under different mining heights. It can be observed that for a coal pillar width of 2.0 m, the required side guard support forces for mining heights of 4.0, 3.5, and 3.0 m are 1.19 MPa, 0.89 MPa, and 0.64 MPa, respectively. As the mining height increases, the required support force increases. Additionally, as the working face advances and the coal pillar width decreases, the required support force to maintain stability increases.

Figure 13b shows the relationship between coal pillar width and side guard support force under different roof and floor pressures. For a coal pillar width of 2.0 m, the required side guard support forces for roof and floor pressures of 8.95 MPa, 9.95 MPa, and 10.95 MPa are 1.19 MPa, 1.42 MPa, and 1.65 MPa, respectively. Higher roof and floor pressures require greater support forces. Similarly, as the working face advances and the coal pillar width decreases, the required support force to maintain stability increases.

The macroscopic manifestations caused by the microstructural changes in the coal quality near the fault can be represented by the integrity of coal wall. The difference in integrity can be quantified according to the strain assumption proposed by J. Lemaitre in 197240. The difference in the integrity of the coal pillar and the reinforced coal before and after reinforcement can be considered as damage to the elastic modulus, with the elastic modulus of coal pillar as the benchmark (100%). The relationship between coal pillar width and side guard support force at different integrities is analyzed, as shown in Fig. 13c. For a coal pillar width of 2.0 m, the required side guard support forces for coal pillar integrities of 100%, 60%, and 20% are 1.19 MPa, 1.63 MPa, and 3.49 MPa, respectively. The lower the coal pillar integrity, the higher the required support force. As the working face advances and the coal pillar width decreases, the required support force to maintain stability increases.

Since the support force that hydraulic supports can provide is limited, the stability criterion of the coal wall can be taken as the upper limit of the side guard support force provided by the hydraulic support:

$$\frac{1}{2}\frac{{\sigma _{{h{\text{max}}}} H\left[ { - u^{2} {\text{tan}}\;u + \left( {{\text{sec}}\;u - 1} \right)\left( {{\text{tan}}\;u + u} \right)} \right]}}{{\left[ {\left( {{\text{tan}}\;u - u} \right){\text{tan}}\;u - \left( {{\text{sec}}\;u - 1} \right)^{2} u} \right]}}P \le \left[ P \right]$$
(35)

Equation (35) represents the stability criterion of the coal pillar under the combined effect of tectonic stress and mining-induced stress q, where [P] is the upper limit of the side guard support force that hydraulic supports can provide. Taking the hydraulic support with a working resistance of 17,000 kN from the Wangyun Coal Mine as an example, and according to the calculation method in the literature41, the upper limit of the side guard support force provided by side guard plate is 1,786.6 kN (approximately 0.53 MPa). In Fig. 13a–c, [P] is represented as a horizontal line. The areas above the line indicate coal pillar instability zones, whereas the areas below the line indicate stable zones.

Industrial experiment

Control concepts of working faces crossing faults

Based on the above analysis, the following control techniques can be employed when working faces crossing faults: (1) reducing mining height; (2) increasing the support force of side guard plate on coal pillars; (3) enhancing the flexural stiffness of coal seams (elastic modulus and coal pillar width). The stability of coal pillars is related to the roof and floor pressure, the flexural stiffness of coal pillars, mining height, and the support force of side guard plate. Therefore, to maintain coal pillar stability, pre-grouting ahead of the coal pillars is advantageous for enhancing their stability and integrity42. Adjusting the inclination angle of hydraulic supports during inclined mining can increase the support force of side guard plate on coal pillars.

Control techniques of working faces crossing faults

Based on the above control techniques, a comprehensive technical plan named “inclined mining with slope adjustment” and “pre-grouting of coal pillars” has been developed for safely and smoothly crossing the F36 fault at Wangyun Coal Mine:

  1. (1)

    Reducing mining height: Before encountering structural coal at the fault, reduce the mining height from 4.0 m to 3.5 m.

  2. (2)

    Inclined mining with slope adjustment: Progress the working face with a 9° inclination. At this point, the coal pillars change from a rectangular section to a trapezoidal section (as shown in Fig. 14), increasing the width of the coal pillars and thereby enhancing their flexural stiffness to resist higher horizontal structural stresses in the middle and lower parts of the coal pillars.

  3. (3)

    Pre-grouting of coal pillars: Drill holes at an angle of 12° with a diameter of 42.0 mm, spacing and row spacing of 1.5 m, and a depth of 5.0 m at positions 0.5 m from the roof between hydraulic supports. Grout injection is performed every 4.0 m. The specific layout is shown in Fig. 14.

Fig. 14
figure 14

Pre-grouting of coal pillars and inclined mining across the fault.

Full size image

On-site effects

As shown in Fig. 15a,b, after implementing the measures proposed in this paper, the hydraulic supports in the working face are no longer tilted and are uniformly flat.

As shown in Fig. 15c, the grouting slurry spreads to the lower part of the coal wall, demonstrating effective grouting with minimal coal fragment shedding, resulting in stable coal pillars.

As shown in Fig. 15d, prior to implementing control measures, cutting a knife of coal seam required 4.5 shifts (each shift of 8 h). After implementing control measures, mining operations returned to normal, requiring only 2 shifts to cut a knife of coal seam.

Fig. 15
figure 15

On-site effects: (a)-(c) construction effects; (d) comparison of working face advancement time.

Full size image

Conclusions

  1. (1)

    Field observations and data indicate significant variations in coal quality near the fault. There is a distinct boundary between primary coal and tectonic coal. When the working face crosses this boundary, there is considerable roof pressure and frequent coal pillar spalling.

  2. (2)

    Theoretical analysis results indicate that the angle factor k0 determines the form of the horizontal tectonic stress function. When k0<1, the horizontal tectonic stress function is a negative exponential function; otherwise, it is a positive exponential function. The deflection of coal pillars is directly proportional to the support force of side guard plate, maximum horizontal tectonic stress, and equivalent moments of cohesion. Roof and floor pressures and mining height are positively correlated with the required support force of side guard plate. Coal pillar integrity and width are negatively correlated with the required support force needed to maintain coal pillar stability.

  3. (3)

    Combining the actual conditions of the 15,106 working face, a combined technique of “inclined mining” and “grouting” for working faces crossing faults is proposed. The grouting material effectively diffuses within the tectonic coal, controlling the frequent coal pillar spalling and the tilting of hydraulic supports. Ultimately, the working face crossed the fault smoothly and efficiently, providing a reference for controlling coal pillar spalling under similar engineering geological conditions.