Introduction

With the progress of science and technology, industrial products have brought convenience to people lives, but at the same time, the pollution of the environment is also significant. Noise pollution, as an essential type of pollution, is widely distributed in industrial production, transport, and daily life. Ventilation is necessary in many noise scenarios. Efficient absorption of low-frequency sound while maintaining fluid flow remains a significant challenge in acoustic engineering due to the strict trade-off between absorption and ventilation performance.

Conventional acoustic materials are unsuitable due to size, difficulty recycling and disposal, and poor low-frequency effectiveness. Acoustic metamaterials are capable of controlling noise through subwavelength and deep-subwavelength dimensions1. As an emerging acoustic modulation method, it has been investigated in the fields of acoustic cloaking2,3,4, acoustic focusing5,6,7, and noise reduction8,9,10. In recent years, as an extension, it has also been applied in the fields of acoustic metamaterial coding11,12 and fault diagnosis13,14. Various metamaterial absorbers have been proposed with the continuous advances in acoustic metamaterials, but most of them work adequately only under conditions without sound transmission. When a complete fluid channel is required, their absorption performance drops drastically. Numerous scholars have extensively studied this to ensure ventilation while improving noise attenuation performance. Kim15 designed a transparent acoustic window using diffraction theory and acoustic metamaterial theory which consists of a three dimensional array of strongly diffractive resonators. The negative effective bulk modulus of the resonant cavity generates an evanescent wave, and the effectiveness on airflow is experimentally verified. Ghaffarivardavagh16 demonstrated that acoustic properties of a two-layer medium differ and exhibit an asymmetric transmission, similar to the Fano interference phenomenon. This work proposed a deep-subwavelength acoustic metasurface unit cell comprising nearly 60% open area for air passage while serving as a high-performance selective silencer. Fano-like interference provides a viable solution for permeability barriers. The mechanism of Fano-like interference, on the other hand, suggests a narrow frequency range for its operation. Since noise usually covers a wide frequency range, designing broadband acoustic barriers remains a challenge. Sun17 proposed a hypersurface consisting of a central hollow hole and two helical channels with different pitches. The response strengths of the monopole and dipole modes of the system are almost balanced in a specific frequency range and can effectively block more than 90% of the incident energy. The proposed design is experimentally validated and the results are consistent with analytical predictions and simulations. The design has potential for air permeability and acoustic insulation applications. Xiang18 proposed an ultra-open ventilated metamaterial absorber, elaborating the mechanism from an effective model of coupled lossy oscillators, targeting low-frequency sounds while ensuring high-performance absorption and ventilation. Zhang19 proposed an acoustic metamaterial muffler for grazing flow pipelines and established the related analytical and numerical calculation models. By analyzing the impedance at the inlet of the side branch, the influence law of the swept flow velocity on the performance of the acoustic metamaterial is obtained. This work provides a new solution for the application of acoustic metamaterials.

The analysis of the thermal viscous effect (TVE) on waves is often neglected in previous studies on ventilated acoustic metamaterials, and the volume of ventilated acoustic metamaterials needs to be further reduced. In this paper, a ventilated acoustic metamaterial labyrinth (VAML) is proposed that fully utilizes the space and reduces the volume by channel folding. The analytical and numerical computational model of the VAML is developed considering TVE, and the experimental results are compared to verify the accuracy of the model. The effect of TVE is analyzed quantitatively and its impact on macroscopic acoustic performance is described. The geometrical parameters of the VAML are quantitatively analyzed to obtain the influence law of the structure parameters on the transmission coefficient. Finally, the effect of fluid flow velocity on the transmission coefficient is quantitatively investigated by building a CFD model.

Methods

Analytical model

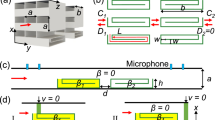
The ventilated acoustic metamaterial model proposed in this paper is shown in Fig. 1 and consists of four metamaterial units arranged circumferentially. The waveguide of the metamaterial unit is divided into two parts, denoted by channels 1 and 2, and the lengths were labeled \(l_{1}\) and \(l_{2}\). The thickness of the VAML is labeled t, the width of the labyrinth channel is labeled d, the wall thickness is labeled w, and the radius of the ventilated area is R.

Fig. 1
figure 1

Ventilated acoustic metamaterial labyrinth. (a) 3D model. (b) Structural schematic.

Full size image

In order to reveal the mechanism of action of VAML, the analytical models are developed. The TVE of the acoustic wave and the entrance loss due to the sudden change in cross section are considered in the model20. The impedance at the entrance can be calculated as21

$$\begin{aligned} {Z_1} = {Z_{1JCA}}\frac{{ - i{Z_s}\cot \left( {{k_{1JCA}}w} \right) + {\mathrm{{Z}}_{1JCA}}}}{{Zs - i{Z_{1JCA}}\cot \left( {{k_{1JCA}}w} \right) }} \end{aligned}$$
(1)

where \(\textit{Z}_{1JCA}\) is the acoustic impedance of the porous substrate based on the JCA model22,23, \({Z_{1JCA}} = {\rho _{JCA}}{c_{JCA}}\), \({\textit{k}_{1jca} = \omega /\textit{c}_{JCA}}\), and the effective sound velocity is calculated as \({c_{JCA}} = \sqrt{{\kappa _{JCA}}/{\rho _{JCA}}}\). The effective density and bulk modulus are calculated as

$$\begin{aligned} {\rho _{JCA}}= & \frac{{{\alpha _t}{\rho _0}}}{\phi } + \frac{\sigma }{{i\omega }}\sqrt{1 + \frac{{4i\alpha _t^2\eta {\rho _0}\omega }}{{{\sigma ^2}{\zeta ^2}{\phi ^2}}}} \end{aligned}$$
(2)
$$\begin{aligned} {\kappa _{JCA}}= & \frac{{\gamma {P_0}/\phi }}{{\gamma - \left( {\gamma - 1} \right) {{\left[ {1 + \frac{{8\eta }}{{i{\rho _0}\omega \Pr {{\zeta '}^2}}}\sqrt{1 + \frac{{i{\rho _0}\omega \Pr {{\zeta '}^2}}}{{16\eta }}} } \right] }^{ - 1}}}} \end{aligned}$$
(3)

where \(\eta\) and Pr are the kinetic viscous of the air and Prandtl’s number. \(\sigma\) is the airflow resistivity24. Porosity \(\phi\) and tortuosity \(\alpha _{t}\) equal to 1. \(\zeta\) and \(\zeta '\) are the viscous and thermal characteristic lengths, respectively25,26. \(\gamma\) is the specific heat ratio equal to 1.4. \(P_{0}\) is the standard atmospheric pressure.

\(Z_s\) is the effective impedance under the influence of TVE and is calculated as

$$\begin{aligned} {Z_s} = {\mathrm{{Z}}_{e1}}\frac{{ - i\left( {{Z_2}/{\phi _s}} \right) \cot \left( {{k_1}{l_1}} \right) + {Z_{e1}}}}{{{Z_2}/{\phi _s} - i{Z_e}\cot \left( {{k_1}{l_1}} \right) }} \end{aligned}$$
(4)

where \(Z_{e1} = \rho _e c_e\), \(l_e\) is the effective length, and the effective complex wave number \(k_e = \omega /c_e\). The effective density \(\rho _e = \rho _0/\psi _\nu\) and the effective speed of sound \(c_e = \omega /k_c\).

$$\begin{aligned} k_c^2 = k_0^2\frac{{\gamma - \left( {\gamma - 1} \right) {\psi _h}}}{{{\psi _\nu }}} \end{aligned}$$
(5)

where \(\psi _i\),\(i = h, \nu\), denote the viscous and thermal fields, respectively, are expressed as

$$\begin{aligned} {\psi _i} = k_i^2\sum \limits _{m = 0}^\infty {\left[ {{{({\alpha _m}m')}^{ - 2}}\left( {1 - \frac{{\tan \left( {{\alpha _m}W/2} \right) }}{{{\alpha _m}W/2}}} \right) + {{({\beta _m}m')}^{ - 2}}\left( {1 - \frac{{\tan \left( {{\beta _m}H/2} \right) }}{{{\beta _m}H/2}}} \right) } \right] } \end{aligned}$$
(6)

where W and H are the channel width and height. m is the number of summation terms and it is found through analysis that the equation reaches convergence when m is equal to 100.\({\alpha _m} = \sqrt{k_i^2 - \left( {2m'/W} \right) }\), \({\beta _m} = \sqrt{k_i^2 - \left( {2m'/H} \right) }\), where \(m' = \left( {m + 1/2} \right) \pi\), \({k_\nu } = \sqrt{ - i\omega {\rho _0}/\mu }\),\({k_h} = \sqrt{ - i\omega {\rho _0}{C_p}/{\kappa _0}}\)27.

Then, for channel 2, \(Z_2\) is the acoustic impedance at the beginning of channel 2, which can be calculated as

$$\begin{aligned} {Z_2} = {Z_{2JCA}}\frac{{ - {Z_{e2}}\cot ({k_2}{l_2})\cot ({k_{2JCA}}w) + {Z_{2JCA}}}}{{ - i{Z_{e2}}\cot ({k_2}{l_2}) - i{Z_{2JCA}}\cot ({k_{2JCA}}w)}} \end{aligned}$$
(7)

where \(Z_{2JCA}\) is calculated in the same way as \(Z_{1JCA}\), and \(Z_{e1}\) is calculated in the same way as \(Z_{e1}\).

Considering the fluid effects, the impedance \(Z_1\) at the entrance of the side branch can be corrected by the correction term \(\Gamma\)28, \({\Gamma } = {\rho _0}{c_0}\kappa \mathrm{{Ma}}/\sigma\). In this paper, \(\kappa\) is the semi-empirical correction coefficient, \(\textrm{Ma}\) is the Mach number, and \(\sigma\) is the spatial opening ratio in this case \(\sigma = 4WH/\pi {R^2}\). Finally, the impedance Z at the entrance of the side branch is calculated as \(Z = Z_1 + \Gamma\).

The transmission coefficient is calculated as29

$$\begin{aligned} \tau = 1 - \frac{{\sigma {\rho _0}{c_0}}}{{\sigma {\rho _0}{c_0} + 2Z}} \end{aligned}$$
(8)

The sound transmission loss (STL) can be calculated as \(\mathrm{{STL}} = - 20\log _{10}\left( {\left| \tau \right| } \right)\).

Table 1 Physical parameters of materials.
Full size table

Numerical model

The finite element model is established through COMSOL Multiphysics, and thermal viscous acoustic interfaces and pressure acoustic interfaces are used, as shown in Fig. 2a, assuming that the TVE of the wave propagating through the straight tube is neglected. The contact surface between the pressure acoustic zone and the thermal viscous acoustic zone is defined as a multi-physics field coupling. Ports 1 and 2 are set on both sides of the straight tube, where the incident excitation amplitude of port 1 is defined as 1 Pa. A tetrahedral mesh is used for the thermal viscous influence zone and a hexahedral mesh for the other zones, as shown in Fig. 2b. The model contains 337340 tetrahedral meshes and 65520 hexahedral meshes, all of which are 4mm in size. In the thermal viscous acoustic zone, the boundary layer is defined with a layer number of 5 and a total thickness that corresponds to the characteristic thickness of the TVE. The material parameters during numerical computation are shown in Table 1.

Fig. 2
figure 2

Finite element model. (a) Physical field setup. (b) Delineation of mesh.

Full size image

The amplitude of the acoustic wave decays exponentially, influenced by the large thermal viscous damping at the boundary30. As a result, a viscous wave is generated, defined as \(u\left( z \right) ={{u}_{0}}\exp \left[ -\pi f{{\rho }_{0}}{{u}^{-1/2}}\left( 1+i \right) z \right]\), and the viscous penetration depth is \({{\delta }_{v}}={{\left[ \mu /\left( \pi f{{\rho }_{0}} \right) \right] }^{1/2}}\). Similarly, a thermal wave is generated at the wall, defined as \({{\delta }_{h}}={{\left[ {{k}_{h}}/\left( \pi f{{\rho }_{0}}{{C}_{p}} \right) \right] }^{1/2}}\). The ratio of \({\delta }_{v}\) and \({{\delta }_{h}}\) is related to the randtl’s number31.

$$\begin{aligned} \frac{{{\delta _v}}}{{{\delta _{h}}}} = \sqrt{\frac{{\mu {C_p}}}{{{k_h}}}} = \sqrt{\Pr } \end{aligned}$$
(9)

This ratio is close to 0.84 in the air, so the viscous and thermal thickness is of the same order of magnitude. In the numerical model, the thermal-viscous losses are calculated in the form of energy disturbances.

$$\begin{aligned} \frac{{\partial E}}{{\partial t}} + \nabla \cdot \mathbf{{W}} = - D \end{aligned}$$
(10)

where E is the second-order disturbance energy density, \(\textbf{W}\) is the flux vector, and D is the second-order source term.

$$\begin{aligned} E= & \frac{1}{2}\left( {{\rho _0}{u^2} + \frac{{{p^2}}}{{{\rho _0}c_0^2}} + \frac{{{\rho _0}{T_0}{s^2}}}{{{C_p}}}} \right) \end{aligned}$$
(11)
$$\begin{aligned} \mathbf{{W}}= & p\mathbf{{u}} - {\left( {{\mathbf{{u}}^\text {T}} \cdot \tau } \right) ^\text {T}} - \frac{{{k_h}}}{{{T_0}}}T\nabla T \end{aligned}$$
(12)
$$\begin{aligned} D= & \tau :\nabla \mathbf{{u}} + \frac{{{k_h}}}{{{T_0}}}{\left( {\nabla T} \right) ^2} \end{aligned}$$
(13)

where s is the entropy, \(\text {T}\) indicates the transpose of vector, and \(\tau\) is the viscous stress tensor. \(T_0\) and f are the amplitude and frequency of the thermal viscous wave, respectively. \(\textbf{u}\) is the particle vibration velocity. In Eq. (13), the first term is the viscous dissipation function, and the second term is the thermal dissipation function on the right side of the equal sign.

Analysis and validation of results

Analyze and experiment for TVE

To study the macroscopic acoustic performance of VAML, the analytical model, the numerical computational model and the experimental STL is calculated, as shown in Fig. 3. The structural parameters of the three cases are shown in Table 2. In case 1, for example, the STL peak is located at 328 Hz. In the model, the TVE of the wave is taken into account, leading to a smooth transition of the STL curve at the peak rather than tending to infinity. The results of the analytical and numerical models are in good agreement, which verifies the accuracy of the model. With a noise reduction target of 5 dB, the effective bandwidth is 300 Hz-357 Hz. The experimental results are smaller than the theoretical calculations at the resonance frequency, which is caused by the fact that the samples are fabricated using fused deposition modeling (FDM) technology, and there are certain manufacturing errors, which affect the roughness and dimensional accuracy of the wall surface. In addition, in the theoretical model, hard boundaries are defined in the ideal state. However, it is difficult to achieve complete reflection of sound waves at the wall in experiments. The cases 2 and 3 show a shift in resonance frequency compared to case 1, but the general trend is similar to case 1.

Fig. 3
figure 3

Sound transmission loss of VAML.

Full size image
Table 2 Structural parameters.
Full size table

The impedance tube experiments are carried out using the test system as shown in Fig. 4a, where the hardware consists of an upstream tube, a downstream tube, a power amplifier and a signal collector. The specimen is fabricated using the FDM technique with a layer height of 0.1 mm, nozzle diameter of 0.2 mm and filament diameter of 1.75 mm, as shown in Fig. 4b. In the experiment, the relationship between acoustic pressure and particle vibration velocity is expressed as32,33

$$\begin{aligned} \begin{array}{l} {\left[ {\begin{array}{*{20}{c}} {{p_{0m}}}\\ {{u_{0m}}} \end{array}} \right] _{x = 0,load = m}} = T \times {\left[ {\begin{array}{*{20}{c}} {{p_{0m}}}\\ {{u_{0m}}} \end{array}} \right] _{x = t,load = m}}\\ {\left[ {\begin{array}{*{20}{c}} {{p_{tn}}}\\ {{u_{tn}}} \end{array}} \right] _{x = 0,load = n}} = T \times {\left[ {\begin{array}{*{20}{c}} {{p_{tn}}}\\ {{u_{tn}}} \end{array}} \right] _{x = t,load = n}} \end{array} \end{aligned}$$
(14)

where m, n are the loading conditions. T is the transfer matrix associated with the four microphones

$$\begin{aligned} T = \left[ {\begin{array}{*{20}{c}} {\frac{{{p_{0m}}{u_{tn}} - {p_{0n}}{u_{tm}}}}{{{p_{tm}}{u_{tn}} - {p_{tn}}{u_{tm}}}}}& {\frac{{{p_{0m}}{p_{tn}} - {p_{0m}}{p_{tn}}}}{{{p_{tm}}{u_{tn}} - {p_{tn}}{u_{tm}}}}}\\ {\frac{{{u_{0m}}{u_{tn}} - {p_{0n}}{p_{tm}}}}{{{p_{tm}}{u_{tn}} - {p_{tn}}{u_{tm}}}}}& {\frac{{{p_{tm}}{u_{0n}} - {p_{tn}}{u_{0m}}}}{{{p_{tm}}{u_{tn}} - {p_{tn}}{u_{tm}}}}} \end{array}} \right] \end{aligned}$$
(15)

The parameters in equation 15 are expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {p_0} = A + B,{p_t} = C{\mathrm{{e}}^{ - jkd}} + D{\mathrm{{e}}^{jkt}}\\ {u_0} = \frac{{A - B}}{{{Z_0}}},{u_t} = \frac{{C{\mathrm{{e}}^{ - jkd}} - D{\mathrm{{e}}^{jkt}}}}{{{Z_0}}} \end{array} \right. \end{aligned}$$
(16)

where A, B, C and D are the complex sound pressure at each of the four microphones and the air impedance \(Z_0 = \rho _0c_0\).

The transmission coefficient is calculated as34

$$\begin{aligned} \tau = \frac{{2{e^{jkt}}}}{{{T_{11}} + \frac{{{T_{12}}}}{{{Z_0}}} + {T_{21}}{Z_0} + {T_{22}}}} \end{aligned}$$
(17)
Fig. 4
figure 4

Sound transmission loss experiment. (a) Impedance tube test system. (b) Specimens.

Full size image

The STL in the experiment is calculated based on the transmission coefficient results. As shown in Fig. 3, the STL curve has an obvious peak at 330 Hz, and the error of the theoretical calculation results is 0.6% compared with it, which verifies the validity of the theoretical model. The experimental results are higher than the theoretical calculations in most of the frequency ___domain. This phenomenon is because the inner diameter of the impedance tube is larger than the ventilation radius R, which is neglected in theoretical calculations.

For case 1, the sound pressure distribution in the VAML at the resonance frequency is shown in Fig. 5a. The sound pressure is more significant inside the channel and the maximum amplitude reaches 3 Pa, indicating that the resonance is obvious inside the channel. As the position is close to the entrance, the amplitude of the sound pressure gradually decreases, and the sound pressure is close to 0 Pa at the entrance. The distribution of the sound pressure level is shown in Fig. 5b. It can be seen that the plane wave is attenuated dramatically when it passes through the entrance of the side branch. The sound pressure level inside the channel is affected by the resonance of the sound wave and appears higher.

Fig. 5
figure 5

VAML sound pressure and sound pressure level distributions. (a) sound pressure. (b) sound pressure level.

Full size image

TVE inside the channel is not negligible and the comparison of the VAML transmission coefficients when TVE is considered and not considered is shown in Fig. 6. As can be seen from the figure, the minimum value of the transmission coefficient is 0.08 when TVE is considered, and correspondingly, a smooth transition is presented at the peak of the STL shown in Fig. 3. Without TVE, the transmission coefficient is equal to zero at a specific frequency, and the corresponding peak of the STL curve should tend to infinity. In addition, the TVE causes the resonant frequency to drop from 334Hz to 328Hz, which is equivalent to adding the weight of the mass block to the spring-mass system. Thus, TVE has a negative effect on sound transmission loss, but a positive effect on low-frequency noise blocking.

Fig. 6
figure 6

Effect of TVE on transmission coefficient.

Full size image

To further investigate the mechanism of TVE on VAML, the transmission coefficient \(\tau\), reflection coefficient r, and absorption coefficient \(\alpha\) of VAML are calculated as shown in Fig. 7. At the resonance frequency, the value of the transmission coefficient is small, and correspondingly, the reflection and absorption coefficients appear to have a higher value. The sound wave is reflected by the near-field radiation at the entrance of the side branch, and the attenuation of the incident sound wave is caused, which leads to an increase in the reflection coefficient and an attenuation of the transmission coefficient. In addition, when resonance occurs inside the channel, the violent oscillation of the sound wave significantly improves their energy conversion at the near wall, and thus the absorption coefficient is increased.

Fig. 7
figure 7

Multi-coefficient distribution of VAML.

Full size image
Fig. 8
figure 8

Variation of TVE with distance.

Full size image

The variation in thermal and viscous dissipation in the near-wall with the distance from the wall is shown in Fig. 8. The thermal dissipation near the wall is more significant, reaching 1.0 mW/m3, and the viscous dissipation is more negligible, with a maximum value of 0.2 mW/m3. With the increase of the distance from the wall, the thermal and viscous losses gradually decrease, and the reduction rate of the thermal dissipation is larger than the reduction rate of the viscous dissipation. At 1.5 mm from the wall, the thermal and viscous dissipation tend to be zero.

To investigate the mechanism of the effect of TVE on the transmission coefficient, the impedance Z at the entrance of the side branch is shown in Figure 9. When TVE is considered, the impedance is shown in Fig. 9a. The real part of Z, real(Z), is significantly larger than 0 under the influence of TVE, representing the loss. The imaginary part of Z, imag(Z), denoting the reactance, tends to increase. The minimum value of the modulus of Z, \(\left| Z \right|\), leads to the valley of the transmission coefficient. However, the minimum value of \(\left| Z \right|\) is not equal to 0, and it can be thought that the side branch entrance presents an imperfect match between acoustic resistance and reactance. When TVE is neglected, the impedance Z is shown in Fig. 9b, and it is observed that the real(Z) value is always close to 0. Therefore, the minimum value of \(\left| Z \right|\) tends to be 0 at 334 Hz, and acoustic resistance and reactance can be regarded as perfectly matched.

Fig. 9
figure 9

Variation of TVE on impedance at the channel inlet. (a) Considering TVE. (b) Neglecting TVE.

Full size image

According to Eq. (6), the effect of structural parameters on TVE and transmission coefficient is significant. The effect of the structure parameters on the transmission coefficient is shown in Fig. 10. The change in color corresponds to a change in the value of the transmission coefficient. The variation of the transmission coefficient with the length of channel 1 \(l_1\) is shown in Fig. 10a when the channel 2 length \(l_2\) = 95 mm, the width of channel d = 10 mm, and the ventilation radius R = 10 mm. As \(l_1\) increases, the transmission coefficient valley increases, and the corresponding resonant frequency gradually decreases. The variation in the transmission coefficient with the length of channel 2 \(l_2\) is shown in Fig. 10b when \(l_1\) = 200 mm, d = 10 mm, and R = 10 mm. As \(l_2\) increases, the transmission coefficient valley increases, and the corresponding resonant frequency decreases. The variation in the transmission coefficient with channel width d is shown in Fig. 10c when \(l_1\) = 200 mm, \(l_2\) = 95 mm, and R = 10 mm. The valley of the transmission coefficient decreases gradually with increasing channel width d. This phenomenon is attributed to the fact that as d increases, the spatial openness ratio \(\phi _0\) increases, improving the efficiency of near-field radiation at the entrance of the side branches and positively affects STL. At the same time, the resonant frequency decreases. The variation of transmission coefficient with ventilation radius R is shown in Fig. 10d when \(l_1\) = 200 mm, \(l_2\) = 95 mm, and d = 10 mm. As the ventilation radius R increases, the transmission coefficient valley increases, and the reason can be attributed to the fact that the increase in the ventilation radius R decreases the spatial openness ratio \(\phi _0\). In difference to the other parameters, the variation of the ventilation radius R has little effect on the resonant frequency.

Fig. 10
figure 10

Variation of transmittance coefficient distribution with structural parameters. (a) Channel 1 length \(l_1\). (b) Channel 2 length \(l_2\). (c) Channel width d. (d) Ventilation radius R.

Full size image

Fluid effects analysis

When the VAML is placed in the fluid, the fluid passes through the ventilated region and generates a time-___domain perturbation to the impedance at the inlet of the side branch. In order to reveal this phenomenon, the change rule of transmission coefficient under different flow velocities is calculated, which is of great significance to advance the practical application of VMAL. Correction for acoustic impedance was accomplished by introducing the fluid flow velocity into the analytical model. As shown in Fig. 11, the flow of the fluid causes the transmission coefficient to increase at the resonance frequency with a positive correlation, thus the fluid flow has a negative effect on the performance of the VAML.

Fig. 11
figure 11

Variation of transmission coefficient with flow velocity.

Full size image
Fig. 12
figure 12

Variation of transmission coefficient minimum with Ma.

Full size image

Further, the variation of transmission coefficient minimum with Ma is shown in Fig. 12. In noisy industrial scenarios, the fluid flow velocity usually does not exceed 0.3 Ma. The corresponding transmission coefficient in this case has a minimum value of 0.13, which can still provide an excellent noise reduction effect in practical applications. The transmission coefficient increases as Ma increases, but this growth is not linear. Compared to the red curve in the figure, its growth rate gradually decreases, and the value of growth is also decreasing.

To further reveal the effect of flow velocity on the transmission coefficient, the Turbulent Flow, SST Interface in COMSOL Multiphysics was employed for CFD modeling. In the model, the boundary conditions at the inlet were set to be a fully developed flow with a velocity of 0.2 Ma, as shown in Fig. 13a. The outlet boundary condition was set to pressure outlet. The tetrahedral and hexahedral meshes are defined together to improve calculation efficiency. The model contains 165317 tetrahedral meshes and 11912 hexahedral meshes, while the boundary layer is defined to accurately calculate the flow near the wall. The velocity distribution results are shown in Fig. 13b. As can be seen from the figure, in the area near the entrance of the side branch, vortices are generated and the fluid transition is significantly enhanced. The process of vortex formation and shedding generates non-linear pressure pulsations that directly affect the propagation of acoustic waves at this ___location.

Fig. 13
figure 13

CFD model and calculation results. (a) Boundary conditions and meshes. (b) Velocity distribution near the entrance of the branch.

Full size image

Discussion

In this paper, a ventilated acoustic metamaterial labyrinth is proposed and a corresponding analytical model is established. The transmission coefficient, STL, and impedance at the entrance of the VAML side branches are obtained quantitatively. The TVE is comparatively analyzed, and its influence law is elaborated. The corresponding numerical computational model and experiments are conducted to verify the accuracy of the analytical model. The structure parameters are quantitatively analyzed. Finally, the influence law of the fluid flow velocity on the transmission coefficient is revealed. The following conclusions are obtained.

  1. (1)

    Resonance of specific frequency waves in the VAML produces a peak STL with a certain bandwidth, indicating that the proposed VAML can achieve noise attenuation while ensuring ventilation.

  2. (2)

    The VAML has an impedance imperfect match at the entrance of the side branch due to TVE. Thus, the transmission coefficient at the resonance frequency is not 0 and leads to an absorption coefficient. In the near-wall region, the thermal dissipation is larger than the viscous dissipation.

  3. (3)

    The results of structural parameter analysis show that the resonance frequency decreases with the increase of channel 1 length \(l_1\), channel 2 length \(l_2\), and channel width d. In addition, with the increase of \(l_1\), \(l_2\), and ventilation radius R, the valley value of transmission coefficient increases, which means that the noise reduction effect is weakened. The channel width d is negatively correlated with the valley value of transmission coefficient.

  4. (4)

    As Ma increases, the vortex strength increases and the transmission coefficient minimum rises, thus the fluid flow has a negative effect on the macroscopic acoustic performance.