Introduction

Since its discovery in 1956, vancomycin, a glycopeptide antibiotic, has been integral in combating bacterial infections, particularly drug-resistant Gram-positive bacteria such as methicillin-resistant Staphylococcus aureus (MRSA)1. MRSA is responsible for a wide range of diseases, from skin and soft tissue infections to severe conditions like pneumonia, bacteremia, osteomyelitis, meningitis, endocarditis, and sepsis2. Elderly patients, due to physiological degeneration and diminished immune function, are particularly susceptible to healthcare-associated infections (HAIs), often caused by multidrug-resistant organisms3. Epidemiological studies, such as those by Cairns et al., have shown that the risk of HAIs increases linearly with age, underscoring the impact of aging on infection susceptibility and the pharmacokinetics of antibiotics4.

Elderly individuals exhibit significant inter- and intra-individual variability in pharmacokinetics. Renal function, which declines with age, plays a crucial role in the metabolism of vancomycin, a drug primarily excreted via glomerular filtration5. This decline can lead to elevated vancomycin levels and an increased risk of nephrotoxicity6,7. More studies have shown that similar dosing regimens lead to different vancomycin concentration levels in elderly and young patients8. Furthermore, the hydrophilic nature of vancomycin means its concentration can increase as body water content decreases in older adults, adding to the complexity of dosing in this population. Vancomycin is also associated with serious adverse effects such as acute kidney injury, ototoxicity, and red man syndrome9,10. Thus, therapeutic drug monitoring (TDM) is recommended to optimize efficacy and minimize adverse reactions, particularly for those over 65 years of age1,11,12. However, the necessity for TDM to reach a steady state before effective monitoring can delay treatment initiation, posing a significant challenge in acute settings.

Population pharmacokinetics (popPK) is used to quantitatively describe a patient’s drug exposure over time and can also identify sources of differences between patients, such as age, weight, and renal function. Although past studies have leveraged popPK models to optimize vancomycin dosing in elderly patients13,14, these models often include limited covariates such as gender, age, weight, serum creatinine (Scr), and creatinine clearance (CLcr), which may not fully capture the complexities of elderly patient physiology. The pathophysiological status of elderly individuals is intricate, influenced by factors such as inflammatory status, organ function degeneration, concurrent medication use, and comorbid conditions, all of which affect vancomycin metabolism and necessitate more personalized dosing strategies.

In response to these complexities, machine learning (ML) has emerged as a powerful tool for enhancing medication precision. ML models are adept at detecting statistical patterns within large datasets, drawing on comprehensive electronic health records to improve outcome predictions and personalize treatment approaches. Recent expert opinions have advocated for the complementary use of popPK models and ML techniques15,16. Research has shown that incorporating individual parameter estimates from the popPK model as features in a ML model improves predictive performance compared to using either the ML model or the popPK model alone17. However, few studies have integrated these approaches to predict drug plasma concentrations effectively.

Based on these, our study aimed to establish a prediction model for Vancomycin plasma concentration in elderly patients by incorporating popPK parameters as new features into the ML modeling to combine traditional popPK and ML methods. By employing multiple algorithms to identify key determinants of drug plasma concentration, this approach seeks to enhance the practical clinical application of personalized medication, optimizing therapeutic outcomes while mitigating risks associated with vancomycin treatment.

Methods

Patients and data

The trial was a single-center, retrospective study in elderly patients of the First Affiliated Hospital of Army Medical University from November 2013 to July 2022. Another dataset was collected as the clinical validation group enrolled from August 2022 to May 2023. Patients with suspected or documented Gram-positive bacterial infection receiving vancomycin who underwent TDM were enrolled. The inclusion criteria were as follows: (1) age ≥ 65 years; (2) treatment with vancomycin for ≥ 2 days. The exclusion criteria were as follows: (1) underwent irregular administration of vancomycin (13 samples); (2) failure to reach the lower limit of quantification (LLOQ) for the vancomycin plasma concentration assay. The blood sample was collected within 30 min before the next morning dose after reaching steady-state concentration (continuous vancomycin administration for at least two days). Demographic data and laboratory data were collected from the Electronic Medical Record System (EMRS) of the hospital.

Ethics approval

This study was approved by the Institutional Review Board (IRB) of the Southwest Hospital of Army Medical University ([B]KY2023074) and performed in accordance with the Declaration of Helsinki. Due to the retrospective nature of the study, IRB of the Southwest Hospital of Army Medical University waived the need of obtaining informed consent.

Data collection and processing

The vancomycin dataset, including vancomycin administration, demographic information, laboratory parameters, concomitant therapy and diseases, was obtained from the hospital’s EMRS. All serum concentrations of vancomycin were determined via the enzyme-multiplied immunoassay technique (EMIT) method with the Viva-ProE™ system (Syva, USA). As shown in Figure S1, there were no missing values in categorical variables. The median imputation method in Python (version 3.8, Python Software Foundation) was applied to handle missing values for continuous variables, resulting in a dataset of 383 × 34 (33 features and 1 target variable [Drug concentration]). In the overall dataset, only three features have a missing rate exceeding 20%: Cys-C (39.16%), PCT (27.94%), and BMI (26.37%). The final outcome suggested vancomycin plasma concentrations as the target variable, while the whole dataset was randomly divided into a training group and a testing group at a ratio of 8:2.

Population pharmacokinetic analysis

PopPK modeling was using a nonlinear mixed-effects model (NONMEM, version 7.5.1, Icon Development Solutions, Ellicott City, MD, USA). The first-order conditional estimation with interaction of inter-individual and intra-individual variation (FOCE-I) was utilized for parameter estimation and model fitting. The visualization of the different models were conducted using Perl-speaks-NONMEM (PsN, version 5.3.0, [https://uupharmacometrics.github.io/PsN/]), and R (version 4.2.2, [https://r-project.org/]). First, one- and two-compartment models were chosen to fit popPK data and establish the base model. To estimate the inter-individual variability of the pharmacokinetic parameters, an exponential model was applied. The residual variability was compared across additive, proportional, exponential, and mixed models. The selection of the base model was performed guided by the objective function value (OFV), the goodness-of-fit plot (GOF), and the relative standard errors (RSE) of the pharmacokinetic parameters.

Once the base model was built, the impact of covariates on pharmacokinetic parameters was evaluated. Before using the standard stepwise method for covariate analysis, the correlations between covariates and individual empirical Bayesian estimates (EBE) of pharmacokinetic parameters were assessed using Spearman correlation analysis. Covariates included all features listed in Table 1, excluding vancomycin concentration, vancomycin administration, and pop PK parameters. Likelihood ratio tests were used for the validation of statistically significant effects. In the forward inclusion process, each covariate was sequentially incorporated into the model to assess its impact on the OFV. A reduction in OFV values greater than 3.84 (p < 0.05, χ2, df = 1) following the inclusion of covariates implied a significant enhancement in model fit, leading to their retention within the model. The full regression model was obtained after repeating the above steps to include all the covariates that had significant effects on the model. In the backward elimination step, a covariate would remain in the final model if its removal from the full model led to an increase in the OFV greater than 10.83 (p < 0.001, χ2, df = 1). The above steps were repeated to obtain the final model. The predictive performance of the final model was assessed using bootstrap and visual predictive check (VPC) methods.

Table 1 The description of the study samples.
Full size table

Individual pharmacokinetic parameters (e.g., CL and Vd) and predicted concentrations were estimated using the POSTHOC option in NONMEM. Then, each patient’s individual pharmacokinetic parameters calculated by the EBE method were used as new features added to the ML training and testing groups, while predicted concentrations were used only for performance comparison between the popPK and ML models.

Modeling and validation

Nine common supervised ML algorithms were used for modeling, including support vector regression (SVR), light gradient boosting machine (LightGBM), categorical boosting (CatBoost), gradient boosted regression trees (GBRT) and eXtreme Gradient BoostingX (XGBoost), random forest (RF), adaptive boosting (AdaBoost), bootstrap aggregating (Bagging), and back propagation neural network (BPNN)18,19. A grid search was used to optimize the hyperparameters20.

To evaluate the predictive performance of the model, the metrics of R-squared (R2), mean square error (MSE), and mean absolute error (MAE) were used. R2 indicates the fit of the model to the observed data21. The calculation formulas are as presented in our previous study22. The predictive performance of each individual algorithm was evaluated using a five-fold cross-validation approach. Based on R2 value, top three algorithms were selected to create an ensemble model.

In the modeling process, the popPK model was employed to derive the parameters CL and Vd, which were subsequently incorporated as new features into the machine learning models. The feature selection of variables was carried out in two steps. First, Shapley Additive exPlanations (SHAP) was used to obtain the importance ranking of each variable. Starting from the variable with the highest importance, each was gradually included in a single algorithm, and the R2 value was calculated for each combination. The variable combination that resulted in the highest R2 value was selected as the important feature set for a single algorithm. In the second step, the union of the important feature sets obtained from three different algorithms was taken as final result of feature selection.

The ensemble model was constructed including the variables selected. A computer grid search was employed on the weight proportion (accurate to one decimal place) of the three algorithms. Then, the R2 of each model was calculated. The ensemble model with the highest R2 was selected as the final model.

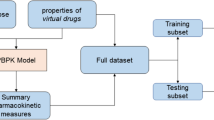
To further evaluate the performance of the ensemble model, the accuracy of the predicted concentration compared to the observed concentration was investigated. The absolute accuracy represented the accuracy of the predicted plasma concentration to be within ± 5 mg/L of the observed plasma concentration, while the relative accuracy showed that the predicted plasma concentration was within ± 30% of the observed plasma concentration. Additionally, three groups of patients (enrolled from August 2022 to September 2024) were included in the dataset to serve as the clinical validation group for corroborating the performance of the prediction models: (a) 27 patients with 37 TDM measurements of vancomycin, for whom individual pharmacokinetic parameters were estimated using the EBE method; (b) 40 patients with 40 TDM measurements, where each patient had a single TDM measurement, and pharmacokinetic parameters were calculated based on population typical values; (c) 25 patients with 40 TDM measurements, excluding the first TDM result for each patient, where multiple TDM measurements were obtained from each patient, and individual pharmacokinetic parameters were estimated using the EBE method combined with the PSN proseval tool. The workflow of data processing, algorithm selection and modeling were displayed in Fig. 1.

Fig. 1
figure 1

The workflow of data processing and algorithm selection. TDM, therapeutic drug monitoring; LLOQ, lower limit of quantification; popPK, population pharmacokinetics; CL, clearance; Vd, volume of distribution; CatBoost, categorical boosting; LightGBM, light gradient boosting machine; SVR, Support Vector Regression; MAE, mean absolute error; MSE, mean squared error. EBE, empirical Bayesian estimates.

Full size image

Model interpretation

SHAP values were employed to interpret our ensemble prediction model22. The SHAP Python package (version 0.39.0) and its permutation explainer (KernelExplainer) were used to demonstrate the SHAP summary plot, importance ranking, SHAP dependence plot, and SHAP decision plot for the relevant features23. As an additive feature attribution method, SHAP value represents contributions of each feature in a certain sample, in which each feature is regarded as a “contributor”. A feature with positive SHAP value contributes to the output value, hence greater contributions account from larger numerical values.

Statistical analysis

Statistical analysis was performed using IBM SPSS version 25.0 (IBM Corp., Armonk, NY, USA). The Kolmogorov‒Smirnov test was used to evaluate whether the measurement data were normally distributed. Measurement data are presented as the median and interquartile range (IQR) for non-normally distributed variables and the mean ± standard deviation for normally distributed variables. Measurement data were analyzed by the Mann‒Whitney U test (non-normal distribution) and independent t test (normal distribution). Categorical data were expressed as n (%) and analyzed by the Chi-square test (n ≥ 5). The tests were two-sided, with a p value of < 0.01 deemed statistically significant.

Results

Baseline patient characteristics

This study was performed on 383 TDM measurements obtained from 245 elderly patients treated with vancomycin. The baseline information of 33 variables and the comparison between the training and testing groups are shown in Table 1, without any significant difference between the variables of the two groups (p > 0.01).

Population pharmacokinetic model

A one-compartment model with first-order elimination accurately described the pharmacokinetics of vancomycin. The combined model was selected to evaluate the residual variability. CLcr was identified as the only significant covariate for CL. The final popPK model of vancomycin was described by the following equations:

$${\text{CL}}\left( {{\text{L}}/{\text{h}}} \right) = {3}.0{2}*\left( {{\text{CLcr}}/{65}.{24}} \right)^{{0.{856}}} *{\text{exp}}\left( {\eta {\text{CL}}} \right)$$
$${\text{V}}\left( {\text{L}} \right) = {83}.{3}*{\text{exp}}\left( {\eta {\text{V}}} \right)$$

where CL represents the clearance, Vd represents the volume of distribution, ηCL and ηVd represent the interindividual variability of clearance and volume of distribution, respectively. CLcr was calculated according to the Cockroft-Gault Equations24:

The popPK estimates of the final model and bootstrap results are shown in Table 2. In the 1000 generated datasets using the bootstrap method, 981 were successfully fitted. The final model parameters were included in the 95% confidence interval of the bootstrap estimates. The above steps were repeated to obtain the final model. The results of VPC (Fig. 2) show that the median and 5th, 95th percentiles of the observed data are mostly distributed in the 95% confidence interval of the simulated data, which indicates the good performance of the final model.

Table 2 Final population pharmacokinetic model estimates and bootstrap results.
Full size table
Fig. 2
figure 2

Visual predictive check of final population pharmacokinetic model. The solid red line represents the median of the observed data. Dash lines depict the 5th and 95th percentiles of the observed data, respectively. Shadow areas correspond to the 95% confidence interval of the median, 5th, and 95th percentiles based on simulations, respectively.

Full size image

Algorithm selection

Nine common ML algorithms were used for modeling. The R2 values of different algorithms calculated by five-fold cross-validation were shown in Table 3. Among the nine algorithms, CatBoost, LightGBM and SVR had high goodness of fit, of which R2 were 0.564, 0.536 and 0.524, respectively. As a result, these three algorithms were chosen for the ensemble model.

Table 3 The R2 results of algorithms are based on fivefold cross-validation.
Full size table

Feature selection of variables

The results of performance metrics of single algorithms showed that the R2 and accuracy with popPK parameters (CL and Vd) were higher than those without popPK parameters (Table 4). Forward stepwise inclusion method was employed for feature selection. Based on the SHAP importance ranking of single algorithms, features were gradually included in order of importance until the R2 value reached a plateau. The feature combination at this point was considered the important feature set for the algorithm. As shown in Figure S2, the highest R2 value was achieved when CatBoost included 9 features, LightGBM and SVR included 10 features. The importance ranking of the top three algorithms was visualized by SHAP, and important feature sets were shown in Figure S3. Finally, the union of the important feature sets (CL, Total daily dose, time since last dose [TSLD], total duration of treatment, Cr [creatinine], Dialysis, Respiratory failure, Single dose, UA [uric acid], Hgb [hemoglobin], Age, SOFA [sequential organ failure assessment], Vd, TP [total protein], ALT [alanine aminotransferase], Cys-C [cystatin C]) was taken as the final important feature set for the model. This approach ensured that only the most relevant and important variables were included in the final feature set.

Table 4 The comparison of model performance of different algorithms with or without popPK parameters.
Full size table

Modeling and validation

With 16 variables obtained by feature selection, the R2 values of 66 permutations and combinations (from 0:0:1 to 1:0:0) of CatBoost, LightGBM and SVR were calculated. This rigorous approach ensures that the ensemble model achieves the best possible performance by finding the optimal combination of weights for the algorithms used. Ultimately, the composition of SVR, LightGBM and CatBoost (6:3:1) with the highest R2 was determined as the final ensemble model. The ensemble model takes advantage of the strengths of each individual algorithm and improves the overall predictive performance by combining their predictions. Interestingly, our results showed that the performance metrics of the model including 16 feature-selected variables were superior to those of the model including all 33 variables. Furthermore, the ML ensemble model incorporating popPK parameters demonstrated significantly better predictive performance compared to both the standalone ensemble model and the popPK model (Table 5). The exact distribution of predicted and observed values in the testing group was shown in Fig. 3.

Table 5 Comparison of model performances for testing group among different ensemble models and the popPK model.
Full size table
Fig. 3
figure 3

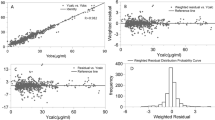
Comparison of predicted and observed value. (A) The blue dots represented testing sample, with observed values on the x-axis and predicted values on the y-axis. The blue dots between the dotted lines indicated that the predict values were within ± 30% of the observed values. (B) The blue dots represented testing sample, with observed values on the x-axis and predicted values on the y-axis. The blue dots between the dotted lines indicated that the predict values were within ± 5 mg/L of the observed values. (C) The x-axis represents the sample numbers in the testing set, which consists of a total of 77 samples. The red dots indicated the observed values, and blue dots indicated the predicted values. The green shade represented within ± 30% of the observed values, and the red shade represented within ± 5 mg/L of the observed values.

Full size image

The absolute accuracy represented the accuracy of the predicted plasma concentration to be within ± 5 mg/L of the observed plasma concentration, while the relative accuracy showed that the predicted plasma concentration was within ± 30% of the observed plasma concentration. As demonstrated in Table 6, the performance of the final ensemble model across three different clinical external validation groups showed that the absolute accuracy (± 5 mg/L) and relative accuracy (± 30%) of the groups whose individual PK parameters were calculated using population typical values or the EBE method combined with the proseval tool were superior to those of the group whose individual PK parameters were obtained using only the EBE method. However, the R2 values for the latter two groups were lower compared to the first group (0.353, 0.443 vs 0.635).

Table 6 The model performance metrics of the ensemble model in different clinical external validation groups.
Full size table

Interpretation of the ensemble model

As shown in Fig. 4A, each feature value of a certain variable corresponds to a SHAP value (x-axis), and the aggregation of the SHAP values of each variable equals the predicted vancomycin plasma concentration. The mean absolute SHAP values of each relevant variable was demonstrated in Fig. 4B. The SHAP value of popPK parameter was found to be high, with CL ranking first. Four of the six variables of vancomycin administration were included in the final model by the feature selection. Moreover, their SHAP values were in the upper half of the ranking, indicating their importance on the model’s predictions.

Fig. 4
figure 4

The model’s interpretation by SHAP. CL, clearance; TSLD, time since last dose; Cr, creatinine; UA, uric acid; Hgb, hemoglobin; SOFA, sequential organ failure assessment; Vd, volume of distribution; TP, total protein; ALT, alanine aminotransferase; Cys-C, cystatin C. (A) The SHAP summary plot of the top 16 relevant variables. The SHAP value (x-axis) is a unified index responding to the effect of a variable in the ensemble model. In each variable importance row, all patients’ attributes to the outcome were plotted using different colored dots, in which the red (blue) dots represent high (low) values. The higher the SHAP value of a variable, the higher vancomycin concentration. (B) The importance ranking of the top 16 variables according to the mean (|SHAP value|).

Full size image

The SHAP dependence plot of the variables showed that higher total daily dose, single dose, total duration of treatment, UA, as well as lower CL, TSLD, Cr, Hgb, Age, and SOFA were related to higher vancomycin plasma concentration (Fig. 5). Figure 6 illustrated the SHAP decision plot of the model, where each line represented one sample of the testing group. The prediction for single sample was demonstrating how the model reaches the final prediction result from the baseline value through the contributions of each feature. The SHAP decision plot demonstrated the cumulative process of the influence of each variable on the output value of SHAP (predicted concentration value), providing insights into the cumulative effect of the interaction and the typical predicted path.

Fig. 5
figure 5

SHAP dependence plot of model. CL, clearance; TSLD, time since last dose; Cr, creatinine; UA, uric acid; Hgb, hemoglobin; SOFA, sequential organ failure assessment; Vd, volume of distribution; TP, total protein; ALT, alanine aminotransferase; Cys-C, cystatin C. Dialysis included CRRT, continuous renal replacement therapy; PD, peritoneal dialysis; HD, hemodialysis. 0: no dialysis; 1: one or more modes of dialysis. Respiratory failure included type I and type II. 0: no respiratory failure; 1: type I; 2: type II. The SHAP dependence plot showed how the relevant variable affected the output of the ensemble prediction model. SHAP values for specific relevant variable exceed 0, representing an increased vancomycin concentration.

Full size image
Fig. 6
figure 6

SHAP decision plot of model for different samples. The SHAP values accumulation process for a single sample is represented by the colored lines indicating whether each feature moves the output value above or below the average prediction, with the gray vertical line marking the model’s baseline value. The feature values are provided for reference next to the prediction lines. Starting from the bottom of the graph, the prediction lines show how the SHAP values accumulate from the baseline to the top of the graph, representing the model’s final score (predicted concentration value). Each line represented a single sample of the testing group. CL, clearance; TSLD, time since last dose; Cr, creatinine; UA, uric acid; Hgb, hemoglobin; SOFA, sequential organ failure assessment; Vd, volume of distribution; TP, total protein; ALT, alanine aminotransferase; Cys-C, cystatin C.

Full size image

Discussion

This study represents the first instance of integrating ML techniques with popPK models to create a predictive model for vancomycin plasma concentrations specifically designed for elderly patients. This model incorporates key variables that influence plasma concentration, utilizing a combination of multiple algorithms and SHAP for robust feature selection. Notably, the model’s predictive performance with 16 selected variables was found to be superior to choose all 33 variables. This demonstrates that strategic feature selection not only enhances model performance but also improves its practical utility, thereby facilitating the clinical application of personalized vancomycin dosing.

PopPK models have long been a cornerstone in quantitative pharmacology, known for their effectiveness in enhancing therapeutic outcomes of vancomycin through precise dosage adjustments and monitoring for adverse reactions13,14,25. However, the real-world applicability of these models is often limited by their inclusion of only basic covariates, which fails to capture the full spectrum of pharmacokinetic and pharmacodynamic alterations in elderly patients. These alterations include reduced organ function, altered receptor sensitivity, and shifts in homeostatic patterns, which are compounded by concurrent medication usage and complex disease states26.

In response to these complexities, the integration of ML with popPK models offers a groundbreaking approach that maintains the interpretability inherent in traditional pharmacokinetic models while significantly improving their predictive accuracy. This dual approach not only preserves the model’s interpretability but also expands its capability to handle complex datasets, enhancing overall model utility27. Indeed, while there have been instances like Bo Hao Tang’s work, which refined clearance predictions in neonates using a similar methodology28, our study is unique in its focus on elderly patients and represents a significant advancement in the field of pharmacokinetics.

In this study, we developed a popPK model of vancomycin specifically for elderly patients, integrating individual PK parameters as key features within our machine learning model. Notably, CL and Vd emerged as critical features that significantly enhance the model’s predictive performance. Our final popPK model estimated interindividual variability (IIV) at 30.8% for CL and 48.8% for Vd, which were higher than those reported by Zhou et al. for elderly patients29. IIV refers to the variation in pharmacokinetic parameters caused by these inter-individual differences. The state of the patients, such as inflammatory states or other complex pathophysiological conditions in our datasets, may explain the higher IIV observed in our study compared to others. Nonetheless, the typical values from our model-CL of 3.02 L/h and Vd of 83.3 L-align with those reported in other studies, where CL ranged from 2.45 to 7.98 L/h and Vd ranged from 60.2 to 154 L29,30,31,32.

In our study, Cr levels emerged as a critical feature, negatively correlating with plasma concentration. Given that 80–90% of vancomycin is eliminated via the kidneys in individuals with normal renal function, accurate renal assessment is essential for safe vancomycin administration, particularly in elderly patients13. Typically, vancomycin therapy is guided by CLcr, calculated using the Cockcroft-Gault formula based on estimated serum Cr. This method is supported by numerous popPK models that identify CLcr as a key determinant of vancomycin clearance30,33. Liu et al. and Frazee EN et al. have shown that CysC-based glomerular filtration rate assessments provide superior predictive value for therapeutic vancomycin levels compared to traditional serum Cr measurements34,35. However, in our popPK and ensemble models, both Cr and Cys-C are relevant, with Cr remaining significant, especially where routine Cr measurements are more feasible.

Dialysis significantly influenced vancomycin plasma concentrations in our study. The drug’s binding to proteins, its interaction with the filtration membrane, the blood’s viscosity, and the drug’s volume distribution are all critical factors that affect vancomycin clearance during dialysis36. Given the variability and complexity of dialysis modalities, including factors such as sieving coefficient, treatment fluid flow rate, filter surface area, filter lifespan, and the site of replacement fluid administration37, we did not conduct an in-depth analysis of these parameters. There is a pressing need for prospective studies in critically ill patients undergoing continuous renal replacement therapy to refine vancomycin administration strategies, ensuring optimal plasma concentrations are achieved for effective treatment outcomes.

Our study further elucidates how the body’s altered inflammatory state significantly impacts vancomycin concentrations. The Sequential Organ Failure Assessment (SOFA) score, which evaluates organ dysfunction, revealed that sepsis—diagnosed with a SOFA score of ≥ 2 was present in 43.14% of our study cohort (132 patients), correlating with decreased vancomycin concentrations. In elderly patients, severe infections leading to sepsis and heart failure may induce an inflammatory response that increases vascular permeability and fluid accumulation at infection sites, thereby elevating the Vd. This physiological alteration, coupled with sepsis-induced hyperdynamic states, can increase cardiac output, enhancing renal blood flow and glomerular filtration, which in turn may increase vancomycin clearance. Notably, the standard dosing recommendations often fail to achieve desired therapeutic levels in patients with sepsis or septic shock38. Consequently, the revised guidelines from the Infectious Diseases Society of America (IDSA) now suggest an initial dose of 15–20 mg/kg every 8–12 h and a loading dose of 20–35 mg/kg to swiftly attain target concentration in critically ill patients1. Additionally, our findings indicate that vancomycin trough concentrations are notably higher in patients with type 2 respiratory failure compared to type 1, and that prolonged mechanical ventilation (≥ 10 days) can significantly reduce the formation and elimination of metabolites by more than 30%, primarily due to reductions in cardiac output and renal blood flow affecting drug excretion39.

As individuals age, physiological changes such as a decrease in muscle mass, an increase in fat percentage, and a resultant reduction in total body water content significantly alter drug distribution profiles40. Vancomycin, being a hydrophilic agent, may see increased blood concentrations as the total body water content decreases. Compounded by the age-related decline in renal function, these factors contribute to the potential accumulation of vancomycin in the body, necessitating adjustments in dosing strategies to avoid toxicity. Typically, lower doses might be required to maintain therapeutic levels in older patients41. Contrary to these expectations, our findings indicate a decreasing trend in vancomycin concentrations with advancing age. This observation suggests that clinicians might be preemptively lowering doses for elderly patients, potentially to mitigate the risks of drug accumulation and adverse reactions. The SHAP dependence plot supports this, showing a trend towards lower dosing in patients over the age of 80 (shown in figure S4). Another potential explanation is that clinicians may be opting for less frequent dosing intervals, such as 1 g every 24 h instead of 0.5 g every 12 h. While this approach results in the same total daily dose and area under the curve (AUC), it could lead to lower trough concentrations. Although such dose adjustments are prudent to prevent toxicity, there is a concurrent risk of subtherapeutic dosing, which could compromise the effectiveness of infection treatment in this vulnerable population. Therefore, it is crucial for healthcare providers to balance reduced dosing with the need to achieve sufficient drug levels to ensure effective antimicrobial therapy.

Our study, conducted at a single center with a limited sample size, may not fully represent broader patient populations. To validate our findings, future research should involve multiple centers. Given the growing recognition of AUC-guided dosing as an important method for optimizing vancomycin therapy42, future work could explore integrating our prediction model with AUC-guided dosing to enhance dosing accuracy and improve patient outcomes. It is acknowledged that that data leakage occurred during the modeling and testing stages of our ensemble model, which may have contributed to some degree of overfitting. This limitation was further supported by the external validation results, where the R2 values for the groups using individual pharmacokinetic parameters calculated through population typical values or the EBE method combined with the proseval tool were lower than those using only the EBE method. Notably, data leakage in the training dataset is unavoidable. Population typical values are derived from models that take into account all observed levels, meaning that even for patients with only a single TDM measurement, the pharmacokinetic parameters based on population typical values were influenced by these observed levels. For future studies involving datasets that are not part of the model development process (i.e., test sets or external validation sets), we strongly recommend directly using population typical values or calculating individual pharmacokinetic parameters through the EBE method combined with the proseval tool. This approach would help mitigate data leakage, reduce overfitting, and improve the clinical applicability of the prediction model. Despite these limitations, our study successfully develops a quick and cost-effective method for predicting vancomycin levels in critically ill elderly patients. By integrating classical pharmacokinetics with machine learning, our model enhances clinical decision-making and supports tailored dosing strategies for vulnerable patients.