Introduction

Pandemics, such as COVID-19, can impose harm and loss on human life and the social economy 1,2. Vaccines are among the most important medical resources in the fight against a pandemic, but they can face shortages in many countries 3, especially at the early stage of vaccine distribution. Therefore, it is imperative to distribute such crucial public goods effectively. The utilization of Social Network Analysis (SNA) in public health, particularly in the field of immunization, represents a significant intersection of epidemiology and network theory4. This approach is predicated on the understanding that human interactions and social structures play a critical role in the spread of infectious diseases. Identifying and targeting those influential individuals within these networks can be an effective strategy for disease control and prevention 5. As we know, not every node plays the same role in the network 6,7. Some individuals can have greater influence than others 8.

In the last few years, researchers have proposed various centrality-based measures, like degree centrality (number of direct connections), betweenness centrality 9 (role in connecting different parts of the network), and closeness centrality 10 (proximity to all other nodes), for identifying influential individuals in the networks. One of the challenges in using centrality measures is the dynamic nature of real-world networks. Networks evolve over time, and so do node centralities. Additionally, these measures, while powerful, can sometimes oversimplify the complexities of real-world networks. To incorporate more information of networks, some new centrality measures have been proposed, such as PageRank 11, Coreness 12, LocalRank 13, VoteRank 14, ClusterRank 15, LeaderRank 16, and TwitterRank 17. Each of these measures provides a unique lens through which to view and analyze network influencers. Their effectiveness and applicability can vary significantly based on the unique characteristics of each network being analyzed, such as its size, density, the nature of connections, and the context in which the network operates (e.g., social, biological or technological).

Another research direction is to split the network into various levels. In these studies, higher levels represent the network’s core and lower levels refer to its periphery. This approach ranks nodes by assuming those at the center of the network wield greater influence. The k-core decomposition 18 is one representative of such a technique. Drawing inspiration from this, several methodologies 19,20,21,22 have been developed that adapt the k-core concept. These methods modify the basic k-core approach for determining influential nodes. Their findings indicated that the identified nodes surpass traditional measures in terms of spreading efficiency. Nonetheless, a significant limitation of these models is their relatively blunt precision. Depending on the network’s structure, numerous nodes might share the same k-core value, yet their actual influence may vary.

Apart from the centrality-based methods and k-core based algorithms, researchers also proposed heuristics to identify influential nodes efficiently. Chen et al. 23 developed an algorithm based on degree discounting that outpaces the typical greedy algorithm by over a million times 24, while achieving a similar level of accuracy. For networks featuring community structures, He et al. 25 have proposed a method centered on communities, employing algorithms for detecting communities 26 to pinpoint essential nodes within different groups. Additionally, Morone and Makse 27 have redefined the task of vital node identification as an optimal percolation problem, focusing on identifying the smallest group of pivotal nodes.

Recently, some studies proposed methods grounded in data-driven machine learning to identify influential nodes in complex networks. Zhao et al. 28 approached the issue of vital node identification through a classification model trained on a large subset of nodes from the original network. In a different study, Yu et al. 29 employed network embedding techniques in temporal networks to pick out influential nodes. Similarly, Khajehnejad et al. 30 applied adversarial graph embedding in networks with distinct communities to find influential nodes. Hao et al. 31 adopted network representation learning techniques for identifying influential nodes in networks with overlapping communities. Nevertheless, most of the methods above focus on ranking nodes based on finding individual influential nodes. In numerous practical scenarios, the task is often to locate a subset of influential nodes that are key to maintaining network connectivity and facilitating the dissemination of information or pathogen. Finding a group of influential nodes is more difficult than finding individual ones because the selected nodes can affect each other 32.

We propose a graph learning and reinforcement learning based vaccination strategy to identify a group of critical nodes in the network. It combines Graph Neural Networks (GNN) with Deep Reinforcement Learning (DRL), which brings together GNN’s ability to efficiently process and learn from graph-structured data with DRL’s prowess in learning optimal decision-making strategies in complex environments. In this hybrid approach, a GNN is used to represent the state of the environment in DRL. The graph-structured data is fed to the GNN, which effectively captures the relationships and interactions between different nodes in the network and generates a detailed representation of the network’s structure33. This enriched state representation is then piped to the DRL system. DRL, with its capabilities in learning optimal policies over time, can make use of the structured data provided by GNN to make informed decisions about which nodes in a network are influential.

Model

Framework

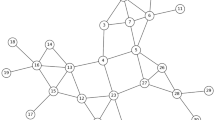
Figure 1 illustrates the proposed framework. It employs a model-free RL approach in conjunction with a graph representation learning module. There are two key components – the encoder and the decoder. The encoder’s role is to produce representations for both the states and actions within this context. Subsequently, the decoder utilizes these representations to construct a score function, guiding the selection of the appropriate action for a given state.

The algorithm follows a greedy approach, where it progressively builds a viable solution by adding nodes based on the underlying graph structure. This solution is continually updated to fulfill the stated objective. Greedy algorithms are commonly employed as a strategy for creating approximation and heuristic algorithms for various graph-related problems.

Fig. 1
figure 1

Illustration of the proposed framework.

Full size image

The encoder can either be a graph embedding model or a graph neural network. Specifically, this study uses Graph Convolutional Networks (GCN) 34, which are a type of GNN. Networks from the training set are fed into the encoder. It maps the structural information of the network into a low-dimensional latent space. Following multiple recursive iterations, all nodes acquires their own embedding vectors that encompass their structural position information within the network with the extensive interplay among node features. A virtual node that represents the whole graph is added in order to extract further information about the network. It is connected to all real nodes. The representation of the whole graph then can be obtained by the summation of those of all nodes. The decoder is implemented as a multi-layer perceptron (MLP). This component utilizes the representations derived from the encoder for both states and actions to compute a score that serves as a quantitative assessment of potential actions.

During the training phase, a graph is chosen at random from a set of synthetic graphs. This graph is subsequently processed through the proposed framework, where the agent engages in a game-like scenario to identify influential nodes. In this context, the state refers to the remaining network after node removals, the action is the elimination of an influential node, and the reward stands for the reduction in the number of infected nodes resulting from the action. To ascertain the appropriate action for a given state, GCN is employed to derive an embedding vector for each node (represented by orange bars in Figure 1). The embedding vectors are then utilized to compute scalar Q values (depicted as green bars with heights indicative of the values in Figure 1) for all nodes, forecasting the potential long-term benefits of the action.

In practical scenarios, the finely-tuned agent can be deployed on actual networks once the training is complete. The procedure is as follows. First, the network under consideration would be transformed into compact vectors. Then, the Q values for each node are estimated using these vectors. The node with the highest Q value is selected at every iteration, and the network is modified accordingly. This procedure is repeated until the network arrives at a predetermined terminal condition (such as maximum number of nodes). The series of nodes that are sequentially removed during this process form the ideal group of influential nodes.

The principal strength of this framework lies in its capacity to effectively handle deferred rewards, which can in turn be used by a simple greedy algorithm to achieve incremental improvement of the objective function. Updates to the network embeddings are made based on the partial solution at each stage of the greedy algorithm, enabling the integration of fresh insights regarding the contribution of every node to the ultimate solution.

Q-learning

The node identification process can be considered as a Markov Decision Process (MDP) using a quintuple \((\mathscr {S}, \mathscr {A}, \mathscr {T}, \mathscr {R}, \gamma )\) in line with standard RL. In this formulation, \(\mathscr {S}\) represents the collection of states, \(\mathscr {A}\) corresponds to the collection of available actions, \(\mathscr {T}: \mathscr {S} \times \mathscr {A} \times \mathscr {S} \rightarrow [0,1]\) denotes the transition function, \(\mathscr {R}: \mathscr {S} \rightarrow \mathbb {R}\) represents the reward function, and \(\gamma\) serves as the discount-rate parameter. Within this framework, a policy denoted as \(\pi : \mathscr {A} \times \mathscr {S} \rightarrow [0,1]\) indicates the probability of taking an action when the agent is in a given state. Here, with a given policy \(\pi\), a value-function is formulated to quantify the long-term accumulated rewards of states over the future in an episode. The value function represents the expected discounted return, defined as:

$$\begin{aligned} V^\pi (s)=E\left[ R\left( s_0\right) +\gamma R\left( s_1\right) +\gamma ^2 R\left( s_1\right) +\ldots \mid s_0=s, \pi (s)\right] . \end{aligned}$$
(1)

The policy of optimizing the expected return can be determined by:

$$\begin{aligned} J(\pi )&=\max _\pi E\left[ V^\pi (s)\right] \nonumber \\ \pi ^*(s)&=\arg \max _\pi J(\pi ) \end{aligned}$$
(2)

Then, we can establish a policy \(\pi\) consisting of a sequence of selected nodes, strategically devised to maximize the expected discounted return, spanning from the initial state to the terminal state.

Q-learning 35 stands as one of the frequently employed algorithms for tackling the MDP problem. Its main task is to estimate value functions. The action-value function under a policy \(\pi\) is defined as,

$$\begin{aligned} Q^\pi (s, a)=\mathbb {E}\left[ \sum _{t=0}^{\infty } \gamma ^t \times \mathscr {R}\left( s_t\right) \mid s_0=s, a_0=a, \pi \right] , \end{aligned}$$
(3)

where \(s_0\) and \(a_0\) represent the state and the action taken in the beginning, respectively. The Q-learning algorithm operates on the foundation of the Bellman equation:

$$\begin{aligned} Q_{t+1}(s, a) \leftarrow Q_t(s, a)+\alpha \times \left[ r+\gamma \times \arg \max _{a^{\prime }} Q_t\left( s^{\prime }, a^{\prime }\right) -Q_t(s, a)\right] . \end{aligned}$$
(4)

The Temporal Difference (TD) incremental learning 36 is applied to recursively update the Q-table. An episode in the Q-learning algorithm consists of numerous steps, spanning from the initial state to the terminal state. During each step, the agent operating under a policy chooses an action based on the observation of the environment. Subsequently, it receives an associated reward and transitions to the next state. This iterative process persists until either the action-value function converges or a predetermined number of episodes is completed.

For discrete states, it is relatively straightforward to represent the action-value function as a table. However, this representation becomes increasingly challenging as the number of states grows and is often infeasible when dealing with continuous states. In these scenarios, we can use a parameterized function to represent the action-value function. The task will focus on determining the optimal values for the parameter \(\theta\). With this approach, it becomes manageable to utilize a Deep Neural Network (DNN) to approximate the action-value function. Upon completion of training the DNN, it is ready to derive an approximation of the optimal policy by adopting a greedy strategy based on the predicted values.

Reinforcement learning formulation

States

In this context, a state denoted as S is defined as a series of actions, which correspond to nodes within a graph denoted as G. With the nodes in the graph already being represented by their embeddings, this state can be thought of as a vector in a p-dimensional space, mathematically expressed as the summation over all nodes in V, i.e., \(\sum _{v \in V} \mu _v\). This embedding-based state representation offers the advantage of versatility, as it can be applied across a range of distinct graphs. Moreover, it is important to note that the determination of the terminal state \(\hat{S}\) is contingent upon the specific number of nodes requiring vaccination.

Actions

An action denoted as v corresponds to the removal of a node from the current state S within the graph G. Furthermore, we will depict actions by employing their corresponding p-dimensional node embeddings, represented as \(\mu _v\). Here, we underscore that this definition remains applicable across graphs of diverse sizes.

Rewards

The primary aim of the exploratory agent is to identify the optimal solution, characterized by the highest resistance to the spreading, at any point within an episode. In a formal context, the reward function, denoted as r(S, v), is represented as the alteration in the influence of the spreading that occurs subsequent to the execution of action v, leading to a transition to the next state \(S^{\prime }\), which can be expressed as:

$$\begin{aligned} r(S, v)=\frac{I(h(S), G)-I\left( h\left( S^{\prime }\right) , G\right) }{|V|}, \end{aligned}$$
(5)

where I(h(S), G) is the number of infected nodes using SIR simulation and \(I(h(\phi ), G)=|V|\). To address potential variations in reward scales stemming from different graph sizes, the reward is standardized by dividing it by the total number of vertices, denoted |V|. In this work, we chose a discount factor \(\gamma = 0.95\), which is a commonly used value in reinforcement learning literature to balance immediate and future rewards effectively 37.

Policy

In reinforcement learning, a policy represents the agent’s behavioral strategy, which guides the agent in selecting subsequent actions. The policy established is deterministic greedy, which is defined as \(\pi (v \mid S) = \operatorname {argmax}_{v^{\prime } \in \bar{S}} \widehat{Q}\left( h(S), v^{\prime }\right)\). Under this policy, taking an action means removing a node from the graph, consequently resulting in the accrual of a reward r(S, v).

Results

To demonstrate the effectiveness of the proposed model, it is compared with Graph Dismantling with Machine learning (GDM) 38, Generalized Network Dismantling (GND) 39, and Explosive Immunization (EI)40. The GDM method utilizes machine learning, specifically graph convolutional-style layers, to efficiently dismantle complex networks by identifying and removing critical nodes. The GND method optimizes the process of fragmenting a network by removing nodes with varying costs, utilizing a spectral bisection approach combined with a weighted vertex cover problem to break the network into isolated components. The EI method combines the explosive percolation paradigm with a strategy that incrementally selects nodes to immunize by evaluating their potential to maintain network fragmentation.

The experiment was conducted on an Ubuntu 20.04.4 LTS system with Lenovo ThinkStation, Xeon 5118, 256 GB RAM and NVIDIA RTX 2080 Ti with 12GB memory size. The proposed model was trained on 10 small synthetic random networks, each consisting of 40 nodes with an average degree of 6. The training process took approximately 6 hours.

Comparative analysis of the degradation in network structures

The network connectivity serves as the conduit through which pathogens can propagate to a greater scope. The topological structure of the network determines its suitability for the dissemination of pathogens or information. This section assesses the proposed framework’s ability to disrupt network structure 41 considering five key aspects: edge quantity, connectivity, epidemic threshold, largest component size, and the count of network components. These dimensions collectively provide a comprehensive evaluation of the framework’s impact on network integrity and dynamics. Each dimension is associated with a specific network structural property, and measurements are conducted on the residual network following the removal of a specific number of nodes. The epidemic threshold is a pivotal measure indicating a network’s defense against pathogen spread. For a pathogen to successfully propagate, its propagation rate must exceed the network’s epidemic threshold 42. Hence, networks with higher epidemic thresholds are more challenging for pathogens to infiltrate and propagate within. The largest component in a network refers to the largest set of nodes within a network where any node is reachable from every other node. This component is often of particular interest because it represents the most significant and interconnected part of the network and plays a crucial role in determining the overall structure and connectivity of the network. The component number indicates how many separate groups of nodes exist in a network, each of which is internally connected but not connected to nodes outside their respective group. It is an important topological property of a network and can provide insights into its structure and connectivity.

Graph Dismantling with Machine learning (GDM) 38, Generalized Network Dismantling (GND) 39, and Explosive Immunization (EI)40 strategies are used as comparison baselines. To demonstrate the broad versatility of our proposed approach, we carried our experiments on five distinct synthetic network types and four real-world networks. Synthetic networks include Erdős-Rényi (ER) random networks, ER random networks with communities, scale-free networks, scale-free networks with communities, and small-world networks. The presence of communities within a network can significantly impact the spreading phenomenon, as nodes within the same community often exhibit more connections with one another compared to nodes in separate communities. In our experiments, communities are introduced into ER random networks and scale-free networks to assess the adaptability of the proposed method to networks with varying characteristics.

Fig. 2
figure 2

The degradation of network structures resulting from the removal of 20% nodes by different models on synthetic datasets with various properties. Each dimension has been scaled to fall within a range of 0 to 1 to enhance visualization. To ensure consistency in the result display, we use the inverse of component number and epidemic threshold as the measurement. This means a lower reciprocal value signals a stronger ability of the network to prevent the spread of pathogens. The proposed method proves to be the most effective in dismantling the network structure, leaving the smallest area remaining in each dataset.

Full size image
Fig. 3
figure 3

The degradation of network structures resulting from the removal of 20% nodes by different models on real-world datasets. Consistent with the findings in synthetic networks, the proposed method demonstrates superior effectiveness in breaking down the network structure, resulting in the smallest area remaining across each dataset.

Full size image

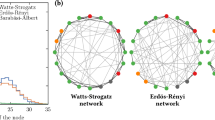
Figures 2 and 3 show that all five metrics of interest are improved (e.g., networks are compromised) after the removal of 20% selected nodes. The proposed strategy consistently outperformed the GDM, GND and EI methods for both the synthetic and real-world networks. The three plots in the top row of Figure 2 illustrate that small-world networks exhibit the highest resilience against structural disruption, while scale-free networks are the most susceptible to immunization. This distinction is primarily due to the presence of prominent high-degree nodes, often referred to as hubs, within scale-free networks, which play a pivotal role in the spread of information or pathogens. Detecting and immunizing these hubs can have a substantial effect on the network’s propagation potential. Nevertheless, small-world networks tend to exhibit greater homogeneity and lack conspicuous hubs. Each node can rapidly reach out to others in a small number of steps, making it intricate to disrupt the network structure by immunizing only a limited number of nodes. In contrast, random networks do not display a bias towards hubs or short network distances, falling somewhere in between. It is also worth noting that the proposed approach demonstrates consistent performance across networks with or without community structures, underscoring its resilience to community variations. The performance improvement of the proposed method over the three baseline methods varies across the different real-world datasets illustrated in Figure 3, likely due to the distinct characteristics of each dataset. Nevertheless, the proposed method consistently outperforms the baselines in all datasets, highlighting its adaptability and effectiveness.

The spreading simulation on the immunized networks

The SIR (Susceptible-Infected-Recovered) model, as implemented in the EoN (EpidemicsOnNetworks) framework 43,44, is employed to simulate network spreading events across five different synthetic network types and four real-world networks. Simulations are performed with a transmission rate per edge (\(\beta\)) of 0.1, a recovery rate per node (\(\gamma\)) of 0.01, and an initial infection ratio (\(\rho\)) of 0.1, representing the proportion of initially infected nodes to the total network nodes.

Fig. 4
figure 4

The infection scale on five synthetic networks with 20% of nodes removed by various models, where \(\beta\) = 0.1, \(\gamma\) = 0.01 and \(\rho\) = 0.1. Each network consists of 500 nodes. The proposed approach outperforms the baseline methods across all datasets. This is primarily because it more effectively reduces the network’s conductivity and leads to smaller peaks in infection scale compared to the baselines. For instance, in the ER random network, immunizing 20% of the nodes identified by the proposed method results in a decrease of the infection scale peak from 86.8% to 75.6%, compared to using the GDM method. These results represent the average of 100 independent runs.

Full size image
Fig. 5
figure 5

The infection scale on four real-world networks with 20% of nodes removed by various models, where \(\beta\) = 0.1, \(\gamma\) = 0.01 and \(\rho\) = 0.1. The presented approach surpasses the baseline methods in every dataset tested. For example, in the weaver network, targeting 20% of the nodes as identified by this new method leads to a reduction in the peak of infection scale from 83.2% to 35.8%, a notable improvement over the GDM method. These results represent the average of 100 independent runs.

Full size image

Figures 4 and 5 present the infection scale outcomes of SIR simulation for the GDM, GND, EI, and the proposed strategies, applied to synthetic and real-world datasets, respectively. The y-axis represents the scale of infection over time. All curves follow a similar pattern: they show a swift increase in infection rates at the initial stages, reach a peak, and then gradually decrease to nearly zero. This pattern occurs because there is an abundance of susceptible nodes initially, allowing for a high potential for infection. As the number of susceptible nodes diminishes, the recovery rate surpasses the infection rate, leading to a decline in the infection levels.

There are distinctions between the timing and magnitude of peak infection for the different networks and strategies. Both the three baseline approaches and the proposed strategy can reduce the peak of infection scale. However, the proposed method outperforms the all the baselines, resulting in a consistently lower peak of infection scale across all different types of networks (i.e., both synthetic and real-world datasets). For example, in the ER random network, immunizing 20% of the nodes identified through the proposed method leads to a reduction in the peak of infection scale from 86.8% to 75.6%, in contrast to employing the GDM method. In the random network with community, the performance of the four methods is comparable to that observed in the ER random network. Here, the infection scale peak for the proposed method is 63.4%, while the GDM method exhibits a peak infection scale of 82.5%. This indicates that the proposed method has strong resilience to community variations.

Fig. 6
figure 6

The cumulative infection scale on five synthetic networks with 20% of nodes removed by various models, where \(\beta\) = 0.1, \(\gamma\) = 0.01 and \(\rho\) = 0.1. Each network consists of 500 nodes. The proposed approach outperforms the baseline methods across all datasets. For instance, in the scale-free network, immunizing 20% of the nodes identified by the proposed method results in a decrease of the final infection scale from 95.3% to 69.1%, compared to using the GND method. These results represent the average of 100 independent runs.

Full size image
Fig. 7
figure 7

The cumulative infection scale on four real-world networks with 20% of nodes removed by various models, where \(\beta\) = 0.1, \(\gamma\) = 0.01 and \(\rho\) = 0.1. The presented approach surpasses the baseline methods in every dataset tested. For example, in the weaver network, targeting 20% of the nodes as identified by this new method leads to a reduction in the final infection scale from 98.8% to 47.9%, compared to using the GDM method. These results represent the average of 100 independent runs.

Full size image

Comparing the performance of our method in random, scale-free, and small-world networks, the lowest infection peak (43.8%) occurs within the scale-free network, the highest (75.6%) in the random network, and an intermediate peak (61.3%) is observed in the small-world network. This occurs due to the scale-free network’s heterogeneous degree distribution, which features more hubs. Our method is capable of efficiently identifying these hubs and preventing the virus spreading in the scale-free network. On the other hand, the small-world network is conducive to rapid virus spreading due to their unique combination of high clustering and short path lengths. It is challenging to stop the spread by immunizing only a subset of nodes. This is mainly because the small-world network contains highly interconnected clusters that enable rapid local spreading, while the presence of shortcuts between distant nodes ensures that the virus can quickly bridge otherwise distant parts of the network.

Figures 6 and 7 show the cumulative infection scale results of the synthetic and real-world datasets, respectively. The presented approach surpasses the baseline methods in every dataset tested, which underscores the versatility and effectiveness of the proposed method. For some networks, the cumulative infection scale is reduced by over 10 percentage points. Table 1 provides a summary of infection scale peak and final infection scale of all the methods.

Another notable observation is that, in random, scale-free and small-world networks, the proposed approach can delay the occurrence of the infection scale peak when compared to the other three strategies. This indicates that the proposed strategy surpasses the other strategies in targeting influential nodes to hinder the spread of disease.

Table 1 Infection scales for different networks and methods
Full size table

Discussion

Managing the spread of phenomena in complex networks is crucial in fields such as disease spread and viral marketing. An essential element in this context is the challenge of pinpointing key nodes with strong dissemination abilities that are capable of projecting information broadly across the network. Practical observations reveal that common measures of node importance, such as degree and betweenness, fall short in identifying nodes with effective dissemination capabilities. For instance, a node might be connected to many others, but if it is on the network’s fringe, its influence is diminished.

Influence maximization and epidemic control in networks are well-known examples of combinatorial optimization problems. IMM 45, a traditional method, utilizes a martingale-based statistical approach to estimate influence spread. While traditional methods are typically highly efficient and come with strong theoretical guarantees, they often involve complex dependencies in their analysis and rely on approximations. In recent years, rapid developments in machine learning have paved the way for a new, learning-based approach to solving combinatorial optimization problems. For instance, GLIE 46 employs a GNN to address influence maximization with high scalability by predicting the influence of nodes and ranking them to optimize seed set selection. A key practical advantage of neural network approaches is their ability to easily integrate additional node information by incorporating the corresponding embeddings into the input. Another notable work, FINDER 47, utilizes a deep Q-learning architecture, where node representations are derived through three GraphSage layers, to solve the network dismantling problem. In this approach, the reward is based on the size of the giant connected component; each node chosen aims to dismantle the network as effectively as possible. FINDER further demonstrates the potential of learning-based methods in tackling combinatorial optimization challenges in complex networks. The proposed approach in this paper combines a graph representation learning model and DRL to process and learn from graph-structured data and make informed decisions in complex environments. The framework proposed employs a model-free RL approach working in the environment extracted from the network structure by a GNN module, aiming to disrupt network structure and hinder disease spread effectively. It is accomplished by a one-time offline training on small synthetic graphs for a specific application scenario without the need for specialized ___domain knowledge.

The adaptability and effectiveness of the proposed approach was investigated by conducting experiments on both synthetic and real-world networks. Removing nodes identified by the proposed method enhances the uniformity of the residual network and is more successful in breaking down the network structure than the baseline methods. SIR simulations on networks immunized by this method reveal its higher efficacy in targeting influential nodes to impede disease transmission, significantly lowering the peak of the infection scale, e.g., from 86.8% to 75.6%, compared to using the GDM method in the ER random network. Our experimental results reveal that halting the spread of a virus within a random network presents a more significant challenge than scale-free networks and small-world networks. The final infection scale in the small-world network is 93.4%, in the scale-free network it is 69.1%, and in the random network it is 94.6%. The results also demonstrate the model’s effectiveness across various network types and scenarios, emphasizing its potential in real-world applications. This shows an encouraging potential of applying deep learning methods to grasping the fundamental principles governing complex networked systems. This advancement enables the design of networks that are more robust and capable of resisting attacks and breakdowns.

This research is not without certain limitations. Learning the embeddings can be time consuming when the network is very large, as embeddings need to be learned before each action. The group of individuals whose vaccination can generate the most benefit to the whole society depends upon demographic properties, such as age and profession, which is not included in our framework. This makes it hard to achieve social utility and equity simultaneously. Nonetheless, this study uncovers a more effective strategy for identifying influential nodes in a deep learning manner.

The introduced framework is versatile and can be applied in various scenarios, including halting the spread of infectious diseases or misinformation, preventing cascading failures in cyber-physical systems, and identifying high-risk accounts in financial networks. On the other hand, reinforcing important nodes in large networks can effectively increase the systems’ robustness against malfunctions, attacks, and deterioration in the food security 48, human gene regulatory network 49, and supply chains 50.

Finally, this method paves the way for using artificial intelligence to understand the spreading phenomena in complex networked systems, which enables us to design dependable networks from the ground up. For the future research, we could consider utilizing other metrics as rewards, such as IMM 45, to enhance the efficiency of the framework. We could also enhance node characteristics by including supplementary details like the node’s age, vaccination costs, and vaccine effectiveness. This method will shift the objective from simply identifying influential nodes to incorporating probabilistic features of nodes. As a result, the issue our study tackles will be more practical and closely aligned with real-world scenarios.

Methods

Datasets

To assess the versatility and effectiveness of our method, experiments were conducted using both synthetic network and real-world network datasets. The statistical characteristics of these networks are presented in Table 2.

Synthetic networks used include random, scale-free, and small-world. Each has distinctive features. Community structures were also considered in random and scale-free networks, as community structures influence network spreading. Note that the small-world network did not have an accompanying community variant by definition. Random networks were generated via the Erdős-Rényi (ER) model 51, scale-free networks through the Barabási-Albert (BA) model 52, and small-world networks using the Watts-Strogatz (WS) model 53. All the network generators above are available in NetworkX 54. Additionally, a random modular network generator 55 was employed for creating networks with community features. It was run with a desired value of modularity, Q, of 0.5 and number of community, m, of 3.

Four real-world network datasets were used in the experiments. Netscience 56 is a collaboration network of scientists working on network theory and experiment. In this network, nodes represent scientists, and an edge between two scientists is included if they have co-authored a research paper. Weaver 57 describes a real-world animal interaction network, specifically focusing on the social interactions among weaver birds. Each node in the network represents an individual weaver bird from a specific colony observed within a particular year. An edge is drawn between two individual birds if they used the same nest chambers. Mammalia 58 is a vole interaction network dataset. Each node in the network represents an individual vole. An edge is added between two nodes if those individuals were caught in the same trap at any point during the primary trapping sessions. Tortoise 59 is structured to map the interactions among tortoises based on their shared use of burrows. Each node in the network represents an individual tortoise. An edge is established between two tortoise nodes if they share the same burrow.

Table 2 Properties of network datasets
Full size table

Metrics of interest

The aim of the proposed approach is to maximize network disruption with a limited number of node removals. To evaluate its effectiveness, five key performance indicators are used to assess the extent of network destruction following node removal by both the proposed method and other baseline approaches.

Edge quantity: In the context of complex networks, the edge quantity refers to the total number of edges (or connections) in a network. Each edge represents a connection or link between two nodes in the network. This metric is crucial in understanding the structure and connectivity of the network, as it indicates how many pairs of nodes are directly connected to each other. A lower edge count in the remaining networks indicates that an approach is more effective in disrupting the network, thereby making it more challenging for a virus to spread.

Count of network components: In a complex network, the count of network components refers to the number of distinct sub-networks or clusters within the entire network that are not connected to each other. Each component is a subset of nodes and edges, where every node in a component is connected directly or indirectly to every other node in the same component, but there are no connections between nodes in different components. This concept is key to understanding the network’s structure, as it reveals how the network is partitioned or fragmented. A larger number of components in the residual networks suggests that a method is more efficient in fragmenting the network, consequently enhancing the network’s ability to impede the spread of a virus. To ensure consistency in the result display, we use the reciprocal of the number of components as the measurement, such that a smaller reciprocal indicates a greater capability of the network in hindering pathogen propagation.

Size of the largest component: The size of the largest component refers to the number of nodes in the largest sub-network within the entire network. This largest component, also known as the giant component, is the biggest group of nodes that are interconnected either directly or indirectly through a series of edges. The size of this component is a key metric in network analysis, as it reflects the extent of connectivity and can indicate the robustness or vulnerability of the network, especially in the context of processes like information dissemination or disease spread. A smaller size of the largest component in the remaining networks implies that a approach is more effective in breaking down the network.

Epidemic threshold 60: Two key factors influencing a pathogen’s spread through a network are its spreading rate and the network’s epidemic threshold. The spreading rate is influenced by the pathogen’s biological traits, while the epidemic threshold represents the network’s ability to withstand such a spreading. An epidemic occurs when the pathogen’s spreading rate surpasses the network’s epidemic threshold; otherwise, the pathogen’s spread diminishes. We assess the impact on the network’s epidemic threshold following node removal using the proposed approach and other baseline methods. Prior research 60 suggested that in an SIS (Susceptible-Infected-Susceptible) model, a network’s epidemic threshold, denoted as \(\tau\), is determined by the equation

$$\begin{aligned} \tau = \frac{1}{\lambda _{\max }} , \end{aligned}$$
(6)

where \(\lambda _{\max }\) represents the largest eigenvalue of the network’s adjacency matrix. This equation is used to compute the epidemic thresholds for networks.

Average node connectivity 61: The definition of average node connectivity in a complex network is the average, over all pairs of vertices, of the maximum number of internally disjoint paths connecting these vertices 61. It can be calculated as

$$\begin{aligned} \bar{\kappa }(G)=\frac{\sum _{u, v} \kappa _G(u, v)}{\left( \begin{array}{l} n \\ 2 \end{array}\right) }, \end{aligned}$$
(7)

where \(\kappa _G(u, v)\) is defined to be the maximum value of k for which node u and node v are k-connected, and n is the size of graph G. Average node connectivity in a network refers to the expected number of nodes that need to be removed to disconnect a pair of non-adjacent nodes. This concept is crucial for assessing the network’s resilience. It also focuses on the maximum number of distinct paths that can be formed between any two nodes, offering a deep insight into the network’s overall interconnectedness and robustness.

SIR simulation

The Susceptible-Infected-Recovered (SIR) epidemic model is utilized to evaluate the influence of particular nodes on network spread. This model categorizes a population of N individuals into three distinct stages:

  1. 1.

    Susceptible (S): These individuals have not yet contracted the infection and are vulnerable to catching it.

  2. 2.

    Infected (I): Individuals in this category have caught the disease and are capable of transmitting it to the susceptible ones.

  3. 3.

    Recovered (R): Once individuals have gone through the infection phase, they are deemed removed from the cycle of the disease, meaning they can neither contract nor spread the infection again.

Initially, all nodes are classified as susceptible (S), except for the specific node being scrutinized for its spreading efficiency, which is classified as infected (I). During each time step t, each node in the infected state (I) has a probability \(\beta\) (infection rate) of infecting adjacent susceptible nodes. Subsequently, these infected nodes have a probability \(\gamma\) (recovery rate) of moving to the recovered state (R).

This approach allows for a detailed understanding of how specific nodes affect the spread within a network, underlining the dynamics of disease or information propagation in a structured population. The parameters \(\beta\) and \(\gamma\) are crucial in determining the speed and extent of spread within the network. The SIR model is extensively employed in various fields for its effectiveness in simulating the spread of infectious diseases and behavioral patterns in social and information networks.