Introduction

In recent years, stock price prediction has been a hot topic in academia. As an important component of the financial market, the stock market plays a crucial role in national economic development, corporate financing, and investor asset al.___location. The stock market provides a platform for capital flows, promotes optimal resource allocation, and drives sustained economic growth. However, the complexity and uncertainty of the stock market pose unprecedented challenges to prediction tasks1. Market volatility, rapidly changing information, unpredictable investor behavior, and the evolving macroeconomic environment are intertwined factors that make accurately predicting future stock prices an extremely challenging task. Stock data often contains many random and irregular fluctuations, which may be mistakenly regarded as important features by models during the training process. Noise can obscure the true trends and patterns of stock prices, making it difficult for models to capture useful information. Therefore, in the presence of significant noise, the predictive accuracy of models can drop significantly. Despite significant efforts by scholars in model construction, algorithm optimization, and data analysis, effectively dealing with noisy data in the stock market and improving prediction accuracy remain important challenges to be overcome in this field.

In the early stages, models based on statistical methods2 were used to predict stocks. Traditional time series analysis methods are primarily based on linear assumptions and statistical regularities to predict future trends. Although traditional time series analysis is a commonly used prediction method in the financial field, it has limitations in dealing with the nonlinearity and high noise of stock data. Time series models are often based on linear assumptions, whereas fluctuations in stock data are not simple linear functions but are influenced by nonlinear interactions among multiple variables. Consequently, the performance of traditional time series analysis methods in stock prediction models is often less than satisfactory. With the continuous advancement of machine learning technology, researchers are using its algorithms to predict stock trends, such as the Autoregressive Moving Average Model (ARMA)3, Support Vector Machines (SVM)4, K-Nearest Neighbors5, and the bagging algorithm6. Zhenkun Liu et al.6 proposed a new profit-oriented PPer prediction fusion framework that combines bagging (specifically Random Forest, RF) and boosting (using Categorical Boosting, CatBoost) algorithms, replacing the base learner with CatBoost and using grid search to fine-tune hyperparameters for profit maximization. However, the performance of machine learning models often highly depends on data quality and feature selection. In high-noise environments, the noise in the data may obscure useful information, resulting in the model’s inability to accurately extract features and make predictions. With the rise of deep learning, more and more scholars are applying neural networks to the field of stock prediction, such as Recurrent Neural Networks (RNN)7, Long Short-Term Memory Networks (LSTM)8, and Gated Recurrent Units (GRU)9. Luo et al.10 proposed the Causality-Guided Multi-Memory Interaction Network (CMIN), which models the multimodal relationship between financial text data and causality-enhanced stock correlations to achieve higher prediction accuracy. Due to the nonlinearity and instability of stock data, a single prediction model cannot accurately predict stock prices. An increasing number of scholars are beginning to apply ensemble models to stock prediction. Zhenkun Liu et al.11 combined the Bayesian optimization algorithm with the Extreme Gradient Boosting algorithm, using Bayesian methods to optimize the class weights and other hyperparameters of Extreme Gradient Boosting to improve the accuracy of predicting profit-driven customer churn. Yu L et al.12 used a hybrid model combining LSTM and CEEMDAN to predict the realized volatility (RV) of the CSI 300 Index, the S&P 500 Index, and the STOXX50 Index.

From the research mentioned above, it becomes evident that the task of reducing the adverse effects of noise on the accuracy of stock market predictions poses a significant challenge. In response to this challenge, researchers have explored innovative methods, one of which is the introduction of the CEEMDAN technology. This technology is particularly promising for processing noisy stock data, as it can effectively decompose complex signals into simpler, more manageable components. However, despite its potential, these studies have typically not carried out detailed segmentation when dealing with the decomposed components of the stock data. This oversight has limited the ability to fully capture and exploit the potentially intricate patterns and relationships that may exist within each of these components. Consequently, the denoising effect of the stock data, while improved to some degree by the application of CEEMDAN, still leaves room for further enhancement.

On the other hand, the pursuit of accuracy in stock prediction has led some scholars to explore the integration of optimization algorithms with stock prediction models. This approach aims to fine-tune the parameters of the prediction models, thereby improving their performance. Many optimization algorithms are susceptible to the problem of converging prematurely to local optimal solutions. This limitation means that they may fail to identify the global optimal parameter combination that could maximize the performance of stock prediction models. As a result, despite the efforts made in combining optimization algorithms with prediction models, the desired improvements in accuracy have often been elusive.

Addressing the issue of low prediction accuracy in stock forecasting due to noise interference, this study delves into three core technologies: CEEMDAN, the Encoder-Decoder framework, and the PSO algorithm. The aim of this research is to fully leverage the advantages of these technologies and propose a new time series model based on CED-PSO-StockNet to solve the problem of noise interference and improve prediction accuracy. To reduce noise interference and enhance the stability of components, the model utilizes the CEEMDAN technique to decompose stock data and then reclassifies the decomposed components into high-frequency, mid-frequency, and low-frequency components using the extreme point method. To deeply extract features from the reconstituted components and improve stock prediction accuracy, an Encoder-Decoder model incorporating an attention mechanism is employed in the construction of the stock prediction framework, with separate prediction models established for each. At the same time, to further optimize prediction performance, the inertia weight and learning factors of the PSO algorithm are refined, and the improved algorithm is used to fine-tune the parameters of each component prediction model. To comprehensively validate the performance of the proposed model, we conducted the detailed experimental analysis using the Shanghai Pudong Development Bank dataset. Initially, ablation experiments were designed to observe the impact on prediction performance by gradually removing key components of the model, thereby verifying the effectiveness of the improved parts of each component. Additionally, benchmark model comparison experiments were conducted to compare the proposed model with current mainstream single and ensemble stock prediction models, in order to evaluate its advantages in prediction accuracy. The experimental results demonstrate that the proposed model performs exceptionally well on the Shanghai Pudong Development Bank dataset, exhibiting higher prediction accuracy compared to the benchmark models and being more suitable for stock prediction tasks.

The main contributions of this paper are summarized as follows:

  1. (1)

    The application of CEEMDAN to stock data preprocessing, where the decomposed IMFs are further classified into high-frequency, mid-frequency, and low-frequency components using the extreme point method. Prediction models are then established for each component to capture key information from different frequency components.

  2. (2)

    Based on the classic Encoder-Decoder framework, an innovative introduction of the attention mechanism enables the model to adaptively allocate different levels of attention according to the characteristics of the input data, capturing information crucial to prediction results.

  3. (3)

    Addressing the parameter optimization problem of component prediction models, an IPSO algorithm is employed to automatically find the optimal parameter combination.

  4. (4)

    Using a high-noise stock dataset from Shanghai Pudong Development Bank, this study conducts ablation experiments and benchmark model comparison experiments to verify the outstanding performance of the proposed CED-PSO-StockNet model in the field of stock prediction, contributing a new method to the stock prediction ___domain.

The rest of this paper is organized as follows: Sect. 2 presents related work. Section 3 introduces the methodology. Section 4 describes the construction and methodology of the CED-PSO-based StockNet model. Section 5 presents the experiment. Finally, Sect. 6 concludes the paper.

Related work

Application of decomposition algorithms in Time Series Prediction

Decomposition algorithms have shown great potential in time series analysis. They can decompose complex stock price series into multiple simple modal components, enabling models to gain a deeper understanding of the intrinsic structure and characteristics of the series and achieve the effect of data denoising. Currently, scholars have combined decomposition algorithms with various prediction models to fully leverage the advantages of different models and improve the accuracy of stock prediction. A common strategy is to input the decomposed components into prediction models separately and then integrate the prediction results from each model to obtain the final prediction. This flexible combination approach helps the model to more comprehensively capture and utilize key information in the stock price series. For example, Yi Cai et al.13 proposed a stock prediction method that combines the Ensemble Empirical Mode Decomposition (EEMD) algorithm with the CNN-BiLSTM-Attention network to address the issue of low accuracy in noisy stock prediction. On the other hand, Kai Lv et al.14 adopted a similar strategy when predicting the Remaining Useful Life (RUL) of lithium-ion batteries. They first decomposed the Health Indicator (HI) into multiple components using CEEMDAN and then input these components into component prediction models for prediction. Finally, they fused the prediction results and input them into a capacity prediction model to indirectly predict RUL. Decomposition algorithms have significant advantages in reducing the complexity of time series and removing noise. By combining them with different prediction models, decomposition algorithms can more comprehensively capture and utilize key information in stock price series, thereby improving the accuracy of stock prediction.

Application of encoder-decoder framework in stock prediction

The Encoder-Decoder framework excels in handling time series tasks such as stock price prediction due to its outstanding sequence-to-sequence processing capabilities. The Encoder part of this framework encodes historical stock data sequences into a fixed-length vector, while the Decoder part generates future stock price predictions based on this vector. This design enables the Encoder-Decoder model to better capture and utilize the temporal dependencies of stock prices. For the problem of predicting non-stationary stock sequences, scholars such as HuiHuiZ15 have proposed an innovative new framework based on the Encoder-Decoder. In this framework, the encoding and decoding processes use GRU as the core unit structure to extract and utilize continuous and useful feature information. However, as the length of stock sequences increases, the issue of information loss gradually becomes prominent. To effectively address this issue and further enhance the performance of the Encoder-Decoder framework in stock prediction, researchers have introduced the Attention Mechanism. The introduction of this mechanism allows the model to focus more on the input parts most relevant to the current prediction during the decoding process, thereby effectively mitigating the problem of information loss. For example, Yao Qin16 proposed a Recurrent Neural Network (DA-RNN) based on a two-stage attention mechanism. In the first stage, the network introduces an input attention mechanism that adaptively extracts relevant driving sequences at each time step by referencing the previous encoder’s hidden state. In the second stage, it uses a temporal attention mechanism to select relevant encoder hidden states from all time steps, further enhancing the model’s ability to capture and utilize key information.

Application of optimization algorithms in stock prediction

The precise setting of model parameters has a crucial impact on the performance of the model, and optimization algorithms play a central role in this process. Through intelligent search strategies, optimization algorithms can autonomously discover the optimal combination of parameters, thereby effectively improving the accuracy of the model and providing strong support for optimizing model performance. For example, Bayesian optimization algorithms12, Artificial Bee Colony optimization algorithms17, and PSO algorithms18 have all demonstrated their optimization potential in practice. Currently, many scholars are dedicated to combining these advanced optimization algorithms with machine learning or deep learning models to tackle more complex stock prediction tasks. Ping Jiang et al.17 adopted the Artificial Bee Colony optimization algorithm to fine-tune model parameters to improve the accuracy of customer churn prediction. Addressing the issue that the PSO algorithm can easily fall into local optima during the optimization process, which hinders the performance improvement of stock prediction models, Yang et al.18 proposed an improved PSO algorithm. This algorithm aims to find the optimal parameter combination for the stock price prediction model to achieve more accurate stock predictions. In summary, optimization algorithms have a significant effect on improving model performance. Especially in complex tasks such as stock prediction, precise setting of model parameters can effectively enhance the accuracy of predictions.

Methodology

CEEMDAN principle

EMD (empirical mode decomposition)19 is a method for processing nonlinear and non-stationary signals. It aims to break down complicated signals into intrinsic mode functions (IMFs), ensuring each IMF adheres to certain criteria. First, across the entire span of the data, the quantity of local extremities and zero-crossings should be identical or have a maximum disparity of one; Second, the mean value of the local maxima’s envelope (upper envelope) and the local minima’s envelope (lower envelope) needs to be zero at any time. However, there will be the problem of mode aliasing in the decomposition process of EMD. To reduce the problem of mode aliasing, EEMD(ensemble empirical mode decomposition)20 as well as CEEMD(complete ensemble empirical mode decomposition) introduce both positive and negative white Gaussian noise pairs into the targeted signal. The basic idea of these algorithms is to use the statistical characteristics of white noise to average the results of repeated decomposition, to eliminate mode aliasing. However, when these algorithms decompose the signal, some white noise often remains in the IMFs component, which is disadvantageous to the subsequent signal analysis.

To solve the problem of residual white noise, Torres et al. Proposed the CEEMDAN algorithm21. CEEMDAN improves the performance of EMD by introducing adaptive noise and ensemble averaging. The specific steps of the CEEMDAN algorithm are as follows:

  1. 1.

    Similar to the EEMD algorithm, CEEMDAN adds pairs of positive and negative Gaussian white noise to the original signal, and the calculation formula is shown in Eq. 1. However, unlike EEMD, CEEMDAN only adds noise to the remaining signal in each iteration, not to the entire original signal.

    $${a^l}(t)=a(t)+{s^l}(t)$$
    (1)

    Among them, a(t) is the decomposed signal, sl(t) is the Gaussian white noise satisfying the standard normal distribution added for the l time, and al(t) is the new signal after adding the white noise for the l time.

  2. 2.

    After adding noise, the new signal shall be EMD decomposed and the first IMFs shall be taken. The calculation formula is shown in Eq. 2.

    $$C_{1} = E_{1} (a^{l} (t))$$
    (2)

    Where EN(x) represents the Nth IMFs after EMD decomposes signal x; C1 represents the first IMFs obtained after decomposing the new signal with white noise.

  3. 3.

    To eliminate the influence of the added white noise on the decomposition results, CEEMDAN adopts the set average method, and the calculation process is shown in Eq. 3. Specifically, for each IMFs component, the decomposition results after adding different noises for many times are averaged to obtain the final IMFs component. This can eliminate the random error caused by noise and improve the stability of decomposition results.

    $${\bar {C}_1}({\text{t}})=\frac{1}{L}\sum\limits_{{l=1}}^{L} {C_{1}^{l}} (t)$$
    (3)
  4. 4.

    Subtract the first IMFs component from the original signal to obtain the remaining signal. The calculation process is shown in Eq. 4.

    $${\text{r}}_{1} (t) = a(t) - \bar{C}_{1} (t)$$
    (4)

    Where r1(t) represents the residual signal.

  5. 5.

    Continue to add noise to the remaining signals, and then perform EMD decomposition. The decomposition results are collectively averaged to obtain the second IMFs. The calculation process is shown in Eq. 5.

    $$\bar{C}_{2} ({\text{t}}) = \frac{1}{L}\sum\limits_{{l = 1}}^{L} {E_{1} (r_{1} (t) + s^{l} (t))}$$
    (5)
  6. 6.

    Repeat the above steps until the remaining signal becomes a monotonic function, unable to EMD decomposition, and the algorithm stops. Finally, the original signal is decomposed into multiple IMFs and residual signals. The expression of the original signal is shown in Eq. 6.

    $$a(t) = \sum\limits_{{q = 1}}^{Q} {\bar{C}_{q} (t) + r_{q} (t)}$$
    (6)

Through the above steps, CEEMDAN algorithm can obtain a series of IMFs components, which represent the changes of the original signal in different frequencies and time scales. Compared with EMD, CEEMDAN has higher decomposition accuracy and stability, especially suitable for processing nonlinear and non-stationary time series data. But the stock data contains a lot of noise, which increases the difficulty of extracting effective information from the data. Although CEEMDAN can deal with noise to some extent, noise may still be a problem in some cases. Frequency division processing helps to divide the components into different frequency ranges, making the proportion of noise and signal more reasonable in each frequency range, so it is easier to identify useful information.

Encoder-decoder framework

The encoder-Decoder framework22 is a deep learning model, which is mainly used for sequence-to-sequence tasks. Such tasks usually need to convert one input sequence into another output sequence, such as machine translation, time series prediction, etc. The Encoder-Decoder framework contains two main components: an encoder and a decoder. Figure 1 shows the Encoder-Decoder framework.

Fig. 1
figure 1

Encoder-decoder frame diagram.

Full size image

The encoder is responsible for receiving the input sequences xt and ht-1 and converting them into an internal representation (“encoding”). Then this internal representation is calculated by a recursive neural network to obtain a context vector C. This context vector C contains all the information of the input sequence, which can be used by the decoder to generate the output sequence. The calculation process is shown in Eqs. 7–8.

$${\rm h}_{\rm t}=f(h_{t-1},\,x_{t})$$
(7)
$$C = {\text{g}}(h_{1} ,h_{2} ,h_{3} ,h_{4} , \cdots ,h_{n} )$$
(8)

In this paper, g(x) is selected as the BiGRU network. Where ht represents the hidden state at time t, ht-1 represents the hidden state at time t-1, xt represents the input sequence at time t, and C represents the context vector.

At each time step, the decoder uses the output Yt-1 of the previous time step as the input of the current time step and combines with the context vector C to generate the output Yt of the current time step. The calculation process is shown in Eq. 9.

$$Y_{{\text{t}}} = g(Y_{{t - 1}} ,C)$$
(9)

Where Yt represents the output value at time t, Yt-1 represents the output value at time t-1, C is the context vector calculated from the encoder, and g(x) uses the same BiGRU network as the encoder.

Attention mechanism

Attention mechanism23 is a mechanism that simulates human attention distribution and can help neural networks pay more attention to important parts when processing sequence or image data. In deep learning, the attention mechanism is widely used in natural language processing, time series prediction, image processing, speech recognition, and other tasks. Figure 2 is the schematic diagram of the attention mechanism. The specific steps of the attention mechanism are as follows:

  1. 1.

    Calculate the attention weight24 of each input data through the scoring function. This weight vector represents the relative importance of the input data. The calculation process is shown in Eq. 10.

    $$a_{i} = s(x_{i} ,q)$$
    (10)

    Where ai is the attention weight, xi is the input vector, q is the query vector, and s() is the scoring function.

  2. 2.

    Normalization of attention weight using the softmax function. The calculation process of weight normalization is shown in Eq. 11.

    $$a^{\prime}_{i} = soft\max (a_{i} ) = \frac{{\exp (a_{i} )}}{{\sum\nolimits_{{j = 1}}^{n} {\exp (a_{i} )} }}$$
    (11)
  3. 3.

    The attention weight is multiplied by the input data to obtain a weighted input representation. The calculation process is shown in Eq. 12.

    $${\text{context}} = \sum\nolimits_{{i = 1}}^{n} {a^{\prime}_{i} \cdot x_{i} }$$
    (12)
  4. 4.

    Combine weighted inputs to generate a more targeted representation.

Fig. 2
figure 2

Schematic diagram of attention mechanism.

Full size image

BiGRU

BiGRU (bidirectional gated recurrent unit)25 is a model of the bidirectional gated cyclic unit, which is used to process the modeling task of sequence data. It is a combination of bidirectional RNN26 and GRU (gated recurrent unit)27. In traditional RNN, information can only be transferred in one direction, from the past time step to the future time step. While BiGRU introduces bidirectionality, taking into account the past and future information in the sequence, to better capture the context and long-term dependencies in the sequence. It is widely used in natural language processing, speech recognition, text generation, and other fields, and has achieved good results. The principle of BiGRU is that at each time step, the input sequence will be input into the forward GRU unit and the backward GRU unit respectively. The forward GRU unit calculates the hidden state and output based on the input of the current time step and the output of the previous time step. Conversely, the backward GRU unit calculates the hidden state and output based on the input of the current time step and the output of the next time step. Finally, the outputs of forward and backward GRU units will be combined for subsequent tasks.

PSO

The particle Swarm Optimization algorithm (PSO)28 is rooted in swarm intelligence and takes its inspiration from the patterns of birds searching for food and the migration behavior of fish. PSO searches for the optimal solution by simulating the cooperation and information sharing among individuals in a flock of birds. In PSO, each individual in the solution space is represented as a particle, its position represents the candidate solution of the solution, and the speed represents the moving direction and speed of the particle in the search space. Each particle searches for the optimal solution by constantly updating its speed and position. In the application of stock forecasting, appropriate parameter selection can help improve the performance of the algorithm.

Huber loss function

Huber29 is a loss function for robust regression, which is widely used in statistics. The Huber loss function combines the characteristics of mean square error (MSE) and mean absolute error (MAE). When the error is small, it uses MSE; When the error is large, it uses the linear loss function. This design reduces the sensitivity of the Huber loss function to outliers or noise and improves the robustness of the model. The mathematical expression of the Huber loss function is shown in Eq. 13.

$$L_{{{\text{huber}}}} (f,y) = \left\{ {\begin{array}{*{20}c} {(f - y)^{2} ,\left| {f - y} \right| \le \& } \\ {2\& \left| {f - y} \right| - \& ^{2} ,\left| {f - y} \right| > \& } \\ \end{array} } \right.$$
(13)

Where f is the predicted value, y is the real value, and & is a super parameter used to control the conversion point of the Huber loss function between MAE and MSE. The choice of hyperparameter & is crucial to the impact of the Huber loss function29.

Construction based on CED-PSO-StockNet model

Construction of time series model based on CED-PSO-StockNet

The CED-PSO-StockNet model mainly solves the problem that the prediction accuracy of stock data is affected by excessive noise. The model first decomposes the stock data into multiple IMFs and residual signal R by using the CEEMDAN method. Then, the frequency of each component is evaluated by the extreme point method and recombined into high-frequency, medium-frequency and, low-frequency components to extract the characteristics of each component more accurately. Given the large amount of noise contained in high-frequency components, the combination mode is optimized to reduce noise interference and improve prediction accuracy.

An Encoder-Decoder framework integrating the attention mechanism is used to construct efficient prediction models for each component after reconstruction. Due to the frequent and complex changes in high-frequency component and medium-frequency component signals, a deeper network structure is needed to capture the details and patterns. Therefore, for high-frequency and medium-frequency component signals, the encoder and decoder adopt two-layer BiGRU networks respectively to enhance the processing ability of the model for complex signals. In contrast, the change of low-frequency component signal is relatively stable, and its internal structure and mode are relatively simple. To balance the complexity and computational efficiency of the model, the network structure is simplified for low-frequency component signals. The encoder and decoder adopt a layer of the BiGRU network respectively. This can maintain a certain prediction performance, reduce the number of parameters and calculations of the model, and improve the training speed and efficiency of the model.

At the same time, the improved PSO algorithm is used to adjust the parameters of the three component prediction model to optimize the performance of the model. In the process of model training, the Heber loss function is selected, and the super parameters in the loss function are optimized by the improved PSO algorithm to ensure that the model can better fit the change law of stock data. Finally, the final stock prediction results are obtained by summing the prediction results of each component, providing investors with a more accurate and reliable decision-making basis. The training process of the model is shown in algorithm 1. The model structure diagram of CED-PSO-StockNet is shown in Fig. 3.

Algorithm 1 Training process of model

Input: The closing price of stock S = s1,…., sn

Output: Model predictions

Step1: IMF1,IMF2,…,IMFn, r = CEEMDAN(S)

Step2: high_freq_imfs[], medium_freq_imfs[], low_freq_imfs[] = frequency division (IMF1,IMF2,…,IMFn, r) and optimize the combination of high_freq_imfs

Step3: Build the component prediction model as shown in Fig. 4

Step4: High frequency loss = Heber(predicted value of high_freq_imfs, true value, delat1); Medium frequency loss = Heber(predicted value of medium_freq_imfs, true value, delat2); Low frequency loss = Heber(predicted value of low_freq_imfs, true value, delat3)

Step5: The optimal parameter combination [] = IPSO(prediction model parameters constructed from high, medium, and low frequency components, delat1, delat2, delat3)

Step6: Final prediction result = Composite prediction result (high frequency prediction result, medium frequency prediction result, low frequency prediction result)

Fig. 3
figure 3

CED-PSO-StockNet model structure diagram.

Full size image

Frequency division processing

In stock data analysis, a significant challenge is the presence of a large amount of noise in the data, which greatly increases the difficulty of extracting useful information from it. Although the CEEMDAN method can effectively handle noise to some extent, the noise problem cannot be ignored in certain specific situations. Li et al.30 has proposed using the zero-crossing rate for frequency division processing of components. However, the zero-crossing rate does not directly reflect turning points or extreme situations in market trends, which limits its application in stock prediction to some extent. Inspired by the work of Lirong Sun31, we applied extreme points to the frequency division of IMFs. Extreme points are often closely associated with turning points in market trends. The extreme point method is not confined to the zero crossings of signals but is capable of comprehensively capturing the local maximum and minimum values of signals within a given range, thus more accurately reflecting the signal’s variation characteristics and trends. This feature enables the extreme point method to maintain high accuracy and robustness even when dealing with complex signals or situations with significant noise interference. Secondly, the extreme point method exhibits greater versatility and applicability. Regardless of whether a signal has zero crossings, the extreme point method can effectively extract the modes and features of the signal, providing strong support for subsequent analysis and processing. In contrast, the zero-crossing rate method is constrained by the zero-crossing characteristics of signals, and its effectiveness may be significantly reduced for certain special signals or in noisy conditions. Therefore, this paper proposes using extreme points to estimate the frequency of components. The basic idea of this method is to infer the oscillation frequency of the signal through the number of local minimum and maximum values in the signal, which helps to divide the components into different frequency ranges. Such division makes the ratio of noise to signal within each frequency range more reasonable, making it easier to identify useful information. The specific steps are as follows:

  1. 1.

    Begin by analyzing the provided IMFs to identify all local minimum and maximum values.

  2. 2.

    Subsequently, calculate the respective counts of these local minimum and maximum values. The number of such extreme points serves as an indicator of the oscillation periodicity within the signal. Typically, a higher count of extreme points suggests that the signal contains a greater number of oscillation periods.

  3. 3.

    The frequency of the signal can be approximately estimated based on the count of these extreme points. The calculation process of frequency is shown in Eq. 14.

$$fre = \frac{{f_{{{\text{sum}}}} ({\text{argrelextrema}}(x,p)) + f_{{{\text{sum}}}} ({\text{argrelextrema}}(x,q))}}{{2*f_{{{\text{sum}}}} (x)}}$$
(14)

Where fre is the frequency; fsum() is the function for calculating the count; p and q are comparison functions, with p being the function for comparing minimum values and q for comparing maximum values; x represents the frequency data; argrelextrema() is the function for calculating local extrema points.

After frequency division, the IMFs decomposed by the CEEMDAN algorithm are reconstructed into high-frequency components, medium-frequency components, and low-frequency components. Subsequently, the improved PSO algorithm can effectively optimize the parameters of the prediction model constructed for these three categories, and the model’s prediction performance and accuracy can be enhanced significantly.

Encoder-decoder framework with an attention mechanism

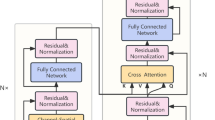
The Encoder-Decoder framework can learn effective feature representation from a variety of complex stock data and accurately capture context information. However, it needs an extensive volume of training data to achieve gratifying results. When faced with a long input sequence, the Encoder-Decoder framework may be affected by the lack of information, because the later input information may cover the previous input information, which makes it difficult for the model to capture the long-term dependency and context information. Such a scenario could diminish the model’s effectiveness in performing prediction tasks. To tackle the issue of cumulative error stemming from the copious amounts of training data required for generating long sequences, this paper proposes to add an attention mechanism between the encoder and decoder to dynamically weight the output state of the encoder, so as to better focus on the more important part of the previous input information. The framework is composed of three core components: encoder, attention layer, and decoder. Among them, the encoder and decoder adopt the BiGRU network to make full use of the dependent information before and after the sequence.

The attention mechanism assigns a weight to each element, deriving these weights from the similarity measured between encoder output elements. These weights reflect the importance of information from different locations for the current prediction. Then, the attention weight is multiplied by the output of the encoder element by element, and the context vector is obtained by summing along the dimension of the time step. This context vector not only contains the global information of the input sequence but also highlights the most relevant part of the current prediction. This allows the model to more precisely focus on crucial information within lengthy sequences and prevents the issue that the early information is covered by the subsequent information. Figure 4 shows the Encoder-Decoder framework with an attention mechanism.

Fig. 4
figure 4

Encoder-Decoder framework with an attention mechanism.

Full size image

Improved particle swarm optimization algorithm

Through continuous iterative updating and information exchange, PSO can gradually converge to the optimal solution. However, PSO also has some disadvantages and limitations, such as easy to fall into local optimization, sensitivity to parameter settings, and so on. In this paper, by improving the inertia weight w and the learning factor c, we address the shortcomings of traditional PSO and effectively enhance the performance of the algorithm.

Improvement of inertia weight w

The inertia weight w holds a pivotal role within the framework of the PSO algorithm, which reflects the influence of the current particle speed on the previous generation of particles. Selecting the appropriate value for w significantly influences the algorithm’s performance and its effectiveness in optimization. The existing inertia weights are mainly divided into three types: constant, time-varying inertia weight, and adaptive inertia weight. The constant w means that each particle moves at the same speed, while the time-varying and adaptive weights allow w to change dynamically during the execution of the algorithm.

Compared to static values, dynamically changing ω often achieves better results in the optimization process. This is because dynamically adjusted ω can flexibly adjust the velocity of particles based on the nature of the problem and the search status of the particles, thereby better exploring and utilizing the search space. Therefore, in many cases, using an adaptive inertia weight model can enhance the global optimization ability of the PSO algorithm. Wen et al.32 proposes a linearly decreasing weight strategy. Although this strategy provides a larger inertia weight in the early stages of search to enhance global search capability, in the later stages of search, as the inertia weight decreases linearly, the velocity of the particles also decreases correspondingly, leading to a potential slowdown in the convergence speed of the algorithm. To improve the convergence speed of the PSO algorithm in the later stages of the search, this paper proposes an adaptive nonlinear inertia decreasing weight, calculated as shown in Eq. 23. Figure 6 illustrates the time variation of the inertia weight w.

$${\text{w}} = w_{{\max }} - (w_{{\max }} - w_{{\min }} )\cos (\tan (1 - (t/T)^{2} ))$$
(15)

Where wmax and wmin are the maximum and minimum values of inertia weight respectively; T is the maximum iteration number of particles.

Fig. 5
figure 5

Time variation diagram of inertia weight w.

Full size image

It can be seen from Fig. 5 that the adaptive inertia decreasing weight w proposed in this paper is large in the early stage of the search process, which can improve the global search ability of particles. As the search goes on, w gradually decreases, and particles focus more on the search of local areas to enhance the optimization ability of particles. The strategy helps to strike a balance between global and local search abilities throughout the process, so as to obtain a better optimal solution.

Improvement of learning factors

In the PSO algorithm, learning factors c1 and c2 are key parameters to adjust the speed of particles in the search space. c1 controls the movement speed of particles to their best position in history (individual optimal solution). A large c1 value helps the algorithm quickly locate the possible optimal region in the initial stage, but too large a value may lead to the algorithm falling into the local optimal solution. A smaller c1 value may slow down the moving speed to the individual optimal solution and affect the global search ability of the algorithm. c2 controls the speed of particles moving to the global optimal position (global optimal solution) of the population. A large c2 value helps the algorithm converge to the optimal solution accurately in the later stage of the search, but too large a value may make the algorithm lose its exploratory ability in the initial stage. A small c2 value may slow down the moving speed to the global optimal solution and affect the local search ability of the algorithm.

The traditional PSO algorithm33 often sets c1 and c2 as fixed constants, which can not meet the needs of practical applications. To improve the probability of finding the global optimal solution, the values of c1 and c2 need to be adjusted dynamically. This method facilitates achieving a more balanced approach between global and local searches, thereby reducing the duration of the search. To solve this problem, this paper improves the update formula of learning factors c1 and c2, and the calculation method is shown in Eqs. 16–17. Figure 6 shows the time variation of learning factors c1 and c2.

$${\text{c}}1=2 - \arccos w$$
(16)
$${\text{c}}2=\arccos w$$
(17)
Fig. 6
figure 6

Time variation of learning factors c1 and c2.

Full size image

From Eqs. 16–17, we can see that the values of c1 and c2 can be dynamically adjusted with the change of the search process by using acos function. This dynamic adjustment can adapt to different search stages. For example, in the initial stage of search, c1 is larger and c2 is smaller, which is conducive to global search; At the later stage of search, c1 is smaller and c2 is larger, which is helpful for local search. This method integrates the three parameters of the PSO algorithm into one. By adjusting the value of w, you can affect c1 and c2 at the same time, and then affect the speed and search behavior of particles. This integration can significantly enhance the algorithm’s efficiency and precision.

Experiment

Experimental data

The experimental data selected for this study is sourced from the Tushare interface, specifically focusing on the stock of Shanghai Pudong Development Bank (600000.SH) listed on the Shanghai and Shenzhen stock exchanges. The time range covers from January 1, 2019, to January 1, 2024, totaling 1,214 data records (https://www.tushare.pro.). To construct and validate the stock prediction model, the dataset is divided into a training set and a testing set, with the first 80% of the data used as the training set and the remaining 20% as the testing set. Since its listing on the Shanghai Stock Exchange in 1999, Shanghai Pudong Development Bank has accumulated a rich history of transaction data, providing a solid foundation for model construction and validation in this study. As an important component of the financial market, the stock of Shanghai Pudong Development Bank holds significant implications for deeply understanding the operating mechanisms of the financial market and optimizing investment strategies through the study of its price volatility patterns. The financial market is a complex and ever-changing system, and the stock price volatility of Shanghai Pudong Development Bank is influenced by a multitude of factors, making it an ideal dataset for examining the diversity and complexity of stock prediction models. As illustrated in Fig. 7, the stock of Shanghai Pudong Development Bank exhibits instability and a high level of noise, further demonstrating the suitability of this dataset for predictive research using the CED-PSO-StockNet time series model.

Fig. 7
figure 7

Stock closing price trend chart.

Full size image

Evaluating indicator

This experiment uses three evaluation indicators to measure the accuracy of the model, namely MAPE, RMSE, and R2.

Mean Absolute Percentage Error (MAPE) is a measure of the percentage error between predicted results and actual observations. When evaluating predictive models, the MAPE metric can be used to understand the relative error between the predicted results and the true values. The smaller the average absolute percentage error, the better the performance of the model. The calculation process is shown in Eq. 18.

$$MAPE = \frac{1}{{\text{n}}}\sum\limits_{{i = 1}}^{n} {\left| {\hat{y}_{{\text{i}}}^{{}} - y_{i} } \right|} * 100$$
(18)

Root Mean Square Error (RMSE) can effectively measure the degree of deviation between model predictions and actual values. Specifically, the calculation of RMSE involves calculating the square of the difference between the predicted and actual values for each observation point, then averaging all these square differences, and finally taking the square root to obtain the final result. The smaller the root mean square error, the better the performance of the model. The calculation process is shown in Eq. 19.

$$RMSE = \sqrt {\frac{1}{{\text{n}}}\sum\limits_{{i = 1}}^{n} {(\hat{y}_{i} - y_{i} )^{2} } }$$
(19)

The coefficient of determination (R2) refers to the quotient of SSR and SST. SSR is the sum of squared residuals, representing the sum of squared differences between actual values and model predictions. SST is the total sum of squares, which represents the sum of squares of the difference between the actual value and its mean. The size of the value is between [0, 1]. The larger the coefficient of determination, the better the performance of the model. The calculation process is shown in Eqs. 20–22.

$$RMSE = \sqrt {\frac{1}{{\text{n}}}\sum\limits_{{i = 1}}^{n} {(\hat{y}_{i} - y_{i} )^{2} } }$$
(20)
$$SSR = \sum\limits_{{{\text{i}} = 1}}^{{\text{n}}} {{(\hat{\text{y}}}_{{\text{i}}} - y_{i} )} ^{2}$$
(21)
$$SST = \sum\limits_{{{\text{i}} = 1}}^{{\text{n}}} {({\bar{\text{y}}}{}_{i} - y_{i} )} ^{2}$$
(22)

Among them, n represents the number of samples, \({\hat{\text{y}}}_{{\text{i}}}\)represents the model output value, yi represents the actual value, and \({\bar{\text{y}}}_{{\text{i}}}\)represents the average value.

Experimental configuration

This experiment is implemented based on the TensorFlow framework. The experimental environment configuration is shown in Table 1. In this experiment, the sliding window is set to 10, which means using the stock data from the first 10 days to predict the closing price of the stock on the 11th day. The optimization function used in the model is Adam34, which has the advantages of adaptive learning rate, fast convergence, adaptability to large-scale data, and high-dimensional parameter space in stock prediction models, and also demonstrates a certain degree of robustness. To enhance the model’s predictive accuracy and efficiency, varying iteration counts were assigned to the prediction models for the high-frequency, medium-frequency, and low-frequency components. Due to the presence of a significant amount of noise in the high-frequency component, the complexity of its prediction model is relatively high. Therefore, the number of iterations for the high-frequency component prediction model is set to 300. The medium-frequency component prediction model is set to have 200 iterations to improve the training speed while maintaining prediction accuracy. For low-frequency components, due to their stable changes and relatively simple prediction models, the iteration number of the low-frequency component prediction model is set to 100 times to quickly converge and obtain accurate prediction results.

Table 1 Experimental configuration.
Full size table

Data preprocessing

Data decomposition

The original stock closing prices in the experimental dataset are decomposed using CEEMDAN, resulting in six IMFs and one residual signal. As observed in Fig. 8, the frequencies of these six IMFs gradually decrease from top to bottom, and the residual signal exhibits a monotonic variation. With the decrease in frequency, the variation patterns of each IMF become simpler and more stable.

Fig. 8
figure 8

CEEMDAN decomposition view.

Full size image

Data frequency division and recombination

When reorganizing the subsequences decomposed by CEEMDAN using the extremum method, two thresholds were set: 0.005 and 0.1. If the frequency fre of the subsequence is greater than 0.1, it is classified as a high-frequency component; If fre is between 0.005 and 0.1, it is considered as the medium-frequency component; And the remaining subsequences are classified as low-frequency components. According to this standard, imf1 and imf2 are divided into high-frequency components, imf3, imf4, and imf5 are medium-frequency components, and imf6 and the remaining signals are classified as low-frequency components. Figure 9 shows the high-frequency component diagram before optimization. Figure 11 shows the medium-frequency component diagram. Figure 12 shows the low-frequency component diagram. However, imf1 and imf2 contain a large amount of information and relatively more noise, resulting in more significant noise components in the high-frequency components. Therefore, to optimize the combination of high-frequency components, special consideration was also given to the issue of whether to retain or remove imf1. Because the frequency of imf2 is lower than that of imf1 and it contains relatively less noise, imf2 is essential in the high-frequency component. For this purpose, two comparative experiments were conducted: one group removed imf1, and the other group retained imf1. From Table 4, it can be seen that the high-frequency component combination method after removing imf1 is more effective. The final choice is to retain only imf2 in the high-frequency component. This improvement helps to reduce noise interference and improve the accuracy of signal processing. Figure 10 shows the high-frequency component diagram after optimization.

Fig. 9
figure 9

High-frequency component diagram before optimization.

Full size image
Fig. 10
figure 10

High-frequency component diagram after optimization.

Full size image
Fig. 11
figure 11

Medium-frequency component diagram

Full size image
Fig. 12
figure 12

Low-frequency component diagram.

Full size image

Ablation experiment

To comprehensively verify the effectiveness of each part of the proposed CED-PSO-StockNet model in this study, we have carefully designed five sets of comparative experiments. The first set of experiments presents the complete experimental results of the CED-PSO-StockNet model. The second set of experiments removes the IPSO module from the CED-PSO-StockNet model, aiming to explore the role of this module in improving the prediction accuracy of the model. The third set of experiments removes the high-frequency component optimization improvement to evaluate its impact on model performance. The fourth set of experiments removes the frequency division processing step to observe its role in the model. The fifth set of experiments removes the attention mechanism to observe its impact on model performance. Figures 13, 14, 15, 16 and 17 respectively show the comparison between the predicted values and the true values for Exp.1-Exp.5.

Fig. 13
figure 13

Comparison between the true and predicted closing prices of stocks in the Exp.1.

Full size image
Fig. 14
figure 14

Comparison between the true and predicted closing prices of stocks in the Exp.2.

Full size image
Fig. 15
figure 15

Comparison between the true and predicted closing prices of stocks in the Exp.3.

Full size image
Fig. 16
figure 16

Comparison between the true and predicted closing prices of stocks in the Exp.4.

Full size image
Fig. 17
figure 17

Comparison between the true and predicted closing prices of stocks in the Exp.5.

Full size image

From Table 3, it can be observed that Exp.1, the proposed CED-PSO-StockNet time series model in this paper, exhibits significant advantages in stock data prediction. The model’s R2 value is as high as 0.9875, close to the ideal value of 1, indicating its excellent fitting effect. To further explore the effectiveness of the improvements in each module of the CED-PSO-StockNet model, a series of comparative experiments were conducted (Table 2).

Exp.2 is designed to verify the effectiveness of the IPSO algorithm. To more fully extract feature information from high-frequency, medium-frequency, and low-frequency components, the improved PSO algorithm is used to optimize key parameters in the prediction models for each component. These optimized parameters include the number of neurons in each layer of the BiGRU in the high-frequency, medium-frequency, and low-frequency component prediction models, the number of neurons in the dense layer in the attention mechanism, and the hyperparameters in the Huber loss function. The specific optimized parameter information is shown in Table 4. From the table, it can be seen that the optimal parameter combination is [262, 434, 313, 541, 556, 273, 503, 45, 295, 439, 382, 615, 496, 439, 66, 526]. To verify the superiority of the improved PSO algorithm in the stock prediction field, this paper specifically compares it with the traditional PSO algorithm. As can be seen from Table 3, compared to Exp.1, the R2 of Exp.2 decreases by 1.12%, and RMSE and MAPE increase by 0.0155 and 0.01% respectively. This demonstrates the effectiveness of the improved PSO algorithm proposed in this paper in enhancing model performance.

Exp.3 is based on Exp.2 but removes the optimization of high-frequency components. Compared to Exp.2, the R2 of Exp.3 decreases by 1.41%, and RMSE increases by 0.0241. This indicates that optimizing high-frequency components can effectively improve prediction accuracy. Exp.4 is based on Exp.3 but removes frequency division processing. Compared to Exp.3, the R2 of Exp.4 decreases by 5.56%, and MAPE increases by 6.34%, but RMSE slightly increases. This may be due to the introduction of a small amount of white noise by the CEEMDAN technique. Overall, frequency division processing has a positive effect on improving model performance. Exp.4 is based on Exp.3 but removes the attention mechanism. Compared to Exp.4, the R2 of Exp.5 decreases by 1.12%, and RMSE and MAPE increase by 0.0155 and 0.01% respectively. This demonstrates that the attention mechanism can enhance the feature extraction capability of the Encoder-Decoder framework. Although the RMSE of Exp.1 is slightly higher than that of Exp.4, the difference is not significant. This may be because the optimization of high-frequency components discards IMF1, which may contain a small amount of useful information. However, overall, it is clear that the improvements in each module have a positive effect on enhancing the prediction accuracy of the model.

Table 2 Improving the PSO algorithm to optimize parameters.
Full size table
Table 3 Experimental results of the ablation experiment.
Full size table
Table 4 Comprehensive performance of the model.
Full size table

Benchmark model comparison experiment

To evaluate the performance of our proposed model, this section conducts a comparative analysis with five existing benchmark models. The selected single prediction models include LSTM35, GRU36, and BiGRU37, which are widely used in the field of stock prediction. Additionally, comparisons will be made with three combining models, namely DA-RNN16, Ensemble Model38 and CNN-BiLSTM-AM39. DA-RNN16 is a two-stage attention-based recurrent neural network model. In the first stage, it introduces an input attention mechanism to adaptively extract relevant input features at each time step by referencing previous encoder hidden states. In the second stage, it employs a temporal attention mechanism to select relevant encoder hidden states across all time steps. The Ensemble Model38 integrates three RNN models by averaging their outputs. The CNN-BiLSTM-AM model39, on the other hand, combines Convolutional Neural Networks (CNN), Bidirectional Long Short-Term Memory (BiLSTM), and Attention Mechanism (AM). The CNN is used to extract features from input data, while the BiLSTM utilizes these extracted feature data to predict the stock’s closing price for the next day. Simultaneously, the attention mechanism is employed to capture the impact of past feature states at different times on the stock’s closing price, thereby enhancing prediction accuracy. Figures 18, 19, 20, 21, 22 and 23 represent the comparison charts of actual and predicted stock values for the above six baseline models, respectively.

Fig. 18
figure 18

Comparison between the true and predicted closing prices of stocks in the LSTM model.

Full size image
Fig. 19
figure 19

Comparison between the true and predicted closing prices of stocks in the GRU model.

Full size image
Fig. 20
figure 20

Comparison between the true and predicted closing prices of stocks in the BiGRU model.

Full size image
Fig. 21
figure 21

Comparison between the true and predicted closing prices of stocks in the Ensemble Model.

Full size image
Fig. 22
figure 22

Comparison between the true and predicted closing prices of stocks in the DA-RNN model.

Full size image
Fig. 23
figure 23

Comparison between the true and predicted closing prices of stocks in the CNN-BiLSTM-AM model.

Full size image

From the data analysis in Table 2, it can be observed that the single prediction models LSTM and GRU exhibit similar performance in evaluation metrics, with GRU having a slight advantage. This marginal superiority may stem from GRU’s fewer gating mechanisms, which result in a relatively reduced number of parameters and subsequently mitigate the risk of overfitting. The BiGRU network, incorporating a bidirectional information processing mechanism based on GRU, shows a significant performance improvement. Specifically, R2 increases by 23%, while RMSE and MAPE decrease by 0.037 and 9.44% respectively. The advantages of BiGRU over GRU are mainly attributed to its bidirectional information processing mechanism, which enables a more comprehensive understanding of the contextual meaning of sequences and enhances the ability to capture long-term and bidirectional dependencies.

Furthermore, the data in Table 2 reveal the superiority of combining models compared to single prediction models. For instance, compared to a single model, the evaluation metrics of the Ensemble Model are all superior. Compared to LSTM, DA-RNN achieves a 32.88% increase in R2, with a reduction of 0.054 and 15.78% in RMSE and MAPE, respectively. Similarly, the ensemble model CNN-BiLSTM-AM also demonstrates significant performance improvements, with a 40.68% increase in R2 and reductions in RMSE and MAPE reaching 0.062 and 22.7%, respectively. These results indicate that ensemble models can integrate the advantages of multiple models, compensate for their respective deficiencies, and thereby more comprehensively capture data features to improve overall prediction performance. It is noteworthy that among these six sets of experiments, the proposed CED-PSO-StockNet model performs the best, outperforming all baseline models. Specifically, the R2 value of the CED-PSO-StockNet model is closest to 1, reaching 0.9875, while its RMSE and MAPE are also the lowest, at 0.0598 and 6.24, respectively. This outstanding performance fully demonstrates the applicability and superiority of the CED-PSO-StockNet model in stock prediction tasks.

To comprehensively and deeply evaluate the generalization capability of our model in practical applications, this study specifically selects the representative dataset of Ping An Bank (000001.SZ) for testing and validation. As a crucial component of China’s financial industry, Ping An Bank’s dataset is not only massive but also covers various business scenarios and complex market changes, providing a rigorous and comprehensive test for the model’s generalization performance. On this basis, we conducted detailed and systematic comparative experiments between our model and the selected baseline models in this paper. The experimental results are shown in Table 5, from which it can be clearly observed that the CED-PSO-StockNet model demonstrates significant advantages in terms of R2, MAPE, and RMSE evaluation metrics, comprehensively outperforming other baseline models. This result not only verifies the rationality and advancement of the CED-PSO-StockNet model in theoretical design but also fully proves its excellent performance and wide applicability in practical applications. Figure 24 presents a comparison of the actual and predicted stock closing prices of Ping An Bank using the CED-PSO-StockNet model.

Table 5 Comprehensive performance of the model on Ping An Bank’s dataset.
Full size table
Fig. 24
figure 24

Comparison between the true and predicted closing prices of stocks in the CED-PSO-StockNet model.

Full size image

Conclusion

The paper proposes the CED-PSO-StockNet time series model to address the challenges of inaccurate stock prediction arising from high noise in stock data. This model innovatively integrates CEEMDAN decomposition and reconstruction techniques, component modeling, and an optimized PSO algorithm, significantly enhancing the accuracy of stock prediction. Through a series of ablation experiments and comparative analyses with benchmark models, the effectiveness of each component of our model is verified, demonstrating its superior performance over other baseline models in various evaluation metrics.

Despite the overall superiority of the CED-PSO-StockNet model, a thorough analysis of the comparison between actual and predicted stock closing prices reveals certain limitations. Notably, when stock prices reach their peaks, a non-negligible error persists between the predicted and actual values. This phenomenon suggests that the model’s predictive performance requires further improvement in handling extreme market volatility, especially during peak price levels. To enhance prediction accuracy, future research may consider incorporating more complex network structures or adopting advanced feature extraction methods to comprehensively capture latent information in stock data. Furthermore, integrating knowledge and techniques from other domains, such as market sentiment analysis and macroeconomic indicators, may also lead to breakthroughs in stock price prediction.

In practical applications, the CED-PSO-StockNet model holds immense potential value. Financial institutions can leverage this model for more accurate market trend prediction, enabling them to formulate more effective investment strategies. Investors can utilize the model’s prediction results to assist in timing stock purchases and sales, thereby reducing investment risks. Therefore, further optimizing and refining this model to improve its prediction accuracy in real-world scenarios holds significant practical implications and valuable insights.