Introduction

The indirect-drive approach to inertial confinement fusion (ICF) is to achieve ignition through the spherical compression of a deuterium–tritium (DT)-filled capsule driven by X-rays generated from the laser irradiation of a high-Z hohlraum1,2. In laser ICF experiments, hydrodynamic instability of the inner interface of the pellet during the implosion deceleration stage seriously affects the compression density and intensifies hot spot mixing, considering reducing the overall implosion performance3,4,5,6,7,8,9. ICF diagnostic systems are required to study the involvement of the Rayleigh–Taylor (R–T) instability in mixing and the transition to turbulence in the high-energy density regime. To effectively diagnose the growth of microstructures due to hydrodynamic instability, the diagnostic system must realize a high spatial resolution of < 3 μm in a 1-mm FOV10,11,12,13.

Several methods have been developed for high-resolution diagnosis of hydrodynamic instability in laser ICF. The Crystal Backlighter Imager (CBI) is a spherically-bent crystal imager at the National Ignition Facility (NIF) with a resolution limit of 7 μm14,15. However, further improvement of the resolution requires using a toroidal crystal, and the near-normal incidence requires an overly large diagnostic stereo angle, which will occupy the diagnostic optical path of other devices. A Fresnel zone plate (FZP)16,17,18,19 design has been calibrated at the NIF with a 9 keV zinc (Zn) backlighter, demonstrating a resolution of 2.3 ± 0.4 μm2. However, FZPs have severe chromatic aberration, and their high spatial resolution depends on the monochromaticity of the light source, so they have limited application to ICF and are more commonly used in synchrotron radiation.

Kirkpatrick–Baez (KB) microscopes are diagnostic devices based on grazing incidence reflection that can achieve a high resolution of 4–6 μm for a central field of view (FOV) of 200–300 μm20,21. The optimal resolution of a KB microscope is limited by spherical aberration, and the high-resolution FOV is limited by off-axis aberration. The KBA configuration can effectively correct the off-axis aberration and expand the FOV by adding a spherical mirror with the same curvature in each of the two-dimensional directions22. The quadratic surface effectively eliminates spherical aberration at points on the axis, a spatial resolution of < 2 μm has been achieved in the central FOV in the laboratory23. The advanced KB (AKB) configuration proposed by Kodama et al. achieved a spatial resolution of better than 3 mm in an FOV of 800 mm24. The AKB configuration comprises two pairs of hyperbolic and elliptical cylindrical mirrors, which satisfies the Abbe sine condition for high spatial resolution. However, this study used the 25–75% criterion for resolution calibration while subsequent studies on the AKB configuration focused on synchrotron radiation25,26.

In this study, we developed an AKB configuration based on the quadratic-aberration theory to realize an X-ray microscope with a large FOV and resolution of < 1 μm at the central FOV. The large FOV is realized by using a metal monolayer with a large angle bandwidth, and the initial positions of two quadratic surfaces are located by machining two ultra-smooth reflecting surfaces on a mirror base. To evaluate the performance, offline X-ray imaging and resolution calibration experiments were performed in the laboratory, and grid resolution and hydrodynamic instability tests were conducted at the Shenguang III (SG-III) prototype laser facility.

System design

Optical design

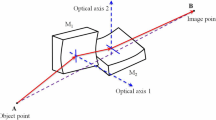
The AKB configuration focuses separately in the meridional and tangential directions with two reflections in a given direction. Figure 1 shows a schematic of the AKB microscope in one-dimensional, which is based on hyperbolic and elliptical mirrors. The object point is located at the right focus F3 of the hyperbolic surface. The rays emitted by the object point first pass through the hyperbolic surface to form a virtual image at the common focus F2 of the hyperbolic and elliptical surfaces. The actual rays are reflected by the hyperbolic surface, and they finally converge at the right focus F1 of the elliptical surface to form a real image. Because the two surfaces are quadratic, the central object point F3 satisfies the Fermat principle, so the ideal image ultimately appears there.

Fig. 1
figure 1

Schematic of the AKB microscope.

Full size image

Suppose that the angle between the incident main ray F3M1 and optical axis is θ3 and that the angles between the main ray and optical axis after one and two reflections are θ2 and θ1, respectively. Then, M1 and M2 are the central positions of the two mirrors, the first and second theoretical angles of incidence are θ10 and θ20, and the magnification of the system is M. Based on geometric optics and conics properties, the following can be deduced using the law of reflection:

$$\left\{\begin{array}{l}{\theta }_{1}=\frac{2\left({\theta }_{10}+{\theta }_{20}\right)}{1+M}\\ {\theta}_{2}=\frac{2\left(M{\theta }_{10}-{\theta}_{20}\right)}{1+M}\\ {\theta }_{3}=\frac{2M\left({\theta }_{10}+{\theta }_{20}\right)}{1+M}\end{array}\right.$$
(1)

Equation (1) can be employed to determine the angles between the main ray and optical axis. For one hyperbola, these are easily obtained from the law of reflection and the geometric relations of triangles:

$$\left\{\begin{array}{l}{a}_{1}=\frac{{u}_{10}}{2}\left({M}_{h}-1\right)\\ {b}_{1}=\frac{{u}_{10}}{2}\sqrt{{M}_{h}^{2}-\left(2cos2{\theta }_{10}+1\right){M}_{h}+2}\end{array}\right.$$
(2)

where u10 is the object distance, Mh is the magnification of the hyperbolic mirror, a1 is the semi-real axis of the hyperbola, and b1 is the semi-imaginary axis of the hyperbola. The same method can be used to calculate the parameters of an elliptical surface:

$$\left\{\begin{array}{l}{u}_{20}=d+{M}_{h}{u}_{10}\\ {a}_{2}=\frac{{u}_{20}}{2}\left({M}_{e}+1\right)\\ {b}_{2}=\frac{{u}_{20}}{2}\sqrt{2\left(1-cos2{\theta }_{20}\right){M}_{e}}\\ M={M}_{e}{M}_{h}\end{array}\right.$$
(3)

where u20 is the object distance of the elliptical mirror, Me is the magnification of the elliptical mirror, M is the magnification of the optical system, a2 is the semi-major axis of the ellipse, and b2 is the semi-minor axis of the ellipse. With the above equations, if we are given the object distance u10, magnification M, and grazing incident angle θ10 and θ20, then the initial structural parameters of the hyperbolic and elliptical mirrors can be obtained. Because one-dimensional direction mirrors can only achieve one-dimensional focusing, the meridional and sagittal directions need to be calculated independently.

For the conventional KB configuration, the mirror length acts as an aperture diaphragm, and the grazing incidence angle bandwidth acts as a FOV diaphragm. However, for the AKB configuration of the two-mirror structure, the distance between the two reflecting surfaces separates the FOV diaphragm from the aperture diaphragm. As shown in Fig. 2a, the schematic diagram of the optical path over a certain range of central FOV is given as FOVcen. The hyperbolic mirror predominates in limiting the range of the rays passing through the system and acts as the aperture diaphragm. Elliptical mirror acts as FOV diaphragm and determines the FOV angle σ of the system. For marginal FOV, the role of the apertures and FOV diaphragms of the two mirrors becomes complicated. In order to analyze the effective FOV of the system we need to solve for the variation of the geometric solid angle with the FOV by using the ray-tracing procedure.

Fig. 2
figure 2

Schematic of the FOV diaphragm and angular bandwidth of an AKB microscope. (a) Optical path diagram of the elliptical mirror as a FOV diaphragm, (b) schematic diagram of the angular bandwidth optical path of AKB microscope.

Full size image

The angular bandwidth of an optical system is determined by the superimposed effects of aperture and FOV. As shown in Fig. 2b, considering the edge rays reflection at full aperture and full FOV of the system. The angle between the two mirrors is κ. The positive and negative FOV edge rays are reflected from the hyperbolic edge and incident on the edge of the elliptical mirror. At this point the grazing incidence angle of the elliptical mirror ranges from θ2min to θ2max. Thus, the geometric angular bandwidth of the system is ∆θ2. The following expression can be given based on the geometric relationship:

$$\left\{\begin{array}{l}{u}_{10}{\theta }_{10}+q=\left({u}_{10}-\frac{{d}_{1}}{2}\right)*\left(\kappa -{\theta }_{2\text{min}} \right)\\ {u}_{10}{\theta }_{10}-q=\left({u}_{10}+\frac{{d}_{1}}{2}\right)*\left(\kappa -{\theta }_{2\text{max}} \right)\\ {\Delta\theta }_{2}={\theta }_{2max}-{\theta }_{2\text{min}} \end{array}\right.$$
(4)

where q is the half-FOV and d1 is the hyperbolic mirror length. The geometric angular bandwidth in the FOV of 2q can be estimated by the above method, and the angular bandwidth of the film coated on the mirror surface needs to be matched with ∆θ2.

To facilitate X-ray plasma diagnosis of high-power laser equipment, the working energy point of the microscope was set to 8.0 keV (corresponding to the Cu Ka1 line) to ensure a large observation depth. To consider the influence of the detector pixel size on the spatial resolution, the magnification of the microscope was designed at 20.0 to 25.0 times. Based on the experimental conditions of the laser facility and the requirements for diagnosis hydrodynamic instability, we set the initial parameters of the microscope to an object distance of 200 mm and central incident angle of 0.45° for the hyperbolic and elliptical mirrors. Specifically, the hyperbolic magnification Mh is 2 times in both the sagittal and meridional directions, and the elliptical magnification Me is 12.5 and 10.65 times, respectively. These parameters were employed to calculate a geometric solid angle of 1.2 × 10−7 sr. Table 1 presents further details on the optical parameters.

Table 1 Parameters of the AKB Microscope.
Full size table

Simulation

We have compiled ray-tracing program for the AKB microscope, and we can simulate the optical performance of the system under full-FOV conditions. For the same object distance of 200 mm, grazing incidence angle of 0.45° and magnification of 25, the resolution curves of KB configuration, elliptical KB configuration and AKB configuration are shown in Fig. 3a. Due to the limitations of spherical and off-axis aberrations, KB microscopes are unable to achieve high resolution in the full-FOV. The ellipsoidal KB guarantees high resolution in the central FOV, but the high-resolution area is small. A simulation of the resolution of the AKB microscope in the two-dimensional direction is shown in Fig. 3b. It can be seen that a resolution better than 1.3 μm can be achieved in 1-mm FOV. As a result of the greater magnification, the resolution in meridional direction will be better than in sagittal direction.

Fig. 3
figure 3

Resolution curves of KB configuration, elliptical KB configuration and AKB configuration. (a) The resolution simulations of KB configuration, elliptical KB configuration and AKB configuration, (b) resolution of the AKB configuration in two-dimensional direction.

Full size image

For the AKB microscope, we adopted a Pt monolayer design with flat response characteristics, and each working surface has a grazing incident angle of 0.45°. The reflectivity–angle curve can be obtained in ray-tracing simulations. The corresponding distribution can be obtained based on the film structure and solid angle for geometric light collection. As shown in Fig. 4a, the reflective efficiency of the AKB microscope was symmetric in the meridian and sagittal directions with a peak reflectance of 39% at the center of the FOV and reflectance of 28% at the edge of the FOV. The incident angle and actual object distance corresponding to different positions in the object FOV are slightly different from the theoretical calculation, so the geometric solid angle for light collection of the full-FOV should be calculated to determine the overall response efficiency. Because part of the rays at the edge of the FOV fail to enter the elliptical mirror after being reflected by the hyperbolic mirror, this causes a loss of the solid angle for light collection. Thus, we need to normalize the amount of ray passing through. The light collection capacities can be calculated in two dimensions and multiplied to obtain the geometric solid angle, as shown in Fig. 4b. For a FOV of ± 500 μm, the geometric solid angle varies from 3.3 × 10−8 to 1.2 × 10−7sr, and the response distribution of the microscope can be obtained by multiplying the reflectivity distribution of the system, as shown in Fig. 4c. The peak response efficiency of the AKB microscope was obtained at 4.7 × 10−8 sr. The angular bandwidth of the system is 0.28°in meridional direction and 0.26°in sagittal direction, which can have a reflectivity of 70% in a 600-µm FOV and a reflectivity of 31% in a 1-mm FOV.

Fig. 4
figure 4

Reflective strength of the AKB microscope in ray-tracing simulations. (a) efficiency, (b) geometric solid angle, and (c) response efficiency of the AKB microscope.

Full size image

Results and methods

Laboratory resolution testing

Figure 5 shows the experimental arrangement of the AKB microscope in the X-ray imaging laboratory. The high-precision electronic control displacement table has an adjustment accuracy of 10 μm. The reflector substrate was made of Si, and the effective area of the hyperbolic and elliptical surfaces was 2 × 10 mm. Through surface characterization with a phase-shift interference microscope, the average values of the shape error, slope error, and roughness were determined to be 0.694 nm, 0.158 µrad, and 0.179 nm, respectively. The non-central working area of the mirror was in contact with a pair of high-precision prisms with tightly controlled dimensions and inclination that were fixed by rear reclining. The prisms provided the initial spatial attitude of the mirrors to guarantee that the vector height of the working area of the mirror matched the theoretically calculated value from the conic curve. The parallelism between the optical axis of the microscope and the axis of the experimental platform was judged by a position sensor. The six-axis precision electronic control adjustment frame was used to carry the microscope and adjust the two axes to coincide with a pitch and roll alignment accuracy of ~ 0.5 µrad. The center of the image point on the image surface was always near the optical axis, and the position of the charge-coupled device (CCD) or framing camera was easily determined by laser indication.

Fig. 5
figure 5

Experimental arrangement of the AKB microscope.

Full size image

The target material of the X-ray backlight was a Cu anode with Kα1 characteristic line emission at 8.0 keV. The focal spot size of the backlight was 1 × 1 mm2. A gold grid with a diameter of 2 mm and a marked center was placed on the object, and the number of periods varied from 150 to 2000 mesh grids. A mixed mesh grid was used to mark the center of the FOV, and high-mesh grids were used to test the spatial resolution of the system. Meshes were replaced under the supervision of two high-precision CCDs from different directions, and the replacement accuracy was < 5 μm, which corresponded to half the line width of the mesh. A Hard X-ray scintillation detector was used as the image recording equipment with a pixel size of 4.54 μm and maximum acquisition area for a single image of 12.5 mm × 10 mm. A 5-m-long helium tube with a concentration of more than 90% was placed in the optical path to reduce X-ray attenuation and improve the air environment and signal-to-noise ratio.

Resolution calibration

Figure 6 shows X-ray grid backlight images and the results of the laboratory test to determine the resolution of the AKB microscope. The spatial resolution was calibrated by using 10–90% of the grid shadow edge27. The 1000-mesh Au grid shown in Fig. 6a was imaged at 40 kV by using a 30-mA continuous X-ray source with an exposure time of 20 min. The grid period was ~ 25 μm, the grid width was ~ 6 μm, and the thickness was ~ 20 μm. The initial position of the grid was set to (0, 0), which was centered on the marked point. The grid was moved to the positions of (+ 250, 0), (+ 250, + 250), (0, + 250), (− 250, + 250), (− 250, 0), (− 250, − 250), (0, − 250), and (− 250, − 250) to obtain mesh imaging results for a FOV of 1 mm. For each move to a different set of coordinates, the X-ray backlight and CCD needed to be moved proportionally and simultaneously to ensure that the edges of the grid were also illuminated. Figure 6a shows the imaging result of the 1000-mesh Au grid within a FOV of ± 500 μm comprising nine pictures. The red circle is the positioning center of the image stitching, 75 μm away from the center of the FOV. A clear and sharp grid line can be observed at the central FOV that gradually blurred toward the edge, and a good resolution was maintained throughout the FOV. These results showed that a spatial resolution of < 4.5 μm could be achieved even at the edge of the FOV.

The high spatial resolution of the microscope can be characterized by using a high mesh grid. Figure 6b shows the backlit imaging results of a 1000-mesh grid and intensity profiles in the central 200-µm FOV in the two-dimensional direction. Figure 6c,d show the measurements of black and red lines used to obtain the spatial resolution of the entire FOV in two directions. Specifically, we perform rectangular integration on the single direction intensity profiles and then use Boltzmann function fitting to obtain the edge response. A polynomial fit was performed to estimate the resolution curve. The optimal spatial resolution of the AKB microscope reached ~ 0.53 and ~ 0.40 μm in the meridional and sagittal directions, respectively. The resolution was better in the sagittal direction than in the meridional direction due to greater magnification, which is consistent with the trend of the simulation curves. The AKB microscope had a spatial resolution of < 1.5 μm in a 300-µm FOV and < 4.5 μm in a 1-mm FOV. Compared with conventional KB diagnostic equipment, the AKB microscope has a much larger high-resolution area.

Fig. 6
figure 6

Grid imaging results of the AKB microscope in laboratory tests. (a) 1000-mesh grid imaging of a 1-mm FOV; (b) 1000-mesh grid imaging of the central FOV; Spatial resolutions of the FOV in the (c) meridional and (d) sagittal directions measured using the 10–90% criterion.

Full size image

Online experimental arrangement

The AKB microscope was applied in the X-ray radiography of the R–T instabilities growth on the SG-III prototype laser facility. Two types of targets were used: an Au mesh, and an R–T perturbation target. First, grid backlighting experiments were performed on the facility with the aim of testing the static resolving power of the microscope and locating the recording equipment which is a scintillation detector. The imaging grid was employed with a position sensor to locate the center of the chamber. A diaphragm hole was placed in front of the diagnostic module to effectively shield stray light from outside the FOV while a 100-µm-thick Kapton layer and 200-µm-thick polycarbonate layer were installed to shield against debris. Further, by adjusting the laser parameters and replacing the target, the study of the R–T instabilities can be conducted.

In the experiments, the V backlighter was driven by four laser beams from the chamber bottom, and other four laser beams directly drive the planar CH-Al target with the preset perturbations on the Al surface. The pulse width of the backlighter and driving laser are 0.5 ns and 1 ns. Each laser beam is a square pulse with 800 J of energy. The experimental optical path layout is shown in Fig. 7, the driving laser is injected from the top. The R–T perturbation target mainly includes two CH ablator layers, the perturbation samples and the CH foam. The target is wrapped in an Al shielding case. The diagnostic direction of the microscope is perpendicular to the perturbation growth plane, and the center of the FOV can be calculated from the shock wave velocity.

Fig. 7
figure 7

Online experimental arrangement of the laser facility.

Full size image

Imaging results at the SG-III prototype

The time integral images of the Au mesh and the R-T instability were recorded with a pixel size of 13.5 μm. Figure 8a shows the 1000-mesh Au grid imaging results with the V backlight, and Fig. 8b shows the obtained spatial resolution. The backlight impingement point was slightly off-center with a resolution of up to 1 μm for the central FOV and a resolution of < 3 μm for a ± 250 μm FOV. The resolution at the edge of the FOV was slightly reduced compared to the laboratory results. Figure 8c shows the imaging results for the R–T sinusoidal perturbation target with the V backlight and the spikes and protrusions of the perturbed interface can be observed. For the reduction of resolution at the laser facility, we believe the reason for this is that a shock wave with a velocity of 40 km/s produces a temporal blur of about 20 μm for 0.5-ns backlight time, and this effect can be effectively reduced by using the framing camera. Using a 10-ps time-resolved framing camera can reduce temporal blur to less than 1 μm under current conditions. However, effective diagnosis of hydrodynamic fine structure also requires backlight imaging with a certain contrast. It is not the case that the shorter the gating time the better the resolution, this needs to be considered in conjunction with the following factors. The specific value of the temporal blur that can be reduced needs to be combined with hydrodynamic model simulations, plasma backlighting efficiency, mirror reflection efficiency, and quantum efficiency of the recording device.

Fig. 8
figure 8

Imaging results of the laser facility with the AKB microscope. (a) 1000-mesh grid imaging of the central FOV, (b) spatial resolution using the 10–90% criterion, and (c) imaging results for an R–T sinusoidal perturbation target with V backlight.

Full size image

Conclusion

We developed an AKB microscope that is suitable for diagnosing hydrodynamic instability in ICF research. The large FOV and high resolution of < 1 μm at the central FOV are effective for diagnosing the fine structure of cusps and bubbles during ICF implosions. Moreover, the AKB microscope has a wide energy spectrum of ~ 8.0 keV. Laboratory results showed that the AKB microscope could achieve an optimal resolution of ~ 0.53 and ~ 0.40 μm in the meridional and sagittal directions, respectively, and spatial resolutions of < 1.5 μm within a 300-µm FOV and < 4.5 μm in a 1-mm FOV. The microscope was used in studying R–T instabilities in a planar geometry at the SG-III prototype laser facility and successfully observing the hydrodynamic instability of a sinusoidal perturbation target during implosion.