Introduction

Honeycomb, honeycomb-like structures, are widely used in industry and daily life due to their lightweight and high specific energy absorption characteristics. Honeycomb structures have appeared in landing gear legs of spacecraft, aircraft skin, anti climbing energy absorption components of high-speed rail, vehicle body components, and hull structures1,2. With the development of the technology, more and more advanced porous structures have emerged, such as lattice structured materials, negative poisson’s ratio materials, zero poisson’s ratio materials, etc.3,4, which have good mechanical performance. In recent years, the research on three period minimal curved surface structures (TPMS) has become a hot topic, and this structure has also provided us with new ideas for preparing shock absorption materials for nuclear equipment5,6.

To ensure the safety of nuclear equipment, impact limiters are installed at both ends of the transportation cask. The interior of the devices is made of energy absorbing materials, and the common energy absorbing material is wood. Wood has good energy absorbing properties7,8, but there are also defects. Due to the texture of wood, the mechanical properties are differences in three directions, which makes it difficult to ensure the internal safety of the transportation cask. In limited design space, the mechanical properties of wood must reach a certain strength to make it safe enough, so the selection of wood is particularly strict and difficult9,10, which limits its application in nuclear equipment shock absorption filling materials. PU foam and honeycomb aluminum are also used as shock absorption filler materials for nuclear equipment. However, PU foam and honeycomb aluminum are subjected to the plateau stress11,12, so they also need larger dimensions. Due to the limited preparation process, foam aluminum is difficult to homogenize13,14, which still needs further research. New types of 3D printing materials, lattice materials, and other metal porous structures have also been extensively studied, but limited by the preparation process, they are difficult to produce in large size15,16. As a shock-absorbing filling material for nuclear equipment transportation casks, the key point of its preparation and research is to ensure as much as possible the similarity of mechanical properties in 2 or 3 directions (reducing the design and layout) and stable energy absorption (energy absorption protection effect). In addition, easy preparation, large size, and low price are also key considerations.

It is necessary to obtain the constitutive relationship of a new material through experimental or theoretical analysis methods, and studying its constitutive relationship can reduce the cost of testing. In 1960, Alexander17first established a kinematic deformation field when thin-walled tubes undergo axisymmetric progressive expansion and contraction deformation, proposed a circular tube axial compression symmetric deformation mode, and established a theoretical model to predict the energy absorption of axial circular ring deformation mode in metal circular tubes. Abramowicz18 and Wierzbicki19 improved the Alexander model and improved the theoretical prediction accuracy of the axial pressure characteristics of thin-walled circular tubes. Wierzbicki and Abramowicz20 established a superfolding element model to analyze the axial compression behavior of rectangular thin-walled tubes, and established the superfolding element theory. Chen and Wierzbicki proposed a simplified theoretical model of superfolded units21. For the study of energy absorption in single and multiple cell tubes, a combination of experimental, simulation, and theoretical methods is mostly used. Eyvazian22 proposed an improved simplified superfolding element theoretical solution under axial load conditions. The theoretical solution depends on the number of plastic hinges, wall thickness, length of the structure, and material flow stress. The comparison between the theoretical solution and experimental results shows that corrugated pipes have good energy absorption performance. With the development, there are more and more means to study porous materials, and more and more mechanisms and methods have been proposed.

Lan23 developed an analytical model to investigate the in-plane mechanical properties of a thin-walled honeycomb structure. Nonlinear constitutive relations of honeycombs are presented based on in-plane large deformation analysis of a beam. Zhao24 introduced a detailed finite element model to analyze the mechanical response and deformation mechanism of curved honeycombs and then verified through experiments using a specially designed set-up. Qi25 aimed to investigate the in-plane dynamic crushing responses of the novel REC honeycombs through numerical simulations and theoretical analyses. The theoretical predictions were in good agreement with the numerical simulation results. Niu26 established the in-plane mechanical properties and energy absorption performance of bio-honeycombs under different impact speeds, finite element (FE) models and verified by empirical formulas and current experiments. The results indicate that the bio-honeycombs outperform the Hex in terms of energy absorption capacity, and the nominal stress–strain curves of the bio-honeycombs show two prominent stages under quasi-static and mid-impact.

The structural morphology of materials has a significant impact on their mechanical properties, and optimizing the material structure to obtain better mechanical properties is also the pursuit of many scholars. Studying the influence of structural parameters on the deformation mode of thin-walled components can lead to the design of high-performance energy absorbing components. A large number of scholars have conducted extensive research on the energy absorption performance of thin-walled structures27,28. Metal thin-walled pipes can dissipate a large amount of impact kinetic energy through plastic deformation, fracture and other damage forms when subjected to impact loads, making them a very effective energy absorption device29. Scholars have shown that the geometric characteristics and mechanical properties of eight types of honeycomb structures, including hexagonal, triangular, regular, circular, concave hexagonal, double V-shaped, chiral, and star structures, are not suitable for all application scenarios. Some special application scenarios urgently require materials with higher stiffness/strength, better energy absorption capacity, and a wider poisson’s ratio range. On the basis of these classic honeycomb materials, more advanced design solutions are constantly being proposed and developed. Yu30 proposed a novel 3D negative poisson’s ratio material design method based on the coupling effect of tension and torsion. The concept of gradient is to construct some sub cells with different properties, and the assembly of all sub cells forms a complete gradient changing honeycomb structure. Research has shown that gradient honeycomb has better mechanical properties than uniform honeycomb, so the introduction of gradient design in honeycomb has attracted widespread attention. However, the research on gradient structural materials is still in the laboratory stage, and there are still significant limitations in their application in engineering. Researchers have proposed many new structures and new morphologies of porous materials, all of which have certain energy absorption capabilities. However, the emergence of new structures mostly uses 3D printing preparation, which increases the difficulty of application. For the shock absorption filling of nuclear equipment transportation casks, it is difficult to adopt the above structures.

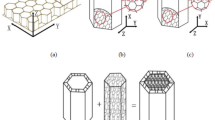
The orthogonal trapezoidal aluminum honeycomb prepared in this paper is a bi-directional material with a structure similar in the Y and Z directions. When a bi-directional structure is applied as a energy-absorbing filling material in nuclear equipment impact limiters, a simple design can protect the safety of the transport cask in all directions (each direction can be carried by the material in the Y or Z direction), as shown in Fig. 1.

Fig. 1
figure 1

Application of orthogonal trapezoidal honeycomb aluminum in nuclear equipment.

Full size image

The arrangement of this paper is as follows: Firstly, two different structures of orthogonal trapezoidal aluminum honeycomb were prepared using rolling and welding methods. Then, the mechanical properties of the material were studied using quasi-static and dynamic loading methods. Through simulation, the experimental process was compared to obtain the performance effects of the material at different pore sizes and loading rates. The energy absorption of the material after loading was studied through theoretical analysis and compared with the energy absorption results obtained during the experimental process. Based on the experimental results, a C-S dynamic constitutive relationship based on strain rate was derived. Finally, the feasibility of using orthogonal trapezoidal aluminum honeycomb as a shock absorption filling material was characterized by comparing with wood.

Experiments

Specimen manufactured

This paper manufactured two materials with different pore sizes, one is a 4 mm trapezoidal hole (with a trapezoidal upper edge length of 4 mm and lower edge length of 8 mm), and the other is a 3 mm trapezoidal hole (with a trapezoidal upper edge length of 3 mm and lower edge length of 6 mm). The thickness of the plate layer t0 is 0.3 mm, and the overall height is about 50 × 50 × 50 mm.

The preparation process of the material is as follows: Firstly, the aluminum plate is rolled with rollers to form a corrugated plate. Different roller shaped corrugated aluminum plates have different hole shapes, and the other plate is cut for backup. Secondly, place a flat plate and a corrugated plate in a staggered manner in the direction of 0/90°, and apply solder (approximately 0.2 mm thickness) in the middle. Finally, place it in the furnace for heating, with a heating temperature controlled at 600 ℃ and a duration of 100 s. To prevent warping and deformation during the heating process, clamping fixtures will be installed at both ends of the material, and the maximum preparation size of the material in the furnace can reach 1000 × 1000 × 1000 mm. Finally, a complete large-size orthogonal trapezoidal aluminum honeycomb is formed, and the material is insulated and pressurized. Then, a 50 × 50 × 50 mm sample is cut using wire cutting method (as shown in Fig. 2).

Fig. 2
figure 2

Preparation process of orthogonal trapezoidal aluminum honeycomb.

Full size image

WOTAH is selected from 3003 aluminum alloy, and the relevant parameters are derived from the Ref31.. The lateral sides of WOTAH were symmetrical (Y and Z directions), and a quasi-static compression test was performed on one lateral direction (Fig. 3).

More details we can refer paper32. In this study, 2 materials with different cell thickness/cell size ratios were prepared, the stress-strain curves of the materials were obtained, and the deformation process of the materials was analyzed. When the WOTAH is deformed by compression, the energy absorption per volume (SEAV) is represented by W1. The calculation Formula (1) of SEAVis shown as follows33,34.

$$W_{1} = \int\limits_{0}^{\varepsilon } {\sigma {\text{d}}\varepsilon } .$$
(1)

σ-compressive stress, ε-strain.

Fig. 3
figure 3

Material structure and loading direction.

Full size image

Test procedure

Static compression

For the compression performance testing of materials under quasi-static conditions, a universal compression testing machine is used for the experiment. The maximum pressure of the compression test device can reach 3000 kN, using the method of loading at the lower end and fixing at the upper end. The testing speed is 5 mm/min, when the compression reaches 70% of the material height, it stops. The loading direction of the material is in the Y or Z direction. The data obtained from the test is automatically recorded by the program, and the engineering stress and strain data is automatically saved in the hard drive. The quasi-static compression test is illustrated in Fig. 4.

Fig. 4
figure 4

Quasi-static compression experiment.

Full size image

Dynamic compression

The impact test was carried out on a Hopkinson compression bar testing device (as shown in Fig. 5), which can study the mechanical properties of materials under high-speed loading. The system can test and convert stress, strain, strain rate, strain energy, etc. The speed testing range is 0.5–300 m/s, and the accuracy is within 1%. The maximum rod diameter can reach ø 100 mm. The WOTAH samples used in this section were tested at high strain rates of 338/s, 269.4/s, 212.8/s, and 149.2/s (corresponding to initial velocities of 16.9 m/s, 13.47 m/s, 10.64 m/s, and 7.46 m/s, respectively).

Fig. 5
figure 5

Hopkinson compression bar test equipment.

Full size image

Simulation

The base material of sample is aluminum, and the orthogonal trapezoidal aluminum honeycomb material parameters used in the simulation are set to the default, mainly including density, elastic modulus, poisson’s ratio, yield stress, and tangent stress35. The upper and lower pressure plates were set to structural steel plates, and the parameters of the stainless steel plate were selected by the system36. To speed up the calculation and reduce the use of computer resources as much as possible, the WOTAH and the upper and lower pressure plates were set to different mesh sizes, as can be seen from Ref.37. When the mesh size to cell size ratio was 0.125, the simulation agreed well with the experimental results; thus, the mesh size of the WOTAH can be obtained from this formula. The mesh sizes of the upper and lower pressure plates were set to 2 mm (Fig. 6). The contact form of the WOTAH and the upper and lower pressure plates was set to “bonded,” and the WOTAH was set to “material body self-contact”; the type was “frictional,” and the static friction was set to 0.3; the dynamic friction was set to 0.238,39. For statics simulation, a smaller speed should be loaded. However, a too small loading speed will result in the consumption of a large amount of calculation time. According to Ref.40. the quasi-static condition can be satisfied when the loading speed is less than 2 m/s. The lower plate was completely fixed, and the upper pressure plate was assigned a speed of 500 mm/s to conduct simulation analysis.

The dynamic simulation adopts the Ls-dyna module, which sets the initial speed loading. The loading speed is the same as the experiment, and the loading time is set to 0.05 s. Static loading does not consider the strain rate effect of the material, while dynamic loading needs to be considered1.

Fig. 6
figure 6

Mesh contour.

Full size image

Results and discussion

Static test results

By observing the deformation process of the small hole material in Fig. 7, it can be seen that the material gradually compresses and deforms until densification. Observing the deformation of the material during the experiment, the top of the material first deformed, twisted, and tilted towards one end, which corresponded to the first peak point of the curve. Afterwards, the material buckled and tilted towards one end, causing each hole to compress and shrink. At this point, the curve fluctuated up and down. However, the fluctuation range was relatively small and stable within the range of 20–25 MPa. Afterwards, each hole was further compressed and compacted, which corresponded to the rapid rise stage of the curve.

Observing the deformation process of the material under simulation is relatively similar to the experimental results. Comparing the curves of the experiment and simulation, it can be seen that the curves of the two are also relatively similar. The initial peak stress is 33.5 MPa, and then the stress decreases and stabilizes between 20 and 25 MPa. The effective strain is about 0.5, then the stress rises rapidly. Observing the energy absorption curve of the material, the energy absorption gradually increases within the strain range of 0-0.6, indicating that within the effective strain range, the material gradually deforms and absorbs energy. The effective energy absorption of the material at 0.5 strain can reach 11.3 MJ/m3.

Fig. 7
figure 7

The result of small hole (quasi-static).

Full size image

Observing the deformation process of large hole materials (Fig. 8), it can be seen that the deformation process of the material is similar to the small hole materials. However, the deformation of the large hole material first occurs at the bottom of the material, and the material also twists and tilts towards one end, which corresponds to the first peak point of the curve. Afterwards, the material buckles and tilts towards one end, causing each hole to compress and shrink. At this point, the curve fluctuates up and down. However, the fluctuation range is more stable than that of small hole materials, ranging from about 11–14 MPa. Subsequently, each hole is further compressed and compacted, which corresponds to the rapid rise stage of the curve.

The experimental results showed tilting deformation, and the simulation process involved outward expansion and compression. There were slight differences between the experimental and simulation results, mainly due to the fact that the simulation model is idealized and has no defects, while the experimental model has local defects, which will cause deformation at the weakest point first, leading to tilting buckling. However, the experimental and simulated stress and energy absorption curves are relatively similar. Comparing the curves of the experiment and simulation, it can be seen that the curves of the two are relatively similar. The initial peak stress is 26.5 MPa, and then the stress decreases and stabilizes between 11 and 14 MPa. The effective strain is about 0.5, then the stress rises rapidly. Observing the energy absorption curve of the material, the energy absorption gradually increases within the strain range of 0-0.6, indicating that within the effective strain range, the material gradually deforms and absorbs energy. The effective energy absorption of the material at 0.5 strain is about 8.2 MJ/m3.

Through the comparison of mechanical properties of large and small hole materials under static conditions, it was found that the deformation curve of large hole materials is smoother and the peak stress is lower than that of small hole materials. However, the energy absorption performance of small hole materials is better than that of larger hole materials.

Fig. 8
figure 8

The result of big hole (quasi-static).

Full size image

Dynamic test results

Observing the dynamic deformation results of the small hole material in Fig. 9, the deformation of the material under high-speed impact is very small. For the large hole material, the deformation is from 50 mm to about 48.6 mm under a loading rate of 149.2/s, from 50 mm to about 47.9 mm under a loading rate of 212.8/s, from 50 mm to about 46.3 mm under a loading rate of 269.4/s, and from 50 mm to about 44.8 mm under a loading rate of 338/s. At a rate of 149.2/s, the small hole material undergoes deformation from 50 mm to approximately 48.7 mm, at a rate of 212.8/s, the material undergoes deformation from 50 mm to approximately 48 mm, at a rate of 269.4/s, the material undergoes deformation from 50 mm to approximately 47 mm, and at a rate of 338/s, the material undergoes deformation from 50 mm to approximately 45.9 mm. Under the same hole size material, the bigger the strain rate, the greater the impact on the material and the huger the material deformation. At the same loading rate, the deformation of macroporous materials is greater than that of microporous materials, indicating that macroporous materials are more prone to deformation. Observing the results of material deformation, for loading at a strain rate of 149.2/s, the deformation of the sample after impact is very small. For loading at higher strain rates, the deformation of the material significantly increases, and the energy of the Hopkinson bar is absorbed by the material deformation. Observing the deformation of the material, it is not a layer by layer folding deformation mode. Under high strain rates, the material exhibits a tilted deformation mode, which can also be demonstrated through simulation of the deformation process. Through the simulation process, it can also be seen that the deformation of the material in the simulation is relatively similar to that in the experiment. Under the strain rate loading of 149.2/s, the deformation of the material is very small. For larger strain rate loading, the deformation of the material is relatively large, and there is a phenomenon of buckling tilt in the deformation of the material. From the force flow line of the material, it can also be seen that the force flow line of the material is not always perpendicular to the material, and there will be a certain tilt, this indicates that the material does not undergo vertical deformation but rather inclined deformation. From the simulation results, it can also be seen that when the material is the same and the loading rate is different, the deformation amount of the material is different. The larger the strain rate, the greater the deformation. When the materials are different and the loading rate is the same, the deformation of the material is also different, and the larger the holes, the larger the deformation of the material.

Fig. 9
figure 9

Comparison of deformation results of materials with big and small hole.

Full size image

Comparing the stress and energy absorption of materials under different loading rates (Fig. 10), it can be seen that for small hole materials, the stress curves of materials under different strain rates are different. Under four sets of high-speed strain rate impacts, the materials all exhibit two segmented curves, namely the elastic stage and the strengthening stage. However, the initial peak stress points of the materials are different. At a loading rate of 149.2/s, the initial peak stress is about 19.5 MPa, afterwards, the material stress continued to rise until it stopped at 29 MPa. There is an error of stress between simulation and experimental results. Although the stress under simulation is also a two-stage curve, there is no very clear boundary between the two curves.

At a loading rate of 212.8/s, the initial peak stress is about 30.5 MPa, while the simulated initial peak stress is about 36.5 MPa. Afterwards, the material stress continues to rise until it stops at 40 MPa. There is a certain error between the simulated stress and the test results, and the simulated stress is also a two-stage curve. However, there is a slight difference between the latter half of the curve and the test, and the climbing rate slows down. At a loading rate of 269.4/s, the initial peak stress is about 39.5 MPa, while the simulated initial peak stress is about 35.5 MPa. Afterwards, the material stress continues to rise until it stops at 44 MPa. There is a certain error between the stress under simulation and the experimental results, and the first half of the curve under simulation rises slowly compared to the experimental results. At a loading rate of 338/s, the initial peak stress is about 47.5 MPa, while the simulated initial peak stress is about 40.5 MPa. Afterwards, the material stress slowly increases until it stops at 49 MPa. There is a certain error between the simulated stress and the test results. The stress curve under the test is a two segment curve with fluctuating rise, while the stress curve under the simulation is relatively flat.

For the energy absorption under simulation and experiment, the energy absorption of the material is determined by the initial loading speed, and under effective strain, the material can absorb load impacts at different loading rates. The stress and strain of the material vary at different loading rates, indicating that it is a strain rate dependent material. The situation of large hole materials under high rate stress loading is similar to that of small hole materials, and we will not expand on the description here. However, for the loading of 338/s strain rate, the curve of the second stage of large hole materials is relatively flat and there is no obvious upward trend, indicating that the material enters a stable plastic deformation stage at this strain rate.

Compared with small hole materials, the initial peak stress of large hole materials under strain rate loading of 149.2/s is about 21 MPa, and then the material stress continues to rise until it stops at 29 MPa. The initial peak stress under strain rate loading of 212.8/s is about 31 MPa, and then the material stress continues to rise until it stops at 44 MPa. The initial peak stress under strain rate loading of 269.4/s is about 32 MPa, and then the material stress continues to rise until it stops at 42 MPa. The initial peak stress under 338/s strain rate loading is about 48 MPa, and then the material stress slowly fluctuates, about 48 MPa. This indicates that materials with different hole sizes exhibit different performance under the same or different external loads, and the material structure can affect the mechanical properties of the material.

Fig. 10
figure 10

Stress-strain and energy absorption curves under different loading rates.

Full size image

Derivation of material strain rate effect

From the experimental curve, it can be seen that the material exhibits different properties under different loading rates, indicating a strong rate correlation. The mechanical properties of different structural materials under different loading rates can be obtained through the experimental results, and the material parameters under the C-S (Cowper-Symond) constitutive law can be fitted using the least squares method.

In this section, the material properties are set to aluminum, and the relevant data will not be repeated here. The C-S constitutive model is represented by Formula (2), and the dynamic yield stress:

$${\sigma _{\text{d}}}={\sigma _{\text{y}}}{(1+\varepsilon ^{\prime}/D)^{(1/{\text{P}})}}$$
(2)

σd is dynamic yield stress, σyis the static yield stress, εʹ is the strain rate, and D and P are constants41. By calculation, D = 25.97 and P = 1.54.

By obtaining the C-S constitutive model, a solid model was used to replace the honeycomb structure (Fig. 11) to simulate the stress-strain curve of the compression process. The results are shown in Fig. 12. From the Fig. 12, it can be seen that using the dynamic C-S constitutive model to replace the honeycomb structure, the deformation curve is very similar to the deformation curve of the honeycomb structure, but the solid structure cannot characterize the microscopic characteristics of the material, that is, the deformation characteristics of the hole cannot be seen, it can only be used as a configuration for displaying curves.

Fig. 11
figure 11

The mesh comparison of two materials.

Full size image
Fig. 12
figure 12

Comparison of simulation curves for small and large hole materials use honeycomb and solid structures.

Full size image

Unit cell theory analysis based on quasi-static loading

The process of compression and deformation of porous metal materials leads to continuous energy absorption, and during the process, external loads are continuously dispersed. Many scholars have theoretically studied the compression properties of porous materials. Alexander42 first established the kinematically admissible deformation field when a thin-walled tube undergoes axisymmetric progressive telescopic deformation. Abramowicz43 and Wierzbicki44improved the Alexander model and improved the theoretical prediction accuracy of the pressure characteristics of the thin-walled round tube shaft. Wierzbicki and Abramowicz45 established a super-folding element model for analyzing the axial crushing behavior of rectangular thin-walled tubes. Since then, the simplified super-folding element theoretical model proposed by CHEN and Wierzbicki has been used21. The external work produced by a period folding with a wavelength of 2 H is mainly dissipated through two approaches: the bending energy E and the membrane energy UV46. The total energy is marked by A.

In this study, we take the unit cell of WOTAH as the analysis object. The basic element is composed of two trapezoidal plates and two square plates. As shown in Fig. 13, the energies absorbed by the four plates under the external load are W1, W2, W3, and W4. According to the energy conservation of Formula (3),

$${\text{E}}\,=\,{{\text{W}}_{\text{1}}}\,+\,{{\text{W}}_{\text{2}}}\,+\,{{\text{W}}_{\text{3}}}+{{\text{W}}_{\text{4}}}.$$
(3)

In the formula, P is the average stress of the unit cell during compression; ηis the effective compression stroke coefficient, which is set to 0.547 in this study; 2 H is the height of unit cell; and S is the bottom area. The energy absorption of W1 includes the plastic hinge (W11) caused by the bending of the plate and the energy consumption of film extension W1248. W2 and W4 have the same energy absorption, mainly composed of the plastic hinge energy absorption generated by the bending of the plate. W3 is mainly composed of the plastic hinge energy absorption (W31) formed by the bending of a trapezoidal plate and tilting energy absorption (W32). The Formulas (4) and (5) are given as following:

$$\begin{aligned}W_{1} &= W_{{11}} + W_{{12}} = M_{0} \times \theta \times \frac{H}{2} + \frac{{23.9 \times M_{0} \times \left( {\frac{H}{2}} \right)^{2} }}{{t_{0} }}\left( {\frac{1}{{\left( {a/t_{0} } \right)^{{0.6}} }}} \right) \\ &= 2 \times \pi \times M_{0} \times \frac{3}{2}{\text{a}} + \frac{{23.9 \times M_{0} \times \left( {\frac{3}{2}{\text{a}}} \right)^{2} }}{{t_{0} }}\frac{1}{{\left( {a/t_{0} } \right)^{{0.6}} }}\end{aligned}$$
$$W_{2} = W_{4} = M_{0} \times \theta \times \frac{H}{2} = 2 \times \pi \times M_{0} \times \frac{3}{2}a$$
$$W_{3} = W_{{31}} + W_{{32}} = M_{0} \times \theta \times \frac{H}{2} + 4 \times M_{0} \times \theta _{1} \times \frac{H}{6} = M_{0} \times \frac{\pi }{2} \times \frac{3}{2}{\text{a}} + 4 \times M_{0} \times \frac{5}{9}\pi \times \frac{a}{2}$$
(4)

The bending energy consumption represents the sum (Formula 5) of the bending deformation energy of each plastic hinge line. Each unit cell has a total of four plate bending plastic hinge deformation energy absorptions, four film extension energy consumptions, and two inclined plane bending energy consumptions (Fig. 13B).

$${\text{E}} = \frac{{645.3}}{{48}} \times \sigma _{0} \times {\text{t}}_{0}^{{1.6}} \times {\text{a}}^{{1.4}} + \frac{{21}}{8} \times \pi \times \sigma _{0} \times {\text{t}}_{0}^{2} \times {\text{a}}$$
$$S = 11 \times a \times t_{0} + \frac{{\sqrt 3 }}{8}a^{2} - \frac{2}{3}\sqrt 3 t_{0}^{2}$$
(5)

where M0 is full plastic bending moment, \(M_{0} = \frac{1}{4}\sigma _{0} \times {\text{t}}_{0}^{2}\); θ is bending rotation angle of each hinge line; θ1 is the trapezoidal hypotenuse rotation angle; a is the edge length of the plate unit; t0 is the thickness of the honeycomb cell; and σ0 is the flow stress value, which can be expressed as \(\sigma _{0} = \sqrt {\frac{{\sigma _{y} + \sigma _{u} }}{{1 + n}}}\) or \(\:{\sigma\:}_{0}=\frac{{\sigma\:}_{y}+{\sigma\:}_{u}}{2}\)49.

n is power law exponent (n= 0.18)50; σy is the yield limit of the material; and σuis the ultimate strength of the material51. According to the folding wavelength H, to obtain the average load, we make \(\frac{{\partial P}}{{\partial H}} = 0\).

For a V-element with an angle of ω, the membrane energy is denoted as UV. The distribution of the extensional and compressional regions in three basic folding elements has been observed and studied by many researchers, and the corresponding membrane energy UV has also been derived and modified21 (Formula 6):

$$\:{\text{U}}_{\text{V}}=\int\:{{\upsigma\:}}_{0}\text{t}\text{d}\text{s}=2{\text{M}}_{0}\frac{{\text{H}}^{2}}{\text{t}}=2\times\:\frac{1}{4}{{\upsigma\:}}_{0}\times\:{\text{t}}_{0}^{2}\times\:\frac{{9\text{a}}^{2}}{\text{t}}$$
(6)

Observe the deformation process of the material, the folding wavelength of the material is half of the unit cell height52. By substituting the obtained bending energy consumption and film extension energy, we can obtain the average stress load using Formula (7):

$${\text{A}}\,=\,{\text{E}}\,+\,{{\text{U}}_{\text{V}}}={\text{P}}*{\text{2 H}}*{\text{S}}*{\text{h}}$$
$$\:\text{P}=\bigg(\frac{21}{8}{\uppi\:}\times\:{{\upsigma\:}}_{0}\times\:{\text{t}}_{0}^{2}+\frac{645.3}{48}{{\upsigma\:}}_{0}\times\:{\text{t}}_{0}^{1.6}\times\:{\text{a}}^{0.4}+\frac{9}{2}{{\upsigma\:}}_{0}{\text{t}}_{0}{\text{a}}^{2}\bigg)/\bigg[\bigg(33\text{a}{\text{t}}_{0}+\frac{3\sqrt{3}}{8}{\text{a}}^{2}-\frac{2\sqrt{3}}{3}{\text{t}}^{2}\bigg)\times\:0.5\bigg].$$
(7)
Fig. 13
figure 13

Basic folding element.

Full size image

Table 11 presents the relationship between the theoretical results and the experimental results. The result shows the error is small, indicating the accuracy of the theoretical results.

The theoretical derivation can calculate the SEA in the ideal state53. However, the experiment has various unsatisfactory conditions. The plateau stress obtained through theory can be compared with experiments to analyze the accuracy of experimental results and reduce the effect of material preparation defects. It can be compared with the mechanical properties of wood, which is more convenient for analysis. The plateau stress is calculated by formula \(\sigma _{{{\text{pl}}}} = SEA_{V} /\varepsilon _{{\max }}\). The error in Table 1 includes two aspects. First is the influence of the adhesive. In the theoretical derivation, we use the unit cell, and the influence of the adhesive on the mechanical properties is not considered, which will cause an error. Second is the influence of the deformation process, in the theoretical analysis, the main deformation of the material is a plastic hinge, which is a very ideal condition. However, in the actual compression process, the energy absorption of the material is affected by the deformation process. Because the material always has some defects in the manufacturing process, the material is difficult to appear completely plastic hinge, resulting in incomplete energy absorption. This will cause an error.

Table 1 Comparison of theoretical and experimental results of different kinds WOTAH.
Full size table

Mechanical properties comparison with wood

Through the paper54, we can conclude that when using wood as the shock absorption filling material of the NAC-STC transport cask, the unit volume energy absorption of the wood can fully meet the shock absorption when reaches 10 MJ/m3 (Table 2). Therefore, the energy absorption of WOTAH can also meet the shock absorption effect when it can reach 10MJ/m3 (Fig. 14). Comparing the energy absorption of 2 kinds of materials (Fig. 8), it is found that the energy absorption of the small hole structure material can meet the usage conditions, and other materials need to further improve their structural configuration or size. Small hole material can meet the application conditions of nuclear equipment. The SEAV of 0.3/4 decrease 24.7% than 0.3/3.

The structural dimensions of materials suitable for nuclear equipment can be calculated using the energy absorption formula and it can reduce experimental validation.

Table 2 The comparison of energy absorption under static loading of different material.
Full size table
Fig. 14
figure 14

The usage of WOTAH in transport cask.

Full size image

Conclusion

This paper manufactured two types of WOTAH with different structures through welding technology, and analyzed the mechanical properties of the material under different loading rates through experiments and simulations. The following results were obtained.

Materials with different hole sizes exhibit different performance under the same rate of loading. Under quasi-static loading, the initial peak stress and plateau stress of small hole structure materials are higher than those of large hole materials, but the time to enter the densification strain is also earlier. Overall, the specific energy absorption of small hole materials can reach 11 MJ/m3, which is greater than that of large hole materials 6 MJ/m3. Under high-speed loading, the characteristics of different hole size materials are also different, and small hole materials have better impact resistance. Under absorbing large impact loading, the deformation is small.

The performance of materials with the same hole size varies under different loading speeds. Under quasi-static loading, materials have good energy absorption characteristics. Under high-speed loading, the deformation of the material is more severe, and when the rate is higher, the kinetic energy is greater. Therefore, the deformation of the material increases in order to absorb the initial kinetic energy.

The D and P values of the material based on the C-S dynamic constitutive effect were obtained through experimental data. The mechanical properties of the material were simulated using a solid structure instead of a honeycomb structure. The simulation results showed that the solid structure instead of a honeycomb simulation results were consistent, but the solid structure deformation could not reflect the deformation process of the material.

Taking a unit honeycomb structure as an example, the energy absorption process of a unit cell was studied. Combined with the quasi-static deformation process, the results obtained by the theoretical method are relatively similar to the experimental results, indicating the feasibility of theoretical derivation guiding the experiment.

Finally, by comparing the energy absorption performance of the obtained material with wood, it was found that the material with a performance of 0.3/3 is superior to wood, so it can be used as a shock-absorbing filling material for nuclear equipment.