Introduction

In offshore structures, submarines, and aerial boats, the cylinder shells of functionally classed materials are essential architectural elements. A cylindrical shell is a section between two cylinders that are similarly high and have the same dominant axis. Functionally Graded Material (FGM) cylindrical shells, which have material properties that vary gradually along their thickness, are widely used in various engineering applications. Vibration analysis of these shells plays a crucial role in ensuring the safety, durability, and performance of structures. Here are some real-life applications where vibration analysis of FGM cylindrical shells is important: FGM cylindrical shells are used in rocket and missile casings to reduce weight while maintaining strength and thermal resistance. Vibration analysis is crucial to prevent resonance and structural failure during launch or re-entry. In aerospace structures, FGM cylindrical shells can help in optimizing the thermal and mechanical properties for better performance under varying operational conditions. FGM cylindrical shells are applied in submarine and deep-sea vessel hulls due to their ability to withstand high pressure. Vibration analysis ensures structural stability under underwater pressure and external vibrations. Underwater and offshore pipelines made from FGMs can better resist the harsh marine environment. Vibration analysis helps in preventing failure caused by dynamic loads such as ocean waves. FGM cylindrical shells are used in components like reactor pressure vessels and steam generators, where a balance between thermal resistance and structural integrity is needed. Vibration analysis helps in predicting the behavior under thermal and mechanical loads, thus avoiding catastrophic failures. Functionally graded materials (FGMs) are unique composites that vary easily and continuously in material characteristics from one layer to the next. The frequency of the cylindrical shell is seen for shells of different widths. The frequency of vibration is a method for measuring vibration and frequency levels. A lot of studies have been done on vibration frequency analysis, and some of them are listed here.

Loy et al.1 investigated how the stiffness moduli and characteristics of a three-layered cylindrical shell, made of functionally graded and isotropic materials, are influenced by vibration analysis. They used the Rayleigh-Ritz approach to convert the shell problem into integral form. Liew et al.2 studied the free vibration in thin conical shells using the kp-Ritz element-free kernel particle technique. This study simulated the two-dimensional field of displacement, the effects of semi-vertex angle conical shells on frequency characteristics, and boundary constraints. Kim3 developed a technique for studying the vibratory characteristics of initially strained, functionally graded rectangular plates made of metal and ceramic in thermal conditions. Zhang et al.4 introduced the local adaptive differential square method (LaDQM), which uses locally interpolated basis functions and external grid points for boundary treatments. They found that appropriate natural frequencies can be achieved by using a limited number of grid points with additional points to satisfy boundary constraints. Haddadpour et al.5 analyzed vibration-free FG cylindrical shells with temperature-dependent material properties that change gradually across the shell thickness. Arshad et al.6 investigated comparative shell frequencies for FGM using algebraic polynomial, exponential, and trigonometric fraction rules. Pellicano7 studied linear and nonlinear vibrations in circular cylindrical shells with shifting boundaries, using a combination of harmonic functions and Chebyshev polynomials. The technique described can analyze vibrations in both linear and nonlinear cylindrical shells. Isvandzibaei8 utilized a functionally graded material (FGM) consisting of stainless steel and nickel to study the vibration of cylindrical shells. Cylindrical shells with random ring support exhibit zero lateral deflection. The study employs the third-order shell theory (T.S.D.T) and presents findings on the frequency characteristics, ring support ___location, and boundary conditions. The study by Yuan and Ning9 focused on the free vibration analysis of functionally graded (FGM) cylinder shells with holes.

Meanwhile, Li et al.10 examined a circular cylindrical three-layer shell with interior and external layers made of the same homogeneous material and an intermediate layer of a functionally graded material. Their findings indicated that the fundamental natural frequency decreases as the radius increases, and the ratio of the modulus at the central surface to the outer (or inner) layer increases. In cylindrical shells, layers help distribute stress more evenly, increase strength, and provide resistance to thermal or corrosive damage. Using varied materials across layers allows for tailored performance, enhancing the shell’s durability and efficiency in demanding applications like aerospace and structural engineering.

Additionally, Sofiyev and Avcar11 investigated the stability of ceramic, FGM, and metal coatings on Winkler-Pasternak foundations. They found that the composite layer, consisting of a functionally graded material and another isotropic material, as utilized by Arshad et al.12, yielded noteworthy results.This technique involves regulating frequency equations to reduce Lagrangian functionality to a value problem. Arshad et al.13 conducted a study on a bi-level cylindric shell with two functionally graded layers, assuming the shell’s thickness is constant. Naeem et al.14 investigated the vibration of a three-layer cylindrical shell with functionally distinct inner and outer layers. Wang et al.15 studied the free flexural vibration of a cylindrical shell immersed in low water using wave propagation and imaging. The modal frequency increases if the shell is near the free surface or a stiff wall, and decreases if it is in low water. Low water has a considerable impact on linked modal frequencies when the shell is submerged relatively shallowly.

To address the issue of planar vibration in parallelogram-shaped piezoceramic sheets, Mobarakeh et al.16 developed a series of equations to describe the movement of piezoceramic plate elements. Ghamkhar et al.17 [examined the vibration analysis of three layers of a CS with homogenous interior and external layers, a core layer made of FGMs, and so on. Under various edge conditions, the thickness, length, and radius ratio were shown to have distinct results. The mathematical expressions of polynomial, exponential, and trigonometric functions are described by three-volume fractional laws (VFLs). FGM (functionally graded material) shells with homogeneous inner and exterior layers were studied by Ghamkhar et al.18 Varying thicknesses of the medium layer have an impact on natural frequencies (NFs). Several boundary conditions affect the ratios of thickness to radius length. Khalmuradov and Yalgashev19 solved the problem of an end-to-end circular cylindrical shell with free ends. They used the Rayleigh-Ritz technique to investigate the free vibration and flutter of multi-layered cylindrical shells. The critical value of free vibration for composite cylindrical shells increases with changes in layer orientation (fall). Augustyn et al.20 discussed free vibration and flutter in multi-layered cylindrical shells using the Rayleigh-Ritz method. Their focus was on optimal design constraints and fiber orientations. Anwar et al.21 studied the analysis of natural frequencies for different layered cylindrical shells, those constructed from FGMs. Ghamkhar et al.22 examined the vibration analysis of a CS having FGM layers as a cylinder, with the FGM core layer and identical isotropic materials making up the external and interior layers. Ghamkhar et al.23 examined in depth the bilayered FGM cylindrical shells’ vibrational frequency both with and without the impact of internal pressure on ring support. The FG materials of a cylindrical shell were investigated under various boundary circumstances and created with specific goals in mind. The link between the curvature displacement and strain displacement was discovered using the Love shell theory. A polynomial volume fraction law was used to evaluate the natural frequency vibrations of a bi-layered FGM shell under ring support.

Ghamkhar et al.24 examined the vibrations of four-layered cylindrical shells with a ring support along the axial direction. The two internal layers were composed of isotropic materials, and the external two layers were composed of functionally graded materials. The outer functionally graded material layers considered were stainless steel, zirconia, and nickel. The inner two isotropic layers considered of aluminum and stainless steel. The shell frequency equation was acquired by employing the Rayleigh–Ritz method under the Sander’s shell theory. The trigonometric volume fraction law is used to sort the functionally graded material composition of the FGM layers. The natural frequencies were attained under simply supported–simply supported and clamped–clamped edge conditions. Talebitooti and Zarastvand25 examined the propagation of waves on an infinite doubly curved laminated composite shell enclosing a porous material, commonly seen in aerospace structures, by means of a diffuse acoustic field. As a result, the poroelastic material was modelled using Biot’s theory, which took into account three different wave propagation scenarios two compressions and one shear terms. Zarastvand et al.26 examined the vibroacoustic properties of shell constructions. To categorise the issues that need to be searched, a number of categories were initially highlighted for this purpose. Then, the review was focused on the various geometries of shells, including doubly curved and cylindrical shells. Afterward, a perfect explanation of he significance of modelling the structures according to the different materials was revealed. The various acoustic excitations involving plane wave and point source incidences were used to characterise the structure since the type of incident field can have a significant impact on the sound insulation specification of these shells. Talebitooti et al.27 examined the laminated composite cylindrical shell’s acoustic response to an oblique plane sound wave. It was thought that the cylindrical shell had an infinite length and that the fluid medium outside of it had uniform airflow. Third-order Shear Deformation Theory (TSDT) was used to produce an analytical solution for Sound Transmission Loss (STL), and the displacements were developed as the cubic order of the thickness coordinate. Talebitooti and Zarastvand28 studied the result, based on Third-order Shear Deformation Theory (TSDT), also known as HSDT, the displacements were extended up to cubic order of thickness coordinate with no effect from the shear correction factor. Thus, to display the Sound Transmission Loss (STL) of the current model, the structure was excited using an oblique plane sound wave in the proper order. Also, by providing greater clarity on the more exact results, their findings highlighted the significance of researching TSDT.

Talebitooti et al.29 observed the acoustic analysis based on Third Order Shear Deformation Theory (TSDT) of a four-sides simply supported doubly curved composite shell interlayered with porous material used in aerospace applications. They focused on the poroelastic structure’s Sound Transmission Loss (STL). A novel method was developed to take the number of modes for the finite composite structure that was coated in porous material into account. This procedure led to the discovery of the unknown constants in the porous core, upper and bottom composite shells, and other structural components. As a result, the structure’s STL was shown on a logarithmic scale.

There are four separate layers in the shells. FGM is used to build the first and third layers, whereas isotropic materials are used to build the second and fourth layers. By selecting the combined stress and strain energy of CS, the shell problem is expressed. The Lagrangian function is determined by comparing the two shell energies. The shell frequency equations are eigenvalue-formed by Sander’s shell theory and the Rayleigh-Ritz approach. Natural frequency (NF) decreases with rising N and rises with decreasing L/R (length to radius ratio). To approximate the axial deformation function, a beam function that satisfies the edge condition is employed. It is recognised that the circumferential wave number, length-to-radius ratio, and thickness-to-radius ratio all affect the four-layered CS’s frequency fluctuation. The eigenvalue problems are solved using MATLAB.

Theoretical consideration

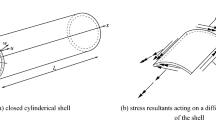
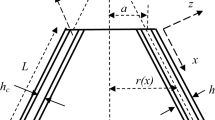
For the FGM round cylindrical coating of L, the average vibration width of R is h. The material properties, including CS Poisson’s ratio λ, Young’s modulus E, and mass density η, have their own limitations. A cylindrical coordinate system is located on the central surface of the shell (refer to Fig. 1). The strain energy of CS is

$$\:{E}_{strain}=\frac{1}{2}\:{\int\:}_{0}^{L}{\int\:}_{0}^{2\pi\:}{\left\{C\right\}}^{{\prime\:}}\left[{M}_{s}\right]\left\{C\right\}Rd\theta\:dx,$$
(1)
Fig. 1
figure 1

Four layers FGM CS.

Full size image

where

$${\left\{ C \right\}^{\prime}} = \left\{ {{e_1},~{e_2},~\ell ,~{\kappa _1},~{\kappa _2},~2\rlap-\,t\:} \right\}$$
(2)

in which \(\left\{ {{e_1},~{e_2},~\ell } \right\}\)and \(\left\{ {{\kappa _1},~{\kappa _2},~\rlap-\,t\:}\right\}\)are strains and curvatures reference surface relations, respectively. These equations are developed from the shell theory of Sander’s and are designated as:

$$\{ {e_1},{e_2},\ell \} =\left\{ {\frac{{\partial \alpha }}{{\partial x}},\frac{1}{R}\left( {\frac{{\partial \beta }}{{\partial \theta }}+\gamma } \right),\left( {\frac{{\partial \beta }}{{\partial x}}+\frac{1}{R}\frac{{\partial \alpha }}{{\partial \theta }}} \right)} \right\}$$
(3)
$$\left\{ {{\kappa _1},{\kappa _2},2\rlap{--} t} \right\}=\left\{ { - \frac{{{\partial ^2}\gamma }}{{\partial {x^2}}}, - \frac{1}{{{R^2}}}\left( {\frac{{{\partial ^2}\gamma }}{{\partial {\theta ^2}}} - \frac{{\partial \beta }}{{\partial \theta }}} \right), - \frac{2}{R}\left( {\frac{{{\partial ^2}\gamma }}{{\partial x\partial \theta }} - \frac{3}{4}\frac{{\partial \beta }}{{\partial x}}+\frac{1}{{4R}}\frac{{\partial \alpha }}{{\partial \theta }}} \right)} \right\}$$
(4)

and

$$\:\left[{M}_{s}\right]=\left[\begin{array}{cc}\begin{array}{ccc}{p}_{11}&\:{p}_{12}&\:0\\\:{p}_{12}&\:{p}_{22}&\:0\\\:0&\:0&\:{p}_{66}\end{array}&\:\begin{array}{ccc}{q}_{11}&\:{q}_{12}&\:0\\\:{q}_{12}&\:{q}_{22}&\:0\\\:0&\:0&\:{q}_{66}\end{array}\\\:\begin{array}{ccc}{q}_{11}&\:{q}_{12}&\:0\\\:{q}_{12}&\:{q}_{22}&\:0\\\:0&\:0&\:{q}_{66}\end{array}&\:\begin{array}{ccc}{r}_{11}&\:{r}_{12}&\:0\\\:{r}_{12}&\:{r}_{22}&\:0\\\:0&\:0&\:{r}_{66}\end{array}\end{array}\right],\:\left(i,j=\text{1,2},6\right)$$
(5)

in which \(\:{p}_{ij}\) extensional, \(\:{q}_{ij}\) coupling, and \(\:{r}_{ij}\) bending stiffness respectively and defined:

$$\left\{ {{p_{ij}},{q_{ij}},{r_{ij}}} \right\}=~~\mathop \smallint \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rlap{--} Q_{ij}}\left\{ {1,z,{z^2}} \right\}dz~$$
(6)

Classification of materials

The current study is divided into four layers: the second and fourth levels are isotropic, while the first and third layers are made up of FG materials such as aluminum, nickel, zirconia, and stainless steel. Aluminum, zirconia, and stainless steel are important materials for their distinctive properties. Aluminum is lightweight and resistant to corrosion, making it suitable for aerospace and automotive uses. Zirconia is strong and provides excellent thermal insulation, often used in ceramics and implants. Stainless steel is durable and highly resistant to corrosion, essential in construction and medical applications. Nickel is significant for its excellent corrosion resistance and ability to withstand high temperatures, making it ideal for applications in chemical processing, aerospace, and power generation.

FGMs are advanced materials with gradually varying properties that improve performance in challenging conditions. They reduce stress concentrations, enhance thermal and mechanical resistance. Isotropic materials have uniform properties in all directions, meaning their mechanical, thermal, and electrical behavior is the same regardless of orientation. This makes them predictable and easy to model, commonly used in engineering applications like metals, ceramics, and polymers. Their consistent behavior simplifies design processes and ensures reliable performance under different loading conditions.

The links below show the shell inner layer volume fractions built with two components using trigonometric VFL:

$$\:{V}_{f1}={\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{1}}{{h}_{2}-{h}_{1}}\right\}}^{N}\right],\:{V}_{f2}={\text{cos}}^{2}\left[{\left\{\frac{z-{h}_{1}}{{h}_{2}-{h}_{1}}\right\}}^{N}\right],\:0\le\:N\le\:\infty\:$$
(7)

These relations satisfy the VFL i.e., \(\:{V}_{f1}+{V}_{f2}=1\), here \(\:h\) is the thickness of the shell, and \(\:N\) indicates the power law exponent. It is assumed that every layer is of the thickness \(\:h/4\). Material parameters: \(\:{E}_{1},{\lambda\:}_{1},{\eta\:}_{1}\) are for nickel, \(\:{E}_{1},{\lambda\:}_{1},{\eta\:}_{1}\) for Zirconia, \(\:{E}_{3},{\lambda\:}_{3},\:{\eta\:}_{3}\) for stainless steel, \(\:{E}_{4},{\lambda\:}_{4},\:{\rho\:}_{4}\) is for Aluminum, \(\:{E}_{5},{\lambda\:}_{5},{\eta\:}_{5}\) for stainless steel and \(\:{E}_{6},{\lambda\:}_{6},{\eta\:}_{6}\) for Zirconia. Then the effective material quantities

$$\:\left.\begin{array}{c}{E}_{{fgm}1}=\left[{E}_{1}-{E}_{2}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{1}}{{h}_{2}-{h}_{1}}\right\}}^{N}\right]+{E}_{2},\\\:{\lambda\:}_{{fgm}1}=\left[{\lambda\:}_{1}-{\lambda\:}_{2}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{1}}{{h}_{2}-{h}_{1}}\right\}}^{N}\right]+{\lambda\:}_{2},\\\:\begin{array}{c}{\eta\:}_{{fgm}1}=\left[{\eta\:}_{1}-{\eta\:}_{2}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{1}}{{h}_{2}-{h}_{1}}\right\}}^{N}\right]+{\eta\:}_{2},\\\:{E}_{{fgm}2}=\left[{E}_{4}-{E}_{5}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{3}}{{h}_{4}-{h}_{3}}\right\}}^{N}\right]+{E}_{5},\\\:\begin{array}{c}{\lambda\:}_{{fgm}2}=\left[{\lambda\:}_{4}-{\lambda\:}_{5}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{3}}{{h}_{4}-{h}_{3}}\right\}}^{N}\right]+{\lambda\:}_{5},\\\:{\eta\:}_{{fgm}2}=\left[{\eta\:}_{4}-{\eta\:}_{5}\right]{\text{sin}}^{2}\left[{\left\{\frac{z-{h}_{3}}{{h}_{4}-{h}_{3}}\right\}}^{N}\right]+{\eta\:}_{5}.\end{array}\end{array}\end{array}\right\}$$
(8)

The stiffness moduli are modified as, where \(\:i=\text{1,2},6\).

$$\:\left.\begin{array}{c}{p}_{ij}={p}_{ij}\left(FGM\right)+{p}_{ij}\left(iso\right)+{p}_{ij}\left(FGM\right)+{p}_{ij}\left(iso\right),\\\:{q}_{ij}={q}_{ij}\left(FGM\right)+{q}_{ij}\left(iso\right)+{q}_{ij}\left(FGM\right)+{q}_{ij}\left(iso\right),\\\:{r}_{ij}={r}_{ij}\left(FGM\right)+{r}_{ij}\left(iso\right)+{r}_{ij}\left(FGM\right)+{r}_{ij}\left(iso\right).\:\:\:\end{array}\right\}$$
(9)

In this research, we have examined the four-layer cylindrical shell (1st and 3rd layers are of FGM and the other two are of Isotropic Materials).

Now by using Eqs. (2)–(4) and (6) in (1),

$$\begin{aligned}{E}_{strain}&=\frac{1}{2}\:{\int\:}_{0}^{L}{\int\:}_{0}^{2\pi\:}\left\{{p}_{11}{\left(\frac{\partial\:\alpha\:}{\partial\:x}\right)}^{2}+\frac{2}{R}{p}_{12}\frac{\partial\:\alpha\:}{\partial\:x}\left(\frac{\partial\:\beta\:}{\partial\:\theta\:}+\gamma\:\right)\right. \\ & \quad -2{q}_{11}\frac{\partial\:\alpha\:}{\partial\:x}\frac{{\partial\:}^{2}\gamma\:}{\partial\:{x}^{2}}-{q}_{12}\frac{1}{{R}^{2}}\frac{\partial\:\alpha\:}{\partial\:x}\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)+{p}_{22}{\left[\frac{1}{R}\left(\frac{\partial\:\beta\:}{\partial\:\theta\:}+\gamma\:\right)\right]}^{2}\\ & \quad +{r}_{12}\frac{1}{{R}^{2}}\frac{{\partial\:}^{2}\gamma\:}{\partial\:{x}^{2}}\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)+{r}_{11}{\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{x}^{2}}\right)}^{2}\left[-2{q}_{12}\frac{1}{R}\left(\frac{\partial\:\beta\:}{\partial\:\theta\:}+\gamma\:\right)\frac{{\partial\:}^{2}\gamma\:}{\partial\:{x}^{2}}\right] \\& \quad -\frac{2}{{R}^{3}}{q}_{22}\left(\frac{\partial\:\beta\:}{\partial\:\theta\:}+\gamma\:\right)\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)+{p}_{66}{\left(\frac{\partial\:\beta\:}{\partial\:x}+\frac{1}{R}\frac{\partial\:\alpha\:}{\partial\:\theta\:}\right)}^{2} \\ & \quad -\frac{8}{R}\left(\frac{\partial\:\beta\:}{\partial\:x}+\frac{1}{R}\frac{\partial\:\alpha\:}{\partial\:\theta\:}\right)\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:x\partial\:\theta\:}-\frac{3}{4}\frac{\partial\:\beta\:}{\partial\:x}+\frac{1}{4R}\frac{\partial\:\alpha\:}{\partial\:\theta\:}\right){q}_{66}+4\left[\frac{2}{R}{\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:x\partial\:\theta\:}-\frac{3}{4}\frac{\partial\:\beta\:}{\partial\:x}+\frac{1}{4R}\frac{\partial\:\alpha\:}{\partial\:\theta\:}\right)}^{2}\right]{r}_{66}\\ & \quad \left.-{q}_{12}\frac{1}{{R}^{2}}\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)\frac{\partial\:\alpha\:}{\partial\:x}+{r}_{12}\frac{1}{{R}^{2}}\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)\frac{{\partial\:}^{2}\gamma\:}{\partial\:{x}^{2}}+{r}_{22}\left(\frac{1}{{R}^{2}}{\left(\frac{{\partial\:}^{2}\gamma\:}{\partial\:{\theta\:}^{2}}-\frac{\partial\:\beta\:}{\partial\:\theta\:}\right)}^{2}\right)\right\}Rd\theta\:d\end{aligned}$$
(10)

The shell’s kinetic energy \(\:{E}_{kinetic}\) is specified as

$$\:{E}_{kinetic}=\frac{1}{2}{\int\:}_{0}^{L}{\int\:}_{0}^{2\pi\:}{\eta\:}_{t}\left[{\left(\frac{\partial\:\alpha\:}{\partial\:\tau\:}\right)}^{2}+{\left(\frac{\partial\:\beta\:}{\partial\:\tau\:}\right)}^{2}+{\left(\frac{\partial\:\gamma\:}{\partial\:\tau\:}\right)}^{2}\right]Rd\vartheta\:dx,$$
(11)

where time denotes by \(\:\tau\:\), \(\:{\eta\:}_{t}\) is the mass density for each length, given as

$$\:{\eta\:}_{t}={\int\:}_{-\frac{\hslash\:}{2}}^{\frac{\hslash\:}{2}}\eta\:\:dz$$
(12)

The Lagrange energy function \({E_{lagrange}}\) is defined as

$$\:{E}_{lagrange}={E}_{kinetic}-{E}_{strain}$$
(13)

Numerical procedure

The Rayleigh-Ritz parameter controls the normal frequencies of CS. The distortion defects in the longitudinal \(\:\alpha\:\), transverse \(\:\beta\:\), and angular directions \(\:\gamma\:\) are taken into account. The displacement domains are now assumed by the following relationships.

$$\:\left.\begin{array}{c}\alpha\:\left(x,\vartheta\:,\tau\:\right)={x}_{n}D\left(x\right){cos}\left(m\vartheta\:\right)sin\left(\varpi\:\tau\:\right),\\\:\beta\:\left(x,\vartheta\:,\tau\:\right)={y}_{n}E\left(x\right){sin}\left(m\vartheta\:\right)cos\left(\varpi\:\tau\:\right),\\\:\gamma\:\left(x,\vartheta\:,\tau\:\right)={z}_{n}F\left(x\right){cos}\left(m\vartheta\:\right)sin\left(\varpi\:\tau\:\right).\end{array}\right\}$$
(14)

\(\:{x}_{n}\), \(\:{y}_{n}\), \(\:{z}_{n}\) amplitudes of frequency in the \(\:x\), \(\:\vartheta\:\), and \(\:z\) axis respectively, \(\:n\) circumferential frequency, \(\:m\) axial numbers, and \(\:\varpi\:\) circular vibration for the shell wave. \(\:D\left(x\right)\), \(\:E(x)\) and \(\:F\left(x\right)\) are axial model dependencies in the longitudinal, circumferential, and transverse directions respectively.

Here

$$\:\left.\begin{array}{c}D\left(x\right)\:=\:\frac{d\phi\:}{dx}\:,\\\:E\left(x\right)\:=\:\varphi\:\left(x\right),\\\:F\left(x\right)\:=\:\varphi\:\left(x\right),\end{array}\right\}$$
(15)

where \(\:\phi\:\left(x\right)\) is the axial function that meets the geometric requirement of the edge and is defined as

$$\:\varphi\:\left(x\right)=\:{\beta\:}_{1}{cosh}\left({\mu\:}_{m}x\right)+\:{\beta\:}_{2}{cos}\left({\mu\:}_{m}x\right)-{\sigma\:}_{m}{\beta\:}_{3}\text{sinh\:}\left({\mu\:}_{m}x\right)+{\sigma\:}_{m}{\beta\:}_{4}\text{sin\:}\left({\mu\:}_{m}x\right)$$
(16)

\(\:{\mu\:}_{m}\) are roots of some transcendental equations, \(\:{\sigma\:}_{m}\) are parameters that depend on the values of \(\:{\mu\:}_{m}\) and \(\:{\beta\:}_{i}\:\:(i=\text{1,2},\text{3,4})\) are changed with respect to the edge conditions.

To generalize this issue, we use the following non-dimensional parameters.

(17)

The term (3.14) is now changed to form

(18)

The Lagrangian function \(\:{\text{\pounds\:}}_{\text{m}\text{a}\text{x}}\)transformed by applying the principle of maximum energy.

(19)

To minimize Lagrangian energy functional \(\:{E}_{lagrange}^{max}\) w.r.t amplitudes \(\:{x}_{n},{y}_{n}\) and \(\:{z}_{n}\), as follow,

$$\:\frac{\partial\:{E}_{lagrange}^{max}}{\partial\:{x}_{n}}=\frac{\partial\:{E}_{lagrange}^{max}}{\partial\:{y}_{n}}=\frac{\partial\:{E}_{lagrange}^{max}}{\partial\:{z}_{n}}=0.$$
(20)

The produced solutions are written in the form of the matrix

$$\:\left\{\left[K\right]-{\varOmega\:}^{2}\left[L\right]\right\}X=0$$
(21)

where \(\:{{\Omega\:}}^{2}={R}^{2}{\omega\:}^{2}{\rho\:}_{t},\)\(\left[ K \right]\)Stiffness matrices of the cylindrical shell,\(\left[ L \right]\) Mass matrices of the cylindrical shell, and \(\:\left[X\right]\) Contains the terms related material moduli

$$\:X=\left[{x}_{n},{y}_{n},{z}_{n}\right]$$

Results and discussion

To demonstrate the precision and understanding of the precise conclusion, functionally graded materials (FGM) and isotropic cylindrical shells (CS) are utilized to describe the present outcome for simply supported-simply supported (SS) edge circumstances. The shells confiscated were constructed in four distinct layers. The first and third layers are constructed of FGM, whereas the remaining two levels are built of isotropic materials. The shell problem is stated by choosing the stress and strain energy of CS in combination. By contrasting the two shell energies, the Lagrangian function is established. The Rayleigh-Ritz technique and Sander’s shell theory are used to eigenvalue-formulate the shell frequency equations. When \(\:N\) rises, natural frequency (NF) drops and increases with L/R. A beam function that fulfills the edge condition is used to approximate the axial deformation function. It is understood that the frequency fluctuation of the four-layered CS depends on the circumferential wave number, the length-to-radius ratio, and the thickness-to-radius ratio. The eigenvalue problems are solved using MATLAB. Three materials (stainless steel, zirconia, and nickel) are combined to create two distinct forms of FG materials dubbed FGM cylindrical layers. FGM Variability by material type is seen in Fig. 2.

Fig. 2
figure 2

Configurations FGM CS.

Full size image

Type 1

The inner surfaces of type 1 FGM CS are composed of Nickel and Stainless Steel. The outer layers, on the other hand, are made of zirconia.

Type 2

The inner surfaces of type 2 FGM CS are composed of zirconia, while the outside layers are constructed of nickel and stainless steel.

Variability of natural frequencies

Table 1 shows the variance in natural frequency for (\(\:m=1\), \(\:R=1\), \(\:h=0.002\), \(\:L=20\)). As the circumferential frequency of wave n increases from 1 to 10, the value of natural frequency decreases. Additionally, the values of natural frequencies decrease somewhat for power law exponents \(\:N=1\) to \(\:N=20\), from 14.0244 to 13.8455 for \(\:N=1\) to \(\:N=20\). Variation in the natural frequency of L/R in proportion to the circumferential frequency of wave \(\:n\) was observed and reported for shells with parameters (\(\:m=3\), \(\:R=1\), \(\:h=0.002\), \(\:L=30\)) in Table 2. For \(\:n=1\) to \(\:n=10\), frequency values ranged from 51.4000 to 0.8205. Additionally, results for exponential laws \(\:N=1\) to \(\:N=20\) range from 51.400 to 50.6680. Table 3 plots the natural frequency for L/R in opposition to the circumferential frequency of wave \(\:n\) for a shell with parameters (\(\:m=1\), \(\:R=1\), \(\:N=1\), \(\:L=20\)) under the S-S Edge condition (thickness of the layer). The value of natural frequency falls from 14.0244 to 0.2053 when the frequency of wave n increases from 1 to 10. The frequencies remain almost constant as the shell thickness changes between 0.001 and 0.07. It’s worth noticing that even when the thickness varies slightly, the natural frequency values remain constant. Additionally, when \(\:h=0.07\), the frequency value decreases from 14.0246 to 5.6681 when \(\:n=1\) to \(\:n=2\), and then increases to 125.5347 at \(\:n=10\). Additionally, we can observe from this table that the value of frequency remains constant for the frequency of wave 1 but increases as the frequency of the wave increases.

Table 4 illustrates the natural frequency of L/R in opposition to the circumferential frequency of wave \(\:n\) for a shell with the parameters (\(\:m=4\), \(\:R=1\), \(\:N=3\), \(\:L=60\)) under the S-S Edge condition. Thickness values 0.001 and 0.005 decrease, but thickness values \(\:h=0.007\) and \(\:h=0.01\) decrease from \(\:n=1\) to \(\:n=8\), then progressively rise. When h=0.0.05, values decrease until \(\:n=3\), at which time they climb steadily. For \(\:h=0.07\), values decreased from 24.1572 to 8.6636 between \(\:n=1\) and \(\:n=2\), then rapidly increased from 8.6636 to 125.1045 between \(\:n=2\) and \(\:n=10\).

Tables 5 and 6 illustrates the natural frequency of L/R in opposition to the circumferential frequency of wave n for a shell with the parameters (\(\:m=1\), \(\:R=1\), \(\:N=1\), \(\:h=0.005\)) under the S-S Edge condition. Natural values for cylindrical shells with lengths ranging from 10 to 70 are presented in this table, and it is noticed that as the wave frequency goes from 1 to 10, the value for \(\:L=10\) decreases from 51.4337 to 1.0305. Another interesting finding in this table is that when the duration of CS increases, the frequency values decrease rapidly. As the wavelength increases from \(\:L=10\) to \(\:L=70\), the natural frequency decreases from 51.4337 to 1.1805 for wave \(\:n=1\), a rather rapid decrease compared to the preceding tables.

The natural frequency for L/R is found to be opposite the circumferential frequency of wave n for a shell with the parameters (\(\:m=3\), \(\:R=1\), \(\:N=15\), \(\:h=0.04\)) under the S-S Edge condition. It’s worth mentioning that the consequences shown in this table vary depending on the settings. NFs decrease from 208.3126 to 24.2820 between \(\:n=1\) and \(\:n=6\) and increase to 41.6529 between \(\:n=6\) and \(\:n=10\). Furthermore, this effect is valid for all other values of \(\:L\). When \(\:L=70\) is utilised, the frequency value decreases from 10.2644 to 3.4856 at \(\:n=1\) to \(\:n=2\), and then increases to 40.7207 when \(\:n=10\).

The results of this study are compared to those of previous research in Tables 7, 8, 9 and 10 to verify they are correct. It looks to have a striking resemblance to previous outcomes as well as to the same outcomes as previously. Figure 3 shows the behavior of natural frequencies (Hz) versus circumferential wave numbers with various \(\:L/R\) ratios for type 1 CS. It is seen that the natural frequencies (Hz) are decreased when the wave number increase from 0 to 2 and then start increasing onwards. It is also noted that changing the value of \(\:N\) does not affect the natural frequency. Figure 4 shows the behavior of natural frequencies (Hz) for different \(\:L/R\) ratios versus circumferential wave numbers for type 1 Cylindrical shell. It is seen that the natural frequencies (Hz) are decreased when the wave number increase from 0 to 2 and then start increasing onwards. It is also noted that varying the value of thickness \(\:h\) has an effect on the natural frequency. As the value of \(\:h\) increases the NF also increases. As \(\:h\) varies from 0.001 to 0.01 has a very small change in frequency but when changing the h by 0.01 to 0.7 it shows a notable change in NF. Figure 5 shows the behavior of natural frequencies (Hz) versus circumferential wave number for edge conditions S-S. It is seen that the natural frequencies (Hz) are decreased when the wave number increase. It is also noted that varying the value of \(\:L\) has an effect on the natural frequency. As the value of \(\:L\) increases the natural frequency decreases. By increasing the value of \(\:L\) from 10 to 70, it is noted that the value of frequency fall has a big change from 10 to 20 but when the value change from 20 to 70, the change is small.

Figure 6 shows the behavior of natural frequencies (Hz) versus circumferential wave numbers with various \(\:L/R\) ratios for type II CS. It is seen that the natural frequencies (Hz) are big decreased when the wave number increase from 0 to 2 and from 2 to 6 has a slight decrease then becomes nearly linear onwards. It is also noted that changing the value of \(\:N\) does not affect the natural frequency. Figure 7 shows the behavior of natural frequencies (Hz) for different \(\:L/R\) ratios versus circumferential wave numbers for type II cylindrical shells. It is seen that the natural frequencies (Hz) are decreased when the wave number increase from 0 to 4 then scatter for different value oh h. It is seen that varying the value of thickness \(\:h\) has no effect on the natural frequency for small wave numbers and has a different value for wave numbers 4 to 10.

Figure 8 shows the behavior of natural frequencies (Hz) with circumferential wave numbers. It is seen that the natural frequencies are decreased when the wave number increase. It is also noted that varying the value of \(\:L\) changes the natural frequency from 1 to 7 and then becomes constant onward. The value of \(\:L=20\) has a big fall of frequency for small values of wave numbers and values 40 and 50, which has a small change as compared to 10.

Table 1 Variability of natural frequency averse to circumference frequency of wave \(\:n\) for the shell with parameters (\(\:m=1\), \(\:R=1\), \(\:h=0.002\), \(\:L=20\)) under simply supported-simply supported (S-S) edge condition.
Full size table
Table 2 Aversion of the natural frequency of the shell by the circumferential frequency \(\:n\) (\(\:m=3\), \(\:R=1\), \(\:h=0.002\), \(\:L=30\)) under S-S edge condition.
Full size table
Table 3 Under the S-S edge condition, the natural frequency of a shell with parameters (\(\:m=1\), \(\:R=1\), \(\:N=1\), \(\:L=20\)) varies in relation to the circumferential frequency of wave \(\:n\).
Full size table
Table 4 Under S-S edge condition, variation of natural frequency vs. circumferential frequency of wave \(\:n\) for the shell with parameters (\(\:m=4\), \(\:R=1\), \(\:N=3\), \(\:L=60\)).
Full size table
Table 5 Natural frequency variation versus circumference frequency for the shell with parameters (\(\:m=1\), \(\:R=1\), \(\:N=1\), \(\:h=0.005\)).
Full size table
Table 6 Natural frequency vs. circumferential frequency of wave \(\:n\) for a shell with parameters (\(\:m=3\), \(\:R=1\), \(\:N=15\), \(\:h=0.04\)).
Full size table
Table 7 A comparison of the behavior of natural frequencies in relation to n for simply supported-simply supported shells (\(\:m=1\), \(\:R=1\), \(\:h=0.002\), \(\:L=20\)).
Full size table
Table 8 Contrast the behavior of natural frequencies in the presence of \(\:n\) for simply supported-simply supported shells (\(\:m=1\), \(\:R=1\), \(\:h=0.001\), \(\:N=1\)).
Full size table
Table 9 Contrast the behavior of natural frequencies in the presence of \(\:n\) for simply supported-simply supported shells (\(\:m=1\), \(\:R=1\), \(\:h=0.001\), \(\:N=1\)).
Full size table
Table 10 Contrast the behavior of natural frequencies in the presence of \(\:n\) for simply supported-simply supported shells (\(\:m=1\), \(\:R=1\), \(\:h=0.001\), \(\:N=1\)).
Full size table
Fig. 3
figure 3

Natural frequency variation of wave \(\:n\) concerning its circumferential frequency for type I with parameters (\(\:m=4\), \(\:R=1\), \(\:h=0.06\), \(\:L=20\)).

Full size image
Fig. 4
figure 4

Variation of the natural frequency of a wave with its circumferential frequency for type I with parameters\(\:\left(m=1,\:R=1,\:L=20,\:N=1\right)\) under S-S edge condition.

Full size image
Fig. 5
figure 5

Change of natural frequency versus the wave frequency circumference \(\:n\) for type with parameters (\(\:m=1\), \(\:R=1\), \(\:h=0.005\), \(\:N=1\)) under the edge conditions S-S.

Full size image
Fig. 6
figure 6

Natural frequency variation of L/R concerning the circumferential frequency of wave \(\:n\) for type II with parameters (\(\:m=3\), \(\:R=1\), \(\:h=0.002\), \(\:L=30\)).

Full size image
Fig. 7
figure 7

Natural frequency fluctuation vs. wave n circumferential frequency for type II (\(\:m=1\), \(\:R=1\), \(\:L=20\), \(\:N=1\)).

Full size image
Fig. 8
figure 8

Under S-S edge condition, natural frequency vs. wave \(\:n\) circumferential frequency (\(\:m=1\), \(\:R=1\), \(\:h=0.005\), \(\:N=10\)).

Full size image

Conclusion

This paper examined the frequency response of a tetra-layer cylinder-shaped shell formed by the composition of FGM and Isotropic materials, for a variety of shell thicknesses, heights, and exponential coefficients. The FGM Cylindrical shell is made of four materials sucha as aluminum, nickel, zirconia, and stainless steel. The strain and curvature displacement relationships are derived using Sander’s theory. To handle the current problem, the Rayleigh-Ritz method is utilized. Natural frequencies are analyzed to see whether or not they are simply supported. Natural frequencies decrease as the thickness of the shell rises. These, too, decreased when L/R ratios rose. Frequencies grew in proportion to the increase in h/R ratios. Frequencies remain almost constant by changing the exponential coefficients. The fact that the frequency curves of the shells follow each other is investigated in all comparisons for shell parameters. The natural frequencies of the shell are clearly influenced by its length, radius, and width. The approach is easy to understand and straightforward. It can be extended to multilayered structures having different boundary conditions and different volume fraction laws.This work can extended to study the vibration frequencies of submerged FGM multi-layered shells.

To sum up, this research significantly advances our understanding of the natural frequencies and vibrational characteristics of orientated cylindrical structures composed of FGM nad Isotropic materials. By employing advanced analytical techniques and examining a range of material compositions and boundary conditions, the study sheds light on the complex dynamics of these hybrid systems, which could have implications for a wide range of real-world applications.