Introduction

In the past, electricity production mainly depended on non-renewable resources (coal, oil, and gas) to run thermal facilities using steam turbines and combustion. Hydropower was helpful in areas with plenty of water, and nuclear power was also practical despite safety concerns. However, the depletion of natural resources, their adverse effects on the environment, and the cost of these conventional approaches have forced a paradigm change in favour of renewable energy sources.

In recent times, renewable energy resources (RES) have attracted much attention from researchers because of the promise to provide sustainable and environmentally friendly energy solutions. Compared to non-renewable energy sources that harm the environment and human health, renewable energy sources like solar PV, WT, and EV are better options. A more affordable option to fossil fuels, which are limited resources that worsen the environment, is provided by renewable energy sources. Researchers are developing and improving renewable energy solutions to lessen society’s reliance on non-renewable resources and lessen the adverse consequences of climate change. Development is guided and incentivised by the Paris Agreement’s framework for mitigating climate change and national policy changes, such as India’s 500 GW objective and the EU Green Deal1.

However, the advantages mentioned above can only be fully realised if the ideal sizes of DG units are identified and subsequently deployed in the appropriate locations within distribution networks; failure to do so may lead to increased PLoss and voltage deviation. Driven by environmental and electricity demand concerns, numerous strategies have been proposed in the literature to place DGs into the RDS. To harness the optimal benefits of the DGs, it is crucial to place them optimally at a better ___location. Therefore, various researchers have come up with different types of optimisation techniques. The major goal of power systems is to supply all necessary power while preserving security, dependability, and cost-effective operation. Relying on additional generation sources and strengthening transmission capacity is crucial to addressing problems like the rise in power consumption and environmental concerns2. In3, an Artificial hummingbird algorithm (AHA) is used to place biomass-based DGs into the three test systems to mitigate the targets of reducing network losses and voltage deviation. In4, the authors analysed the impact of integrating DGs using an effective Jellyfish Search Algorithm (JSA) to minimise real PLoss and maximise profits. This article addresses a recent swarm optimisation technique, a backtracking search optimisation algorithm (BSOA), to assign distributed generators (DGs) along radial distribution networks to reduce active and reactive PLoss5. To minimise PLoss and enhance voltage profile and voltage stability index6, suggests a high-convergence optimisation technique for the best placement of distributed generation (DG) in distribution networks. Authors in7 describe a novel combination of genetic algorithm (GA)/particle swarm optimisation (PSO) for optimal placement of DGs to reduce network PLoss, enhance voltage regulation, and increase voltage stability. The Particle Swarm Optimisation (PSO) algorithm finds DG’s best ___location and optimal size8. Several methods are available in the literature for locating and sizing active and reactive power sources in radial distribution networks9,10,11,12,13,14. The primary goals of these articles are to lower network losses while raising the stability index and voltage profile. It is implemented in various IEEE test systems and verifies the robustness of the algorithms. In15,16 The authors aim to minimise total real PLoss and the total voltage deviation to enhance the distribution system performance using an improved genetic algorithm combined with local search (EGA) and salp swarm algorithm (SSA). It is implemented in various test systems. Authors17 study the economic benefits of integrating DGs into DS using the PSCAD/EMTDC simulation software package. An effective method is put forth to improve radial distribution networks’ security and dependability and optimise the planning of wind turbine generators and electric vehicle charging. In the IEEE 33-bus distribution test network, the method effectively increased security and reliability indices by sizable percentages18.

An RDS that uses renewable energy sources may suffer a significant loss because of the unpredictability of wind and solar irradiance. The intermittent and unpredictable nature of these sources can cause sudden changes in power output, leading to imbalances in the system and increased PLoss. Accurate solar irradiance and wind speed prediction are fundamental in managing the PLoss of RDS. Forecasting the potential variations in renewable energy sources provides valuable information to operators so they can plan and adjust power generation accordingly. By doing so, they can minimise PLoss and ensure a stable and reliable power supply. Advanced monitoring and control systems can also be used to manage the power flow and reduce losses in the distribution network.

In conclusion, accounting for the uncertainty associated with solar irradiance and wind speed is critical in managing the PLoss of RDS. It makes system planning and execution more effective while guaranteeing a steady and dependable power supply. Therefore, precise forecasting models and sophisticated monitoring and control systems must be developed to lower uncertainty and boost RDS efficiency. Electric vehicles (EVs) are becoming increasingly ubiquitous; by 2030, there will be over 40 million EVs on the road, drastically changing the nature of electric transportation and posing opportunities and challenges for the power grid19. EVs provide better performance and zero carbon emissions, but their integration requires careful thought because of the possibility of grid congestion. Electric vehicles (EVs) are generally known for their benefits to the environment, but integrating them into RDS can be tricky since, if not appropriately placed, they overwhelm the grid. The possible adverse effects of widely integrating electric vehicle charging stations (EVCS), such as voltage deviations, power factor degradation, harmonic distortion, and higher peak load demands, have been noted in several studies20,21,22.

Accordingly, to address the abovementioned problem, numerous research studies were conducted on the design, sizing, and optimal placement of the EVCS in Distribution Systems. In23, a novel method based on the Voltage stability, Reliability and PLoss (VRP) index is proposed to place the EV into the distribution system. It is analysed using the IEEE 33 test system. Similarly, the authors of24,25,26 studied the impact of placing the EVs optimally into the distribution system.

The interconnection of EVs increases the peak demand and degrades the voltage profile of the DS. Therefore, it is necessary to schedule the charging of EVs at suitable locations and time intervals. In27 authors discuss how to manage the burden of the EVCS by adding the DGs into the distribution systems. Additionally, studies have explored the co-optimisation of EV placement and DG allocation within RDS to minimise PLoss, improve voltage profiles, reduce the grid’s stress and maximise EVs’ benefits. The following literature contains a comprehensive analysis of the allocation problem for DGs and EVs: Kumar et al.28, Dharavat et al.29, Golive et al.30, Wang et al.31, Mehroliya et al.32, CB et al.33, Gampa S et al.34, Gautam et al.35 and Babu et al.36. In37, a new approach for optimizing the placement of shunt capacitors, electric vehicle charging stations, and distributed generation resources in power distribution networks is introduced. The suggested model integrates fuzzy and chaotic theory with competitive search optimization (CSO) to enhance power efficiency and voltage profiles. Plug in electric vehicles along with PVDG are optimized using the east delta network considering the reduced power loss, reactive power loss and minimum investment cost in38.

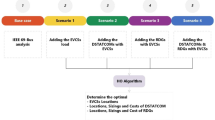
More studies in the existing literature about the joint optimisation of the architecture of electric vehicle charging stations (EVCS) and distributed generation (DG) deployment, as well as their combined effects on PLoss, voltage profiles, and environmental sustainability, need to be conducted This research suggests a novel method for placing DG optimally within RDS to fill this gap. The methodology considers the risks of renewable energy sources, including wind turbines (WT) and solar photovoltaic (PV) systems. It also discusses the best way to distribute EVs and the benefits of combining solar PV and wind turbines with EVCS. The efficacy of the suggested method is assessed using the Indian 28-bus test system and the MEWOA.

The following sums up this paper’s contribution:

Using the MEWOA algorithm, we developed a novel optimisation method for improving the voltage profile and active loss of renewable DG units in RDS.

  1. i.

    Determine the ideal size or sizes for RDGs and EVs using the suggested MEWOA algorithm.

  2. ii.

    Determine the solar PV array’s power production and WT for a year or four seasons using the Beta and Weilbull PDF.

  3. iii.

    Giving input to the suggested algorithms, the actual power output of the solar PV and WT, to determine the real active and reactive loss and how it affects the voltage profile.

  4. iv.

    When the EV is connected to the RDS, its fixed rating is considered to study its effects on active and reactive PLoss and the RDS’s voltage profile, with the EV acting as the additional load.

  5. v.

    A system with 28 tests evaluates the suggested algorithm’s robustness and effectiveness.

The best places for distributed generation (DG) are identified using the Voltage Stability Index (VSI), and the sizes of the EV and DG are determined by the MEWOA. The remaining portion of the paper follows the following structure:

Probabilistic modelling of RDGs

Solar and wind power generation is essential to a sustainable energy system. However, because wind speed, ambient temperature, and solar irradiation are all closely correlated with geographic ___location, their effectiveness heavily depends on these meteorological factors. To guarantee the effective use of photovoltaic (PV) arrays and wind turbines (WTs), it is crucial to thoroughly examine the features of solar radiation and wind conditions at possible installation locations. By paying close attention to details, renewable energy systems may be implemented more intelligently and effectively, leading to a more sustainable and eco-friendly future. When wind and solar generation units are deployed in distributed generation, a more comprehensive uncertainty analysis is necessary due to the load demand uncertainty on the power grid.

Modeling of solar irradiance

The Beta PDF39 estimates the sporadic nature of solar irradiance and is provided below:

$$\:{f}_{b}\left(s\right)=\frac{{\Gamma\:}(\alpha\:+\beta\:)}{{\Gamma\:}\left(\alpha\:\right)\:\cdot\:{\Gamma\:}\left(\beta\:\right)}\cdot\:\:{S}^{(\alpha\:-1)}\cdot\:{(1-S)}^{(\beta\:-1)}\:for\:\alpha\:>0;\:\beta\:>0$$
(1)

Where.

S is the solar irradiance (kW/m2).

\(\:{f}_{b}\left(s\right)\) is the Beta distribution function

\(\:\alpha\:\:\&\:\beta\:\) are the parameters of the Beta distribution function, and \(\:{\Gamma\:}\) represents the Gamma function.

The mean (µ) and standard deviation (σ) of the random variable are used in the following manner to get the parameters of the Beta distribution function [39]:

$$\:\beta\:=\:(1-\mu\:)\cdot\:(\frac{\mu\:(1+\mu\:)}{{\sigma\:}^{2}}\:-\:1)$$
(2)
$$\:\alpha\:=\:\frac{\mu\:\cdot\:\beta\:}{(1-\mu\:)}$$
(3)

The power generation of the PV array at solar irradiance (s) for the nth states is evaluated as

$$\:{P}_{PVn}\left(S\right)={N}^{PVm}*FF*{V}_{n}\:*{I}_{n}$$
(4)
$$\:FF=\:\frac{{V}_{MPP}*{I}_{MPP}}{{V}_{OC}*{I}_{SC}}$$
(5)
$$\:{V}_{n}={V}_{OC}*{K}_{v}*{T}_{cn}$$
(6)
$$\:{I}_{n}={S[I}_{SC}+{K}_{i}({T}_{C}-25)]$$
(7)
$$\:{T}_{cn}={T}_{A}+S\left(\frac{{N}_{OT}-20}{0.8}\right)$$
(8)

Where \(\:{N}^{PVm}\) is the total number of PV modules,

FF is the fill factor.

\(\:{T}_{A}\) is the ambient temperature (°C)

\(\:{T}_{cn}\) is the cell temperature at nth states

\(\:{K}_{v}\:\&\:{K}_{i}\) are the voltage and current temperature co-efficient (A/°C and V/°C)

\(\:{N}_{OT}\) is the normal operating temperature of a cell (°C)

\(\:{V}_{OC}\:and\:{I}_{SC}\) are the open circuit voltage (V), and short circuit current (A) at maximum power point.

$$\:P\left(S\right)\:={P}_{PVn}\left(S\right)*\:{f}_{b}\left(s\right)$$
(9)
$$\:Total\:Expected\:power\:output\:\left(TEPO\right)=\:\underset{0}{\overset{1}{\int\:}}P\left(S\right)$$
(10)

Modelling of the wind speed

Weibull PDF39 is used to estimate the stochastic behaviour of wind speed in a time segment as below:

$$\:{f}_{w}\left(\nu\:\right)\:=\frac{K}{C}\cdot\:{\left(\frac{\nu\:}{C}\right)}^{k-1}\cdot\:exp(-({\left(\frac{\nu\:}{C}\right)}^{k-1}\left)\right)\:for\:c>1;\:k>0.$$
(11)

Where,

K it the shape parameter and.

C is a scale factor.

The mean (µ) and standard deviation (σ) of the random variable are used in the following manner to get the shape parameter and scale factor of the Weibull distribution function;

$$\:k={\left(\frac{\sigma\:}{\mu\:}\right)}^{-1.086}$$
(12)
$$\:c\:=\frac{\mu\:}{\gamma\:(1+\frac{1}{k})}$$
(13)

The power generation of the wind turbine for the nonlinear performance curve for the nth state is provided below equation:

$$\:{P}_{WT}\left(\vartheta\:\right)=\:\left\{\begin{array}{c}0\:for\:\:\vartheta\:\le\:{\vartheta\:}^{cut-in}{\:and\:\:\vartheta\:\ge\:\vartheta\:}^{cut-out}\\\:a\cdot\:{\vartheta\:}^{3}+b\cdot\:{P}^{rated}\:for\:{\vartheta\:}^{cut-in}\le\:\vartheta\:\le\:{\vartheta\:}^{rated}\\\:{P}^{rated}\:\:for\:{\vartheta\:}^{rated}\le\:\vartheta\:{\:and\:\:\vartheta\:\ge\:\vartheta\:}^{cut-out}\end{array}\right.$$
(14)
$$\:a=\frac{{P}^{rated}}{{{\vartheta\:}^{rated}}^{3}-{{\vartheta\:}^{cut-in}}^{3}}$$
(15)
$$\:b=\frac{{{\vartheta\:}^{cut-in}}^{3}}{{{\vartheta\:}^{rated}}^{3}-{{\vartheta\:}^{cut-in}}^{3}}$$
(16)
$$\:P\left(WT\right)=\:{P}_{WT}\left(\vartheta\:\right)*\:{f}_{w}\left(\nu\:\right)$$
(17)
$$\:Total\:Expected\:power\:output\:\left(TEPO\right)=\:\underset{0}{\overset{1}{\int\:}}P\left(WT\right)$$
(18)

Modeling of EV charging station (EVCS)

EVCS is considered the additional load and depends on the charging of the SoC, trip distance and charge power29. The SoC of the kth EV at ith hour is given below equation:

$$\:{\text{S}\text{o}\text{C}}_{\text{i}}^{\text{k}}=\left(1-\frac{\text{t}\text{*}\text{d}}{{\text{d}}_{\text{c}}}\right)\cdot\:100\text{\%}$$
(19)

Battery Storage constraints of the EV is given by:

$$\:{SoC}^{min}\le\:{SoC}_{i}^{EV}\le\:{SoC}^{max}$$
(20)
$$\:{P}_{i,d}^{ch}\le\:{P}_{max,\:i}^{ch}$$
(21)
$$\:{P}_{i,d}^{disch}\le\:{P}_{max,\:i}^{disch}$$
(22)

Where,

t is the no. of trips, d is the distance travelled by EV, \(\:{d}_{c}\) is the distance covered by EV in the range

Problem formulation

The unique methodology focuses primarily on maximising PLoss reduction and voltage profile improvement by allocating solar, wind, and electric vehicles (EVs) in the RDS in the best possible way. The overall real PLoss is expressed below:

$$\:min\sum\:_{b=1}^{24}{P}_{LOSS}$$
(23)
$$\:{P}_{LOSS}=\sum\:_{b=1}^{24}\left({I}^{2}*{R}_{b}\right)$$
(24)

The bus voltage should be maintained within the permissible limits and power generation should be equal to the power demand and PLoss in the RDS. The voltage and power constraints are provided below:

$$\:{V}_{min}^{b,\:i}\le\:{V}_{b,\:i}\le\:{V}_{max}^{b,i}$$
(25)
$$\:{P}_{DG}^{min}\le\:{P}_{DG}\le\:{P}_{DG}^{max}$$
(26)
$$\:\sum\:_{b=1}^{24}{P}_{G}^{SS}+\sum\:_{b=1}^{24}{P}_{DG}^{PV}+\sum\:_{b=1}^{24}{P}_{DG}^{WT}={\sum\:}_{b=1}^{24}\left[{P}_{Demand}+{P}_{EV}+{P}_{Loss}\right]$$
(27)

Where,

\(\:{P}_{G}^{SS}\) is power generated from the grid substation,

\(\:{P}_{DG}^{PV}\) is power generated by solar PV DGs

\(\:{P}_{DG}^{WT}\) is power generated by WT DGs

\(\:{P}_{Demand}\) is the total demand of the system

\(\:{P}_{EV}\) is the power consumed by the EV while charging

\(\:{P}_{Loss}\) total system losses.

Voltage stability index (VSI)

The voltage stability indicator (VSI)40, is a vital power system tool. It helps to understand the probability of voltage collapse and identify weak or strong buses in the system. Additionally, the VSI can help find the best places to distribute energy resources (DERs). Using the VSI, power system operators can better decide where to put DERs and how to improve their system’s voltage stability. The bus is stronger if the VSI value is closer to 1, and the weak bus is if the VSI value is closer to 0. Figure 1represents the VSI value of each bus without considering any DG and EV. The red column indicates the weak bus, and the green column indicates the stronger bus, according to the VSI. The solar PV and WT will be placed in the weaker buses, and EVs will be placed in the stronger buses identified by VSI. VSI is calculated from the load flow solution data as given in the equation below41:

$$\:VSI=2{V}_{1}^{2}{V}_{2}^{2}-{V}_{2}^{4}-{2 V}_{2}^{2}\left(PR+QX\right)-\left({P}^{2}+{Q}^{2}\right){\left|Z\right|}^{2}$$
(28)
Fig. 1
figure 1

The VSI value at the base case (without DG and EV) shows the weak and strong buses.

Full size image

Optimisation algorithm

WOA is an optimisation technique developed by Mirjalili S. in 2019 to solve single and multi-objective optimisation problems in various fields. However, WOA frequently experiences rapid local optimum and delayed convergence and may become trapped in undesirable outcomes. Additionally, it can be challenging to investigate the entire solution space efficiently. Therefore, Ya Shen et al. developed improved versions of the WOA addressing these shortcomings in 2022. MEWOA unveils a unique feature based on the evolution of multi-population and is a vital tool for optimising complicated problems in power systems, such as integrating PV, WTs, and EVs into RDS. MEWOA imitates humpback whale hunting techniques, such as encircling prey to investigate it and using bubble nets to harvest it with exploration and exploitation methods. The MEWOA algorithm groups the whale population into three sub-populations based on their fitness levels. Individuals with poor fitness levels are categorised as exploratory sub-populations, those with good fitness levels as exploitative sub-populations, and those in between, good and bad, are classified as modest sub-populations. Each sub-population consists of an equal number of individuals and follows a distinct moving strategy, as shown in Fig. 2.

Fig. 2
figure 2

Evolution strategy of MEWOA.

Full size image

Each moving strategy of each sub-population can be represented using the following equations:

  1. i.

    Exploratory sub-population.

The movement of the whale moving randomly to explore globally is represented by Eq. 6, when the |A|>1;

$$\:X(t+1)={X}^{rand}\left(t\right)-A\cdot\:|C\cdot\:{X}^{rand}(t)-X(t\left)\right|$$
(29)

Where: \(\:{X}^{rand}\) is the random whale picked from the current population at the \(\:{t}^{th}\) iteration. |A| is the absolute value of A. X(t) is a whale whose position vector needs to be updated. A and C are the coefficient random vectors between (0,1).

  1. ii.

    Exploitative sub-population.

Usually, the whales swim in the decreasing circle of the prey, so there is a 50% probability of catching the prey and a 50% possibility of not getting the prey. Therefore, this process can be represented by Eq. 5.

$$\:X(t+1)=\left\{\begin{array}{c}X*\left(t\right)-A\cdot\:|C\cdot\:X*(t)-X(t\left)\right|\:\:if\:p<0.5\\\:\left|X*\right(t)-X(t\left)\right|\cdot\:{e}^{bl}\cdot\:cos\:\left(2\pi\:l\right)+X*\left(t\right)\:if\:p\ge\:0.5\end{array}\right.$$
(30)

Where X*(t) is the position vector of the best whale, p is the random vector between (0,1). b is the constant number usually set at 1, and l is the random number between [−1,1].

  1. iii.

    Modest sub-population.

$$\:X(t+1)=\left\{\begin{array}{c}\left\{\begin{array}{c}X*\left(t\right)-A\cdot\:|C\cdot\:X*(t)-X(t\left)\right|\:\:if\:{p}_{1}<0.5\\\:\left|X*\right(t)-X(t\left)\right|\cdot\:{e}^{bl}\cdot\:cos\:\left(2\pi\:l\right)+X*\left(t\right)\:if\:{p}_{1}\ge\:0.5\end{array}\right.\:if\:{p}_{2}<0.5\\\:{X}^{rand}\left(t\right)-A\cdot\:|C\cdot\:{X}^{rand}(t)-X(t\left)\right|\:if\:{p}_{2}\ge\:0.5\end{array}\right.$$
(31)

Once the positions of the individuals are updated, with every iteration, the population evolution is also considered to increase the population’s search diversity, escape local optima, and accelerate convergence. The following equations represent the population evolution of the sub-populations.

  1. i.

    Exploratory sub-population.

$$\:X(t+1)=X\left(t\right)\cdot\:{r}_{1}$$
(32)

Where \(\:{r}_{1}\) is the random number between (1,2).

  1. ii.

    Exploitative sub-population.

$$\:X(t+1)={X}^{*}\left(t\right)\cdot\:{r}_{2}$$
(33)

Where \(\:{r}_{2}\) is the random number between (0,2) and \(\:{X}^{*}\left(t\right)\) is the position vector of a present optimal solution.

  1. iii.

    Modest sub-population.

$$X(t+1) = \left\{ \begin{array}{ll} X^{(t)}\, if\, fit (X^{(t)})\, is\, better\, then\, fit (X(t))\\ X(t)\, else \end{array} \right.$$
(34)
$$\:X^{(t)}=lb+ub-X(t)$$
(35)

Where \(\:X^{(t)}\) is the new position of the objective function, lb is the lower boundary, ub is the upper boundary and fit () is the objective function of the problem.

The sequence of steps of MEWOA is provided as follows:

Step 1. Read the system data of the proposed test system.

Step 2. Run the Backward Forward DLF.

Step 3. Using the VSI method, calculate the VSI of each bus.

Step 4. Identify the weak and strong buses for allocating DGs and EVs, respectively. Accordingly, the information will be provided to the MEWOA algorithm.

Step 5. Initialize the parameters of the MEWOA (population sizes, maximum iteration, lower bound, upper bound, and the dimension of the fitness function, and set the current iteration to 1).

Step 6. Compute the fitness of all individuals and select the best fitness values as the current optimal solution.

Step 7. Divide the population into three sub-populations based on fitness levels: exploratory, exploitative, and modest.

Step 8. According to the current iteration number, update the position as per Eqs. 29, 30, and 31 if the iteration is odd and update the population as per Eqs. 32, 33, and 34 if it is even.

Step 9. Then, update the fitness values (PLoss).

The MEWOA flow chart is represented in Fig. 3.

Fig. 3
figure 3

Flow chart of MEWOA.

Full size image

Results and discussion

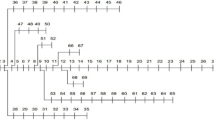
This section describes implementing the proposed technique in the Indian 28 test system. Figure 4 depicts the single-line diagram of the 28-bus test system, which consists of 27 branches and 28 buses operating at a base voltage of 11 kV. The system’s total demand load is 776.42 kVar and 761.04 kW. The main objectives of this paper are to optimise the goal functions of the RDS, which include minimising PLoss, improving the voltage profile, and maximising VSI. Several possibilities are examined in this work in the following ways:

  1. i.

    Effects of RDGs on system losses and voltage profile.

  2. ii.

    Solar PV and WT affect system losses and voltage profile considering uncertainty for different seasons.

  3. iii.

    Effects of EVs on system losses and voltage profile without DGs.

  4. iv.

    Effects of DGs and EVs on system losses and voltage profile.

Fig. 4
figure 4

Single-line diagram of 28 test systems with two DGs and two EVs.

Full size image

Effects of RDGs on system losses and voltage profile

The suggested method was first implemented and evaluated for the base case, which uses the standard line and bus data of the 28-test system to perform the backwards-forward distribution load flow (DLF) to obtain the active PLoss. This article also simulates the various load profiles 24 h after integrating one DG and two DGs into the RDS. Table 1 lists the simulated outcomes of the base case, one DG and two DGs active and reactive PLoss. As per the findings presented in Table 1, it is evident that the PLoss experienced by the system is directly proportional to the load demand of the customers. At full load demand (at 18 h), the active PLoss reaches its maximum value of 68.8189 kW, and the reactive PLoss reaches its maximum value of 46.0416 kVar. However, at 50% load demand (4 & 5 h), the active PLoss is 21.751 kW, and the reactive PLoss is 14.55 kVar.

To validate the objective of reducing PLoss and enhancing the voltage profile, a distributed generator (DG) was incorporated at bus ___location 7 in the RDS. The results of this addition revealed a significant decrease in active PLoss to 37.0066 kW and reactive PLoss to 24.3207 kVar at full load demand (18 h) and active PLoss to 12.1178 kW and reactive PLoss to 7.9626 kVar at 50% load demand. Further, two DGs are added into the RDS, and the active and reactive PLoss is further reduced to 36.53 kW and 24.12 kVar, respectively, for full load demand. Therefore, adding DGs can significantly lower the PLoss and raise overall voltage profiles and VSI. The effects of DGs on voltage profile and VSI are graphically represented in Figs. 5 and 6, respectively.

Table 1 Analysis of active/reactive PLoss in DN: base case vs. single/double DG scenarios.
Full size table
Fig. 5
figure 5

Voltage profile of the 28-bus system with different scenarios.

Full size image
Fig. 6
figure 6

Voltage stability index (VSI) of the 28-bus system with different scenarios.

Full size image

Solar PV and WT affect system losses and voltage profile considering uncertainty for different seasons.

A 250 kW WT and a 600 PV module 132 kW Solar PV array are used to precisely analyse wind and solar power’s erratic and intermittent characteristics. The Solar PV and WT specifications are provided in Tables 2 and 3, respectively. This study chose a year as the study period, which was divided into four seasons. A typical day is generated for each season to reflect the random behaviour of the various renewable resources over time. It is standard procedure to employ probability density functions (PDFs) to estimate the hourly wind speed and solar irradiance data in this investigation. The Weibull and Beta distributions are two popular PDFs. These distributions are often discretised by dividing the data into a predetermined number of states. In this case, the number of states chosen for the Beta and Weibull PDFs were 20 and 15, respectively. The distribution of hourly wind speed and solar irradiance at the research ___location can be more precisely modelled and analysed by discretising the data in this way. The power output of solar irradiance at 11 h during summer and autumn and 12 h during winter and spring has been graphically represented in Fig. 7.

Similarly, Fig. 8 depicts the power output of wind speed for specific hours during the four seasons. These representations provide a comprehensive and visual understanding of the power output fluctuations of both solar irradiance and wind speed throughout the year. The summarised power output generated by the solar irradiance and wind speed are illustrated in Fig. 9. The total of 96-time segments representing four seasons is depicted in Fig. 9. It can be seen that solar irradiance is maximum during noon for all four seasons, and wind speed is maximum during the spring and summer seasons.

Table 2 Specification of Solar PV39.
Full size table
Table 3 Specification of WT39.
Full size table
Fig. 7
figure 7

Power output of solar irradiance for four seasons.

Full size image
Fig. 8
figure 8

Power output of wind speed for four seasons.

Full size image
Fig. 9
figure 9

Hourly power output of solar and wind for four different seasons.

Full size image

After obtaining the actual power output of the solar photovoltaic (PV) and wind turbine (WT), their outputs are incorporated into a 28-test system to investigate the impacts of these distributed generators (DGs) on PLoss and voltage profiles. Initially, a single solar PV with a rating of 132 kW is connected to the 28-test system at bus ___location 7. Subsequently, two solar PVs are connected at bus locations 7 and 25, respectively, to study the effects of the uncertainty of solar irradiance. The results obtained from the experiments are carefully tabulated in Table 4. The methodology used in this investigation offers empirical evidence that integrating single and two Solar PVs results in a slight decrease in PLoss, specifically to 57.0926 kW and 47.6817 kW during the 11 h in summer. It should be noted that this methodology has applicability across all seasons, given that the solar irradiance is at its maximum during the 11 h across all seasons. These findings underscore the potential of Solar PVs as a viable solution to address PLoss, highlighting the significance of considering seasonal variations in solar irradiance when designing solar PV systems.

Table 4 Comparison of active PLoss for integrating single SPV and two SPV DGs to the DN considering the uncertainty of solar irradiance for four seasons.
Full size table

Like solar PVs, wind turbines are integrated into the 28-test system to examine their effect on power system stability. To begin with, a 250 kW-rated WT is linked at bus ___location 7. Following that, two wind turbines are connected at bus locations 7 and 25 to analyse how wind speed unpredictability affects the system. The outcomes from these trials are meticulously documented in Table 5. According to the data in Table 5, the wind speed reaches its highest during spring, specifically at noon, resulting in a PLoss of 40.1782 kW.

Conversely, wind speeds are noticeably lower during autumn, resulting in a corresponding decrease in PLoss. The presented study focuses on the effects that wind turbine and solar PV penetration have on RDS concerning PLoss and voltage profiles during different seasons. Figure 10 illustrates the different scenarios of PLoss. The voltage profiles at three different times, considering the uncertainty of WT, are represented in Fig. 11. The figures indicate that the voltage profiles vary according to their power output.

Table 5 Comparison of active PLoss for integrating single WT and two WT DGs to the DN considering the wind speed uncertainty for four seasons.
Full size table
Fig. 10
figure 10

Hourly PLoss of Solar and Wind for four seasons (Summer, Autumn, Winter, and Spring) considering uncertainty.

Full size image
Fig. 11
figure 11

Voltage profile graph of 1 WT integration considering the wind speed uncertainty at three different times (summer).

Full size image

Effects of EVs on system losses and voltage profile without DGs

Reducing carbon emissions and supporting sustainable mobility are two reasons the distribution system’s integration of electric vehicles (EVs) has attracted much interest. However, the integration of these vehicles can have a significant impact on PLoss and voltage profile within the RDS. Therefore, EV charging stations are connected to the RDS at different bus locations identified by VSI to verify its effects on RDS. This paper uses the proposed algorithm to study the effects on PLoss and voltage profile. The detailed specifications for EVs are provided in Table 6. Using the specification provided in Table 6, the rating of the EV charging station is calculated as 142 kW. One EV charging station is initially connected to charge at bus ___location 2. Subsequently, two EV charging stations are connected to the RDS at bus locations 2 and 11. The simulated results of PLoss and voltage profile for 24 h are tabulated in Table 7. With the addition of the EV, the load demand in the RDS increases, and based on the rating of the EV charging station, the PLoss increases slightly based on the power consumed by the EV while charging. From Table 7, results clearly show that with the addition of one EV at ___location 2, the PLoss increased to 70.6467 kW from 68.8195 kW, and when two EVs were added to the RDS at 2 and 11, PLoss increased to 84.3528 kW from 68.8195 kW. However, the voltage profile is decreased to 0.9108 (p.u) and 0.9048 (p.u) from 0.9123 (p.u) with the addition of single and two EVs into RDS, respectively.

Table 6 Specification of EV29.
Full size table
Table 7 Active and reactive PLoss with integration of EVs.
Full size table

Effects of DGs and EVs on system losses and voltage profile

With DG integration, there were benefits such as reduced PLoss and improvement. However, with the addition of an EV charging station into RDS, the PLoss increased, and the voltage profile was affected. So, to study the effects of DGs along with EVs, the proposed technique is implemented into the Indian 28 test system. This work uses VSI to determine the optimal ___location of DG and EV, and the MEWOA technique is used to determine their optimal sizes. We consider the EV charging station to have a fixed rating. Among 60 EVs, this paper considered placing 30 EVs into the two bus locations, 2 and 11. Initially, 30 EVs each, along with PV and WT at different locations, are integrated and simulated results are tabulated in Table 8. From Table 8, as highlighted in bold, the active and reactive PLoss decreases with the integration of two DGs as it compensates for the power consumed by the EVs. Figures 12 and 13 present the voltage profile and VSI under various circumstances. The MEWOA results are compared with six optimisation techniques: GWO, WOA, POA, FPA, and GOA. The parameters of each algorithm are set as follows: search agent = 20, and maximum number of iterations as 50. Table 9 tabulates the simulated results. It is clear from Table 9 that the proposed algorithm provides the best (lower) value of power losses and improved voltage profile. Results of MEWOA are highlighted in bold in Table 9. The convergence curve of different algorithms is shown in Fig. 14. However, there is no convergence curve for FPA, and the GOA convergence curve is omitted as its final values are very high (42.097 kW) for full load demand. Figure 15 depicts the voltage profile of different algorithms.

Table 8 Active and reactive PLoss with integration of DGs along with EVs.
Full size table
Fig. 12
figure 12

Voltage profile of different scenarios.

Full size image
Fig. 13
figure 13

VSI of different scenarios.

Full size image
Table 9 System performance with different algorithms.
Full size table
Fig. 14
figure 14

Convergence curve for different algorithms.

Full size image
Fig. 15
figure 15

Voltage profile of different algorithms.

Full size image

Conclusion

This paper discusses identifying the weak and strong buses using the VSI for the Indian 28 test system and the optimal allocation of the general RDGs and Solar PV and WT considering uncertainty. The MEWOA algorithm has been adopted to allocate the DGs and EVs optimally. The Beta and Weibull probability distribution functions are employed to model the uncertainties of the Solar PV and WT DGs. The distribution system is integrated with different scenarios considering the combination of DGs, Solar PV, WT, and EVs at various bus locations. The simulated results show that the power losses decrease when the single or double DGs are integrated into RDS. However, when the EVs with fixed ratings are connected to the RDS, the power losses increase slightly depending upon the rating of the EV charging stations. To harness the optimum benefits from the RDGs, DGs and EVs are integrated simultaneously into the RDS, obtaining the optimal power losses and improved voltage profile. In addition, the effects of uncertainties of solar PV and WT are studied in this paper. Uncertainties of solar PV and WT are generated for 24 h for a year. Due to dependency on solar irradiance and wind speed, the power outputs vary throughout the day. However, with uncertainty, the planning engineers will benefit precisely during load generation and planning process forecasting. The future scope of this work, related to different types of EVs and its charging and discharging patterns and driving patterns, needs to be considered for better assessment.