Exploring optimal control strategies in a nonlinear fractional bi-susceptible model for Covid-19 dynamics using Atangana-Baleanu derivative

The emergence of the novel SARS-CoV-2 led to the Coronavirus pandemic, marking one of the most substantial global challenges in recent history. In December 2019, health authorities identified the virus as the main culprit behind multiple cases of pneumonia in Wuhan, China¹. The Coronavirus outbreak began in China that year and quickly disseminated across borders, escalating into a pandemic by March 2020. Its widespread impact extended to over 223 countries and territories across Asia, Australia, America, Europe, and other regions. The virus, officially named Covid-19, belongs to the family of Coronaviruses, which also includes viruses like SARS and MERS. Covid-19 has indeed resulted in millions of deaths worldwide and has had far-reaching effects on economies, including those of well-developed nations. Lockdowns, travel and trade restrictions, disruptions to supply chains, unemployment, and changes in consumer behavior have all played a significant roles in economic downturns and fluctuations in Gross domestic product (GDP). The virus is highly transmissible among individuals, spreading through both direct and indirect physical contact². The virus primarily spreads through respiratory droplets when an infected person coughs, sneezes, talks, or breathes. These droplets can land in the mouths or noses of people nearby or be inhaled into the lungs, thus infecting them. Additionally, touching surfaces contaminated with the virus and then touching the face (mouth, nose, or eyes) can also contribute to the transmission of the virus³. Therefore, practicing good hygiene, wearing masks, and maintaining physical distance are important measures to reduce the risk of transmission.

The incubation period of Covid-19, which is the time between exposure to the virus and the onset of symptoms, typically ranges from 2 to 14 days. However, it is essential to note that some individuals infected with the virus may remain asymptomatic throughout the entire incubation period and still be able to transmit the virus to others⁴. This aspect of asymptomatic transmission has been one of the challenges in controlling the spread of Covid-19. The majority of individuals who contract Covid-19 typically undergo mild to moderate respiratory symptoms, which may include severe headaches, muscle pains, cough, runny nose, exhaustion, fever, bloody diarrhea, sore throat, trouble sleeping, and vomiting. However, there are more severe symptoms that could indicate a potentially dangerous condition, including chest pain, confusion, difficulty breathing, loss of speech or mobility^5,6,7. Seeking emergency medical help for these severe symptoms is essential for timely treatment and preventing complications. Individuals with co-morbid conditions, including hypertension, diabetes, those aged 60 years or older, respiratory infections, and compromised immune systems are indeed at higher risk for severe illness from Covid-19^8,9. Such individuals often experience more severe symptoms and complications if they contract the virus compared to younger, healthier individuals. Taking extra precautions, such as following hygiene protocols, wearing masks, practicing social distancing, and getting vaccinated, can help mitigate the risk of contracting the virus. Moreover, consulting with healthcare professionals for personalized guidance on managing underlying health conditions during the pandemic is advisable. The recovery rate from Covid-19 can vary depending on various factors such as age, underlying health conditions, access to healthcare, and the strain of the virus. During the early stages of the Covid-19 pandemic, it was estimated that around 80–85\(\%\) of people who contracted the virus experienced mild to moderate symptoms and recovered without needing hospitalization or significant medical intervention^4,5. This percentage might include asymptomatic cases as well.

Mathematical modeling of infectious diseases offers a multitude of benefits in our quest to understand, manage, and mitigate the impact of epidemics^10,11,12. These models provide the capacity to predict and forecast disease trajectories by considering factors like transmission rates, population dynamics, and intervention strategies, helping healthcare systems and policymakers to prepare for potential challenges^13,14,15. Moreover, they evaluate the effectiveness of various interventions, offering insights into social distancing measures, vaccination campaigns, and treatments options. By simulating diverse scenarios, these models help identify the most efficient and cost-effective strategies for controlling disease spread. Additionally, mathematical models also aid in the optimization of resource allocation, guiding decisions on hospital capacity, resource management, and medical supply distribution during an epidemic. Furthermore, they can serve as early warning systems, alerting authorities to potential outbreaks and facilitating proactive containment efforts. These models are invaluable for hypothesis testing, contributing to a deeper understanding of infectious disease dynamics and guiding experimental research. Policymakers rely on mathematical modeling to shape public health policies based on evidence and data-driven recommendations. Beyond this, epidemic models help address ethical considerations, balancing the protection of public health with individual freedoms and rights, including privacy and informed consent. By learning from past outbreaks, adapting to changing conditions, and promoting global collaboration, mathematical modeling enhances our preparedness and response to infectious diseases, contributing to better outcomes for affected populations¹⁶. Overall, mathematical modeling plays a pivotal role in aiding public health, medical research, and the allocation of resources during epidemics, ultimately leading to better outcomes for affected populations.

In epidemic models, ’memory effects’ refer to how past events or interactions influence the current state of the epidemic. These effects acknowledge that the dynamics of an epidemic are influenced not only by present factors but also by historical trends, such as previous outbreaks, interventions, population behaviors, and healthcare infrastructure. By incorporating these memory effects, epidemic models can provide more accurate predictions and insights into ongoing epidemic, intervention effectiveness, and the resilience of healthcare systems. This comprehensive understanding facilitates better-informed decision-making for public health authorities, policymakers, and stakeholders involved in epidemic control and preparedness efforts. Traditional integer-order models, which assume instantaneous reactions, fail to capture adequately their complex dynamics influenced by past events^17,18,19. To better understand these memory effects, fractional-order models or other advanced mathematical frameworks may be necessary. Fractional-order models^{20,21,22,23,24,25,26,27} can accommodate non-instantaneous reactions, memory, and hereditary effects, providing a more nuanced depiction of the epidemic dynamics and improving the accuracy of predictions and intervention strategies.

Fractional calculus applied to epidemic models represents a sophisticated advancement in the mathematical modeling of infectious diseases²⁸. Traditional epidemic models, relying on ordinary differential equations, are enhanced by replacing these standard derivatives with fractional derivatives. This adaptation introduces the concept of memory effects, allowing the model to capture the nuanced dynamics of diseases where individuals retain immunity or susceptibility over extended periods²⁹. As a result, fractional-order models offer a more precise and accurate depiction of the intricate behavior of infectious diseases in contrast to integer-order models. The fractional models also excel in representing long-range dependencies inherent in the spread of infectious diseases, contributing to a more realistic portrayal of real-world scenarios. Applications of fractional epidemic models include the fitting of real-world epidemiological data with increased accuracy, accommodating the complexities of disease transmission and recovery³⁰. However, challenges in solving fractional differential equations exist, often necessitating specialized numerical techniques. Despite these challenges, ongoing research explores various applications of fractional calculus in epidemic modeling, considering different diseases and population structures, with the potential to further improve predictive capabilities and enhance our understanding of the intricate interactions within populations during epidemics^31,32.

The literature has introduced various fractional operators that include both singular and non-singular kernels^28,33. These operators have found application in various recent studies^34,35 aimed at understanding the dynamics of infectious diseases. The fundamental limitation of operators like the Riemann-Liouville and Caputo derivatives lies in the inherent singularity property of their kernels^28,36. Recognizing this limitation, some researchers have identified the need for fractional operators incorporating non-singular kernels. Significant progress has been made in developing fractional operators with non-singular kernels, as demonstrated by the Caputo-Fabrizio (CF) fractional operator^37,38,39. Atangana and Baleanu made an innovative contribution by introducing the ABC fractional derivative operator featuring a Mittag-Leffler kernel characterized by a single parameter^40,41. The ABC operator offers a key advantage due to its non-local and non-singular kernel, making it an invaluable asset for researchers within this ___domain. Recent studies has explored novel developments and extensive inquiries into fractional biological systems using the ABC derivative operator^{42,43,44,45,46,47,48}. These studies contribute to advancing our understanding of complex biological systems through the application of refined fractional operators with non-singular kernels.

Optimal control theory finds applications in analyzing fractional epidemic models and offers several distinct advantages⁴⁹. Firstly, it provides a sophisticated framework to systematically optimize control strategies for containing infectious diseases, such as Covid-19. This optimization is crucial for minimizing infection rates and public health impacts. Secondly, fractional order models, which represent a more nuanced and realistic approach to capturing the complexities of epidemics, can be effectively integrated with optimal control theory^50,51,52. This collaboration facilitates a deeper comprehension of the fundamental dynamics and characteristics of infectious diseases. Furthermore, the use of fractional calculus enables the modeling of memory effects and long-range interactions, which are often observed in real-world epidemiological data. As a result, optimal control strategies designed within this framework tend to be more adaptable and responsive to the evolving nature of the disease and the efficacy of interventions. The combination of optimal control theory and fractional epidemic models offers a powerful toolset for both comprehending and mitigating the spread rate of infectious diseases, making it valuable in the context of contemporary global health challenges.

In particular, fractional optimal control analysis of epidemics presents a cutting-edge approach with several notable advantages. Firstly, fractional calculus, which allows for modeling non-integer order derivatives, is instrumental in capturing the long-term memory effects and complex dynamics often observed in infectious disease spread. This advanced modeling approach enables a more accurate representation of real-world epidemiological data. When integrated with optimal control theory, fractional models provide a systematic means to optimize intervention strategies. These strategies can include a wide range of measures, such as vaccination campaigns, quarantine protocols, healthcare resource allocation, and public health policies. The fractional optimal control framework allows for the fine-tuning of these strategies to minimize infection rates and mitigate the impact of epidemics. Moreover, fractional optimal control analysis offers the flexibility needed to adapt control measures as the epidemic evolves. It takes into account the effectiveness of interventions and their impact over time, making it a valuable tool in dynamic and unpredictable disease scenarios. Optimal control strategies have been widely applied in numerous mathematical models related to Covid-19^49,50,51,52 to curb pandemic outbreaks. These articles deeply investigate the creation of mathematical frameworks for understanding Covid-19, employing diverse analytical and numerical methods to identify essential optimization criteria for both control and state variables. Consequently, control methodologies have become a highly versatile tool for modeling biological challenges, offering valuable insights into the management and mitigation of infectious disease outbreaks.

Motivation and problem description

Multi-susceptible epidemic models categorize the susceptible population into two or more primary groups, irrespective of gender distinctions. These groups may exhibit varying susceptibilities to the virus, influenced by factors such as age, pre-existing health conditions, genetic predisposition, access to healthcare, behavioral tendencies, and other relevant characteristics affecting the likelihood of contracting the disease. It is worth mentioning that not all susceptible individuals within a population face the same risk of contracting Covid-19 due to variations in exposure risk, immune response, adherence to preventive measures, and vaccination status. Through this categorization, the multi-susceptible system enhances understanding of disease transmission patterns and facilitates more precise predictions and interventions for controlling the spread of infectious disease spread.

In our latest research, we have successfully developed a novel \(S_{1}S_{2}V_{1}V_{2}IHR\) Covid-19 model by incorporating two distinct compartments for both the susceptibility and vaccination. To our knowledge, there have been no prior investigations into the mathematical aspects of the fractional version of this model particularly when considering the application of the ABC derivative and its implications in optimal control analysis. This nonlocal fractional operator has proven to be remarkably robust and an ideal choice for capturing complex dynamics in various scientific domains. By employing this operator, we can investigate the fractional version of newly constructed bi-susceptible model, allowing us to gain a more profound understanding of its behavior and implications. As the world continues to navigate the complexities of the Coronavirus pandemic, ongoing efforts focus on vaccination campaigns, public health measures, and adapting to a changed societal landscape. The pandemic has prompted reflection on global preparedness for health emergencies and the need for collaborative approaches to address future challenges. Our research thus breaks new ground and offers a novel perspective on the dynamics of Covid-19. In this endeavor, we aim to offer valuable insights to support the ongoing fight against the Covid-19 pandemic. Our goal is to inform potential strategies for vaccination and treatment campaigns, alongside other public health interventions.

Details of the research work

To better understand the infection dynamics in humans, we suggest employing the Atangana-Baleanu operator in conjunction with the developed Coronavirus model. Our model accounts for two vaccinated groups of people who have completed an adequate vaccination programme at their susceptibility levels, reflecting the efficiency and safety of vaccination in preventing Corona infectious disease. Throughout history, vaccination has proven to be the most effective and reliable approach to halt the spread of all contagious illnesses, serving as a crucial intervention in public health^48,53,54. Using the ABC fractional model, we aim to assess comprehensively the combined impact of well-established hospitalization and vaccination techniques on individuals of the host population. We are particularly interested in identifying both time-dependent and consistent (constant in time) control strategies for the Covid-19 host population. Our analytical work focuses on key model features, such as solution positivity, invariant regions, threshold values, and stability analysis. We employed well-known Toufik-Atangana numerical approach^55,56 to address the developed model, aiming to examine the impacts of hospitalization and vaccination strategies on the spread of Coronavirus disease. Additionally, we conduct sensitivity analysis to pinpoint parameters exhibiting the highest sensitivity indices. Furthermore, we explore an optimal control problem to identify the most efficient time varying mandatory measures for susceptible and infected individuals^57,58,59. We derive necessary conditions for optimally designed controls using the Hamiltonian and Pontryagin’s Maximum Principle (PMP)^60,61,62. We utilize the Toufik-Atangana numerical method and have developed its backward in time version to effectively solve these optimality conditions. This specific numerical approach has not previously been applied to fractional optimal control problems, particularly in solving adjoint systems that require a backward-in-time version. To improve our understanding of the biological factors associated with the control problem, we perform supplementary numerical simulations both before and after the optimization process. The numerical results illustrate that the proposed numerical scheme preserves the fundamental characteristic of the model, providing a robust depiction of the fractional problem.

Manuscript structure

The manuscript consists of six distinct sections. In Section “Coronavirus disease modeling”, we provide a comprehensive explanation of our process in deriving the compartmental model, utilizing the ABC operator to transform it into a fractional form. Section “Analytical investigation of fractional model”, we delve into an analytical exploration of essential mathematical properties associated with the ABC fractional model to assess its qualitative behavior. It has been established that the solutions persist within positive bounds, maintaining their positivity and boundedness. Additionally, we ascertain the equilibrium states in a dynamical system and calculate the threshold number analytically, which provides insights into the prospective dynamics of the disease. The stability of the fractional model at equilibrium points is rigorously demonstrated both in local and global context. In Section “Analysis of a model under constant controls”, we conduct a comprehensive numerical analysis and provide associated discussions, graphical representations, and vital predictions. A numerical approach is employed to estimate solutions for the model and assess the influence of the fractional order. Further investigation is conducted into the effects of consistent, time-invariant mandatory measures on the disease dynamics. Moreover, a comprehensive sensitivity analysis of the Covid-19 model is carried out. Section “Optimal control design” introduces an optimal control problem that integrates time-dependent controls. The main goal is to identify the most efficient strategies for implementing hospitalization and vaccination for the eradication of Covid-19. Seeking to minimize the number of infected individuals while minimizing costs, we examine the control problem and the related Pontryagin-type optimality conditions. The backward-in-time implemented Toufik-Atangana scheme is utilized to solve the optimum problem and obtain extremals for various fractional order values. The examination of the Corona optimum problem reveals the efficacy of the implemented controls and their influence on population dynamics both prior to and following optimization. We draw conclusions of our work and offer suggestions for potential avenues of further research in Section “Conclusions and recommendations”.

Multiple methods exist to model the spread of Covid-19 within human communities, each built upon distinct assumptions, offering diverse perspectives on transmission dynamics^63,64,65. One potential model is the proposed real-world \(S_1S_2V_1V_2IHR\) model, called bi-susceptible system, which examines the dynamics of the seven distinct human groups or compartments outlined below:

The bi-susceptible system categorizes the susceptible population into two primary groups, regardless of gender differences. These groups exhibit different susceptibilities to the virus due to various factors such as age, pre-existing health conditions, genetic predisposition, healthcare access, behavioral patterns, or other relevant characteristics that may influence the likelihood of contracting the disease. However, within a human population, not every susceptible individual is equally likely to become infected with Covid-19 due to variations in exposure risk, immune response, adherence to preventive measures, and vaccination status. By partitioning the susceptible population into two distinct groups, the bi-susceptible system enables a deeper comprehension of disease transmission patterns and can lead to more accurate predictions and interventions for controlling the spread of infectious diseases. These susceptible classes can be categorized as follows

• \(S_{1}(t)\): refers the population of susceptible individuals who are generally in good health, with no underlying medical conditions that significantly compromise their immune systems or respiratory functions.

• \(S_{2}(t)\): denotes the count of individuals who are susceptible and belong to one of two categories: either they are older in age or they are experiencing another significant medical condition or disease such as diabetes, heart disease, respiratory disorders, or compromised immune systems. They have not yet contracted Covid-19 but these conditions can increase susceptibility to severe illness or complications from the virus.

We assume that the vaccination process is not perfect. That is, during the vaccination period, individuals with certain underlying conditions might face the possibility of becoming seriously ill and needing hospitalization, while others in \(S_{1}\) group may stay healthy throughout this period. Indeed, healthy individuals in \(S_{1}\) group may engage in behaviors that promote overall well-being, such as regular exercise and a balanced diet, which could potentially lower their risk of contracting Covid-19 compared to individuals with pre-existing diseases who may have to take extra precautions.

Recognizing the distinction between two types of susceptible individuals and understanding that not all susceptible individuals in a population are equally likely to become infected, we propose an assumption. Our assumption suggests that individuals without underlying health conditions may exhibit a stronger immune response to Covid-19 compared to those with such conditions. Therefore, individuals in group \(S_{1}(t)\) transition directly to the recovered state after vaccination. Conversely, those in group \(S_{2}(t)\) still have a chance of contracting the virus and may require additional time for complete recovery even after vaccination. Given this assumption, the categories of vaccination can be described as follows:

• \(V_{1}(t)\): denotes individuals who have received vaccination and were previously categorized in group \(S_{1}(t)\). As a result of vaccination, they have developed full immunity against the virus and move directly into the recovered class.

• \(V_{2}(t)\): represents individuals who have been vaccinated and were previously categorized in group \(S_{2}(t)\). Despite being vaccinated, they still carry a risk of of getting infected before achieving full recovery.

The descriptions for the remaining classes are as follows:

• I(t): represents the number of individuals within the infectious compartment at time t.

• H(t): signifies individuals who have been admitted to a hospital because of Corona infection. These individuals have developed severe symptoms and necessitate medical care within a hospital environment.

• R(t): represents the number of people who have effectively recovered from Covid-19. After being infected previously, they have completely recovered, eliminating their capability to transmit the disease.

• N(t), as the sum of all the sub-populations, specifies the complete human population under consideration at a given time t.

A diagram depicting the physical phenomenon of Covid-19 in seven classes.

Full size image

Figure 1 presents a schematic illustration depicting the impact of Corona infection on individuals. The constituted Covid-19 model and its associated parameters, along with their physical interpretation, are described as follows:

The rate at which new individuals enter the susceptible category \(S_{1}(t)\) influenced by factors such as births and immigration, is denoted by the symbol \(\Lambda _{1}\). The rate at which disease transmission occurs within \(S_{1}(t)\) community, due to their contact with infectious individuals, moves some humans from \(S_{1}(t)\) class to the infected class at rate \(\beta _{1}\), referred to as ’force of infection’. Additionally, susceptible people in class \(S_{1}(t)\) are vaccinated at the rate \(\beta _{3}\). The term \(\alpha\) indicates the natural mortality rate of susceptible class \(S_{1}(t)\). Consequently, the overall rate of change of susceptible individuals \(S_{1}(t)\) can be expressed as the following differential equation

The rate at which new individuals enter the susceptible category \(S_{2}(t)\) influenced by factors previously mentioned, is denoted by the symbol \(\Lambda _{2}\). Disease transmission within this category, caused by their contact with infectious individuals, transfers some individuals from \(S_{2}(t)\) class to infectious class at the rate \(\beta _{2}\). Moreover, the susceptible people in class \(S_{2}(t)\) receive vaccination at the rate \(\beta _{4}\), while \(\alpha\) signifies the natural mortality rate. Hence, the change in susceptible individuals \(S_{2}(t)\) is expressed by the following equation

The rate at which susceptible individuals \(S_{1}(t)\) transition to the vaccinated category \(V_{1}(t)\) is \(\beta _{3}\). Vaccinated individuals \(V_{1}(t)\) recover at the rate \(\beta _{6}\). The term \(\alpha\) indicates the natural mortality rate of the vaccinated class \(V_{1}(t)\). Consequently, the overall rate of change of vaccinated individuals \(V_{1}(t)\) can be expressed as the following differential equation

Susceptible individuals \(S_{2}(t)\) transition to the vaccinated category \(V_{2}(t)\) at rate \(\beta _{4}\). Disease transmission within the vaccinated class \(V_{2}(t)\) results in some vaccinated individuals moving to the infected class I(t) at rate \(\beta _{5}\), while recovery in \(V_{2}(t)\) occurs at rate \(\beta _{7}\). The parameter \(\alpha\) represents the natural mortality rate of vaccinated class \(V_{2}(t)\). Thus, the overall rate of change of vaccinated individuals \(V_{2}(t)\) is described by the following equation

The infected class I(t) receives new members at rates \(\beta _{1}\), \(\beta _{2}\), and \(\beta _{5}\) from the susceptible classes \(S_{1}(t)\), \(S_{2}(t)\), and the vaccinated class \(V_{2}(t)\), respectively. Individuals in the infectious class transition to the hospitalized class H(t) at a rate of \(\mu\), while natural mortality causes individuals to leave the infectious class at a rate of \(\alpha\). Therefore, the net rate of change of individuals in the infectious class I(t) is expressed by the following ordinary differential equation

Infected individuals joins the hospitalized class at rate \(\mu\). Within the hospitalized class, individuals move to the recovered class at rate \(\rho\), while exiting the hospitalized class due to natural mortality occurs at rate \(\alpha\). Thus, the ordinary differential equation describing the net rate of change of individuals in the treatment class is as follows.

The recovered class is comprised of individuals transitioning from the vaccinated, infectious, and hospitalized classes at the rates \(\beta _{6}\), \(\beta _{7}\) and \(\rho\) respectively. Additionally, some individuals exit the recovered class due to the natural mortality rate \(\alpha\). As a result, the following ordinary differential equation represents the net rate of change of individuals in the recovered class

Therefore, the \(S_1S_2V_1V_2IHR\) model utilizes a nonlinear set of differential equations to describe transitions between the seven compartments depicted below:

with non-negative initial conditions,

The state variables \(S_{1}\), \(S_{2}\), \(V_{1}\), \(V_{2}\), I, H, and R within model (1) are smooth real-valued functions, continuously defined across the time interval \([0,+\infty )\). A comprehensive breakdown of the parameters employed in the research work, including their physical interpretations and connections to particular phenomena, is detailed in the Table 1.

Fractional version

First, let’s review some fundamental concepts related to Caputo²⁸ and Atangana-Baleanu fractional derivatives^69,70.

Definition 1

Let \(\Omega\) be an open subset of \({\mathbb {R}}\) and \(p\in [1,\infty )\), the Sobolev space \(H^{p}(\Omega )\) is defined by

Definition 2

The Caputo fractional derivative of order \(\eta \in (n-1, n)\), \(n\in {\mathbb {N}}\), for a given function \(v:[a, b]\rightarrow {\mathbb {R}}\), is stated as:

Clearly, \(^{C}_{a}D^{\eta }_{t}v(t)\) tends to \({\dot{v}}(t)=\dfrac{dv}{dt}\) as \(\eta \rightarrow 1\).

Definition 3

If \(v:[a,b]\rightarrow {\mathbb {N}}\) is a differentiable function defined on [a, b] such that \(v\in H^{1}(a,b)\), \(b>a\) and \(\eta \in (0,1]\), then the Atangana-Baleanu fractional derivative of v in Caputo sense (ABC) is defined as:

where \(E_{\eta }\) is the well-known one parameter Mittag-Leffler function and \(B(\eta )>0\) is a normalization function satisfying \(B(0)=B(1)=1\).

Definition 4

The Laplace Transform of the Atangana-Baleanu operator is defined as follows:

Definition 5

The associated fractional integral with non-local kernal is defined by

Theorem 2.1

The fractional order differential equation

has the following unique solution

For additional information on the properties of the Atangana-Baleanu fractional derivative, we direct readers to^34,47,48.

Classical integer-order models often fail to capture the memory effects present in various biological systems. To address this limitation within the model (1) for the present study, we exchange the conventional integer-order derivative \(D_{t}\) with the fractional Atangana-Baleanu derivative \(^{ABC}_{0}D^{\eta }_{t}\). This adjustment enables us to observe and understand the memory effects inherent in the dynamics of the Corona disease more comprehensively. Before proceeding further, it is crucial to revisit key properties related to Caputo and Atangana-Baleanu derivatives. For more details, we recommend referring to⁴⁸.

Therefore, considering \(t\ge 0\) and \(\eta \in (0,1]\), the subsequent formulation represents the anticipated Covid-19 model incorporating the Atangana-Baleanu derivative

incorporating the initial conditions (1h). Expressing the system (2) in its simplified form yields:

where \(v:[0,+\infty )\rightarrow {\mathbb {R}}^{7}\) and \(F:{\mathbb {R}}^{7}\rightarrow {\mathbb {R}}^{7}\) are vector valued functions with

The constituted model (2) or model (3) which distinguishes among susceptible individuals, considers the different stages of the disease and their interactions within the human community. Analyzing the Covid-19 flow pattern through this model enables a deeper understanding of the disease spread. Our analysis is crucial as it enables the evaluation of vaccination and hospitalization strategies in real-world scenarios, acknowledging the challenges where achieving perfect vaccination remains unattainable. Our goal is to ensure that our research findings make a substantial contribution to the development of the most efficient control strategies for effectively managing and reducing the spread of the Coronavirus disease. These strategies involve finding the appropriate balance between vaccination rates, hospitalization measures, and other control variables to effectively manage and contain the spread of diseases like Covid-19.

Analytical study of an epidemic model involves employing mathematical tools and techniques to comprehensively examine the dynamics, behaviors, and solutions of the model. This approach often employs methods such as differential equations, fractional calculus, statistical analysis, and mathematical frameworks tailored specifically for epidemiological systems. The goal is to gain insights into the key factors influencing the spread of infectious diseases, analyze the stability of various equilibrium states, and explore potential interventions or control strategies. Through rigorous mathematical analysis, researchers can contribute to a deeper understanding of epidemic dynamics, informing public health policies and strategies for disease management^{71,72,73,74,75}. The computations associated with these considerations will be carried out in the subsequent stages.

Theorem 3.1

The function F in (3) exhibits Lipschitz continuity with respect to v. That is,

which holds for all \(v_{1},v_{2}\in {\mathbb {R}}^{7}\) with \({\mathcal {M}}>0\).

Theorem 3.2

Assuming that the function F(t, v(t)) fulfills the Lipschitz condition (4), the problem (3) will have a unique solution for the specified initial population under the conditions \(F(0,v(0))=0\) and \({\mathcal {M}}^{*}<1\).

Remark 1

The existence and uniqueness of solutions have been previously established in our prior work. Hence, for the proofs of Theorems 3.1 and 3.2, we suggest referring to the sources^19,48.

Key characteristics

In this segment, we explore certain essential properties of the dynamical system (2). We focus on the positivity and boundedness of solutions^49,50 throughout the time ___domain \([0,+\infty )\). Consequently, we establish the problem (2) as well-posed, ensuring that the solution derived is not only attainable but also practical.

Theorem 3.3

The solutions to the system (2) exhibit positively bounded behavior for all \(t\ge 0\), with the condition that the initial states remain non-negative.

Proof

Letting \(\Lambda =\Lambda _{1}+\Lambda _{2}\), the entire population dynamics is described as follows:

After conducting an extensive calculation, we deduce that

where \(E_{\eta }(-\alpha t^{\eta })\) signifies the one parameter classical Mittag-Leffler function displays an asymptotic behavior⁴⁰. As \(0<E_{\eta }(-\alpha t^{\eta })\le 1\) and \(1-E_{\eta }(-\alpha t^{\eta })\le 1\), it follows that

Hence, N(t), starting in \({\mathbb {R}}^{7}\) remains bounded for all \(t\ge 0\). The inequality above incorporates N(0), indicating the initial population size of humans. Consequently, all other variables (solutions) in model (2) are also bounded for all \(t\ge 0\).

To establish the non-negativity of solutions, re-arranging the first equation of the model (2) yields

As all the solutions are bounded, let I(t) be bounded by \(\varrho\). Then,

where \(K=\alpha +\beta _{3}+\beta _{1}\varrho\) is a constant. After applying the Laplace transform to both sides of inequality (6), we derive

Upon applying the Inverse Laplace, the above inequality transforms to

Clearly, the solution \(S_{1}(t)\) is greater than the product of positive terms, it is positive for all \(t\ge 0\). Likewise, we can demonstrate that all remaining solutions are positive for all \(t\ge 0\). Therefore, each solution within \({\mathbb {R}}^{7}_{+}\) subject to any nonnegative set of initial conditions tends asymptotically towards in finite time t, enters and remains in the feasible region

Hence, the enclosed set \(\Pi\) maintains its positive invariance property^29,30 with respect to system (2). \(\square\)

States of equilibrium and threshold parameter

The determination of equilibrium points involves setting the right-hand side of the equations in model (2) to zero and subsequently solving for the state variables. To simplify the notations, we assume that

The model (1) exhibits a unique Covid-19-free equilibrium at the point

with coordinates

Threshold number, often denoted by \(\Re _{0}\), is indeed a critical factor in understanding the dynamics of diseases within populations. As a dimensionless quantity, it provides a quantitative measure of the potential for an infectious disease to propagate throughout a population. It signifies the anticipated number of new infections generated by a single infected individual within a population entirely susceptible to the infection. In straightforward terms, if we bring one person who is infectious with the disease into a group of people entirely susceptible to the infection, \(\Re _{0}\) quantifies the average number of fresh infections produced by that individual during the time they are infectious. If \(\Re _{0}\) exceeds one, it suggests that each infected person, on average, will infect more than one other person. This leads to exponential spread of the disease because each new infection leads to multiple additional infections. This can result in a rapid increase in the number of cases within the population. Conversely, if \(\Re _{0}\) is less than one, the disease is likely to die out eventually as the number of new infections per case diminishes over time. This parameter holds immense significance in epidemiology as it helps in predicting the trajectory of a disease outbreak. Moreover, it guides public health interventions by indicating the effectiveness of various control measures. For instance, if \(\Re _{0}\) is high, interventions like vaccination, quarantine, or social distancing become crucial in lowering the reproduction number to curb the disease’s spread. On the other hand, if \(\Re _{0}\) is relatively low, the disease might naturally die down without extensive intervention. Understanding \(\Re _{0}\) enables health authorities to make informed decisions regarding resource allocation, preparedness, and the most suitable strategies to manage and control the spread of diseases within populations.

Mathematically, the computation of \(\Re _{0}\) involves determining the dominant eigenvalue of the matrix that characterizes the transmission patterns of the illness. This matrix considers various factors including the time duration in which they are infectious, the frequency of interactions among people, and the probability of transmission after contact between an infected individual and a susceptible person. The method of next generation, as outlined in various works^29,30,38,48, provides a mathematical framework for calculating \(\Re _{0}\) in infectious disease models. This approach becomes especially valuable in situations where the model’s complexity poses challenges for obtaining analytical solutions. Here, we will highlight some key aspects of this method. Our attention is directed toward the behaviors and changes within compartments I and H. The matrices which relate to the emergence and shift rates of new and current infections are symbolized and described in the following manner:

The Jacobians of the matrices \({\mathcal {F}}\) and \({\mathcal {G}}\), assessed at the specific point \({\mathcal {C}}^{0}\), are:

The essential threshold parameter,

for the proposed model (2) is determined by computing the spectral radius of the product matrix \(\bar{{\mathcal {F}}}\bar{{\mathcal {G}}}^{-1}\).

Alternatively, model (2) possesses a unique Covid-19-present equilibrium at the point

where

To compute the value of \(I^{*}\), we use Eq. (2e), which is

\(I^{*}\ne 0\) signifies an endemic state, therefore,

Putting the values of \(S_{1}^{*}\), \(S_{2}^{*}\), and \(V_{2}^{*}\) in above equation, we have

The simplified form of the above equation is

where

Descartes rule of signs is a mathematical principle employed to predict the potential count of negative and positive real roots present in a polynomial Eq. (9) containing real coefficients, all without explicitly solving the equation. The count of positive real roots within a polynomial Eq. (9) corresponds to the number of alterations in signs among its coefficients. On inspection, \(a_{1}\), \(a_{2}\), and \(a_{3}\) are strictly positive and \(a_{4}<0\) whenever \(\Re _0>1\). This implies that there is only one change in sign among the coefficients of polynomial (9) Hence, by Descartes rule of sign, the polynomial (9) in \(I^{*}\) possesses precisely one positive real root if \(\Re _0>1\). Consequently, the existence of the endemic equilibrium point \({\mathcal {C}}^{*}\) is confirmed when \(\Re _0>1\).

Analysis of stability

This section entails a theoretical examination of both local and global stabilities of model (2) at its equilibrium states, employing specific conditions imposed on the threshold parameter \(\Re _{0}\). Achieving global stability will involve applying Lyapunov theory^68,48 in conjunction with the LaSalle Invariance Principle (LIP)⁷⁶.

Theorem 3.4

The Corona free equilibrium \({\mathcal {C}}^{0}\) exhibit local asymptotic stability (LAS) when \(\Re _{0}<1\). Conversely, it becomes unstable if \(\Re _{0}>1\).

Proof

The Jacobian matrix \(J(S_{1},S_{2},V_{1},V_{2},I,H,R)\) for model (2) at \({\mathcal {C}}^{0}\) is given by

The eigenvalues associated with the Jacobian matrix \(J({\mathcal {C}}^{0})\) are listed below

The first six eigenvalues are evidently negative as the quantities \(K_{1}\), \(K_{2}\), \(K_{3}\), \(K_{4}\), \(K_{6}\), and \(\alpha\) are strictly positive. Considering that \(K_{5}\) is also positive, it follows that \(\lambda ^{0}_{7}<0\) if and only if \(\Re _{0}<1\). So, with \(\Re _{0}\) below unity, all the eigenvalues of \(J({\mathcal {C}}^{0})\) are negative, signifying the local asymptotic stability (LAS) of the system (2) at \({\mathcal {C}}^{0}\). Consequently, there is no imminent threat of a pandemic. In addition, \(\lambda ^{0}_{7}\) becomes positive when \(\Re _{0}>1\), indicating the instability of system (2) at \({\mathcal {C}}^{0}\) for \(\Re _{0}>1\). This proves the desired claim. \(\square\)

Theorem 3.5

The Covid-19-present equilibrium \({\mathcal {C}}^{*}\) exhibit local asymptotic stability (LAS) when \(\Re _{0}>1\). However, when \(\Re _{0}<1\), the point \({\mathcal {C}}^{*}\) becomes unstable.

Proof

The Jacobian matrix \(J(S_{1},S_{2},V_{1},V_{2},I,H,R)\) for model (2) at \({\mathcal {C}}^{*}\) takes the following form

where

The Jacobian matrix \(J({\mathcal {C}}^{*})\) possesses the following eigenvalues:

Hence, when \(\Re _{0}\) exceeds unity, all eigenvalues of \(J({\mathcal {C}}^{*})\) turn negative, signifying the local asymptotic stability (LAS) of \({\mathcal {C}}^{*}\). Once the dynamic system (2) stabilizes at the Covid-19-present point \({\mathcal {C}}^{*}\), the disease will spread within the human population. \(\square\)

Theorem 3.6

A Corona free equilibrium \({\mathcal {C}}^{0}\) achieves global asymptotic stability (GAS) within the ___domain \(\Pi\) if \(\Re _{0}<1\).

Proof

Consider a Volterra type candidate Lyapunov function^29,30 for the system (2) outlined below

Upon applying the ABC fractional operator on both sides, we obtain

Substitution of fractional derivatives leads to

After some useful substitutions, the above expression will transform to

By Arithmetic-Geometric inequality

Hence, \(^{ABC}_{0}D_{t}^{\eta }L_{0}\le 0\), whenever \(\Re _{0}<1\). Particularly, \(_{0}^{ABC} D^{\eta }_{t} L_{0}=0\), when \(S_{1}=S_{1}^{0}\), \(S_{2}=S_{2}^{0}\), \(V_{1}=V_{1}^{0}\), \(V_{2}=V_{2}^{0}\), \(I=I^{0}\). Consequently, the singleton set \(\{{\mathcal {C}}^{0}\}\) stands as the largest invariant set found within

In this situation, regardless of the initial nonnegative conditions, all solution trajectories will eventually converge to the correct steady state \({\mathcal {C}}^{0}\). Thus, in accordance with the LaSalle Invariance Principle, the point \({\mathcal {C}}^{0}\) achieves global asymptotic stability within the region \(\Pi\). \(\square\)

Theorem 3.7

A Covid-19-present equilibrium \({\mathcal {C}}^{*}\) achieves global asymptotic stability (GAS) within the feasible region \(\Pi\) when \(\Re _{0}>1\).

Proof

Let us examine a candidate Lyapunov function defined as follows

Applying ABC fractional operator on both sides, we get

The incorporation of fractional derivatives results in

This can be written as

By Arithmetic-Geometric inequality, one can show that

Therefore, \(^{ABC}_{0}D_{t}^{\eta }L_{1}<0\). In particular, \(_{0}^{ABC} D^{\eta }_{t} L_{1}=0\) if and only if \(S_{1}=S_{1}^{*}\), \(S_{2}=S_{2}^{*}\), \(V_{1}=V_{1}^{*}\), \(V_{2}=V_{2}^{*}\), and \(I=I^{*}\). Corona present equilibrium \({\mathcal {C}}^{*}\) exists when \(\Re _{0}>1\). The singleton set \(\{{\mathcal {C}}^{*}\}\) constitutes the largest invariant set within

In this scenario, all solution trajectories will converge towards the correct steady state \({\mathcal {C}}^{*}\) irrespective of the initial nonnegative conditions. Consequently, according to the LaSalle Invariance Principle⁷⁶, \({\mathcal {C}}^{*}\) achieves global asymptotic stability (GAS) within region \(\Pi\). \(\square\)

In dynamical systems theory, local and global stability are properties that describe the behavior of solutions to the system over time. When we say a system is locally stable, it means that small perturbations occurring around an equilibrium point do not cause the system to diverge over time; rather, it tends to return to that equilibrium. On the other hand, global stability means that the entire system, not only a neighborhood but the system as a whole remains bounded over time, regardless of initial conditions or perturbations.

In the context of the present study, the local and global stability of \({\mathcal {C}}^{0}\) implies that the transmission of Coronavirus disease has been effectively halted within the population. These stability findings demonstrate the successful deployment of measures, interventions, or factors to curb further spread. The containment efforts have proven successful, effectively preventing new infections and ensuring the safety and well-being of the human population. Alternatively, local and global stability of \({\mathcal {C}}^{*}\) suggests that Corona disease will persist in propagating and transmitting within the human population, ultimately leading to a pandemic. This scenario indicates that preventive interventions or measures have proven insufficient in halting the spread of the disease.

Remark 2

Establishing the existence of unique solutions, along with proving their boundedness and positivity of solutions, and then stability for the problem (2), leads to the conclusion that it is mathematically well-posedness. This ensures that the solution obtained is both achievable and practical.

In this section, our aim is to evaluate the numerical stability of system (2) at its equilibrium points using the Toufik-Atangana numerical method^40,55. Therefore, the model (3) in discrete form is given as

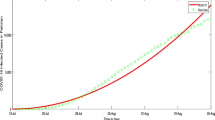
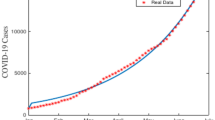
For numerical simulations, we shall consider days as time unit. By applying this scheme across various order \(\eta\) values, we simulate the dynamic behavior of the Covid-19 disease. The numerical results, obtained with parameters from Table 1, consistently match the continuous model (2), confirming the reliability of the Toufik-Atangana scheme. Moreover, we explore the consequences of constant (consistent) hospitalization and vaccination strategies on the population under different coverage levels. Detailed sensitivity analysis of parameters influencing \(\Re _{0}\) is also presented.

Impact of fractional order on disease dynamics

Impact of fractional order \(\eta\) on Coronavirus dynamics: Decreasing value of \(\eta\) leads to increased individuals in \(S_{2}\) and R classes, while gradually decreasing the infected individuals.

Full size image

In this section, we investigate how fractional values of order \(\eta\) influence model (2). Figure 2 shows the graphical results obtained using (14) to depict the impact of \(\eta\) on individuals within each distinct compartment. The model was simulated for \(\eta =0.6,0.7,0.8,0.9,1.0\). Starting from the endemic state \({\mathcal {C}}^*\) when \(\eta =1.0\), decreasing the value of \(\eta\) leads to an increase in susceptible people within the \(S_2\) class. Additionally, there is a slight increase in the community of recovered humans. However, the humans in the infected compartment consistently decreases as \(\eta\) decreases from 1.0. Therefore, it becomes possible to reduce the Corona-infected cases by decreasing the fractional order values from 1.0.

Effects of vaccination policies

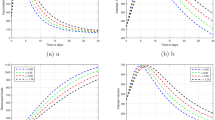
In this subsection, a quantitative study was conducted to investigate the influence of mandatory vaccination program on the propagation of Coronavirus disease. Our approach involved various conducting multiple numerical experiments of the model (2) utilizing a numerical scheme (14). This allowed us to observe the spread of disease under different vaccination levels. These simulations extended up to 200 days, and the results were presented in Figs. 3, 4, 5, 6 and 7. By introducing a fractional order parameter \(\eta\) different from 1, our numerical analysis yielded biologically relevant and insightful outcomes, shedding light on stability patterns within the disease dynamics.

Figures 3, 4, 5, 6 and 7 depict the impact of the vaccination parameter \(\beta _{3}\) levels and the order \(\eta\) on the total count within each compartment. Our findings suggest a notable reduction in Corona virus infections with increased fractional order derivatives and vaccination levels. As \(\beta _{3}\) and \(\eta\) rise, the count of susceptible individuals in class \(S_{1}\) gradually decreases, while the infected and hospitalized people declines. At the same time, the count of recovered individuals rises. Our analysis indicates that for vaccination levels from \(0\%\) up to \(20\%\), the Corona disease persists in the human population. However, surpassing a \(20\%\) vaccination level \((\beta _{3})\), each population tends toward the equilibrium state \({\mathcal {C}}^{0}\), as depicted in Fig. 7.

On the other hand, the infectivity reduces with vaccination of susceptible individuals \(S_{2}\) at varying rates \(\beta _{4}\) as illustrated in Figs. 8, 9, 10, 11 and 12. Despite high vaccination coverage levels (\(\beta _{4}\)) reaching \(80\%\) or more, the disease persists in the population, indicating the existence of other factors that contribute to its transmission even among vaccinated individuals. However, vaccination efforts show promising outcomes in mitigating the severity of the disease, as evidenced by a slight decline in hospitalizations, with higher \(\eta\) and \(\beta _4\) values. This indicates that vaccination not only mitigates infectivity but also alleviates the burden on healthcare systems by reducing severe cases. Additionally, increased vaccination levels (\(\beta _{4}\)) for \(S_{2}\) individuals lead to improvements in the recovery rate from Corona disease. These results emphasize the importance of vaccination campaigns in controlling disease spread and severity, and improving overall recovery outcomes, although complete eradication may require complementary measures in conjunction with vaccination efforts.

Our analysis suggests that eradicating the Corona disease becomes achievable when at least \(20\%\) of the population in class \(S_{1}\) receives vaccination. Vaccinating individuals in \(S_{2}\) also proves beneficial, reducing infections while maximizing recoveries. This conclusion supports our paper’s title and highlights the pivotal role vaccination measures can play in curbing disease spread.

Susceptible humans (\(S_{1}\)) decrease continuously with increasing vaccination levels when \(\eta =0.6\). A slight decrease in hospitalized people is noticed. However, there is an improvement in the recovery rate.

Full size image

Susceptible humans (\(S_{1}\)) decrease continuously with increasing vaccination levels using \(\eta =0.7\). Infected humans also decrease, while the the number of recovered people increases. In addition, a slight reduction in the hospitalized humans is noticed.

Full size image

Impact of vaccination rate \(\beta _{3}\) at \(\eta =0.8\): Gradual reduction in infectivity with increasing vaccination levels, decreased individuals in \(S_{1}\) class, a slight decline in hospitalizations, and continuous increase in the number of recoveries.

Full size image

Impact of vaccination rate \(\beta _{3}\) on disease dynamics at \(\eta =0.9\): Gradual reduction in infectivity with increasing vaccination levels, decreased individuals in \(S_{1}\) class, a small regression in the hospitalized class, and a continuous increase in the recovered class with higher vaccination levels.

Full size image

Effect of vaccination rate \(\beta _{3}\) on sub-populations is explored for \(\eta =1.0\). It is evident that the Coronavirus disease will vanish from the population if a minimum of \(20\%\) of the susceptible population in the \(S_{1}\) class is vaccinated.

Full size image

For \(\eta =0.6\), vaccination results in: Reduced susceptibility among the \(S_{2}\) category, a continuous drop out in infected humans, a consistent rise in recoveries, and a minor decline in hospitalizations.

Full size image

Impact of vaccination rate when \(\eta =0.7\): Decreased \(S_{2}\) individuals, lower infections, increasing recoveries, and slight regression in hospitalizations.

Full size image

Impact of \(\beta _{4}\) vaccination rate on Corona virus dynamics when \(\eta =0.8\): Gradual decrease in infectivity with higher vaccination levels, reduced \(S_{2}\) individuals, slight regression in hospitalizations, and steady increase in recoveries.

Full size image

For \(\eta =0.9\), the vaccination rate \(\beta _{4}\) effects the model dynamics: Gradual reduction in infectivity with increasing vaccination levels, decreased individuals in \(S_{2}\) class, small regression in hospitalizations, and continuous increase in recovery.

Full size image

Impact of \(\beta _{4}\) vaccination rate on Corona virus dynamics for \(\eta =1.0\): Reduced infectivity with higher vaccination levels, decreased \(S_{2}\) individuals, slight regression in hospitalizations, and continuous increase in recoveries.

Full size image

Impact of hospitalization policy

We analyzed the impact of the hospitalization rate \(\mu\) in Figs. 13, 14, 15, 16 and 17 on the population dynamics. Increasing both the hospitalization rate and fractional order \(\eta\) leads to a significant decrease in Corona infections. However, with the rise in hospitalization levels, there is a small increase in the hospitalized people, consistent with the natural flow pattern depicted in model (2). Additionally, an increase in hospitalization levels results in a slight increase in the count of susceptible humans of classes \(S_{1}\) and \(S_{2}\) respectively. Additionally, the curves representing the count of recovered individuals exhibit a slight increment with increased hospitalization rates \(\mu\). The Figs. 13, 14, 15, 16 and 17 also demonstrate that the the eradication of the Corona pandemic from the population is achievable by hospitalizing at least \(20\%\) of the infected individuals, as the fractional order \(\eta\) increases. Thus, relying solely on hospitalization as a strategy, especially in conjunction with vaccination, can prove advantageous in completely eradicating the Corona disease.

For the case \(\eta =0.6\): Increasing hospitalization rate leads to decreased infections, higher recoveries, and an increase in both categories of susceptible individuals.

Full size image

For the case \(\eta =0.7\): Increasing hospitalization reduces infections, boosts recoveries, and raises susceptible individuals.

Full size image

With \(\eta =0.8\), higher hospitalization leads to reduced infections, increased recoveries, and an upsurge in susceptible individuals.

Full size image

For \(\eta =0.9\), increasing hospitalization results in fewer infections, higher recoveries, and an increase in susceptible individuals. The reduction in infected cases is more significant as compared to \(\eta =0.6\), \(\eta =0.7\), and \(\eta =0.8\).

Full size image

For \(\eta =1.0\), the hospitalization rate \(\mu\) has a crucial impact on the diseased human population. It is observed that Covid-19 will be eradicated from the population when a minimum of \(20\%\) of the infected population is hospitalized.

Full size image

Influence of constant controls on \(\Re _{0}\)

Determining the threshold parameter value \(\Re _{0}\) across various levels of mandatory measures holds significant importance. Figure 18 displays \(\Re _{0}\) corresponding to varying levels of vaccination and hospitalization, represented by \(\beta _{3}\), \(\beta _{4}\), and \(\mu\). This provides insights into the impact of different preventive measures on the transmission of Covid-19 within the human community.

Figure 18 shows that increasing vaccination coverage levels reduces \(\Re _{0}\). This implies higher vaccination levels effectively curb virus spread. The virus persists in the population until we vaccinate \(S_{1}\) individuals up to \(17\%\) vaccination. Below \(17\%\), \(\Re _{0}\) is above one, indicating ongoing virus spread. At \(17\%\) or more, \(\Re _{0}\) drops below one, signifying disease control. The infectivity rate hits zero at \(17\%\), emphasizing the effectiveness of vaccination in managing virus transmission.

However, when examining \(\Re _{0}\) versus different vaccination rates \(\beta _{4}\) for \(S_{2}\) people is illustrated in Fig. 18. We noticed a decrease in \(\Re _{0}\) as vaccination levels of \(\beta _{4}\) rise. Yet, even with high vaccination rates, the disease is not completely controlled. Indeed, in this scenario, the \(\Re _{0}\) value remains above one. Additionally, \(\Re _{0}\) drops below one when \(\mu\) reaches 0.20 or higher. This indicates that Covid-19 would be eradicated if at least \(20\%\) of infected individuals were hospitalized.

Graphs depicting the threshold parameter \(\Re _{0}\) in relation to constant vaccination and hospitalization rates.

Full size image

Sensitivity assessment

Sensitivity analysis is an essential tool in epidemic modeling, offering insights into the behavior and robustness of mathematical models used for simulating infectious disease dynamics. By systematically varying input parameters and assumptions, sensitivity analysis identifies critical factors that significantly influence model outcomes, such as transmission rates and population density. This analysis not only aids in understanding uncertainties inherent in the model but also guides efforts to refine parameter estimates and prioritize data collection. Moreover, sensitivity analysis plays a crucial role in evaluating the effectiveness of control measures by assessing how interventions like vaccination coverage or social distancing impact disease transmission dynamics. By providing a comprehensive understanding of model sensitivities and uncertainties, sensitivity analysis enables policymakers and public health officials to make informed decisions and allocate resources effectively to mitigate the spread and impact of epidemics.

We explored the influence of certain parameters in system (2) that significantly affect the threshold parameter \(\Re _{0}\). Parameters exhibiting the highest absolute sensitivity index are regarded as highly and proportionally sensitive concerning \(\Re _{0}\). The normalized forward sensitivity index⁷⁷ for a parameter p is calculated utilizing the method described in⁷⁸, denoted by \({\mathcal {S}}_{p}^{\Re _{0}}\), and is given by the relation

The sensitivity indices for the parameter(s) affecting \(\Re _{0}\) are computed as follows:

where

The \(\Re _{0}\) value fluctuates according to the involved parameter(s). The absolute value of the parameter’s sensitivity index indicates the directional impact on \(\Re _{0}\). When the sensitivity index is positive, it means that raising the value of the parameter(s) will result in an increase in \(\Re _{0}\). If the sensitivity index is negative, it implies that raising the value of the parameter(s) will cause a decrease in \(\Re _{0}\). This information is detailed in Table 2.

Table 2 illustrates that the parameters \(\Lambda _{1}\), \(\Lambda _{2}\), \(\beta _{1}\), and \(\beta _{2}\) have a positive impact on \(\Re _{0}\). Physically, it indicates that a \(10\%\) increase or decrease in these parameters would correspondingly increase or decrease \(\Re _{0}\) by the same proportion. For instance, a \(10\%\) increase or decrease in the values of parameters \(\Lambda _{1}\), \(\Lambda _{2}\), \(\beta _{1}\), and \(\beta _{2}\) leads to an approximate \(8.271\%\), \(1.387\%\), \(8.271\%\), and \(1.225\%\) increase or decrease in the threshold parameter, respectively. On the other hand, the parameter(s) \(\beta _{3}\), \(\beta _{4}\), \(\beta _{5}\), \(\beta _{7}\), \(\mu\), and \(\alpha\) exhibit an inverse relationship with \(\Re _{0}\). That is to say, increasing any of these parameters results causes a reduction in \(\Re _{0}\) value. As per our findings, the negative index associated with these parameters indicates that a ten percent increase in their values would lead to a decrease in the threshold parameter \(\Re _{0}\) by approximately \(1.809\%\), \(4.550\%\), \(0.161\%\), \(0.126\%\), \(2.857\%\), and \(8.475\%\), respectively. The response of \(\Re _{0}\) to variations in these parameters is depicted in Figs. 18 and 19.

Graph depicting \(\Re _{0}\) and its corresponding sensitive parameters.

Full size image

Ignoring the sensitivity of birth rates \(\Lambda _{1}\) and \(\Lambda _{2}\), the observation emphasizes that \(\Re _{0}\) demonstrates the highest sensitivity to changes in \(\beta _{1}\). Following \(\beta _{1}\), the parameter \(\beta _{2}\) significantly influences \(\Re _{0}\) compared to other parameters, including \(\beta _{3}\), \(\beta _{4}\), \(\beta _{5}\), \(\beta _{7}\), \(\mu\), and \(\alpha\). It is worth mentioning that the natural death rate \(\alpha\) poses challenges in controlling Corona virus spread, as it cannot be physically altered. Hence, it is crucial to prioritize reducing the transmission rate \(\beta _1\) through mandatory measures such as social distancing, mask-wearing, and hygiene practices, followed by addressing the reduction of \(\beta _{2}\).

Continuous refinement of Corona models through sensitivity analysis is vital for accurately representing the disease dynamics. Iteratively incorporating new data and parameter estimates ensures these models reflect the evolving dynamics of the pandemic aiding policymakers in making informed decisions to control the spread and mitigate impact. Performing a sensitivity analysis aids in identifying optimal values of parameter in our model, crucial for effectively controlling and potentially eradicating the Covid-19 virus. The analysis underscores the effectiveness of preventive measures like social distancing, mask-wearing, and maintaining hygiene compared to sole reliance on vaccination and hospitalization measures. Early adoption of safety measures such as mask usage, hand hygiene, social distancing, and sanitizer usage is imperative. Neglecting these protective strategies often results in costly consequences like community quarantine, extensive treatment and vaccination efforts to eradicate the Corona disease.

Optimal control design refers to the process of developing a systematic approach to determining the most effective strategy for managing a dynamic system. This involves optimizing the control inputs over time to achieve specific objectives while considering constraints and minimizing costs. In various applications, including areas such as engineering, economics, and public health, optimal control design holds significant importance in improving the performance and efficiency of nonlinear models.

The primary objective behind studying the impact of vaccination and hospitalization on Covid-19 transmission is to formulate an optimized control approach. This approach seeks a time-varying strategy to effectively decrease in infected humans while maximizing the count of recovered and susceptible individuals at the lowest control cost. The ultimate objective is to create an optimal control strategy for Corona disease, supporting healthcare experts and policymakers in making well-informed decisions. This strategy aims to effectively manage the spread of disease and reduce its societal impact. The Pontryagin Maximum Principle (PMP), a powerful optimization method^79,80,81,82, is employed here to derive necessary conditions indicating potential optimal control in the model (2). To regulate the Covid-19 spread within the community, three different control variables, labeled as \(u_{1}(t)\), \(u_{2}(t)\), and \(u_{3}(t)\), are incorporated into model (2). These controls are responsible for adjusting the vaccination and hospitalization rates, represented as \(\beta _{3}(t)\), \(\beta _{4}(t)\), and \(\mu (t)\), respectively.

The fractional Corona pandemic model, integrating controls \(u_{i};\ i=1,2,3\) is depicted as follows:

subject to the initial conditions (1h). The comprehensive objective cost function comprising of both state and control variables, can be expressed as

where I(t) represents the state variable, \(T_{f}\) is the pre-determined terminal time, and the control spaces are defined by \(0\le u_{1}(t)\le 1\), \(0\le u_{2}(t)\le 1\), and \(0\le u_{3}(t)\le 1\), signifying the permissible intervals for controls. Each \(u_{i}\) belongs to the presumed control space \({\mathcal {U}}\) of Lebesgue measureable functions defined on interval [0, 1]. The constant \(a_{1}\) represents the coefficient associated with the count of infectious people within the population. Moreover, \(\frac{1}{2}a_{2}u_{1}^{2}(t)\), \(\frac{1}{2}a_{3}u_{2}^{2}(t)\), and \(\frac{1}{2}a_{4}u_{3}^{2}(t)\), represents the cost functions linked to the employed control strategies for vaccinations and hospitalizations. Specifically, \(a_{2}\), \(a_{3}\) and \(a_{4}\) represent the costs associated with controls \(u_{1}(t)\), \(u_{2}(t)\), and \(u_{3}(t)\), respectively.

Our goal is to identify the most effective controls, denoted as \(u^{*}_{1}\), \(u^{*}_{2}\), and \(u^{*}_{3}\), for the vaccination and hospitalization rates \(\beta _{3}(t)\), \(\beta _{4}(t)\), and \(\mu (t)\). These controls belong to the admissible control space \({\mathcal {U}}\) and are aimed at minimizing the cost function (16). That is

To derive the optimal controllers for the control problem (17), we apply PMP method to derive necessary optimality conditions. This process involves constructing the Hamiltonian for controlling the epidemic model (15) in conjunction with (17) as follows:

where \({{\textbf {v}}}\) represents a column vector containing state variables, and \(\Lambda _{S_{1}}\), \(\Lambda _{S_{2}}\), \(\Lambda _{V_{1}}\), \(\Lambda _{V_{2}}\), \(\Lambda _{I}\), \(\Lambda _{H}\), and \(\Lambda _{R}\) denote adjoint variables that corresponds to the state equations presented in (15).

The permissible control functions \(u^{*}_{1}\) and \(u^{*}_{2}\) are obtained by setting (First optimality condition of PMP)

and we obtain

Considering the boundaries, we obtain the characterization of optimal controls as under

The adjoint system of differential equations

with the transversality conditions

can be derived by employing the second optimality condition

of Pontryagin’s Maximum Principle (PMP).

Numerical study for optimization

At this stage, our objective is to compute the numerical solution for an control problem (15). We aim to ascertain the most effective strategies for the vaccinations and hospitalization. We discuss the solution to the optimal control problem (15) alongside the associated cost functionals. The numerical approach employed to determine solutions for systems (20) and (22) is detailed below.

Numerical strategy-II

We utilize the Toufik-Atangana scheme (14) in a forward time progression to approximate the solution of the state system

along with the initial conditions (1h), with three controls. However, the adjoint system (20) is solved numerically by utilizing the reversed version of a numerical scheme (14), operating backward in time, and incorporating the transversality conditions (20h). This process facilitates the update of the controls \(u_{i}(t)\) at discrete time grid points \(t_{n}=n\Delta t\).

Solution algorithm

We can use the following algorithm to numerically solve the discrete necessary conditions:

1. 1.

   Consider an initial control \(u_{k}\in {\mathcal {U}}\) for \(k=0\).

2. 2.

   Approximate state and adjoint variables for the system (20) and (22) using the numerical scheme (14). Implement this scheme in both forward and backward in time with control \(u_{k}\).

3. 3.

   Determine the control \(u^{*}\) using equation (19).

4. 4.

   Update control using \(u_{k}=\dfrac{u^{*}+u_{k}}{2}\).

5. 5.

   If \(\delta \Vert \theta _{k}\Vert -\Vert \theta _{k}-\theta _{k-1}\Vert \ge 0\), then stop, otherwise \(k\rightarrow k+1\) and move to step 2.

Here \(\theta\) represents each of the state, adjoint and control variables and \(\delta\) signifies the required tolerance level.

Optimal vaccination and hospitalization strategies

The primary focus of this investigation was to ascertain the most effective rates \(\beta _{3}(t)\) and \(\beta _{4}(t)\), along with the optimal hospitalization rate \(\mu (t)\), aimed at minimizing the count of infectious people within the human population. To address this objective, we formulated an optimal control problem (17). We showcase simulation outcomes achieved through solving the derived necessary optimality conditions from the problem (17). MATLAB software was employed to execute the algorithmic steps, and simulations were conducted using the Toufik-Atangana numerical approach. The parameter values employed in these simulations are listed in Table 1. For a comprehensive analysis, we explore three different cases.

Case-I: We intend to identify optimal vaccination rate \(\beta _{3}(t)\) that solves the control problem (17). We examined the objective cost functional (16) with \(a_{1}=a_{2}\ne 0\) and \(a_{3}=a_{4}=0\). This indicates that both the vaccination rate \(\beta _{4}\) and hospitalization rate \(\mu\) are regarded as constant controls. In practical terms, the non-zero values assigned to weighting constants \(a_{1}\) and \(a_{2}\) denote the relative importance of disease burden terms and the cost associated with controls, respectively. For instance, a higher value assigned to \(a_{1}\) signifies a greater priority in reducing the disease burden especially within the compartment I, prioritizing it over other variables and the cost associated with control \(u_{1}(=\beta _{3})\). The Fig. 20 displays curves for the optimizer \(u_{1}(=\beta _{3})\) of the control problem (17) for various values of the order \(\eta\), alongside the corresponding cost functional. It is evident that the optimal vaccination rate \(\beta _{3}\) consistently minimizes the cost functional for each fractional order \(\eta\). Specifically, for \(\eta =0.7\), the optimal rate \(\beta _{3}(t)\) incurs the lowest cost for implementing the vaccination strategy among all other values. This observation highlights a continuous reduction in the cost of implementing the vaccination strategy for individuals in compartment \(S_{1}\) as the value of order \(\eta\) decreases from \(\eta =1.0\). Furthermore, The optimal vaccination rate \(\beta _{3}\), varied across different order values \(\eta\), played a significant role in reducing the number of infectious humans while simultaneously increasing recovery. This trend in illustrated in Figs. 21, 22, 23 and 24. Remarkably, following optimization, infectivity reaches zero when \(\eta =1.0\).

Case-II: In the second scenario, we address the problem (17) to find the most efficient vaccination rate \(\beta _{4}(t)\), considering both \(\beta _{3}\) and \(\mu\) as constant controls. Specifically, we explore the cost functional (16) with \(a_{1}\ne 0\), \(a_{2}=0\), \(a_{3}\ne 0\), and \(a_{4}=0\). The consideration of non-zero values for both \(a_{1}\) and \(a_{3}\) emphasizes the reduction of infected individuals in class I by minimizing the control \(u_{2}(=\beta _{4})\) cost intended for vaccinating individuals in \(S_{2}\) class. The solution curves for the optimizer \(u_{2}(=\beta _{4})\) of problem (17), along with the cost functional for different values of order \(\eta\), are plotted in Fig. 25. The optimally devised vaccination rate \(\beta _{4}\) effectively minimizes the cost functional across all fractional order \(\eta\) values. Specifically, for \(\eta =0.7\), the optimal vaccination rate \(\beta _{4}\) incurs the lowest cost among the costs associated with other fractional order values. This showcasing a continuous increase in the cost of implementing the vaccination strategy as the order \(\eta\) rises. Moreover, the optimal vaccination rate contributes to reducing the count of infected humans and elevating individuals in recovered class, as depicted in Figs. 26, 27, 28 and 29.

Case-III: In the third case, the control problem (17) was solved to identify the most suitable hospitalization rate \(\mu (t)\), keeping both the vaccination rates constant, using specifications, \(a_{2}=a_{3}=0\). By considering non-zero values for \(a_{1}\) and \(a_{4}\), our objective is to reduce the infected population while minimizing the cost associated with controlling hospitalization (\(u_{3}=\mu\)). The results for different \(\eta\) values are depicted in Fig. 30, illustrating how \(\mu\) optimally minimizes the cost for each \(\eta\) value. Notably, the optimal hospitalization rate yields the lowest cost for \(\eta =0.7\) compared to higher \(\eta\) values. Additionally, it significantly lowers infection rates and boosts the number of recoveries, as clearly shown in the Figs. 31, 32, 33 and 34.

Optimal control \(u_{1}(=\beta _{3})\) for vaccination of \(S_{1}\) individuals and corresponding cost for different \(\eta\) values. Costs minimized at \(\eta =0.7\) for the implementation of vaccination strategy.

Full size image

Disease dynamics in the fractional model for \(\eta =0.7\), both before and after the optimizing the vaccination rate \(\beta _{3}\) of \(S_{1}\) people.

Full size image

Dynamical behavior of fractional Corona model for the case \(\eta =0.8\) before and after optimizing the vaccination rate \(\beta _{3}\) of \(S_{1}\) individuals.

Full size image

Corona fractional model dynamics for the case \(\eta =0.9\) before and after optimization of vaccination rate \(\beta _{3}\) of \(S_{1}\) people.

Full size image

Disease dynamics in the fractional model for \(\eta =1.0\) before and after optimization of vaccination rate \(\beta _{3}\) of \(S_{1}\) people. Post-optimization, Covid-19 infectivity reduces to zero, signifying effective spread control.

Full size image

Optimal control \(u_{2}(=\beta _4)\) for vaccination of \(S_{2}\) individuals and corresponding cost for different \(\eta\) values. Costs minimized at \(\eta =0.7\) as \(\eta\) increases.

Full size image

Profile of the Corona disease dynamics in the fractional model for \(\eta =0.7\) before and after optimization of vaccination rate \(\beta _{4}\) of \(S_{2}\) people.

Full size image

Profile of the Corona disease dynamics in the fractional model for \(\eta =0.8\) before and after optimization of vaccination rate \(\beta _{4}\) of \(S_{2}\) people.

Full size image

Dynamics of Corona fractional model for \(\eta =0.9\) before and after optimization of vaccination rate \(\beta _{4}\) of \(S_{2}\) people.

Full size image

Dynamics of Corona fractional model for \(\eta =1.0\) before and after optimization of vaccination rate \(\beta _{4}\) of \(S_{2}\) people.

Full size image

Optimal control \(u_{3}(=\mu )\) for the hospitalization strategy introduced for infected individuals and corresponding cost for different \(\eta\) values. Costs minimized at \(\eta =0.7\) as \(\eta\) increases for the implementation of hospitalization strategy.

Full size image

Dynamics of the Corona fractional model for \(\eta =0.7\) before and after optimization of hospitalization for the infected people.

Full size image

Dynamics of Corona fractional model for \(\eta =0.8\) before and after optimization of hospitalization for the infected people.

Full size image

Dynamics of Corona fractional model for \(\eta =0.9\) before and after optimization of hospitalization for the infected people.

Full size image

Dynamics of Corona fractional model for \(\eta =1.0\) before and after optimization of hospitalization for the infected people.

Full size image

The conclusions and future recommendations of the study are summarized below in the form of bullets to provide a clear and concise overview.

• This study examined the dynamic behavior of a novel Covid-19 model formulated as a fractional order \(S_{1}S_{2}V_{1}V_{2}IHR\) system, utilizing the fractional Atangana-Beleanu derivative in conjunction with the generalized Mittag-Leffler function.

• The choice of the ABC operator was based on its advantageous non-singular and non-local properties, which enhance the model’s ability to capture complex Covid-19 dynamics.

• A threshold parameter, computed analytically, was used to evaluate the model’s dynamics at equilibrium points.

• Local and global asymptotic stability of equilibrium states was established using necessary conditions on the threshold parameter. To demonstrate global asymptotic stability, we used Lyapunov function theory.

• Validation of theoretical findings was achieved through the Toufik-Atangana numerical scheme, exhibited compatibility with the continuous model and preserved essential dynamic properties.

• The fractional ABC derivative operator significantly influenced the long-term dynamics of Covid-19, impacting population numbers in each class.

• A substantial reduction in total infected cases was achieved by lowering the fractional order value from 1.0, along with a slight increase in recovered cases.

• Increasing vaccination levels and the fractional order effectively reduced infective cases. For \(\eta =1\), eradicating Covid-19 is feasible with at least \(17\%\) vaccination coverage among \(S_{1}\) individuals, while vaccinating \(S_{2}\) individuals also aids in reducing infectivity.

• Higher hospitalization rates are beneficial in controlling virus spread, resulting in a minor increase in susceptible individuals but a significant decrease in infected cases. It is observed that Covid-19 will be eradicated from the population when a minimum of \(20\%\) of the infected population is hospitalized.

• The combination of hospitalization and vaccination strategies is beneficial for controlling Covid-19 transmission. A comprehensive strategy involves vaccinating a large proportion of \(S_{2}\) individuals, \(17\%\) of \(S_{1}\), and ensuring hospitalization for at least \(20\%\) of the infected population.

• Sensitivity analysis revealed that the contact rate \(\beta _{1}\) between susceptible and infected individuals and transmission rate \(\beta _{2}\) are the most sensitive parameters affecting the threshold.

• Raising public awareness through advocates is essential to promote strategies that reduce transmission rates, such as mask-wearing, social distancing, and hygiene practices.

• A modified fractional model was created to include time-dependent vaccination and hospitalization rates as controls, aiming to minimize infections and boost susceptible and recovered populations.

• The study constructed an optimal control problem and derived the optimality conditions, employing the Toufik-Atangana technique for numerical solutions.

• Simulations indicated that optimal vaccination rates positively affect susceptible individuals, while hospitalization also demonstrates significant benefits.

• The findings highlight the advantages of combining vaccination and hospitalization strategies for effective disease mitigation and public health improvement.

• The mathematical analysis provided a deeper understanding of Covid-19 dynamics, guiding health authorities in decision-making.

• Future work will focus on delay and stochastic optimal control analysis of the developed \(S_{1}S_{2}V_{1}V_{2}IHR\) model to explore optimal control strategies.