Introduction

The recent technological advents in remote sensing, particularly with Synthetic Aperture Radar (SAR) imaging, have opened the doors of earth observations for many probable applications in both military and civilian domains1. Amongst these, ship detection has attracted significant interest because of its utmost importance in numerous surveillance and disaster management applications, such as maritime surveillance, military reconnaissance, fishery management, and seaborne traffic services2. Therefore, SAR-based ship detection has been considered one of the most lucrative applications of ocean surveillance. The shipping industry also plays a vital role in the global economy as most of the trade has been carried out by sea. Similarly, with more than 200 seaports in India, this industry has also contributed significantly toward sustainable development and economic well-being. However, these extensive coastlines also present some key challenges, such as effective border patrolling, traffic management, illegal migrations, etc.3. Therefore, efficient and robust ship detection has been the most demanding application field for SAR. Further, it can also help the authorities for overall navigation safety by providing useful information regarding pirates and traffickers.

Usually, with the availability of SAR-enabled satellites such as Gaofen-3, COSMO-SkyMed, ALOS, Sentinel-1, Kompsat-5, etc., a large number of ship-SAR datasets have been introduced4. However, only Gaofen-3 and Sentinel-1 have been popularly employed for maritime applications. Further, though both operate in C-band, their images vary in resolution, imaging mode, polarization, incidence angle, and background. The Sentinel-1 has four acquisition modes, whereas Gaofen-3 has 12 imaging modes that have been further classified into six groups. A detailed comparison between the SAR payload characteristics of Gaofen-3 and Sentinel-1 has been presented in Table 1. It reveals that Gaofen-3 offers high-resolution imaging, whereas Sentinel-1 provides broad area coverage. Therefore, Gaofen-3 has been found suitable for detailed local monitoring, whereas Sentinel-1 is for continuous environmental monitoring. Moreover, the open data policy of Sentinel-1 significantly enhances its accessibility and utility in various applications worldwide.

Table 1 Comparison between SAR payload characteristics of Gaofen-3 and Sentinel-1.
Full size table

Traditionally, ship detection using SAR imagery has been accomplished by employing the Constant False Alarm Rate (CFAR) and generalized likelihood ratio test5,6. These frameworks detect ships by identifying the handcrafted features after segmenting the background (sea and land). However, these models greatly struggle to achieve acceptable accuracy, particularly in the inshore area of SAR images, because of the artificially designed features for identification7. On the contrary, the advancements in neural networks, especially Convolutional Neural Networks (CNNs), established their dominance in object detection8. Further, with the availability of large data, recently significant progress has been made in the deep learning (DL) based object detection frameworks for remote sensing images9,10,11. These modern DL models employ deep CNNs to automatically extract the vital discriminative features and become the primary choice for ship detection.

Earlier, the DL models have been employed to match the features of the cropped patch with the target object12. However, these methods find difficulties in handling the large geometric variation of ships. Therefore, to overcome this problem, the literature reveals many prominent works based on two-stage detectors, such as Region-based CNN (RCNN) and its family13. These models mostly employ feature fusion techniques before the region proposal network (RPN) to develop an end-to-end ship detection framework14,15. Though these frameworks achieved good accuracy, they require higher computation time. Therefore, in later literature, single-stage detectors, primarily You Only Look Once (YOLO), have been employed for object detection tasks16. Motivated by this, many versions and modifications have been developed and utilized for ship detection in SAR imagery. For example, the ship has been detected from low-resolution wide-band SAR images using YOLOv217 and YOLOv318. The Hybrid YOLO model has been developed for ship detection from open-source SAR images19. Further, the noise level classifier has been appended to distinguish images with noise levels effectively20. The Duplicate Bilateral YOLO (DB-YOLO) has been evolved to detect multi-scale ships21. More recently, the SSS-YOLO model has been developed to detect small ships in SAR images22. These mentioned approaches utilized pre-defined anchors to localize the objects, whereas other algorithms based upon anchor-free mechanisms also exist and have been employed for ship detection23.

The above-mentioned DL approaches consider only one detector at a time to recognize the ship in the image. These models generate their final prediction using the Non-Maximum Suppression (NMS) method. The NMS retains only that predicted box that has the maximum score and eliminates all other redundant boxes based on the predefined threshold24. This approach works efficiently in most cases but often results in high missed detection with objects near each other. Consequently, soft-NMS has been proposed to improve the final predictions25. Nevertheless, these filtering approaches lag in producing averaged localization of predictions by combining multiple models.

Though the traditional NMS approach struggles with fused models, the literature suggests that ensemble models can uplift performance26. On the contrary, the Weighted Box Fusion (WBF) technique fuses the predicted boxes of all the ensemble models based on their confidence score and, thus, constructs average boxes27. Therefore, the WBF approach has shown tremendous capability to improve the performance of object detection models by fusing multiple detectors for natural ground images. Additionally, the performance of any detection model has been highly influenced by the methodology employed to estimate and minimize the loss, usually Intersection over Union (IoU) loss. This approach works satisfactorily in most cases but fails to optimize the loss, especially when the predicted and ground truth bounding boxes do not overlap. Therefore, the literature reveals other loss functions such as Generalized IoU (GIoU)28, Distance IoU (DIoU)29, and Complete IoU (CIoU)30 to handle this issue for object detection using natural images effectively. DIoU focuses on minimizing the distance between the centers of the predicted and ground-truth bounding boxes, whereas CIoU adds aspect ratio consideration. Both these are more effective when the bounding boxes already overlap. However, due to low object contrast and noisy backgrounds in SAR imagery, GIoU can be much more effective than DIoU and CIoU. Because it focuses more on the target objects, which helps maintain robustness against false object edges. Moreover, the effectiveness of WBF and GIoU loss functions in ship detection from SAR images has neither been exhaustively investigated nor well documented.

Based on these observations, it has been perceived that the generalization ability of DL models should be increased to develop an efficient ship detection model from SAR. Also, the limitation of IoU necessitates the exploration of other alternatives to optimize the losses more efficiently. Therefore, the present work focuses on the development of a highly robust generic ship detection framework with better loss optimization capabilities in a reliable manner. Summarizing, the main contribution of the present work has been listed as:

  • The GIoU loss has been incorporated into the loss function, which reduces the scale sensitivity of the network and ensures a better multiscale feature learning capability of the model.

  • Based on the modified loss function, YOLOv4 (G-v4) and YOLOv5 (G-v5) models have been developed to detect ships from SAR imagery.

  • Considering the complexities associated with SAR images containing ships, an ensemble YOLO (eYOLO) framework has been proposed to enhance the generalization capability of the model. The eYOLO has been developed as an end-to-end network that fuses the G-v4 and G-v5 models via WBF.

The rest of this work has been organized as follows: section “Dataset description” describes the dataset being utilized. Section “Preliminary knowledge” briefly provides the preliminary information regarding YOLOv4 and YOLOv5 along with the loss function and employed fusion mechanism. The proposed methodology for the development of eYOLO has been presented in section “Proposed methodology”. The results obtained by eYOLO and comparative analysis have been provided in section “Experiments”. Finally, section “Conclusion and future scope” concludes the present work with directions for future work.

Dataset description

This study utilizes the open-source SAR-ship dataset provided by the Chinese Academy of Sciences, which contains ships of various shapes and sizes in relatively low-resolution SAR images31. This dataset considers 102 Gaofen-3 and 108 Sentinel-1 images to generate a total of 39,729 images with 50,885 ship appearances, and the size of all these ships has been kept at 256 pixels for both range and azimuth. The sample images from this dataset have been presented in Fig. 1. Further, the distribution of the dataset is depicted in Fig. 2, where the number of ships in each image and the bounding box area are demonstrated in Fig. 2a and b, respectively. This indicates that the employed dataset mostly has a single ship in each image chip with a median box size of 897. This median box area has been estimated to be only 1.37% of the total image size, whereas around 85.85% of ships have less than 3.05% representation of image size. Further, the relative box size has been calculated by \(\sqrt {\left( {box size/image size} \right)}\), which reflected that approximately 92.91% of ships have a relative size of less than 0.2. These observations reveal that the dataset has ships of various shapes and has been highly populated with small-sized ships. These small-sized ships added the difficulties associated with already complex ship detection from SAR because now the deep CNNs may miss the distinguishable attributes of ships from the background on the feature map, particularly after several rounds of sub-sampling. Additionally, similar scattering patterns have been witnessed in the presence of tides or ships near shore, which significantly uplifts the difficulties of this task.

Fig. 1
figure 1

Sample images in SAR-ship dataset (a) Sentinel-1, (b) Gaofen-3.

Full size image
Fig. 2
figure 2

Dataset (a) number of ships per image, (b) available box area.

Full size image

The acquired dataset has been randomly subdivided into training, validation, and test datasets by adopting an empirically verified policy of 85:10:5. Therefore, the dataset has 33,769 images with 44,239 ship instances for training, 3993 images with 4589 ship appearances for validation, and 1967 images with 2057 ship occurrences for testing.

Preliminary knowledge

This section develops a brief concept of the two most popular versions of YOLO (v4 and v5) in sub-sections “YOLOv4” and “YOLOv5”. The loss function utilized by both versions has been discussed in sub-section “Weighted box fusion”, and the basic idea of WBF in sub-section “Weighted box fusion”.

YOLOv4

Before the inception of YOLO, two-stage detectors have been commonly accepted. However, they failed to balance the speed-accuracy trade-off. Therefore, YOLO transforms object detection into regression to effectively mitigate this issue, which remains the core idea of all the versions of YOLO. The YOLOv4 incorporates a mosaic data augmentation technique to enhance the prediction capability of the model. Further, it optimizes and updates the backbone, incorporates advanced activation functions, and improves the training methodology to balance the speed-accuracy trade-off32,33. It employs CSPDarknet53 as the backbone network for feature extraction, PANet (Path Aggregation Network) to fuse the extracted attributes, and YOLOv3 as the head for object detection.

The basic structure of the ship detection model based on YOLOv4 has been presented in Fig. 3. It combines Convolution and Batch Normalization with the Leaky-ReLU activation function to develop a CBL block, whereas the MISH activation function for the CBM block. Further, Spatial Pyramid Pooling (SPP) transforms convolutional features into pooled features of the same length.

Fig. 3
figure 3

YOLOv4-based ship detection model.

Full size image

YOLOv5

YOLOv4 enhances the detection capability of object detection models, reduces the computational complexity, and can be trained with a single graphical processing unit (GPU). However, it still has a large model size because of the large number of training parameters. Therefore, to reduce the model size for lightweight characteristics, with high detection accuracy and less inference time, YOLOv5 evolved. It incorporates a focus module and redefines the CSP module in the existing backbone of YOLOv4. The focus module slices the image to retain more information with a reduced computational burden. It also has two CSP modules (CSP1_X and CSP2_X) modified from the CSPNet. The CSP module first divides the earlier layers’ features into two parts, processes them, and then combines them hierarchically. The CSP1_X module has been utilized in the backbone, whereas CSP2_X in the neck to strengthen the integration capability of the network and reduce the computational complexities with improved accuracy. Besides these modules, the SPP module in the ninth layer of the backbone has been employed to generate the feature vector of the length of the fully connected layer. The basic structure of the YOLOv5 and various modules has been presented in Fig. 4.

Fig. 4
figure 4

The basic structure of YOLOv5 with various modules.

Full size image

Loss function

The loss function has been the most crucial part of any learning algorithm as it allows the model to learn the differences between the predicted and actual values. In both the studied versions of YOLO, the loss function has been typically defined by the summation of bounding box regression loss (loss1), confidence loss (loss2), and classification loss (loss3). The loss1 has been expressed by Eq. (1).

$$ loss_{1} = - \sum\limits_{m = 0}^{{S^{2} }} {\sum\limits_{n = 0}^{B} {1_{m,n}^{obj} M} } \, $$
(1)

where, S2 and B represent the number of grids and the number of bounding boxes in each grid, respectively. M denotes the mean square error (MSE) between the estimated and actual values of bounding boxes. The confidence loss has been mathematically represented by Eq. (2).

$$ \begin{gathered} loss_{2} = - \sum\limits_{m = 0}^{{S^{2} }} {\sum\limits_{n = 0}^{B} {T_{m,n}^{obj} \left[ {K_{m}^{n} \log \,(C_{m}^{n} ) + (1 - K_{m}^{n} )\log (1 - C_{m}^{n} )} \right]} } \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \lambda_{noobj} \sum\limits_{m = 0}^{{S^{2} }} {\sum\limits_{n = 0}^{B} {(1 - T_{m,n}^{obj} )\,\left[ {K_{m}^{n} \log \,(C_{m}^{n} ) + (1 - K_{m}^{n} )\log (1 - C_{m}^{n} )} \right]} } \hfill \\ \end{gathered} $$
(2)

where, \(\lambda_{noobj}\) symbolizes the weight parameter. \(T_{m,n}^{obj}\) represents the function of objects and \(T_{m,n}^{obj} = 1\) if and only if the nth bounding box of the mth grid detects the current object. \(K_{m}^{n}\) and \(C_{m}^{n}\) have been used to represent the confidence score of predicted and target bounding boxes, respectively. The classification loss has been generally defined by Eq. (3).

$$ loss_{3} = - \sum\limits_{m = 0}^{{S^{2} }} {\sum\limits_{n = 0}^{B} {T_{m,n}^{obj} \sum\limits_{c = 1}^{C} {\left[ {E_{m}^{n} (c)\log \,(F_{m}^{n} (c)) - (1 - E_{m}^{n} (c))\log (1 - F_{m}^{n} (c))} \right]} } } \, $$
(3)

where, \(E_{m}^{n} (c)\) and \(F_{m}^{n} (c)\) denote the prediction and actual probability that the object belongs to the true category. Therefore, the final loss function has been defined as in Eq. (4).

$$ Loss = loss_{1} + loss_{2} + loss_{3} $$
(4)

Weighted box fusion

As discussed earlier, the NMS and soft-NMS provide acceptable results but have often encountered difficulties, especially for the ensemble approach. Therefore, techniques like non-maximum weighted (NMW) and WBF have been proposed27. In these techniques, the predicted bounding boxes from one or more than one model have been used to estimate the average bounding box so that a more reliable and robust detection algorithm can be developed. The NMW considers IoU values to build a weight matrix of predicted boxes. This method improves the drawbacks associated with NMS; however, as these weight matrices employ only IoU, they fail to attract general acceptability. On the other hand, WBF ensemble models by fusing multiple bounding boxes for a single object using their confidence score. Further, on every addition of the bounding box in the fused list, it recalculates the coordinates and confidence score of the fused box using Eqs. (5–7) and, therefore, performs very efficiently.

$$ C = \frac{{\sum\limits_{n = 1}^{N} {C_{n} } }}{N} $$
(5)
$$ X_{12} = \frac{{\sum\limits_{n = 1}^{N} {C_{n} \times X_{12,n} } }}{{\sum\limits_{n = 1}^{N} {C_{n} } }} $$
(6)
$$ Y_{12} = \frac{{\sum\limits_{n = 1}^{N} {C_{n} \times Y_{12} } }}{{\sum\limits_{n = 1}^{N} {C_{n} } }} $$
(7)

where, C represents the confidence score. X and Y symbolize the x and y coordinates of the bounding box, respectively.

Proposed methodology

Generally, all object detection models use Intersection over Union (IoU) to estimate their accuracy. This measure the similarity between the predicted bounding boxes and the ground truth and is mathematically expressed by Eq. (8).

$$ IoU = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}} $$
(8)

where, A and B represent the area of the predicted and ground truth bounding boxes, respectively. The value of IoU lies in the range of [0, 1]. This method performs satisfactorily in most of the cases. However, it finds reliable assessment difficult, especially when the bounding boxes do not overlap or have different overlapping directions. Therefore, in this work, despite IoU loss (Eq. 1), Generalized IoU (GIoU) has been adopted to evaluate the bounding box regression loss28. The basic methodology to estimate the GIoU has been presented in Fig. 5, and its mathematical formulation by Eq. (9).

$$ GIoU = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}} - \frac{{\left| {C\backslash (A \cup B)} \right|}}{{\left| {C\,} \right|}} $$
(9)

where, A and B represent two arbitrary-shaped bounding boxes. C depicts the smallest enclosing box, and GIoU lies between − 1 and 1.

Fig. 5
figure 5

Generalized Intersection over Union (GIoU).

Full size image

Therefore, if AC represents the area of box C, then the box regression loss can be framed by Eq. (10), which replaces the loss1 in Eq. 4.

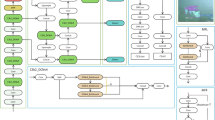
$$ loss_{4} = \sum\limits_{m = 0}^{{S_{{}}^{2} }} {\sum\limits_{n = 0}^{B} {1_{m,n}^{obj} \left[ {1 - IoU + \frac{{A^{C} - \left( {A \cup B} \right)}}{{A^{C} }}} \right]} } $$
(10)

The preprocessed dataset has 33,769 and 3993 images for training and validating the ship detection models. Further, data augmentation techniques such as rotation, flip, and crop have also been employed. These techniques help the model to achieve better generalization capability. Both YOLOv4 and YOLOv5 have been trained for 100 epochs with a batch size of 16 and an image size of 256 × 256. Once trained, the weights of these models have been saved. Then, the WBF technique has been employed to ensemble these models. Further, the performance of these models has been evaluated and compared with each other. This whole methodology has been represented in Fig. 6.

Fig. 6
figure 6

Methodology for the development of eYOLO.

Full size image

Experiments

Simulation settings

In the present work, the proposed model has been implemented by employing the PyTorch framework. For this purpose, a DL environment has been built on CUDA and cuDNN-enabled Ubuntu 18.04 LTS system having an Intel Xeon Gold processor with 48-GB QUADRO RTX-8000 GPU. Further, this work considers YOLOv5s as the baseline model. However, this model has been trained on ground-image-based datasets having entirely different viewpoints. Therefore, it cannot be directly employed to detect the object from SAR images. Hence, the baseline model has also been trained by fine-tuning the provided final weights (v5_T). Also, YOLOv5 has been trained from scratch (v5_S). Further, both YOLOv4 and YOLOv5 have been trained by employing GIoU loss to develop an ensemble object detection model. These ensemble models have been represented by G-v4 (GIoU + YOLOv4), G-v5 (GIoU + YOLOv5), and eYOLO (G-v4 + G-v5), respectively. The image size has been fixed to 256 × 256 during the entire simulation work. All these models have been developed by employing the ADAM optimizer with a learning rate of 0.001, weight decay of 0.0005, and momentum of 0.93734,35. These models have been trained for 100 epochs, and the batch size has been set to 16.

Evaluation metrics

The performance of the developed ensemble model has been compared with the v5_T and v5_S based on mean Average Precision (mAP), considering it the most crucial factor in analyzing the generalization ability of any object detection model. Further, various other performance metrics such as precision (P), recall (R), and F1 score have been utilized to compare the model performance with other reported works. These indicators have been computed by Eqs. (11–14). Also, as the F1 score gives a higher weightage to P, another measure of the F2 score has been introduced in Eq. (15), which gives a higher weightage to R.

$$ mAP = \int\limits_{0}^{1} {P(R)\,dR} $$
(11)
$$ P = \frac{{T_{P} }}{{T_{P} + F_{P} }} $$
(12)
$$ R = \frac{{T_{P} }}{{T_{P} + F_{N} }} $$
(13)
$$ F_{1} \,score = \frac{2 \times P \times R}{{P + R}} $$
(14)
$$ F_{2} \,score = \frac{5 \times P \times R}{{4 \times P + R}} $$
(15)

Result analysis

As mentioned earlier, the SAR images have significantly different characteristics. Therefore, the open-source DL object detection models cannot be directly applied. First, the YOLOv5 model with open-source pre-trained weights has been tested to review this critically. From this analysis, it has been revealed that although it achieved mAP of 0.689 on the COCO dataset, only 0.048 mAP has been attained on the employed dataset. Therefore, two models of YOLOv5 (v5_T and v5_S) have been trained with the aforementioned hyperparameters by employing transfer learning and from scratch, respectively. These models help to analyze the impact of these techniques on the model performance for an entirely different representative dataset. The performance of these models has been compared based on mAP, and it has been witnessed that v5_T achieved the mAP of 0.909. Therefore, it performs slightly better (0.44%) than v5_S on the unseen dataset. This also verifies that the transfer learning approach should be preferred over training from scratch because this approach with the pre-trained backbone has superior capabilities.

Further, two other models (G-v4 and G-v5) were trained to incorporate GIoU loss. These models have been trained from scratch because of the unavailability of their trustworthy weights with this loss. On comparing their performance, it has been observed that G-v5 dominates G-v4 by a comprehensive margin of 16.92% for mAP. Consequently, G-v5 has a more overwhelming ship detection capability than G-v4. Also, the mAP of G-v5 has been computed as 0.77% and 0.33% higher than v5_S and v5_T, respectively. Therefore, it has been perceived that the GIoU enhances the model’s prediction ability and should be preferred over IoU. Lastly, the developed G-v4 and G-v5 models have been fused to create an eYOLO by employing the WBF technique. It has been witnessed that eYOLO attained the mAP of 0.920 and dominated G-v4, G-v5, v5_T, and v5_S with an encouraging margin of 17.95%, 0.88%, 1.21%, and 1.66%, respectively. Therefore, eYOLO has better generalization capability and can detect ships with higher P and R. The computed mAP values of all the models have been tabulated in Table 2, and their impact has been depicted by the P-R curve, as shown in Fig. 7.

Table 2 Performance comparison.
Full size table
Fig. 7
figure 7

P-R curve for ship detection models.

Full size image

The ships detected by these models have been visually compared against the ground-truths for test images, and a sample of these has been demonstrated in Fig. 8. The bounding boxes generated by all the models for the detected ships in each image have been compared against the ground truths, and it has been computed that eYOLO predicts better and crisper bounding boxes than all others. This also verifies that eYOLO has better detection capability because of the fusion. Occasionally, eYOLO also detects some false ships (Image 4); however, considering the complexities associated with SAR, these may be neglected because the number of these false detections has been computed very little.

Fig. 8
figure 8

Ships detected (a) ground truth, (b) G-v4, (c) G-v5, (d) eYOLO, (e) v5_T, (f) v5_S.

Full size image

The developed models have also been compared for qualitative analysis based on the false detection rate (FDR) and missed detection rate (MDR). The values of these rates for all the developed models have been mentioned in Table 3. Based on FDR, the eYOLO outperforms v5_T and v5_S by a significant margin of 35.16% and 54.70%, respectively. Similarly, it outclasses G-v4 and G-v5 for the same parameter by 160.49% and 25.2%, respectively. For MDR, the developed eYOLO also dominates others by a minimum margin of 28.42%. Therefore, the developed eYOLO has been examined as more robust than others.

Table 3 Qualitative analysis of developed ship detection models.
Full size table

Comparison and validation

The results obtained by eYOLO have been compared against other reported work on the same dataset to validate the proposed model. For this purpose, a comparative table has been framed and presented in Table 4. The developed eYOLO conquered the other developed models for P by the minimum and maximum margins of 0.82% and 19.72%, respectively. It also achieves a 4.28% higher value of R as compared with the reported literature36 and has been found comparable with others. Based on the F1 score, it outclasses most of the reported models by at least 0.32%. However, the achieved F1 score has been found to be slightly lower than the value attained by CR2A-Net37. This may be because the hyperparameters of G-v4 can be further improved, and this model finds difficulty detecting small-size ships in complex scenarios, which has also been witnessed in the higher MDR (Table 3). On the basis of mAP also, the developed eYOLO significantly outperformed all the other compared models, which suggests that algorithmic enhancements, such as loss functions, optimization techniques, etc., might improve other aspects of model performance (robustness, generalization ability, etc.), with only slight improvement in mAP 38. Therefore, it has been concluded that the developed eYOLO has better adaptability and generalization capability. Further, the higher values of both the F1 score and F2 score concealed that the developed eYOLO may be very effective for the marine industry.

Table 4 Comparative analysis with state-of-the-art models.
Full size table

Conclusion and future scope

In this work, a novel ensemble object detection framework has been proposed for efficient ship detection from SAR imagery, and the effectiveness of the model has been analyzed on the open-source SAR-Ship dataset. Firstly, the GIoU loss function has been incorporated to modify the loss, which has been further utilized to train G-v4 and G-v5. Then, the WBF technique has been employed to develop the proposed ensemble object detection model (eYOLO) by fusing G-v4 and G-v5. The developed eYOLO model has been compared against other developed models on the basis of mAP, FDR, and MDR, which establishes the superiority of eYOLO over others for this specific task. Further, the efficacy of eYOLO has been validated by comparing it with other reported works. The simulated results endorsed that the eYOLO has a better adaptability and generalization capability. Though the proposed eYOLO performed satisfactorily and has shown tremendous ability to detect ships of several scales, it still suffered from false alarms, particularly at the edges, which will be addressed in the future.