Introduction

A transversal or lateral shift known as the Goos-Hänchen (GH) shift or the Imbert-Fedorv (IF) shift occurs when a linearly polarized light is incident on an optical interface. The GH shift was found by F. Goos and H. Hänchen for the total internal reflection in 19471 and further confirmed by Artmann through experiments2. After that, Fedorv proposed the hypothesis of lateral shift, which was experimentally verified by Imbert3,4. The GH shift is determined mathematically by calculating the gradient of the coefficient phase to the incident angle and directly associated with the incident beam and the material properties. It is caused by the dispersive properties of the material for reflected or refracted light beams. Conversely, the IF shift originates from the spin-orbit interaction in the beam and is considered one of the spin-Hall effects (SHE) related to the geometric Berry phase5. The GH and IF shifts are very small, typically in the order of wavelength, which makes the phenomenon extremely challenging to observe and quantify. In recent years, numerous methods for measuring the beam shift have been proposed and practiced. For example, it is possible to magnify spatial shifts using the weak measurement6. To perform a direct measurement, a variety of intriguing structures, such as metamaterials7, metasurfaces8,9, Dirac materials10,11, and epsilon near-zero (ENZ) materials12,13, were employed to amplify the shifts. In addition to materials, the enhanced spatial shifts are also dependent on the type of light beam, i.e. Gaussian beams14,15, Laguerre-Gaussian beams16, Bessel beams17,18, rotating elliptical Gaussian beams19,20, and Airy beams21,22.

A novel class of quantum-effect insulator known as a topological insulator (TI) has an energy gap in its interior and exhibits an insulating state, while its surface is a conducting state shielded by the time-reversal symmetry23. Controlling the spatial shifts generated by the TI’s surface state allows for more precise beam adjustment24,25. The interaction of intrinsic and extrinsic angular momentum plays a vital role in the increased SHE of light produced by a reflected Airy beam off the interface of an air-topological insulator (TI)24. Under the influence of an external magnetic field, a tunable magneto-optical SHEL on the surface of TIs is examined25. The time-reversal symmetry of TI can be broken by coating a thin magnetic layer on the surface of TI or applying an external magnetic field perpendicular to the surface26,27. Under such conditions, the TI’s surface state will be fully gapped and exhibit unusual electromagnetic properties, such as the topological magnetoelectric effect (TME, the axion coupling effect). The electric field induces the magnetization while the magnetic field causes the electric polarization28,29,30,31,32. The constituent relation between the magnetic field and electric field becomes \(\mathbf{D}={\varepsilon }_{0}\varepsilon \mathbf{E}+\frac{\Theta }{\pi }(\alpha \mathbf{B})\) and \(\mathbf{H}=\frac{\mathbf{B}}{{\mu }_{0}\mu }-\frac{\Theta }{\pi }(\alpha \mathbf{E})\)33, where the fine-structure constant of the material \(\alpha ={e}^{2}/\hslash c\approx 1/137\)34, and \(\Theta\) is called the axion field33. The axion field \(\Theta\) closely corresponding to the TME is quantized and expressed as \(\Theta =(2n+1) \pi ,\) where \(n\) is an integer35. Two general cases will be presented, for example, \(\Theta =0\) showing an ordinary insulator and \(\Theta =1 \pi\) displaying a three-dimensional TI. The values of \(\Theta\) are normally governed by the perturbation of breaking time-reversal symmetry, whose sign depends on the magnetization direction of the surface magnetic layer. \(\Theta\) takes positive values when the magnetization is parallel to the normal of the surface and negative values when it is antiparallel to the surface’s normal direction36. Recently, the dynamical TME in antiferromagnetic MnBi2Te4 films can be adjusted by engineering the thickness of the films, temperature or element substitutions37. Through a variety of plateau states, a tunable TME with ion-gel gating was accomplished using a unique ionic gel gating approach to adjust the chemical potential of Bi2Se3 thin film38. Thus, the optical properties of TIs can be controlled by adjusting the axion field \(\Theta\)39,40,41. The IF shifts of a reflected Gaussian beam from anisotropic TIs are studied, where two types of TI surface perturbations, namely, a magnetic coating and an applied magnetic field, are taken into account39. It is suggested that a TI-based cavity structure can significantly increase the lateral shift, which is explained by the presence of the TME in TIs40. In the presence of a static magnetic field, the massive and quantized lateral and angular GH shifts can be produced from the surface of a hybridized TI thin film41. It demonstrates that the spatial shifts are feasible to be controlled by using the TI with an external perturbation.

Two-dimensional (2D) Dirac materials, such as graphene, have analogous surface state characteristics to TIs. Though graphene lacks topological protection for the Dirac state, the band structures of TI and graphene are remarkably similar42. To improve and precisely control the spatial shifts, numerous works on different graphene-based nanostructures have been conducted43,44,45. By efficiently modifying the appropriate graphene parameters, the graphene/hexagonal boron nitride (hBN) metamaterials’ surface may produce huge and controllable GH and IF shifts with higher reflectivity43. Large quantized GH shifts in graphene that are electrically tunable have been investigated by varying the Fermi energy in the terahertz (THz) range44,45. Nevertheless, the situation where 2D Dirac materials blanket the surface of TI with perturbations has not been extensively studied. Specifically, a hyperbolic metasurface can be formed when the graphene ribbons are placed on the TI surface. By constructing the metasurfaces, the desired reflected and transmitted waves can be manipulated. It has been discovered in recent years that reflected light beams off the gradient metasurface show special spatial-shift characteristics8,39,46,47,48. For example, the influence of the cross-anisotropic metasurface coating on the spatial and angular GH shifts is theoretically investigated in Ref.46, where a larger positive or negative spatial GH shift appears, accompanied by pairs of greater positive or negative angular GH shifts. The evident tunability is presented by the spatial shifts or spin splitting of the reflecting Gaussian beams47 or vortex beams48 incident on the metasurface based on the hBN crystal.

Motivated by these advances in the investigation of GH and IF shifts on the metasurface based on TIs, we theoretically investigate the GH and IF shifts of a reflected Gaussian beam on the hyperbolic metasurface of graphene grating/TI structure, where the TI is coated with a thin magnetic layer of negligible thickness. A remarkable phenomenon could potentially arise from the combined action of the hyperbolic metasurface and the TME. Additionally, as the Fermi energy of graphene can be influenced by an external electric field, the controllability of the GH and IF shifts will be enhanced. An extensive analysis is carried out regarding the effects of the GH and IF shifts by the chemical potential, filling ratio, rotation angles of graphene, and TME of TI. The maximum GH and IF shifts for the case with a single layer of graphene or without graphene on the surface of TIs are also provided to serve as a standard reference for comparison. This paper is organized as follows. The GH and IF shifts analytical formulas for the reflected Gaussian beams are given in Sect. “Theoretical model”. Section “Numerical results and discussion” displays the findings and conversations. Finally, a useful conclusion is drawn in Sect. “Conclusions”.

Theoretical model

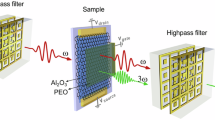
Figure 1 depicts a semi-infinite anisotropic topological insulator (TI) coated by a periodic graphene grating. The width of graphene strips is represented by \({W}_{g}\) and \(D\) is the periodic length. In addition, the graphene grating is rotated from the principal-axis coordinate system \(({x}{\prime}{y}{\prime}{z}{\prime})\) by an angle \(\beta\) with respect to the x-axis. The optical axis (OA) of the TI is in the x–z plane (the incident plane) along the z-axis. Consider a Gaussian beam impinging on the metasurface at the incident angle \(\theta\), and the central rays of the incident and reflected beams are denoted by I and R, respectively. \(\Delta x\) and \(\Delta y\) indicate the shifts of the reflected beam along the x and y axes.

Fig. 1
figure 1

Schematic illustration of the GH and IF shifts when a Gaussian beam is incident on the metasurface of graphene grating/TI. The magnetic coating on the TI surface is the cause of breaking the time-reversal symmetry.

Full size image

The effective medium theory can be applied since the operating wavelength is substantially larger than the graphene grating thickness43. Then, the expression of the effective permittivity of the graphene grating in the principal-axis coordinate system (\({x}{\prime}{y}{\prime}{z}{\prime}\)) is expressed as

$$\overleftrightarrow \varepsilon_{g}^{e} = \varepsilon_{0} \left( {\begin{array}{*{20}c} {{{\varepsilon_{g} } \mathord{\left/ {\vphantom {{\varepsilon_{g} } {(\varepsilon_{g} f_{a} + f_{g} )}}} \right. \kern-0pt} {(\varepsilon_{g} f_{a} + f_{g} )}}} & 0 & 0 \\ 0 & {f_{a} + f_{g} \varepsilon_{g} } & 0 \\ 0 & 0 & {f_{a} + f_{g} \varepsilon_{g} } \\ \end{array} } \right),$$
(1)

where \({f}_{g}=\frac{{W}_{g}}{D}\) represents the filling ratio of the graphene ribbons, and the filling ratio of air \({f}_{a}=1-{f}_{g}\). \({\varepsilon }_{g}\) indicates the permittivity of graphene, which is expressed as \({\varepsilon }_{g}=1+i\sigma /{\varepsilon }_{0}\omega {d}_{g}\)41. \({\varepsilon }_{0}\) is the dielectric constant in vacuum and \({d}_{g}\) is the thickness of graphene.\(\sigma\) represents the surface conductivity of the graphene and is simplified as \({{\sigma =i{e}^{2}\mu }_{c}/\pi \hslash }^{2}(\omega +i{\tau }_{g}^{-1})\) at the room temperature42. The parameters \(e\), \({\mu }_{c}\), \(\hslash\) and \({\tau }_{g}\) are the electron charge, the chemical potential, the Planck constant and the damping of the graphene, respectively. After rotating the graphene ribbons around the z-axis by an angle \(\beta\), the equivalent permittivity is a non-diagonal matrix in the xyz coordinate system and will be

$$\overleftrightarrow \varepsilon = \varepsilon_{0} \left( {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{xy} } & 0 \\ {\varepsilon_{xy} } & {\varepsilon_{yy} } & 0 \\ 0 & 0 & {\varepsilon_{zz} } \\ \end{array} } \right),$$
(2)

where

$$\varepsilon_{xx} = \cos^{2} \beta \varepsilon_{g} /(\varepsilon_{g} f_{a} + f_{g} ) + \sin^{2} \beta (f_{a} + f_{g} \varepsilon_{g} ),$$
(3a)
$$\varepsilon_{yy} = \sin^{2} \beta \varepsilon_{g} /(\varepsilon_{g} f_{a} + f_{g} ) + \cos^{2} \beta (f_{a} + f_{g} \varepsilon_{g} ),$$
(3b)
$$\varepsilon_{xy} = \varepsilon_{yx} = - \sin \beta \cos \beta \varepsilon_{g} /(\varepsilon_{g} f_{a} + f_{g} ) + \sin \beta \cos \beta (f_{a} + f_{g} \varepsilon_{g} ),$$
(3c)
$$\varepsilon_{zz} = f_{a} + f_{g} \varepsilon_{g} .$$
(3d)

The perturbation of breaking the time-reversal symmetry is produced by coating a magnetic layer on the surface of the TI, where the thickness of the magnetic coating is assumed to be ignored. In the principal axis coordinate system, the permittivity of the TI is represented as \({\varepsilon }_{t}=diag({\varepsilon }_{tx},{\varepsilon }_{tx},{\varepsilon }_{tz})\), in which the OA is parallel to the z-axis. It is evident that the TI is isotropic in the x–y plane, and \({\varepsilon }_{tx}=1+{\omega }_{e}^{2}/({\omega }_{0}^{2}-{\omega }^{2}-i\omega \gamma )\), where \({\omega }_{e}\) represents the strength of the oscillation, \({\omega }_{0}\) is the resonance frequency, and γ is the damping coefficient. The level of anisotropy, namely,\({\varepsilon }_{tz}\)/\({\varepsilon }_{tx}\) determines the value of \({\varepsilon }_{tz}\)39.

In the layer of the graphene grating, based on the Helmholtz equation ∇ × (∇ × E) = \({\omega }^{2}{\mu }_{0}{\varepsilon }_{0}\varepsilon \mathbf{E}\), the field amplitudes satisfy the following equations,

$$- k_{x} k_{z} E_{z} + (k_{z}^{2} - \varepsilon_{xx} f^{2} )E_{x} - f^{2} \varepsilon_{xy} E_{y} = 0,$$
(4a)
$$k_{x}^{2} E_{y} + k_{z}^{2} E_{y} - f^{2} \varepsilon_{yy} E_{y} - f^{2} \varepsilon_{yx} E_{x} = 0,$$
(4b)
$$- k_{x} k_{z} E_{x} + (k_{x}^{2} - f^{2} \varepsilon_{zz} )E_{z} = 0,$$
(4c)

here \(f=\omega /2\pi c\), where \(c\) is the velocity in vacuum48. Due to the anisotropy of the graphene grating, two wave solutions for \({k}_{z}\) are obtained,

$$k_{ \pm }^{2} = \frac{1}{{2\varepsilon_{zz} }}( - a \pm \sqrt {a^{2} - 4\varepsilon_{zz} b} ){\kern 1pt} ,$$
(5)

where

$$a = \varepsilon_{xx} (k_{x}^{2} - \varepsilon_{zz} f^{2} ) + \varepsilon_{zz} (k_{x}^{2} - \varepsilon_{yy} f^{2} ){\kern 1pt} ,$$
(6a)
$$b = (k_{x}^{2} - \varepsilon_{zz} f^{2} )(\varepsilon_{xx} k_{x}^{2} - \varepsilon_{xx} \varepsilon_{yy} f^{2} + \varepsilon_{xy}^{2} f^{2} ){\kern 1pt} ,$$
(6b)

\({k}_{\pm }\) corresponds to the two wave solution branches in the effective graphene grating layer, respectively. The choice of the sign for \({k}_{\pm }\) must guarantee attenuation of electromagnetic waves along the direction perpendicular to the surface. The three electric field components are coupled together due to the existence of non-diagonal terms of the effective permittivity when the graphene grating is rotated around the z-axis or the incident plane is rotated at a certain angle. Based on Eqs. (4b) and (4c), the x- and z-components of the electric fields are expressed as a function of the y-component, i.e.

$$E_{x}^{ \pm } = (k_{x}^{2} + k_{ \pm }^{2} - \varepsilon_{yy} f^{2} )E_{y}^{ \pm } /\varepsilon_{xy} f^{2} = \Lambda_{ \pm } E_{y}^{ \pm } ,$$
(7a)
$$E_{z}^{ \pm } = k_{ \pm } k_{x} (k_{x}^{2} - \varepsilon_{zz} f^{2} )^{ - 1} E_{x}^{ \pm } = k_{ \pm } k_{x} \Lambda_{ \pm } (k_{x}^{2} - \varepsilon_{zz} f^{2} )^{ - 1} E_{y}^{ \pm } .$$
(7b)

By a similar process, we can easily obtain two wave solutions in semi-infinite TIs, namely,\({k}_{o}=\sqrt{{\varepsilon }_{tx}{f}^{2}-{k}_{x}^{2}}\) and \({k}_{e}=\sqrt{{\varepsilon }_{tx}{f}^{2}-{\varepsilon }_{tx}{k}_{x}^{2}/{\varepsilon }_{tz}}\).\({k}_{o}\) is the TE wave with the electric field perpendicular to the incident plane, while \({k}_{e}\) represents the TM wave with the electric field parallel to the incident plane. In the graphene grating layer, only the y-component of the electric field needs to be shown, while the x- and y-components of the electric field in the other spaces will have to be given. The expressions of the electric fields in each space are as follows,

$$\left\{ {\begin{array}{*{20}c} {E_{x,y} = (E_{x,y}^{i} e^{{ik_{z} z}} + E_{x,y}^{r} e^{{ - ik_{z} z}} )e^{{i(k_{x} x - \omega t)}} \quad {\kern 1pt} \;\;\;\;\;\quad \quad \;\quad \;\,\;\quad \,\,\;\;\;(z < 0)} \\ {E_{y} = (Ae^{{ik_{ + } z}} + Be^{{ - ik_{ + } z}} + Ce^{{ik_{ - } z}} + De^{{ - ik_{ - } z}} )e^{{i(k_{x} x - \omega t)}} \quad \quad \,\,(0 < z < d_{g} )} \\ {E_{x} = F_{x} e^{{ik_{e} z}} e^{{i(k_{x} x - \omega t)}} ,\quad E_{y} = F_{y} e^{{ik_{o} z}} e^{{i(k_{x} x - \omega t)}} \quad \quad \,\,\quad \;\quad \,\,\;\;\;(z > d_{g} )} \\ \end{array} } \right..$$
(8)

The upper indexes i and r of the electric fields represent the incident and reflected electric fields, respectively. The magnetic field in each space can be obtained from Maxwell’s equation. By using the electromagnetic boundary continuity condition, we can obtain the electromagnetic field relationship at the upper surface:

$$E_{x}^{i} + E_{x}^{r} = \Lambda_{ + } (A + B) + \Lambda_{ - } (C + D),$$
(9a)
$$E_{x}^{i} - E_{x}^{r} = \lambda_{ + } (A - B) + \lambda_{ - } (C - D),$$
(9b)
$$E_{y}^{i} + E_{y}^{r} = A + B + C + D{\kern 1pt} ,$$
(9c)
$$E_{y}^{i} - E_{y}^{r} = \left[ {k_{ + } (A - B) + k_{ - } (C - D)} \right]/k_{z} ,$$
(9d)

here \({\lambda }_{\pm }={k}_{\pm }{k}_{z}{\varepsilon }_{zz}{\Lambda }_{\pm }/({\varepsilon }_{zz}{f}^{2}-{k}_{x}^{2})\). Similarly, the relationship at the interface between the graphene grating layer and the TI is as follows,

$$\Lambda_{ + } (Ae^{{ik_{ + } d_{g} }} + Be^{{ - ik_{ + } d_{g} }} ) + \Lambda_{ - } (Ce^{{ik_{ - } d_{g} }} + De^{{ - ik_{ - } d_{g} }} ) = F_{x} ,$$
(10a)
$$\gamma_{{_{ + } }}^{ + } Ae^{{ik_{ + } d_{g} }} - \gamma_{ + }^{ - } Be^{{ - ik_{ + } d_{g} }} + \gamma_{ - }^{ + } Ce^{{ - ik_{ - } d_{g} }} - \gamma_{ - }^{ - } De^{{ - ik_{ - } d_{g} }} = F_{x} ,$$
(10b)
$$Ae^{{ik_{ + } d_{g} }} + Be^{{ - ik_{ + } d_{g} }} + Ce^{{ik_{ - } d_{g} }} + De^{{ - ik_{ - } d_{g} }} = F_{y} ,$$
(10c)
$$\psi_{ + }^{ - } Ae^{{ik_{ + } d_{g} }} - \psi_{ + }^{ + } Be^{{ - ik_{ + } d_{g} }} + \psi_{ - }^{ - } Ce^{{ik_{ - } d_{g} }} - \psi_{ - }^{ + } De^{{ - ik_{ - } d_{g} }} = k_{o} F_{y} ,$$
(10d)

where

$$\psi_{ \pm }^{ \pm } = k_{ \pm } \pm \frac{\alpha f}{\pi }\Lambda_{ \pm } \Theta = k_{ \pm } \pm \zeta_{ \pm } \Theta {,}$$
(11a)
$$\gamma_{ \pm }^{ \pm } = [k_{e} k_{ \pm } \Lambda_{ \pm } \varepsilon_{zz} \pm \Theta \frac{\alpha }{\pi f}k_{e} (\varepsilon_{zz} f^{2} - k_{x}^{2} )]/[\varepsilon_{tx} (\varepsilon_{zz} f^{2} - k_{x}^{2} )] = Z_{ \pm } \pm \delta \Theta {,}$$
(11b)

For convenience, we transform Eqs. (9a–9d) and (10a–10d) into the following matrix forms,

$$\left( {\begin{array}{*{20}c} {E_{x}^{i} } \\ {E_{x}^{r} } \\ {E_{y}^{i} } \\ {E_{y}^{r} } \\ \end{array} } \right) = T_{1} \left( {\begin{array}{*{20}c} A \\ B \\ C \\ D \\ \end{array} } \right),$$
(12)

Then,

$$T_{1} = \frac{1}{2}\left( {\begin{array}{*{20}c} {\Lambda_{ + } + \lambda_{ + } } & {\Lambda_{ + } - \lambda_{ + } } & {\Lambda_{ - } + \lambda_{ - } } & {\Lambda_{ - } - \lambda_{ - } } \\ {\Lambda_{ + } - \lambda_{ + } } & {\Lambda_{ + } + \lambda_{ + } } & {\Lambda_{ - } - \lambda_{ - } } & {\Lambda_{ - } + \lambda_{ - } } \\ {1 + k_{ + } /k_{z} } & {1 - k_{ + } /k_{z} } & {1 + k_{ - } /k_{z} } & {1 - k_{ - } /k_{z} } \\ {1 - k_{ + } /k_{z} } & {1 + k_{ + } /k_{z} } & {1 - k_{ - } /k_{z} } & {1 + k_{ - } /k_{z} } \\ \end{array} } \right),$$
(13)

and

$$T_{2} \left( {\begin{array}{*{20}c} A \\ B \\ C \\ D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {F_{x} } \\ 0 \\ {F_{y} } \\ 0 \\ \end{array} } \right),$$
(14)

The effect of Θ mainly is represented in the matrix \({T}_{2}\). In order to show the role of Θ more clearly and compare with the previous works, we write the \({T}_{2}\) matrix as follows,

$$T_{2} = \Pi_{1} + \Theta \Pi_{2} ,$$
(15a)

where,

$$\Pi_{1} = \frac{1}{2}\left( {\begin{array}{*{20}c} {(\Lambda_{ + } + {\rm Z}_{ + } )p_{ + } } & {(\Lambda_{ + } - {\rm Z}_{ + } )/p_{ + } } & {(\Lambda_{ - } + {\rm Z}_{ - } )p_{ - } } & {(\Lambda_{ - } - {\rm Z}_{ - } )/p_{ - } } \\ {(\Lambda_{ + } - {\rm Z}_{ + } )p_{ + } } & {(\Lambda_{ + } + {\rm Z}_{ + } )/p_{ + } } & {(\Lambda_{ - } - {\rm Z}_{ - } )p_{ - } } & {(\Lambda_{ - } + {\rm Z}_{ - } )/p_{ - } } \\ {(1 + k_{ + } /k_{o} )p_{ + } } & {(1 - k_{ + } /k_{o} )/p_{ + } } & {(1 + k_{ - } /k_{o} )p_{ - } } & {(1 - k_{ - } /k_{o} )/p_{ - } } \\ {(1 - k_{ + } /k_{o} )p_{ + } } & {(1 + k_{ + } /k_{o} )/p_{ + } } & {(1 - k_{ - } /k_{o} )p_{ - } } & {(1 + k_{ - } /k_{o} )/p_{ - } } \\ \end{array} } \right),$$
(15b)

and

$$\Pi_{2} = \frac{1}{2}\left( {\begin{array}{*{20}c} {\delta p_{ + } } & {\delta /p_{ + } } & {\delta p_{ - } } & {\delta /p_{ - } } \\ { - \delta p_{ + } } & { - \delta /p_{ + } } & { - \delta p_{ - } } & { - \delta /p_{ - } } \\ { - \xi_{ + } p_{ + } /k_{o} } & { - \xi_{ + } /p_{ + } k_{o} } & { - \xi_{ - } p_{ - } /k_{o} } & { - \xi_{ - } /p_{ - } k_{o} } \\ {\xi_{ + } p_{ + } /k_{o} } & {\xi_{ + } /p_{ + } k_{o} } & {\xi_{ - } p_{ - } /k_{o} } & {\xi_{ - } /p_{ - } k_{o} } \\ \end{array} } \right),$$
(15c)

where \({p}_{\pm }=\text{exp}(i{k}_{\pm }{d}_{g})\). After eliminating the amplitudes A, B, C and D, the above matrix can be changed into,

$$\left( {\begin{array}{*{20}c} {F_{x} } \\ 0 \\ {F_{y} } \\ 0 \\ \end{array} } \right) = T\left( {\begin{array}{*{20}c} {E_{x}^{i} } \\ {E_{x}^{r} } \\ {E_{y}^{i} } \\ {E_{y}^{r} } \\ \end{array} } \right),$$
(16)

here \(T={\Pi }_{1}{T}_{1}^{-1}+\Theta {{\Pi }_{2}T}_{1}^{-1}\). According to the matrix (16), we can get the relationship between the reflective field and the incident field in the xyz laboratory coordinate system, which is expressed as,

$$\left( {\begin{array}{*{20}c} {E_{x}^{r} } \\ {E_{y}^{r} } \\ {E_{z}^{r} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {m_{11} } & {m_{12} } & 0 \\ {m_{21} } & {m_{22} } & 0 \\ 0 & {m_{12} \tan \theta } & { - m_{11} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{x}^{i} } \\ {E_{y}^{i} } \\ {E_{z}^{i} } \\ \end{array} } \right),$$
(17)

in which,

$$m_{11} = \frac{{T_{21} T_{44} - T_{24} T_{41} }}{{T_{24} T_{42} - T_{22} T_{44} }},\,\,\,m_{12} = \frac{{T_{23} T_{44} - T_{24} T_{43} }}{{T_{24} T_{42} - T_{22} T_{44} }}.$$
(18a)
$$m_{21} = \frac{{T_{42} T_{21} - T_{22} T_{41} }}{{T_{22} T_{44} - T_{42} T_{24} }},\,\,\,m_{22} = \frac{{T_{42} T_{23} - T_{22} T_{43} }}{{T_{22} T_{44} - T_{42} T_{24} }}.$$
(18b)

It is well known that \({E}_{y}^{r}\) is the electric field amplitude of the s-polarization state of the reflected beam, but \({E}_{x}^{r}\) and \({E}_{z}^{r}\) are the two electric field amplitude components of the p-polarized reflected beam. Transforming the laboratory coordinate system to the central beam coordinate system gives the expression for the reflected electric field, i.e.

$$\left( {\begin{array}{*{20}c} {E_{p}^{r} } \\ {E_{s}^{r} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - m_{11} } & { - m_{12} /\cos \theta } \\ {m_{21} \cos \theta } & {m_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{p}^{i} } \\ {E_{s}^{i} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {r_{pp} } & {r_{ps} } \\ {r_{sp} } & {r_{ss} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{p}^{i} } \\ {E_{s}^{i} } \\ \end{array} } \right).$$
(19)

The matrix (19) is generally defined as the Fresnel reflection coefficient matrix. The off-diagonal components appear as a result of the rotation of the graphene grating, which leads to the surface anisotropy. In addition, if we set \(\Theta =0\) where the TI crystal will become the ordinary anisotropic material, the matrix \(T\) will be reduced to the known expression in Ref.47, where \({r}_{ps}={r}_{sp}=0\) for the isotropic materials and \({r}_{ps}=-{r}_{sp}\) for the anisotropic materials. It is clear that \({r}_{ps}\ne {r}_{sp}\) due to \(\Theta \ne 0\) which exhibits the impact of TME on the reflection coefficient.

The incident beam, being a paraxial beam, has a narrow plane wave distribution along the central wave in momentum space, where the electric-field can be expressed by \({E(\mu ,\nu )=E}_{j }exp[-{({w}_{0}/2)}^{2}({k}_{\mu }^{2}+{k}_{v}^{2})]\) in the k-space. \({w}_{0}\) represents the beam waist. \({k}_{\mu }={k}_{0}{\beta }_{s}sin\theta\) is the wave vector perpendicular to the incident plane, where \({\beta }_{s}\) is a tiny rotation angle of the incident plane. \({k}_{v}={k}_{0}{\theta }_{p}\) indicates the wave vector in the incident plane and normal to the central beam, where \({\theta }_{p}\) represents a slight changing angle of the incident angle49. \({k}_{0}=\omega \sqrt{{\mu }_{0}{\varepsilon }_{0}}\) is the wave vector in the vacuum. From Eq. (19), it can be seen that all the components of the reflective coefficient are dependent on the \(\theta\) and \(\beta\). Therefore, we provide the GH shift without considering \({\beta }_{s}\), and the reflected electric field given in the central beam coordinate system is further expanded to the first order of \({\theta }_{p}\), while the advanced items are ignored, resulting in,

$$\left( {\begin{array}{*{20}c} {E_{p}^{r} } \\ {E_{s}^{r} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - (m_{11} + m_{11}{\prime} \theta_{p} )} & { - \frac{{(m_{12} + m_{12}{\prime} \theta_{p} )}}{\cos \theta }} \\ {(m_{21} { + }m_{21}{\prime} \theta_{p} )\cos \theta } & {m_{22} + m_{22}{\prime} \theta_{p} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{p}^{i} } \\ {E_{s}^{i} } \\ \end{array} } \right) = M_{p} \left( {\begin{array}{*{20}c} {E_{p}^{i} } \\ {E_{s}^{i} } \\ \end{array} } \right),$$
(20)

where \({m}_{ij}{\prime}(i=j=\text{1,2})\) denotes the the first derivative to \({\theta }_{p}\) and the advanced terms are neglected. The reflective electric field can be expressed by \(\left|{{\varvec{E}}}_{r}\rangle ={M}_{p}E(\mu ,\nu ){{\varvec{E}}}_{i}\right.\). The expression for GH shift can be written as47,49:

$$\Delta x = \frac{1}{{2\pi k_{0} }}{\text{Im}} \left\langle {{{\text{E}}^{r} }} \mathrel{\left | {\vphantom {{{\text{E}}^{r} } {\frac{\partial }{{\partial \theta_{p} }}{\text{E}}^{r} }}} \right. \kern-0pt} {{\frac{\partial }{{\partial \theta_{p} }}{\text{E}}^{r} }} \right\rangle /\left\langle {{{\text{E}}^{r} }} \mathrel{\left | {\vphantom {{{\text{E}}^{r} } {{\text{E}}^{r} }}} \right. \kern-0pt} {{{\text{E}}^{r} }} \right\rangle ,$$
(21)

The analytical expression is,

$$\begin{aligned} \Delta x = & \frac{1}{{2\pi k_{0} R}}{\text{Im}} \{ [m_{11} E_{p}^{i} + m_{12} E_{s}^{i} \cos^{ - 1} \theta ]^{*} [m_{11}{\prime} E_{p}^{i} + m_{12}{\prime} E_{s}^{i} \cos^{ - 1} \theta ] \\ &+ [m_{21} E_{p}^{i} \cos \theta + m_{22} E_{s}^{i} ]^{*} [m_{21}{\prime} E_{p}^{i} \cos \theta + m_{22}{\prime} E_{s}^{i} ]\} \\ \end{aligned}$$
(22)

where \(R={\left|{E}_{p}^{r}\right|}^{2}+{\left|{E}_{s}^{r}\right|}^{2}\) is the reflectivity. \({E}_{s}^{i}\)=0 for p-polarized incidence while \({E}_{p}^{i}\)=0 for s-polarized incidence. We may similarly get the expression of the IF shift when only \({\beta }_{s}\) is considered. This tiny rotation of the plane of incidence will influence the elements of the reflection coefficient matrix in addition to altering the polarization direction of the incident or reflected beam. For the small rotation \({\beta }_{s}\), the reflected electric field in the central beam coordinate system becomes,

$$\left( {\begin{array}{*{20}c} {E_{p}^{r} } \\ {E_{s}^{r} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {Z_{11} } & {Z_{12} } \\ {Z_{21} } & {Z_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{p}^{i} } \\ {E_{s}^{i} } \\ \end{array} } \right),$$
(23)

where

$$Z_{11} = - m_{11} + \beta_{s} (m_{12} + m_{21} \cos^{2} \theta - m_{11}{\prime} ),$$
(24a)
$$Z_{12} = - m_{12} /\cos \theta + \beta_{s} ( - m_{11} \cos \theta + m_{22} \cos \theta - m_{12}{\prime} /\cos \theta ),$$
(24b)
$$Z_{21} = m_{21} \cos \theta + \beta_{s} (m_{11} \cos \theta - m_{22} \cos \theta + m_{21}{\prime} \cos \theta ),$$
(24c)
$$Z_{22} = m_{22} + \beta_{s} (m_{12} + m_{21} \cos^{2} \theta + m_{22}{\prime} ),$$
(24d)

The marked coefficients in Eq. (24a–24d) represent the derivatives to \({\beta }_{s}\). The IF shift can be expressed as follows47,49:

$$\Delta y = - \frac{1}{{2\pi k_{0} \sin \theta }}{\text{Im}} \left\langle {{E^{r} }} \mathrel{\left | {\vphantom {{E^{r} } {\frac{\partial }{{\partial \beta_{s} }}E^{r} }}} \right. \kern-0pt} {{\frac{\partial }{{\partial \beta_{s} }}E^{r} }} \right\rangle /\left\langle {{E^{r} }} \mathrel{\left | {\vphantom {{E^{r} } {E^{r} }}} \right. \kern-0pt} {{E^{r} }} \right\rangle .$$
(25)

A relatively complicated analytical expression for IF shift is achieved, i.e.

$$\Delta y = - \frac{1}{{2\pi k_{0} R\sin \theta }}{\text{Im}} [( - m_{11} E_{p}^{i} - m_{12} /\cos \theta E_{s}^{i} )^{*} Q_{1} + (m_{21} \cos \theta E_{p}^{i} + m_{22} E_{s}^{i} )^{*} Q_{2} ],$$
(26)

where

$$Q_{1} = (m_{12} + m_{21} \cos^{2} \theta - m_{11}{\prime} )E_{p}^{i} + ( - m_{11} \cos \theta + m_{22} \cos \theta - m_{12}{\prime} /\cos \theta )E_{s}^{i} ,$$
(27a)
$$Q_{2} = (m_{11} \cos \theta - m_{22} \cos \theta + m_{21}{\prime} \cos \theta )E_{p}^{i} + (m_{12} + m_{21} \cos^{2} \theta + m_{22}{\prime} )E_{s}^{i} ,$$
(27b)

It is commonly known that on an isotropic surface of an ordinary medium, the off-diagonal components of the Fresnel coefficient matrix must meet the requirement \({r}_{sp}{ =r}_{ps}=0\). Thus, the first-order derivation to \({\beta }_{s}\) disappears so that the IF shift will not be generated by linearly polarized beams. However, due to the effect of \(\Theta\), neither \({r}_{sp}\) nor \({r}_{ps}\) will go to zero, whose values are dependent on \(\Theta\). It suggests that even at the isotropic surface, IF shifts induced by linearly polarized beams can also be observed. Once the graphene grating layer is laid on the surface of the TI, an anisotropic surface with a rotation angle will result in relatively larger non-zero off-diagonal components. The generated IF shifts will be significantly enhanced and effectively adjusted by changing the corresponding parameters of graphene. The combined interaction between the axion coupling and the rotated graphene grating will provide us with new possibilities to control IF shifts.

Numerical results and discussion

The thickness of monolayer graphene is known to be \(0.335\text{ nm}\), and then changing the number of graphene layers allows us to calculate the thickness of the upper graphene grating, namely, \({d}_{g}=N*0.335\text{ nm}\). \(N\) indicates the layer number of graphene. The electronic relaxation time of graphene is fixed as \({\tau }_{g}=0.5\text{ ps}\). Figure 2a shows the variation of the real and imaginary parts of the permittivity of graphene with the frequency at \(N=8\) and \({\mu }_{c}=0.2 \text{eV}\). The epsilon-near-zero (ENZ) of \({\varepsilon }_{g}\) is observed at \(\omega =158.24\text{ THz}\), which can be tuned by \(N\) and \({\mu }_{c}\)43. Figure 2b presents the real parts of the effective permittivity of graphene grating at \({f}_{g}=0.7\) versus the frequency in the principal axis coordinate system. The other parameters are the same as in Fig. 2a. It is evident that two residual frequency bands (RBs) appear. The first RB defined as RB-I is in the region of \(\omega <86.66\text{ THz}\) where \({\varepsilon }_{gx}^{e}\)>0 and \({\varepsilon }_{gy}^{e}\)<0. The second one named RB-II lies in \(132.4\text{ THz}<\omega <158.24\text{ THz}\), where \({\varepsilon }_{gx}^{e}\)<0 and \({\varepsilon }_{gy}^{e}\)>0. The right boundary of the RB-II is roughly consistent with the ENZ of graphene, implying that the frequency band of the RBs can be adjusted by controlling the graphene. The permittivity of the semi-infinite TI varies with the frequency in Fig. 2c, where the OA is perpendicular to the surface with \({\varepsilon }_{tz}=1.05 {\varepsilon }_{tx}\). The other physical parameters are \({\omega }_{0}=1.68\text{ THz}\), \(\gamma =0.01 {\omega }_{0}\) and \({\omega }_{e}=0.9 {\omega }_{0}\), respectively36,39. A transition around \(1.68\text{ THz}\) occurs, where the real part of the permittivity jumps from positive to negative. Furthermore, the imaginary part also fluctuates around this frequency. In comparison to Fig. 2b, the resonance frequency of the TI just falls in the RB-I of the graphene grating.

Fig. 2
figure 2

Permittivity with the frequency at \(N=8\), \({\mu }_{c}=0.2\text{ eV}\) for (a) graphene and (b) graphene grating with \({f}_{g}=0.7\). RB-I and RB-II are denoted by the colored regions in (b,c) Permittivity of TI in the x-direction versus frequency in the case of \({\varepsilon }_{tz}=1.05 {\varepsilon }_{tx}\).

Full size image

The anisotropy of the surface is obviously induced by the graphene grating, which should be responsible for the enhanced GH and IF shifts. A comparison with two cases at \({f}_{g}=0\) and \({f}_{g}=1.0\) will be exhibited for p-polarized incidence, which is shown in Fig. 3a–d, respectively. For \({f}_{g}=0\), the graphene grating/TI structure will be transformed into a semi-infinite TI with an OA perpendicular to the surface. The maximum GH shift about \(\Delta {x}_{max}=33.68 {\lambda }_{0}\) is achieved at \(\omega =1.39\text{ THz}\), however, it becomes negative and is increased to \({114 \lambda }_{0}\) at \(\omega =1.58\text{ THz}\) once the graphene film (\({f}_{g}=1.0\)) is put on the surface of the TI, as shown in Fig. 3a and b. \({\lambda }_{0}\) is the wavelength in vacuum. It is generally known that IF shifts typically do not occur when a linearly polarized beam incident on an isotropic surface because the off-diagonal components of the reflecting coefficient matrix become zero. Surprisingly, IF shifts are produced, as Fig. 3c illustrates, when the p-polarized incident beam impinges on the isotropic surface (x–y plane) of the TI. It is worth noting that due to the existence of the TME, the off-diagonal terms \({r}_{ps}\) and \({r}_{sp}\) still are not zero at either \({f}_{g}=0\) or \({f}_{g}=1.0\), resulting in the generation of IF shifts even with the linearly polarized beam. If we set \(\Theta\) to be zero, the medium degenerates to an ordinary medium, where \({r}_{ps}={r}_{sp}=0\) is easy to achieve. Then, it has demonstrated that IF shifts will disappear47. As shown in Fig. 3c and d, the maximum IF shifts are \(\Delta {y}_{max}=-4.03 {\lambda }_{0}\) at \(\omega =3.35\text{ THz}\) and \(\Delta {y}_{max}=-6.54 {\lambda }_{0}\) at \(\omega =2.34\text{ THz}\), respectively. A red-shift phenomenon occurs when the graphene is put on the surface of the TI.

Fig. 3
figure 3

For p-polarized incidence, GH and IF shifts with frequency are shown in (a) and (c) without the graphene layer and in (b) and (d) with a single layer of graphene.

Full size image

The influence of the surface anisotropy on the spatial shifts will be emphasized when the graphene grating is taken into account. Meanwhile, as seen in Fig. 2b, the hyperbolic characteristic is displayed. Figure 4 shows the maximum of GH and IF shifts along with the related reflectivity at the following conditions, \(\theta =81.7^\circ\), \(\beta =0.14^\circ\), \({\mu }_{c}=0.2\text{ eV}\), \(N=8\), \({f}_{g}=0.7\), \(\Theta =1\) π and \({\varepsilon }_{tz}=1.05 {\varepsilon }_{tx}\) for GH shifts and \(\theta =32^\circ\), \(\beta =0.01^\circ\), \({\mu }_{c}=1.0\text{ eV}\), \(N=1\), \({f}_{g}=0.96\), \(\Theta =-1\uppi\) and \({\varepsilon }_{tz}=0.82 {\varepsilon }_{tx}\) for IF shifts, respectively. As shown in Fig. 4a, three clear peaks for GH shifts are observed. The first peak emerges at \(\omega =1.66\text{ THz}\) with \(R\approx 0\), situated close to the TI’s resonant frequency. Consequently, the GH shift that manifests near this frequency will be independent of the graphene grating, which is primarily governed by the TI. The maximum GH shift, which can reach about \(\Delta {x}_{max}=405.92 {\lambda }_{0}\) at \(\omega =86.66\text{ THz}\) with \(R\approx 0\), is represented by the third peak. The frequency precisely lies around the right border of RB-I, indicating that the graphene grating should be the reason for this highest GH shift when compared to Fig. 2b. This makes it possible to effectively regulate the GH shift produced by adjusting the metasurface’s characteristics. Since the reflectivity related to the first and third GH-shift peak is close to zero, the incident angles can be regarded as the Brewster angles where substantial GH shifts always can be produced. It is remarkable that the reflectivity of the second peak about \(\Delta x=-18.29 {\lambda }_{0}\) is as high as \(69.9\text{\%}\) at \(\omega =6.06\text{ THz}\). In Fig. 4b, the wave vector of the e-wave with the frequency change is examined in order to shed more light on the cause of the GH shift with high reflectivity. A transition between the imaginary part and the real part of \({k}_{e}\) is found just at \(\omega =6.06\text{ THz}\). From the expression of \({k}_{e}\), it is evident that if \({\varepsilon }_{tx}{f}^{2}(1-{\text{cos}}^{2}\theta /{\varepsilon }_{tz})>0\) a real solution of \({k}_{e}\) is achieved, implying that the e-wave is a type of surface wave. On the other hand, if \({\varepsilon }_{tx}{f}^{2}(1-{\text{cos}}^{2}\theta /{\varepsilon }_{tz})<0\), \({k}_{e}\) is an imaginary solution connected to the bulk wave. Upon satisfying condition \({\text{cos}}^{2}\theta ={\varepsilon }_{tz}\), the critical frequency of the transition between the bulk wave and surface wave can be determined. It is found that the jumping point for Fig. 4b is about \({\omega }_{c}=6.06\text{ THz}\). Therefore, a conclusion may be made that the transformation between the propagation models will lead to the obvious GH shifts with a considerable reflectivity. The phase of the reflection coefficient \({\varphi }_{p}\) with the frequency also is displayed in Fig. 4c. It is clear that the maximum values of the GH shifts correspond to the abruptly changing phase of the reflected coefficient. Two clear peaks of IF shifts in Fig. 4d with \(R\approx 0\) are observed. In contrast to the peaks in Fig. 3c and d, we discover that the IF shift in Fig. 4 is the result of the combined action of the graphene grating and the TI. As can be observed that for the first peak about \({\Delta y}_{max}=174.42 {\lambda }_{0}\), the corresponding resonant frequency around \(\omega =2.94\text{ THz}\) is close to the one of the dip in Fig. 3d, where a single layer of graphene is deposited on the surface of TI. We believe that the graphene grating is the primary cause of this peak for the IF shift. Conversely, the second peak’s resonant frequency around \(\omega =3.63\text{ THz}\) is close to the one in Fig. 3c, where simply the TI remains. Thus, TI’s impact on the second peak should be significant. A relatively larger IF shift is achievable in a continuous region of \(2.94\text{ THz}<\omega <3.63\text{ THz}\). In the following discussions, we set the parameters to produce the highest GH and IF shifts and consider how these parameters affect the spatial shifts.

Fig. 4
figure 4

(a) GH shifts and reflectivity, (b) wavevector of e-wave and (c) phase of reflective coefficient with frequency at \(\theta =81.7^\circ\), \(\beta =0.14^\circ\), \({\mu }_{c}=0.2\text{ eV}\), \(N=8\), \({f}_{g}=0.7\), \(\Theta =1\) π and \({\varepsilon }_{tz}=1.05 {\varepsilon }_{tx}\). (d) IF shifts and reflectivity with frequency at \(\theta =32^\circ\), \(\beta =0.01^\circ\), \({\mu }_{c}=1.0\text{ eV}\), \(N=1\), \({f}_{g}=0.96\), \(\Theta =-1\uppi\) and \({\varepsilon }_{tz}=0.82 {\varepsilon }_{tx}\).

Full size image

To get additional insight into the off-diagonal terms \({r}_{ps}\) and \({r}_{sp}\), Fig. 5 illustrates their impact in several cases at \(\Theta =0\) and \(1\uppi\), including a TI surface without graphene (\({f}_{g}=0\)), a single layer of graphene (\({f}_{g}=1.0\)), and graphene grating (\({f}_{g}=0.96\)). For \(\Theta =0\), the TI becomes a regular anisotropic media without taking into account the surface state. Therefore, the \({r}_{ps}\) and \({r}_{sp}\) will be equal to zero in the case of \({f}_{g}=0\) and \(1.0\) since the surface is isotropic, as demonstrated in Fig. 5a. However, the anisotropic surface will cause clear peaks at \(\omega =86.66\text{ THz}\) with the opposite sign once the graphene grating is attached to the surface. Combined with Fig. 2, the non-zero \({r}_{ps}\) and \({r}_{sp}\) originate from the graphene grating. For \(\Theta =1\uppi\), as shown in Fig. 5b, the \({r}_{ps}\) and \({r}_{sp}\) will not be zero and are relatively small values at \({f}_{g}=0\) and \(1.0\). The obvious asymmetric peaks are presented at \(\omega =86.66\text{ THz}\), as shown in Fig. 5c. From Eqs. (15a–15c) and (19), it can be seen that this asymmetrical phenomenon mainly stems from the effect of Θ related to the TME and becomes more pronounced as Θ increases. When Θ is positive, the magnitude of \({r}_{sp}\) is evidently larger than that of \({r}_{ps}\). It is worthy to note that the magnitude of \({r}_{ps}\) grows larger than the one of \({r}_{sp}\) as soon as Θ takes a negative value. Therefore, the off-diagonal components of the reflection coefficients will be influenced by the magnetization direction of the surface magnetic layer.

Fig. 5
figure 5

Changes of the off-diagonal terms \({r}_{ps}\) and \({r}_{sp}\) with the frequency at (a) \(\Theta =0\) at \({f}_{g}=0\), 0.7 and \(1.0\), (b) \(\Theta =1 \pi\) at \({\text{f}}_{\text{g}}=0\) and \(1.0\) and (c) \(\Theta =\pm 1 \pi\), \(\pm 3 \pi\) at \({f}_{g}=0.7\).

Full size image

The distribution of the GH shifts, IF shifts and the reflection versus the incident angle and the frequency is displayed in Fig. 6, where the other conditions will be fixed at the values needed to achieve the maximum (refer to Fig. 4). It is evident from Fig. 6a and b that the three peaks of the GH shifts shown in Fig. 4a rely on the incidence angle and frequency in distinct ways. The comparatively strong GH shifts for the first peak primarily center around \(55^\circ <\theta <80^\circ\) in the region of \(\omega <2 \text{THz}\). With the rising of the incident angles, the blue-shift phenomenon arises and a maximum roughly about \({\Delta x}_{max}=34.7 {\lambda }_{0}\) appears at \(\theta =60^\circ\). The second peak will be positive around \(2.6 \text{THz}\) for \(20^\circ <\theta <45^\circ\). And the negative peak progressively grows as the incident angle and frequency rise. For the third peak shown in Fig. 6b, the negative and positive maxima of the GH shift are very demanding on the incident conditions and are only observed in a very narrow range of incident angles and frequencies. Figure 6c displays the impact of incident angles on the IF shifts where the highest value is found in the region of \(\theta <33^\circ .\) With the reduction of the incident angles, the maximum of IF shifts will move to the higher frequency, in addition, the frequency band is gradually widened. Thus, if a relatively large IF shift is expected over a broad frequency spectrum, the angle of incidence can be selected in the range of \(\theta <20^\circ\). Finally, the dependence of the reflection on the incident angle and frequency is also examined in Fig. 6d. An obvious high reflection region is observed, which becomes wider with the increasing of the incident angle and frequency. In addition, the second peak in Fig. 6a is just located in this area, indicating that direct observation is possible.

Fig. 6
figure 6

Variation of (a,b) GH shifts, (c) IF shifts and (d) reflection versus the incident angles and frequency. The other parameters is fixed at the conditions for obtaining the maximum.

Full size image

As indicated in Fig. 4a, the graphene grating is mostly responsible for the peaks that arise at \(\omega =86.66\text{ THz}\). Figure 7a illustrates that an evident red-shift phenomenon occurs with the increasing of \({f}_{g}\). The positive maximum roughly \({\Delta x}_{max}=38.81 {\lambda }_{0}\) at \({f}_{g}=0.68\) and the negative maximum around \({\Delta }_{max}=-36.67 {\lambda }_{0}\) at \({f}_{g}=0.72\) are available. The effect of the filling ratio on the other two peaks is slight and almost negligible. Figure 7b shows two clear peaks of IF shifts that grow as \({f}_{g}\) rises. When \({f}_{g}>0.8\), the maximum of the IF shift is located at the first peak within a restricted frequency range. Of course, once \({f}_{g}=\) 1.0, the IF shifts will rapidly decrease. Figure 7c and d examine the impact of the chemical potential \({\mu }_{c}\) on the GH and IF shifts because the Fermi energy can be readily adjusted by the external electric field. In contrast to Fig. 7a, an obvious blue-shift phenomenon is observed with the increasing of \({\mu }_{c}\). The maximum of GH shifts is produced in the vicinity of \({\mu }_{c}=0.21 \text{eV}\). It can be expected that the GH shifts will decrease to a small value when \({\mu }_{c}\gg 0.24 \text{eV}\). However, the relatively larger IF shifts should be excited in the region of \({\mu }_{c}>0.3 \text{eV}\), and achieve the maximum at \({\mu }_{c}=1.0 \text{eV}\).

Fig. 7
figure 7

Variation of GH and IF shifts with frequency under the different (a) and (b) \({f}_{g}\) and (c) and (d) \({\mu }_{c}\).

Full size image

Obtaining substantial GH and IF shifts simultaneously under the same chemical potential is evidently difficult. The rotation angle of the graphene grating modifies the magnitude of the effective permittivity component without affecting the resonant frequency’s ___location. Figure 8a and b show the influence of the graphene grating’s rotation angle, where the peak positions of the IF and GH shifts are independent of the rotation angle. It can be seen that a slight rotation will result in a significant enhancement of GH and IF shifts, such as \({\Delta x}_{max}=405.92 {\lambda }_{0}\) at \(\beta =0.14^\circ\) and \({\Delta y}_{max}=174.42 {\lambda }_{0}\) at \(\beta =0.01^\circ\). Rotating the incident plane makes it simple to achieve in experiments.

Fig. 8
figure 8

Variation of (a) GH shifts at \(\Theta =1\uppi\) and (b) IF shifts at \(\Theta =-1\uppi\) with frequency under the different \(\beta\).

Full size image

For the various \(\Theta\), Fig. 9 describes the GH and IF shifts with the incidence frequency. We found that the GH shifts in Fig. 9a present apparent changes at \(\omega =86.66\text{ THz}\). The maximum is observed at \(\Theta =1\uppi\), and the GH shifts corresponding to the positive \(\Theta\) are higher than those connected to the negative \(\Theta\). As analyzed in Fig. 4, the peak appearing at this frequency is induced by the graphene grating, since it will disappear at \({f}_{g}=\) 0 or 1.0. In this case, although the non-diagonal components that depend on \(\Theta\) are relatively small, they are not zero. As a result, the TME does not play a significant role in the spatial shifts. However, if \({f}_{g}\ne\) 0 or 1.0, the anisotropy of the surface will be stronger. The greater spatial shifts are the result of the combined action of the TME and the stronger anisotropy of the surface. For the other two peaks in Fig. 9a, the GH shifts remain unchanged because the permittivity of TI will not be influenced by \(\Theta\) and the anisotropy of the surface. The different influence on IF shifts is exhibited in Fig. 9b, where the symmetric distribution with \(\Theta\) is found. For example, the magnitudes of IF shifts are the same, but the directions are just opposite when \(\Theta\) only changes the sign. The maximum of IF shifts can be obtained at \(\Theta =\pm 1\uppi\), and rapidly reduce with increasing \(\Theta\). The frequencies achieving the maximum are always kept around \(\omega =2.94\text{ THz}\) for the first peak and \(\omega =3.63\text{ THz}\) for the second peak. Obviously, the first peak is slightly higher than the second one.

Fig. 9
figure 9

Variation of (a) GH shifts and (b) IF shifts with frequency under the different \(\Theta\).

Full size image

Finally, under the assumption of getting the greatest spatial shifts, the variations of the GH and IF shifts with the extent of anisotropy, namely, \({\varepsilon }_{tz}/{\varepsilon }_{tx}\), are examined in Fig. 10. It is found that the relatively larger GH shifts can be observed in the lower frequency region shown in Fig. 10a, where \({\varepsilon }_{tz}/{\varepsilon }_{tx}>1\). In addition, the GH shifts at \(\omega >86.67\text{ THz}\) will not depend on the anisotropy of the TI. In the higher frequency region, the negative and positive maximum values are mainly located around \({\varepsilon }_{tz}/{\varepsilon }_{tx}=1.05\) and sensitive to the frequency, as illustrated in Fig. 10b. Figure 10c presents that the obvious IF shifts are located in the region of \({0.8<\varepsilon }_{tz}/{\varepsilon }_{tx}<\) 1.0. Consequently, a material with \({\varepsilon }_{tz}/{\varepsilon }_{tx}\approx 1.0\) should be chosen for investigations if significant GH and IF shifts are required. It can be seen that the degree of anisotropy of the material has an important influence on the excitation of large spatial shifts.

Fig. 10
figure 10

Variation of (a) and (b) GH shifts and (c) IF shifts with the degree of TIs’ anisotropy.

Full size image

In the above analysis, we assumed that the beam waist of the incident beam is much larger than its wavelength, which leads to the neglect of the terms containing \({\lambda }_{0}/{w}_{0}\). As shown in Fig. 11, the impact of the beam waist on the maximum of GH and IF shifts displayed in Fig. 4 is investigated. The simulation results demonstrate that the GH and IF shifts essentially match those peaks when the beam waist is sufficiently large. A theoretical upper limit of the GH and IF shifts can be achieved. When \({w}_{0}/{\lambda }_{0}>15\) or \(100\) depicted in the inset of Fig. 11a, the limited simulation results are just consistent with the maxima of GH shifts in the lower frequency in Fig. 4a. But for the peaks around \(86.66\text{ THz}\), the beam waist needs to be much larger than the incident wavelength. On the other hand, the two peaks corresponding to the IF shifts in Fig. 4d will agree with the ones with \({w}_{0}/{\lambda }_{0}>200\). As discussed above, under certain specific conditions, the GH and IF shifts generated by the provided theory or formulae are reasonable.

Fig. 11
figure 11

The maximum of (a) GH shifts and (b) IF shifts presented in Fig. 4a and d versus the beam waist. The other parameters are same as the ones in Fig. 4.

Full size image

Conclusions

In this work, we have investigated the enhanced GH and IF shifts in the reflective beams as a p-polarized Gaussian beam is incident on the graphene grating/TI metasurface, which is rotated by an angle. The conditions for the maximum of GH and IF shifts are determined, moreover, the corresponding physical mechanism is explored in detail. The magnetic coating on the TI surface is used to induce a time-reversal breaking perturbation, which leads to the TME in the TI. On the other hand, due to the graphene grating, the isotropic surface transforms into a hyperbolic and anisotropic metasurface. As a result of the combined interaction of the metasurface and the TME, the GH and IF shifts are significantly increased, especially, since the maximum magnitude of IF shifts is roughly two orders of magnitude greater than that of the situation with no graphene or with only a single layer of graphene. One remarkable occurrence observed in TI is that a relatively large GH shift accompanying the high reflection is produced when the transition between the different types of propagated models occurs, such as \(\Delta x=-18.29 {\lambda }_{0}\) with \(R=0.699\) at \({\omega }_{c}=6.06\text{ THz}\). In addition, the critical frequency is only dependent on the incident angles. Due to the hyperbolicity of the graphene grating, the peak values of GH and IF shifts are mainly produced in or near the right boundary of the RB-I. Thus, the tunability for GH and IF shifts can be realized by adjusting the filling ratio, chemical potential, and also the rotation angles of graphene. Finally, it can be seen that as the increasing of \(\Theta\), the GH and IF shifts will quickly reduce. Further, a material should be selected with \({\varepsilon }_{tz}/{\varepsilon }_{tx}=1.05\) for the maximum of GH shifts and \({0.8<\varepsilon }_{tz}/{\varepsilon }_{tx}<0.85\) for the maximum of IF shifts in experiments. It has been demonstrated that the theoretical results obtained are reasonable when the beam waist is large enough in relation to the wavelength. The manipulation of the TI surface, such as laying down a graphene grating structure or adding a surface perturbation, is experimentally controllable. Thus, we provide a new insight into the use of the hyperbolic metasurface of TI with a surface`s perturbation and their potential applications in optical electric devices.