Introduction

The geometric errors of a hydrostatic thrust bearing structure affect the motion error at different assembly positions. During the assembly process of thrust bearings, insufficient knowledge of the value and direction angle of the geometric error of machined parts introduces randomness into the process. Therefore, measuring these geometric errors is crucial for improving bearing performance.

At present, many scholars have done research on geometric error measurement methods. Zhang et al.1 proposed a geometric error measurement and coaxiality evaluation method by installing a laser sensor outside the hole, which can characterize multiple holes at a time with high accuracy. Experiments verify the effectiveness of this method. Gao et al.2 proposed a non-contact measuring system based on laser displacement sensors to measure the coaxiality of the hole. The results show that the system has high detection accuracy for large-span small holes. Song et al.3 developed a multi-sensor integrated system based on laser displacement sensors, circular grating, a two-dimensional position-sensitive detector and a laser interferometer, which can simultaneously measure the roundness error and axis straightness error of the hole and verified the effectiveness of the measurement system through experiments. In the above measurement methods, the rotation and lifting of the sensor movement errors will have a great influence on the measurement. Wu et al.4, based on fringe projection, applied a non-contact rapid measurement technique of a 3D scanner to measure the root diameter error of the hole combined with the subpixel edge detection method. But the detection accuracy cannot reach the micron level. Katsuki et al.5 constructed a small-size hole measurement system including a laser interferometer, a probe and an optical device used to detect probe attitude. They analyzed and corrected the errors generated by the device. The results show that the device can accurately evaluate the hole deviation and roundness error of the deep hole after correction. However, the friction of the contact has a great influence on the measurement accuracy. Zangl et al.6 proposed a pure optical 3D micro coordinate machine measurement method based on focus change, and the results show that this device can accurately measure the geometric structure parameters of micro holes. However, the equipment is only suitable for micropore measurement, and the equipment is large, expensive and complicated to operate. Liu et al.7 measured the thickness of a deep hole online by circumferential three-point ultrasonic thickness measurement to calculate the straightness error of the axis of the hole. They proposed a geometric method for evaluating the deviation and direction of the axis of the deep hole in real time by using the error limit and verifying it through actual measurement. However, using the three-point method to locate the center of the circle may have a large deviation. Xin et al.8 used a dual confocal probe measurement system to evaluate the inner and outer cylindricity and thickness of a circular cylinder by spiral scanning accurately and synchronously. The results showed that the geometrical error of the circular cylinder evaluated by this method is in good agreement with the measurement results of CMM. However, measuring aperture parts is limited by the size of the sensor. Sun et al.9 designed a cylindrical measurement model considering five systematic errors. Based on the proposed model and measurement strategy, the coaxiality and cylindricity of a low-pressure turbine shaft were evaluated. The experimental results showed that the proposed method is especially suitable for low-pressure turbine shafts with large radii. Sun et al.10,11 proposed a morphological filter based on sample angle distribution to achieve high precision roundness and coaxiality error measurement based on considering multiple systematic error measurement models. However, the above equipment is a single probe contact measurement. Zhang et al.12 established a more comprehensive measurement model based on two-dimensional linear laser sensor measurement technology for measuring the cylindricity error of cylindrical components. The results showed that this method could improve the accuracy of cylindricity measurement, especially for large-radius cylindrical parts. But this device also uses a single probe measurement, and measurement efficiency is low. Zha et al.13 considered that the motion error of the turntable is directly affected by the geometric error of the rotor system and proposed a method based on coordinate transformation and the principle of least squares for the assessment of geometric errors in rotor systems using an ultraprecision coordinate measuring machine (CMM) and proposed an optimization method for improving the assembly accuracy of the rotor system based on this method. Chen et al.14 proposed a method to measure the roundness of a small cylinder by using a stitching linear scan with a stylus profilometer, and experiments verified the effectiveness of this method. But this method is only suitable for the roundness measurement of small cylinders. Jin et al.15 proposed a non-contact optical method for measuring the diameter of a cylindrical opening with a disc beam probe. The measurement results were consistent with those of a vernier calliper, which was suitable for simple and rapid measurement but not suitable for measuring a cylindrical opening with a diameter smaller than the probe. Nemedi et al.16 proposed a new method based on CMM that can display both the roundness error and the actual shape of the workpiece section, which can greatly improve the efficiency of some measurement and detection processes. Gu et al.17 proposed an improved calibration method for the straightness error of CMM. They proposed an improved total least squares fitting method for fitting the straight lines and planes of asymmetric variables and verified the effectiveness of the method through experiments. Zhang et al.18 proposed a rotor coaxiality measurement method based on a common reference axis, and the results showed that the measurement accuracy of this method is higher than that of the rotor coaxiality measurement model based on a connected center line and a single reference axis. Zhang et al.19 proposed a multistage rotor perpendicularity detection method considering reference error compensation, which can be used to detect the perpendicularity tolerance of the rotor end face. Zhou et al.20 proposed a submicron precision measurement separation method of perpendicularity error based on a confocal sensor and optical plane, and the results showed that this method can measure the perpendicularity error of the rotation shaft with high accuracy. References 18, 19, and 20 require many displacement sensors and complex data processing. Peng et al.21 proposed a hexahedral perpendicularity error measurement method based on a wavefront interferometer and collimator and verified the effectiveness of the method by comparing it with the measurement results of CMM. This method can be extended to other polyhedral parts for high-precision shape and position error measurement. However, it can only be used to measure the perpendicularity error of the hexahedron. Chen et al.22 proposed a new method for measuring the perpendicularity of the narrow deep groove wall of a micro die based on micro-spark corrosion, automatic optical inspection (AOI) technology and capacitive sensing (CS) technology. Experiments verify the feasibility of the method, and the method can be extended to the measurement of small holes and grooves on a sub-micron or even nanometer scale. But the method uses a special microprobe that is only suitable for measuring perpendicularity between surfaces. Zhang et al.23,24 used a CMM for measurement and used a particle swarm optimization algorithm to evaluate the cylindricity error of the cylinder. Pathak et al.25 used a CMM for measurement and proposed an improved particle swarm optimization algorithm to determine the straightness, flatness, perpendicularity and parallelism of a plane. The results showed that the algorithm has higher efficiency and accuracy and can evaluate the planar surface features effectively and accurately. Huang et al.26,27 used a CMM for measurement and used a search algorithm for evaluating the sphericity and cylindricity. Chiabert et al.28 used a CMM for measurement, introduced three evaluation methods for the roundness tolerance area of cylindrical workpieces, including the least square method, probability method and standardized minimum region method, and proposed an evaluation method based on the probability density function of roundness tolerance bandwidth. The results showed that probability method is more suitable for production process. Wang et al.29 used a vertical crankshaft comprehensive measuring instrument for measurement. They proposed an optimization algorithm for crankshaft journal cylindricity error based on step acceleration and verified the practicability of the algorithm through experiments. However, the equipment covers a large area, and the operation is complicated.

Based on the above analysis, the high-precision measurement equipment for the geometric error of parts mainly involves two types: general measurement products (such as laser interferometers, CMM, profilometers, etc.) and special measurement equipment based on high-precision displacement sensors (such as laser sensors, inductive sensor, etc.). General measuring equipment has formed fixed products. Their measuring principle and data processing methods are relatively mature, have high precision, and have a wide range of applications. Still, the cost is high, they occupy a large area, they need full-time personnel to operate, and they are not easy to field measure. Among them, the CMM is a single probe and can only measure one point at a time. Although the profilometers can be continuously measured, it is also a single-probe device. The special measuring equipment based on high-precision displacement sensors will configure different sensors according to different types of geometric errors and establish the measurement model and data processing method by themselves. The high-precision displacement sensor is divided into contact and non-contact; the contact sensor is generally low sampling frequency, measurement speed is slow, and non-contact sensors measure fast and do not harm the part surface. At present, in addition to measuring the perpendicularity error and direction angle of the two end faces of the rotating part relative to the center line in the hydrostatic thrust bearing with CMM, special measurement models are rarely discovered. Therefore, this study proposes a non-contact measurement method for the perpendicularity error value and direction angle of hydrostatic thrust bearings. Compared with CMM, this method uses two non-contact sensors to measure simultaneously, which is suitable for on-site rapid measurements. It can be measured continuously, and the error value and error direction angle can be found by fitting. In addition, a method of correcting the perpendicularity error of the thrust surface is proposed, and the error size and position can be determined according to the measurement results for timely repair to improve the real-time working accuracy of thrust bearings. Finally, the experiment verifies the accuracy of the measurement method and the effectiveness of the error correction.

Research objective

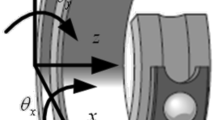
Figure 1 shows a structural diagram of the hydrostatic rotary table. The table comprises an upper thrust plate, lower thrust plate, shaft, and bearing bush. The thrust plate and the shaft are fixed with bolts. The recesses of the hydrostatic thrust bearings and the hydrostatic journal bearing are machined on the bearing bush.

Fig. 1
figure 1

Schematic diagram of the hydrostatic rotary table.

Full size image

The thrust plate is an essential part of the hydrostatic thrust bearing. As shown in Fig. 1, the thrust surface 1 of the upper thrust plate is the rotary working table, and the thrust surface 2 is the working face of the hydrostatic thrust bearing. Flatness errors may be introduced into the thrust surface during machining. The shaft is part of the rotor system of the hydrostatic thrust bearing and includes a cylindrical surface, surface 1, and surface 2 of the hydrostatic rotary table. Roundness error can be introduced into the cylindrical surface during machining and mainly affects the motion error of the journal bearing of the turntable30. Only the thrust bearing is discussed in this paper. The surface 1 and surface 2 of the shaft will have a perpendicularity error relative to the axis during processing. The thrust plate is bolted to the shaft, and the shaft and thrust surface are treated as a whole in subsequent analysis. The bearing bush is the stator of the hydrostatic thrust bearing, and the working faces of the thrust bearing part are surfaces 1 and 2. Processing and assembly may also introduce errors in the perpendicularity and flatness between the surfaces and the axis.

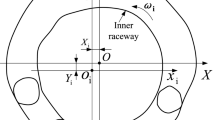
Figure 2 is the schematic diagram of the working principle of a pair of opposite oil pads of hydrostatic thrust bearings. The hydrostatic thrust bearing is divided into three parts: constant pressure oil supply system, constant temperature system, and bearing body. The oil cooler circulation cools the oil in the oil tank so that the oil temperature is within a certain set range, the motor drives the oil pump to work, and the oil suction filter prevents the oil pump from inhaling pollution impurities. The overflow valve keeps the oil pressure constant, and the check valve prevents the hydraulic oil backflow. The two-stage oil filter ensures the cleanliness of the hydraulic oil, the pressure of the outgoing oil is Ps, and the pressure gauge shows the pressure reading. The hydraulic oil enters the oil chamber through the restrictors and then flows out into the clearance. The pressure is reduced to atmospheric pressure (There is a large difference between atmospheric pressure and oil film pressure, so the atmospheric pressure is recorded as 0). According to the principle of liquid flow continuity, the oil chamber pressure can be obtained as follows:

$$P_{i} = \frac{{P_{s} }}{{1 + \frac{{R_{ci} }}{{R_{hi} }}}}, \, \left( {i = 1, \, 2} \right)$$
(1)

where Pi is the pressure of the ith oil chamber, Ps is the constant oil supply pressure, Rci is the flow resistance of the ith restrictor, and Rhi is the flow resistance of the ith clearance.

Fig. 2
figure 2

Working principle of the hydrostatic thrust bearing.

Full size image

When the external load is 0, P1 and P2 are equal. When there is an external load F, clearance 1 becomes larger, clearance 2 becomes smaller, Rh1 becomes smaller, Rh2 becomes larger. According to Eq. (1), P1 becomes smaller, and P2 becomes larger. The pressure difference between P1 and P2 creates the oil film force to balance the external load and rebuild the equilibrium state.

$$\Delta P = \left( {P_{2} - P_{1} } \right)A_{e}$$
(2)

where Ae is the effective area of a single oil chamber31.

Based on the above analysis, it can be found that the clearance will affect the performance of the hydrostatic thrust bearings (including bearing capacity, motion accuracy, etc.). Due to the perpendicularity error of the shaft and bearing bush, the distribution of clearance will be uneven, which will affect the motion accuracy of the hydrostatic thrust bearing. Therefore, this paper proposes a method of evaluating and correcting the perpendicularity error of the shaft and bearing bush.

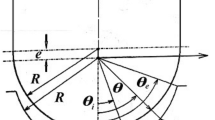
Figure 3 shows the overall perpendicularity error. In Fig. 3, a is the center point of the thrust surface 1, b is the center point of the thrust surface 2, and ab represents the axis. The establishment of the rectangular coordinate system in Fig. 3 is explained as follows: the origin point is the center point of ab, the X-axis points to the center of the oil pad , and the Z-axis is perpendicular to the X-axis upward, so the Y-axis is set according to the Cartesian establishment rule, as shown in Fig. 3. The perpendicularity error is a spatial concept that needs to be represented by different view directions. In space, when the end face of the rotary part is not perpendicular to the center line, the spatial position between the end face and the center line is arbitrary.

Fig. 3
figure 3

Schematic diagram of the overall perpendicularity error.

Full size image

In the xy plane, there must be an angle starting from the X-axis counterclockwise (there will be two angles in the circumferential direction, and the difference is 180°; the first angle is taken in this paper). When projected along this angle, the end face is a straight line. This angle is called the direction angle of the perpendicularity error between the end face and the center line. Therefore, the perpendicularity error of the two ends of the shaft and bearing bush to the center line will have 4 of the above direction angles. As mentioned above, the bearing bush is fixed in the coordinate system, and the shaft can be rotated so that the perpendicularity error direction angle of surfaces 1 of the shaft and the bearing bush to the center line is the same (both Δθd). On this basis, the perpendicularity error direction angles of surfaces 2 of the shaft and bearing bush relative to the center line are Δθd + θd and \(\Delta \theta_{d} \, + \theta_{d}^{\prime }\), respectively. Where θd and \(\theta^{\prime}_{d}\) are the difference of the perpendicularity error direction angles of the two ends of the shaft and bearing bush, respectively. The directions A, B and C in Fig. 3 correspond to the above three directions respectively. The three directions of A, B, and C will change with the actual error direction angle of the part.

Figure 4 shows the mapping relationship between the perpendicularity error of the thrust surfaces and the axis. In Fig. 4, the view of the shaft projected along directions A and B is shown. From the perspective of direction A, surface 1 of the shaft is a straight line. Only when the surface is viewed as a straight line is it convenient to characterize the perpendicularity error of the end face of the shaft and its center line, the difference between point a and the edge of thrust surface 1 is the perpendicularity error δ1 of thrust surface 1. From the B direction, surface 2 of the shaft is a straight line, the difference between point b and the edge of thrust surface 2 is the perpendicularity error δ2 of thrust surface 2. The thrust surface only needs to ensure the flatness error, while the perpendicularity error needs to be ensured by controlling the shaft end face error. In this paper, the rotation error of the journal bearing is not considered. The centerline of the shaft in the figure can be regarded as the centerline of the rotation of the journal bearing.

Fig. 4
figure 4

Schematic diagram of the thrust surface perpendicularity error relation.

Full size image

Figure 5 shows the perpendicularity error of the bearing bush. In Fig. 5, the view of the bearing bush projected along directions A and C is shown. From the perspective of direction A, surface 1 of the bearing bush is a straight line, the difference between point \({\text{a}}^{\prime }\) and the edge of surface 1 of the bearing bush is the perpendicularity error δ3 of surface 1 of the bearing bush. From the C direction, surface 2 of the bearing bush is a straight line, the difference between point \(b^{\prime }\) and the edge of surface 2 of the bearing bush is the perpendicularity error δ4 of surface 2 of the bearing bush.

Fig. 5
figure 5

Schematic diagram of the perpendicularity error of the bearing bush.

Full size image

Experimental design and analysis

Measurement method for the perpendicularity error of the thrust surface

An analysis of the mapping relationship between the perpendicularity errors of the shaft end face and thrust surface presented in Fig. 4 shows that the perpendicularity error of the thrust surface is caused by the perpendicularity error between the axis and the shaft end face introduced during the machining of the shaft. Therefore, the measured perpendicularity of the thrust surface of the hydrostatic thrust bearing can be transformed into the perpendicularity error of the shaft end face.

A method for measuring the perpendicularity of the thrust surface of a hydrostatic thrust bearing is presented in this paper. In the rotary measurement method, the shaft rotates synchronously with the precision air-floating turntable while the position of the displacement sensor remains fixed. By contrast, the traditional CMM measurement method requires point-by-point capture. The rotary measurement method can be used to make continuous measurements, where the displacement in the X- and Y-directions can be measured through one circular rotation. Two sensors are used to make simultaneous measurements, improving measurement efficiency.

The rotary measurement method uses equipment such as precision air-floating turntables, air pumps, eddy current displacement sensors, and data acquisition cards. The journal and axial rotation accuracy of the spindle of the precision air-floating turntable is less than 0.2 μm. The compressed air pressure of the air pump is 0.4–0.6 MPa. The MICRO-EPSILON eddy current sensor (Model DT3010-U05-M-C2), with a static resolution of 0.025 μm and a sampling rate of up to 25 kHz. The data acquisition card model is an Advantech PCI-1812, with 16-bit resolution and 8-channel differential analog input. The maximum sampling rate can reach 250 kHz.

Figure 6 is a schematic showing how the perpendicularity error of the thrust surface is measured via the rotary method. In Fig. 6b, lm is the distance between the two sensors, and lab is the height of the shaft. The measurement steps are given below.

  1. 1.

    The air pump is connected to the precision air-floating turntable, the bottom of which is placed on a granite plate. The surface 1 of the shaft is fixed to the turntable.

  2. 2.

    The displacement sensor is fixed by attachment to the rigid rod.

  3. 3.

    The shaft rotates with the turntable, and the displacement sensor collects data and performs multiple groups of measurements.

  4. 4.

    After surface 1 is measured, the shaft is flipped, and surface 2 is fixed to the turntable. To ensure that the coordinate system is consistent with that used for measuring surface 1, the turntable drives reverse rotation of the shaft. Rotation of the shaft around the Y-axis shifts the direction of the X-axis in the coordinate system by 180°, while the position of the displacement sensor remains unchanged. Therefore, the data collected when the turntable is rotated by 180° should be used as the initial data to ensure the same initial positions for surfaces 2 and 1. The measurement steps are repeated.

Fig. 6
figure 6

Measurement of the perpendicularity error of the thrust surface via the rotary method.

Full size image

Figure 7 shows the data collected via the rotary measurement method. Different amplitudes are measured by the two displacement sensors because different eccentric errors are introduced during sensor installation. Thus, data processing must include eccentricity elimination and smoothing.

Fig. 7
figure 7

Data processing of the rotary measurement method.

Full size image

The circle’s center was fitted with the least square method from the processed data32. Table 1 shows the least squares center data obtained by fitting. The coordinates of the four points A, B, C, and D are (a, b), (c, d), (e, f), and (g, h), respectively.

Table 1 Least squares center of a circle.
Full size table

In the measurement process, because the eddy current displacement sensor is fixed and the precision of the precision air float turntable is high, the measurement points on the surface of the shaft rotating synchronously with the turntable are always in two fixed planes. Figure 8 shows the schematic diagram of two measurements of the shaft. The left part shows the measurement of surface 1 of the shaft placed on the air-floating turntable, and the right part shows surface 2 of the shaft placed on the air-floating turntable. The axis of rotation and the coordinate system are the same in both cases. By marking the center of the least square circle measured by sensor 1 and sensor 2 in the coordinate system, the inclination of the axis when surface 1 and surface 2 of the shaft are placed can be analyzed. Point E is the projection of point A on the surface 1 of the shaft, and point F is the projection of point B on the surface 2 of the shaft. The length lEC of line segment EC can be obtained according to the coordinates of point E and point C; the length lDF of line segment DF can be obtained according to the coordinates of point D and point F; the length of line segment AE and BF is the height of the shaft; the expressions of γ1 and γ2 can be obtained according to the geometric relationship:

$$\gamma_{1} = \arctan \left( {\frac{{l_{ab} }}{{l_{EC} }}} \right)$$
(3)
$$\gamma_{2} = \arctan \left( {\frac{{l_{ab} }}{{l_{DF} }}} \right)$$
(4)
Fig. 8
figure 8

Coordinate diagram of the center of the least squares circle.

Full size image

In the experimental measurement, knowing the direction angle of the perpendicularity of surface 1 and surface 2 in three-dimensional space is also necessary. Figure 9 shows a schematic diagram of the thrust surface perpendicularity error direction angles. In the xoy coordinate system, line EC and line DF are drawn according to the coordinates of four points C, D, E, and F. The angle between line EC and the x-axis is the error direction angle of thrust surface 1, the angle between line DF and the x-axis is the error direction angle of thrust surface 2, and the angle between line EC and line DF is θd.

Fig. 9
figure 9

Schematic diagram of the thrust surface perpendicularity error direction angle.

Full size image

Figure 10 is a schematic of the perpendicularity error of the thrust surface. The geometric relationship shown in Fig. 10 is used to derive formulas for the perpendicularity errors δ1 and δ2 of the thrust surfaces as follows:

$$cos\gamma_{1} = \frac{{\delta_{1} }}{R}$$
(5)
$$cos\gamma_{2} = \frac{{\delta_{2} }}{R}$$
(6)

where R is the radius of the thrust plate.

Fig. 10
figure 10

Structural diagram of the thrust surface perpendicularity error.

Full size image

Comparative experiments were carried out to verify the accuracy and feasibility of the proposed method. The value and direction angle of the perpendicularity error of the thrust surface were measured by CMM (Brand: HEXAGON, Model: INSPECTOR 10.12.08), as shown in Fig. 11. A measurement point was set every 15° on the cylindrical surface of the shaft near surfaces 1 and 2, and 24 measurement points were equally divided to measure the perpendicularity error of surfaces 1 and 2 of the shaft, respectively. The measurement positions on surface 1 of the shaft are shown in Fig. 12.

Fig. 11
figure 11

CMM measurement.

Full size image
Fig. 12
figure 12

Measurement positions on surface 1 of the shaft.

Full size image

The results of the comparative experiments are shown in Table 2. The value and direction angle difference of the perpendicularity error of the thrust surface measured via the rotary method are basically consistent with the CMM results.

Table 2 Comparison of measurement results.
Full size table

Measurement of the perpendicularity error of the bearing bush

Considering that the bearing bush has a large volume and mass, the rotary method is used to measure the bearing bush. Unlike in the rotary measurement method of the thrust surface, the bearing bush remains fixed during this measurement, and the sensor follows the rotary motion of the precision air-floating turntable.

Figure 13 shows the structural diagram of the perpendicularity error of the bearing bush by the rotary measurement method. In Fig. 13, \({\text{l}}_{{a^{\prime}b^{\prime}}}\) is the height of the bearing bush. The specific measurement steps are as follows.

  1. 1.

    Surface 1 of the bearing bush is placed on a standard granite plate with a hole. The lower surface of the standard plate is placed parallel to the plane of the precision air-floating rotary table (the standard plate can be measured separately using a group of positions, and the results can be superposed on the original data to ensure parallelism).

  2. 2.

    The positions of the two displacement sensors are fixed on the air-floating turntable by attachment to the rigid rod.

  3. 3.

    During measurement, the bearing bush and the standard plate remain static, and the air-floating rotary table drives the displacement sensor to rotate. The displacement sensor collects data and carries out multiple groups of measurements.

  4. 4.

    After measuring surface 1 of the bearing bush, the bearing bush is turned over, and surface 2 is placed on the standard plate. The coordinate system for the measurement should be consistent with that used for surface 1. The measurement steps are repeated.

Fig. 13
figure 13

Measurement of the perpendicularity of the bearing bush.

Full size image

The least squares circular center solution and the direction angle solution of the bearing bush measurement method are like the above thrust surface rotation measurement method, and the linear inclination angle data γ3 and γ4 are obtained. Figure 13 shows a schematic diagram of the bearing bush perpendicularity error. From the geometric relationship in Fig. 14, the formulas for calculating the bearing bush perpendicularity δ3 and δ4 are derived as follows:

$$cos\gamma_{3} = \frac{{\delta_{3} }}{R}$$
(7)
$$cos\gamma_{4} = \frac{{\delta_{4} }}{R}$$
(8)
Fig. 14
figure 14

Schematic of the geometric relation of the bearing bush perpendicularity error.

Full size image

The measured perpendicularity error and direction angle difference of the bearing bush are shown in Table 3.

Table 3 Measured results for the bearing bush.
Full size table

Correction method for the perpendicularity error of the thrust surface

The above measurements obtained the perpendicularity error value and direction angle of the thrust surface. Therefore, the installation perpendicularity error of the rotating shaft and the thrust surface can be corrected by placing precision shims on one side between the contact surface connected by bolts.

Figure 15 shows the placement of the precision shim. The precision shim is 5 μm thick. The geometric relationship can be used to derive the following theoretical formula for the perpendicularity error δis of the thrust surface after shim placement:

$$\delta_{is} = \delta_{i} - \frac{R}{2r}\lambda \quad \left( {i = {1},{2}} \right)$$
(9)

where λ is the thickness of the precision shims, and r is the shaft radius.

Fig. 15
figure 15

Repair method of the thrust surface perpendicularity error.

Full size image

Table 4 shows the theoretical and measured perpendicularity errors of thrust surface 1 corrected with one and two shims. The theoretical values agree well with the measured values, showing that the correction method is accurate.

Table 4 Corrected results.
Full size table

Experimental verification

Figure 16 shows the device employed for measuring the motion error of the hydrostatic rotary table using the multisensor method. This experimental device was built to meet ANSI/AMSE B89.3.4 standards33. The oil supply pressure of the experimental device is 1 MPa, and the ambient temperature is 20 ± 1 °C. A master dual ball (brand: LION PRECISION) is installed on the surface of the workbench. The master ball has a diameter of 25.4 mm and a roundness of less than 26 nm. The eccentricity of the master ball is adjusted by the micrometre. Five sensors are used in the device. Sensor 1 and sensor 2 are eddy current displacement sensors. Sensors 3, 4, and 5 are spectral confocal displacement sensors; the sensor brand is STIL, and the sensor model is GL3-MG70. The vertical installation of Sensor 5 can directly collect the initial axial motion error data of the rotating shafting system. Sensors 1 and 2 (3 and 4) are installed along the directions of the X-axis and Y-axis of the upper (lower) master ball, respectively. The distance between the upper and lower master balls is Ld, which is equivalent to the distance between the upper and lower groups of sensors. Sensors 1, 2, 3 and 4 all directly collect the initial journal motion errordata of the rotating shaft system.

Fig. 16
figure 16

Motion error measuring device.

Full size image

Figure 17 shows the experimental measurement results of the motion error before and after the shims adjustment (the speeds are 10 rpm, 30 rpm, and 50 rpm, respectively). Table 5 shows the comparison of motion errors at different speeds before and after shim adjustment. Table 6 shows the situation of the motion error reduction after placing shims at different speeds. Through the analysis of the experimental results of the motion error before and after correction, the results show that repair considerably reduces the errors in the axial and tilt displacements. At 10 rpm, the errors in the axial and tilt displacements are reduced by 66.39% and 28%, respectively. At 30 rpm, the errors in the axial and tilt displacements are reduced by 71.39% and 25.13%, respectively. At 50 rpm, the errors in the axial and tilt displacements are reduced by 67.44% and 53.19%, respectively.

Fig. 17
figure 17

Experimental results of the motion error before and after the shims adjustment.

Full size image
Table 5 Comparison of motion error at different speeds before and after shim adjustment.
Full size table
Table 6 Situation of the motion error reduction after placing 2 shims at different speeds.
Full size table

After shim correction, the motion accuracy of the rotary table can be greatly improved.

Results and discussion

According to the above analysis, the geometric error of hydrostatic thrust bearings can cause an uneven distribution of oil film clearance and affect motion accuracy. For the perpendicularity error of a planar surface related to a datum straight line, the tolerance zone of the perpendicularity error is defined as the area limited by two parallel planes with a distance equal to the tolerance value and perpendicular to the datum34, ignoring the tilt direction of the plane to the datum. However, the author believes that the measurement of the tilt direction of the plane relative to the line can be used to guide the effective correction of the perpendicularity error in the assembly process. To reduce the impact of the geometric errors of hydrostatic thrust bearings on workbench performance at the assembly site, a method is proposed for rapid onsite measurement of the geometric error of the thrust surface and bearing bush. The measured data are processed, the centers of surfaces 1 and 2 of the thrust surface and bearing bush are fitted via the least squares method, and an evaluation model is derived. The perpendicularity error value and the error direction angle can be obtained based on the evaluation method.

In addition, it is important to correct geometric errors. Due to the large volume and mass of the bearing bush, it is not easy to correct its perpendicularity, so consider changing the perpendicularity of the thrust surface to improve the motion accuracy. Presented a method of correcting the perpendicularity error of thrust surface by placing precision shims. Based on the evaluation method, knowing where to place shims to correct. This method has good stability and reliability and can quickly correct the geometric errors of rotating parts when machining and assembling on-site. It should be noted that the number of precision shims placed on the contact surface should not be too much. Otherwise, the oil leaked during the use of hydrostatic bearings will enter the contact surface and affect the sealing of the contact surface.

Conclusions

A rotary measurement method is presented in this paper to rapidly measure the value and direction angle of the perpendicularity error of the thrust surface and bearing bush of hydrostatic thrust bearings. The measurement results are in good agreement with those obtained by CMM, validating the proposed method. Based on the measurement results, a method to correct the perpendicularity error of the thrust surface is proposed that involves placing precision shims on the contact surface. The correction changes the perpendicularity error of the thrust surface 1 from 31.1 μm to 19.9 μm. At different speeds (10 rpm, 30 rpm, and 50 rpm), the errors in the axial and tilt mean displacements of the thrust bearing are reduced by 68.41% and 35.44%, respectively.

It can be found that rapidly measuring the value and direction angle of the perpendicularity error of the shaft and the bearing bush onsite can be used to determine the position of the precision shims that can considerably reduce the perpendicularity error of the shaft and thereby improve the motion accuracy of the turntable.