An integrated CRITIC and EDAS model using linguistic T spherical fuzzy Hamacher aggregation operators and its application to group decision making

Environmental sustainability refers to the prudent use and preservation of natural resources and ecosystems to satisfy the present generation’s requirements without jeopardizing the ability of future generations to satisfy their own needs. It is a persistent problem and calls for a paradigm shift in our thinking to decouple resource use and environmental destruction from economic and social progress. Presently, green technologies actively contribute to reshaping the worldwide economic trajectory in favour of sustainability. They provide an alternative socio-economic paradigm that paves the way for present and future generations to inhabit a pristine, healthful environment in harmony with the natural world. Environment protection became a point of concern after significant incidents happened worldwide. For example, the oil crisis (1970–1980), the massive industrial catastrophe (India 1984), the destruction of the Amazon rainforest, and the hole in the ozone layer¹. The significance of environmental health has become more widely recognized due to these incidents. Environmental policies and guidelines for green management have been put in place by several companies, governments, and organizations.

Sustainability and the environment are important aspects of green management. Making a company’s operations more environmentally friendly may significantly impact its business. Their sustainability business may alter, giving them benefits over competitors. Businesses and organizations that embrace green innovation promote a clean and healthy environment. This can be accomplished by utilizing products, services, and technology that don’t deplete the resources of the natural environment. For example, manufacturers and software solutions prevent damaging technological waste from polluting the environment². Two of the numerous natural resources in the world that have already run out are electronics and household batteries. Some of these materials include dangerous chemicals that contaminate soil and groundwater³. According to the United Nations’ report on green technology⁴, nations’ environmental policies are crucial. The Millennium Development Goals (MDGs) goal of preserving and enhancing the environment for civilization to thrive will be facilitated by the principles of GTs if they are accepted and implemented into everyone’s life⁵. As part of “The 2030 Agenda for Sustainable Development,” the United Nations General Assembly adopted the Sustainable Development Goals (SDGs) in 2015. The SDGs serve as an indicator and gauge of progress toward the primary goal of sustainable development by balancing stakeholders’ requirements on a global scale in terms of economic, social, and environmental development^6,7. Several technologies are necessary to achieve the SDGs of the United Nations (UN) on a global and local level. Green technology is one of these; it aims to lessen the negative effects of the conventional economic development paradigm and raise living standards⁸. When using or adopting green technologies, it is crucial to consider economic and environmental implications because these aspects determine how effective they will be⁹.

Furthermore, the available GT alternatives must be evaluated while considering several frequently competing criteria that address their effects on the economy, the environment, and society. The GT selection problem involves choosing environmentally sustainable solutions to address various challenges, such as energy efficiency and reduced environmental impact. The selection of GTs can become an MCGDM problem when it involves various stakeholders, such as governmental agencies, environmental groups, and business professionals, all with different priorities and preferences. This change often occurs when it’s necessary to compromise opposing points of view, gather various criteria, and agree among different stakeholders, guaranteeing that the selected green technology aligns with more general sustainability and social objectives^10,11. MCGDM is a recognized cognitive tool designed to identify the optimal choice among a limited range of options based on input from experts’ viewpoints. Different MCGDM methods have been designed to select GT options. For selecting cleaner production (CP) practices, Laforest et al.¹² suggested using ELECTRE I, while Khalili and Duecker¹³ used ELECTRE III to create a sustainable environmental management system for CP implementation. Si and Marjanovic¹⁴ employed a weighting technique for criteria in GT selection as part of the retrofit decision making (DM) process based on the Analytical Hierarchy Process (AHP). Wen et al.¹⁵ employed a new DM method to evaluate two heating systems while considering various conflicting criteria regarding a sustainable environment. When analyzing complicated DM issues where the expert evaluation data takes the form of linguistic terms, all of these earlier methodologies have shown significant achievements. All these studies are beneficial for decision-makers who want to tackle MCGDM selection and evaluation problems. However, there are still research gaps:

1. (1)

   The lack of methods for accurately determining the criteria weights that represent the relative importance or significance of each criterion in the DM process; the CRITIC method is the newly designed and widely used method for determining weights in MCGDM;

2. (2)

   The vital role that AOs play in information fusion emphasizes the constant need for developing novel aggregation techniques to improve DM processes and extract meaningful insights from diverse data sources.

3. (3)

   The dearth of techniques for MCGDM under uncertainties: the majority of earlier published research requires specific information on alternative green technologies concerning their criteria, while it is frequently challenging to get all the information, and the techniques for making decisions under uncertainty are crucial;

To produce democratic and scientific decisions for choosing the most appropriate green technology option, this study aims to address three key research gaps and develop a generic sustainability assessment method for ranking alternative green technologies comprehensively while considering a variety of sustainability criteria based on current conditions and expert preferences. The contributions of this study are outlined as follows:

1. (1)

   We establish an LT-SF-CRITIC method to meet the need for an effective criterion weighting procedure.

2. (2)

   We defined some new Hamacher operations for LT-SFNs, and then, based on these defined operations a series of AOs for LT-SFNs are proposed, including the LT-SF Hamacher weighted average (LT-SFHWA) operator, the LT-SF Hamacher ordered weighted average (LT-SFHOWA) operator, the LT-SF Hamacher weighted geometric (LT-SFHWG) operator and the LT-SF Hamacher ordered weighted geometric (LT-SFHOWG) operator.

3. (3)

   We design a novel LT-SF-EDAS technique based on LT-SFHWA operator to get an efficient alternative ranking methodology that does not require burdensome computations and a method that can reveal all kinds of information hidden in the data and analyze it with statistical techniques.

4. (4)

   Finally, we evaluate the effectiveness of our established LT-SF-CRITIC-EDAS model by applying it to solve problems related to selecting the most suitable green technology for promoting environmental sustainability.

The remainder of this study is summed up as follows: “Introduction” reviews the literature of study, motivation, and declaring the contributions. “Preliminaries” provides the basic concepts related to LT-SFSs and Hamacher operations. Hamacher operations and AOs under LT-SF information are developed, and some of their prominent properties are discussed in “Operational Laws of linguistic T-spherical fuzzy numbers based on Hamacher t-norm and t-conorm” and “Linguistic T-spherical fuzzy HAOs”, respectively. “MCGDM algorithm using LT-SF information” is devoted to developing the MCGDM approach based on modified LT-SF-EDAS. In the same section, we additionally introduce the LT-SF-CRITIC method as a means to establish criterion weights. “Numerical illustration” employs an example of the best suitable green technology for promoting environmental sustainability to showcase the practicality of the developed model. The same section explained the impact of parameters on outcomes and comparison analysis with existing studies. “Conclusions” serves as a conclusion, summarizing the study’s findings and offering insights into potential future directions.

Literature review

Fuzzy group decision making

Experts often face challenges in providing precise judgments when evaluating criteria for different alternatives. Estimating evaluation values in decision-making scenarios can be difficult due to the inherent uncertainty and complexity of decision making. Experts frequently employ fuzzy set (FS) theory Zadeh¹⁶ in group DM problems because it helps them handle ambiguity efficiently while delivering assessments for objects or available options. Decision analysis is only one of the many areas where FS has advanced significantly since its start. Many extensions of FS theory have been provided since its inception. Interested readers are referred to^{17,18,19,20,21,22,23,24,25,26,27,28,29,30} for further details. The membership degree (MD) of an object to a given target is the only information provided by FS theory. To address the shortcomings of FS, Atanassov³¹ introduced the concept of an intuitionistic fuzzy set (IFS), which is a helpful extension of FSs that incorporates non-membership degrees (NMD). The IFSs cannot simulate such decision information when the total of MD and NMD is more than one. Yager^32,33 introduced the concept of the Pythagorean fuzzy set (P_yFS) to deal with such decision data by easing the requirements for FSs and IFSs. Compared to other FSs, P_yFS is more effective and flexible in managing MCGDM issues involving ambiguity.

MD and NMD characterize this with the restriction that the square sum of each degree should not exceed one. However, certain issues arise when the square sum of the MD and NMD exceeds one. To tackle this weakness, Yager³⁴ presented the q-rung orthopair fuzzy set (q-ROFS) as a valuable solution. The q-ROFS is defined by MD and NMD so that the qth power sum of each degree falls within the range of [0,1]. It’s worth noting that IFS and P_yFS represent special cases of q-ROFS. It can be argued that q-ROFS is a more general framework because the permissible range expands as the parameter ‘q’ increases. The q-ROFS gives experts more flexibility in communicating their unclear knowledge. Later, Cuong and Kreinovich³⁵ proposed another extension of the FSs mentioned above, picture fuzzy sets (PFSs). It includes MD, NMD, and the abstinence degree (AD). However, PFSs can take the ambiguity and uncertainty in the information more consistently. Due to the requirement that the sum of MD, AD, and NMD be less than one, this kind of fuzzy setting is limited to a very specific data set. In reality, it is not always possible to provide information data for which the sum of the MD, AD, and NMD does not exceed one. To address this, Mahmood et al.³⁶ developed spherical fuzzy sets (SFSs) to expand PFS by modifying the restriction from the sum of MD, AD, and NMD to the square sum of MD, AD, and NMD. In the same research, they proposed an expanded version of SFS by adding a condition that requires \(\:qth\:\)power sum of these three degrees to lie in the unit interval. This type of set was named as T-SFS. PFS and SFS are special cases of T-SFS as if the value of parameter ‘\(\:q=1\)’, then T-SFS degenerated to PFS, and if ‘\(\:q=2\)’ then T-SFS is restricted to SFS. The theory of T-SFSs provides a thorough model of some well-known and accepted fuzzy frameworks due to the generality of the T-SF framework. This supports the usefulness, adaptability, and flexibility of T-SF sets in manipulating imprecision and vagueness for solving complex uncertain MCGDM problems.

The methods discussed above primarily deal with uncertainty from a quantitative perspective. However, many attributes are subjectively evaluated and cannot be easily quantified. Addressing Multi-Criteria Group Decision Making (MCGDM) in such scenarios can be achieved by incorporating linguistic variables. Zadeh³⁷ introduced the concept of linguistic term sets (LTSs) to express assessment information using linguistic terms (LTs). For instance, when evaluating a smartphone’s performance, we often use phrases like “poor,” “below average,” “average,” “good,” and “excellent” rather than specific numerical values. Therefore, using linguistic variables to communicate imprecise and subjective assessment data aligns better with individual reasoning capabilities. Xu³⁸ introduced a concept known as the continuous linguistic term set (CLTS) to preserve information integrity throughout computational processes. Additionally, Zhang³⁹ is credited with pioneering the notion of a linguistic intuitionistic fuzzy set (LIFS), which integrates linguistic methodologies with IFS, creating a unique and innovative approach. To manage the qualitative data, Garg⁴⁰ introduced the theory of linguistic P_yFS (L_yPFS) by combining the concepts of PFSs and LT. L_yPFS is characterized by linguistic MD (LMD) and linguistic NMD (LNMD). Khan et al.⁴¹ proposed the concept of linguistic q-ROFS (Lq-ROFS). The idea of linguistic picture fuzzy set (LPFS) was derived from⁴², characterized by linguistic MF, linguistic AF and linguistic NMF. A further extension of LPFS called linguistic spherical fuzzy set (LSFS) was proposed by Jin et al. (2019). However, there are some situations in which LSFS failed. To further explain the situation, we discuss an example from this perspective. Suppose an expert provides his evaluation information in the format of LSFS as \(\left( {{s_7},{s_4},{s_6}} \right)\), where \({s_\tau }\)representing the linguistic variable in the range of [0,9]. According to the LSFS restriction,\({\left( {LMD} \right)^2}+{\left( {LAD} \right)^2}+{\left( {LNMD} \right)^2} \leqslant {\tau ^2}\), if we apply this to the given example data, the results don’t satisfy this primary condition of LSFS. Clearly \({\left( 7 \right)^2}+{\left( 4 \right)^2}+{\left( 6 \right)^2}=101>{9^2}=81\). In order to provide experts greater flexibility in handling information of this type, Gurmani et al. (2022) introduced a novel extension of LSFS known as the linguistic T-spherical Fuzzy Set (LT-SFS). This extension, LT-SFS, is noted for its heightened generality compared to other existing extended fuzzy sets. The authors introduced a parameter ‘q’ into the constraints such as \({\left( {LMD} \right)^q}+{\left( {LAD} \right)^q}+{\left( {LNMD} \right)^q} \leqslant {\tau ^q}\), where this parameter play a crucial role. If we take \(q=1,{\text{ }}q=2\)then LT-SFS degenerates into LPFS and LSFS, respectively. In cases where both LPFS and LSFS prove ineffective for handling the information provided in the earlier example, LT-SFS emerges as a valuable and effective tool. For instance, if we take \(q=3\); \({\left( 7 \right)^3}+{\left( 4 \right)^3}+{\left( 6 \right)^3}=623<{9^3}=729\) holds. This adaptability underscores the utility of LT-SFS in addressing complex information scenarios.

Therefore, we use LT-SFS in this article because they effectively handle the uncertainty and vagueness inherent in green technology selection, where expert assessments are often qualitative and imprecise. LT-SFS allow decision-makers to express their evaluations using linguistic terms such as “high” or “low,” reflecting their knowledge’s uncertainties. This method is particularly useful when experts face challenges in quantifying criteria, as it captures not only membership and non-membership degrees but also hesitancy, providing a more comprehensive representation of real-world DM. In practice, LT-SFS information is obtained through expert surveys or workshops, where stakeholders provide their assessments based on available data and personal expertise, making it a valuable tool for real-world DM scenarios.

Hamacher aggregation operators

Aggregation operators (AOs) in MCGDM are helpful tools for combining several decision values into a single value. Various AOs have been developed to handle imprecise DM scenarios^45,46. Numerous linguistic operators^47,48 are commonly used in fuzzy settings as well. Jin et al.⁴³ introduced LSF-weighted geometric AOs to aggregate the expert’s evaluation information characterized by LSF numbers. Gurmani et al.⁴⁴ suggested Dombi AOs for LT-SFS numbers to tackle MCGDM difficulties, which were motivated by the characteristics of Dombi operations. The justification demonstrates that most AOs developed had their primary inspirations in the algebraic product and sum. Other AOs relying solely on algebraic sum and product may fail to adequately represent the interactions within aggregated data. Furthermore, it’s worth noting that Hamacher t-norm and t-conorm, as introduced by Oussalah⁴⁹, represent important categories within the realm of t-norms. These t-norms serve as generalizations of algebraic and Einstein norms. Consequently, Hamacher AOs (HAOs) have proven to be highly valuable and advantageous compared to their existing counterparts. There have been a number of HAOs introduced in the literature thus far, and each of these has its own restrictions. When it comes to intuitionistic fuzzy settings, Huang⁵⁰ introduced the HA operators. Tang and Meng⁵¹ established HAOs in the context of LIF environment and series of HAOs under LP_yF setting have been developed in⁵². According to a review of the LT-SF-AOs, there hasn’t been any research on the development of new operators employing Hamacher operations. Consequently, there is a clear need for conducting research on AOs that leverage Hamacher operations within the context of LT-SF information. In this study, HAOs are used to integrate expert evaluations of green technologies due to their flexibility and ability to model varying degrees of interaction among criteria. Unlike traditional aggregation operators, Hamacher operators account for both the intensity and uncertainty of expert opinions, making them particularly suitable for complex DM environments where information is often imprecise or conflicting.

CRITIC method

In MCGDM problems, assigning weights is a crucial stage that genuinely affects the final outcome of the DM process. Various authors have offered different frameworks for evaluating the criteria weights^53,54. The objective and subjective weights are referred to as the weighting structures of the criterion Peng⁵⁵. The CRITIC model was established by Diakoulaki et al.⁵³ to determine objective weights while simultaneously considering the variations and correlations among multiple criteria⁵⁶. This method establishes the attribute weights using a decision matrix. The main strength of this method is that it can be employed for both dependent and independent criteria. The CRITIC method offers advantages that can be summarized as follows: it concurrently addresses the normalization of the decision matrix by considering the ideal values for cost and benefit criteria together, in contrast to other methods that handle them separately. The sole method gauges criterion similarity using the correlation coefficient derived from values within the decision matrix. Furthermore, it assesses the relative importance of a given criterion compared to others by computing the standard deviation of the normalized values associated with that specific criterion. The literature has integrated the CRITIC model with various DM techniques, such as^57,58,59.

Although the CRITIC method has been employed in various MCGDM techniques recently, it hasn’t yet been extended to the LT-SF context. Therefore, in this study, the CRITIC method is extended using the LT-SF environment to calculate the importance of evaluation criteria of alternative green technologies for environmental sustainability. This method is well-suited for capturing the relative importance of criteria, which is crucial in a multi-criteria decision making (MCDM) problem like green technology evaluation, where the criteria are often interdependent.

EDAS method

When handling complex and multifaceted real-world challenges, multi-criteria group DM procedures, also known as multi-attribute group DM (MAGDM), are considered straightforward yet incredibly powerful DM tools^60,61. MCGDM approaches address two key concerns in DM problems: first, determining the relevance of the decision criteria and, second, comparatively prioritizing or ranking a set of options concerning the criteria. It has been crucial for management science and other sectors to develop MCGDM techniques. These methods have been applied to various DM problems in different fields, such as waste management⁶², defence industry⁶³, healthcare management⁶⁴, and humanitarian and disaster management⁶⁵. Recently, several MCGDM techniques have been developed to improve the DM capabilities of real-world decision-makers in actual practices. EDAS (Evaluation Based on Distance from Average Solution) is one of the most recently created methodologies with broad applicability in challenging DM. EDAS method proposed by Ghorabaee et al.⁶⁶ is an emerging DM method that belongs to the family of distance-based DM techniques such as TOPSIS and VIKOR. The best alternative is chosen using the EDAS technique based on its distance from the average solution, as compared to TOPSIS and VIKOR, which choose the best alternative based on ideal solutions (positive and negative). This distinction removes the need to choose positive or negative ideal solutions, which might be complicated in some circumstances. It offers a straightforward methodology, quick computation, and a strong rating of alternatives. Tang et al.^67,68,69,70 proposed various DM techniques using different structures of fuzzy sets.

In many uncertain situations, including picture fuzzy⁷¹, spherical fuzzy⁷², and linguistic Pythagorean fuzzy⁵². environments, the EDAS model has been extended. However, the EDAS method has not yet been extended into the LT-SF setting to address uncertainties like imprecision, vagueness, and inconsistency. To fill this research gap, in this study, the EDAS (Evaluation based on Distance from Average Solution) method is employed to rank the alternatives for green technology selection due to its simplicity, computational efficiency, and strong ability to handle uncertainty in DM. The EDAS method is particularly suitable for real-world applications like green technology evaluation, where experts provide qualitative assessments that may be imprecise or inconsistent. The key advantage of EDAS is that it ranks alternatives by evaluating their distance from the average solution, which eliminates the need for ideal or non-ideal solutions, which are often difficult to define in complex problems like green technology selection. This makes it more practical when the decision-makers face challenges in clearly defining perfect solutions. Moreover, EDAS is efficient in capturing the overall performance of each alternative across multiple criteria, making it an ideal choice for evaluating green technologies where different stakeholders might have varying priorities but need a straightforward way to identify the best alternatives.

This section provides an overview of fundamental concepts related to LT-SFSs and Hamacher’s operation.

Definition 2.1

⁴⁴ Let be a universal set, and be a continuous LTS. Then,

is called as LT-SFS is defined. Where \(\:{s}_{\mu\:}\left(u\right),{s}_{\eta\:}\left(u\right),{s}_{\nu\:}\left(u\right)\in\:S\) are the LMD, LAD and LNMD of the element \(\:u\) to\(\:\:T\). Each triplet \(\:\left({s}_{\mu\:}\right(u),{s}_{\eta\:}(u),{s}_{\nu\:}(u\left)\right)\) is simplified as \(\:({s}_{\mu\:},{s}_{\eta\:},{s}_{\nu\:})\) called as LT-SFN and meets the condition \(\:0\le\:{\mu\:}^{q}\left(u\right)+{\eta\:}^{q}\left(u\right)+{\nu\:}^{q}\left(u\right)\le\:{t}^{q}\) for any positive number \(\:q\ge\:1\). Further, \(\:{\pi\:}_{T}={s}_{\sqrt[q]{{t}^{q}-\left({\mu\:}^{q}\right(u)+{\eta\:}^{q}(u)+{\nu\:}^{q}(u\left)\right)}}\) is called as linguistic hesitancy function of \(\:u\) in \(\:T\).

Definition 2.2

⁴⁴ Let be a LT-SFN. Then, the score function is defined as

and accuracy function \(\:\mathfrak{R}\left(T\right)\) for LT-SFN is expressed as

where \(\:q\ge\:1\).

For comparing laws for two LT-SFNs \(\:{T}_{1}=({s}_{{\mu\:}_{1}},{s}_{{\eta\:}_{1}},{s}_{{v}_{1}})\) and \(\:{T}_{2}=({s}_{{\mu\:}_{2}},{s}_{{\eta\:}_{2}},{s}_{{v}_{2}})\) are given as follows:

1. (1)

   If \(\:S\left({T}_{1}\right)>S\left({T}_{2}\right),\) then \(\:{T}_{1}>{T}_{2};\)

2. (2)

   If \(\:S\left({T}_{1}\right)<S\left({T}_{2}\right),\) then \(\:{T}_{1}<{T}_{2};\)

3. (3)

   If \(\:S\left({T}_{1}\right)=S\left({T}_{2}\right),\:\)then,

1. i.

   If \(\:H\left({T}_{1}\right)>H\left({T}_{2}\right),\) then \(\:{T}_{1}>{T}_{2};\)

2. ii.

   If \(\:H\left({T}_{1}\right)=H\left({T}_{2}\right),\) then \(\:{T}_{1}={T}_{2}\).

Definition 2.3

⁷³ Hamacher product (t-norm) and the Hamacher sum (t-conorm) are defined as follows:

Note that when\(\:\:\gamma\:=1\), the Hamacher product and Hamacher sum are reduced to algebraic product and sum; the Hamacher product and Hamacher sum are degenerated into Einstein sum and product for \(\:\gamma\:=2\), respectively.

In this section, some operational Laws of LT-SFNs based on Hamacher t-norm and t-conorm have been defined.

Definition 3.1

Let and be two LT-SFNs defined on continuous linguistic term set (CLTS), and. Then, the Hamacher operations defined for two LT-SFNs are as follows:

i.

ii.

iii.

iv.

where \(\:A=({s}_{{\mu\:}_{A}},{s}_{{\eta\:}_{A}},{s}_{{v}_{A}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{A}=\frac{{\psi\:}_{A}}{t}\\\:{\eta\:}_{A}=\frac{{\theta\:}_{A}}{t}\\\:{v}_{A}=\frac{{\varsigma\:}_{A}}{t}\end{array}\right.\), \(\:B=({s}_{{\mu\:}_{B}},{s}_{{\eta\:}_{B}},{s}_{{v}_{B}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{B}=\frac{{\psi\:}_{B}}{t}\\\:{\eta\:}_{B}=\frac{{\theta\:}_{B}}{t}\\\:{v}_{B}=\frac{{\varsigma\:}_{B}}{t}\end{array}\right.\), and \(\:f\) is transferred function such that

\(\:A=f\left({A}^{{\prime\:}}\right)={I}_{t}\odot\:f\left({A}^{{\prime\:}}\right)\) for any LT-SFN \(\:A=({s}_{{\psi\:}_{A}},{s}_{{\theta\:}_{A}},{s}_{{\varsigma\:}_{A}})\) with \(\:A=({s}_{{\mu\:}_{A}},{s}_{{\eta\:}_{A}},{s}_{{v}_{A}})=({s}_{\frac{{\psi\:}_{A}}{t}},{s}_{\frac{{\theta\:}_{A}}{t}},{s}_{\frac{{\varsigma\:}_{A}}{t}})\).

Remark 3.1

1. 1.

   For \(\:\gamma\:=1\), the LT-SF Hamacher operational laws are reduced into the LT-SF algebraic operational laws.

2. 2.

   For \(\:\gamma\:=2\), the LT-SF Hamacher operational laws are diminished into LT-SF Einstein operational laws.

Theorem 3.1

Let and are two LTSFNs defined on CLTS, then

1. (1)
   $$\:A\oplus\:B=B\oplus\:A$$
2. (2)
   $$\:A\otimes\:B=B\otimes\:A$$
3. (3)
   $$\:\lambda\:(A\oplus\:B)=\lambda\:A\oplus\:\lambda\:B$$
4. (4)
   $$\:{(A\otimes\:B)}^{\lambda\:}={A}^{\lambda\:}\otimes\:{B}^{\lambda\:}$$
5. (5)
   $$\:{\lambda\:}_{1}A\oplus\:{\lambda\:}_{2}A=({\lambda\:}_{1}\oplus\:{\lambda\:}_{2})A$$
6. (6)
   $$\:{A}^{\left({\lambda\:}_{1}\right)}\oplus\:{A}^{\left({\lambda\:}_{2}\right)}={A}^{({\lambda\:}_{1}\oplus\:{\lambda\:}_{2})}$$

where \(\:A=({s}_{{\mu\:}_{A}},{s}_{{\eta\:}_{A}},{s}_{{v}_{A}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{A}=\frac{{\psi\:}_{A}}{t}\\\:{\eta\:}_{A}=\frac{{\theta\:}_{A}}{t}\\\:{v}_{A}=\frac{{\varsigma\:}_{A}}{t}\end{array}\right.\), \(\:B=({s}_{{\mu\:}_{B}},{s}_{{\eta\:}_{B}},{s}_{{v}_{B}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{B}=\frac{{\psi\:}_{B}}{t}\\\:{\eta\:}_{B}=\frac{{\theta\:}_{B}}{t}\\\:{v}_{B}=\frac{{\varsigma\:}_{B}}{t}\end{array}\right.\), and \(\:\lambda\:>0\).

Proof

It is obvious.

Definition 4.1

Let be a collection of LT-SFNs defined on a CLTS. The LT-SFHWA operator is thus defined as follows:

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})=({s}_{\frac{{\psi\:}_{j}}{t}},{s}_{\frac{{\theta\:}_{j}}{t}},{s}_{\frac{{\varsigma\:}_{j}}{t}})\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Based on Hamacher sum operations of LT-SFNs described in definition 3.1, we can drive the Theorem 1.

Theorem 4.1

Let be a collection of LT-SFNs defined on CLTS, then their aggregated values by using LT-SFHWA is also a LT-SFNs, and

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\:\:\right.\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Proof

We will use mathematical induction to verify Eq. (11).

For \(\:l=2\), Let \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\text{\hspace{0.17em}\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) be two LT-SFNs. Then, by Eqs. (3.1), (3.3), and (11), we get,

\(\begin{gathered} =\left( \begin{gathered} {s_{t\left( {\frac{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{1}^{q}} \right)}^{{w_1}}} - {{\left( {1 - \mu _{1}^{q}} \right)}^{{w_1}}}}}{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{1}^{q}} \right)}^{{w_1}}}+\left( {\gamma - 1} \right){{\left( {1 - \mu _{1}^{q}} \right)}^{{w_1}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}},{s_{t\left( {\frac{{\sqrt[q]{\gamma }\eta _{1}^{{{w_1}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{1}^{q}} \right)} \right)}^{{w_1}}}+\left( {\gamma - 1} \right){{\left( {\eta _{1}^{q}} \right)}^{{w_1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }v_{1}^{{{w_1}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{1}^{q}} \right)} \right)}^{{w_1}}}+\left( {\gamma - 1} \right){{\left( {v_{1}^{q}} \right)}^{{w_1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right)\, \hfill \\ \oplus \left( \begin{gathered} {s_{t{{\left( {\frac{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{2}^{q}} \right)}^{{w_2}}} - {{\left( {1 - \mu _{2}^{q}} \right)}^\lambda }}}{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{2}^{q}} \right)}^\lambda }+\left( {\gamma - 1} \right){{\left( {1 - \mu _{2}^{q}} \right)}^\lambda }}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}},{s_{t\left( {\frac{{\sqrt[q]{\gamma }\eta _{2}^{{{w_2}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{2}^{q}} \right)} \right)}^{{w_2}}}+\left( {\gamma - 1} \right){{\left( {\eta _{2}^{q}} \right)}^{{w_2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }v_{2}^{{{w_2}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{2}^{q}} \right)} \right)}^{{w_2}}}+\left( {\gamma - 1} \right){{\left( {v_{2}^{q}} \right)}^{{w_2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered}\)

\(\begin{gathered} =\left( {{s_{t{{\left( {\frac{{\prod\nolimits_{{j=1}}^{2} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}} - \prod\nolimits_{{j=1}}^{2} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}{{\prod\nolimits_{{j=1}}^{2} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{2} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}},} \right. \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{2} {\eta _{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{2} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{2} {{{\left( {\eta _{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ \left. {{s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{2} {v_{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{2} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{2} {{{\left( {v_{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}} \right) \hfill \\ \end{gathered}\)

For \(\:l=2\), the result in Eq. (11) is true. We now assume that the outcome is true for \(\:l=k\). i.e.

when \(\:l=k+1\), according to Eq. (12), we get

\(\begin{gathered} =\left( \begin{gathered} {s_{t{{\left( {\frac{{\prod\nolimits_{{j=1}}^{k} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}} - \prod\nolimits_{{j=1}}^{k} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}{{\prod\nolimits_{{j=1}}^{k} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{k} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{k} {\eta _{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{k} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{k} {{{\left( {\eta _{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{k} {v_{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{k} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{k} {{{\left( {v_{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \oplus \left( \begin{gathered} {s_{t\left( {\frac{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{{k+1}}^{q}} \right)}^{{w_{k+1}}}} - {{\left( {1 - \mu _{{k+1}}^{q}} \right)}^{{w_{k+1}}}}}}{{{{\left( {1+\left( {\gamma - 1} \right)\mu _{{k+1}}^{q}} \right)}^{{w_{k+1}}}}+\left( {\gamma - 1} \right){{\left( {1 - \mu _{{k+1}}^{q}} \right)}^{{w_{k+1}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}},{s_{t\left( {\frac{{\sqrt[q]{\gamma }\eta _{1}^{{{w_{k+1}}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{{k+1}}^{q}} \right)} \right)}^{{w_{k+1}}}}+\left( {\gamma - 1} \right){{\left( {\eta _{{k+1}}^{q}} \right)}^{{w_{k+1}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }v_{1}^{{{w_{k+1}}}}}}{{{{\left( {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{1}^{q}} \right)} \right)}^{{w_{k+1}}}}+\left( {\gamma - 1} \right){{\left( {v_{1}^{q}} \right)}^{{w_{k+1}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered}\)

\(\:LT-SFHWA({T}_{1},{T}_{2},\ldots,{T}_{k+1})=\)\(\left( \begin{gathered} {s_{t{{\left( {\frac{{\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}} - \prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}{{\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}},{s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{{k+1}} {\eta _{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {\eta _{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{{k+1}} {v_{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{{k+1}} {{{\left( {v_{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right)\)

Hence, the result holds for \(\:l=k+1\), and thus, Eq. (11) holds for all positive integers \(\:l\).

Theorem 4.2

Let, be two collections of LT-SFNs and is the weight vector of the with and We can define the following properties:

P1 (Idempotency): For all LT-SFNs \(\:{T}_{j}=({s}_{{\psi\:}_{j}},{s}_{{\theta\:}_{j}},{s}_{{\varsigma\:}_{j}})\text{\hspace{0.17em}\hspace{0.17em}}\:(j=\text{1,2},\ldots,l)\) be equal to \(\:T=({s}_{\psi\:},{s}_{\theta\:},{s}_{\varsigma\:})\text{\hspace{0.17em}\hspace{0.17em}}\)

P2 (commutativity): Let \(\:{T}_{j}=({s}_{{\psi\:}_{j}},{s}_{{\theta\:}_{j}},{s}_{{\varsigma\:}_{j}})\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) be the collection of LT-SFNs and \(\:{T}_{j}=({s}_{{\psi\:}_{\left(j\right)}},{s}_{{\theta\:}_{\left(j\right)}},{s}_{{\varsigma\:}_{\left(j\right)}})\text{\hspace{0.17em}\hspace{0.17em}}\)be the permutation of\(\:\:{T}_{j}\), \(\:(j=\text{1,2},\ldots,l)\) then,

Proof

Since, are the two collections of LT-SFNs. Then.

(P1) When \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{\nu\:}_{j}})=T=({s}_{\mu\:},{s}_{\eta\:},{s}_{\nu\:})\) for all \(\:j\) and \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\)

with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\). Then, based on Definition 4.1, we have

\(=\left( \begin{gathered} {s_{t{{\left( {\frac{{\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}} - \prod\nolimits_{{j=1}}^{l} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}{{\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\mu _{j}^{q}} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {1 - \mu _{j}^{q}} \right)}^{{w_j}}}} } }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{l} {\eta _{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta _{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {\eta _{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{l} {v_{j}^{{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v_{j}^{q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {v_{j}^{q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right)\)

\(=\left( \begin{gathered} {s_{t{{\left( {\frac{{\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right){\mu ^q}} \right)}^{{w_j}}} - \prod\nolimits_{{j=1}}^{l} {{{\left( {1 - {\mu ^q}} \right)}^{{w_j}}}} } }}{{\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right){\mu ^q}} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {1 - {\mu ^q}} \right)}^{{w_j}}}} } }}} \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}},{s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{l} {{\eta ^{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - {\eta ^q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {{\eta ^q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}}, \hfill \\ {s_{t\left( {\frac{{\sqrt[q]{\gamma }\prod\nolimits_{{j=1}}^{l} {{v^{{w_j}}}} }}{{{{\left( {\prod\nolimits_{{j=1}}^{l} {{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - {v^q}} \right)} \right)}^{{w_j}}}+\left( {\gamma - 1} \right)\prod\nolimits_{{j=1}}^{l} {{{\left( {{v^q}} \right)}^{{w_j}}}} } } \right)}^{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}}}} \right)}} \hfill \\ \end{gathered} \right)\)

\(=\left( \begin{gathered} \left( {\frac{{\left( {1+\left( {\gamma - 1} \right)\mu - \left( {1 - \mu } \right)} \right)}}{{\left( {1+\left( {\gamma - 1} \right)\mu +\left( {\gamma - 1} \right)\left( {1 - \mu } \right)} \right)}}} \right),\left( {\frac{{\gamma \left( \eta \right)}}{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - \eta } \right)+\left( {\gamma - 1} \right)\left( \eta \right)} \right)}}} \right), \hfill \\ \left( {\frac{{\gamma \left( v \right)}}{{\left( {1+\left( {\gamma - 1} \right)\left( {1 - v} \right)} \right)+\left( {\gamma - 1} \right)\left( v \right)}}} \right) \hfill \\ \end{gathered} \right)\)

(P2) The result can be easily verified by Definition 4.1.

Example 4.1

Let be CLTS. We assume three experts are tasked with evaluating and selecting the best mobile phone. They will consider multiple criteria such as performance, design, camera quality, battery life, and price. Each expert has assessed each alternative based on the elective criterion using LT-SFNs. Let the information given by experts be as follows:, and. The weight vector for experts is given as, and the two parameters are assumed as,. Then, by Eq. (11),

Remark 4.1

1. 1.

   When \(\:\gamma\:=1\), the LT-SFHWG degenerated into the LT-SF algebraic weighted average operator.

2. 2.

   When \(\:\gamma\:=2\), the LT-SFHWG degenerated into LT-SF Einstein weighted average operator.

3. 3.

   When \(\:\gamma\:=1\) and \(\:q=1\), the LT-SFHWG is transformed into a linguistic picture fuzzy algebraic weighted average operator.

4. 4.

   When \(\:\gamma\:=2\) and \(\:q=1\), the LT-SFHWG is replaced by linguistic picture fuzzy Einstein weighted average operator.

5. 5.

   When \(\:\gamma\:=1\) and\(\:\:q=2\), the LT-SFHWG is reduced to the LSF algebraic weighted average operator.

6. 6.

   When \(\:\gamma\:=2\) and\(\:\:q=2\), the LT-SFHWG is reduced to the LSF Einstein weighted average operator.

Here, it is worth noting that the LT-SFHWA AO exclusively assigns weight to the LT-SFN. There are several situations in the context of MCGDM problems where the precise sequence or position of the LT-SFN becomes important. In such cases, the idea of ordered weighted averaging operators is critically important. For this reason, the LT-SFHOWA operator is presented with the following formulation.

Definition 4.2

Let be a collection of LT-SFNs, then we define the LT-SFHOWA operator as follows:

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})=({s}_{\frac{{\psi\:}_{j}}{t}},{s}_{\frac{{\theta\:}_{j}}{t}},{s}_{\frac{{\varsigma\:}_{j}}{t}})\), \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})=({s}_{\frac{{\psi\:}_{j}}{t}},{s}_{\frac{{\theta\:}_{j}}{t}},{s}_{\frac{{\varsigma\:}_{j}}{t}})\) and \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) is a permutation of \(\:(\text{1,2},\ldots,l)\) such that \(\:{T}_{\sigma\:(j-1)}\ge\:{T}_{\sigma\:(j-1)}\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Theorem 4.3

Let be a collection of LT-SFNs, then their aggregated values obtained by applying LT-SFHOWA is still an LT-SFNs, and

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\) and \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) is a permutation of \(\left( {1,2,\ldots,l} \right)\), such that \(\:{T}_{\sigma\:(j-1)}\ge\:{T}_{\sigma\:(j-1)}\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Proof

Theorem 4.3’s proof is similar to that of Theorem 4.1. Thus, we won’t include its proof here.

Definition 4.3

Suppose is a set of LT-SFNs, then the LT-SFHWG operator is defined as follows:

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Based on Hamacher product operations of LT-SFNs described in definition 3.1, The Theorem 4.4 can be expressed as follows:

Theorem 4.4

Let be a collection of LT-SFNs, then their aggregated values by using LT-SFHWG is also LTSFNs, and

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Proof

Since Theorem 4.4’s argument is similar to that of Theorem 4.1, we won’t include it here.

Example 4.2

By using the example 4.1 data and Eq. 16,

\(=\left( \begin{gathered} {s_{8 \times \left( {\frac{{\sqrt 3 \times \left( {{{\left( {\frac{6}{8}} \right)}^{0.3}} \times {{\left( {\frac{3}{8}} \right)}^{0.2}} \times {{\left( {\frac{1}{8}} \right)}^{0.5}}} \right)}}{{{{\left( {1+2 \times \left( {1 - {{\left( {\frac{6}{8}} \right)}^3}} \right)} \right)}^{0.3}} \times {{\left( {1+2 \times \left( {1 - {{\left( {\frac{3}{8}} \right)}^3}} \right)} \right)}^{0.2}} \times {{\left( {1+2 \times \left( {1 - {{\left( {\frac{1}{8}} \right)}^3}} \right)} \right)}^{0.5}}+2 \times \left( {{{\left( {{{\left( {\frac{6}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {{{\left( {\frac{3}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {{{\left( {\frac{1}{8}} \right)}^3}} \right)}^{0.5}}} \right)}}} \right)}} \hfill \\ {s_{8 \times {{\left( {\frac{{{{\left( {1+2 \times {{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+2 \times {{\left( {\frac{6}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+2 \times {{\left( {\frac{2}{8}} \right)}^3}} \right)}^{0.5}} - {{\left( {1+{{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+{{\left( {\frac{6}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+{{\left( {\frac{2}{8}} \right)}^3}} \right)}^{0.5}}}}{{{{\left( {1+2 \times {{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+2 \times {{\left( {\frac{6}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+2 \times {{\left( {\frac{2}{8}} \right)}^3}} \right)}^{0.5}}+2 \times \left( {{{\left( {1+{{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+{{\left( {\frac{6}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+{{\left( {\frac{2}{8}} \right)}^3}} \right)}^{0.5}}} \right)}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}}} \hfill \\ {s_{8 \times {{\left( {\frac{{{{\left( {1+2 \times {{\left( {\frac{1}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+2 \times {{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+2 \times {{\left( {\frac{5}{8}} \right)}^3}} \right)}^{0.5}} - {{\left( {1+{{\left( {\frac{1}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+{{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+{{\left( {\frac{5}{8}} \right)}^3}} \right)}^{0.5}}}}{{{{\left( {1+2 \times {{\left( {\frac{1}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+2 \times {{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+2 \times {{\left( {\frac{5}{8}} \right)}^3}} \right)}^{0.5}}+2 \times \left( {{{\left( {1+{{\left( {\frac{1}{8}} \right)}^3}} \right)}^{0.3}} \times {{\left( {1+{{\left( {\frac{4}{8}} \right)}^3}} \right)}^{0.2}} \times {{\left( {1+{{\left( {\frac{5}{8}} \right)}^3}} \right)}^{0.5}}} \right)}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}}} \hfill \\ \end{gathered} \right)\)

Remark 4.2

1. 1.

   When \(\:\gamma\:=1\), the LT-SFHWG degenerated into an LT-SF algebraic weighted geometric operator.

2. 2.

   When \(\:\gamma\:=2\), the LT-SFHWG degenerated into LT-SF Einstein weighted geometric operator.

3. 3.

   When \(\:\gamma\:=1\) and \(\:q=1\), the LT-SFHWG is transformed into a linguistic picture fuzzy algebraic weighted geometric operator.

4. 4.

   When \(\:\gamma\:=2\) and \(\:q=1\), the LT-SFHWG is replaced by linguistic picture fuzzy Einstein weighted geometric operator.

5. 5.

   When \(\:\gamma\:=1\) and \(\:q=2\), the LT-SFHWG is reduced to an LSF algebraic weighted geometric operator.

6. 6.

   When \(\:\gamma\:=2\) and \(\:q=2\), the LT-SFHWG is reduced to LSF Einstein weighted geometric operator.

Furthermore, it is clear that the suggested LT-SFHWG operator also satisfies the properties P1 and P2, which are expressed in Theorem 4. 2 for a collection of LT-SFNs.

Definition 4.4

Let be a collection of LT-SFNs, then we define the LT-SFHOWG operator as follows:

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\) and \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) is a permutation of \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) such that \(\:{T}_{\sigma\:(j-1)}\ge\:{T}_{\sigma\:(j-1)}\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Theorem 4.5

Let be a collection of LT-SFNs, then their aggregated values by using LT-SFHOWG is also an LTSFNs, and

where \(\:{T}_{j}=({s}_{{\mu\:}_{j}},{s}_{{\eta\:}_{j}},{s}_{{v}_{j}})\) with \(\:\left\{\begin{array}{c}{\mu\:}_{j}=\frac{{\psi\:}_{j}}{t}\\\:{\eta\:}_{j}=\frac{{\theta\:}_{j}}{t}\\\:{v}_{j}=\frac{{\varsigma\:}_{j}}{t}\end{array}\right.\) and \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) is a permutation of \(\:\left(\sigma\:\right(1),\sigma\:(2),\ldots,\sigma\:(l\left)\right)\) such that \(\:{T}_{\sigma\:(j-1)}\ge\:{T}_{\sigma\:(j-1)}\) and \(\:w={({w}_{1},{w}_{2},\ldots,{w}_{l})}^{T}\) be the weighting vector of \(\:{T}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,l)\) and \(\:{w}_{j}>0\), \(\:\sum\:_{j=1}^{l}{w}_{j}=1\).

Proof

The proof of Theorem 4.5 is similar to Theorem 4.1, so we omit its proof here.

Furthermore, it is clear that the suggested LT-SFHOWG operator also satisfies the properties P1 and P2, which are expressed in Theorem 4.2 for a collection of LT-SFNs.

To solve the MCGDM problem, we presented a novel ranking mechanism in this section. To do so, the LT-SF-MCGDM problem is first developed. In light of this, we use the LT-SFHWA operator to compile the decision-makers’ input arguments into a comprehensive opinion. Meanwhile, the CRITIC method under LT-SF information determines the criteria weights. Then, a modified EDAS method-based MCGDM technique is constructed to solve real-world problems.

Let \(\:X=\{{x}_{1},{x}_{2},\ldots,{x}_{m}\}\) be the set of ‘\(\:m\)’ alternatives and \(\:A=\{{a}_{1},{a}_{2},\ldots,{a}_{n}\}\) be the set of ‘\(\:n\)’ criteria. \(\:w=({w}_{1},{w}_{2},\ldots,{w}_{n})\) is called the weighting vector of criterion, which is based on the condition \(\:0\le\:{w}_{j}\le\:1\) and \(\:{\sum\:}_{j=1}^{n}{w}_{j}=1\). Consider that \(\:E=\{{e}_{1},{e}_{2},\ldots,{e}_{l}\}\) be the set of experts with the corresponding vectors\(\:\lambda\:=({\lambda\:}_{1},{\lambda\:}_{2},\ldots{\lambda\:}_{l})\). Assume that there are ‘\(\:l\)’ experts who have evaluated the alternatives \(\:{X}_{i}\text{\hspace{0.17em}}(i=\text{1,2},\ldots,m)\) under the criterion \(\:{A}_{j}\text{\hspace{0.17em}}(j=\text{1,2},\ldots,n)\) and provided their assessment information in the form of LT-SFNs, \(\:{Y}^{\left(k\right)}=\left({y}_{ij}^{\left(k\right)}\right),\text{\hspace{0.17em}}(k=\text{1,2},\ldots,l)\) where \(\:{y}_{ij}^{\left(k\right)}=\left({s}_{{\psi\:}_{ij}}^{\left(k\right)},{s}_{{\theta\:}_{ij}}^{\left(k\right)},{s}_{{\varsigma\:}_{ij}}^{\left(k\right)}\right)\). The EDAS method is enhanced using LT-SF data to identify the optimal solution in decision making problems.

Modified EDAS method-based MCGDM technique

The novel EDAS technique has been proven to be a useful tool for dealing with group DM issues. So, it is crucial to develop a new method by extending the EDAS methods into LT-SFNs to deal with linguistic assessment information. Therefore, this subsection develops the LT-SF-CRITIC-EDAS model based on the LT-SFHWA and the LT-SFHWG AOs by considering the flexibility of LT-SFNs. The framework of the proposed LT-SF-CRITIC-EDAS model is expressed in Fig. 1, and its specific computing steps are executed as follows:

Flowchart of the proposed LT-SF-CRITIC-EDAS model.

Full size image

Step 1. Construct the decision matrix.

The decision matrix involving the alternatives and criteria afforded by experts is given in the form of LT-SFS:

Here, \(\:{y}_{ij}^{\left(k\right)}=\left({\mu\:}_{ij}^{\left(k\right)},{\eta\:}_{ij}^{\left(k\right)},{v}_{ij}^{\left(k\right)}\right)=\left({s}_{{\psi\:}_{ij}}^{\left(k\right)},{s}_{{\theta\:}_{ij}}^{\left(k\right)},{s}_{{\varsigma\:}_{ij}}^{\left(k\right)}\right)\)

Step 2. Normalize the decision matrix.

The normalized decision matrix \(\:{\chi\:}_{ij}^{\left(k\right)}\) can be obtained from the following Eq. (20):

where \({\upchi _{ij}}\) represents the standard value of the decision matrix for the ith alternative with respect to jth criteria and.

Step 3. Compute the collective decision matrix.

By using the weights of experts and Eq. (11), the combined decision matrix is computed as follows:

where \(\:\lambda\:={({\lambda\:}_{1},{\lambda\:}_{2},\ldots{\lambda\:}_{l})}^{T}\)be the weighting vector with \(\:{\lambda\:}_{k}>0\) and \(\:\sum\:_{k=1}^{l}{\lambda\:}_{k}=1\).

Step 4. Determination of criteria weights.

The criteria weights can be calculated from the following steps:

Step 4.1 Generate the score matrix by using the following equation.

Step 4.2 Calculate the correlation coefficients (CC) between the criterion with the help of the following Eq. (23).

where \(\:{\stackrel{-}{\chi\:}}_{j}\) and \(\:{\stackrel{-}{\chi\:}}_{k}\) are the means of jth and kth criteria. \(\:{\stackrel{-}{\chi\:}}_{j}\) is computed by the following Eq.

Similarly \(\:{\stackrel{-}{\chi\:}}_{k}\) also can be calculated.

Step 4.3 Compute the standard deviation \({\sigma _j}\) of each criterion by using the following Eq. (23).

Step 4.4 The index \({I_j}\) is calculated with the help of Eq. (25).

Step 4.5 Then, the criterion weights are calculated using the Eq. (26).

Step 5. Compute the average solution matrix based on all criteria according to Eq. (27).

Step 6. This step is for the calculation of LT-SF positive distance from average (LT-SFPDA) and LT-SF negative distance from average (LT-SFNDA) from the by using the average solution matrix using Eqs. (28), (29), (30) and (31).

Here

Step 7. This step is used to get the weighted LT-SFPDA and weighted LT-SFNDA by using the weights of criterion and Eqs. (32) and (33).

Step 8. Calculate the normalized weighted LT-SFPDA and weighted LT-SFNDA by utilizing Eqs. (32) and (33).

Here \(\:S\left(W{P}_{i}\right)\) and \(\:S\left(W{N}_{i}\right)\) are the score functions of \(\:W{P}_{i}\) ad \(\:W{N}_{i}\) respectively.

Step 9. Each alternative’s appraisal values are calculated using the Eq. (36).

Step 10. Rank the alternatives based on the score function values in descending order. The alternative with the highest value will be considered the best choice among the available options.

This section uses a practical MCGDM problem involving green technology for environmental sustainability to ensure that the designed approach is applicable and feasible.

Explanation of problem

Environmental sustainability is a multi-faceted concept that embodies the ethical and practical imperative to safeguard the health of our planet. Its fundamental goal is to ensure the availability of natural resources, including water, energy, forests, and minerals, for present and future generations. This calls for decreasing waste production, minimizing soil, water, and air pollution, and safeguarding and maintaining ecosystems and biodiversity. Environmental sustainability also necessitates a dedication to limiting climate change through renewable energy sources, lowering greenhouse gas emissions, and promoting resistance to its effects. Additionally, it encompasses eco-friendly/green technology and consumer habits, responsible land use planning, and sustainable agricultural practices. To secure a prosperous and peaceful future for everybody, attaining environmental sustainability ultimately needs a collaborative effort at the individual, community, corporate, and governmental levels to strike a delicate balance between human progress and environmental conservation. Green technology, also called eco-friendly or clean technology, is essential for tackling pressing environmental issues and helping humanity shift to a more resource- and ecologically-conscious way of life. These technologies deal with developing and applying breakthroughs that have minimal environmental impact. The broad category of GTs includes renewable energy, energy efficiency, waste reduction, water conservation, sustainable agriculture, pollution avoidance, and other topics.

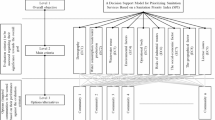
The municipal government of Hefei, Anhui province, China, is committed to enhancing environmental sustainability and reducing its carbon footprint. The city is investigating the adoption of GT across several industries, such as energy generation, transportation, waste management, and urban planning, to meet these objectives. The government’s DM team involves stakeholders, including environmental experts, community representatives, and financial analysts. These three stakeholders/experts \(\:\left\{{e}^{\left(1\right)},{e}^{\left(2\right)},{e}^{\left(3\right)}\right\}\) are tasked with evaluating four alternatives \(\:\{{A}_{1},{A}_{2},{A}_{3},{A}_{4}\}\) of green technology for reducing energy consumption in their manufacturing process, which is expressed as follows:

\(\:\left({A}_{1}\right)\) Green Building: The design, construction, and use of buildings that prioritize sustainability and reduce their adverse environmental effects are referred to as “green building” as a GT concept. These buildings are designed to be energy-efficient, water-efficient, and resource-efficient, using eco-friendly materials and technologies to reduce their carbon footprint. Improved interior air quality, lower energy use, and support for ecologically responsible practices are all goals of green buildings. They play a critical role in mitigating climate change, conserving natural resources, and improving the effectiveness and health of living environments.

\(\:\left({\text{A}}_{2}\right)\) Solar photovoltaic power: Solar power is a key pillar of the transition to a more sustainable and environmentally friendly energy system, and its continued development and widespread adoption play a crucial role in reducing the environmental impact of electricity generation. Photovoltaic cells or solar thermal systems collect energy from sunlight for solar power, a well-known GT. Unlike photovoltaic cells, more commonly known as solar panels, solar thermal systems use solar energy to produce heat that can be used to generate electricity or supply hot water.

\(\:\left({\text{A}}_{3}\right)\) Green Transport: In GT parlance, “green transport” refers to low-impact, ecologically friendly forms of transport that reduce pollution, carbon emissions, and resource usage. It includes shared mobility choices, electric and hybrid vehicles, bicycles, and public transportation. Fuel efficiency and the use of clean energy sources, such as hydrogen or electricity, are given priority by green transportation technology. Green transportation minimizes traffic, mitigates climate change, and reduces air pollution by reducing reliance on fossil fuels. This results in better urban air quality and a healthier planet. To provide accessible and environmentally friendly mobility options for communities worldwide, green transport initiatives must include investments in public transport, pedestrian-friendly infrastructure, and sustainable urban design.

\(\:\left({\text{A}}_{4}\right)\) Energy-efficient Equipment: As a core component of GT, energy-efficient equipment includes machinery, appliances, and systems that are made to use as little energy as possible without sacrificing performance. By utilising cutting-edge engineering and design principles, these technologies lower the energy needed to complete tasks, such as heating and cooling buildings, running industrial operations, or running domestic appliances. Energy-efficient equipment often incorporates LED lighting, high-efficiency HVAC systems, and smart thermostats. By optimizing energy use, these technologies help reduce greenhouse gas emissions, lower utility bills, and decrease the overall environmental impact, making them crucial in pursuing a more sustainable and eco-conscious future. Moreover, the decision hierarchy of the decision making problem is illustrated in Fig. 2.

Hierarchy structure of green technology selection problem.

Full size image

These experts have supposed five criteria \(\:\left\{{\mathcal{H}}_{1},{\mathcal{H}}_{2},{\mathcal{H}}_{3},{\mathcal{H}}_{4},{\mathcal{H}}_{5}\right\}\) while evaluating the above-mentioned four alternatives \(\:\{{A}_{1},{A}_{2},{A}_{3},{A}_{4}\}\) of green technologies explained as follows:

Environmental impact: Environmental impact as a criterion in GT evaluation assesses how a particular technology affects the environment throughout its lifecycle. It involves examining factors such as carbon emissions, resource consumption, pollution, and habitat disruption. The goal is to prioritize technologies that minimize these negative effects, reduce their ecological footprint, and promote sustainability. By emphasizing low environmental impact, GTs contribute to mitigating climate change, conserving natural resources, and preserving the planet’s health, aligning with broader environmental sustainability goals.

Cost-effectiveness: The economic efficacy of a technology’s installation and operation concerning its environmental advantages is referred to as cost-effectiveness, which is a criterion in the evaluation of GT. It entails examining the upfront investment, ongoing expenses, and possible long-term savings connected with implementing a GT. The objective is to find economically feasible solutions and provide significant environmental benefits. Prioritizing cost-effective GTs guarantees that sustainability initiatives help the environment and make financial sense, increasing the possibility that organizations and people will embrace and invest in environmentally friendly alternatives.

Maintenance and reliability: The ability of the technology to operate consistently and effectively over time with little or no need for maintenance or downtime is what is meant by “maintenance and reliability” as a criterion in assessing GT. This criterion evaluates the technology’s robustness, dependability, and maintenance-friendliness. Since they contribute to long-term sustainability by lowering the frequency of repairs, replacements, and related resource consumption, GTs with high maintenance and reliability scores are preferred. Green solutions are trustworthy and economical in pursuing sustainability goals due to their capacity to consistently bring environmental advantages.

Social acceptance: “Social acceptance” in GT analysis refers to how well society and the local community accept and support technology. This criterion assesses factors like popular opinion, cultural fit, and the likely effects of technology on society. It is more probable that GT will be adopted and successfully assimilated into society if they’re given a high social acceptability rating. This criterion recognizes that community engagement and participation are essential to sustainable technologies’ effective adoption and long-term viability, making them vital in transitioning to a more sustainable and ecologically friendly future.

Long-term sustainability: “Long-term Sustainability” is a rating criterion for GT that looks at how effectively the technology can maintain its positive social and environmental impacts over an extended length of time. This criterion focuses on robustness, flexibility, and durability. GTs that continue contributing to social well-being, resource conservation, and environmental preservation throughout their lifetimes receive high marks for long-term sustainability. By prioritizing long-term sustainability, we ensure that the chosen technologies can give long-term advantages, decrease the need for frequent replacements, and enable a more resilient and environmentally responsible future.

The three stakeholders/experts \(\:\{{e}^{\left(1\right)},{e}^{\left(2\right)},{e}^{\left(3\right)}\}\) with weighting vector \(\:{\left(\text{0.41,0.24,0.35}\right)}^{T}\) have provided their evaluation information in the form of LT-SFN while evaluating each alternative \(\:\{{A}_{1},{A}_{2},{A}_{3},{A}_{4}\}\) against four criteria \(\:\left\{{\mathcal{H}}_{1},{\mathcal{H}}_{2},{\mathcal{H}}_{3},{\mathcal{H}}_{4},{\mathcal{H}}_{5}\right\}\) with unknown criteria weights based on linguistic term set:

\(S=\{ {s_1}=very\,poor,\,{s_2}=poor,\,{s_3}=slightly\,poor,\,{s_4}=medium,\,{s_5}=slightly\,good,{s_6}=good,\,\)

\({s_7}=very\,good,\,{s_8}=Excellent\}\), and the results are given in Tables 1, 2 and 3. The algorithm designed in Sect. 5 is employed to get the weight vector of the supposed criteria and the best alternative. In this example, we assume the parameters \(\:q=3\:\)and \(\:\gamma\:=3\). The following are the steps of the proposed methodology:

Step 1. Decision matrices obtained from three experts are given in Tables 1, 2 and 3.

Step 2. In the following, only one criterion ‘\(\:{\mathcal{H}}_{2}\)’ is cost type criteria. So, we will compute the normalized decision matrices using Eq. (20) shown in Tables 4, 5 and 6.

Step 3. The comprehensive decision matrix is constructed by combining the evaluation inputs from three experts using the LT-SFHWA operator and Eq. (21), as shown in Table 7.

Step 4. The CRITIC method under the LT-SF setting designed in Sect. 5 is applied to compute the criteria weights, according to Eqs. (22), (23), (24), and (25), the results are shown in Table 8.

Step 5. We produce the average solution matrix by using Eq. (26) (see Table 9).

Step 6. We compute LT-SF positive distance from average (LT-SFPDA) and LT-SF negative distance from average (LT-SFNDA) by using Eqs. (27), (28), (29) and (30) (see Tables 10 and 11).

Step 7. We get the weighted LT-SFPDA \(\:W{P}_{i}\text{\hspace{0.17em}}(i=\text{1,2},\text{3,4})\) and weighted LT-SFNDA \(\:W{N}_{i}\text{\hspace{0.17em}}(i=\text{1,2},\text{3,4})\) by using the weights of criterion and Eqs. (5.13) and (5.14) as follows:

Step 8. The normalized weighted LT-SFPDA ‘\(\:NW{P}_{i}\)’ and normalized weighted LT-SFNDA ‘\(\:NW{N}_{i}\)’ are computed by using Eqs. (31) and (32) as follows:

Step 9. The appraisal values \(\:\wp\:{s}_{i}\text{\hspace{0.17em}}(i=\text{1,2},\text{3,4})\) of each alternative are computed by using the Eq. (33) as follows:

Step 10. Using the appraisal values, we arrange the alternatives in descending order, resulting in the final ranking as follows:

\(\:{A}_{2}>{A}_{1}>{A}_{4}>{A}_{3}\). This shows that Solar photovoltaic power is the best option among those four options.

Sensitivity investigation

In this section, we investigate the influence of parameters \(\:{\prime\:}q{\prime\:}\) and \(\:{\prime\:}\gamma\:{\prime\:}\) on decision outcomes using the approach proposed in this study. Keeping the parameter \(\:\gamma\:=3\) fixed and varying \(\:{\prime\:}q{\prime\:},\) we iterate through all steps of our suggested methodology. The analysis presented in Table 12 reveals that within the range of parameter \(\:q=3\) to\(\:\:q=9\), the optimal choice consistently remains \(\:{A}_{2}\). Slight changes in ranking are observed for alternatives when \(\:9\le\:q\ge\:10\), which are \(\:{A}_{2}>{A}_{4}>{A}_{1}>{A}_{3}\), and \(\:{A}_{2}>{A}_{4}>{A}_{1}>{A}_{3}\). Despite adjustments to the parameters, the identification of the best and worst alternatives remains unchanged. These findings are visually depicted in Fig. 3, illustrating the persistent selection of the best alternative across varying q values, highlighting the robustness of our proposed approach. In this methodology, a higher ‘q’ value signifies increased complexity in the decision making context. Experts are encouraged to select parameter values based on specific circumstances and considerations carefully.

Influence of parameter ‘q’ on final ranking order.

Full size image

Comparative analysis

To prove the feasibility and superiority of the established method, it is compared with traditional models and current novel techniques, respectively, and the outcomes are shown in Table 13. Analysis of Table 13 reveals that employing the linguistic P_yF-CRITIC-EDAS proposed in⁵², the linguistic spherical fuzzy weighted average operator (LSFSWAO) method from⁴³, and the technique using the linguistic P_yF weighted average operator (LPFWAO) described in⁴⁰ on the given dataset did not yield defined results due to limitations inherent in their structures. The example presented in this paper includes a linguistic abstinence degree that the aforementioned fuzzy sets cannot handle or accommodate. Additionally, we applied existing methods to the provided data, including the LT-SF-TOPSIS method⁴⁴, LT-SF-MABAC method⁷⁴, and linguistic T-spherical fuzzy-combinative distance-based assessment (CODAS) (LT-SF-COAS)⁷⁵ method. Table 13 provides the final rankings obtained and their graphic representation in Fig. 4. Table 13 illustrates that the ranking order of the options generated with the LT-SF-MABAC method⁷⁴ differs somewhat. Still, the best and worst alternatives for using different approaches are the same. In this study, the CRITIC method is extended under the LT-SF environment to determine the weights of experts, and the EDAS approach is integrated to establish the final ranking order of the available alternatives, which have never been used before in the LT-SF scenario. Through this comparative analysis, we can conclude that the methodology designed in this paper exhibits a higher level of generality and significantly contributes to our understanding of group DM. In conclusion, the combined application of LT-SF-CRITIC-EDAS demonstrates the flexibility and effectiveness of the designed model.

Comparative analysis of proposed technique with existing methods.

Full size image

Advantages of the proposed method

When making judgments, decision-makers must choose effective approaches based on their real-world surroundings because different tactics serve different purposes. Comparing our approach to other methods, we have found it to have positive impacts and superiorities, which are described as follows:

• The LT-SFHWA and LT-SFHWG operators enhance the reliability and effectiveness, facilitating a more realistic resolution of MCGDM problems for independent attributes.

• The LT-SF format represents information in the LT-SFHWA and LT-SFHWG operators. Linguistic terms are combined with T-SFS to form LT-SFS, which provides detailed information on the assessment procedure. The suggested operators are more broadly applicable due to LT-SFS’s adaptability in handling quantitative and qualitative data.

• It is crucial to highlight that LT-SFFWA and LT-SFWG are specific instances derived from our developed operators. Nevertheless, these limitations do not effectively reduce the uncertainty of decision data. Therefore, our enhanced operators are much more efficient in addressing this concern.

• The process of making decisions heavily relies on attribute weights, which have a substantial impact on the outcome. For this reason, the CRITIC method is used to determine the weights of attributes under the LT-SF environment.

• Further, the EDAS method is a recently developed MCDM model employed for ranking and selecting alternatives, considering their proximity to the average solution for a set of criteria. This is the first time the EDAS method has been modified using the LT-SF information to get the ranking of alternatives.

Table 14 presents the aspects of the proposed technique and existing models to further demonstrate the recommended approach’s superiority in modeling fuzzy information.

This study develops a novel DM methodology for selecting green technology, addressing the problem of choosing the most suitable green technology for environmental sustainability. For this purpose, linguistic T-spherical fuzzy CRITIC integrated EDAS methodologies are proposed. The CRITIC method enables objectively determining the weights of criteria, and the EDAS model ranks the alternatives by considering the experts’ assessments with respect to the criteria. Before all else, some fundamental concepts related to this research have been reviewed. Considering the importance of LT-SFSs that allow for independent modeling of experts’ hesitancy, the HAOs under the LT-SF environment are introduced for information fusion during the decision process. Some prominent properties of these newly established operators are also discussed. Then, the LT-SF-CRITIC-EDAS model is designed to tackle the complex MCGDM problems in the context of LT-SFSs. Furthermore, to show the viability and acceptability of the planned strategy, we have provided a real-world example of the selection of green technology for environmental sustainability. In the end, sensitivity and comparison analyses are also discussed to show the reliability of alternatives found using the planned strategy. The assessment outcomes effectively showcased the excellence and credibility of our developed method compared to existing approaches.

However, as expected, the present research model also has its limitations, such as (i) This study did not take into account a method to determine expert weights that may be employed to enhance the suggested approach; (ii) In contemporary information-driven societies, the concept of large-scale group decision making (LSGDM) has garnered considerable attention among academics. LSGDM involves decision making processes that engage a substantial number of participants and entail the evaluation of diverse viewpoints, preferences, and criteria. This complexity inherently increases the challenge of arriving at a final decision; and (iii) The choice of technology and its implementation can vary significantly depending on the area’s specific needs, existing infrastructure, environmental conditions, and local priorities. For example, the selection of solar photovoltaic power will be different for sunny and cloudy regions. Some of these shortcomings of the suggested study will be addressed as part of future research directions. Further, different types of AOs can be proposed in future research. Additionally, these proposed operators may be utilized with a larger number of criteria. On the other hand, we may implement the established technique into different real-world problems such as waste management⁶², defense industry⁶³, healthcare management⁶⁴, and humanitarian and disaster management⁶⁵.