Abstract
The optimal integration of Photovoltaic (PV) systems into an electric grid is dependent upon the total output power of the PV system. To optimize the output power of a PV system, the modules must be positioned at an optimal tilt angle (OTA) to maximize the absorption of solar radiations. This research focused on a mathematical model to optimize incident solar radiation. The proposed model is used to determine the OTA and evaluate its impact on the optimum configuration and power output capacity using MATLAB for six cities located in different temperature zones across Pakistan. The isotropic and anisotropic models have been used to calculate the total solar radiations (HT) on a sloped surface. During the summer season, all four selected models present similar findings in terms of the monthly average daily solar radiations on the tilted surface. During the winter season, the anisotropic models performed better than the isotropic models. The anisotropic model achieved a 14.82% energy increase in January and a 0.16% increase in June compared to the isotropic model. We present monthly and annual OTA calculated from the anisotropic model. The OTA has been determined for the HT across slope values ranging from 0° to 90° with a 1° resolution. The monthly OTA using anisotropic model for the Faisalabad, Lahore, Multan, RYK, Islamabad and Karachi ranges from 7° to 54°, 7° to 53°, 6° to 52°, 5° to 52°, 10° to 58° and 1° to 50° and the annual OTA for cities has been calculated to be 30.5°, 30.25°, 29.33°, 28.66°, 33.34° and 25.5° respectively. Utilizing the OTA calculated from the selected model, a PV array with a rated power of 52.200 kW has been used to analyze the system performance. The annual average output power at the monthly OTA results in gains of 8.83%, 9.40%, 9.78%, 9.77%, 9.82%, and 9.91% compared to the annual OTA. This research study is particularly beneficial for researchers and the industry in deploying PV systems across different climatic zones of Pakistan, intending to maximize output power while minimizing energy costs.
Similar content being viewed by others
Introduction
Fossil fuels continue to be the predominant energy source consumed globally, and their combustion is the primary driver of greenhouse gas emissions that contribute to climate change1. The ongoing exploitation of conventional fossil fuels at the current rate will eventually lead to their depletion2. Consequently, there is an immediate need to adopt renewable resources for energy generation. Meanwhile, the global ecosystem is at risk due to the significant emissions of pollutants and greenhouse gases (GHG) generated by fossil fuels3. The efficient use of renewable energy is a critical approach to reducing the consumption of fossil fuels and associated GHG4,5. Solar energy is considered the most abundant and readily accessible source of renewable energy, and it also offers significant environmental advantages6. Photovoltaic (PV) energy generation technology has emerged as one of the most crucial solutions to the global energy crisis and the attainment of carbon neutrality7. These benefits have been achieved due to the substantially reduced cost of solar PV modules8. Thus, the assessment of the energy generation potential and spatial distribution of solar energy resources is an important basis for countries around the globe for planning, decision-making, and installation of this sustainable form of energy. This also significantly impacts the development and formulation of legislation as well as regulations for the use of renewable energy, which aims to enhance the adoption of reliable and economically favorable energy sources9.
The low maintenance and operating costs of PV systems, the prolonged lifespan of approximately 25 years, and the ubiquitous features of solar radiation have made them an attractive source of energy for adaptation10. Nevertheless, a single PV module cannot generate a significant amount of power enough to meet a specific demand due to losses that occur throughout the physical process, which also hampers conversion efficiency11.. Furthermore, the output of the PV system is primarily influenced by ambient temperature, environmental conditions, and radiations12. PV systems are confronted with partial shading conditions (PSCs) circumstances due to the unpredictable nature of weather, the irregularity in sunlight accessibility, and the existence of physical obstacles (e.g., overhead cables, and trees)13,14,15. Hotspots are generated under non-homogeneous irradiance conditions, resulting in persistent damage to PV modules and significant voltage drops on the terminals of the shaded module16,17. The extraction of the utmost available power becomes challenging due to the presence of numerous peaks in the power-voltage curve of a PV module18. In addition, the need for PSCs is inevitable as a result of mutual shading between adjacent PV modules and limited available space19.
The possibility of improper interconnections in series or parallel configurations among modules in the photovoltaic system can reduce its expected lifespan, cost-effectiveness, efficiency, and performance reliability. Additionally, the installation cost of the system increases due to the requirement of additional wires20. However, maximum power point trackers (MPPTs) can enhance the efficiency of PV arrays in converting sunlight into power, but this is only possible under uniform shading conditions21,22. MPPTs cannot extract the maximum available power when multiple local peaks are found in the power-voltage (P–V) curve. The Global Maximum Power Point Trackers (GMPPTs) approach has been used to overcome this problem. GMPPTs identify the peak point on the P–V curve with the highest value among numerous points, thus optimizing the performance of the PV array23,24,25,26. Despite the fact that GMPPTs handle the problem of low efficiency in the PV modules, they continue to be considered a costly solution that involves additional circuitry and the implementation of complex algorithms27.
Another research approach to improve the efficiency and reduce the impact of PSCs has been proposed28. The authors introduced the adoption of either double-axis or single-axis sun tracking as a feasible option. These techniques offer benefits but also impose significant financial burdens, especially for utility-scale solar PV projects, and require sophisticated control systems and optimization algorithms to handle weather fluctuations. The combination of PSCs and the low efficiency of the modules needs larger areas to achieve higher energy generation. This emphasizes the significance of meticulous PV system installation to maximize power production and minimize expenses29. The tilt angle of the photovoltaic modules is the primary factor contributing to the optimization of power production. However, if the photovoltaic modules are not appropriately tilted and oriented, a significant quantity of energy may be lost30,31. The current studies on optimizing tilt angle exclude essential parameters. Therefore, their results are unsatisfactory and undermine the validity of their findings32. In addition, several methods for optimizing the tilt angle of photovoltaic modules are season-specific and do not consider the entire calendar year33.
Researchers from multiple countries conducted studies to determine the OTA. The research34examined the tilt angle (TA) of photovoltaic modules in low-latitude regions. The authors develop a strategy to enhance solar photovoltaic efficiency for sites located near the Tropic of Cancer35. The yearly energy increase has been calculated to be 18.35%, which subsequently improved to 34.16%. A study has been performed to establish a correlation between economics and the TA, aiming to decrease energy costs and installation expenses simultaneously36. The authors37conducted research in China to calculate tilt angle using collected data but did not provide specific numbers for OTA. The study38introduces a regression model that determines the OTA for flat-plate fixed-mode solar collectors at numerous places throughout Libya. The suggested model adjusts the OTA by considering the three different components of solar radiations: direct-beam radiations, diffuse radiations, and ground-reflected solar radiations. A technique has been proposed in39to determine the OTA of a PV module at the equator which calculates the optimal monthly TA based on the equatorial declination angle. The authors determined that the absence of a monthly tilt angle for the PV module would result in a power loss of 12%. The researchers developed a mathematical model using MATLAB software to calculate the OTA and sun radiations for a south-facing surface in the United Arab Emirates over various periods. The analysis concludes that using a fixed annual OTA of 23° results in approximately 8% more energy gain compared to using a horizontal photovoltaic array40. The authors41 proposed a method to calculate the OTA in hilly regions. The monthly and annual OTA enhanced the solar energy collections by 398.3 kWh/m2 and 238.7 kWh/m2 per year respectively.
A mathematical model to assess the OTA for Baghdad, Iraq has been introduced in42and the OTA for the whole year has been calculated to be 30.6°. A study was conducted in Senegal to determine the OTA43and demonstrated that the maximum potential energy production was not achieved by maintaining the tilt angle the same as the latitude. Optimizing the TA of solar energy conversion systems monthly is more beneficial than keeping it fixed, as it allows for more electricity generation. The study44was conducted in Basra city and the authors performed a computational and experimental investigation to assess the impact of changing TA of PV modules on their energy generation. The findings demonstrate that this model is highly precise in determining tilted angles and suggest that the annual OTA for a PV system in Basra city is 28°. Multiple techniques for determining the OTA have been proposed in45. The authors claimed that solar radiations will also increase as the number of variations in the tilt angle increases. A similar research study conducted in Turkey46 found that the annual average fixed monthly OTA is 38.14°, with solar radiations around 6866.12 Mj/m2per year. A technique for calculating the OTA while considering the shadow cast by nearby buildings has been proposed in47. Similar objectives can be mentioned in references48,49,50,51. The OTA for the PV systems for several countries was determined using HelioScope software29, NREL’s PVWatts, and PVGIS52,53,54.
Assessing the quantity of solar radiation (SR) at a specific geographical site is crucial for the planning and financial evaluation of photovoltaic systems. However, long-term data are often unavailable in numerous regions worldwide. Researchers have developed multiple empirical models using climate data to estimate the availability of solar energy. These empirical algorithms and models aim to estimate SR on a tilted surface for different geographical regions and varying atmospheric conditions55. The mathematical methodologies used to calculate solar radiation in these models are similar, except for the diffuse radiation component. This component is typically divided into the isotropic as well as anisotropic models. Isotropic diffuse models solely examine the intensity of solar radiations and do not consider orientation. In contrast, anisotropic models incorporate the horizontal-brightening or/and the circumsolar diffuse components on an inclined surface56,57,58. Several studies59,60,61,62have been reported in the literature on isotropic models (Badescu, Karonakis, and Liu and Jordanmodels) and anisotropic models (Hay and Davies, Reindle, and Hay Davies Klucher Reindle (HDKR)) models. The research63demonstrated that while determining the OTA for Canada, the isotropic model provided lower tilt angle predictions compared to the ___location’s latitude. On the other hand, the anisotropic model provided comparatively greater tilt angle values. In the same manner, the anisotropic model attained a higher TA for different sites in India64. Researchers have developed many mathematical models and correlations to determine the OTA of PV systems in order to achieve optimum power production65. Multiple mathematical models of diffuse solar irradiance were considered to find the OTA of PV modules that would maximize the amount of solar radiation they receive66,67.
The majority of researchers focus on determining the annual OTA for a particular ___location and then using it as a benchmark for the entire country. Due to the substantial variation in weather conditions across various geographic regions in Pakistan, it is not appropriate to estimate a single average OTA that accurately represents the entire country. The literature comprehensively demonstrates that the power production of photovoltaic systems depends on the tilt angle and the temperature of the solar PV cells. By considering both the solar radiations incident on the inclined surface and the temperature implications, it is possible to improve power production and decrease the expenses associated with PV energy systems and the cost of energy produced. Therefore, it is highly significant to conduct comprehensive research that examines the combined impact of TA and ambient temperature on optimizing the output power of photovoltaic arrays in different locations in Pakistan.
Methodology
Solar photovoltaic modules directly convert solar energy into electric energy. The quantity of power produced by a module is directly related to the amount of solar energy that reaches or strikes its surface. Therefore, it is crucial to comprehend the correlation between the position of the sun and the angle at which the PV module is tilted29. Various approaches to optimizing the tilt angle (TA) of photovoltaic modules have been suggested in28,29, such as manual and automatic sun-tracking techniques that utilize different mathematical models. In the proposed research a concise description of a mathematical model used to optimize the TA of PV modules has been presented.
Mathematical model of solar angles
Photovoltaic arrays mounted on tracking systems follow the trajectory of the sun. However, fixed systems need to be kept at a specific angle relative to the horizontal plane to maximize the utilization of sunlight at the given position. Accurate estimation of the slope angle increases both the amount of sunlight received (radiations) and the amount of energy generated. The solar constant \({G}_{SC}\) refers to the amount of solar energy received per unit time and per unit area, which is derived from the SR released by the sun. The World Radiation Centre has established a solar constant value of 1367 W/m268.
The declination angle formed between the earth’s equator and a line drawn from the center of the earth toward the center of the sun . The main reason for the variation in solar declination is the rotation of the Earth on an axis. The declination angle varies within the range of −23.45 degrees to + 23.45 degrees, as shown in Fig. 1. The equation of Cooper (1) can be used to determine the fluctuation of the declination angle throughout the year69.
The number “n” represents the specific (nth) day in the calendar year i.e. when n = 1, it corresponds to the 1st of January. During equinox days (Mar 20 and Sep 23), the declination angle is zero as the incident light is parallel to the equator. Furthermore, the declination angle has a value of + 23.45° at the summer solstice and −23.45° during the winter solstice.
Incidence angle refers to the angle formed between the solar radiations and the perpendicular line to the surface at the specific point where the radiations strike. The incidence angle that occurs on the flat horizontal plane is calculated by using Eq. (2)70.
where \(\omega\) represents the hour angle and \(\varnothing\) represents the latitude of the site. For an inclined surface in the northern hemisphere oriented towards the south (as Pakistan is located in the northern hemisphere), Eq. (2) can be rewritten as Eq. (3).
where \(\beta\) represents the angle of inclination between the horizontal plane and the surface where the radiation is being captured.
Solar hour angle is the angular distance between the sun’s position at solar noon and local solar time. This angle is precisely 0° at the solar noon. The earth completes a full rotation of 360° in one day, which means it rotates at a rate of 15° per hour (360° divided by 24 h equals 15°). The hour angle is expressed by using Eq. (4) and is derived from Atlantic Standard-Time (AST). A positive value indicates afternoon-hours, whereas a negative value indicates morning-hours70.
Azimuth angle \({\gamma }_{S}\) is the angle formed by the projection of the radiation on a flat horizontal surface. The azimuth angle has been determined by using Eq. (5). The given equation is utilized to compute the azimuth angle, which depends upon the solar hour angle, declination angle, and zenith angle (\({\theta }_{zen}\))70,71.
Solar zenith angle \({\theta }_{zen}\) is the angle formed between the sun and the vertical plane. The zenith angle resembles the altitude angle; however, it is measured with respect to the vertical instead of the horizontal plane. The calculation for the zenith angle is described by Eq. (6)71.
Solar altitude angle (SAA) is a key indicator used to determine the optimum inclination of a PV module. The SAA provides a visual representation of the sun’s height at any given time. To determine the solar altitude angle, it is necessary to compute both the declination angle and the hour angle. Solar altitude angle can be calculated using the Eq. (7 & 8) which establishes a relationship between the solar altitude and zenith angles72.
The sunrise and sunset angles for the northern hemisphere have been calculated using Eq. (6) when the zenith-angle on the horizontal plane is zero \({\theta }_{zen}\) = 0. The sunset hour angle \({\omega }_{sunset}\) is computed using Eq. (9)65.
The following Eq. (10) is used to calculate the sunset time \({t}_{sunset}\)65.
The sunset and sunrise times of an inclined surface may be shorter than those for the same events on a flat horizontal plane. For the surface that faces south, the \({t}_{sunset.south}\) can be calculated using Eq. (11)65.
Mathematical model of solar radiation
The solar radiation model comprises a collection of mathematical equations for total solar radiation on sloped surfaces. The surface area of the SR for photovoltaic modules involves calculations of integrated modeling, dynamic solar inclination on surfaces with varying orientations, TAs, and diverse geographical locations with diverse foreground surfaces. Factors like the geographical ___location, solar time model, time data, and solar geometry model determine the total solar radiation. Total solar radiation that strikes on the inclined surface is the combination of three types of SR: direct-beam radiation (\({H}_{B}\)), diffuse radiation (\({H}_{D}\)), and ground reflected radiation (\({H}_{R}\)) as shown in Fig. 2. Total SR are calculated by using Eq. (12)73.
Approximately, direct-beam radiation consists of the largest proportion of total radiation, whereas diffuse radiation represents the second largest proportion. Typically, the percentage of ground-reflected radiation is fairly minimal, except for places surrounded by extremely reflecting surfaces. The Eq. (12) could have been rewritten as Eq. (13).
\({H}_{g}\) defines the monthly averaged daily solar radiation that is incident on a global horizontal plane. The value of \({H}_{d}\) can be determined using the equation (\({\overline{H} }_{B}/{\overline{H} }_{o}\)) that relates to the monthly fraction of diffuse radiation. The parameters \({R}_{b}\) and \({R}_{d}\) represent the ratio of the mean daily beam as well as diffuse radiations on an inclined surface, respectively. \({R}_{b}\) is determined by the Eq. (14)73.
The Eq. (14) has been modified using the incidence angle Eq. (3) and zenith angle Eq. (6) for the surface inclined towards the equator in the northern hemisphere region, described in Eq. (15).
Isotropic and anisotropic models are used to describe the models that have been used to calculate the ratio of diffused solar radiations \({R}_{d}\) on an inclined surface compared to that on a horizontal surface. The hourly sky-diffuse solar radiation incident on an inclined surface is determined by multiplying the hourly diffuse solar radiation incident on a flat horizontal surface by the surface-sky configuration factor. Numerous anisotropic and isotropic models can be utilized to describe \({R}_{d}\). The isotropic model presented by Liu and Jordan is represented by Eq. (16)74,75.
The isotropic model proposed by Badescu is represented by Eq. (17)74,75.
Hay and Davies (HD) introduced an anisotropic indicator which is determined by the transmittance of the atmosphere for beam radiation and the anisotropic index is denoted as \({H}_{B}\)/\({H}_{o}\). HD model calculates the proportion of the diffuse component, which typically refers to the sunlight scattered by the atmosphere, and assumes that it is in the same direction as direct beam radiations. The expression for HD is represented by Eq. (18), where \({H}_{o}\)represents the daily average mean extraterrestrial radiations74,75.
Reindel et al. improved the HD model by incorporating a horizontal-brightening component, denoted as \(f= \sqrt{{H}_{B}/{H}_{g}}\)as recommended by Klucher. The model had been considered as a combination of HD, Klucher, and Reindel models referred to as the HDKR model. HDKR model was formulated using SR equations for, reflected beam and diffuse radiation terminologies, such as isotropic, circumsolar, and horizontal-brightening. The anisotropic model known as HDKR, which is a modified version of the HD model, is expressed by Eq. (19)74,75.
Extraterrestrial radiation refers to the hypothetical quantity of SR that would reach the Earth’s surface without atmospheric attenuation. The alteration in extraterrestrial radiation is attributed to fluctuations in SR and variations in the earth’s distance from the sun. The incident solar radiations \({I}_{o}\) on a flat horizontal plane outside the earth’s atmosphere, arising between sunrise and sunset is calculated by dividing the normal incident SR by the average daily beam (\({R}_{b}\)). Extraterrestrial radiation at the top of the earth’s atmosphere can be determined using Eq. (20)72,75.
\(D\) indicates the calendar day in a year ranges from 1 to 365, while \({G}_{SC}\) refers to the solar constant. \({H}_{o}\) indicates the horizontal extraterrestrial radiations expressed in joule per square meter per day and can be calculated by Eq. (21).
Liu and Jordan determined the monthly average clearness index \({K}_{t}\), which is calculated as the ratio of monthly average daily total radiations on the horizontal surface \(H\) to the monthly averaged daily extraterrestrial radiations \({H}_{o}\). The \({K}_{t}\) fluctuates with global irradiance, indicating the variation in meteorological conditions across different areas. Therefore, the \({K}_{t}\) can be considered an atmospheric characteristic that reduces the radiation intensity and is represented by the Eq. (22)76.
The monthly average percentage of the diffuse component has been estimated using the correlations established in Eq. (23) and Eq. (24).
PV array output power
The power output of a PV array is determined as the product of current and voltage. This output is influenced by factors such as the amount of SR striking a tilted or inclined surface, specific features of the photovoltaic module, and ambient temperature.
Temperature model of PV cell
The operational temperature of the PV module is estimated by the energy balance equation. A certain amount of solar energy absorbed by the PV module is transformed into thermal energy, while the rest is converted into electrical energy. The module’s temperature is expected to peak at midday while the temperature in the evening is expected to be equivalent to the ambient temperature. The present research study aims to determine the PV module/cell temperature by considering factors such as electricity conversion efficiency, ambient temperature, fluctuations in irradiance, and heat dissipation to the environment. The calculation is derived by utilizing the energy balance Eq. (25) to the specific area of the PV module that cools as a result of environmental losses76.
where \(\tau\) represents the solar transmittance of PV modules, \(\alpha\) represents the solar absorbing capacity of PV modules, and \({\eta }_{c}\) represents the efficiency of the module in transforming incident radiations into electric energy. Depending on how close the PV module is to the maximum power point (MPP) at which it is operating, the efficiency of the module can range from 0 to the maximum module efficiency. Convection and radiation losses from the top and bottom surfaces, as well as conduction through the related mounting system, are all taken into account by the loss coefficient \({U}_{l}\) in relation to the ambient temperature \({T}_{amb}\). If the PV cells have not been installed under the same conditions as when they were tested, the nominal operating cell temperature (NOCT) condition may have a significant impact on their performance. The data of cell temperature, ambient temperature, and solar radiation under NOCT circumstances can all be incorporated into Eq. (25) and rewritten as Eq. (26)77.
By adding the established values for NOCT (800 W/m2 incident radiations, AM 1.5G, wind speed 1 m/s) in the above equation and considering the efficiency changes linearly with cell temperature, expressed as Eq. (27).
where \(\alpha\) represents the solar absorbing capacity of PV modules (α = 90%) and \(\tau\) represents the solar transmittance of PV modules (τ = 90%). \({T}_{amb.NOCT}\) refers to the surrounding ambient air temperature at NOCT of 20℃. \({T}_{Cell.STC}\) represents the PV module’s temperature in standard test conditions (STC) which is 25℃. \({T}_{cell.NOCT}\) refers nominal operating temperature range spans from 45℃ to 48℃ and \({G}_{T.NOCT}\) refers to the solar irradiances level of 800W/m2 as specified by NOCT. \({G}_{T}\) refers to global solar irradiations on the tilted surface of the PV module, \({\alpha }_{\rho }\) represents the temperature coefficient of the power (–0.350%/℃ to –0.29%/℃) and \({\eta }_{mp.STC}\) represents the efficiency at the MPP (22.45%).
Power output model of PV module
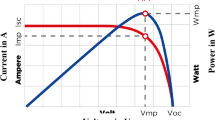
A PV cell can be represented by a simplified model known as a single-diode model. This model consists of a current source and a diode connected in parallel. The I-V and P–V curves of the photovoltaic cell demonstrate the non-linear correlation due to variations in cell temperature and radiations intensities. In this research study, a single-diode method has been utilized for assessing the I-V curves due to its simplicity and high level of accuracy. Eq. (28) accurately represents the I-V curve of a single diode cell under constant solar radiations and temperature78..
\({I}_{ph}\) represents the current produced at incident light, \({I}_{o}\) represents the reverse saturation current, \({N}_{series}\) represents series-connected solar cells per module, \(k\) represents the Boltzmann constant (1.381 × 10–23 J/K) and \(e\) represents the charge of an electron (1.6022 × 10–19C). \({R}_{P}\) and \({R}_{S}\) denotes a parallel resistor and series resistor respectively. \({I}_{ph}\) and \({I}_{Ph.n}\) are both influenced by the SR and temperature. This relationship can be mathematically explained using the Eq. (29)78.
The variable \({I}_{Ph.n}\) represents the current produced by the light under nominal conditions. \({G}_{T.STC}\) indicates the radiations at STC, whereas \({G}_{T}\) refers to global solar radiations on the tilted surface of the PV module. \({T}_{n}\) and \(T\) represents nominal and actual temperatures (kelvin), whereas \({k}_{i}\) is a coefficient for short circuit current. The output power is defined as the multiplication of voltage and current and is represented by Eq. (30).
The output of the PV module has been determined by utilizing parameters included in the datasheets issued by the manufacturers. The parameters normally include the number of the PV cells, maximum power \({P}_{max},\) maximum power voltage \({V}_{mp}\), open-circuit voltage \({V}_{oc}\), maximum power current \({I}_{mp}\), short-circuit current \({I}_{sc}\), efficiency at STC (%), the operating temperature ℃, temperature coefficients for \({P}_{max}\), \({I}_{sc}\), and \({V}_{oc}\) and power tolerance. These parameters are provided in accordance with STC, as demonstrated in Table 1. Eq. (31) represents the general I-V relationship at maximum power as shown below78.
The MATLAB tool has been used for the simulations in the proposed research to determine the optimum power produced by a PV array installed at an OTA for any specified ___location. Figure 3 presents a flow chart that summarizes the fundamental steps needed to calculate the optimum output power of a PV array. The initial step includes finding the latitude, calculating the ambient temperature \({T}_{amb}\), monthly global horizontal irradiance \({H}_{g}\) and monthly diffuse horizontal irradiance \({H}_{d}\) of the desired ___location. After selecting a ___location, declination angle \(\delta\), incidence angle \(\theta\), and sunset hour angle \({\omega }_{sunset}\) have been determined. Following that, the extraterrestrial radiation \({H}_{o}\) and clearness index \({K}_{t}\) has been calculated for each of the 365 days in a year. The range of slope values \(\beta\) from 0 to 90° is computed using the above-specified parameters.
A decision block evaluates if the sunset hour angle meets the specified criteria or not (\({\omega }_{sunset}\le 81.4\)). The monthly diffuse fraction is determined based on this condition and by utilizing Eqs. (23) and (24). In order to determine the OTA, the total solar radiation HT that strikes the module surface for different tilt angles \(\beta\) throughout the calendar year has been calculated. The OTA for every single day is determined by calculating/ measuring the slope values that maximize the total solar radiation. The tilt angle that maximizes the average total radiation is referred to as the average monthly optimal tilt angle (\({\beta }_{m.opt}\)) and annual optimal tilt angle (\({\beta }_{a.opt}\)). The monthly averages for twelve months have been used to estimate the HT and the OTA.
The PV system consists of five strings, with each string consisting of 18 modules in series. This configuration results in a rated peak power of 52.200 kWp. The power output of the PV array is determined for both the monthly OTA and the annual OTA until the array’s optimum output is achieved. Finally, the energy generation and losses of PV systems for a single ___location have been analyzed.
Results and discussion
A MATLAB-based mathematical model has been developed to optimize incident solar radiations by determining the OTA. This leads to the generation of maximum power by the photovoltaic array. The monthly average daily solar radiation data, including global and diffuse horizontal irradiance (GHI and DHI), ambient air temperature, linke turbidity factor, wind speed, latitude and longitude, and relative humidity have been obtained from the meteonorm database29. The data obtained from the meteonorm database assisted in the estimation of many factors related to total solar radiations HT on a tilted surface, direct-beam radiation \({H}_{B}\), diffuse radiation \({H}_{D}\), ground-reflected radiation \({H}_{R}\), and the OTA for every single day of the year. The initial case study examined the city of Faisalabad, where the monthly average daily direct-beam, diffuse, and ground-reflected radiations have been evaluated using two isotropic and two anisotropic models. The most precise model has been selected as a framework for a subsequent case study, aiming to conduct a thorough comparison of six different locations in Pakistan.
Optimal tilt angle and power for single ___location
This section presents a case study to estimate the maximum power generation of a photovoltaic array in Faisalabad, a city situated in the center of the largest province of Pakistan. The meteorological station situated on the campus of GC University Faisalabad at coordinates 31.4161° N, 73.0700° E. Table 2 presents the monthly irradiances data (GHI and DHI), ambient air temperature, wind speed, linke turbidity factor, and relative humidity for the proposed ___location. Table 2 indicates that the SR level reaches its peak during the summer season, particularly in the months from May–July. The proposed ___location has an annual average GHI of 1558.4 kWh/m2/month and a DHI of 902.2 kWh/m2/month. The maximum monthly GHI is 181.9 kWh/m2 for May and DHI is 106.7 kWh/m2 for June. Table 2 also shows that the ambient air temperature increases during the summer season and declines during the winter season. The monthly average ambient temperature is 24.4 °C. The proposed ___location has usually moderate winds, with annual average wind speeds of 1.4 m/s. Relative humidity levels are consistently high throughout the winter months and low during the summer season, with an increase during the monsoon season. The monsoon season spans from July to September with humidity levels ranging from 71% to 73.5%. The data analysis suggests that there is a substantial and reliable availability of solar energy that is captured by a PV system.
Table 3 demonstrates the average monthly daily global and diffuse horizontal irradiance (Hg and Hd respectively), ambient air temperature \({T}_{amb}\), and annual and monthly OTA determined for the proposed ___location (Faisalabad) using four mathematical models (two isotropic as well as two anisotropic). The monthly average daily SR for Faisalabad as shown in Fig. 4 varies between 2.18 and 5.89 kWh/m2 throughout the year. The maximum Hg is recorded for June. However, the models used in this research provide a more accurate estimation of total solar radiations HT on tilted or inclined surfaces compared to total solar radiations on flat horizontal surfaces. This can be seen in Fig. 4 and Table 3.
During the summer season, it is determined that all four selected models present similar findings in terms of the monthly average daily solar radiations on the tilted surface. During the winter season, the anisotropic models (HD and HDKR) performed better than the isotropic models (LJ, Badescu models) as shown in Fig. 4. In January, the Liu and Jordan (LJ) model anticipated a monthly average total solar radiations of 2.70 kWh/m2, however, the HDKR model estimated 3.17 kWh/m2, resulting in a 14.82% increase compared to isotropic-model. In June, the LJ model anticipated a monthly average total solar radiations of 5.91 kWh/m2, however the HDKR model estimated 5.92 kWh/m2, resulting in a 0.16% increase compared to the isotropic model. Similarly in November, the LJ model anticipated a monthly average total SR of 2.90 kWh/m2, however the HDKR model estimated 3.33 kWh/m2, resulting in a 12.91% increase compared to the isotropic model. The isotropic diffuse models by Badescu estimated the lowest annual average total SR at 4.43 kWh/m2/day. This is followed by Liu and Jordan’s models at 4.51 kWh/m2/day. On the other hand, the anisotropic models indicated higher annual HT values of the HD model 4.75 kWh/m2/day, and the HDKR model 4.77 kWh/m2/day, resulting in energy gains. The inclusion of the horizontal brightening and circumsolar components into the isotropic-diffuse model accounts for this phenomenon. The impact of these components is particularly noticeable on global SR during the winter season when the atmosphere is cloudy. In clear summer weather situations, assuming that the diffused component of SR is scattered. Anisotropic models provided identical results to the isotropic model. The highest temperature is measured in May and June at 32.8 °C, while the lowest temperature is measured in January at 12.2 °C. The annual average ambient air temperature is 24.4 °C as shown in Table 3.
The monthly OTAs, which are derived from using isotropic as well as anisotropic models, indicate that the total solar radiations reaches its maximum in May–June and it is lowest in December-January. The OTA varies from 4° (June) to 54° (December) as indicated in Table 3 and Fig. 5. Anisotropic models generated a slightly higher OTA in comparison to isotropic models. The monthly OTA for the LJ model ranges from 5° to 44°, ranges from 4° to 36° for the Badescu model, ranges from 7° to 52° for the HD model, and ranges from 7° to 54° for HDKR model as shown in Fig. 5. The HDKR, HD, LJ, and Badescu models generated annual OTAs of 30.5°, 29.25°, 23.75°, and 18.08°, respectively. In addition, the isotropic models estimated an annual OTA that is significantly lower than the latitude of Faisalabad, whereas the anisotropic model estimated a slightly lower TA than the latitude.
After conducting a comparative assessment of four models, the HDKR anisotropic model was selected for further investigation. Although isotropic models are simplistic and provide conservative estimates, numerous experimental and theoretical research have indicated that HDKR-generated findings are more closely aligned with experiment data. The estimated radiation results and OTA for Faisalabad city, calculated with the HDKR anisotropic model, are presented in Figs. 6 and 7. The bar graph (Fig. 6) displays the average monthly daily direct-beam radiations \({H}_{B}\), diffuse radiation \({H}_{D}\), and ground-reflected radiation \({H}_{R}\). The direct-beam component is the main component in determining the total solar radiations HT strikes on the tilted surface. Figure 7 demonstrates that to maximize the amount of available energy, OTA during the summer season might be lower in comparison with the latitude of the proposed ___location, whereas during the winter it might be higher. In addition, the annual calculated TA for the Faisalabad city is 30.5°, which is lower than the latitude of the city.
The relationship between the PV cell temperature and its ambient temperature for each month is described in Fig. 8 and Table 4. The highest calculated temperature of the photovoltaic cell is 39.982 °C in June, with an ambient temperature of 32.8 °C. The lowest calculated temperature of PV cell is 14.943 °C in January, with an ambient temperature of 12.2 °C. The average annual PV cell temperature is calculated to be 29.61 °C, indicating a 17.56% rise in temperature relative to the average annual ambient temperature.
The present research study also investigated the power produced by the proposed PV system that consisted of ninety (PV) modules (580W monocrystalline bifacial). The average power production of the installed PV system at the monthly OTA and annual OTA is indicated in Table 4 and Fig. 9. The PV system generates its highest power output during the summer season and has a decline in power output during the winter season. The maximum power production of 37.1334 kW has been achieved in June with a monthly tilt angle, marking the highest level reached during the year. The maximum power production of 35.2031 kW has been achieved with Annual TA. When comparing the percentage gain in power production between monthly and annual tilt angles, in May, the power output reached its highest level at the monthly OTA, resulting in a 29.21% increase in power compared to the annual OTA. Despite the fact that the radiation is at its highest level in June (5.89 kWh/m2/day), the PV cell temperature is also at (39.982 °C) during that month. Therefore, June produced the most amount of PV power compared to any other month.
The difference between the monthly OTA and annual OTA in September and March is low. The power output in September is approximately equivalent, with minor difference in OTA, whereas in March, there is a variation of 23.67%. Despite the nearly similar OTA (monthly OTA of 33° and annual OTA of 30.5°), a significant difference in power output has been observed for March, due to several technological and geographical factors, including declination and incidence angle sensitivity. The declination angle in March fluctuates substantially as the sun approaches the equinox. Additional factors include the influence of direct and diffuse SR, variations of solar altitude angle, temperature coefficients, and atmospheric impacts, as well as daytime duration and distribution of SR. The high sensitivity of PV module efficiency to small alterations in OTA during March is the result of the relationship among the dynamic ranges of declination angle, enhanced diffuse SR, fluctuation in climatic conditions, and solar elevation. The OTA is nearly the same, but these parameters correlate non-linearly with the OTA, which causes a substantial difference in power output. The stable atmospheric and solar conditions in September significantly reduce climate sensitivity, leading to a much lower output power difference. Table 4 shows that the annual average output power of the PV system installed at a monthly OTA is 26.19 kW and the annual average output power of the PV system installed at an annual OTA is 23.63 kW. Based on the research investigation, the optimal monthly tilt angle of the PV system increased output power by 9.77% when compared to the annual OTA.
Optimal tilt angle and power for multiple locations
This section aims to examine how climatic conditions, such as temperature, SR, and latitude impact the OTA of PV modules in various locations across Pakistan, as well as the associated maximum output power. Six locations are selected that represent a range of climate conditions in the central, eastern, western, southern, and northern areas of the country. Pakistan occupies an extensive land area and comprises regions with diverse climatic conditions, including variations in ambient temperature and humidity. For instance, Faisalabad and Lahore represent hot and humid climates, Islamabad demonstrates comparatively low temperatures, while Multan and RYK have hot and dry weather. The geographical coordinates of the locations under the proposed research in Pakistan are as follows:
-
1.
Location 1 (Faisalabad 31.4161° N, 73.0700° E)
-
2.
Location 2 (Lahore 31.4790° N, 74.2662° E)
-
3.
Location 3 (Multan 30.2606° N, 71.5071° E)
-
4.
Location 4 (Rahim Yar Khan (RYK) 28.3808° N, 70.3744° E)
-
5.
Location 5 (Islamabad 33.6995° N, 73.0363° E)
-
6.
Location 6 (Karachi 24.9389° N, 67.1237° E)
The monthly fluctuations in the average monthly daily GHI, \({T}_{amb}\), and PV cell temperatures for the different research locations are presented in Table 5. The average monthly daily total solar radiations on the flat horizontal plane is shown in Fig. 10. Table 5 and Fig. 10 demonstrate that among all the locations examined, Karachi city received the highest average monthly daily GHI during the month of April-June, reaching up to 6.71 kWh/m2/day in May. Conversely, Karachi has the most modest GHI during the winter season, with a value of 3.84 kWh/m2/day. Faisalabad, Multan, and Islamabad have the highest average monthly daily GHI in June. The values for Faisalabad, Multan, and Islamabad are 5.89 kWh/m2/day, 5.96 kWh/m2/day, and 6.22 kWh/m2/day, respectively. Lahore, RYK, and Karachi have the highest average monthly daily GHI in May. The values are 5.68 kWh/m2/day, 6.49 kWh/m2/day, and 6.71 kWh/m2/day, respectively. The cities of RYK, Multan, Lahore, Faisalabad, Islamabad, and Karachi experienced their highest average monthly ambient temperatures in June, with measured values of 34.6 °C, 34.1 °C, 33.3 °C, 32.8 °C, 31.7 °C and 31.6 °C respectively. The PV cell temperature variation in relation to the ambient temperature for the six locations under research is presented in Fig. 11. In the hottest month of June, RYK experienced the highest PV cell temperature of 42.343 °C, leading to a reduction in maximum power efficiency. However, Islamabad has the lowest photovoltaic cell temperature among all the locations. The measured PV cell temperature for the cities of RYK, Multan, Lahore, Faisalabad, Islamabad, and Karachi are 42.343 °C, 41.367 °C, 40.226 °C, 39.982 °C, 39.284 °C and 39.481 °C respectively.
Table 6 presents the power production of the PV array using both the monthly and annual OTA. Figure 12 shows the monthly TAs of the researched locations in Pakistan. The OTA for Faisalabad city ranges from 7° to 54°, for Lahore city it ranges from 7° to 53°, for Multan city it ranges from 6° to 52°, for RYK city it ranges from 5° to 52°, for Islamabad city it ranges from 10° to 58° and for Karachi it ranges from 1° to 50° as shown in Fig. 12. The annual OTA for Faisalabad, Lahore, Multan, RYK, Islamabad, and Karachi has been calculated to be 30.5°, 30.25°, 29.33°, 28.66°, 33.34° and 25.5° respectively. Figure 13 exhibits the output production of the PV array achieved by utilizing the monthly OTA for the locations under research. In Faisalabad, the highest power generated by the PV array is 37.13 kW, 35.55 kW for Lahore, 37.39 kW for Multan, 40.52 kW for RYK, 39.2 kW for Islamabad, and in Karachi it is 42.58 kW. These maximum power outputs for four locations were measured in June. However, in RYK and Karachi, the highest output power is obtained in May. The annual average output power generated by the PV array installed at monthly OTA in Karachi, RYK, Multan, Faisalabad, Islamabad, and Lahore is 31.01 kW, 29.56 kW, 26.59 KW, 26.19 kW, 26.12 kW, and 25.42 kW respectively. The annual average PV array output power at monthly OTA in Karachi is 15.74% higher than that of Islamabad. Specifically, Karachi produces 31.01 kW while Islamabad produces 26.12 kW. The primary factor behind this is that Karachi experiences a higher annual average solar radiations, measuring at 5.19 kWh/m2/day, whilst Islamabad has a lower solar radiations of 4.30 kWh/m2/day.
The annual average output power at the monthly OTA results in gains of 8.83%, 9.40%, 9.78%, 9.77%, 9.82%, and 9.91% compared to the annual OTA. A monthly OTA generates more output power relative to the annual OTA, which makes it a technically as well as financially viable option. Even though adjustments made monthly generally require additional labor as well as installation efforts, recent advancements in adjustable technology have mitigated particular expenses. Especially considering the typical 20–25-year lifespan of a PV system installation, this upfront energy expenditure, and operational efforts are negligible in comparison to the substantial excess power the system produces over time. The enhanced power generation translates into a higher ROI as it shortens the payback period and enhances power-generating efficiency.
Energy generation and losses of PV system for single ___location
The PV system that has been installed for Faisalabad city with monthly OTA generates an annual energy output of 76.17 MWh. The specific energy yield, which is the amount of energy produced per unit of installed capacity, is 1,407.2 kWh/kWp. The performance ratio (PR), which measures the efficiency of the system, is 83.3%. PV system that has been installed with annual OTA generates an annual energy output of 73.18 MWh. The specific energy yield is 1,401.9 kWh/kWp, whereas PR is 81.7%. Figure 14 presents the monthly energy generation (kWh) of the PV system that has been installed with monthly and annual OTA.
The results have indicated that the PV system achieves peak energy generation from April to August while experiencing a decline in energy generation from November to February. The PV system installed with monthly and annual OTA generates a maximum energy of 7,951.7 kWh and 7,401.2 kWh in May respectively, while in January, it generates a minimum energy of 4,349.3 kWh and 4,195.5 kWh respectively. The annual energy generation of PV systems with nameplate capacity installed at monthly OTA, measured under STC, is 86,463.40, as shown in Table 7. PV system generates an output of 85,944.6 kWh at the total-collector radiation level (with 0.5% losses). After accounting for PV cell temperature losses of 6.0% and mismatch losses of 3.8%, the output has been decreased to 80,787.9 kWh and 77,717.9 kWh, respectively. The optimal DC output of the PV system is 77,484.7 kWh. The annual energy generated by the PV system after inverter losses (1.2%) is 76,554.68 kWh, whereas the total energy supplied into the national utility grid is 76,171.9 kWh. For the annual OTA, the annual energy generation of the PV system with nameplate capacity is 83,300.5 kWh. After accounting for temperature losses of 6.0% and mismatch losses of 4.1%, the output has decreased to 77,904.9 kWh and 74,674.3 kWh, respectively. After inverter losses (1.2%) the output energy is 73,545.3 kWh, whereas the total energy supplied into the national utility grid is 73,177.6 kWh.
The performance efficiency and output energy are significantly influenced by losses in a PV system. For the PV system installed at monthly OTA, irradiation losses attributed to shading are 0.9%, irradiations losses due to the reflection are 3.2%, irradiations losses as a result of soiling are 2.0%, and module low irradiations energy losses are 0.5%. The PV module also incurs energy losses of 6.0% due to temperature, losses due to mismatch are 3.8%, and DC wiring I2R losses are 0.3%. The clipping losses in the system are negligible at 0.0%, and losses due to inverters efficiency are 1.2%. The AC system losses due to AC transformers and conductors are 0.5% as shown in Fig. 15. For the PV system installed at annual OTA, shading causes losses of 2.2%, losses due to reflection amount to 2.9%, soiling leads to losses of 2.0%, while the PV module experiences low irradiation energy losses of 0.5%. The PV module also incurs energy losses of 6.0% due to temperature, energy losses of 4.1% due to mismatch, and DC wiring I2R losses account for 0.3%. The clipping losses are negligible at 0.0%, and inverter efficiency results in energy losses of 1.2%. Lastly, AC system losses due to AC transformers and conductors are 0.5% as shown in Fig. 16.
Conclusion
This research study is proposed to determine the monthly and annual OTA to optimize power output from a PV array, considering GHI, DHI, ambient air temperature, and total solar radiation (HT) for multiple locations in Pakistan. A MATLAB-based mathematical model has been developed to maximize incident solar radiations, determine the OTA, and assess its impact on the power output capacity for 6 cities located in different temperature zones in Pakistan. The initial case study analyzed monthly radiations in Faisalabad using two isotropic and two anisotropic models. During the summer season, all four selected models present similar findings in terms of the monthly average daily solar radiations on the tilted surface. During the winter season, the anisotropic models (HD and HDKR) performed better than the isotropic models (LJ, Badescu models). After conducting a comparative assessment of four models, the HDKR anisotropic model was selected for further investigation.
Utilizing the selected model, an analysis has been conducted for six locations. The measured PV cell temperature for the cities of RYK, Multan, Lahore, Faisalabad, Islamabad, and Karachi are 42.343 °C, 41.367 °C, 40.226 °C, 39.982 °C, 39.284 °C and 39.481 °C respectively. The monthly OTA for Faisalabad city ranges from 7° to 54°, for Lahore city it ranges from 7° to 53°, for Multan city it ranges from 6° to 52°, for RYK city it ranges from 5° to 52°, for Islamabad city it ranges from 10° to 58° and for Karachi it ranges from 1° to 50°. The annual OTA has been calculated to be 30.5°, 30.25°, 29.33°, 28.66°, 33.34° and 25.5° respectively. The annual average output power generated by the PV array installed at monthly OTA in Karachi, RYK, Multan, Faisalabad, Islamabad, and Lahore is 31.01 kW, 29.56 kW, 26.59 KW, 26.19 kW, 26.12 kW, and 25.42 kW respectively. The annual average output power at the monthly OTA results in gains of 8.83%, 9.40%, 9.78%, 9.77%, 9.82%, and 9.91% compared to the annual OTA. The PV system that has been installed for Faisalabad city with monthly OTA generates an annual energy output of 76.17 MWh. The specific energy yield is 1,407.2 kWh/kWp and the PR is 83.3%. At annual OTA, the annual energy output is 73.18 MWh, the specific energy yield is 1,401.9 kWh/kWp, whereas PR is 81.7%.
This research study introduces an innovative way of predicting the output power of a PV system, which leads to a comprehensive and improved forecasting model by incorporating OTA and ambient temperature. Previous research studies primarily focused on solar radiation, however, this research identifies temperature as another crucial factor that affects PV performance. Although the solar radiation patterns are similar in the two cities, Lahore and Multan, inconsistencies in power generation occur due to temperature fluctuations. Future research studies have to broaden this research and incorporate economic assessments, particularly regarding the impact of OTA on the levelized cost of energy (LCOE). Minimizing LCOE is crucial for improving the economic viability of PV systems through the optimization of energy capture and efficiency. Additional research investigating the impact of automated tilt adjustment systems on reducing LCOE and optimized operating expenses (OPEX) is recommended. Research methodology is further optimized by analyzing the significance and interaction of shading, dust deposition, and other environmental variables, which could result in a more accurate evaluation of power output and related system costs.
Data availability
Data generated or analysed during this study is provided within the manuscript.
References
Habib, S. et al. Modeling, simulation, and experimental analysis of a photovoltaic and biogas hybrid renewable energy system for electrification of rural community. Energy Technol. 11(10), 2300474 (2023).
Saleem, S. et al. Power factor improvement and MPPT of the grid-connected solar photovoltaic system using nonlinear integral backstepping controller. Arabian J. Sci. Eng. 48(5), 6453–6470 (2023).
Tamoor, M. et al. Optimal sizing and technical assessment of a hybrid renewable energy solution for off-grid community center power. Front. Energy Res. 11, 1283586 (2023).
Wang, S., Tarroja, B., Schell, L. S., Shaffer, B. & Samuelsen, S. Prioritizing among the end uses of excess renewable energy for cost-effective greenhouse gas emission reductions. Appl. Energy 235, 284–298 (2019).
Al-Ismail, F. S., Alam, M. S., Shafiullah, M., Hossain, M. I. & Rahman, S. M. Impacts of renewable energy generation on greenhouse gas emissions in Saudi Arabia: A comprehensive review. Sustainability 15(6), 5069 (2023).
Algarni, S., Tirth, V., Alqahtani, T., Alshehery, S. & Kshirsagar, P. Contribution of renewable energy sources to the environmental impacts and economic benefits for sustainable development. Sustain. Energy Technol. Assess. 56, 103098 (2023).
Zhao, J., Dong, K. & Dong, X. How does energy poverty eradication affect global carbon neutrality?. Renew. Sustain. Energy Rev. 191, 114104 (2024).
Gerarden, T. D. Demanding innovation: The impact of consumer subsidies on solar panel production costs. Manag. Sci. 69(12), 7799–7820 (2023).
Islam, M. R., Aziz, M. T., Alauddin, M., Kader, Z. & Islam, M. R. Site suitability assessment for solar power plants in Bangladesh: A GIS-based analytical hierarchy process (AHP) and multi-criteria decision analysis (MCDA) approach. Renew. Energy 220, 119595 (2024).
Fazal, M. A. & Rubaiee, S. Progress of PV cell technology: Feasibility of building materials, cost, performance, and stability. Solar Energy 258, 203–219 (2023).
Shen, L., Li, Z. & Ma, T. Analysis of the power loss and quantification of the energy distribution in PV module. Appl. Energy 260, 114333 (2020).
Seapan, M., Hishikawa, Y., Yoshita, M. & Okajima, K. Temperature and irradiance dependences of the current and voltage at maximum power of crystalline silicon PV devices. Solar Energy 204, 459–465 (2020).
Chintapalli, N., Sharma, M. K. & Bhattacharya, J. Linking spectral, thermal and weather effects to predict ___location-specific deviation from the rated power of a PV panel. Solar Energy 208, 115–123 (2020).
Winston, D. P., Kumaravel, S., Kumar, B. P. & Devakirubakaran, S. Performance improvement of solar PV array topologies during various partial shading conditions. Solar Energy 196, 228–242 (2020).
El Iysaouy, L. et al. Performance enhancements and modelling of photovoltaic panel configurations during partial shading conditions. Energy Systems https://doi.org/10.1007/s12667-023-00627-7 (2023).
Clement, C. E., Singh, J. P., Birgersson, E., Wang, Y. & Khoo, Y. S. Hotspot development and shading response of shingled PV modules. Solar Energy 207, 729–735 (2020).
Ghosh, S., Singh, S. K. & Yadav, V. K. Experimental investigation of hotspot phenomenon in PV arrays under mismatch conditions. Solar Energy 253, 219–230 (2023).
Lappalainen, K. & Valkealahti, S. Number of maximum power points in photovoltaic arrays during partial shading events by clouds. Renew. Energy 152, 812–822 (2020).
Tubniyom, C., Jaideaw, W., Chatthaworn, R., Suksri, A. & Wongwuttanasatian, T. Effect of partial shading patterns and degrees of shading on Total Cross-Tied (TCT) photovoltaic array configuration. Energy Procedia 153, 35–41 (2018).
Satpathy, P. R. & Sharma, R. Parametric indicators for partial shading and fault prediction in photovoltaic arrays with various interconnection topologies. Energy Convers. Manag. 219, 113018 (2020).
Da Rocha, M. V., Sampaio, L. P. & da Silva, S. A. O. Comparative analysis of MPPT algorithms based on Bat algorithm for PV systems under partial shading condition. Sustain. Energy Technol. Assess. 40, 100761 (2020).
Kumar, M., Panda, K. P., Rosas-Caro, J. C., Valderrabano-Gonzalez, A. & Panda, G. Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems. IEEE Access. 11, 31778–31812 (2023).
Srinivasarao, P., Peddakapu, K., Mohamed, M. R., Deepika, K. K. & Sudhakar, K. Simulation and experimental design of adaptive-based maximum power point tracking methods for photovoltaic systems. Comput. Electr. Eng. 89, 106910 (2021).
Mohamed-Kazim, H. A., Abdel-Qader, I. & Harb, A. M. Efficient maximum power point tracking based on reweighted zero-attracting variable stepsize for grid interfaced photovoltaic systems. Comput. Electr. Eng. 85, 106672 (2020).
Chao, K. H. & Bau, T. T. T. Global maximum power point tracking of photovoltaic module arrays based on an improved intelligent bat algorithm. Electronics 13(7), 1207 (2024).
Sridhar, R., Subramani, C. & Pathy, S. A grasshopper optimization algorithm aided maximum power point tracking for partially shaded photovoltaic systems. Comput. Electr. Eng. 92, 107124 (2021).
Osmani, K., Haddad, A., Lemenand, T., Castanier, B. & Ramadan, M. An investigation on maximum power extraction algorithms from PV systems with corresponding DC-DC converters. Energy 224, 120092 (2021).
Zhu, Y., Liu, J. & Yang, X. Design and performance analysis of a solar tracking system with a novel single-axis tracking structure to maximize energy collection. Appl. Energy 264, 114647 (2020).
Tamoor, M. et al. Designing and energy estimation of photovoltaic energy generation system and prediction of plant performance with the variation of tilt angle and interrow spacing. Sustainability 14(2), 627 (2022).
Govindasamy, D. & Kumar, A. Experimental analysis of solar panel efficiency improvement with composite phase change materials. Renew. Energy 212, 175–184 (2023).
Al-Ghussain, L., Taylan, O., Abujubbeh, M. & Hassan, M. A. Optimizing the orientation of solar photovoltaic systems considering the effects of irradiation and cell temperature models with dust accumulation. Solar Energy 249, 67–80 (2023).
Yassir, A., Zamzami, U., Fauzan, K., & Hasannuddin, T. (2019). Optimization of tilt angle for photovoltaic: Case study Sabang-Indonesia. In IOP Conference Series: Materials Science and Engineering (Vol. 536, No. 1, p. 012055). IOP Publishing.
Beringer, S., Schilke, H., Lohse, I. & Seckmeyer, G. Case study showing that the tilt angle of photovoltaic plants is nearly irrelevant. Solar Energy 85(3), 470–476 (2011).
Mukisa, N. & Zamora, R. Optimal tilt angle for solar photovoltaic modules on pitched rooftops: A case of low latitude equatorial region. Sustain. Energy Technol. Assess. 50, 101821 (2022).
Agrawal, M., Chhajed, P. & Chowdhury, A. Performance analysis of photovoltaic module with reflector: Optimizing orientation with different tilt scenarios. Renew. Energy 186, 10–25 (2022).
Osmani, K., Ramadan, M., Lemenand, T., Castanier, B. & Haddad, A. Optimization of PV array tilt angle for minimum levelized cost of energy. Comput. Electr. Eng. 96, 107474 (2021).
Liu, Y. et al. Spatial estimation of the optimum PV tilt angles in China by incorporating ground with satellite data. Renew. Energy 189, 1249–1258 (2022).
Nassar, Y. F., El-Khozondar, H. J., Abouhmod, N. M., Abubaker, A. A., Ahmed, A. A., Alsharif, A., Khaleel, M. M., Elnaggar, M., & El-Khozondar, R. J. (2023, May). Regression model for optimum solar collectors’ tilt angles in Libya. In 2023 8th International Engineering Conference on Renewable Energy & Sustainability (ieCRES) (pp. 1–6). IEEE.
Karinka, S. & Upadhyaya, V. Concept of annual solar window and simple calculation for optimal monthly tilt angle to maximize solar power generation. Mater. Today: Proceed. 52, 2166–2171 (2022).
Abdallah, R., Juaidi, A., Salameh, T., Jeguirim, M., Çamur, H., Kassem, Y., & Abdala, S. (2022). Estimation of solar irradiation and optimum tilt angles for south-facing surfaces in the United Arab Emirates: A case study using PVGIS and PVWatts. In Recent advances in renewable energy technologies (pp. 3–39). Academic Press.
Xu, L., Long, E., Wei, J., Cheng, Z. & Zheng, H. A new approach to determine the optimum tilt angle and orientation of solar collectors in mountainous areas with high altitude. Energy 237, 121507 (2021).
Al-Shohani, W. A., Khaleel, A. J., Dakkama, H. J. & Ahmed, A. Q. Optimum tilt angle of the photovoltaic modules in Baghdad, Iraq. Appl. Solar Energy 58(4), 517–525 (2022).
Sarr, A., Kebe, C. M. & Ndiaye, A. Determination of the optimum tilt angle for photovoltaic modules in Senegal. African J. Environ. Sci. Technol. 15(6), 214–222 (2021).
Al-Sayyab, A. K. S., Al Tmari, Z. Y. & Taher, M. K. Theoretical and experimental investigation of photovoltaic cell performance, with optimum tilted angle: Basra city case study. Case Stud. Thermal Eng. 14, 100421 (2019).
Kecili, I., Nebbali, R. & Ait Saada, S. Optimal tilt angle of a solar panel for a wide range of latitudes. Comparison between tilted and horizontal configurations. Int. J. Amb. Energy 43(1), 8697–8709 (2022).
Abed, F., & Al-Salami, Q. H. (2021). Calculate the best slope angle of photovoltaic panels theoretically in all cities in Turkey. International Journal of Environmental Science and Technology, 1–16.
Yadav, S., Hachem-Vermette, C., Panda, S. K., Tiwari, G. N. & Mohapatra, S. S. Determination of optimum tilt and azimuth angle of BiSPVT system along with its performance due to shadow of adjacent buildings. Solar Energy 215, 206–219 (2021).
Awasthi, A. et al. Solar collector tilt angle optimization for solar power plant setup-able sites at Western Himalaya and correlation formulation. J. Thermal Anal. Calor. 147(20), 11417–11431 (2022).
Sharma, A. et al. Correlation formulation for optimum tilt angle for maximizing the solar radiation on solar collector in the Western Himalayan region. Case Stud. Thermal Eng. 26, 101185 (2021).
Elmalky, A. M. & Araji, M. T. A new trigonometric model for solar radiation and shading factor: Varying profiles of building façades and urban eccentricities. Energy Build. 282, 112803 (2023).
Hassan, Q., Abbas, M. K., Abdulateef, A. M., Abdulateef, J. & Mohamad, A. Assessment the potential solar energy with the models for optimum tilt angles of maximum solar irradiance for Iraq. Case Stud. Chem. Environ. Eng. 4, 100140 (2021).
Jacobson, M. Z. & Jadhav, V. World estimates of PV optimal tilt angles and ratios of sunlight incident upon tilted and tracked PV panels relative to horizontal panels. Solar Energy 169, 55–66 (2018).
Dabbousa, T. A., Al-Reqeb, I., Mansour, S., & Zainuri, M. A. A. M. (2021, March). The Effect of Tilting a PV Array by Monthly or Seasonal Optimal Tilt Angles on Energy Yield of a Solar PV System. In 2021 International Conference on Electric Power Engineering–Palestine (ICEPE-P) (pp. 1–5). IEEE.
Abdallah, R., Juaidi, A., Abdel-Fattah, S. & Manzano-Agugliaro, F. Estimating the optimum tilt angles for south-facing surfaces in Palestine. Energies 13(3), 623 (2020).
Habib, S., Tamoor, M., Zaka, M. A. & Jia, Y. Assessment and optimization of carport structures for photovoltaic systems: a path to sustainable energy development. Energy Convers. Manag. 295, 117617 (2023).
Arias-Rosales, A. & LeDuc, P. R. Urban solar harvesting: The importance of diffuse shadows in complex environments. Renew. Sustain. Energy Rev. 175, 113155 (2023).
Sun, B., Lu, L., Yuan, Y. & Ocłoń, P. Development and validation of a concise and anisotropic irradiance model for bifacial photovoltaic modules. Renew. Energy 209, 442–452 (2023).
Kaddoura, T. O., Ramli, M. A. & Al-Turki, Y. A. On the estimation of the optimum tilt angle of PV panel in Saudi Arabia. Renew. Sustain. Energy Rev. 65, 626–634 (2016).
Hafez, A. Z., Soliman, A., El-Metwally, K. A. & Ismail, I. M. Tilt and azimuth angles in solar energy applications–A review. Renew. Sustain. Energy Rev. 77, 147–168 (2017).
Yu, Y., Tang, Y., Chou, J. & Yang, L. A novel adaptive approach for improvement in the estimation of hourly diffuse solar radiation: A case study of China. Energy Convers. Manag. 293, 117455 (2023).
Khatib, T., Mohamed, A., Mahmoud, M. & Sopian, K. Optimization of the tilt angle of solar panels for Malaysia. Energy Sources, Part A: Recovery, Utiliz. Environ. Effects 37(6), 606–613 (2015).
Kellegöz, M. Optimization of solar panel tilt angles using isotropic and anisotropic models at sun-belt boundary regions. Meteorol. Atmos. Phys. 135(4), 38 (2023).
Hailu, G. & Fung, A. S. Optimum tilt angle and orientation of photovoltaic thermal system for application in greater Toronto area, Canada. Sustainability 11(22), 6443 (2019).
Yadav, P. & Chandel, S. S. Comparative analysis of diffused solar radiation models for optimum tilt angle determination for Indian locations. Appl. Solar Energy 50, 53–59 (2014).
Heibati, S., Maref, W. & Saber, H. H. Developing a model for predicting optimum daily tilt angle of a PV solar system at different geometric, physical and dynamic parameters. Adv. Build. Energy Res. 15(2), 179–198 (2021).
Glick, A., Ali, N., Bossuyt, J., Calaf, M. & Cal, R. B. Utility-scale solar PV performance enhancements through system-level modifications. Sci. Rep. 10(1), 10505 (2020).
Tamoor, M. et al. Investigation of dust pollutants and the impact of suspended particulate matter on the performance of photovoltaic systems. Front. Energy Res. 10, 1017293 (2022).
Mehleri, E. D., Zervas, P. L., Sarimveis, H., Palyvos, J. A. & Markatos, N. C. Determination of the optimal tilt angle and orientation for solar photovoltaic arrays. Renew. Energy 35(11), 2468–2475 (2010).
Razzaq, M. E. A., & Hasanuzzaman, M. (2022). Solar thermal power plant. In Technologies for Solar Thermal Energy (pp. 151–213).
Mahmoud, M., Olabi, A. G., Radwan, A., Yousef, B. A., & Abdelkareem, M. A. (2023). Case studies and analysis of solar thermal energy systems. In Renewable Energy-Volume 1: Solar, Wind, and Hydropower (pp. 75–92). Academic Press.
Božiková, M. et al. The effect of azimuth and tilt angle changes on the energy balance of photovoltaic system installed in the Southern Slovakia region. Appl. Sci. 11(19), 8998 (2021).
Behar, O., Khellaf, A. & Mohammedi, K. Comparison of solar radiation models and their validation under Algerian climate–The case of direct irradiance. Energy Convers. Manag. 98, 236–251 (2015).
Khalil, S. A. A comprehensive study of solar energy components by using various models on horizontal and inclined surfaces for different climate zones. Energy Power Eng. 14(10), 558–593 (2022).
Arias-Rosales, A. & LeDuc, P. R. Comparing view factor modeling frameworks for the estimation of incident solar energy. Appl. Energy 277, 115510 (2020).
Khan, M. S., Ramli, M. A., Sindi, H. F., Hidayat, T. & Bouchekara, H. R. Estimation of solar radiation on a PV panel surface with an optimal tilt angle using electric charged particles optimization. Electronics 11(13), 2056 (2022).
Apeh, O. O., Overen, O. K. & Meyer, E. L. Monthly, seasonal and yearly assessments of global solar radiation, clearness index and diffuse fractions in alice, South Africa. Sustainability 13(4), 2135 (2021).
HOMER. How HOMER Calculates the PV Cell Temperature. Available online: Available: https://homerenergy.com/products/pro/docs/latest/howhomer_calculates_the_ pv_cell_temperature.html. (accessed on 12 February 2024).
Abderrahim, T., Abdelwahed, T. & Radouane, M. Improved strategy of an MPPT based on the sliding mode control for a PV system. Int. J. Electr. Comput. Eng. (IJECE) 10(3), 3074–3085 (2020).
Funding
The authors declare no funding available to support this research work.
Author information
Authors and Affiliations
Contributions
All authors have contributed and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interest regarding this paper’s publication.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Tamoor, M., Bhatti, A.R., Farhan, M. et al. Optimizing tilt angle of PV modules for different locations using isotropic and anisotropic models to maximize power output. Sci Rep 14, 30197 (2024). https://doi.org/10.1038/s41598-024-81826-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-81826-9