Introduction

Heart disease remains one of the leading causes of death worldwide1. It imposes a significant burden on the healthcare systems and society as a whole. According to the World Health Organization (WHO), an estimated 17.9 million people died from cardiovascular disease in 2019, accounting for 32% of all global deaths. Despite advances in medical research and treatment options, the incidence of heart disease continues to rise, particularly in regions with aging populations and rapid socioeconomic development2. The management of heart disease, especially coronary artery diseases such as acute coronary syndromes (ACS), unstable angina, and myocardial infarctions (both non-ST-segment elevation[NSTEMI] and ST-segment elevation [STEMI]), requires substantial medical resources. These conditions necessitate immediate thrombolysis and percutaneous coronary intervention, underscoring the critical need for timely and accurate diagnosis to reduce patient mortality risks3. Additionally, heart failure exacerbations (HFE), which can result from infections or increased cardiac load, are a significant concern, with a three-year occurrence rate of 28.2%4.

In clinical practice, cardiac angiography is regarded as the gold standard for diagnosing coronary artery disease. However, its high cost and resource intensity restrict its widespread use in primary care settings. For critically ill patients, there is an urgent need for a diagnostic approach that is stable, reliable, cost-effective, rapid, and highly sensitivity to minimize the risk of missed diagnoses. Such an approach would significantly enhance patient outcomes by facilitating timely interventions.

In recent decades, there has been a paradigm shift in preventive medicine strategies, emphasizing early detection and intervention to mitigate the effects of heart disease5. A promising avenue in this regard is the application of Artificial Intelligence (AI) and Machine Learning (ML) techniques to enhance the accuracy and efficiency of heart disease prediction and diagnosis. Previously, various techniques in data mining and neural networks have been employed to determine the severity of human heart disease6. Predictive models for ACS can assist physicians in quickly identify high-risk patients and implementing timely treatment measures. Several studies have developed models that integrate multiple parameters and biomarkers7.

Machine learning algorithms have shown great potential for analyzing complex medical data and identifying patterns that may not be readily apparent to humans. By utilizing various forms of patient information, including demographic factors, medical history, lifestyle choices, and diagnostic test results, in particular, characteristics such as gender, age, heart rate, and systolic blood pressure have been identified as predictors of cardiac arrest8, High-sensitivity troponin and blood glucose levels can effectively predict the occurrence of cardiac arrest (CA)7. While there are various features, the authoritative datasets for this analysis are the UCI datasets and Kaggle datasets, and the performance of the algorithms will be tested on these two datasets.

There is a substantial body of related work in areas directly pertinent to this paper. Neural networks have been introduced to generate highly accurate predictions in the medical field9,10. G.S. Reddy Thummala et al. employed Random Forest to select features for heart disease prediction11; however, their focus was primarily on demonstrating the statistical significance of the Random Forest algorithm in logistic regression, and their analysis of the data concerning the features was insufficient. Venkatesh R, Anantharajan S et al. predicted heart disease using Multiple Gradient Boosting Adaptive Support Vector Machine (MBASVM) and Kernel-based Principal Component Analysis (K-PCA) and Cardinality Ranking Search provided some ideas for feature filtering12; but their experiments were conducted on only one dataset, making it challenging to validate the robustness of the algorithm. El-Shafiey et al. combined a hybrid Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) with Random Forest (RF)13. Sireesha Moturi et al. utilized a combination of the grey Wolf Optimization Algorithm and the Dragonfly Optimization Algorithm (GWU-DA) for feature selection14,15, as well as for optimizing weighting rules16. This provided us with ideas for reference through the combination of optimization algorithms. However, when they used Support Vector Machine (SVM) and Deep Belief Network (DBN) to build a hybrid classification model, they did not directly use the optimization algorithm to optimize the weights of the neural network. Ahmad combined Jellyfish Optimization Algorithm with SVMs to obtain a highly accurate model17, but this approach still belongs to the traditional machine learning field, although RF and SVMs excel in many problems, Back Propagation (BP) can learn complex nonlinear patterns and features in certain cases (especially small samples), and the model efficacy and robustness are more competitive than those of RF algorithms. Sanjay and Shashidhar et al. used deep two-dimensional convolutional neural networks (CNNs) to predict electrocardiogram (ECG) data18. Jillella and Rohith applied CNNs to heart rate monitoring of ECG data, demonstrating that the current deep learning methods are booming and that are already techniques that can be applied in the field of medical diagnosis and monitoring19. R.Das et al. used the back propagation multilayer perception (MLP) of neural networks to predict heart disease. They compared the obtained results with existing models in the same field and found improvements20, but achieved only 89.01% accuracy in the Cleveland Heart Disease Database. Manomita Chakraborty used convolutional neural network to extract prediction rules for heart disease21, but achieved an accuracy of only 85.19%.W. Zhang et al. used CNN for heart sound classification22. In those works, we found that utilizing ML and Deep Learning (DL) techniques is a viable approach for the prediction and classification of heart disease. However, based on the above research, while ML holds the promise of enhancing heart disease prediction, several gaps that must be addressed to fully realize its potential. These gaps include:

  1. (1)

    Low accuracy and robustness: Despite previous efforts to develop predictive models for heart disease, some methods may still struggle to achieve a satisfactory level of accuracy. This may be due to a variety of factors such as inadequate data representation, model complexity, or fitting limitations of the algorithmic techniques used. In addition, many models are not robust enough to handle predictions from multiple datasets

  2. (2)

    Sensitivity to Initial Weights in Neural Networks: In current perceptron-based classifiers, there is a fatal flaw in that the convergence time and convergence accuracy of the algorithm are highly sensitive to the initial weight configuration. How to overcome the initial weight selection problem to ensure the stability of the algorithm is of great significance to the implementation of expert systems in industry.

  3. (3)

    Inadequate feature selection: Some existing heart disease prediction methods may not adequately address the feature selection problem, resulting in suboptimal performance. In addition, experiments conducted to evaluate these methods may lack rigor and thoroughness, which may overlook important factors and hinder progress in the field.

Given these challenges, this study aims to address the limitations of existing ML-based heart disease prediction methods by proposing an innovative framework that integrates advanced optimization algorithms with neural networks, one-hot encoding, principal component analysis (PCA) to enhance the model’s ability to capture data features and improve data smoothness. Specifically, this paper introduces the EPSOSA-BP algorithm, which combines the particle Swarm Optimization (PSO) algorithm, the Simulated Annealing (SA) algorithm, and the BP neural network. This study uses two datasets for comprehensive validation, training the neural network with the data extracted after feature reduction and continuously optimizing the weights to enhance the accuracy. Experiments results demonstrate that our model achieves high accuracy. According to our proposed structure, this paper is organized as follows: In “Overview of theory” section, the proposed method and related techniques, including BPNN, PSO and SA, are introduced. In “Preliminaries” section, the experimental preparation and algorithm process are briefly described, and the processing architecture chart, model training process diagram, and flow chart of the EPSOSA algorithm are constructed. The algorithm solution steps and pseudocode are also presented. In “Experiment andresult analysis” section, the results of the experiments are presented, including the comparison experiment, ablation experiment, algorithm convergence experiment, and a comparison of the experimental results. Finally, in “Conclusion” section, the conclusions of the paper are summarized.

Overview of theory

In this chapter, the algorithm architecture designed in this paper will be systematically described from the perspective of the three components of optimization algorithm, classifier and data processing, as follows:

BPNN

The Backpropagation Neural Network (BPNN) is an artificial neural network model based on gradient descent optimization algorithm, it consists of an input layer, multiple hidden layers, and an output layer, and its training process mainly utilizes the backpropagation algorithm to adjust the network parameters in order to minimize the error23. Currently, MLP has been widely used in pattern recognition and classification tasks24,25. It not only has a strong linear fitting ability, but also can realize nonlinear fitting through the activation function. The workflow of the MLP is shown in Fig. 1:

Fig. 1
figure 1

Diagram of the BP neural network model.

Full size image

In the neural network shown in Fig. 1, \(V = (v_{11} ,v_{12} ,...,v_{nm} )\) represents the connection weight from the input layer to the hidden layer, \(W = (w_{11} ,w_{12} ,...,w_{mh} )\) represents the connection weight from the hidden layer to the output layer. The mathematical formulas of the activation function, hidden layer output, output layer output and the loss function can be expressed by Eqs. (1–4) :

Activation function:

$$f = \frac{1}{{1 + e^{ - x} }}$$
(1)

Hidden layer:

$$u_{i} = f\left(\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {x_{i} v_{ij} } } + \beta \right)$$
(2)

Output layer:

$$y_{i} = f\left(\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{h} {u_{i} w_{ij} } } + \lambda \right)$$
(3)

loss function:

$$Loss = \frac{1}{2}\sum\limits_{i} {(Y_{i} - y_{i} )^{2} }$$
(4)

where \(Y\) is the expected output and \(y\) is the actual output. Now need to update \(w,v,\beta ,\lambda\) to Update \(\lambda\). First, assume that \(\lambda\) is \(\lambda ^{\prime}\) after updating,then \(\lambda ^{\prime} = \lambda + \Delta \lambda\), and it only need to solve for \(\Delta \lambda\) to find \(\lambda ^{\prime}\) ,The update formula for \(\Delta \lambda\) can be expressed by Eq. (5):

$$\Delta \lambda = - \eta \frac{\partial Loss}{{\partial \lambda }}$$
(5)

Similarly, the update formula of \(\Delta w,\Delta v,\Delta \beta\) can be expressed by Eqs. (6)–(8).

$$\Delta w = - \eta \frac{\partial Loss}{{\partial w}}$$
(6)
$$\Delta v = - \eta \frac{\partial Loss}{{\partial v}}$$
(7)
$$\Delta \beta = - \eta \frac{\partial Loss}{{\partial \beta }}$$
(8)

Particle swarm optimization (PSO)

Particle Swarm Optimization (PSO) is a population-based metaheuristic algorithm developed by Kennedy and Eberhart in 1995. In the optimization process of PSO, each particle adjusts the search direction and step size by using its own and neighboring particles’ historical information through individual communication and information sharing26,27. The whole population is guided to move in the direction where an optimal solution may exist28. This mechanism based on individual cooperation between particles is the unique advantage of PSO compared with other evolutionary algorithms29,30.

In this paper use \(V_{i} = (v_{1} ,v_{2} ,...v_{n} )\) and \(X_{i} = (x_{1} ,x_{2} ,...x_{n} )\) to denote the velocity and position of the particle, and the update of the velocity and position of the particle are shown by Eqs. (9) and (10), respectively.

$$v_{i + 1} = w*v_{i} + c_{1} *rand()*(pbest_{i} - x_{i} ) + c_{2} *rand()*(gbest_{i} - x_{i} )$$
(9)
$$x_{i + 1} = x_{i} + v_{i}$$
(10)

where \(w\) is the inertia weight, which represents the ability of the particle to maintain the current speed. An increased value of \(w\) correlates with a higher velocity of the particle, thereby enhancing the algorithm’s capacity for global exploration but concurrently diminishing its ability to converge locally. Conversely, a reduced \(w\) results in a decreased particle velocity, which in turn weakens the global search capability and strengthens the local convergence propensity. To optimize the global search performance of the particles, it is strategic to initialize \(w\) with a higher value. This approach allows the particles to traverse the search space more extensively, increasing the likelihood of discovering optimal solutions. As the optimization process progresses, however, it becomes necessary to decrement \(w\). This reduction refines the search scope of the particles, facilitating a more precise exploration of potential solutions and hastening the convergence towards an optimal solution. The variables \(p_{ij}\) and \(p_{{{\text{g}}j}}\) represent the optimal solution attained by an individual particle and the best solution discovered by the entire swarm, respectively. These values are crucial for guiding the search process within the particle swarm optimization (PSO) framework. The parameters \(c_{1}\) and \(c_{2}\) are indicative of the learning factors associated with the personal best and the global best solutions, respectively. They influence the particle’s ability to learn from its own historical best position and the best position found by its peers. The terms \(r_{1}\) and \(r_{2}\) are random coefficients uniformly distributed within the interval [0,1]. They introduce an element of randomness into the velocity update equation, which is essential for diversifying the search directions. This randomness ensures a more comprehensive exploration of the search space, thereby enhancing the algorithm’s ability to avoid local optima and promoting a robust search strategy.

At present, the linear decreasing weight strategy proposed by Shi has been widely used, and its expression can be shown in Eq. (11):

$$w = w_{max} - \frac{{(w_{max} - w_{min} )*iter}}{T}$$
(11)

here \(w_{max}\) represents the maximum inertia weight,\(w_{min}\) represents the minimum inertia weight, iter represents the number of iterations, and T represents the maximum number of iterations.

Simulated annealing algorithm (SA)

Simulated annealing algorithm (SA) is derived from the metal cooling process31. The simulated annealing algorithm consists of two parts: Metropolis calculation process and annealing process. The Metropolis criterion is a criterion that replaces the original solution with a new solution with a certain probability when the new solution is inferior to the original one32. In the simulated annealing algorithm, this probability is related to the current temperature and the energy difference between the two solutions. As the temperature decreases, the larger the energy difference, the lower the probability of accepting the new solution. At the same time, the process of high temperature annealing is a process of particle energy change, so that the simulated annealing algorithm can jump out of the local optimal solution33. It is calculated as follows:

Assuming that the previous solution is \(X(n)\), the system calculates a new solution \(X(n + 1)\) according to random disturbance, and the system energy changes from \(E(n)\) to \(E(n + 1)\), the acceptance probability P of the algorithm from \(X(n)\) to \(X(n + 1)\) can be expressed by Eq. (12) :

$$P = \left\{ {\begin{array}{*{20}l} 1 & {E(n + 1) < E(n)} \\ {\exp ( - \frac{E(n + 1) - E(n)}{T})} & {E(n + 1) > E(n)} \\ \end{array} } \right.$$
(12)

here, T is the temperature, let the temperature decay rate be \(\lambda\), then the update formula of T can be expressed by Eq. (13) :

$$T(n + 1) = \lambda {*}T(n)$$
(13)

Algorithm construction

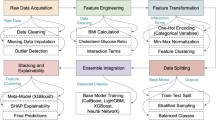
The objective of this paper is to combine the particle swarm optimization (PSO) algorithm and simulated annealing (SA) algorithm, utilizing the back propagation model after processing the data by using the solo thermal coding and principal component analysis, making full use of the advantages of the two algorithms and introducing the particle elimination mechanism, which assists the BP neural network to obtain the optimal network parameters. The processing architecture chart of this paper is schematically shown as Fig. 2:

Fig. 2
figure 2

Processing architecture chart of this paper.

Full size image

In order to find the optimal weight and bias values in the BP neural network, the particle swarm optimization algorithm is used to update the velocity and position of the particles. Subsequently the simulated annealing algorithm is applied to adjust the current position based on Metropolis criterion, allowing the system to escape potential local optimal and explore the global extreme. Finally, an elimination strategy is implemented to enhance the diversity of the population by replacing certain particles with new ones. By combining particle swarm optimization, simulated annealing and elimination strategy, a balance between global exploration and local search can be achieved when updating the weights and bias values of BP neural network, thereby optimizing its performance and generalization capability. The entire process of optimizing the neural network is illustrated in Fig. 3, while the algorithm flowchart of the Enhanced Particle Swarm Optimization with Simulated Annealing (EPSOSA) is presented in Fig. 4.

Fig. 3
figure 3

Model training process diagram.

Full size image
Fig. 4
figure 4

Flow chart of the EPSOSA algorithm.

Full size image

The training process of the entire neural network presented in this paper is illustrated in Fig. 3. this paper employ the backpropagation method to jointly train the parameters using a combination of the particle swarm optimization algorithm and the simulated annealing process, along with an elimination mechanism to enhance the particle swarm. This approach aims to effectively search for and resolve the optimal solution to complex problems.

The flow of EPSOSA optimization algorithm is illustrated in Fig. 4, the dotted line represents the logical data flow, while the solid lines indicate the specific data flow. If the elimination mechanism is completed and the termination condition of the PSO is not met, the particle parameters will be updated through simulated annealing and particle movement until optimal convergence is achieved. The algorithm steps are as follows:

Step1 Initialize the position \(x\) and velocity \(v\) of the particle swarm, where each particle represents a set of parameters of the neural network.

Step2 According to the particle swarm update Eqs. (9) and (10), update the velocity and position of the particle, the individual extreme value and the optimal value;

Step3 Initialize the SA algorithm, and judge whether the new solution is generated according to the Metropolis criterion.

Step4 According to the elimination rules, the particles with poor position are removed and new particles are generated.

Step5 Judge whether the termination condition is satisfied, if it is satisfied, then enter the seventh step, not satisfied, then return to the third step;

Step6 Output the optimal solution as the parameters of the neural network.

The pseudocode of the EPSOSA algorithm is shown in Table 1.

Preliminaries

Experimental dataset

The heart disease data sets used in this paper are from UCI and Kaggle databases respectively. The data set of UCI is Cleveland Dataset, which contains 76 attributes and a total of 303 data. The Kaggle dataset contains Cleveland, Hungary, Switzerland, and the VA Long Beach with a total of 1024 data. This paper focus on selecting some representative features. The experimental data set in this paper contains 13 feature columns and 1 label column. They are age, sex, cp, trestbps, chol, fbs, restecg, thalach, exang, oldpeak, slope, ca, thal and target. Data set of links to: https://www.kaggle.com/datasets/johnsmith88/heart-disease-dataset. The details of the dataset are shown in Table 2.

Table 1 EPSOSA optimization algorithm.
Full size table

Data preprocessing

Before the experimental verification, the heart disease data must be preprocessed. As shown in Table 2, the seven features: sex, cp, fbs, restecg, exang, slope and thal are categorical variables, which are not suitable for direct input into machine learning models. Proper preprocessing is necessary to transform these variables into a format that can be effectively processed by machine learning algorithms. Commonly used methods include one-hot encoding, label encoding, category embedding, target encoding, etc. In this paper, one-hot encoding is used to create new binary feature columns for these seven categorical features. Each feature column represents a category and is represented by 1, and the others are represented by 0.

After using one-hot encoding to process the data features, the features of the data were expanded, from the original 13 features to 32 features. Pearson coefficient is an important index for data screening, which can be expressed by Eq. (14).

$$\rho = \frac{Cov(X,Y)}{{\sigma_{X} \sigma_{Y} }}$$
(14)

In order to show the one-hot encoded data in detail, so as to determine whether there is a need for subsequent dimensionality reduction, this paper conducted Pearson heat map correlation analysis on UCI data and Kaggle data. The one-hot encoded Pearson heat maps can be shown in Figs. 5 and 6, respectively.

Fig. 5
figure 5

Pearson heat map after UCI data augmentation.

Full size image
Fig. 6
figure 6

Pearson heat map after Kaggle data augmentation.

Full size image

According to the formula and heat map, the small grid in the image represents the mathematical representation of the association relationship between features or labels at the horizontal and vertical coordinates. It is easy to find that when the small grid on the graph is red (Pearson coefficient is between 0 and 1), the features or labels at the two positions are correlated to a certain extent, and the data on the red grid is larger, indicating a higher degree of relevance. When the small grid is blue, it indicates that a pair of features or labels are negatively correlated. The bluer the grid, the more discrete the effect34. As shown at Fig. 5, it is believed that this situation is caused by the small number of UCI datasets and the limited ability to mine association relationships. From Fig. 6, it is found that after the one-hot encoding extension data, there are many connected color blocks with the value of 1, indicating that these features are the same feature encoded from the one-hot encoding. There will be some repeatability in the feature learning; therefore, it is necessary to further reduce the feature dimension of the expanded data.

In this paper, Principal Component Analysis (PCA) method is used to reduce the dimension of the data after one-hot encoding. For the n-dimensional sample set \(D = (x^{1} ,x^{1} ,...,x^{n} )\), all samples are first centered, which can be expressed by Eq. (15):

$$x^{i} = x^{i} - \frac{1}{m}\sum\limits_{j = 1}^{m} {x^{j} }$$
(15)

Then \(z^{i}\) is used to recover the original data \(x^{i}\), which can be expressed by Eq. (16):

$$\overline{x}^{i} = \sum\limits_{j = 1}^{n^{\prime}} {z_{j}^{i} w_{j} = Wz^{i} } ,n^{\prime} \le n$$
(16)

where W is the orthonormal basis matrix, in order to make all samples close enough to the hyperplane, that is, to minimize \(\sum\nolimits_{i = 1}^{m} {\left\| {\overline{x}^{i} - x^{i} } \right\|}_{2}^{2}\), when \(z^{i} = W^{T} x^{i}\), it can reduce the dimensionality of the data set n to the n′-dimensional data set with the minimum projection distance.

Unsupervised learning is our primary tool for situations where can’t predict what actions or classifications will lead to. As an unsupervised learning method, PCA has unparalleled advantages in abstract problems and can deal with dimensionality reduction problems in abstract data.

This paper performed PCA on the Cleveland data from UCI database and the multi-source data from Kaggle. Transformed the 32 features of the former data into 9 dimensions, and the features of the latter data into 13 dimensions, realizing the screening of high-dimensional and complex data. The specific projection scatter plot and cumulative variance contribution rate plot under the most important principal components of the first two dimensions after dimensionality reduction are as follows:

Figure 7 shows the projection of the data according to principal component 1 and principal component 2. Through the process of PCA, the spatial scatter points originally scattered on each plane are gathered into a two-dimensional space for representation. After dimensionality reduction, it can be observed that the points in the two-dimensional space are densely clustered, indicating that most of the variance in the original data has been captured by the principal components. The dimensionality reduction process is well preserved to a certain extent, reducing the noise and disturbance of the original features, simplifying the data structure, and improving the training efficiency.

Fig. 7
figure 7

Scatter plot after performing PCA on both data.

Full size image

Figure 8 illustrates the proportion of the total variance of the original data explained by each principal component (PC, or called factor) in principal component analysis (PCA)35,36. In PCA, principal components are ordered by the amount of variance they explain, with the first component (PC1) explaining the largest variance in the data, the second component (PC2) explaining the next largest variance, and so on.

Fig. 8
figure 8

Plot of cumulative variance contribution rate.

Full size image

In order to reduce the interference of complex variables on the model, this paper uses the max–min normalization method37, which will adjust the reference value of the model to between 0 and 1. The normalization formula can be expressed by Eq. (17):

$$x^{*} = \frac{{x - x_{\min } }}{{x_{\max } - x_{\min } }}$$
(17)

Evaluating indicator

In this paper, the Receiver operating characteristic curve (ROC curve), Area under the AUC value (AUC value) are used curve, Accuracy, Precision, Sensitivity(Recall), Specificity, F1 score and confusion matrix are used to measure the performance of the proposed model. The prediction of heart disease is a binary classification problem, where "1" and "0" denote the two predictions, where "1" indicates the presence of heart disease and "0" indicates the absence of heart disease. If the sample is Positive and the prediction is positive, the prediction result is True Positive (TP); if the prediction is Negative, it is False Negative (FN); If the sample is Negative and the prediction is negative, the prediction is True Negative (TN); if the prediction is Positive, it is False Positive (FP). Where TP and TN represent the number of correct predictions, FP and FN represent the number of incorrect predictions. According to TP, TN, FP and FN, the evaluation index Accuracy, Precision, Sensitivity, Specificity, FPR, FNR and F1 values can be expressed by Eq. (18–24) :

$$Accuracy = \frac{TP + TN}{{TP + FP + TN + FN}}$$
(18)
$$\Pr ecision = \frac{TP}{{TP + FP}}$$
(19)
$$Sensitivity = {\text{Re}} call = \frac{TP}{{TP + FN}}$$
(20)
$$Specificity = \frac{TN}{{TN + FP}}$$
(21)
$$FalsePositiveRate(FPR) = \frac{FP}{{FP + TN}}$$
(22)
$$FalseNegativeRate(FNR) = \frac{FN}{{FN + TP}}$$
(23)
$$F1 = \frac{{2*\Pr ecision*{\text{Re}} call}}{{\Pr ecision + {\text{Re}} call}}$$
(24)

ROC curve In the medical field, it is often used as a tool to validate disease prediction models. In the ROC curve, the abscissa is the False Positive Rate (FPR), and the ordinate is the True Posivite Rate (TPR). The higher the TPR, the better the model accuracy. Therefore, the more convex the ROC curve, the stronger the model performance. The AUC value can be represented by the area enclosed by the abscissa and the ROC curve, and the AUC value is usually between 0.5 and 1, the higher the AUC value, the better the prediction performance of the model.

In addition to model accuracy, sensitivity and specificity are also important ways to evaluate expert decision-making systems. In general, a model with high sensitivity means its ability to identify diseases is stronger, which can reduce the risk of missed diagnosis. High specificity means that the model can better distinguish healthy individuals and reduce the risk of misdiagnosis. FPR and FNR are the probability of false detection and missed detection, the lower the better, indicating the higher clinical application value.

Experiment and result analysis

Algorithm verification

In order to verify the reliability of the prediction model in this paper, this paper selected the commonly used logic Regression(LR), eXtreme Gradient Boosting(XGboost), Random Forest (RF), Support Vector Machine (SVM), K nearest neighbor (KNN), and PSO-BP classification algorithm were compared and verified. The above algorithms are simulated on the same data set, and the generated results are compared with the prediction results of the improved PSOSA-BP neural network classification model proposed in this paper. The experimental results on UCI datasets and Kaggle datasets are shown in Tables 3 and 4, and the ROC curves of each algorithm and the confusion matrix of the proposed algorithm are shown in Figs. 9 and 10.

Table 2 Data set characteristic properties.
Full size table
Table 3 Performance comparison of each algorithm on UCI.
Full size table
Fig. 9
figure 9

ROC curves of each algorithm on UCI and confusion matrix of the proposed algorithm.

Full size image
Fig. 10
figure 10

ROC curves of each algorithm on Kaggle and confusion matrix of our algorithm.

Full size image

It can be seen from the data in Table 3 that the performance of the proposed PSOSA-BP heart disease prediction model on the Kaggle data set is not only in terms of accuracy, but also in terms of precision, sensitivity, specificity, FPR, FNR, and F1 value. It is better than the basic RF model, SVM model, KNN model, XGboost model and the unoptimized PSO-BP model, especially in terms of accuracy. It is generally about 10 percentage points higher than other algorithms.

From the ROC curve in Fig. 9, on the UCI dataset, the optimized PSOSA-BP heart disease prediction model is superior to other algorithms in terms of both the image and the area under the AUC curve.

It can be seen from the data in Table 4 that the performance of the PSOSA-BP heart disease prediction model proposed in this paper on the Kaggle data set is not only in terms of accuracy, but also in terms of precision, Sensitivity, Specificity, FPR, FNR and F1 value, which are better than other model. However, because the Kaggle data set is more than two times larger than the UCI data set, other algorithms are easier to learn the characteristics of the data and make the correct prediction than UCI in terms of accuracy, and the difference is further reduced. Therefore, comparing the parameter tables of the two datasets, our PSOSA-BP algorithm has a unique bright performance on small-scale datasets. And the advantage of its specificity is also better than other algorithms on small datasets.

From the ROC curve of Fig. 10, on the Kaggle dataset, the optimized PSOSA-BP heart disease prediction model is superior to other algorithms both on the image and in the area under the AUC curve. However, compared with the UCI data set, the difference is further reduced, which was mentioned in the previous analysis of this paper, and the author believes that it is affected by the size of the data.

In addition, according to our trial chart, there are several additional phenomena: (1) The LR model has strong accuracy and specificity, but its accuracy and sensitivity are low, indicating that the model does a good job in identifying negative samples, almost never misjudge negative samples as positive samples, and has a good ability to resist misdiagnosis and identify healthy people, but it is not enough for the identification of patients, especially in small samples, this defect is more amplified. Inadequate to the clinical needs of the disease. (2) By comparing the experimental results of XGboost, it can be concluded that the performance of XGboost, a typical tree model used to deal with Tabular data, is better in the case of large amount of data, while the performance of EPSOSA proposed by us will not change too much and has good robustness, which will have more outstanding performance in this scenario.

Ablation experiment

In addition, to enhance the scientific rigor and interpretability of the experiment, ablation experiments were conducted on the data preprocessing steps described in this paper. The dataset prior to one-hot coding and PCA dimensionality reduction was compared with the two experimental datasets post one-hot coding and PCA dimensionality reduction, with the corresponding results detailed as follows,

As can be known from Fig. 11 and Table 5, there is a certain gap between the data running before and after preprocessing of the UCI dataset by our EPSO-SA algorithm. Obviously, the accuracy of the results after one-hot encoding and PCA dimension reduction is higher than that of the data before processing, which is increased from 86.44 to 93.22, and the precision, recall and F1 value, sensitivity and specificity are higher than those before processing, especially sensitivity increase of more than 10 percent. In the ROC curve, the area under the curve (AUC) value and curve shape after processing according to our data processing method are also better than those before data processing.

Fig. 11
figure 11

ROC curve and confusion matrix before and after processing of UCI dataset.

Full size image
Table 4 Performance comparison of each algorithm on Kaggle.
Full size table

As shown in Fig. 12 and Table 6, the results of our EPSO-SA algorithm on Kaggle dataset after preprocessing are also better than before preprocessing. After one-hot encoding and PCA dimensionality reduction, the accuracy of the results is improved from 93.00 to 95.52 compared with the data accuracy before processing, and the precision rate, recall rate, F1 value, sensitivity and specificity, are all improved to different degrees. In the ROC curve, our curve shape and area under the curve (AUC) value are also better.

Fig. 12
figure 12

ROC curve and confusion matrix before and after processing of Kaggle dataset.

Full size image
Table 5 Performance before and after processing on UCI datasets.
Full size table

Convergence experiment of algorithm

In order to verify the convergence efficiency of EPSOSA algorithm proposed in this paper, Dung beetle optimization algorithm, particle swarm optimization algorithm, grey Wolf optimization algorithm and sparrow optimization algorithm are selected for comparison, and multiple test functions are selected on CEC2017 benchmark functions to compare the performance of each algorithm. In order to enhance the comparability of the algorithms, the same initial parameters were set for each comparison algorithm, and the population size was N = 30, c1 = c2 = 1.5, inertia weight wmax = 0.9, wmin = 0.4, maximum iteration number Kmax = 100, and test function dimension was set to d = 10.

To evaluate the performance of the algorithm, the following evaluation indicators are used to evaluate the performance of the algorithm: the best value, the average value, the standard deviation, the median value, and the worst value five indicators. Each comparison algorithm solves the test function and runs 100 times independently. The test statistics are shown in Table 7. In order to more intuitively illustrate the test performance of EPSOSA in the above six CEC functions, the variation curve of the population minimum fitness value with the number of iterations in the process of particle swarm optimization of each comparison algorithm is shown in Fig. 13.

Table 6 Performance before and after processing on Kaggle dataset.
Full size table
Table 7 Comparison of various optimization algorithms.
Full size table
Fig. 13
figure 13

Comparison of convergence curves of various optimization algorithms.

Full size image

As can be seen from Table 7, the performance of the proposed EPSOSA algorithm on the five test functions F3, F14, F16, F28 and F29 is better than that of the other several algorithms, and the optimal values are obtained. Only on the F5 test function, it is slightly inferior to the GWO algorithm, but it is also stronger than the other three algorithms. It can also be seen from Fig. 13 that the convergence performance of the EPSOSA algorithm on these several test functions is stronger than that of the other four algorithms. In emergency medicine, the speed of decision-making is crucial, Therefore, the experiments show that the proposed algorithm has more practical application value.

Conclusion

In consideration of the limitations inherent in the Backpropagation (BP) neural network algorithm, such as its sluggish convergence pace, susceptibility to local minima, and sensitivity to initial weights, this study introduces a heart disease prediction model based on Particle Swarm Optimization with Simulated Annealing neural network with elimination mechanism (EPSOSA-BP). Addressing the oversight in previous research regarding the feature selection strategy for datasets, we employ One-hot encoding and Principal Component Analysis (PCA) to filter out a feature set that holds greater learning value for the model, thereby enhancing the performance of the BP neural network in predicting heart disease. Through validation with two datasets sourced from UCI and Kaggle, this paper conducts a comprehensive comparison of the Receiver Operating Characteristic (ROC) curve, Area Under the Curve (AUC) value, Accuracy, Precision, Sensitivity, Specificity, FPR, FNR and F1 score. It is concluded that the model proposed herein leads in all metrics. Our algorithm not only boasts superior accuracy but also exhibits heightened sensitivity and specificity, effectively identifying individuals truly afflicted with heart disease, mitigating the risk of missed diagnoses, and distinguishing more accurately between healthy individuals and those with disease, thus reducing the risk of false positives. Notably, the algorithm’s performance is particularly pronounced in small-sample datasets, which is of significant importance in medical environments with limited resources.

In view of our data preprocessing and feature selection method, this paper also carried out a more detailed ablation experiment. The experimental data show that our data processing method and feature engineering are effective for the heart disease data set, which can provide certain reference for other scholars in the field of related research.

In addition, in terms of the convergence speed of the algorithm, the convergence efficiency of the EPSOSA algorithm is better than that of several classical optimization algorithms and combinatorial optimization algorithms in each test function scenario. It proves that regardless of the complexity of the solution space, the model trained by the algorithm helps to find the optimal solution faster and jump out of the local optimum under the condition of expanding the search horizon. Therefore, it can adapt to the complex and variable relationship between clinical features, and it is efficient and robust when applied to the coronary artery disease prediction model.

The practical implementation of the model faces several challenges that warrant further deliberation. Foremost among these is the issue of technical integration. The existing Hospital Information Systems (HIS) and technological infrastructure are often outdated, with legacy system versions and aging operational equipment, which may pose compatibility issues during deployment. The standardization of data formats is another challenge that needs to be addressed, as outputs from different devices can vary slightly. Additionally, there are heightened concerns regarding privacy protection and compliance with legal and regulatory standards, along with the need to consider user acceptance and the training of personnel.

From a perspective closer to clinical practice, the work presented in this paper has certain limitations. For instance, in emergency departments, it may not be feasible to rapidly collect all data indicators, leading to potential data omissions and measurement errors, which can adversely affect prediction outcomes. It may be necessary to integrate a data imputation module, supported by expert consensus, into the system. Furthermore, measured data can fluctuate rapidly, necessitating the introduction of time series models for subsequent analysis.

However, it is undeniable that our model can assist physicians in identifying high-risk patients earlier, thereby potentially saving lives, improving patient prognoses, and enhancing the efficiency of medical resource utilization. The algorithm proposed in this paper is not only applicable in emergency settings but also has the potential to be employed in community health service centers, after validation, to regularly monitor cardiac risks among community members.