Introduction

Optical communication systems have revolutionized data transmission, offering unprecedented data rates with minimal loss over long distances1,2,3,4,5. Central to this technology is the understanding and manipulation of optical pulses as they propagate through fibers, a phenomenon governed by the nonlinear Schrödinger equation (NLSE). Since its inception, the NLSE has served as a fundamental model6,7, revealing the dynamics of light pulses and the formation of optical solitons8,9,10,11,12,13,14,15,16.

However, the traditional NLSE does not fully encapsulate the complexities of modern optical systems, particularly those involving higher-order nonlinearities and spatiotemporal dispersion. These factors become increasingly significant in modern optical systems designed for ultrafast communication and high-density data storage. Therefore, in order to meet the needs of nonlinear optics research, scientists have introduced different forms of nonlinear terms based on the nonlinear Schrödinger equation, and thus proposed the Schrödinger–Hirota equation(SHE)17,18,19,20. As is well known, these nonlinear equations often have nonlinear terms, dispersion terms, or diffusion terms, making their research often very complex. If its exact solution can be obtained, it will greatly promote scientific research and engineering practice. Therefore, countless mathematical physicists have devoted themselves to exploring exact solutions in engineering, while also obtaining a large number of effective solving methods, such as These include the the enhanced Kudryashovs scheme21, F-expansion technique22, complete discriminant system23, the extended trial function method24, Sardar sub-equation procedure25, planar dynamic system method26,27, Khater method28,29,30,31 and so on32,33,34,35.

In order to study the propagation laws of waves in ultrafast optics, strong field effects in nonlinear media, photonic integrated circuits, and extreme physical conditions, various higher-order nonlinear terms, also known as perturbation Schrödinger–Hilliotta equation (PSHE). PSHE is a critical model designed to capture the complexities of modern optical communication systems with higher-order nonlinearities and spatiotemporal dispersion. This model is particularly significant as it provides a more comprehensive description of soliton dynamics in dispersive media, which is essential for the development of ultrafast communication and high-density data storage technologies. There are various representative forms of PSHE, such as the PSHE with cubic-quintic-septic law nonlinearity36, with anti-cubic law in the presence of spatiotemporal dispersion37, with quadratic-cubic nonlinearity and inter-model dispersion38, with Kerr law nonlinearity39, with spatio-temporal dispersion and kerr law nonlinear40,41, and so forth42,43,44,45. In the context of communication physics, the PSHE model plays a crucial role in understanding the behavior of light pulses as they travel through optical fibers. The ability to predict and control these dynamics is paramount for optimizing system performance, enhancing signal quality, and minimizing errors in data transmission.

The complexity of real optical systems, characterized by spatiotemporal dispersion, self-phase modulation, and other higher-order effects, poses significant challenges for deriving exact solutions from the Schrödinger equation. These optical systems, which simultaneously contain spatiotemporal dispersion and high-order nonlinear terms, are capable of adapting to more complex environments, yet have received relatively little theoretical research attention. While there is a significant amount of work in this field, typically relying on approximations or numerical simulations, it is still necessary to fully capture the rich dynamics of solitons in optical fibers. This has motivated our exploration of the PSHE with cubic-quintic-septic law incorporating spatiotemporal dispersion. The governing model, given by46:

$$\begin{aligned} \begin{aligned}&i U_t+\alpha U_{x x}+\beta U_{x t}+\left( \rho _1|U|^2+\rho _2|U|^4+\rho _3|U|^6\right) U+i\left( \delta _1 U_{x x x}+\delta _2|U|^2 U_x\right) \\ =&i\left( \mu _1 U_x+\mu _2\left( |U|^2 U\right) _x+\mu _3\left( |U|^2\right) _x U\right) , \end{aligned} \end{aligned}$$
(1)

serves as the focal point of our investigation, where \(U(x, t)\) represents the complex soliton profile, and the coefficients \(\alpha\), \(\beta\), \(\rho _1\), \(\rho _2\), \(\rho _3\), \(\delta _1\) and \(\delta _2\) capture the effects of group velocity dispersion, spatiotemporal dispersion, and nonlinearities of varying orders, respectively. The coefficients of \(\mu _1\), \(\mu _2\) and \(\mu _3\) are the inter-modal dispersion, self-steepening and the nonlinear dispersions. Eq. (1) contains higher-order nonlinear terms and serves as a generalization of other nonlinear SHE. When \(\rho _3=0, \mu _1=\mu _2=\mu _3=0\), Eq. (1) reduces to the dispersive SHE36. The PSHE models are considered due to their capacity to account for higher-order nonlinearities and spatiotemporal dispersion effects, which are critical in modern optical systems designed for ultrafast data transmission and high-density data storage. Unlike simpler models that may overlook these complex interactions, the PSHE provides a comprehensive framework that allows for a detailed analysis of soliton propagation and stability. By providing insights into the behavior of optical pulses under various conditions, the PSHE models contribute to the optimization of system performance and the enhancement of signal integrity.

Despite the advances offered by the PSHE, the literature on this topic is sparse, and there remains a significant gap in our understanding of its solutions and their implications for optical communication systems. Previous studies have primarily focused on the NLSE and its basic variants, neglecting the richer dynamics introduced by higher-order terms. Moreover, the existing solutions are often derived under simplified conditions, which may not fully capture the complexity of real-world optical systems. Very recently the perturbed Schrödinger–Hirota equation (PSHE) has been introduced, incorporating cubic-quintic-septic nonlinearity and spatiotemporal dispersion terms that provide a more detailed and accurate description of soliton dynamics in dispersive media.

This research is motivated by the need to bridge this gap and to explore the PSHE in depth. Our aim is to provide a comprehensive analysis of the PSHE, to derive new solutions that account for higher-order effects, and to examine the impact of these effects on soliton propagation. By extending the current theoretical framework, we seek to offer insights that are not only academically significant but also practically relevant for the design and optimization of next-generation optical communication systems.

The present study is meticulously structured to unveil our findings in a coherent and systematic sequence. The paper unfolds as follows: The forthcoming “Mathematical analysis” commences with a strategic transformation of the central model, streamlining the intricate nonlinear ordinary differential equation emergent from our analytical exploration. Advancing to “The modified auxiliary equation method”, we delve into the intricacies of the phase portrait characteristics, leveraging the theoretical frameworks of planar dynamical systems to dissect the underpinning chaotic dynamics within the perturbed system. “Soliton solutions for Eq. (1)” employs the integration principles of dynamical systems to methodically derive exact traveling wave solutions, capturing a comprehensive spectrum of optical solitons and periodic solutions. Subsequent sections integrate our analytical outcomes with the extant body of literature, presenting a thorough discourse and recapitulation of our discoveries, concurrently mapping out prospective avenues for future scholarly investigation. The final section encapsulates the quintessential conclusions drawn from this research, highlighting their theoretical and practical ramifications for the field of nonlinear optics and the advancement of fiber optic communication systems, while also proposing future directions for academic exploration.

Mathematical analysis

To solve Eq. (1), we can utilize the following transformation:

$$\begin{aligned} U(x, t)=R(\xi ) e^{i\left( -\kappa x+\omega t+\varphi _0\right) }, \xi =x-v t, \end{aligned}$$
(2)

where \(\kappa\) is wave number, \(\omega\) is angular frequency, \(\varphi _0\) is phase constant, and v is the velocity. Substituting the transformation (2) into Eq. (1) and separating the real and imaginary parts yields:

$$\begin{aligned} \delta _1 R^{\prime \prime \prime }-\left( (3\mu _2+2\mu _3-\delta _2) R^2+(2 \alpha -\beta v) \kappa +3 \kappa ^2 \delta _1-\beta \omega +v+\mu _1\right) R^{\prime }= & 0, \end{aligned}$$
(3)
$$\begin{aligned} (\alpha -\beta v+3 \delta _1 \kappa ) R^{\prime \prime }-\left( \delta _1 \kappa ^3+\alpha \kappa ^2+(\mu _1-\beta \omega ) \kappa +\omega \right) R\qquad & \nonumber \\ -\left( (a-\delta _2) \kappa -\rho _1\right) R^3+\rho _2 R^5+\rho _3 R^7= & 0. \end{aligned}$$
(4)

If Eq. (3) is integrated and the integration constant is assumed as zero, then we attain,

$$\begin{aligned} \delta _1 R^{\prime \prime }+(\delta _2-3\mu _2-2\mu _3) R^3+3\left( \beta \kappa v-3 \delta _1 \kappa ^2-2 \alpha \kappa +\beta \omega -\mu _1-v\right) R=0 . \end{aligned}$$
(5)

Equation (5) gives the following constraints:

$$\begin{aligned} \delta _1=0,~\delta _2=3\mu _2+2\mu _3, ~v=\frac{2 \alpha \kappa -\beta \omega +\mu _1}{\beta \kappa -1} . \end{aligned}$$
(6)

The substitution

$$R(\xi )=\phi ^{1 / 3}(\xi ),$$

induces a transformation in which Eq. (4) is converted to

$$\begin{aligned} \begin{aligned}&9\left( \rho _1+2 \kappa (\mu _2+\mu _3)\right) \phi ^{\frac{8}{3}}+9 \rho _2 \phi ^{\frac{10}{3}} +3 \left( \alpha - \beta v\right) \phi \phi ^{\prime \prime }\\+&2 \left( \beta v -\alpha \right) \left( \phi ^{\prime }\right) ^2+9\rho _3 \phi ^4+9 \left( -\alpha \kappa ^2+\omega (\beta \kappa -1)-\kappa \mu _1\right) \phi ^2=0. \end{aligned} \end{aligned}$$
(7)

For integrability of Eq. (7), we set

$$\begin{aligned} \rho _1=-2 \kappa (\mu _2+\mu _3),~ \rho _2 =0 . \end{aligned}$$
(8)

Then

$$\begin{aligned} \phi \phi ^{\prime \prime }=\frac{2}{3}\left( \phi ^{\prime }\right) ^2 +p_1\phi ^2+p_2\phi ^4 , \end{aligned}$$
(9)

where \(p_1=-\frac{3(\beta \kappa -1)(\alpha \kappa ^2-\omega (\beta \kappa -1)+\kappa \mu _1)}{\alpha (\beta \kappa +1)-\beta ^2\omega +\beta \mu _1}\),  \(p_2=\frac{3\rho _3(\beta \kappa -1)}{\alpha (\beta \kappa +1)-\beta ^2\omega +\beta \mu _1}\).

The modified auxiliary equation method

In this study, we employ the Modified Auxiliary Equation (MAE) method to analyze the PSHE. Below, we detail the steps involved in each method, highlighting their improvements and applications to our specific problem.

Step 1: Transformation. We start by transforming the PSHE into a form suitable for the MAE method. This involves a change of variables and the introduction of auxiliary functions to simplify the equation. Let the traveling wave transformation \(\phi \left( {x,t} \right) = \phi \left( \xi \right) ,\xi = x - v t\) reduce the nonlinear partial differential equation

$$\begin{aligned} N\left( {\phi ,{\phi _t},{\phi _x},{\phi _{xx}}, \cdots } \right) = 0 \end{aligned}$$
(10)

to a nonlinear ordinary differential equation

$$\begin{aligned} Q\left( {\phi ,\phi ',\phi '', \cdots } \right) = 0. \end{aligned}$$
(11)

Step 2: Auxiliary equation construction. Auxiliary equation construction: Next, we construct an auxiliary equation that approximates the original PSHE. This equation is designed to capture the essential nonlinear dynamics of the system.

Assume that Eq. (10) has the solution of the form:

$$\begin{aligned} \phi \left( \xi \right) = {a_0} + \sum \limits _{i = 1}^N {\left( {{a_i}{K^{if\left( \xi \right) }} + {b_i}{K^{ - if\left( \xi \right) }}} \right) } , \end{aligned}$$
(12)

where \(a_0\), \(a_i\), \(b_i\), \(i = 1, 2,\cdots N,\) are constants to be determined, N can be determined according to the balance principle, and \(f(\xi )\) statisfies the following relationship:

$$\begin{aligned} f'\left( \xi \right) = \frac{1}{{\ln K}}\left( {\sigma _{-1} {K^{ - f\left( \xi \right) }} + \sigma _{0} + \sigma _{1} {K^{f\left( \xi \right) }}} \right) . \end{aligned}$$
(13)

To simplify the notation, we denote: \(\Delta = \sigma _{0}^2 -4\sigma _{-1} \sigma _{1}\). The solutions of Eq. (13) have been found as follows:

(1) \(\sigma _{1} = 0,\sigma _{0} \ne 0\).

$$\begin{aligned} K^{f\left( \xi \right) } = - \sigma _{-1} \pm \frac{1}{\sigma _{0} }{e^{\sigma _{0} \left( {\xi - {\xi _0}} \right) }}. \end{aligned}$$
(14)

(2) \(\Delta < 0,\sigma _{1} > 0.\)

$$\begin{aligned} K^{f\left( \xi \right) } = - \frac{\sigma _{0} }{{2\sigma _{1} }} + \frac{{\sqrt{ - \Delta } }}{{2\sigma _{1} }}\tan \left( {\frac{{\sqrt{ - \Delta } }}{2}(\xi - {\xi _0})} \right) . \end{aligned}$$
(15)

It can also be written in the following special forms:

$$\begin{aligned} K^{f\left( \xi \right) } = - \frac{\sigma _{0} }{{2\sigma _{1} }} + \frac{{\sqrt{ - \Delta } }}{{2\sigma _{1} }}\tan \left( {\frac{{\sqrt{ - \Delta } }}{2}\xi } \right) . \end{aligned}$$
(16)
$$\begin{aligned} K^{f\left( \xi \right) } = - \frac{\sigma _{0} }{{2\sigma _{1} }} + \frac{{\sqrt{ - \Delta } }}{{2\sigma _{1} }}\cot \left( {\frac{{\sqrt{ - \Delta } }}{2}\xi } \right) . \end{aligned}$$
(17)

(4) \(\Delta = 0.\)

$$\begin{aligned} K^{f\left( \xi \right) } = - \frac{\sigma _{0} }{{2\sigma _{1} }} - \frac{1}{{\sigma _{1} \left( {\xi - {\xi _0}} \right) }}. \end{aligned}$$
(18)

(5) \(\Delta > 0.\)

$$\begin{aligned} K^{f\left( \xi \right) }= & - \frac{\sigma _{0} }{{2\sigma _{1} }} - \frac{{\sqrt{\Delta }}}{{2\sigma _{1} }}\coth \left( {\frac{{\sqrt{\Delta }}}{2}(\xi - {\xi _0})} \right) ,\end{aligned}$$
(19)
$$\begin{aligned} K^{f\left( \xi \right) }= & - \frac{\sigma _{0} }{{2\sigma _{1} }} - \frac{{\sqrt{\Delta }}}{{2\sigma _{1} }}\tanh \left( {\frac{{\sqrt{\Delta }}}{2}(\xi - {\xi _0})} \right) . \end{aligned}$$
(20)

Step 3: Solution of coefficients. Substitute Eqs. (11) and (12) together into Eq. (10) to obtain the coefficients \(a_0\), \(a_i\), \(b_i\), \(i = 1, 2,\cdots N\).

Step 4: Solution iteration. Combining the conclusions from Step 1 and Step 3, the solution to Eq. (10) can be derived based on Eq. (11).

Soliton solutions for Eq. (1)

Applying the homogeneous balance principle to Eq. (9), \(n=1\) is obtained. That is to say, Eq. (9) has the following solution:

$$\phi \left( \xi \right) = {a_0} + {{a_1}{K^{f\left( \xi \right) }} + {b_1}{K^{ - f\left( \xi \right) }}}.$$

From the method of constructing solution mentioned above, the solutions of Eq. (9) for different parameter values are as follows:

(1). Given the parameters \(\sigma _{-1} = \sigma _{1}=0,~\sigma _{0} = \sqrt{3p_1},~p_1>0\), \(~p_2={a_0} = {b_1} = 0\), \({a_1} = {a_1}\), the solution is:

$$\begin{aligned} U_1 = \pm e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( {a_1}{e^{\sqrt{3{p_1}} \left( {x - v t - {\xi _0}} \right) }}\right) ^{1/3}, \end{aligned}$$
(21)

where \(U=U(x,t)\).

(2). For \(\sigma _{-1} = \sigma _{1}=0\), \(\sigma _{0} = {\varepsilon _1}\sqrt{3p_1}\),  \(p_1>0\), \({p_2} = {a_0}= {a_1} = 0\), \({b_1} = {b_1}\), the solution is:

$$\begin{aligned} U_2 = \pm e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( {b_1}{e^{-\sqrt{3{p_1}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(22)

(3). With \(\sigma _{-1} = \sigma _{0} = 0\), \(\sigma _{1} = \sigma _{1}\), \({p_1} = {a_0} ={b_1} = 0\), \({p_2} >0\), \({a_1} = \frac{2{\varepsilon _1} \sigma _{1}}{\sqrt{3{p_2}}}\), the solution is:

$$\begin{aligned} U_3 = \pm e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( \frac{2}{{\sqrt{3{p_2}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(23)

(4). For \(\sigma _{-1} = \sigma _{0} = 0\), \(\sigma _{0} = {\varepsilon _1} \sqrt{3{p_1}},\) \({p_1} >0,~{p_2} ={a_0} = {a_1} = 0,~{b_1} = {b_1}\), the solution is:

$$\begin{aligned} U_4 = {\varepsilon _2} e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( {b_1} {e^{{\varepsilon _1}\sqrt{3{p_1}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}, \end{aligned}$$
(24)

where \({\varepsilon _1} = \pm 1\) and \({\varepsilon _2} = \pm 1\).

(5). Given \(\sigma _{-1} = {\varepsilon _1} \frac{{{b_1}}\sqrt{3{p_2}}}{2},\) \(\sigma _{0} = {\varepsilon _1} {a_0} \sqrt{3{p_2}},\) \(\sigma _{1} = {\varepsilon _1} \frac{{a_0^2}\sqrt{3{p_2}}}{{2{b_1}}},\) \({p_1} = a_1=0\), \({p_2}>0,\) \({a_0} = {a_0},\) \({b_1} = {b_1}\), the solution is:

$$\begin{aligned} U_5 = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( \frac{{2{a_0}}}{{2 +{\varepsilon _1} {a_0}\sqrt{3{p_2}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(25)

(6). For \(\sigma _{-1} = \sigma _{-1},\) \(\sigma _{0} = {\varepsilon _1} \sqrt{3{p_1}}\), \(\sigma _{1} = {p_2} = {b_1}= 0\), \({p_1} >0\), \({a_0} = {a_0}\), \({a_1} = {\varepsilon _1} \sqrt{3{p_1}} \frac{{{a_0}}}{\sigma _{-1} }\), the solution is:

$$\begin{aligned} U_6 = e^{i\left( -\kappa x+\omega t+\varphi _0\right) }\left( {a_0}\left( {1 - {\varepsilon _1} {\varepsilon _2} } \right) + \frac{{{a_0}\sqrt{3{p_1}}}}{\alpha }{e^{{\varepsilon _2}\sqrt{3{p_1}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(26)

(7). With \(\sigma _{-1} = {\varepsilon _1} \frac{{a_0^2\sqrt{3{p_2}} }}{{2{a_1}}}\), \(\sigma _{0} = {\varepsilon _1} {a_0} \sqrt{3{p_2}},\) \(\sigma _{1} = {\varepsilon _1} \frac{{{a_1}\sqrt{3{p_2}} }}{2},\) \({p_1} = b_1= 0,{p_2} = {p_2},\) \({a_0} = {a_0}\), \({a_1} = {a_1},\) the solution is:

$$\begin{aligned} U_7 = e^{i\left( -\kappa x+\omega t+\varphi _0\right) }\left( (1+\varepsilon _1)a_0+\frac{2\varepsilon _1}{{\sqrt{3{p_2}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(27)

(8). For \(\sigma _{-1} = \sigma _{0} = 0\), \(\sigma _{1} = {\varepsilon _1} \frac{a_1 \sqrt{3p_2}}{2}\), \({p_1} = {a_0} ={b_1} = 0\), \({p_2}>0\), \({a_1} = {a_1}\), the solution is:

$$\begin{aligned} U_8 = {\varepsilon _1} e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( \frac{2}{{\sqrt{3{p_2}} \left( {x - v t - {\xi _0}} \right) }} \right) ^{1/3}. \end{aligned}$$
(28)

(9). Given \(\sigma _{-1} = {\varepsilon _1} \frac{b_1\sqrt{3p_2}}{2}\), \(\sigma _{0} = 0\), \(\sigma _{1} = -{\varepsilon _1} \frac{3p_1}{2\sqrt{3p_2}}\), \({p_1}=p_1\), \({p_2}=p_2\), \({a_0} = 0\), \({a_1} = \frac{{\sigma _{1} {b_1}}}{\sigma _{-1} }\), \({b_1} = {b_1}\), the solutions are:

$$\begin{aligned} U_9 = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( \sqrt{\frac{{{p_1}}}{{{p_2}}}} \tanh \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) + \sqrt{\frac{{{p_1}}}{{{p_2}}}} \coth \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) \right) ^{1/3}. \end{aligned}$$
(29)
$$\begin{aligned} U_{10} = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( \sqrt{\frac{{{p_1}}}{{{p_2}}}} \tanh \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) - \sqrt{\frac{{{p_1}}}{{{p_2}}}} \coth \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) \right) ^{1/3}. \end{aligned}$$
(30)
$$\begin{aligned} U_{11} = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( - \sqrt{\frac{{{p_1}}}{{{p_2}}}} \tanh \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) + \sqrt{\frac{{{p_1}}}{{{p_2}}}} \coth \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) \right) ^{1/3}. \end{aligned}$$
(31)
$$\begin{aligned} U_{12} = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( - \sqrt{\frac{{{p_1}}}{{{p_2}}}} \tanh \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) - \sqrt{\frac{{{p_1}}}{{{p_2}}}} \coth \left( {\frac{{\sqrt{3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) \right) ^{1/3}. \end{aligned}$$
(32)
$$\begin{aligned} U_{13} = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( - \sqrt{ - \frac{{{p_1}}}{{{p_2}}}} \tan \left( {\frac{{\sqrt{-3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) + \sqrt{- \frac{{{p_1}}}{{{p_2}}}} \cot \left( {\frac{{\sqrt{-3{p_1}} }}{2}\left( {x - v t - {\xi _0}} \right) } \right) \right) ^{1/3}. \end{aligned}$$
(33)
$$\begin{aligned} U_{14} = e^{i\left( -\kappa x+\omega t+\varphi _0\right) } \left( - \sqrt{- \frac{{{p_1}}}{{{p_2}}}} \cot \left( {\frac{{\sqrt{-3{p_1}} }}{2}(x - v t) } \right) + \sqrt{ -\frac{{{p_1}}}{{{p_2}}}} \tan \left( {\frac{{\sqrt{-3{p_1}} }}{2}(x - v t) } \right) \right) ^{1/3}. \end{aligned}$$
(34)

Solutions’ accuracy

Employing the Adomian Decomposition Method (ADM)28,29,30, numerical solutions for Eq. (9) have been individually determined, facilitating the verification of the accuracy of the previously established solutions. This section endeavors to validate the analytical schemes proposed to date by juxtaposing them with their numerical solutions. To adapt the ADM to Eq. (9), a variable substitution was employed, setting \(u(\xi ) = \phi ^2(\xi )\), which effectively reformulates equation (9) into the equivalent form

$$\begin{aligned} u^{\prime \prime }=\frac{15}{6} \frac{\left( u^{\prime }\right) ^2}{u} +2p_1 u+2p_2 u^2. \end{aligned}$$
(35)

Upon the application of the ADM to Eq. (21), the ensuing numerical solution is expressed as a series:

$$\begin{aligned} \small u_{0}= & 1+6 \sqrt{2} \xi , \\ u_{1}= & \left( 5 \sqrt{2}\, \xi +\frac{5}{6}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) +12 \sqrt{2}\, \xi ^{3}-5 \sqrt{2}\, \xi + \xi ^{2}, \\ u_{2}= & \left( \frac{25 \sqrt{2}\, \xi }{12}+\frac{25}{72}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{2}+\left( \frac{325}{432}+10 \sqrt{2}\, \xi ^{3}+5 \xi ^{2}+\frac{25 \sqrt{2}\, \xi }{36}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) \\ & -\frac{25 \xi ^{2}}{4}-\frac{325 \sqrt{2}\, \xi }{72}+ \xi ^{4}-10 \sqrt{2}\, \xi ^{3}+\frac{36 \sqrt{2}\, \xi ^{5}}{5}, \\ u_{3}= & \left( \frac{125 \sqrt{2}\, \xi }{216}+\frac{125}{1296}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{3}+\left( \frac{3125}{5184}+\frac{25 \sqrt{2}\, \xi ^{3}}{6}+\frac{25 \xi ^{2}}{12}+\frac{875 \sqrt{2}\, \xi }{432}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{2}\\ & +\left( \frac{24725}{31104}+6 \sqrt{2}\, \xi ^{5}+5 \xi ^{4}+\frac{25 \sqrt{2}\, \xi ^{3}}{18}+\frac{325 \xi ^{2}}{72}-\frac{4475 \sqrt{2}\, \xi }{2592}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) -2 \sqrt{2}\, \xi ^{5}\\ & -\frac{17405}{62208}-\frac{65 \xi ^{4}}{8}+\frac{72 \sqrt{2}\, \xi ^{7}}{35}+\frac{2 \xi ^{6}}{5}-\frac{4285 \sqrt{2}\, \xi ^{3}}{432}-\frac{1535 \xi ^{2}}{108}+\frac{17405}{62208+373248 \sqrt{2}\, \xi }-\frac{32045 \sqrt{2}\, \xi }{10368},\\ u_{4}= & \left( \frac{125 \sqrt{2}\, \xi }{648}+\frac{125}{3888}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{3}+\left( \frac{3125}{15552}+\frac{25 \sqrt{2}\, \xi ^{3}}{18}+\frac{25 \xi ^{2}}{36}+\frac{875 \sqrt{2}\, \xi }{1296}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{2}+\\ & \left( \frac{24725}{93312}+2 \sqrt{2}\, \xi ^{5}+\frac{5 \xi ^{4}}{3}+\frac{25 \sqrt{2}\, \xi ^{3}}{54}+\frac{325 \xi ^{2}}{216}-\frac{4475 \sqrt{2}\, \xi }{7776}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) +\frac{24 \sqrt{2}\, \xi ^{7}}{35}\\ & +\frac{2 \xi ^{6}}{15}-\frac{2 \sqrt{2}\, \xi ^{5}}{3}-\frac{65 \xi ^{4}}{24}-\frac{4285 \sqrt{2}\, \xi ^{3}}{1296}-\frac{1535 \xi ^{2}}{324}-\frac{32045 \sqrt{2}\, \xi }{31104}+\frac{17405}{186624+1119744 \sqrt{2}\, \xi }\\ u_{5}= & \left( \frac{625 \sqrt{2}\, \xi }{20736}+\frac{625}{124416}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{4}+\left( \frac{23125}{373248}+\frac{125 \sqrt{2}\, \xi ^{3}}{432}+\frac{125 \xi ^{2}}{864}+\frac{8125 \sqrt{2}\, \xi }{31104}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{3}\\ & +\left( \frac{311125}{1492992}+\frac{5 \sqrt{2}\, \xi ^{5}}{8}+\frac{25 \xi ^{4}}{48}+\frac{875 \sqrt{2}\, \xi ^{3}}{864}+\frac{3125 \xi ^{2}}{3456}+\frac{30125 \sqrt{2}\, \xi }{124416}\right) \ln \! \left( 1+6 \sqrt{2}\, \xi \right) ^{2}\\ & + \left( { - \frac{{334105\sqrt{2} {\hspace{0.55542pt}} \xi }}{{746496}} + \frac{{295{{\left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) }^4}}}{{1492992}} + \frac{{{{\left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) }^7}}}{{5225472}} - \frac{{13265{{\left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) }^3}}}{{4478976}}} \right. + \cdots \\ & + \left. {\frac{{23749{{\left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) }^2}}}{{1492992}} + \frac{{11{{\left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) }^5}}}{{373248}}} \right) \ln \left( {1 + 6\sqrt{2} {\hspace{0.55542pt}} \xi } \right) +\frac{3 \sqrt{2}\, \xi ^{9}}{35}+\frac{3 \xi ^{8}}{140}+\frac{\sqrt{2}\, \xi ^{7}}{21}-\frac{115 \xi ^{6}}{144}-\frac{461 \sqrt{2}\, \xi ^{5}}{192}\\ & -\frac{510539 \xi ^{2}}{82944}-\frac{8215691}{53747712}-\frac{2243 \xi ^{4}}{384}+\frac{57053}{331776+1990656 \sqrt{2}\, \xi }-\frac{1026895}{53747712 \left( 1+6 \sqrt{2}\, \xi \right) ^{2}}\\ & -\frac{828463 \sqrt{2}\, \xi }{1119744}-\frac{12031 \sqrt{2}\, \xi ^{3}}{5184}. \end{aligned}$$

Therefore, the approximate solution obtained is \(u_{Approx}(\xi )=u_{0}+u_{1}+\cdots +u_{5}.\) Table 1 delineates the absolute error between the exact and approximate solutions, as revealed by the numerical technique utilized in this study.

Table 1 Adomian decomposition approachs outcome.
Full size table

Modulation instability

Modulation instability is a phenomenon that arises under certain conditions47,48,49, where perturbations to an equilibrium state can lead to significant changes in wave amplitude or phase. This sensitivity to small disturbances, particularly in nonlinear systems, can result in rapid growth of wave amplitudes around specific frequencies, potentially leading to the formation of periodic structures or solitons. Understanding and analyzing modulation instability is crucial for optimizing system performance in various applications, such as optical communications and fluid dynamics.

The foundation of our analysis begins with the steady-state solution of the system, given by Eq. (36).

$$\begin{aligned} U(x,t) = R{e^{{i}\left( { - kx + \omega t} \right) }}, \end{aligned}$$
(36)

This solution represents a steady-state solution of the system before any perturbations are introduced. By substituting Eq. (36) into the governing Eq. (1), we derive the dispersion relation,

$$\begin{aligned} \omega = \frac{{{\rho _{\text {3}}}{R^6} + {\rho _{\text {2}}}{R^4} + \left( {k{\delta _{\text {2}}} - k{\mu _{\text {2}}} + {\rho _{\text {1}}}} \right) {R^2} - ({\delta _{\text {1}}}{\hspace{0.55542pt}} {k^3} + \alpha {k^2} + k{\mu _{\text {1}}}{\text {)}}}}{{1 - \beta k}}, \end{aligned}$$
(37)

which is essential for understanding the system’s behavior under different wave numbers and frequencies:

To examine the system’s response to minor disturbances, we introduce disturbances to the input power as described below

$$\begin{aligned} U(x,t) = \left( {R + \varepsilon V(x,t)} \right) {e^{{\text {i}}\left( { - kx + \omega t} \right) }}, \end{aligned}$$
(38)

where V(x, t) is the perturbation term and \(\left| \varepsilon \right| <1\).

After substituting Eq. (38) into Eq. (1), the linearized equation is obtained

$$\begin{aligned} \begin{aligned}&\beta \frac{{{\partial ^2}V}}{{\partial t\partial x}} + \left( {3{\delta _{\text {1}}}k + \alpha } \right) \frac{{{\partial ^2}V}}{{\partial {x^2}}} + \left( {6{\rho _{\text {3}}}{R^6} + 4{\rho _{\text {2}}}{R^4} + 2\left( {{\delta _{\text {2}}}k - {\mu _{\text {2}}}k + {\rho _{\text {1}}}} \right) {R^2}} \right) V \\ +&i\left( {\beta k - 1} \right) \frac{{\partial V}}{{\partial t}} + i{\delta _{\text {1}}}\frac{{{\partial ^3}V}}{{\partial {x^3}}} - i\frac{1}{{\beta k - 1}}\left( {\left( {2\left( {{\mu _{\text {2}}} + {\mu _{\text {3}}}} \right) \beta k + \beta {\rho _{\text {1}}} + {\delta _{\text {2}}} - 3{\mu _{\text {2}}} - 2{\mu _{\text {3}}}} \right) {R^2}} \right. \\ +&\left. {\beta {\rho _{{\text {3}}{\hspace{0.55542pt}} }}{R^6} + \beta {\rho _{\text {2}}}{\hspace{0.55542pt}} {R^4} + \left( {2\beta {\delta _{{\text {1}}{\hspace{0.55542pt}} }}{k^3} + \left( {\alpha \beta - 3{\delta _{\text {1}}}} \right) {k^2} - 2\alpha k - {\mu _{\text {1}}}} \right) } \right) \frac{{\partial V}}{{\partial x}} = 0. \end{aligned} \end{aligned}$$
(39)

Assuming Eq. (39) has the following form of solution:

$$\begin{aligned} V\left( {x,t} \right) = {C_1}{e^{i\left( { - Kx + \Omega t} \right) }} + {C_2}^*{e^{i\left( { - Kx + {\Omega ^*}t} \right) }}, \end{aligned}$$
(40)

where \(C_1\) and \(C_2\) are the perturbation amplitudes, K and \(\Omega\) are the wave number and frequency of the perturbation, respectively. Substituting Eq. (40) into Eq. (39) results in the following matrix equation:

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{t_1}\Omega + {A_{11}}}& {{A_{12}}} \\ {{A_{21}}}& {{t_2}\Omega + {A_{22}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{C_1}} \\ {{C_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right) , \end{aligned}$$
(41)

where \({t_1} = (\beta k - 1)(\beta K + \beta k - 1)\), \({t_2} = (\beta k - 1)(\beta K - \beta k + 1)\),

$$\begin{aligned} {A_{11}}= & - {\delta _{\text {1}}}\left( {\beta k - 1} \right) {K^3} - \left( {\beta k - 1} \right) \left( {3{\delta _{\text {1}}}k + \alpha } \right) {K^2} + \left( { - 2\beta {\delta _{{\text {1}}{\hspace{0.55542pt}} }}{k^3} + \left( { - \alpha \beta + 3{\delta _{\text {1}}}} \right) {k^2} + 2\alpha k + {\mu _{\text {1}}}} \right) K, \\ {A_{12}}= & \left( { - \beta K + 6\beta k - 6} \right) {\rho _{\text {3}}}{R^6} - {\rho _{\text {2}}}\left( {\beta K - 4\beta k + 4} \right) {R^4} \\+ & \left( {\left( {2\left( {{\delta _{\text {2}}} - {\mu _{\text {2}}}} \right) k + 2{\rho _{\text {1}}}} \right) \left( {\beta k - 1} \right) - \left( {2\left( {{\mu _{\text {2}}} + {\mu _{\text {3}}}} \right) \beta k + \beta {\rho _{\text {1}}} + {\delta _{\text {2}}} - 3{\mu _{\text {2}}} - 2{\mu _{\text {3}}}} \right) K} \right) {R^2}, \\ {A_{21}}= & \left( {K\beta + 6k\beta - 6} \right) {\rho _{\text {3}}}{R^6} + \left( {K\beta + 4k\beta - 4} \right) {\rho _{\text {2}}}{R^4} \\+ & \left( {\left( {2\beta k{\mu _{\text {2}}} + 2\beta k{\mu _{\text {3}}} + \beta {\rho _{\text {1}}} + {\delta _{\text {2}}} - 3{\mu _{\text {2}}} - 2{\mu _{\text {3}}}} \right) K + 2\left( {k{\delta _{\text {2}}} - k{\mu _{\text {2}}} + {\rho _{\text {1}}}} \right) \left( {\beta k - 1} \right) } \right) {R^2}, \\ {A_{22}}= & {\delta _{\text {1}}}\left( {\beta k - 1} \right) {K^3} - \left( {\beta k - 1} \right) \left( {3{\delta _{\text {1}}}k + \alpha } \right) {K^2} + \left( {2\beta {\delta _{\text {1}}}{\hspace{0.55542pt}} {k^3} + \left( {\alpha \beta - 3{\delta _{\text {1}}}} \right) {k^2} - 2\alpha k - {\mu _{\text {1}}}} \right) K. \end{aligned}$$

For non-trivial solutions, the determinant of matrix A must be zero:

$$\begin{aligned} {t_1}{t_2}{\Omega ^2} + \left( {{t_1}{A_{22}} + {t_2}{A_{11}}} \right) \Omega + \left( {{A_{11}}{A_{22}} - {A_{12}}{A_{21}}} \right) = 0. \end{aligned}$$
(42)

This condition yields the expression for \(\Omega\) as follows:

$$\begin{aligned} \Omega = - \frac{{{t_1}{A_{22}} + {t_2}{A_{11}}}}{{2{t_1}{t_2}}} \pm \frac{{\sqrt{{{\left( {{t_1}{A_{22}} + {t_2}{A_{11}}} \right) }^2} - 4{t_1}{t_2}\left( {{A_{11}}{A_{22}} - {A_{12}}{A_{21}}} \right) } }}{{2{t_1}{t_2}}}. \end{aligned}$$
(43)

When \(\left[ t_1 A_{22} + t_2 A_{11} \right] ^2 - 4 t_1 t_2 \left( A_{11} A_{22} - A_{12} A_{21} \right) > 0,\) \(\Omega\) is real, indicating that the solution is stable. Conversely, when \(\left[ t_1 A_{22} + t_2 A_{11} \right] ^2 - 4 t_1 t_2 \left( A_{11} A_{22} - A_{12} A_{21} \right) < 0,\) \(\Omega\) becomes complex. This complex nature implies that infinitesimal perturbations can lead to an exponential change in frequency, signifying the presence of modulation instability. The gain spectrum associated with modulation instability is quantified by the magnitude of the imaginary part of \(\Omega\),

$$\text {Gain} = \left| \text {Im}(\Omega ) \right| ,$$

where \(\text {Im}(\Omega )\) denotes the imaginary component of the solution to the Eq. (43). This measure provides insight into the growth rate of perturbations and is a critical parameter in the analysis of modulation instability.

Figure 1
figure 1

Graphical representation of \(U_1\) at \(\alpha =2, \beta =0.25, \kappa =1,\omega =1,\mu _1=-2\), \(\rho _3=0\), \(v=1.2\) and \(\xi _0=\varphi _0=0\).

Full size image
Figure 2
figure 2

Graphical representation of \(U_7\) at \(\alpha =1, \beta =2, \kappa =2,\omega =2,\mu _1=1\), \(\rho _3=-0.1\), \(v=1.2\) and \(\xi _0=\varphi _0=0\).

Full size image
Figure 3
figure 3

Graphical representation of \(U_9\) at \(\alpha =3, \beta =-1, \kappa =0.15,\omega =1,\mu _1=-2.5\), \(\rho _3=-2\), \(v=1.2\) and \(\xi _0=\varphi _0=0\).

Full size image

Results and discussion

Graphical interpretation

The study of the higher-order PSHE with cubic-quintic-septic nonlinearities provides a theoretical foundation for signal propagation in modern optical systems designed for ultrafast communication and high-density data storage. Optical solitons and their associated effects are pivotal in facilitating efficient and reliable data transmission. By examining various solutions, engineers can optimize system designs to enhance communication performance and storage efficiency. The existence of soliton solutions ensures the feasibility of high-speed data transmission, while periodic solutions are crucial for multi-channel communication, and singular and unbounded solutions aid in the design of interference-resistant systems.

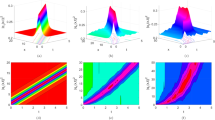
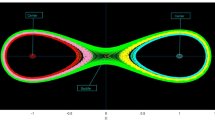
This paper presents exact and approximate solutions of the PSHE using the MAE and the Adomian decomposition method. The obtained solutions encompass a variety of solitary wave forms, including exponential, rational, trigonometric, and hyperbolic functions. Fig. 1, 2 and 3 illustrate the three-dimensional, two-dimensional, and real part of representative solutions \(U_1\), \(U_7\), and \(U_9\), respectively.

Parameter influence

The paper introduces two innovative parameters: the septic nonlinearity coefficient (\(\rho _3\)) and the spatiotemporal dispersion coefficient (\(\beta\)). In nonlinear communication, signals of different frequencies can interact within a nonlinear medium, providing possibilities for the generation and transmission of ultrafast laser pulses. As the degree of nonlinearity increases, signals may exhibit stronger distortion effects, pulse compression or expansion, and inter-channel interference, affecting the signal’s temporal width and spectral characteristics. Spatiotemporal dispersion may lead to more complex pulse dynamics, potentially causing more intricate distortions and interference. These factors are crucial for optimizing signal quality and system performance. The influence of these parameters on the wave propagation behavior of the PSHE is discussed as follows:

Influence of \(\rho _3\): From the definition of parameter \(p_2\), it is evident that \(\rho _3\) solely affects the value of \(p_2\). In this study, only solutions with \(p_2\ge 0\) were constructed. Consequently, when \(\rho _3 = 0\), \(p_2\) equals zero, and Eq. (1) only admits exponential-type solutions, which are unbounded. Otherwise, when \(p_2 > 0\), the system exhibits rational, trigonometric, and hyperbolic function solutions, indicating the presence of periodic and soliton solutions.

Figure 4
figure 4

Three dimensional diagram of the effect of \(\beta\) on the solutions at \(\alpha =2, \kappa =1,\omega =2,\mu _1=0.1\), \(\rho _3=1\), \(v=1.2\) and \(\xi _0=\varphi _0=0\).

Full size image

Influence of \(\beta\): As the spatiotemporal dispersion parameter, \(\beta\)’s impact on the system is demonstrated in Figs. 4 and 5. When \(\beta\) = 0, the system exhibits hyperbolic function solutions, including tanh and coth, with their three-dimensional and two-dimensional graphics shown in Figs. 4a and 5a. When \(\beta\) increases to 2.5, the system presents rational function singular soliton solutions, depicted in Figs. 4b and 5b. As \(\beta\) further increases to 4, the solution behavior changes again, involving trigonometric function solutions with tan and cot, as shown in Figs. 4c and 5c.

In summary, dispersion and nonlinearity significantly affect the system.

Figure 5
figure 5

Two dimensional diagram of the effect of \(\beta\) on the solutions at \(\alpha =2, \kappa =1,\omega =2,\mu _1=0.1\), \(\rho _3=1\), \(v=1.2\) and \(\xi _0=\varphi _0=0\).

Full size image

Literature comparison

This section compares the conclusions drawn in this paper with those from comparable literature. The MAE method was employed to construct exact solutions, and the precision of the Adomian method was validated. The paper presents a variety of analytical solutions, including exponential, rational, trigonometric, and hyperbolic forms. The conclusions of this paper are adaptable to more complex environments, demonstrating the paper’s innovation. To provide a comprehensive view of the advancements in solving the PSHE, we have compiled a comparison table of previous studies alongside our current approach (Table 2).

Table 2 Comparative analysis of studies on the PSHE.
Full size table

Limitation

While the MAE method offers a detailed mathematical analysis, it can be computationally intensive, especially for equations with a large number of terms or high degrees of nonlinearity. The ADM, despite its efficiency, may sometimes struggle with achieving convergence for certain types of nonlinear equations or initial conditions.

To address these limitations, we are exploring the integration of these methods with modern computational tools and algorithms that can enhance their applicability and efficiency. Future research will also focus on developing hybrid methods that combine the strengths of both the MAE and ADM to overcome their individual limitations.

Conclusions

This study has delved into the characteristics of the higher-order PSHE, revealing the impact of nonlinearities on signal propagation behavior through the analysis of exact and approximate solutions. Our research not only confirms the applicability of the theoretical model but also provides new insights into system design and performance optimization in the fields of ultrafast communication and high-density data storage.

The innovation of this paper lies in the introduction of two key parameters, the septic nonlinearity coefficient \(\rho _3\) and the spatiotemporal dispersion coefficient \(\beta\), whose effects on system behavior have been thoroughly analyzed. Furthermore, by employing the MAE method and the Adomian decomposition method, we have successfully constructed various forms of analytical solutions that have significant advantages in adapting to complex environments.

The variety of solutions obtained, including solitary waves, periodic waves, and even complex patterns, reflect the rich dynamics of nonlinear optical systems. Solitary waves, for instance, represent stable light pulses that maintain their shape and speed over long distances, which is crucial for efficient data transmission in fiber optics. Periodic wave solutions, on the other hand, are indicative of stable, repeating patterns that can be harnessed for multiplexing and signal modulation in advanced communication systems. The derived solutions have potential applications in the optimization of fiber optic communication systems. For instance, the control and manipulation of solitary waves can lead to the development of high-speed data transmission technologies with minimal signal distortion. The understanding of periodic wave solutions can facilitate the design of multi-channel communication systems, enhancing the capacity and efficiency of data transmission.

Looking forward, we plan to develop new methods for constructing solutions to overcome the challenges posed by higher-order nonlinearities and spatiotemporal dispersion. Our aim is to further explore the potential impact of these parameters on system performance and to uncover the profound significance of new solutions for system design and research