Introduction

Modern mechanical equipment is widely used in various fields such as construction, aviation, electricity, metallurgy, etc. Mechanical failure can cause huge economic losses and affect the life safety of workers1,2,3. As the core component of rotating machinery, the reliability of rolling bearings in terms of fatigue life, friction torque, vibration and other performance plays a decisive role in the operating status of the main machine4,5,6,7. Based on the vibration performance operation data of rolling bearings at the current time, their failure probability and reliability at a certain time in the future can be predicted, that is, the vibration performance reliability variation process prediction8, which is of great significance to the operation and maintenance of equipment and the dynamic performance evaluation.

Most existing reliability assessment methods rely on the assumption that the sample probability density function and performance failure threshold are known in advance, so as to calculate and analyze the performance reliability. For example, Xia Xintao et al.9 proposed a self-help weighted norm method, assuming that the rolling bearing life obeys the three-parameter Weibull distribution, so as to evaluate the optimal confidence interval of reliability. Zheng Rui10 proposed a new parameter estimation method based on the characteristics of the three-parameter Weibull distribution, combining the graphical method and genetic algorithm. ALI et al.8 assumed that the bearing fatigue life obeys the Weibull distribution to evaluate its reliability. However, during the service life of the bearing, there is a lot of unknown performance degradation and failure probability distribution information. For this kind of unknown or uncertain probability distribution, the reliability assessment problem belongs to the lack of information problem. It is difficult to evaluate the reliability of the bearing under the condition of lack of information, which is still a scientific and technological problem. After the unremitting efforts of scholars at home and abroad, some research results have been achieved. For example, Shinji et al.11 used wavelet transform and fuzzy system theory to diagnose bearing faults; Verma et al.12 used fuzzy set theory to solve the lack of information problem.

The maximum entropy principle can make the best estimate of the unknown probability distribution with the least subjective bias, which plays a key role in the process of analyzing the unknown probability of sample data and has been widely used by domestic and foreign scholars in their scientific research fields. For example, Yang Jie et al.13 put forward the Bayesian uncertainty inverse analysis method based on the principle of maximum entropy and effectively combined the Bayesian method with the entropy of uncertainty inverse analysis to achieve the transformation analysis of the problem. Xia Xintao et al.14 combined the gray self-help principle with maximum entropy to obtain a new data processing method to analyze the output error distribution in the mechanical manufacturing process. Zhang Daobing et al.15 analyzed the reliability of tunnel lining structures based on the maximum entropy principle and optimization method. Dong Xinfeng et al.16 used the maximum entropy principle and the identification information method to analyze the degradation of the workpiece spindle of the grinder. It can be seen that the maximum entropy principle is gradually maturing for the unknown probability distribution, but it is still difficult to apply the maximum entropy principle to analyze the reliability of rolling bearings when there is little or very little sample data.

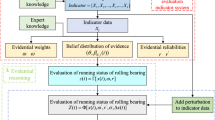
With the rapid development of deep learning in recent years, its application in equipment fault diagnosis and reliability analysis has become more and more common. In the case of incomplete samples, the data generation method has made great contributions to promoting the reliability analysis method in the case of few samples. For example, Yu et al.17 proposed a multi-stage semi-supervised network to detect bearing faults by using data integration and measurement learning; Zhang et al.18 proposed a semi-supervised diagnosis method for coupling faults of key rotating components; He et al.19 proposed an enhanced deep autoencoder for insufficient data, which has a good migration effect; Gao et al.20 used GAN to generate a large number of fault samples and applied them to fault diagnosis based on finite element simulation; Hua et al.21 proposed a GAN-based unbalanced data fault diagnosis method. At the same time, WGAN22, CCAN, and BiGAN have also been proposed successively, making GAN more and more widely used in various fields. Based on this, under the condition of insufficient information, this paper proposes the reliability evaluation of rolling bearings by generative adversarial network sample enhancement and maximum entropy method, and conducts reliability evaluation based on its mutation frequency, mutation speed and mutation acceleration. The scientificity and rationality of the model are verified through experiments, which can make a useful supplement to the existing reliability methods. The specific steps are shown in Fig. 1.

Fig. 1
figure 1

Implementation process.

Full size image

GAN network combined with maximum entropy method

Divide the vibration acceleration collected by the rolling shaft during service into various time series. The time variable was defined as t, and its sampling period was \(\tau\). There \(\tau\) was a constant with a small value. According to the collected vibration acceleration data, it was divided into \(\lambda\) time series. The time series during the period of the optimal running state of the rolling bearing was defined as the eigenstates and denoted as the first time series, represented by the vector X1.

$$X_{1} = (x(1),x(2),..x(k),...x(N))$$
(1)

where x(k) is the kth vibration signal data in the intrinsic sequence, k is the serial number of the signal data in the sequence of this syndrome, k = 1,2,3,… N(N ≥ 600); N is the number of vibration signals collected for each time series. With the progress of time t, the collected vibration acceleration is divided into various time series, and the \(\lambda\) time series vector is \(X_{\lambda }\).\(\lambda\) is the time serial number, n = 1,2,3,…\(\lambda\). Each time series contains N vibration signal data. The obtained time series vector X can be expressed as:

$$X = (X_{1} ,X_{2} ,...X_{\lambda } )$$
(2)

The vibration signals of each time series are trained separately through the GAN network proposed in this paper. The proposed model will print the value of the loss function and generate a sample every 200 rounds, and after 50,000 rounds of iterations, the network training is over. At this time, according to the genetic algorithm, the optimal round of the loss function of the generator and the discriminator is found, and the samples generated by this round of iteration are selected, and the samples collected during the service of the rolling bearing form the vibration signal data of the time series. In this case, the first sequence vector X1 is:

$$X_{1} = (x(1),x(2),..x(k),...x(n),...x(M))$$
(3)

In the formula, x(1) to x(n) is the real data collected by the intrinsic series during the service of rolling bearings, and x(n) to x(M) is the sample data generated by the real data of the time series after the training of the GAN network model, where k = 1,2,3,… n,…, M(M ≥ 10,000).

GAN network sample enhancement

In 2014, Goodfellow et al.23 proposed the Generative Adversarial Network (GAN). As an emerging deep learning model, the GAN network has achieved remarkable application results in speech recognition, image restoration, data generation and other fields. The GAN network consists of two independent network models: a generator and a discriminator. During the model training process, the generator continuously learns the distribution of real sample data. Its goal is to generate false data that the discriminator cannot distinguish. The discriminator’s goal is to continuously distinguish between real data and generated data. The optimization process of alternating training of the two models can be regarded as a minimax game problem. Through the adversarial learning mechanism, the performance of the generator and the discriminator is continuously improved. After a lot of training, the generator and the discriminator reach Nash equilibrium, and its objective function is as follows:

$$\mathop {\min }\limits_{G} \mathop {\max v}\limits_{D} (D,G) = E_{{x \sim P_{data} (x)}} [\log D(x)] + E_{{z \sim P_{z} (z)}} [\log (1 - D(G(z)))]$$
(4)

where: V(D,G) is the objective function; G is the generator; D is the discriminator; x is the real data and its distribution is Pdata (x); z is the random noise of input G, whose distribution is Pz(z); D(x) is the probability that the discriminator determines that the input is true data; G(z) for generated data; D (G (z)) is the probability that the discriminator determines that the input is generated data.

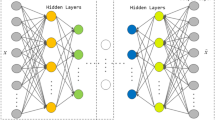
The discriminator and generator networks proposed in this paper are composed of fully connected neural networks. Fully connected neural networks are a standard feedforward neural network in which each neuron is connected to the neurons in the previous layer. The generator network proposed in this paper is constructed as an input layer containing a fully connected layer with 100 neurons, which is used to accept random noise input, and linear transformation and nonlinear activation are performed through the fully connected layer to gradually extract the feature information of the input. These fully connected layers have 128, 256, 512 and 256 neurons respectively, and finally 117 neurons in the output layer, and the output generated sample data enters the discriminator. After the fully connected layer, the output of each layer is standardized through the BatchNormalization layer to ensure that the output distribution of each layer is stable. The generator and discriminator use the LeakReLU activation function, which is mainly used to introduce nonlinearity to help the model learn complex data distribution. Unlike the ReLU function, the LeakyReLU function will not be completely flattened to zero by the activation function when it is negative, but through a small negative gradient, which helps to avoid the gradient vanishing problem and makes the model easier to converge during training.

Maximum entropy principle

The maximum entropy principle enables the best estimate of an unknown probability distribution with minimal subjective bias. For the convenience of narration, the continuous variable x is used to represent the discrete variable in this proof sequence; the discrete data sequence is continuous, and the expression of its maximum entropy is defined as H(x):

$$H(x) = - \int\limits_{w} {f(x)\ln f(x)dx}$$
(5)

where f(x) is the probability density function of x; \(\ln f(x)\) is the logarithm of the probability density function f(x); W is the feasible ___domain of the performance random variable x, \(W = [W_{1} ,W_{2} ]\), W1 is the lower boundary of its feasible ___domain and W2 is the upper boundary of its feasible ___domain.

In the process of solving the problem, the Lagrange multiplier method is introduced to solve the problem, and the probability density function f(x) is adjusted to make H(x) reach the maximum value so that the solution of the probability distribution is transformed into the solution of the Lagrange multiplier. Its Lagrange function can be expressed as:

$$\overline{H} = H(x) + (c_{0} + 1)[\int\limits_{w} {f(x)dx - 1] + \sum\limits_{i = 1}^{j} {c_{i} } } [\int\limits_{w} {x^{i} } f(x)dx - m_{i} ]$$
(6)

where j is the origin moment order; mi is I order origin moment; xi is the coefficient of f(x); c0 is the first Lagrange multiplier; ci is the i + 1 Lagrange multiplier, where i = 1,…j.

Its probability density function can be expressed in terms of f(x) and the first multiplier c0 as:

$$f(x) = \exp (c_{0} + \sum\limits_{i = 1}^{j} {c_{i} x^{i} } )$$
(7)
$$c_{0} = - \ln (\int\limits_{w} {\exp (\sum\limits_{i = 1}^{j} {c_{i} x^{i} } } )dx$$
(8)

It follows that the other j Lagrange multipliers of the probability density function f(x) should satisfy:

$$1 - \frac{{\int\limits_{w} {x^{i} \exp (\sum\limits_{i = 1}^{j} {c_{i} x^{i} )dx} } }}{{m_{i} \int\limits_{w} {\exp (\sum\limits_{i = 1}^{j} {c_{i} x^{i} )dx} } }} = 0$$
(9)

Ci can be solved by formula (9), where i = 1,2,3,…,j; Then c0 is solved according to formula (8), and then f(x) is solved according to formula (7).

Solving the confidence interval of random variables and calculating the mutation frequency

Select the confidence estimates Pq to be 1, 0.999, 0.99, 0.95, 0.9, etc., and use the quantile method to find the confidence interval [XLq, XUq] of the q-th performance random variable. The upper and lower limits should be satisfied:

$$\frac{1}{2}(1 - P_{q} ) = \int_{{X_{Uq} }}^{{w_{2} }} {f(x)dx;q = 1,2,3,...,\lambda }$$
(10)
$$\frac{1}{2}(1 - P_{q} ) = \int_{w1}^{{X_{Lq} }} {f(x)dx;q = 1,2,3,...,\lambda }$$
(11)

Assuming the significance level \(\alpha \in [0,1][0,1]\), the confidence level P is:

$$P = (1 - \alpha ) \times 100\%$$
(12)

For the maximum entropy estimation interval of this evidence sequence, take q = 1, and the maximum entropy estimation interval under the condition of confidence level P is \([X_{L1} ,X_{U1} ]\).

According to the maximum entropy estimation interval calculated by this certificate sequence, based on the Poisson process, record the number \(N_{\lambda }\) of the performance data of the \(\lambda\)-th time series falling outside the estimation interval \([X_{L1} ,X_{U1} ]\) of this certificate sequence, thus obtaining the \(\lambda\)-th mutation frequency of the time series \(f_{\lambda }\).

$$f_{\lambda } = \frac{{M_{\lambda } }}{M}$$
(13)

In the formula, \(M_{\lambda }\) the number of the \(\lambda\)-th time series performance data falling outside the intrinsic sequence, including the number falling greater than the upper limit value and less than the lower limit value. M is the sum of the data generated by the generative adversarial network and the data of real samples.

Reliability function analysis

The rolling bearing reliability function Rn(t) is used to represent the reliability of the n-th time series rolling bearing at time t to maintain the best performance state. Where n = 1,2,3,…,;Rn(t) can be expressed as:

$$R_{n} (t) = \exp ( - f_{n} t)$$
(14)

In the formula,\(f_{n}\) is the variation frequency of the rolling bearing, n is each time series, and t is the time variable. The purpose of solving the reliability function is to calculate the variation velocity and variation acceleration.

Variation velocity and variation acceleration

In the process of predicting the performance reliability of rolling bearings, the variation speed and variation acceleration of vibration performance reliability are used as characteristic parameters. During the operation of rolling bearings, \(f_{\lambda }\) changes as the running time of rolling bearings increases. Define the variation speed of vibration performance reliability at time t as V(t), where V(t) is used to characterize the variation trend of vibration performance reliability of rolling bearings. Define the variation acceleration of vibration performance reliability at time t as \(a(t)\), where \(a(t)\) is used to characterize the change speed of the variation speed V(t) of the vibration performance reliability of the rolling bearing. Its V(t) expression is:

$$v(t) = \frac{\Delta R}{\tau } = \frac{R(t + \tau ) - R + t)}{\tau } \approx \frac{{\exp ( - f_{t + \tau } t) - \exp ( - f_{t} t)}}{\tau }$$
(15)

In the formula, \(\Delta R\) is the reliability change of the rolling bearing performance data within the time interval \(\tau\), \(R(t + \tau )\) and \(R(t)\) are the reliability of the bearing performance at \(t + \tau\) and t times respectively. \(f_{t + \tau }\) is the mutation frequency of time series performance reliability at time \({\text{t + }}\tau\) relative to this certificate sequence, and \(f_{t}\) is the mutation frequency of time series performance reliability at time t relative to this certificate sequence. Therefore, for the performance reliability variation of each time series, the performance reliability variation of the n + 1 time series relative to the n time series can be expressed by Vn(t):

$$v_{n} (t) = \frac{{\exp ( - f_{n + \tau } t) - \exp ( - f_{n} t)}}{\tau }$$
(16)

For the reliability variation acceleration \(a(t)\), its expression is:

$$a(t) = \frac{\Delta v}{\tau } = \frac{v(t + \tau ) - v(t)}{\tau }$$
(17)

where: \(a(t)\) is the variable acceleration of rolling bearing performance reliability at time t; similarly, the variable acceleration of reliability \(a_{n} (t)\) for each time series is defined, and its expression is as follows:

$$a_{n} (t) = \frac{{v_{n + 1} (t) - v_{n} (t)}}{\tau }$$
(18)

Experimental verification

The experimental data comes from the XJTU-SY rolling bearing accelerated life test data set24,25. This dataset was jointly developed by Professor Lei Yaguo’s team from Xi’an Jiaotong University and Zhejiang Changxing Shengyang Technology Co., Ltd., and selected rolling bearings, a typical key component in industrial scenarios, as the test object. The team carried out a two-year accelerated life test of rolling bearings and released the obtained test data, the XJTU-SY rolling bearing accelerated life test dataset, to scholars around the world. The test bench for this dataset consists of an AC motor, a motor speed controller, a shaft, a support bearing, a hydraulic loading system, and a test bearing, as shown in Fig. 2. The test bearing model is LDK UER204 rolling bearing. An accelerometer is used to measure the vibration acceleration signal. The test is designed for three types of working conditions, with five bearings in each type of working condition, as shown in Table 1. This paper selects bearing 1–1 under this working condition for the experiment, and the experimental life of the bearing is 123 min.

Fig. 2
figure 2

Bearing accelerated life test bench.

Full size image
Table 1 XJTU-SY bearing data set information list.
Full size table

1600 vibration signal data of the test bearing during the optimal operating state are taken. After being generated by the GAN network, the data is combined with the real data to be defined as the intrinsic sequence. Based on the maximum entropy principle, the Lagrange multiplier method is used to solve it and the probability density function f(x) of the intrinsic sequence is obtained, as shown in Fig. 3.

Fig. 3
figure 3

Probability density function of this certificate sequence.

Full size image

When the significance level \(\alpha\) is 0.05, P = 95%, the true value of the maximum entropy estimation interval of this evidence sequence at this time is [− 0.8741, 0.7681]. The 1,600 vibration signal data in each subsequent period of time are generated by the GAN network and defined together with the real data as the second, third, and n-th time series. The amount of generated data is 11,934 pieces of vibration data. Find the frequency \(f_{\lambda }\) at which each time series data falls outside the maximum entropy estimation interval of this certificate sequence. The data is shown in Table 2.

Table 2 Variation number and mutation frequency of each time series.
Full size table

It can be seen from Table 2 that as the bearing operation time progresses, the variation frequency of each time series gradually increases, but there are differences in the speed of change. For example, there is a mutation in the second time series, and its variation frequency suddenly increases. In order to further determine the relationship between the mutation point and the variation frequency of the bearing, the variation frequency between the first time series and the second time series is further subdivided, and a more detailed time series is directly divided from the first time series to the second time series. The variation frequency results after subdivision are shown in Table 3.

Table 3 Number of mutations and frequency of mutations in each period time before mutation.
Full size table

As can be seen from Table 3, before the bearing variation frequency mutates, its variation frequency fluctuates stably within a certain range. This is consistent with the fact that under actual working conditions, the rolling bearing has a long-term normal operation stage in the early stage. However, as the rolling bearing continues to operate, its vibration signal will change significantly at a certain point, which we call the beginning of the unhealthy stage. According to the analysis in Table 3, this paper proposes to divide the bearing life stage according to the variation frequency, and the healthy stage is defined before the variation frequency mutation, and the unhealthy stage is defined after the mutation. This is consistent with the actual division of the healthy and unhealthy stages of the bearing. After monitoring the mutation point, the vibration signals of each time series are selected to further analyze the specific situation of the unhealthy stage. At the same time, in order to verify the accuracy and effectiveness of the method proposed in this paper for the bearing stage division, this paper selects the change frequency of each time series of the three methods for comparison, as shown in Table 3.

The reliability variation frequency of vibration performance of each time series under the condition of confidence level P = 95% and the difference in variation frequency of the three methods can be obtained from Table 4. The relationship between the variation frequency of the three methods and remaining life can be drawn from the data in Table 4, as shown in Fig. 4.

Table 4 Comparison of variation frequencies of the three methods.
Full size table
Fig. 4
figure 4

Variation frequency curves of the three methods.

Full size image

As shown in Fig. 4, with the increase of the running time of the rolling bearing, the reliability variation frequency of the vibration performance of each time series relative to the original sequence gradually increases, and according to the speed of the variation frequency increase in Fig. 5, the unhealthy period can be divided into three stages. The first stage is that the reliability variation frequency of the rolling bearing increases rapidly from the time it enters the unhealthy period; the second stage: as the rolling bearing continues to run in the unhealthy period, its reliability variation frequency enters a period of slow increase and slight fluctuation; the third stage: in this stage, the reliability variation frequency of the rolling bearing changes from slow increase and slight fluctuation to rapid increase, which indicates that the rolling bearing enters the final life stage. From the fitting curves of the three methods, it can be concluded that the reliability variation frequency of the rolling bearing under the condition of lack of information (few samples) is quite different from the reliability variation frequency of the rolling bearing under the condition of full life cycle (full samples), and the use of the GAN network for sample generation can make its variation frequency more consistent with the variation frequency under the condition of full life cycle, so the accuracy of the proposed method is greatly improved compared with its accuracy under lack of information.

Fig. 5
figure 5

Variation rate of two methods of sample generation and lack of information in the GAN network.

Full size image

Since the variation frequency can only simply conclude that the unhealthy stage is further divided into three stages, but the specific starting time of each stage cannot be accurately obtained, in order to accurately distinguish the specific starting time of the three stages of rolling bearings, this paper introduces the concepts of variation speed and variation acceleration. First, according to the rolling bearing variation frequency under insufficient information in Tables 2 and 4 and the rolling bearing variation frequency under the GAN network model combined with the maximum entropy method, the rolling bearing reliability function Rn(t) of each time series under the two methods is obtained by combining formula (14). According to the reliability estimation truth function combined with formulas (16) and (17), the variation speed of each time series of the two methods can be obtained. The variation speed image is shown in Fig. 5.

As shown in Fig. 5, the reliability variation rate of the bearing vibration performance is negative. This is because as the running time of the rolling bearing gradually increases, its bearing vibration gradually intensifies, and the reliability of each time series performance decreases successively. According to Fig. 5. A above, when the rolling bearing enters the unhealthy stage, its reliability variation rate changes dramatically. At this time, the absolute value of its reliability variation rate reaches the maximum relative to the absolute value of the reliability variation rate in other stages, so the corresponding two reliability variation rate curves are V(6) and V(7). We call this stage the initial running-in stage of the bearing, which is the first stage after the bearing enters the unhealthy stage. After the bearing has been in the unhealthy stage for a period of time, the wear rate slows down. At this time, the absolute value of its reliability variation rate presents the characteristic of slowly decreasing, and its absolute value is significantly reduced compared with the first stage, indicating that the bearing has entered the second stage of the unhealthy stage. This stage is the stable running-in stage of the bearing, which lasts for a long time. It can be seen from the three reliability variation rate curves of Figure V (3), V(4), and V(5) that they have this characteristic. Therefore, stages V(3), V(4), and V(5) are the second stage of the bearing, that is, the stable running-in stage. After that, the bearing performance began to deteriorate and entered the third stage of severe wear. The absolute value of the reliability variation rate in this stage showed an increase compared with the second stage. The corresponding reliability variation rate curves for this stage are V(1) and V(2), which are the variation rates between the 8th time series and the 7th time series, and the variation rates between the 7th time series and the 6th time series, respectively. As can be seen from Figure A, the absolute value of the reliability variation rate in this stage is larger than that in the late second stage. By specifically dividing the unhealthy stages of the bearing according to the reliability variation rate, the specific starting point of each stage can be accurately found, which provides a new method for dividing the new unhealthy stages of the bearing.

Figure 5B is a reliability variation rate diagram for each time period under information loss conditions. As can be seen from Fig. 5B V(6) and V(7) are the initial stage of bearing running-in, i.e. the first stage, and V(1) is the stage of severe bearing wear, i.e. the third stage. After the bearing enters the unhealthy stage, its vibration performance variation increases. Under the condition of information loss, it has a certain randomness and cannot fully reflect its accurate variation trend, resulting in the inability to accurately distinguish the maximum reliability variation rate in the second stage, i.e. the stable wear stage, and the maximum variation rate in the transition period of the third stage. Therefore, in the absence of information, it is impossible to accurately distinguish the specific start time of each stage. Compared with the images generated by GAN network samples, the distinction accuracy is significantly reduced, which further proves the accuracy of our proposed method in distinguishing the specific time of each stage in the unhealthy stage of the bearing.

In order to further explore the internal connection between the various stages of rolling bearings, we introduce the concept of reliability variation acceleration and use variation acceleration to characterize the speed of change of vibration performance reliability variation. According to Eqs. (18) and (19) and the above, the variation acceleration of each time series generated by the GAN network samples is obtained, and its variation acceleration image is shown in Fig. 6.

Fig. 6
figure 6

GAN network sample generation under each time series variation acceleration.

Full size image

The acceleration of bearing reliability variation is used to reflect the magnitude of bearing reliability variation speed. In the initial running-in stage of the bearing, its reliability variation frequency changes rapidly, and its reliability variation acceleration value should also be large. As shown in Fig. 6, with the increase of time, the absolute value of the acceleration of rolling bearing vibration performance reliability variation in each time series first increases to the maximum value and then gradually decreases to 0, that is, in the first stage, the wear rate is fast, the vibration performance variation frequency increases rapidly, so the reliability variation speed and its acceleration value change rapidly. As the bearing continues to run, its vibration performance continues to deteriorate, and the bearing enters the second stage, that is, the stable wear stage. The running time of this stage is relatively long, and the reliability variation acceleration of each time series gradually approaches 0. This is because the reliability variation rate of the bearing changes slowly in this stage, causing its reliability variation acceleration to approach 0. After the stable wear stage of the bearing ends, it enters the severe wear stage of the bearing. In this stage, the bearing is facing failure at any time. In this stage, its reliability variation rate increases again, causing the reliability variation acceleration to gradually increase from close to 0.

In order to further understand the preliminary relationship between the reliability variation acceleration and the remaining life of the test bearing, we selected a small amount of vibration signal data from the time when the bearing enters the unhealthy stage to the time when the bearing fails completely. After generating samples through the GAN network, the data reliability variation acceleration value of the bearing vibration signal every three minutes is calculated, as shown in Table 5.

Table 5 Variation acceleration of each time series.
Full size table

According to the reliability variation acceleration value of the bering 1–1 test bearing in the XJYU-SY data set in Table 5 every three minutes after entering the unhealthy stage, the preliminary relationship between the maximum value of the reliability variation acceleration of each subdivided time series relative to the verification sequence and the remaining life of the bearing can be obtained, and its fitting function is shown in Fig. 7.

Fig. 7
figure 7

Fitting curve of residual life and variable acceleration.

Full size image

Since the value of the reliability variation acceleration varies in different stages of the bearing, the relationship between the remaining life of the bearing and the reliability variation acceleration can be fitted. As shown in Fig. 7 and Table 5, after the rolling bearing enters the unhealthy stage, its reliability variation acceleration will decrease rapidly. In the remaining life interval of 48 min ~ 36 min, its reliability acceleration curve drops rapidly. Subsequently, the reliability variation acceleration fluctuates around the 0 interval, and its fluctuation amplitude is significantly weakened compared with the initial running-in period. This corresponds to the remaining life interval of 36 min ~ 9 min, and the running time of this stage is longer. Subsequently, as the bearing enters the severe wear stage, the absolute value of the reliability variation acceleration begins to show an upward trend, that is, the change in its reliability variation acceleration value begins to increase again as shown in Fig. 7. This stage corresponds to the remaining life of the bearing of 9 min ~ 1 min. The three stages are reflected in the figure, that is, the value of the reliability acceleration changes from a rapid decline stage to a slow fluctuation and then a rapid decline. From this, the preliminary relationship between the reliability variation acceleration and the remaining life can be obtained, and the stage of the bearing life can be judged according to the fitted curve.

Conclusion

Aiming at the problem that rolling bearing vibration signals are difficult to extract in large quantities under actual working conditions, this paper proposes a rolling bearing reliability method based on sample enhancement and maximum entropy method of generative adversarial network, and obtains the following conclusions through experimental verification:

  1. 1.

    In this paper, according to the reliability analysis of GAN network sample enhancement combined with maximum entropy method, it is concluded that the fitting effect of the variation frequency curve with the whole life cycle is greatly improved compared with the original lack of information (small sample). In this paper, a method is proposed to divide the starting points of the healthy and unhealthy stages of bearings according to the frequency of variation.

  2. 2.

    In order to more accurately distinguish the specific start time of the three stages, this paper proposes to distinguish the start time of the three stages according to the absolute value of the reliability change rate. The first stage is the time series from the sudden change of the reliability change rate to the time series before the reliability change rate changes slowly. The characteristic of this stage is that the absolute value of the reliability change rate is significantly greater than other stages. We call it the initial running-in stage. The second stage is when the reliability change rate fluctuates from a drastic change to a smaller value. This stage corresponds to the second stage, that is, the stable running-in stage. The third stage is when the reliability change rate suddenly increases from a stable fluctuation. This stage is the third stage, that is, the drastic wear stage. According to the absolute value of the reliability change rate, the specific start time of each stage and the stage corresponding to each time series can be accurately located. Compared with the problem that the specific start time of each stage cannot be distinguished when there are few samples, the method proposed in this paper can better avoid the occurrence of this problem.

  3. 3.

    The bearing is subdivided after entering the unhealthy stage, and the preliminary relationship between the remaining operating life of the bearing in the unhealthy stage and the reliability variation acceleration is obtained, which makes a useful supplement for the subsequent research on predicting the bearing life.