Introduction

A comprehensive statistical quality control chart is one of the most crucial and useful instruments in statistical process control (SPC). It is extensively employed in a variety of industries, including the manufacturing, process, and service sectors, to carefully monitor and maintain the quality of products. Since the 1920s, when the first Shewhart charts were introduced, quality control charts have gained importance (Montgomery1). The SPC literature presents a variety of control chart designs, both memoryless and memory-based, including the Shewhart, EWMA, CUSUM, AEWMA, and ACUSUM control charts, among others. Memory-type control charts have drawn a lot of interest because of how fast they can identify slight to moderate changes in process parameters. Their capacity to do so makes them popular in the industrial and production sectors, where even small disruptions can result in substantial financial losses.

Page2 created the CUSUM chart to track process dispersion, while Roberts3 first produced the EWMA chart to track the process mean. Typically, in real-world applications, tracking variations in the process dispersion poses a greater risk than tracking the process mean. In real-world applications, monitoring changes in process dispersion is often more critical than tracking shifts in the process mean, as an increase in dispersion reduces the process efficiency, while a decrease boosts process capability and productivity. Reporting a change in the process mean is worthless if the dispersion of the process is not under control.

While memory-based control charts are commonly employed, their efficacy is limited to situations where shift magnitudes are identified or if the quality practitioner bears the explicit responsibility of generating a shift-specific monitoring chart. Although the conditions in real-world situations are frequently different, shift magnitude might not be known in advance and needs to be calculated first. After this, researchers have focused on the more recent development of adaptive control-charting frameworks to enhance protection in response to different-sized shift adjustments. The authors used several adjustments to normalize the dispersion estimators because their probability distributions are positively skewed. These changes are meant to guarantee the control chart’s unbiased average run length (ARL) performance, which is dependent on the altered dispersion estimator. The predicted number of samples required to control chart to generate an out-of-control signal is represented by the ARL. An ARL is deemed unbiased if its out-of-control ARLs are consistently shorter than its in-control ARL. The AEWMA control chart was introduced by4 and uses a scoring function to track shifts in dispersion operation. The primary approach of this control chart involves adjusting prior observations using a relevant function of the current estimate’s error. Typically, an unbiased estimator is enhanced by the EWMA statistic, which is used in adaptive control charts to estimate process shifts. The shift estimator is then employed to optimize the control chart5.

A large amount of academic research shows that machine learning-based systems for statistical process monitoring are more successful. These machine learning-based tools have shown significant potential in enhancing the oversight and management of diverse procedures. This highlights the increasing acceptance and use of these advanced methods, confirming their value in enhancing the overall efficiency of process monitoring practices. For instance, Walid et al.6, Cuentas et al.7, Machado & Costa8, etc. utilized machine intelligence-based methods that enhance the efficiency of control charting techniques. Khusna et al.9 introduced a multivariate EWMA control chart based on multioutput least squares SVR to address small shifts in auto-correlated processes. The SVR effectively maps multivariate inputs to outputs, reducing serial correlation. Simulation studies using a VARMA model with outliers demonstrate that the proposed chart accurately detects additive outliers at different times across variables. For innovative outliers, it signals double out-of-control conditions. Similarly, Yeganeh et al.10 also proposed a design that focuses on Phase II Poisson profile monitoring and introduces a new robust control chart using SVR with novel input features and an evolutionary training algorithm. The method outperforms conventional techniques in detecting out-of-control signals and is superior in handling fixed explanatory variables and non-parametric models. Although it isn’t the best for all cases with random explanatory variables, it excels in most scenarios. A machine learning-based diagnostic method is also developed, achieving strong results compared to other approaches.

Recently, Kazmi and Noor-ul-Amin11 introduced a parameter-free AEWMA control chart to monitor variations in the process mean. They first trained a support vector regression (SVR) model, which then predicted the smoothing constant based on the shift size. This predicted value was subsequently applied in the final EWMA statistic for charting. Similarly, to track process dispersion, we have created an AEWMA control chart that does not need any pre-defined value of smoothing constant. The approach involves training a machine learning model using optimal smoothing parameter values corresponding to the shift magnitude. The trained model then predicts the appropriate smoothing parameter in response to the detected shift size. The run length profile is determined through Monte Carlo simulations.

The structure of the paper is as follows: “Support vector regression” provides a brief overview of SVR. “Existing control charts” discusses existing control chart techniques. “Proposed AEWMA control chart” outlines the architecture of the proposed control chart. “Main findings” presents the main findings, while “Practical example” demonstrates the practical application of the proposed chart. Finally, “Conclusion” concludes the article.

Support vector regression

Support Vector Machines (SVM), a technique used in data mining and predictive modeling, have been popular in many different fields and provide excellent treatments for a wide range of real-world issues. Vapnik12 presented Support Vector Machines to solve issues with classification and regression. It has been designed for use in classification and regression tasks, either in a supervised or semi-supervised context. Although the majority of SVM work has focused on classification, SVM also provides extremely favorable outcomes for regression purposes13. Smola and Schölkopf14 finished a thorough study on the use of SVM in regression issues. The SVM employed in regression purposes is known as Support Vector Regression (SVR).

Encouragement Reliability is increased while using Vector Regression as it lessens the effect of outliers on the regression equation. The SVR method seeks to identify a function that closely matches the training data while minimizing the estimation error. Finding a line (function) that matches the data with the least amount of inaccuracy is the aim while remaining within the maximum points of a margin15. Figure 1 illustrates the graph of SVR16.

Fig. 1
figure 1

Linear support vector regression.

Full size image

The theory suggests that a linear function can be used to represent the nonlinear relationship between input and output data. The function is defined as follows:

$$f\left(x\right)= {w}^{T}\phi \left(x\right)+b$$

Here, f(x) represents the estimated function, (x) indicates a fixed transformation of the feature space, and w (w ∈ Rn) is the weight and b (b ∈ R) is the bias parameter, respectively. The regularity constant C > 0 limits model complexity by defining the amount of error permitted for training data that exceeds the bound ε (ε ≥ 0). By keeping C > 0 and ε > 0, the standardized form of the SVR is as follows:

$${Min}_{w,b,\xi ,{\xi }^{*}}= \frac{1}{2}{w}^{T}w+C\sum_{i=1}^{l}{\xi }_{i}+{\xi }_{i}^{*}$$

Subject to the

$$\left\{\begin{array}{c}{w}^{T}\phi \left({x}_{i}\right)+b-{y}_{i}\le \epsilon +{\xi }_{i}\\ {y}_{i}-{w}^{T}\phi \left({x}_{i}\right)-b\le \epsilon +{\xi }_{i}^{*}\\ {\xi }_{i},{\xi }_{i}^{*} \ge 0;i=\text{1,2},\dots ,l\end{array}\right.$$

where yi is the objective function value concerning the xi, and ξi and \({\xi }_{i}^{*}\) are slack variables used to handle infeasible limits. ξi represents training errors below ɛ, while \({\xi }_{i}^{*}\) represents training errors above ɛ.

The accuracy of the SVM regression model relies on the selection of the kernel function and the parameter settings. Kernel functions map data into a higher-dimensional feature space to achieve linear separation. This process involves two steps: first, selecting the type of kernel function, followed by determining the appropriate parameters. Choosing a suitable model is essential for enhancing the performance of support vector regression17. Figure 2 illustrates the architecture of the SVM.

Fig. 2
figure 2

Depicting the input and output of the SVR.

Full size image

In Fig. 2, (xi, xj) represents the kernel function that calculates the inner product of the input vectors16. The SVR output is obtained by summing the weighted combinations of these inner products18. SVR typically uses linear, polynomial, and radial basis kernel functions. The equations for these functions are provided in Table 1.

Table 1 Common kernel functions used in SVR.
Full size table

Existing control charts

This section provides a brief overview of some existing control charts used to monitor changes in the variance of a normally distributed process. Let Y represent the quality characteristic of interest, where Y follows a normal distribution with mean μY and variance, i.e., \(Y \sim N({\mu }_{Y,}{\sigma }_{y}^{2})\). We consider a sequence of normally distributed random variables {Yt} for t ≥ 1. The focus of this review is on detecting shifts in the process variance \({\sigma }_{y}^{2}\) . The process Yt is considered to be in control when it remains stable with parameters like \({Y}_{t} \sim N({\mu }_{Y,}{\sigma }_{y}^{2})\) for time t < to, but the process becomes out of control as a result of a change in the process variance then it works on the parameters like \({Y}_{t} \sim N({\mu }_{Y,}{\sigma }_{y,1}^{2})\) for time t > to. Where, \({\sigma }_{y,1}^{2}\) represents the variance of out-of-control process and time to is unknown. Let \(\tau\) show the quantity of shift in the process as \(\tau = {\sigma }_{y,1}^{2}/{\sigma }_{y}^{2}\). When the process is in control such that t < to then \(\tau\) = 1, but \(\tau\) ≠ 1, when the process goes out of control for t > to. As our focus is on the monitoring of process variance then taking a random sample of Yt of size n at time t.

EWMA-S2 control chart

Castagliola19 developed the EWMA-S2 chart, which monitors \({\sigma }_{y}^{2}\) by transforming \({S}_{y}^{2}\) into a 3-parameter logarithmic transformation function to achieve a normally distributed random variable. The goal of transforming \({S}_{y}^{2}\)​ is to approximate normality to achieve nearly impartial ARL performance for the EWMA-S2chart. For the in-control process like t < to, Let \({F}_{t}=a+b \text{ln}({S}_{t}^{2}+c)\), where a, b and c have specific forms like a = A(n) − 2B(n)ln(\({\sigma }_{y}\)), b = B(n), and c = C(n)\({\sigma }_{y}^{2}\). The values of a, b, and c are sensibly set to ensure approximate normality for Ft i. e. \({F}_{t} \sim N({\mu }_{Y}\left(n\right),{\sigma }_{y}^{2}(n))\). Here, the sample size n plays a crucial role because the values of the constants a, b, and c, as well as the mean and variance of Ft, vary with changes in the sample size as reported by (Castagliola). So, the EWMA statistic using the function Ft is defined as:

$${E}_{t}=\lambda {F}_{t}+(1-\lambda ){E}_{t-1}$$

where, the value of λ, constrained to the interval (0, 1], acts as a smoothing parameter and \({E}_{0}=a(n)+b(n)\text{ ln}({S}_{t}^{2}+c(n))\) which relies only on n. Et is the charting statistic of this chart which moves against the LCL and UCL as follows:

$$UCL= \mu F + L \sigma F \sqrt{\frac{\lambda }{2-\lambda }}, CL= \mu F, LCL= \mu F- L \sigma F \sqrt{\frac{\lambda }{2-\lambda }}.$$

Selecting L > 0 ensures that the in-control ARL of the EWMA-S2 chart meets a particular level. The 2-sided EWMA-S2 chart can identify both rises and falls in process dispersion, One-sided EWMA-S2 charts are designed to detect either increases or decreases in variance. An out-of-control signal is triggered when Et exceeds the UCL or falls below the LCL, signaling a rise or drop in σY.

AEWMA-I control chart

Haq and Khoo20 developed a parameter-free AEWMA control to keep an eye on the ___location of the procedure. We have built upon their work to extend the approach for monitoring process variance. As the \({S}_{Y}^{2}={\Sigma }_{i=1}^{n}{\left({Y}_{i}-\overline{Y }\right)}^{2}/(n-1)\) is considered as the unbiased sample estimate of population variance σ2. Where Yi = Y1,Y2,…, Yn and \(\overline{Y }={\Sigma }_{i=1}^{n}{Y}_{i}\). Assuming the underlying process is working in stable conditions, then \({\xi }_{Y}=\left(n-1\right){S}_{Y}^{2}/{\sigma }_{Y}^{2}\) follows a chi-squared distribution with (n—1) degrees of freedom, i.e. \({\xi }_{Y}\sim {\chi }_{n-1}^{2}\). Let for an in-control process \({\phi }^{-1}\left(F\left({\xi }_{Y}\right)\right)\) follows a standard normal distribution i.e. \({\phi }^{-1}\left(F\left({\xi }_{Y}\right)\right)\sim N(\text{0,1})\). Let WY,t = \({\phi }^{-1}\left(F\left({\xi }_{Y}\right)\right)\), so based on the sequence of WY,t the charting statistic of the AEWMA control chart is as follows:

$$B_{t} = \, p\left( {W_{Y,t} } \right)W_{Y,t} + \, \left( {1 \, - \, p\left( {W_{Y,t} } \right)} \right) \, B_{t - 1}$$

where B0 = 0 and p(WY,t) \(\in\) (0,1] which is defined as

$$p\left({W}_{t}\right)= \left\{\begin{array}{c}0.05 if 0.0<{W}_{t}<{m}_{1}\\ 0.25 if {m}_{1}<{W}_{t}< {m}_{2}\\ \begin{array}{c}0.50 if {m}_{2}<{W}_{t}< {m}_{3}\\ 1.00 if {m}_{3}< {W}_{t}\end{array}\end{array}\right.$$

Here, the values of m1, m2 and m3 are wisely chosen like m1 = 3.71902, m2 = 4.09023 and m3 = 5.09023. The reader may refer to Haq and Khoo (2020) for more details. The AEWMA chart signals a process being out of control when the plotted statistic Bt exceeds h or falls below − h, where h is a tunable positive constant that can be adjusted to attain the target in-control ARL.

Proposed AEWMA control chart

In the statistical context, the EWMA technique is well-regarded for its effectiveness in detecting small, persistent changes in a process, making it a valuable tool in SPC applications. Integrating SVR with the AEWMA methodology offers a novel approach to monitoring process dispersion. In the following discussion, we will explore how this combination enhances the capability of the AEWMA control chart by leveraging the strengths of SVR for more accurate and robust process monitoring.

Let Xt be an independent and identically random observations sequence with mean µo and standard deviation σo corresponding to the in-control process. The idea is to first train the SVR model given below with the specified kernel and other parameters of SVR. To accomplish this, utilize the standard normal variable Xt​ and the corresponding values of the smoothing constant (refer to the supplementary file) for training the SVR model outlined below:

$$f\left(x\right)= \sum_{i=1}^{t}{\alpha }_{i}K(x,{x}_{i})+b$$
(1)

αi is the Langrage multiplier for each support vector determined during the training process, K(x, xi) is the kernel function and b is the bias term. The various types of kernels available for use have been previously outlined in “Support vector regression”. Now take the value of Xt of the desired quality characteristic and apply the Ft transformation discussed in the earlier section then predict the value of smoothing constant λ through the trained SVR model given in Eq. (1) for charting statistic AEWMAt.

$${AEWMA}_{t}=\lambda {X}_{t}+(1-\lambda ){\overline{AEWMA} }_{t}$$
(2)

The process triggered out of control signal if |AEWMAt|> h. where ℏ acts as a threshold and is always supposed to be bigger than zero. By finding the value of h, the in-control ARL is fixed at a specific level, let’s say ARL0. The threshold value h of each specified kernel function is found on its own. Unlike existing AEWMA controls, the suggested AEWMA control chart has the advantage of not relying on any pre-specified parameters. Figure 3 provides a quick description of the proposal’s design.

Fig. 3
figure 3

Flow chart of proposed design.

Full size image

Construction of AEWMA control chart

This section will discuss the algorithm for the developed AEWMA control chart.

  1. i.

    Train the SVR model at the optimal values for its parameters, using the data provided in the supplementary file.

  2. ii.

    Now take the data Xt ~ N(µo, σ2) of the desired quality characteristic and apply the Ft transformation.

  3. iii.

    Then predict the values of the weighting parameter through the trained SVR model for the values Ft.

  4. iv.

    Construct the plotting statistic for the developed AEWMA control chart using the predicted smoothing constant obtained from the trained SVR model.

  5. v.

    This constant is adjusted based on the size of the shift observed in the data variance.

Main findings

The results of the advised methodology based on the SVR model are shown in Tables 2, 3, 4 and 5. The following are the key conclusions of the suggested AEWMA control charts:

  1. 1.

    As the variance shift increases, both ARL and SDRL decrease across all sample sizes (n = 3 to n = 7). When the variance shift nears 2.00, ARL values drop significantly, indicating quicker detection of the shift. This pattern of decreasing ARL and SDRL with increasing variance shift is consistent for all sample sizes.

  2. 2.

    When compared to larger sample sizes, the smallest sample size (n = 3) typically yields higher ARL values, indicating a slower rate of shift detection. For example, we can observe from Table 2 that at ARLo = 370 at \(\tau\) = 1.05 the ARL value for n = 3 is 143.03 but at n = 7 at the same shift, the ARL value is 98.98. As represented in the Fig. 4.

  3. 3.

    The trend for the decline in variance is likewise comparable. For all sample sizes, the ARL and SDRL continuously drop as the variance decreases. ARL values drastically decline and approach zero when the variance drops to 0.50, indicating a faster detection of the variance decrease. For instance, in Table 3 for n = 5, the ARL value is 113.14 at

  4. 4.

    \(\tau\) = 0.95, but it decreases significantly to 6.34 at

  5. 5.

    \(\tau\) = 0.50.

Table 2 Run length of the one-sided AEWMA chart for detecting increased process variance.
Full size table
Fig. 4
figure 4

ARL behavior concerning change in variance (increase/decrease).

Full size image
Table 3 Run length of the one-sided AEWMA chart for detecting decreased process variance.
Full size table

Significance of the study

The significance of the proposed design lies in combining SVR with the EWMA control chart, which offers a novel approach to process monitoring. By using SVR, the adaptive EWMA control chart benefits from the model’s ability to handle non-linear relationships and complex data patterns, enhancing the detection of small process shifts more effectively than traditional methods. This integration leads to a more robust and flexible monitoring system, improving both accuracy and responsiveness in real-time applications, particularly in environments where processes change dynamically. Additionally, the proposed design does not require a predefined weighting parameter for the EWMA statistic, unlike the approach advised by Sarwar & Noor-ul-Amin5.

Role of kernel in ARL computations n = 5, C = 0.1, epsilon = 0.1

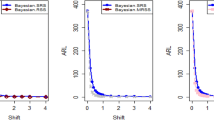
Table 4 demonstrates how the ARL and SDRL for three different control chart types Linear, Radial, and Polynomial vary with increasing shifts in variance. As the shift (increase in variance) intensifies from 1.00 to 2.00, the ARL values for all three methods generally decrease, indicating that the control chart detects the out-of-control signals more quickly with larger shifts. Notably, the Linear and Radial methods show similar ARL and SDRL trends, with the Polynomial method displaying higher ARL and SDRL values, especially at smaller shifts. This implies that, in contrast to the other two approaches, the polynomial method might be less sensitive to slighter disturbances in the dispersion. In addition, the radial kernel function is more appropriate as it consistently yields smaller ARL values compared to the other two kernels. This is visually represented in Fig. 5, where the ARL values for the radial kernel are notably lower, demonstrating its superior performance.

Table 4 Comparison of ARLs across different kernels.
Full size table
Fig. 5
figure 5

Kernel performance in terms of ARLs.

Full size image

Effect of gamma on control charts efficiency

Table 5 demonstrates that as the shift increases, lower ARL values become increasingly significant for effective shift detection. Among the gamma values tested, Gamma = 1 consistently produces lower ARL values compared to Gamma = 1.5, Gamma = 2, and Gamma = 2.5. This trend highlights the importance of lower ARL values for the timely detection of process shifts. Specifically, Gamma = 1 provides the most responsive detection of shifts, with ARL values decreasing from 368.55 at a shift of 1.00 to 3.91 at a shift of 2.00. In contrast, while higher gamma values also show a decrease in ARL with increasing shift, they do not achieve the lower ARL values observed with Gamma = 1. This suggests that Gamma = 1 offers the most effective sensitivity in detecting shifts, as evidenced by its consistently lower ARL values across different shifts. This trend is clearly illustrated in Fig. 6, where the line representing Gamma = 1 consistently remains below those of higher gamma values, emphasizing its superior performance in shift detection.

Table 5 Effect of gamma values on SVR with Gaussian RBF kernel.
Full size table
Fig. 6
figure 6

Impact of Gamma on SVR performance.

Full size image

Comparative analysis

The ability of the AEWMA charts to detect various changes in the process variance in both steady-state and zero-state situations is examined in this section.

The run length patterns for the two AEWMA charts are shown in Table 6 and were determined using 100,000 iterations of the run length for each simulation with upper control limit h = 0.9600 for AEWMA CC and h = 0.3560 for AEWMA-I CC. The instant the variance shift occurs is depicted by the cut. With a cut = 10, for instance, the variance shift is applied following the tenth sample, and the run length is then determined. Setting the cut to 0 compares the charts’ zero-state run duration profiles. Various key points are noted in Table 6.

  1. 1.

    The AEWMA chart consistently behaves better than the AEWMA-I for δ ≤ 0.70, with shorter out-of-control ARLs if the cut = 0. For example, the AEWMA-I chart shows an ARL of 48.22 for the same shift, whereas the AEWMA chart shows an ARL of 39.83 at δ = 1.10.

  2. 2.

    The AEWMA chart’s SDRL values are substantially lower than the AEWMA-I chart at all shift levels when the cut = 0. This implies that the AEWMA chart demonstrates greater consistency in performance compared to the AEWMA-I chart. For example, with a shift of 1.05, the SDRL of the proposed chart is 70.12, notably lower than the competitor’s value of 89.75.

  3. 3.

    Interestingly, both charts in the control state produce ARLs which remain close to ARL0 = 200 across all cut kinds. At every shift level and for every kind of cut, the AEWMA control chart’s ARLs are much lower than the AEWMA-I. For instance, the ARL values of the AEWMA control chart are 77.45,39.88,17.55,11.08,8.18, and of the AEWMA-I are 100.93,47.51,20.18,12.48,9.01 respectively when cut = 50 at shifts 1.05, 1.10,1.20,1.30,1.40.

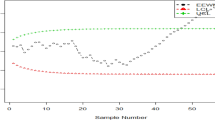
Table 6 Comparison with the competitor in terms of ARL (n = 5).
Full size table

When the in-control ARL0 is adjusted to 200, we compare both charts’ detection capabilities in Fig. 7. As expected, the AEWMA chart outperforms the AEWMA-I chart in terms of ARL. Likewise, the detection capabilities of both charts are evaluated in the steady state (cut = 10) with the in-control ARL0 set to 200. Figure 8 further illustrates that the proposed control chart surpasses its competitor in terms of ARLs.

Fig. 7
figure 7

Zero-state run-length comparisons.

Full size image
Fig. 8
figure 8

Steady-state (cut = 10) run-length comparisons.

Full size image

Practical example

This section presents the real-life data and details the implementation procedures and methodologies for the proposed method and existing control charts applied to real-world data. Using an actual dataset from Jones-Farmer and Champ21, a numerical example is shown to show how the suggested chart examined in this paper can be applied. In Table 7. The patient’s wait durations (in minutes) with µ0 = 8.74 and σ0 = 4.05 for a colonoscopy procedure are included in the dataset. This numerical example includes plots for both the proposed and current charts.

Table 7 Colonoscopy times (minutes) for 30 subgroups of 5 patients.
Full size table

Since the proposed control chart is designed for input data from a standard normal distribution, the normality of the original data is evaluated using a QQ plot. The results appear questionable, prompting the standardization of the input data using the Ft statistic to obtain more efficient outcomes as shown in Fig. 9a, b. Moreover, the histogram clearly illustrates that the data is not symmetrically distributed, highlighting its positive skewness as demonstrated in Fig. 10.

Fig. 9
figure 9

(a) Normality of original data. (b) Normality after applying Ft Statistic.

Full size image
Fig.10
figure 10

Histogram of patients waiting time for colonoscopy.

Full size image

Implementation of the proposed chart

  1. i.

    Use the waiting time values Xt (where t = 1, 2, 3,…, 30) of patients as the variance for each subgroup i (where i = 1, 2, …, 5).

  2. ii.

    Apply the Ft transformation on the Xt series, then train the data with the SVR model that is recommended in "EWMA-S2 control chart".

  3. iii.

    Now, use the trained SVR model to forecast the smoothing constant’s value.

  4. iv.

    Utilizing a smoothing constant, compute the charting statistics given in Eq. (2) and plot the charting statistic.

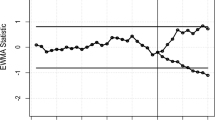
The process remains in control, as illustrated in Figs. 11 and 12, where the control chart remains stable over the initial 25 samples and the process variance increases over the subsequent five samples. The AEWMA and AEWMA-I charts reveal out-of-control conditions in the 26th and 29th samples, respectively, demonstrating that the constructed AEWMA control chart identifies an out-of-control state earlier than the AEWMA-I control chart. This suggests that, on average, the proposed chart exhibits greater sensitivity than the existing chart.

Fig. 11
figure 11

AEWMA-I control chart.

Full size image
Fig. 12
figure 12

Proposed AEWMA control chart.

Full size image

Conclusion

This paper introduces a novel approach for effectively monitoring changes in process dispersion. The charting statistics are calculated using a smoothing constant predicted through an SVR model’s training. A detailed analysis of the SVR model is carried out, focusing specifically on how different kernels impact the performance of the proposed control chart. The performance of the proposed AEWMA chart is evaluated through ARLs and compared with those of existing alternatives. The results show that the proposed AEWMA control chart performs better than the AEWMA-I control chart regarding ARLs. Additionally, a real-life application is demonstrated using patient wait times for a colonoscopy procedure to showcase the practical use of the AEWMA chart. Future research could focus on improving the performance of the AEWMA chart by incorporating different machine-learning techniques.

The use of SVR is limited in the sense that its effectiveness heavily depends on the careful selection of the kernel and its parameters. Additionally, exploring other kernel functions not covered in this study presents a compelling opportunity for future research that can be pursued in later investigations. The proposed methodology may be extended to multivariate cases for complex data sets. Additionally, other machine learning methods can be incorporated to enhance the monitoring ability of the control charts.