Introduction

Orthotropic steel decks (OSDs) have been widely applied in long-span cable-stayed bridges and suspension bridges owing to their advantages of light weight, superior bearing capability, rapid constructability, among other favorable characteristics1,2. Despite these attributes, the inherent welding imperfections, compounded by welding residual stresses (WRS) and the burden of increasing traffic loads, precipitate the consistent emergence of fatigue cracks within the welded joints throughout the service life of OSDs3,4,5. Extensive statistical analysis of numerous data cases and experimental studies have unequivocally demonstrated that OSDs exhibits multiple typical fatigue-prone locations, specifically in the rib-to-crossbeam welded joints, butt welded joints of longitudinal ribs, and the rib-to-deck welded joints6,7,8,9,10. Among these, the fatigue cracks initiating at the rib-to-deck welded joints have been identified as having the most profound impact on the performance of OSDs. An in-depth review of fatigue cracks in conventional single-sided rib-to-deck welded joints has revealed four primary types of fatigue cracking: root-deck, toe-deck, toe-trough, and root-throat cracks. The root-deck and toe-deck cracks, in particular, pose a significant threat due to their potential to penetrate the deck plate, exacerbating pavement damage and intensifying maintenance challenges11,12,13.

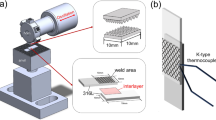
Recently, with the development of intelligent welding technology, China has developed an automatic longitudinal rib internal welding technology that addresses the challenge traditional manufacturing technology faced in welding inside the closed longitudinal ribs with narrow spaces. This innovation involves the application of intelligent robotic automatic welding technology to introduce fillet welds within the U-rib, thereby complementing the conventional single-sided welds and culminating in the formation of innovative double-sided rib-to-deck welded joints. The innovative double-sided rib-to-deck welded joints has been effectively implemented to enhance the fatigue resistance of OSDs, and its application has been successfully implemented in practical engineering projects, as shown in Fig. 1 ref14,15,16. This method involves welding both the internal and external surfaces of the U-ribs connected to the decks, which mitigates stress concentration at the weld root and reduces out-of-plane deformation. However, the double-sided welding process, characterized by multiple passes, results in a complex and inhomogeneous distribution of WRS within the weld heat-affected zone of the rib-to-deck joints. Notably, WRS are a pivotal influencing factor on the fatigue resistance of welded joints. The tensile stress components within the WRS play a particularly detrimental role, exhibiting a direct correlation with the initiation and propagation of fatigue cracks17,18.

Fig. 1
figure 1

Automatic double-sided welding technology16.

Full size image

Recently, researchers have conducted experiments and finite element numerical simulations to investigate the distribution characteristics of WRS, fatigue crack propagation and life assessment19,20,21. Zhang et al.16 and Cui et al.22 employed ultrasonic techniques to measure the WRS at the rib-to-deck double-sided welded joints in OSDs. Their findings indicated that the WRS reaches its peak within the heat-affected zone adjacent to the welded joints and exhibits a rapid decline with increasing distance from the welds. Qiang et al.23 combined experimental measurements with numerical simulations to explore the distribution characteristics of WRS along the deck thickness direction of these joints. Chen et al.24 performed thermo-elastoplastic numerical simulations to investigate the transverse WRS distribution in rib-to-deck double-sided welded joints, revealing that the transverse WRS exhibits a tension–compression-tension stress along the deck thickness direction.

In addition, the inception of cracks or defects within welded steel bridges, particularly in the weld zones, is an unfortunate inevitability. These imperfections are susceptible to further cracking and eventual failure when subjected to the relentless cycle of vehicle loads. Fracture mechanics offers a significant advantage in this context, as it enables a comprehensive assessment of fatigue crack propagation and the prediction of critical crack occurrences. This approach facilitates precise analysis of the remaining fatigue life for structural components that exhibit initial flaws. The fracture mechanics-based fatigue analysis method has been widely adopted for evaluating the fatigue reliability of steel bridges. Yang et al.25 and Liu et al.26 conducted experiments and developed numerical fracture mechanics models to investigate the fatigue crack propagation behavior of rib-to-deck double-sided welded joints in OSDs. Heng et al.27 utilized fracture mechanics analysis to assess the probabilities of fatigue crack growth in rib-to-deck welded joints of OSDs. Miao et al.28 employed the Monte Carlo simulation method to estimate the reliability of fatigue cracks. Deng et al.29 introduced a fatigue reliability analysis method for welds of rib-to-deck welded joints, integrating linear elastic fracture mechanics with long-term monitoring data. Despite these advancements, current studies have limitations in comprehensively assessing the fatigue reliability of rib-to-deck welded joints in OSDs under dynamic vehicle loading. Traditional methods, which do not consider the characteristics of WRS, cannot accurately evaluate the fatigue performance of these joints under the combined influence of WRS and traffic loads. Therefore, considering the effects of WRS in conjunction with the actual effects of traffic loads, real-time evaluation of the fatigue performance degradation process in rib-to-deck welded joints is essential for ensuring the long-term operation safety of OSDs.

This study aims to assess the fatigue reliability of rib-to-deck double-sided welded joints in OSDs subject to dynamic vehicle loading, considering the influence of WRS. Utilizing fracture mechanics theory, a comprehensive fatigue damage equation for the welded joints of OSDs has been developed, which integrates the effects of WRS and dynamic loading. A measurement-based random traffic model was employed to derive the vehicle-induced stress spectra at the rib-to-deck double-sided welded joints in OSDs. The effects of deck thickness, fatigue crack depth and fatigue crack aspect ratio variation on stress intensity factor (SIF) were discussed, and shape functions were construction to calculate the SIF in response to external load. The effect of WRS on the fatigue reliability of the weld toe of rib-to-deck double-sided welded joints in OSD was analyzed. The influence of traffic volume growth on the fatigue reliability was also discussed. The technical route of this paper is seen in Fig. 2.

Fig. 2
figure 2

Flowchart of fatigue reliability assessment in OSD.

Full size image

Fatigue reliability function

The well-known power model for fatigue crack growth rate, formulated by Paris law30, is depicted in Eq. (1).

$$da/dN = C\left( {\Delta K} \right)^{m}$$
(1)

where \(da/dN\) represents fatigue crack growth rate, the material constants of C and m are experimentally determined and ΔK denotes the SIF range, as follows31:

$$\Delta K = K_{{{\text{app}},{\text{ max}}}} - K_{{{\text{app}},{\text{ min}}}} = F\left( a \right) \cdot S_{eq} \cdot \sqrt {\pi a}$$
(2)

where, Kapp, max and Kapp, min represent the maximum SIF and minimum values associated with the applied external load, respectively, \(F(a)\) is the shape function that accounts for the geometry of the crack and the structure, Seq is the equivalent stress range under the applied external load and a is the crack depth.

On this basis, Elber32 introduced the concept of crack closure and applied the effective SIF range \((\Delta K_{eff} )\) instead of the SIF range \(\left( {\Delta K} \right)\) for fatigue crack growth, known as Paris-Elber law:

$$\frac{da}{{dN}} = C\left( {\Delta K_{eff} } \right)^{m}$$
(3)
$$\Delta K_{eff} = U\Delta K = UF\left( a \right) \cdot S_{eq} \cdot \sqrt {\pi a}$$
(4)

where U, the crack closure parameter, is dependent only on the load ratio R. For the application of U to structural steel, the following equation was utilized, as detailed in33:

$$U = \, 0.722 \, + \, 0.278R$$
(5)
$$R = \left( {K_{{{\text{app}},{\text{min}}}} + K_{{{\text{res}}}} } \right)/\left( {K_{{{\text{app}},{\text{max}}}} + K_{{{\text{res}}}} } \right)$$
(6)

where, Kres represents the SIF value associated with the WRS.

Assuming that the crack size increases from \({a}_{0}\) to \({a}_{1}\), and the number of stress cycles experienced by the member accordingly rises from N0 to N1, by substituting Eq. (4) into Eq. (3) and integrating the resulting expression, the following results are obtained:

$$\mathop \smallint \limits_{{a_{0} }}^{{a_{1} }} \frac{da}{{\left( {UF\left( a \right) \cdot \sqrt {\pi a} } \right)^{m} }} = \mathop \smallint \limits_{{N_{0} }}^{{N_{1} }} C \cdot S_{eq}^{m} dN$$
(7)

Subsequently, the critical cumulative fatigue damage function \({\psi (a}_{0},{a}_{c})\), related to the crack growth from the initial crack depth \({a}_{0}\) to the critical crack depth \({a}_{c}\), can be formulated as follows:

$$\psi (a_{0} ,a_{c} ) = \mathop \smallint \limits_{{a_{0} }}^{{a_{c} }} \frac{da}{{\left( {UF\left( a \right) \cdot \sqrt {\pi a} } \right)^{m} }}$$
(8)

Alternatively, the critical cumulative fatigue damage function \({\psi (a}_{0},{a}_{N})\), related to the crack growth from the initial crack depth \({a}_{0}\) to \({a}_{N}\) following N cycles of load, can be formulated as follows:

$$\psi (a_{0} ,a_{N} ) = \mathop \smallint \limits_{{N_{0} }}^{N} C \cdot S_{eq}^{m} dN = C \cdot S_{eq}^{m} \cdot \left( {N - N_{0} } \right)$$
(9)

Therefore, the fatigue reliability limit state equation for the welds in OSD can be expressed as Eq. (10).

$$g\left( X \right) = \psi (a_{0} ,a_{c} ) - \psi (a_{0} ,a_{N} ) = \mathop \smallint \limits_{{a_{0} }}^{{a_{c} }} \frac{da}{{\left( {UF\left( a \right) \cdot \sqrt {\pi a} } \right)^{m} }} - C \cdot S_{eq}^{m} \cdot \left( {N - N_{0} } \right) = 0$$
(10)

where,\({\psi (a}_{0},{a}_{c})\) and \({\psi (a}_{0},{a}_{N})\) represent the resistance term and load effect term of fatigue limit state equation respectively.

The presence of initial cracks or defects in welded steel bridges is inevitable. Consequently, the number of stress cycles,\({N}_{0}\), corresponding to the initial crack depth \({a}_{0}\), is assumed to be zero. The total number of stress cycles, N, experienced by the welding details of OSDs can be calculated as follows:

$$N = 365 \cdot n \cdot N_{d}$$
(11)

where \(n\) is the service time of the bridge and \({N}_{d}\) is the daily number of stress cycles. Considering the wheel track lateral distribution coefficient e of vehicle load on the bridge panel, the fatigue limit state equation is expressed as Eq. (12).

$$g\left( X \right) = \mathop \smallint \limits_{{a_{0} }}^{{a_{c} }} \frac{da}{{\left( {UF\left( a \right) \cdot \sqrt {\pi a} } \right)^{m} }} - e \cdot 365 \cdot n \cdot N_{d} \cdot CS_{eq}^{m}$$
(12)

Considering the traffic growth, the fatigue limit state, specifically Eq. (12), can be reformulated as follows:

$$g\left( X \right) = \mathop \smallint \limits_{{a_{0} }}^{{a_{c} }} \frac{da}{{\left( {U \cdot F\left( a \right) \cdot \sqrt {\pi a} } \right)^{m} }} - e \cdot 365 \cdot n \cdot N_{d} \cdot CS_{e}^{m} \left( {1 + \frac{{\left( {n - 1} \right)\alpha }}{2}} \right)$$
(13)

where, \(\alpha\) the linear growth factor of the traffic volume.

During the service time of the bridge, when fatigue failure occurs in the welded joints, \(g\left(X\right)\)<0, the fatigue failure probability, \({p}_{\text{f}}\), is given by \({p}_{\text{f} }=p(g(X)<0)\). Therefore, the fatigue reliability index \(\beta\) can be determined from Eq. (14).

$$\beta = \Phi^{ - 1} (1 - p_{f} )$$
(14)

where \(\Phi^{ - 1} (X)\) denotes the inverse of the standard normal distribution function.

Random traffic-based derivation of stress spectra

Random vehicle load modeling

Vehicle load is a primary factor contributing to fatigue damage in OSDs. These loads exhibit variability due to the uncertainty in vehicle load rates. In this study, the random vehicle load model proposed in34 is applied to account for this uncertainty. Vehicles are categorized into six typical models, each with different occupancy rates: C2, C3(1), C3(2), C4, C5, and C6, as illustrated in Fig. 3. For each vehicle type, two types of axles are considered, corresponding to two types of wheel landings: a 300 mm × 200 mm (width and length) for the steering axle with a single tire, indicated in green, and a 600 mm × 200 mm (width and length) for the rear axle with dual tires, indicated in blue. To capture the multi-modal characteristics of axle weight distributions, a Gaussian Mixture Model (GMM) is utilized to fit the probability distribution. The GMM can be expressed as follows34:

$$G (x|\theta ) = \mathop \sum \limits_{i = 1}^{M} w_{i} N\left( {x|\mu_{i} , \sigma_{i}^{2} } \right) = \mathop \sum \limits_{i = 1}^{M} w_{i} \frac{1}{{\sqrt {2\pi } \sigma_{i} }}\exp \left[ { - \frac{{\left( {x - \mu_{i} } \right)^{2} }}{{2\sigma^{2} }}} \right]$$
(15)

where the total samples include M types of sub-samples Xi = (X1, X2, …, XM); Xi represents a one-dimensional random variable; wi is the proportion of the i-th Gaussian components, x is the value from the sample of Xi, \({\mu }_{i}\) is the mean value, \({\sigma }_{i}^{2}\) is the variance, and \({\varvec{\theta}}=({w}_{1}, {w}_{2} \dots { w}_{i}; {\mu }_{1}, {\mu }_{2} \dots { \mu }_{i};{\sigma }_{1}^{2}, {\sigma }_{2}^{2} {\dots \sigma }_{i}^{2})\). Figure 4 displays the probability density of the weights for the six typical vehicle models, along with the detailed parameters of the GMM.

Fig. 3
figure 3

Six typical vehicle configurations34.

Full size image
Fig. 4
figure 4

Probability density distribution for six types of vehicle weight.

Full size image

To better capture the load effects of axle load distribution from various vehicle models on OSDs, a linear regression model has been developed to represent the relationship between axle weight and vehicle weight. In this study, the linear regression models were developed based on the findings from Wang et al.35. The linear regression equation is presented in Eq (16).

$${W}_{\text{cij}}={a}_{cij}{G}_{ci}+{b}_{cij}$$
(16)

where \({W}_{\text{cij}}\) is the e axle weight of \({C}_{i}\), \({a}_{cij}\) and \({b}_{cij}\) are the parameters of a partition coefficient. The parameters of the linear regression model for the six typical vehicle models are depicted in Fig. 5, as compiled from the study by34.

Fig. 5
figure 5

Types of vehicle axle weight linear regression model34.

Full size image

FEM of segmental bridge

Obtaining the statistical characteristics of the fatigue stress spectrum under random vehicle loads is essential for the fatigue reliability analysis of OSDs. This study focuses on a typical rib-to-deck double-sided welded joint in OSDs to derive the vehicle-induced stress spectra, as depicted in Fig. 6. The deck and the U-rib have thicknesses of 16 mm and 8 mm, respectively. The U-ribs, which are 300 mm wide and 8 mm thick, are connected to the deck by double-sided welds with an 80% partial penetration rate. Furthermore, the clearance between the U-rib and the deck plate assembly is maintained at no more than 0.5 mm.

Fig. 6
figure 6

FEM of 1/2 segmental steel bridge deck (unit: mm).

Full size image

The effect range of the fatigue stress on the welding details of OSDs is localized, and the segment model, which allows the use of a segment model to obtain calculation results that closely approximate those of a whole bridge model36. Therefore, a multi-scale finite element model (FEM) of an OSD with a 12 m length standard segment is established using ABAQUS37 to obtain the vehicle-induced stress spectra. Figure 6 illustrates a schematic representation of the FEM. The material specified for the FEM is steel Q345qD, characterized by a Young’s modulus of 206 GPa and a Poisson’s ratio of 0.3. To balance accuracy and efficiency, the FEM consists of two parts with distinct meshing strategies: a global model of the segment and a sub-model of the rib-to-deck double-sided welded joints. The global model is simulated using a 4-node shell element (S4R) with a relatively coarse element size of 100 mm, as it primarily serves to transfer boundary conditions from the global model to the sub-model. In contrast, the sub-model employs an 8-node solid element (C3D8R) with a finer element size of 10 mm, with the rib-to-deck double-sided welded joints of interest being refined to 1 mm. The global and sub-models are meshed independently and subsequently coupled through shell-solid interaction37. The global and sub-models are meshed independently and subsequently coupled through shell-solid interaction. A symmetric boundary condition is imposed at the model’s symmetric center line, fixing transverse displacement (Ux = 0) and prohibiting rotations about the y and z axes (Ry = Rz = 0). The longitudinal end of the model is fully fixed in all directions (Ux = Uy = Uz = 0), while the opposite end is restrained against displacement in the y direction only (Uy = 0).

Stress spectra of OSD under dynamic vehicle load

The weigh-in-motion (WIM) system34 is installed on the OSD to record the vehicle parameter data, including truck weight, axle weight and truck type. Stochastic truck data, collected over a 30-day period, were utilized for the probabilistic density modeling of the rib-to-deck welded joints situated in the slow lane. The traffic volume is characterized by an average daily traffic with a Gaussian distribution, as depicted in Fig. 7. Figure 8 illustrates the stochastic stress spectra, which are calculated separately for the outer and inner welded toes under random traffic flow conditions. A database of equivalent stress ranges has been established, approximated using the GMM distribution function, as depicted in Fig. 9. Figure 10 illustrates the probability density function corresponding to the number of daily stress cycles.

Fig. 7
figure 7

Distribution of the average daily traffic.

Full size image
Fig. 8
figure 8

Stress spectra of welded joints in slow lane. (a) Outside weld toe, (b) Inside weld toe.

Full size image
Fig. 9
figure 9

Equivalent stress range probability distribution (a) Outside weld toe, (b) Inside weld toe.

Full size image
Fig. 10
figure 10

Number of daily cycles probability distribution for slow lane.

Full size image

SIF calculation considering WRS

The SIF values of welded joints in OSDs may be significantly influenced by WRS14. The weight function method is recognized as an effective approach to accurately calculate the SIF of welded joints. Bueckner et al.38,39 proposed a weight function method for calculating the SIF of a surface crack under arbitrary load, with the following expression:

$$K = \mathop \smallint \limits_{0}^{a} m\left( {x,a} \right) \cdot \sigma \left( x \right)dx$$
(17)

where, \(\sigma \left(x\right)\) is the stress distribution, a is the crack length of a semi-elliptical crack, and the weight function \(m\left(x,a\right)\) for the deepest points of a semi-elliptical crack can be approximated using the following expression40:

$$m\left( {x,a} \right) = \frac{2}{{\sqrt {2\pi \left( {a - x} \right)} }} \cdot \left[ {1 + M_{1A} \left( {1 - \frac{x}{a}} \right)^{\frac{1}{2}} + M_{2A} \left( {1 - \frac{x}{a}} \right) + M_{3A} \left( {1 - \frac{x}{a}} \right)^{\frac{3}{2}} } \right]$$
(18)

here, \({M}_{1A}\)、\({M}_{2A}\) and \({M}_{3A}\) can be determined by using two reference solutions and a third condition, as follows:

$$\left\{ {\begin{array}{*{20}c} {M_{1A} = \frac{\pi }{{\sqrt {2Q} }}\left( {4F_{0} - 6F_{1} } \right) - \frac{24}{5}} \\ {M_{2A} = 3} \\ {M_{3A} = \frac{2\pi }{{\sqrt {2Q} }}F_{0} - 2M_{1A} - 8} \\ \end{array} } \right.$$
(19)

where, \(Q\) is the shape factor for an ellipse, given by:

$$Q=1.0+1.464{(a/c)}^{1.65},\text{ for} 0\le a/c\le 1.0$$
(20)

Detailed expressions for F0 and F1 derived for surface cracks of rib-to-deck double-sided welded joints in OSDs, are presented in41. The expressions for \({F}_{0}\) and \({F}_{1}\) are as follows:

$${F}_{0}={p}_{0}+{p}_{1}(a/t)+{p}_{2}{(a/t)}^{2}+{p}_{3}{(a/t)}^{3}+{p}_{4}{(a/t)}^{4}$$
(21)

where the coefficients \({p}_{i}\) are defined by Eqs. (22) to (26).

$$p_{0} = \, 0.999 \, {-} \, 0.299 \, \left( {a/c} \right) \, + \, 0.890 \, \left( {a/c} \right)^{2} {-} \, 1.151 \, \left( {a/c} \right)^{3} + \, 0.542 \, \left( {a/c} \right)^{4}$$
(22)
$$p_{1} = \, 0.304 \, {-} \, 1.135 \, \left( {a/c} \right) \, {-} \, 0.881 \, \left( {a/c} \right)^{2} + \, 6.605 \, \left( {a/c} \right)^{3} {-} \, 5.118 \, \left( {a/c} \right)^{4}$$
(23)
$$p_{2} = \, 3.796 \, {-} \, 17.549 \, \left( {a/c} \right) \, + \, 49.627 \, \left( {a/c} \right)^{2} {-} \, 72.615 \, \left( {a/c} \right)^{3} + \, 38.199 \, \left( {a/c} \right)^{4}$$
(24)
$$p_{3} = \, 0.274 \, {-} \, 1.985 \, \left( {a/c} \right) \, + \, 14.906 \, \left( {a/c} \right)^{2} + \, 48.897 \, \left( {a/c} \right)^{3} {-} \, 34.163 \, \left( {a/c} \right)^{4}$$
(25)
$$p_{4} = \, 1.093 \, {-} \, 14.83 \, \left( {a/c} \right) \, + \, 58.092 \, \left( {a/c} \right)^{2} {-} \, 86.607 \, \left( {a/c} \right)^{3} + \, 43.523 \, \left( {a/c} \right)^{4}$$
(26)

and

$$q_{0} = \, 0.361 \, {-} \, 0.113 \, \left( {a/c} \right) \, + \, 0.111 \, \left( {a/c} \right)^{2} {-} \, 0.182 \, \left( {a/c} \right)^{3} + \, 0.073 \, \left( {a/c} \right)^{4}$$
(27)

with the coefficients \({q}_{i}\) are defined by Eqs. (28) to (32).

$$q_{0} = \, 0.361 \, {-} \, 0.113 \, \left( {a/c} \right) \, + \, 0.111 \, \left( {a/c} \right)^{2} {-} \, 0.182 \, \left( {a/c} \right)^{3} + \, 0.073 \, \left( {a/c} \right)^{4}$$
(28)
$$q_{1} = \, 0.464 \, {-} \, 3.956 \, \left( {a/c} \right) \, + \, 12.809 \, \left( {a/c} \right)^{2} {-} \, 18.405 \, \left( {a/c} \right)^{3} + \, 10.068 \, \left( {a/c} \right)^{4}$$
(29)
$$q_{2} = \, 0.732 \, + \, 8.562 \, \left( {a/c} \right) \, {-} \, 48.653 \, \left( {a/c} \right)^{2} + \, 86.723 \, \left( {a/c} \right)^{3} {-} \, 52.641 \, \left( {a/c} \right)^{4}$$
(30)
$$q_{3} = \, 3.381 \, {-} \, 37.278 \, \left( {a/c} \right) \, + \, 137.296 \, \left( {a/c} \right)^{2} {-} \, 211.830 \, \left( {a/c} \right)^{3} + \, 118.534 \, \left( {a/c} \right)^{4}$$
(31)
$$q_{4} = \, {-}1.102 \, + \, 9.793 \, \left( {a/c} \right) \, {-} \, 43.513 \, \left( {a/c} \right)^{2} + \, 80.304 \, \left( {a/c} \right)^{3} {-} \, 51.273 \, \left( {a/c} \right)^{4}$$
(32)

According to the crack orientation, the transverse WRS significantly contributes to fatigue crack growth. Chen et al.24 modeled the distribution of transverse WRS along the deck thickness direction in rib-to-deck double-sided welded joints using a sinusoidal function. In the present study, the distribution of transverse WRS of rib-to-deck double-sided welded joints in OSD is modeled, as depicted in Fig. 11. Details regarding the sinusoidal function utilized in this modeling are provided in reference24.

Fig. 11
figure 11

WRS distribution of rib-to-deck double-sided welded joints24.

Full size image

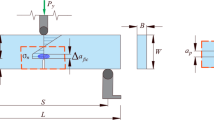
SIF analysis under vehicle load

A multi-scale FEM of an OSD segment with a crack is established using ABAQUS and FRANC3D42, as depicted in Fig. 12. The FEM comprises two levels: a complete model featuring shell-solid elements, and a refined sub-model focusing on the solid elements containing the crack. The dimensions of the complete model are 9 m in length, 4.2 m in width, and 6 m in height, while the refined sub-model has dimensions of 300 mm × 300 mm × 316 mm. In the complete model, shell elements are modeled using a 4-node shell element (S4R) with a mesh size of 100 mm. Solid elements are modeled using a 20-node solid element (C3D20R) with a global mesh size of 10 mm, which is refined to 1 mm around the rib-to-deck welded joints. Within the refined sub-model containing the crack, the elements adjacent to the innermost circle of the crack tip are 15-node wedge elements, and those surrounding the outer circle are C3D20 hexahedral elements. The mesh size for the refined sub-model is a/10, where a is the crack depth. The diaphragm’s lower edge is fully fixed, with zero vertical displacement (Uy = 0) and no rotational freedom (Rx = Rz = 0). Longitudinal movement (Uz = 0) and associated rotations (Rx = Ry = 0) are restricted at both ends of the model. Transverse displacement (Ux = 0) and rotations (Ry = Rz = 0) are prohibited along the two lateral edges of the model. Solid and shell elements interact through shell-solid interaction, ensuring a consistent response between the sub-model and the main model. The contact surfaces between the sub-model and the complete model are tied together using tie constraints, maintaining continuity and interaction across the interface. For the FEM analysis of the rib-to-deck double-sided welded joints in OSDs, a one-sided twin axle loading model is utilized, with each axle weighing 60 kN and a contact surface of 600 mm × 200 mm.

Fig. 12
figure 12

FEM of rib-to-deck double-sided welded joints in OSDs (Unit: mm).

Full size image

Effect of deck thickness

Mode-I SIFs, KI, of initial fatigue crack (a = 0.2 mm, a /c = 0.4) of rib-to-deck double-sided welded joints in OSD are calculated for various deck thicknesses (t = 12 mm, 14 mm, 16 mm, 18 mm and 20 mm). Figure 13 presents the variation of KI values with respect to the deck thicknesses. It is observed that the KI value for a crack at the deepest point of the outside weld toe decreases progressively as the deck thickness increases. Specifically, KI reduces from 44.6 MPa•mm1/2 to 33.7 MPa•mm1/2 with the increase in deck thickness, indicating a reduction of 24.4%. In contrast, the KI value for a crack at the deepest point of the inside weld toe exhibits relative constancy with increasing deck thickness.

Fig. 13
figure 13

KI versus the deck thickness.

Full size image

Effect of crack depth

Mode-I SIFs, KI, of initial fatigue crack (a /c = 0.4) of rib-to-deck double-sided welded joints in OSD are calculated for various fatigue crack depth (a = 0.2 mm, 0.25 mm, 0.30 mm, 0.35 mm and 0.40 mm). Figure 14 presents the variation of KI values with respect to fatigue crack depth. It is observed that the KI value for a crack at the deepest point of the outside weld toe increases gradually with the increase of crack depth. Specifically, KI rises from 38.3 MPa•mm1/2 to 43.5 MPa•mm1/2 with the increase in crack depth, representing an increase of 13.6%. The KI value for a crack at the deepest point of the inside weld toe also increases with crack depth, from 28.0 MPa•mm1/2 to 31.3 MPa•mm1/2, representing an increase of 11.8%.

Fig. 14
figure 14

KI versus the crack depth.

Full size image

Effect of crack aspect ratio

Mode-I SIFs, KI, of initial fatigue crack (a = 0.2 mm) of rib-to-deck double-sided welded joints in OSD are calculated for various fatigue crack aspect ratio (a /c = 0.2, 0.4, 0.6, 0.8 and 1.0). Figure 15 presents the variation of KI values with respect to fatigue crack aspect ratio. It is observed that the KI value for a crack at the deepest point of the outside weld toe decreases gradually with the increase of crack aspect ratio. Specifically, KI reduces from 43.9 MPa•mm1/2 to 27.2 MPa•mm1/2 with the increase in aspect ratio, representing a decrease of 38.0%. Similarly, the KI value for a crack at the deepest point of the inside weld toe also decreases with the crack aspect ratio, from 31.6 MPa•mm1/2 to 19.5 MPa•mm1/2, representing a decrease of 38.3%.

Fig. 15
figure 15

KI versus the crack aspect ratio.

Full size image

In Eq. (2), F(a) represents the shape function, which varies for the deepest points of the fatigue crack at the outside and inside weld toes. Firstly, all the KI data generated in the parametric study are normalized to obtain the shape function F(a), as follows:

$$F(a) = K/\left( {\sigma_{0} \sqrt {\pi a} } \right)$$
(33)

where, \({\sigma }_{0}\) is the stress; a is the crack depth.

Subsequently, a multiple regression analysis is conducted to fit a polynomial function to the normalized data. The specific polynomial model is described as follows:

(1) The shape function for the deepest point of crack at the outside weld toe is

$$F(a) = m_{0} + m_{1} \left( {a/t} \right) \, + m_{2} \left( {a/t} \right)^{2} + m_{3} \left( {a/t} \right)^{3} + m_{4} \left( {a/t} \right)^{4}$$
(34)

where the coefficients \({m}_{i}\) are defined by Eqs. (35) to (39).

$$m_{0} = \, 2.93 \, {-} \, 3.42 \, \left( {a/c} \right) \, + \, 4.31 \, \left( {a/c} \right)^{2} {-} \, 2.49 \, \left( {a/c} \right)^{3}$$
(35)
$$m_{1} = \, {-} \, 18.69 \, + \, 26.79 \, \left( {a/c} \right) \, {-} \, 41.10\left( {a/c} \right)^{2} + \, 25.42 \, \left( {a/c} \right)^{3}$$
(36)
$$m_{2} = \, 61.38 \, {-} \, 100.84 \, \left( {a/c} \right) \, + \, 157.41\left( {a/c} \right)^{2} {-} \, 96.44 \, \left( {a/c} \right)^{3}$$
(37)
$$m_{3} = \, 83.04 \, + 132.50 \, \left( {a/c} \right) \, - 209.87 \, \left( {a/c} \right)^{2} + 131.01 \, \left( {a/c} \right)^{3}$$
(38)
$$m_{4} = \, 38.73 \, {-} \, 58.04 \, \left( {a/c} \right) \, + \, 94.13\left( {a/c} \right)^{2} {-} \, 60.52 \, \left( {a/c} \right)^{3}$$
(39)

(2) The shape function for the deepest point of crack at the inside weld toe is

$$F(a) = n_{0} + n_{1} \left( {a/t} \right) \, + n_{2} \left( {a/t} \right)^{2} + \, n_{3} \left( {a/t} \right)^{3} + n_{4} \left( {a/t} \right)^{4}$$
(40)

where the coefficients \({n}_{i}\) are defined by Eqs. (41) to (45).

$$n_{0} = \, 2.59 \, + \, 1.63 \, \left( {a/c} \right) \, {-} \, 6.88 \, \left( {a/c} \right)^{2} + \, 4.64 \, \left( {a/c} \right)^{3}$$
(41)
$$n_{1} = \, {-} \, 12.50 \, {-} \, 29.73 \, \left( {a/c} \right) \, + \, 82.35 \, \left( {a/c} \right)^{2} {-} \, 53.69 \, \left( {a/c} \right)^{3}$$
(42)
$$n_{2} = \, 40.64 \, + \, 91.42 \, \left( {a/c} \right) \, {-} \, 270.91\left( {a/c} \right)^{2} + \, 181.45 \, \left( {a/c} \right)^{3}$$
(43)
$$n_{3} = \, {-} \, 55.49 \, {-} \, 131.79 \, \left( {a/c} \right) \, + \, 387.39 \, \left( {a/c} \right)^{2} {-} \, 260.27 \, \left( {a/c} \right)^{3}$$
(44)
$$n_{4} = \, 26.07 \, + \, 66.93 \, \left( {a/c} \right) \, {-} \, 192.39 \, \left( {a/c} \right)^{2} + \, 129.05 \, \left( {a/c} \right)^{3}$$
(45)

Figure 16 presents compares the F(a) curves derived from the regression equations with FE data. It is observed that the obtained regression equations provide a good agreement with the FEA results. The error associated with the regression equation is quantified by Eq. (46). Since the error for the majority of the data points is less than 10%, the regression equation is deemed to provide an accurate approximation of the KI value, suitable for engineering applications.

$$Error = (F\left( a \right)_{FE - } F\left( a \right)_{Eq} /F\left( a \right)_{FE} ) \times 100\%$$
(46)
Fig. 16
figure 16

Compare the F(a) curves of equation with FE data. (a) Outside weld toe, (b) Inside weld toe.

Full size image

Results and discussion

Initially, the fatigue reliability index of the rib-to-deck double-sided welded joints in OSDs was calculated using the Monte Carlo method based on the fatigue reliability function presented in Eq. (9) and the statistics of variables shown in Table. 1. This paper employs a Monte Carlo sampling approach with 1.0 × 106 iterations. However, fatigue reliability indices exceeding 5 are not reported due to the inherent limitations in the accuracy of the Monte Carlo simulation method. Figure 17 presents the calculation results of the fatigue reliability index for the outside weld toe and the inside weld toe of rib-to-deck double-sided welded joints in OSDs, both with and without consideration of the effects of WRS. It is observed that when considering the WRS, the fatigue reliability indexes for the outside weld toe and the inside weld toe decrease to 2.1 and 2.7, respectively, after 100 years of service. In contrast, without considering the WRS, the fatigue reliability indexes decrease to 3.9 and 4.4, respectively, after the same period. The fatigue reliability index for the outside weld toe, when considering the influence of WRS, is approximately 0.54 times that when the influence is not considered. Similarly, for the inside weld toe, when considering the influence of WRS, is approximately 0.61 times that when the influence is not considered. It is indicating that WRS has a significant impact on fatigue reliability index of rib-to-deck double-sided welded joints in OSDs. Therefore, the influence of WRS should be thoroughly considered when designing or evaluating the fatigue life of OSDs. Additionally, regardless of whether the effects of WRS are considered. the fatigue reliability index for the outside weld toe is consistently lower than that for the inside weld toe.

Table 1 Statistics of variables in fatigue limit state function.
Full size table
Fig. 17
figure 17

Time-variant fatigue reliability indexes considering the WRS and not considering the WRS. (a) Outside weld toe (b) Inside weld toe.

Full size image

In practice, as urban development accelerates and the urban population expands, an increase in traffic volume is expected. To investigate the effect of this traffic volume growth on fatigue reliability, it is assumed that the growth rates of traffic volume increase linearly. Figure 18 presents the calculation results of the fatigue reliability index for the outside weld toe and the inside weld toe, considering the WRS, when the linear growth factor of the traffic volume is 0, 1, 2, and 3%. It is observed that the fatigue reliability indexes noticeably decrease with an increase in traffic volume during the service time. When the traffic volume growth rate reaches 3%, the fatigue reliability indexes for the outside weld toe and the inside weld toe decreases to 0.3 and 0.8, respectively, in the 100th years of service.

Fig. 18
figure 18

Time-variant fatigue reliability indexes with consideration of traffic volume growth factor. (a) Outside weld toe (b) Inside weld toe.

Full size image

Fatigue reliability assessment is not only to evaluate the safety of structures at probability level, but also to determine the fatigue life of structures within the target reliability index (\({\beta }_{\text{target}}\)), which provides a basis for the inspection and maintenance of bridges. Helmerich et al.43 suggest a \({\beta }_{\text{target}}\) range of 2.0 to 3.5 according to the calibration study of Eurocode 344. In the present study, \({\beta }_{\text{target}}\) is determined to be 2.0. Table 2 shows the structural fatigue life corresponding to the \({\beta }_{\text{target}}\). It is observed that the fatigue life of both the outside weld toe and the inside weld toe decreases significantly with the growth of traffic volume. When the linear annual growth factor of traffic volume,\(\alpha\), exceeds 1%, the fatigue life of the outside weld toe and the inside weld toe is only 78 years and 96 years, respectively, which is less than the expected design service life. Therefore, the traffic volume growth should be effectively controlled during the service time, and the fatigue reliability of the structure should be evaluated in time according to the existing traffic data.

Table 2 Fatigue life prediction for rib-to-deck double-sided welded joints considering traffic volume growth factor.
Full size table

Conclusions

This paper presents a novel method for evaluating the fatigue reliability of rib-to-deck double-sided welded joints in OSDs under traffic vehicle loading, while considering the effects of WRS. The effects of deck thickness, fatigue crack depth and fatigue crack aspect ratio variation on SIF of the crack were discussed. These three variables were regarded as feature vectors, and a polynomial model was built to calculate the shape functions. The fatigue reliability of the rib-to-deck double-sided welded joints was estimated using Monte Carlo simulation, and the influence of traffic volume growth on fatigue reliability was also discussed. Based on the above investigations, the following conclusions can be drawn:

(1) The value of KI of a crack at the deepest point of the outside weld toe can be significantly reduced by increasing the deck thickness. When the initial crack shape ratio remains constant, the KI value of a crack at the deepest point of the weld toe increases gradually with the increase of crack depth. Similarly, when the initial crack depth is consistent, the KI value of a crack at the deepest point of the weld toe decreases gradually with the increase of crack aspect ratio.

(2) After 100 years of service, the fatigue reliability indexes are approximately 0.54 times for the outside weld toe and 0.63 times for the inside weld toe when considering the combined effects of WRS and vehicle load, compared to when only vehicle load is considered. It is crucial to rigorously consider the effects of WRS during the design and evaluation phases to accurately assess the fatigue life of OSD.

(3) The fatigue reliability index of rib-to-deck double-sided welded joints decreased significantly with the growth of traffic volume. A linear annual growth factor of 1% in traffic volume will result in a fatigue reliability index of less than 2 for the prototype bridge. Therefore, it is crucial to effectively manage the growth of traffic volume during the service life of the bridge, and the fatigue reliability of the structure must be promptly assessed based on available traffic data.

(4) To investigate the fatigue reliability of OSDs, this paper draws upon existing results and employs an assumed initial crack size along with a simplified load traffic growth model. In forthcoming studies, we intend to enumerate the initial defect type and size specific to real steel bridge decks. By incorporating the actual initial defect size and a more sophisticated traffic growth model, we aim to augment the veracity of our predictions.