Introduction

Safflower (Carthamus tinctorius L.) is a drought-resilient oilseed crop belonging to the family Asteraceae. It produces oil rich in unsaturated fatty acids viz oleic acid and linoleic acid. Besides oil, safflower can be used as coloring dyes, food flavoring agents, pharma-nutraceutical compounds as well as biofuels1,2,3. With a global production of 6.3 million tonnes, safflower is cultivated in more than 20 countries (https://www.fao.org/faostat/). However, its area under cultivation remains stagnant or decreased over the years due to its low yield, low oil content, highly spinous nature, susceptibility to diseases, and thus faces negligence from the farmers leaving it as a marginal crop. Furthermore, being a geographically and genetically diverse crop4,5, its oil and yield is influenced by the environmental conditions. Thus, the interaction between genotype and environment is crucial in determining this key agronomic trait, underscoring the importance of ___location-specific field management practices. The integration of precision agriculture techniques can further optimize safflower yield by tailoring practices to site-specific conditions. Soil has a direct role in plant growth, and safflower yield is affected by soil salinity, soil fertility, nutrient availability, chemical composition, and water availability6,7,8. Therefore, characterizing the soil through fine-resolution surveying in safflower fields and the use of classification models for correctly grouping the land are important steps for identifying the appropriate soil management practices in precision agriculture9.

Characterizing the physical and chemical properties of the soil helps in identifying the requirements for precision agricultural management. Soil texture and moisture are a couple of the most important physical properties affecting plant growth. Nutrients and water retention capacity of the soil are controlled by texture. Aeration of the soil, root penetration, soil organic matter, nutrient dynamics, movement of water, heat conduction, and susceptibility to erosion are affected by the aggregation of textural components. Soil moisture influences this aggregation and leads to precipitation of the nutrients such as nitrogen for the plants which play a major role in its growth. A combination of different features including clay, and soluble salts such as sodium, calcium, magnesium, and potassium lead to the salinity and electrical conductivity of the soil10. As the salinity increases, water availability decreases, and ultimately affects plant growth. Soil organic carbon (SOC), a proxy of soil organic matter, also influences nutrient retention capacity11 and is a key element in defining soil quality, fertility, and agricultural profitability. The presence of salts, SOC, and pH influences the chemical properties of the soil. The most used indicator for nutrients is soil chemical indicators and for this reason, they are usually referred to as ‘indices of nutrient supply’12, thus their identification plays a significant role in precision agriculture.

Monitoring spatial changes in the soil quality, understanding its dynamic nature, and role in precision agriculture and land management are crucial. The construction of accurate maps based on the spatial variability in physio-chemical soil properties is the first step in this process13. Various attempts have been made to construct soil maps using digital and conventional methods at the global level14,15,16,17,18, national level9,19 and at the local level20,21,22,23,24,25,26,27. However, most of the maps are at low resolution. With the Global Soil Map project28 aimed at fine-resolution mapping using digital soil mapping (DSM) approaches, there has been an exponential growth in high-resolution (> 10,000 km2) soil maps in the last two decades29. Creation of the soil maps requires sampling and measurement of features of interest, followed by statistical analysis involving interpolations, simple regressions, or the use of artificial intelligence models to process the patterns from the datasets. With fine-resolution sampling and robust statistical methods, better interference can be developed with greater confidence for more useful analysis and interpretation.

Linear and non-linear statistical models can be used to evaluate spatial variability in the soil from complex datasets30. Principal component analysis (PCA) has been widely used in soil analysis31,32,33,34,35, as it can correlate several variables simultaneously35. Also, PCA can handle high-dimensional data arrays, e.g., three-way PCA can be useful to analyze many soil variables obtained from multiple locations as a function of other experimental conditions such as sampling time36. Multivariate linear regression (MLR) and correlation are other most used methods37,38,39, to infer the relationship among soil features. MLR has a simple structure, easy calculation, and interpretation, however, it is inadequate to detect non-linear relationships40. Machine learning (ML) and deep learning (DL) approaches have been used to conclude linear and non-linear relations between the soil features and their distribution41. The most popular ML and DL tools for the estimation of the soil features, its classification, and prediction are random forest (RF) and artificial neural network (ANN)42,43. RF is a classification machine learning approach with the ability to model complex and nonlinear relationships44. Besides this, its capacity for determination of the relevant variables, resistance to over-fitting, robustness, and establishment of an impartial measure of error rate45,46,47, are the advantages which made RF most widely applied approach for the analysis of soil variables48,49,50,51. ANN, analog to the biological neural network, is more complex and uses synaptic weights to establish a connection among predictor variables through multiple layers of networks and predicts the classification52. Some of the features of the neural network such as no assumption of a prior relationship, availability of multiple training algorithm detections of complex nonlinear relationships, and detection of all possible interactions between predictor variables53, made it another popular soil classification model54,55,56,57,58,59,60. Self-organizing map (SOM)61 is an ANN that does dimension reduction as well as clustering simultaneously by keeping similar objects together and can be more useful in clustering of the soil62. The application of multiple models for the classification of soil can be useful in arriving at more robust predictions as well as providing a comparison among different models.

Safflower can thrive in diverse soil types63 but grows mainly in black soil types in India (https://eands.dacnet.nic.in/) producing varying phenotypes. In this study, we aim to, (1) classify soil samples collected at fine resolution from target environments (TE) of safflower based on their physicochemical features, (2) evaluate variability in soil features and establish robust soil classification prediction models, and (3) create soil maps for nutrient management, field design, risk assessment, and management during safflower cultivation. To our knowledge, this is the first study on prediction modeling for precision agriculture in safflower using a large set of physiochemical features and fine-resolution soil mapping.

Methods

Experiment design

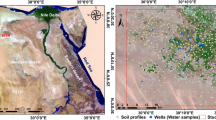
As a part of the safflower crop improvement program, we conducted a multi-environmental trial for a safflower breeding population (recombinant inbred lines (RIL)), hereafter referred to as “Population A” developed from parents contrasting for various traits, at representative TEs in India. Soil samples were collected from these locations for soil profiling. Four soil profiles representing alluvial (Delhi University (DU) Research Field, Delhi, 28°74′ N, and 77°12′ E), black (Nimbkar Agriculture Research Institute (NARI), Pune, 18°57′ N, and 74°05′ E), red and yellow (Ankur seeds (AS) Pvt. Ltd., Nagpur, 21°13′ N, and 79°09′ E), and laterite (a farmer’s field in Haveri, 14°78′ N and 75°39′ E) were collected. In this fine-resolution soil profile study, a total of 288 samples (72 samples × 4 locations) were collected to evaluate the micro and macro variations. Each ___location (representing macro-environment) had four blocks (representing micro-environments) labelled A, B, C, and D placed as far as possible from each other in the given area. The distance between blocks was the furthest in the DU research field where they were kept in a ~ 40,000 m2 land. In other locations, the blocks were placed logistically in ~ 2000 m2 of land.

In general, a block was of dimension 20 m × 17 m which was partitioned into six rectangular plots each of dimension 20 m × 2 m separated by a gap of 1 m along the width. This design was originally created for safflower cultivation. For the fine-resolution soil mapping, the plots were again partitioned into segments of ~ 7 m × 2 m dimension. To understand the micro-variation in the physiochemical characteristics of the soil within the ___location, the samples were collected from these segments in a plot. From each ___location, 72 samples (18 samples × 4 blocks) were collected from pits of depth 30 cm by mixing soils from different layers along the depth. Soil collection was done from five random pits in a segment and later homogenized to make one composite. Samples were carried to a soil laboratory at Delhi University from all sites in airtight zip-lock bags for the physiochemical analysis. The samples were dried, sieved through a 2 mm sieve, and stored at room temperature for analysis. The soil was collected before the start of crop season to make sure that any management or nutrient application were not biasing the soil features.

Physiochemical analysis of soil

Soil features include moisture content, texture, percentage of sand, clay, silt, salinity, electrical conductivity (EC), and pH as well as micro and macro-nutrients such as nitrogen (N), phosphorous (P), potassium (K), calcium (Ca), sodium (Na), sulphur (S), and organic carbon (C), were measured in the soil science laboratory of the University of Delhi and Indian Agricultural Research Institute, Delhi. To determine the soil moisture percentage (gravimetric water content (GWC)), 10 g of fresh soil was taken in petri dish and oven dried at 105°C until constant weight was achieved. Estimation of GWC percentage was done as per the protocol64. The GWC (%) was measured as follows:

$$GWC \left( \% \right) = \frac{{\left( {W_{wet} - W_{dry} } \right)}}{{W_{dry} }} \times 100$$

where \(W_{wet}\) and \(W_{dry}\) are the weights of wet and dry soil in grams respectively.

A soil suspension was prepared using 20 g of soil and 40 ml of deionized water (1:2 soil-to-water ratio). Homogenization of soil sample was done by stirring it on a magnetic stirrer for one hour and later filtered through Whatman filter paper no.1. Electrical conductivity (\({\mu S}/{\text{cm}})\), pH, and salinity (ppm) of the supernatant were measured using a Multiparameter Tester (PCS Tester 35). Soil texture (%) was analyzed using the Bouyoucos Hydrometer method65 Nutrients were measured in the unit mg/100 g of soil. Available K, Na, and Ca were extracted using neutral ammonium acetate and estimated with flame photometric method64. Total available N was estimated with an automatic micro-Kjeldahl distillation unit66. Total organic C was estimated using the wet oxidation method68. Turbidimetric method was used for the estimation of available S67. The available P was estimated using Olsen’s method68.

Statistical analysis

In this study, we evaluated fourteen physiological properties of the soil called “soil features” for the creation of the fine-resolution map. Average value from three replicates was used for analysis except for soil texture, where only one observation was taken. Missing values were imputed as average values from nearest neighbor segments. A correlation analysis was performed and removed EC having high collinearity with salinity (Fig. 1). Thirteen soil features were chosen for further analysis. Graphical soil maps were created showing the variability of these features within blocks in a ___location (Supplementary figure S1).

Fig. 1
figure 1

Correlation and variability of all soil features collected from the field. The electrical conductivity (EC) and salinity showed high correlation. The EC and salinity followed the same pattern of correlation with other variables also. To avoid multicollinearity, variable EC was removed from further analysis.

Full size image

Models

The general model used in this study is

$$Y = f\left( S \right)$$

where Y is the classification labels based on soil features and S is the set of soil features. This generalized model was evaluated using four main model frameworks for narrative and predictive abilities. The features were standardized before modeling.

Four models were used for classification and prediction: Multinomial model using (1) all the variables hereafter called as base model (2) principal component analysis (PCA), a dimension reduction method; the first two principal components (PCs: PC1 and PC2) which explained > 50% of the variation were then used in the model hereafter called as PC model (3) RF, a classification ML model, and (4) SOM, an ANN model. The models were tested for classification prediction for locations using 70:30 training: test datasets cross-validation method which was repeated 100 times. The accuracy in classification and confusion matrix were used as criteria for predictability evaluation. Later, unsupervised models were used for classification of the data based on the similarities of the soil features to overcome the limitation of grouping based on locations. The similarity matrices from the models were used to cluster the soil profile using a k-medoid algorithm. The predictability of all models in correctly classifying the soil profile into clusters were evaluated using proportionately partitioned training: test datasets cross-validation method which was repeated 100 times. Average classification accuracy was used for predictability evaluation.

Multinomial regression models

The model used is as follows:

$$\left( {Y = i | X; \theta } \right)$$
$$Y \sim Bernoulli\left( \theta \right) where \theta = P\left( {Y = i} \right)$$
$$i = \left( {1, 2, 3, 4} \right);$$
$$X = \left( S \right)\; is\; base \;model \; and \; X = \left( {PC1, PC2} \right) \;is\; PC\; model$$

The first two PCs which explained > 50% of the variation was used in the PC multinomial model.

Random Forest model

RF45 is an ensemble classifier machine learning approach growing many classification trees69. Each tree gives a classification giving ‘votes’. The forest choses the classification having the most votes over all the trees. The model uses bootstrap aggregating (bagging) algorithms for an internal cross-validation for getting unbiased estimate of the classification error. The bagging process is repeated ‘B’ times.

$$\hat{h}\left( x \right) = \frac{1}{B}\mathop \sum \limits_{b = 1}^{B} f_{b} \left( x \right)$$

The out of bag (oob), x, would be fitted with the classification function \(f_{b}\) and then all the results from the individual trees are averaged.

Gini impurity measure, G, is used as the classification function in RF. The best classification at a split (node) in a tree is made based on the probability of using a set of variables p, the value of p is held constant during the tree growth. G for the descendent nodes is less than the parent node. Adding up G for each variable set p over all the trees in the RF provides criterion for ranking variables based on importance. The Gini impurity measure for a tree, \(G\left( {p_{t} } \right)\) is

$$G\left( {p_{t} } \right) = arg\mathop \sum \limits_{j}^{{}} P_{{p_{j} |t}} \left( {1 - P_{{p_{j} |t}} } \right)$$
$$P_{{p_{j} |t}} = \mathop \sum \limits_{{c \in \left[ {1, \ldots C} \right]}}^{{}} P_{p|c}^{2}$$

where P is the probability of picking p set of variables; c is the class; j is the node; t is the tree.

A similarity matrix is computed between the observations with classification of oob observation. If two observations are classified in the same tree terminal node, the proximity between them is incremented. One thousand trees are created in the forest using pairwise comparison based on G.

Self-organizing map

SOM61 is an ANN that does dimension reduction as well as clustering simultaneously by keeping similar objects together62. The original ‘online’ algorithm of SOM is used in this study. In the algorithm, the data is described by numerical vectors belonging to K units on a two-dimensional grid, here in a Euclidean space (\(R^{p} )\). A codebook vector (neuron) \(m_{k} \in R^{p}\) is attached to each unit k, the initial value of the vector is chosen based on the distance function.

A random data is mapped to a trained SOM by calculating the distance of the datapoints to the codebook vectors and assigning each datapoint, x, to the unit with the most similar codebook vector called as the best matching unit. The matching units are assigned to clusters. The best matching unit in a cluster c at a time t is defined by minimizing the distance, here Euclidean distance, between x and matching codebook \(m_{k}\) as

$$c^{t} \left( x \right) = \arg arg\mathop {min}\limits_{{k \in \left[ {1, \ldots K} \right]}} \left\| {x - m_{k} \left( t \right)} \right\|$$

And codebook vectors are updated via

$$m_{k} \left( {t + 1} \right) = m_{k} \left( t \right) + \propto \left( t \right)h_{{c^{t} \left( x \right)}} \left( t \right)\left( {x - m_{k} \left( t \right)} \right)$$

where \(\propto \left( t \right)\) is the learning rate; \(h_{{c^{t} \left( x \right)}} \left( t \right)\) is the neighbour function, here Gaussian function, at time t between winner unit, j, and the neighbour unit, i.

$$h_{ji} \left( t \right) = exp\left( { - \frac{{d_{ji}^{2} }}{{\varphi^{2} \left( t \right)}}} \right)$$

where \(d_{ji}\) is the Euclidean distance;\(\varphi\) is the standardization parameter which decrease over time t to reduce the intensity and scope of the neighbourhood relations. One thousand iterations were conducted for the model.

Clustering of observations

The observations were grouped into clusters based on dissimilarity using a k-medoid algorithm. The k-medoid clustering is a robust clustering method70 and is less sensitive to outliers as it uses representative observations called medoids for clustering. Partitioning around medoids (PAM)71 is known as the most powerful k-medoid clustering method72 and is used in this study. PAM was performed on Euclidean distance matrices obtained from (1) normalized data which is used in the base (2) dimension reduced data using PCA where only first two PCs are used (3) proximity matrix from unsupervised RF and (4) unified distance matrix (U-matrix) from unsupervised SOM. The Euclidean distance matrix, \(d_{ab} ,\) from two datapoints a and b is calculated as:

$$d_{ab} = \left\| {a - b} \right\|$$

The distance matrix from proximity matrix, s of RF is calculated as

$$d_{ab} = \sqrt {1 - s}$$

For each randomly selected k medoids, PAM algorithm selects datapoints that decrease the distance within a medoid. The total within-cluster sum of square (wss) is calculated for each datapoint x for a medoid k of a cluster \(c\) as follows:

$$Total\; wss = \mathop \sum \limits_{c = 1}^{C} \mathop \sum \limits_{{x_{i} \in c}}^{{}} \left( {x - k_{c} } \right)^{2}$$

Total ‘wss’ measures the ‘goodness’ of the cluster, the lower the value the better the cluster. Optimal number of clusters was selected using elbow method by plotting the total wss to the number of clusters and choosing number corresponding to the bend (elbow) of this line graph. Best model for partitioning the data was chosen by comparing the wss among the optimal clusters from all the four models.

Predictability testing

The predictability of the classification models was tested using cross-validation (CV). The predictability was tested using ‘___location’ or ‘cluster’ as the response variable using CV method where the datum was randomly partitioning into training and test datasets. A confusion matrix was used to represent the counts of actual vs predicted classification from each iteration of CV. Later, average values were calculated from all the confusion matrices. The accuracy in classification was calculated for each confusion matrix and averaged as follows:

$$Accuracy = \frac{1}{M}\mathop \sum \limits_{m = 1}^{M} \frac{{tpr_{m} }}{{N_{m} }}$$

where M is the total number of confusion matrices from a CV; tpr and N are the counts of truly predicted classes and total counts respectively from a confusion matrix, m.

Impact of training population proportion and versatility of model

Various instances of models were performed to check the robustness and versatility using different proportions of training population in predicting the clusters based on soil features. Clusters created using a specific model was tested using all the models to check the predictability of the models irrespective of the origin of clustering. Predictability was also evaluated with varying training population size which was set as low as 60% to as high as 95%. Also, the models were evaluated by increasing the area of observation from three to nine times. In such instances, observations from segments (area of 1x) were averaged together to produce a single value for an area thus decreasing the number of total observations while increasing the area. For example, a soil feature value for a 3x  area was calculated by averaging the values of the feature from three logistically adjacent segments in that area thus reducing the total number of observations to a third. The most important variables influencing the classification were filtered out based on PCA, RF, SOM. Similar instances as mentioned above were performed based on these fewer number of variables. Evaluating the models for reduced number of variables and observations were practically and economically important. The CV in these simulation settings was repeated 100 times and the average accuracy in correctly predicting the classes were observed.

Use of fine resolution soil mapping in understanding spatial correlation

The fine resolution soil feature collection was done at segment level in a plot within a block in a ___location and the mapping was done for a block. While building the soil classification models, safflower population A was cultivated in the locations. Each rectangular plot in a block had 20 RILs with 10 replicates each, separated by 1 m between the plot cells. On the assumption that spatial correlation within a block can be explained using the fine resolution soil map, we used the following model to check the correlation for safflower yield:

$${\mathbf{Y}}_{n \times 1 = } {\varvec{\mu}} + {\mathbf{Z}}1_{{{\text{n}} \times {\text{g}} }} {\varvec{g}}_{{{\text{g}} \times 1}} + {\mathbf{Z}}2_{{{\text{n}} \times {\text{b}} }} {\varvec{b}}_{{{\text{b}} \times 1}} + {\varvec{\eta}}$$
$${\varvec{g}} \sim N\left( {0, \sigma_{g}^{2} } \right);{\varvec{b}} \sim N\left( {0, \sigma_{b}^{2} } \right); {\varvec{\eta}} \sim N\left( {0,\sigma_{{}}^{2} } \right)$$

where, Y is the vector of observed yield; Z1 and Z2 are the design matrices for RILs and blocks withing a ___location; g and b are the vectors of line and block effects; g and b are the total number of RILs and blocks; \({\varvec{\eta}}\) is the residual error. In the model, after accounting for the known sources of variations, RILs and blocks, the presence of spatial pattern in the residual error can be related to the spatial distribution of soil features.

Software used

The scripts to perform statistical analysis was written in R language (R v4.2.2). Packages ‘nnet’73, ‘randomForest’, and ‘kohonen’ were used for running multinomial regression, RF, and SOM models respectively. PAM clustering was performed using the package ‘pmclust’. Package ‘ggplot2’ was used for graphing.

Results

Evaluation of soil features among different locations

In this study, we analyzed fourteen soil properties across four locations to identify patterns in soil composition and variability. Moisture content and pH exhibited significant variation, with Pune exhibiting the highest mean moisture levels (4.70 mg/100 g) and Haveri the most alkaline pH (mean 8.82). Salinity and electrical conductivity (EC) were similar across locations, averaging approximately 95–109 mg/100 g and 200–232 mg/100 g, respectively, with Nagpur and Pune showing slightly higher values. For particle size distribution, Pune had the highest sand content (54 mg/100 g). Carbon content varied substantially, with Pune having the highest mean value (672.14 mg/100 g) and Delhi the lowest (246.17 mg/100 g), highlighting significant differences in organic matter. Phosphorus levels were highest in Nagpur (mean 2.74 mg/100 g), while nitrogen remained relatively stable across locations, ranging from 6.52 to 9.93 mg/100 g. Sulphur, sodium, calcium, and potassium contents also varied significantly. Calcium levels were notably high in Pune (mean 696.23 mg/100 g) but much lower in Nagpur (70.92 mg/100 g), while sodium was highest in Nagpur (18.72 mg/100 g) and lowest in Haveri (15.05 mg/100 g). The observations from the locations are presented in Supplementary Table S1. The differences across locations highlight distinct soil profiles (Supplementary figure S1) likely influenced by local environmental conditions, with implications for site-specific soil management strategies.

Evaluation of classification prediction models

To distinguish the locations, PCA was performed for all the variables. The first two PCs explaining 54% of the variation (Supplementary figure S2) were chosen for further analysis. The biplot (Fig. 2) indicated that the soil from Pune and Nagpur were clearly distinguishable from each other and also from those in Delhi and Haveri. Delhi and Haveri soils had similar features with Haveri being more alkaline in nature. Soil from Pune was sandier with lower clay content. Soil from Delhi and Haveri were siltier in nature. Both Nagpur and Pune soils had high calcium and carbon content while Nagpur soil had more sodium between the two.

Fig. 2
figure 2

Classification of soil using PCA. The farther the loadings (vectors) are from the origin, the more their influence on the PC. PC1 was predominantly influenced by calcium, carbon, and pH while PC2 by sand, clay, and sodium. Both PC 1 and 2 were similarly influenced by potassium. Pune and Nagpur soil were observed to be clearly distinguishable from each other and those in Delhi and Haveri. There were similar features between Delhi and Haveri soils.

Full size image

PC values were obtained and used as predictors in a multinomial model. The base model provided an average accuracy of 99% (Fig. 3a and b) which could be due to the use of all the variables available. Because of the overlapping features of Delhi and Haveri soil, there were misclassification in prediction of those on an average of 6% (Fig. 3c) from PC model which resulted in an average prediction accuracy of 92% (Fig. 3d). Clustering was performed using PAM and five or four clusters were selected based on the within sum of squares (wss) using the similarity measurements of each model as optimum for base and PC respectively (Fig. 4a–d) and Supplementary Table S1). The clustering indicated that some segments of a ___location had features like those in other locations.

Fig. 3
figure 3

Results obtained from 100 replications of 70:30 training: test cross-validation predicting ___location. Left hand column represents average confusion matrices and right-hand column represents histogram of accuracy. (a) and (b) are results from base multinomial model, (c) and (d) from multinomial model using PC1 and 2, (e) and (f) from random forest model (RF), and (g) and (h) from self-organizing maps (SOM).

Full size image
Fig. 4
figure 4

Soil clusters. Optimum number of clusters of soil types based on the within sum of squares (wss) using the similarity measurements of each model. Left hand column indicates the wss for all the possible clusters and right-hand column indicates the representation of fields using optimum number of clusters. (a) and (b) based on all features after nomalizing (c) and (d) based on PC1 and  PC2 (e) and (f) based on the distance matrix from unsupervised random forest, and (g) and (h) from unsupervised self-organizing maps.

Full size image

RF model was performed with locations as the response variable. Using RF, the locations were predicted with no misclassification error on an average (Fig. 3e and f) with prediction accuracy of 100% (Fig. 3f). Five clusters optimally distinguished the locations as well as blocks within Delhi (Fig. 4e–f and Supplementary Table S1). Calcium content was found to be the most important feature distinguishing the locations (Fig. 5a) as well as the clusters (Fig. 5b).

Fig. 5
figure 5

Variables of importance. Variables of importance based on mean decrease in Gini value from the supervised random forest (RF) model using (a) locations as response variable (b) cluster as response variable. Calcium content was found to be most important in distinguishing locations and clusters.

Full size image

Self-organizing maps were used to evaluate the clustering based on soil features and ability to predict ___location. On average, there was no misclassification error and the predictability was 100% (Fig. 3g, h). An unsupervised SOM was used to identify the most influential variables from the codebook vector (Fig. 6a). A U-matrix (Fig. 6b) was used for visualizing the distances between codebook vectors and clustering those (Fig. 6c). The model converged around 600 iterations (Supplementary figure S3). The re-clustering was done using PAM on U-matrix. Five clusters were chosen as optimum based on the wss (Fig. 4g, h and Supplementary Table S1).

Fig. 6
figure 6

Result from unsupervised SOM. (a) Neighbourhood codes indicating most influential variables (b) U-matrix between neurons (c) cluster map based on optimal number of clusters (five).

Full size image

Based on the wss values and optimal number of clusters, RF and SOM were considered as best models for clustering. They both produced clusters that can be logistically applicable. The clustering based on base also appeared similar to those from RF and SOM but with a higher wss. The macronutrients P and K, the micronutrients Na and Ca, SOC, and the percentage of sand were found to be the most influential variables in classifying the soil profiles used in this study (Figs. 2, 5, and 6a).

Versatility, robustness, and predictability of models

Overall, RF was found to be the most robust, versatile, and best-performing model with accuracy never below 85% irrespective of the training population size, number of features used, total number of observations in the testing population, and the type of cluster (Fig. 7a, b). The prediction accuracy of RF was never below 90% when only the most influencing features were used in the model. RF and SOM performed similarly except when the area of measurement was increased. Since the total area and number of collected observations were constant in this study, on increasing the unit area per observation (for example, from 1× to 3×), the total number of observations reduced proportionately. Additionally, the prediction accuracy of RF and SOM were close to 100%. SOM failed to perform when the number of observations in the testing population was less than five. Out of the two multinomial regression models, base model performed better, even with increase in the proportion of training population.

Fig. 7
figure 7

Average classification accuracies. Average classification accuracies from studies using (a) all the features (variables) (b) most important features which are sodium, calcium, potassium, carbon, phosphorous, and sand. The clusters made from each model (Base, PC—multinomial based on principal components, RF—Random Forest, and SOM—Self Organizing Maps) are represented in horizontal panels while the unit area for observations is represented in the vertical panels. The smallest unit area is a segment in a block (~ 7 × 2 m) which is expressed as ‘x’. The other three areas are represented as the multiples of this segment. The predictability of all the models which are represented in four different colors is checked against the clusters produced by a specific model. The predictability was checked using varying training population size. Overall, RF was found to the most robust, versatile, and best performing model. RF and SOM performed similarly except when (i) the area was increased a.k.a the number of observations was reduced and (ii) clusters were based on PC.

Full size image

In general, predictability can be maintained with fewer number of features, especially when those are the most influencing features in clustering. Size of training population influences the predictability when the number of observations in testing population is reduced to five or less, i.e., when the training population proportion is 90% or above in 6× and 9× unit areas (1× being the area of a segment) with proportionate decrease in the total number of observations. In general, 70–80% of the population can be used for training irrespective of the total number of observations for better accuracy in prediction.

Fine resolution soil mapping to understand spatial correlation

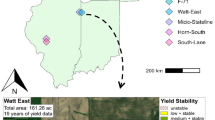
Compared to all other locations and blocks within locations, block B in Delhi exhibited visibly significant spatial correlation of the yield (Fig. 8a). Thus, we used it to demonstrate the influence of soil feature spatial distribution in safflower yield. The residual error showed spatial distribution after taking out the line and block effect on yield (Fig. 8b) indicating the presence of a strong influencing factor in the soil. The model assumed that the lines were independent of each other and the line effect showed no spatial relation and were distributed randomly (Fig. 8c). Sodium was found to be aligning with the yield distribution. The presence of high sodium content reduced the yield (Fig. 8d).

Fig. 8
figure 8

Visualization of the effects from safflower yield model and the distribution of influencing soil feature from block B in Delhi field. Each of the six plots were partitioned into 20 rows for planting safflower lines while soil features were collected from three segments in a plot. Missing lines are indicated by grey cells in the plot. (a) Distribution of safflower yield indicating spatial correlation in low yield, (b) non-random distribution of residual error (eta) showing spatial correlation, (c) random distribution of recombinant inbred line (RIL) effect; RILs were assumed to be independent of each other in the model, and (d) the spatial distribution of sodium in the field. Presence of high sodium concentration was aligned with the spatial distribution of low yield.

Full size image

Discussion

Knowing the characteristics of the field is a critical element for success in precision agriculture for which soil features play a major role. Collecting fine-resolution soil features helps in understanding not only the dissimilarities between distant fields but also within a field. Our study on representative TEs of safflower, found that the different locations can be distinguished based on their unique soil characteristics using robust modeling approaches. Out of the thirteen features we evaluated, calcium, sand, soil organic carbon, phosphorous, potassium, and sodium were found to be most influential in distinguishing the representative TE into unique clusters. These features represent the uniqueness of the soil samples collected before the crop season.

We found that calcium was the most influencing soil feature in distinguishing the clusters. In our study, high calcium content was present in Pune and Nagpur with average values of 696 mg/100 g and 496 mg/100 g respectively. Whereas Haveri (145 mg/100 g) and Delhi (89.5 mg/100 g) had moderate calcium content. Calcium is a macronutrient, which plays a significant role in plant growth74. Its deficiency leads to chlorosis and decreased immunity of the plant, whereas abundant calcium interferes with the uptake of the micronutrient, which creates a deficiency of another nutrient75. Therefore, adjustment of the calcium level in the fertilizers according to the field conditions is important. Sandy soil has good drainage properties. In addition to having high calcium content, Pune soil had relatively high sand content also. Sandy soil is reported to have high topsoil (5000 mg/100 g) and subsoil (2000 mg/100 g) organic carbon content76,77. In safflower, productivity can be increased by loosening the soil and the addition of soil organic matter78. Organic carbon present in the soil can be used as a proxy for organic matter content79. Therefore, an increase in soil organic carbon can be interpreted as an increase in the fertility of the soil. On average, Pune soil had the highest organic carbon (672 mg/100 g) followed by that in Haveri (584 mg/100 g), Nagpur (544 mg/100 g), and Delhi (246 mg/100 g). However, these values were lower compared to the expected value in agricultural fields (3800 mg/100 g)80, and thus application of manure before every crop season in the TE was important. Although the importance of potassium, a major nutrient, in safflower physiology and morphology is still incipient, it is assumed that potassium will positively involve in growth and development81. From our study, Nagpur soil is found to have relatively high average potassium (53 mg/100 g) content while other clusters have less than 20 mg/100 g of this nutrient. A high amount of potassium in the Nagpur soil can be due to chloritized vermiculites and mica in the soil which may play an important role in the dynamics of soil potassium in calcareous soil82. Phosphorus, another major nutrient, stimulates seed yield in safflower83. It is also critical for cellular processes84, cell division, carbohydrate metabolism, and root development85. We found that Nagpur and Haveri soils had relatively high phosphorus content with average values of 2.7 and 2.4 mg/100 g respectively while other clusters had approximately 1.2 mg/100 g of the nutrient. Various factors including pH, clay, and exchangeable Ca in the soil influence the availability of phosphorus. As exchangeable Ca and pH increase, the available phosphorus for the plants decreases due to its solubilization86. Thus, the highly calcareous soil of Pune, with a basic pH of ~ 7.5 was found to have low available phosphorus whereas the soil in Nagpur, again with high Ca content but with an acidic pH of 6.5 was found to have a high amount of the nutrient. Potassium and phosphorus are widely used nutrients in fertilizers. According to the Safflower package of practices (https://icar-iior.org.in/package-practices), safflower required 168 mg/100 g of phosphorus and 56 mg/100 g of phosphorus in Karnataka region, whereas 90 mg/100 g of phosphorus is required in Maharashtra soil. However, in our study, we found that phosphorus and potassium were in less amount in all the soil and thus, required fertiliser treatment throughout growing season. Sodium is a “functional nutrient” as plants can survive without it87. In plants, sodium stimulates plant height and dry matter absorption88. It is assumed that sodium could be used as a substitution for phosphorus in fertilizers, however, in safflower sodium and phosphorus play their independent functions89. Abundance of sodium tends to increase the salinity of the soil and thus causes salt stress in the plant. In our study, we found the sodium levels were beyond the critical value (13 mg/100 g) (https://ucanr.edu/) for Nagpur (71 mg/100 g) and in the cluster formed by blocks A and B in Delhi (26 mg/100 g). Soil salinity depends on the parent rock, soil type, climate, pH, and irrigation routine90. High salinity in Nagpur can be attributed to smectite-dominant shrink-swell soils91 whereas salinity in the Delhi cluster formed by blocks A and B can be attributed to high pH and irrigation routine. Also, that particular cluster in Delhi was nearby the housing locality, which may also contributed to the high salinity in the soil. Being adapted in semi-arid regions, safflower can be expected to grow in high saline conditions provided other nutrients are adequately available. We also found that the Block B in Delhi had spatial pattern in safflower yield. The low yield in the block was influenced mainly by the high concentration of sodium. Knowing this prior to planting would have helped in re-designing the experiment and optimizing the nutrient supply throughout the cropping season.

Moreover, we found dissimilarities in soil characteristics within a ___location. The blocks in Delhi were kept the farthest apart within an area of ~ 40,000 m2 with an arrangement that a pair of blocks were kept at a distance of 160 m apart, and this pair was separated from the other pair by a distance of 350 m. The pairs, although from the same ___location, showed distinct characteristics to be accommodated into separate clusters. Delhi cluster with blocks A and B had higher calcium, sand, and phosphorus as compared to the cluster with blocks C and D with higher organic carbon. This variation even within a field thrusts the importance of fine-resolution soil surveying to facilitate smart farming. This kind of within ___location prior information is even more important for farmers with marginal crops for risk management and on the other hand for crop insurance companies for risk assessment. However, distinction within the field could not be detected in other TEs which could be due to the shorter distance between the blocks. Therefore, we found that an area of 170 m2 is an ideally large area for collecting soil samples. A comprehensive study using edaphic as well as topographic features from blocks in multiple sites within a ___location will provide a better insight into the optimal area for sample collection. Thus, based on the different soil features, the management practices such as dose and frequency of fertilizers as well as macro and micronutrient supply should be customized even within a ___location.

Furthermore, the use of robust modeling approach for distinguishing features became significant due to the magnitude of data required in precision agricultural studies. In this study, we used different supervised and unsupervised models to detect the best modeling approach. PCA, although the most used statistical approach, failed to produce practically useful cluster as the variability of data was limited to the first two PCs. The RF and SOM models consider the underlying relationship among the features while training the model which eventually helps in identifying the clusters with low ‘wss’. RF and SOM from our study can be used to identify the major distinguishable features within and between the locations. In future, collection of soil features from more safflower cultivating farms can be limited to these major distinguishable features and these features can also be used as the base for customizing the management practices in the cropping season. RF model can be adopted for evaluating similarity of a test ___location to any of the clusters in the training data. The soil features collected from the new ___location can be tested using the model to predict their cluster identity. Later, management practices can be optimized to the test ___location to prevent over accumulation in natural resources and toxicity in plants. Contextually, adding more data to train the model would increase the scope of prediction. Representation of variation in the test data influences the prediction accuracy. Therefore, the SOM models failed when the proportion of training population was 90% or higher and when the area of collection were 6× and 9× (1× being the area of segment) with proportionately lower number of total observations. Transferring the codebook information and finding meaningful distance between objects was challenging when the number of observations decrease in the test population. In this context, the higher prediction accuracy of RF model was significant even in small datasets. For very small datasets, a training population proportion varying from 70 to 80% was optimal for all the models for proper distribution of the variation and relationship among the soil features. A marginal decrease in the prediction accuracy from training population proportion of 0.6 compared to 0.7 and 0.8, especially in 6× and 9× unit areas could be because of the under representation of the relationship among features. The concept of design of experiments with optimal area and number of observations should be used in edaphic surveying for smart agriculture to represent the variation.

Fine-resolution mapping of soil provides detailed spatial data on soil properties, enabling precise decision-making in resource management. Our study highlights the significance of such efforts and can pave the way for precision farming and increased agriculture efficiency even for small farms and marginalized crops. Studies of this nature are particularly crucial for agriculture-dependent developing countries such as India, where fine resolution mapping is still in its early stages92,93,94. Notably, resources such as SoilGrids 2.0 (https://soilgrids.org/) and OpenLandMap (https://openlandmap.org/) offer detailed digital soil mapping (DSM) at a fine resolution of 250 m2 across India16. However, the limited density of sampling undermines the accuracy of these maps21. Consequently, there is a pressing need for studies conducted at the plot level (0–1 km2) and local level (1–104 km2) to enhance our understanding of soil variability. By integrating these insights into precision agriculture practices, particularly for safflower cultivation, we can optimize resource management and improve crop yield. The detailed soil information gained from fine-resolution mapping can help farmers make informed decisions about nutrient application and soil management strategies, ultimately leading to sustainable agricultural practices and enhanced productivity in safflower farming. Additionally, detailed soil maps based on high-resolution sampling can act as stepping stones for many conservations policies at the national and international levels.

Conclusions

In conclusion, we present fine-resolution, high-density site-specific digital soil map tailored for safflower cultivation areas. This map is not only unique and significant in its application but also in its innovative methodology, making it a valuable resource for nutrient recommendations within the context of precision agriculture. Based on our study, we recommend collecting fine-resolution edaphic features from marginal farms prior to the crop season. By employing the RF model, we can accurately identify the similarity of a new ___location/field with our trained data and facilitate in (1) designing the field for homogenous yield, (2) effective soil management strategies, and (3) recommending site-specific optimum use of nutrients. Such tailored recommendations rather than a unified package of practice serve as a useful and effective tool for government initiatives in the agriculture sector, including soil health cards and delineation of suitable crop-growing areas26,95.