Introduction

Since the 21st century, the overall scale of China’s logistics industry has been growing rapidly, and the level of logistics services is improving significantly. As a new thing in the field of logistics, China’s emergency logistics is still in its infancy compared with developed countries. Emergencies (e.g., various natural disasters, public health incidents, traffic accidents, etc.) often lead to obstruction or damage to traditional logistics paths, and thus affect the efficiency of logistics and the level of service1. According to the statistics of the Global Natural Disaster Assessment Report, the cumulative number of people affected by natural disasters in China in the period 2019 to 2023 is 582 million, the cumulative crop affected area is 73,564.5 thousand hectares, and the cumulative direct economic loss is up to 1,615.36 billion yuan. This accounts for 26.99% of the total global economic losses from natural disasters2-6,3,4,4,5,-; It is estimated that global earthquake disasters caused a cumulative economic loss of US$33,384 million during 2020–2022. As a serious challenge to nature, the frequency of earthquakes poses a serious threat to human society and has highlighted the importance of emergency logistics in disaster management7.

The frequent occurrence of natural disasters has not only brought severe disasters to human society, but also posed a serious challenge to the emergency response system. Against this background, emergency logistics as a central component of the disaster response system is becoming increasingly important. The aim of emergency logistics is to deliver relief supplies quickly and precisely to the affected areas in order to secure the basic needs of the affected people and reduce the negative effects of the disaster. Among the many aspects of emergency logistics, emergency material distribution is one of the most important functions, and the Vehicle Routing Problem (VRP) has arisen8.

As a classic logistics problem, the use of VRP in emergency logistics is particularly complex and critical. Traditional VRP optimization aims to find the optimal vehicle path to minimize transportation costs, time and other key performance indicators through accurate mathematical models and algorithms. However, the complexity of this problem increases significantly in emergency logistics scenarios. On the one hand, uncertainties such as road damage and post-disaster traffic congestion make it difficult to directly apply the traditional VRP model9; On the other hand, the psychological risk perception of the affected population influences the allocation and distribution of relief supplies, a factor that is often neglected in the traditional VRP model, which leads to the limitations of the traditional model in practical application10.

Psychological risk perception is an important concept at the intersection of behavioral economics and psychology and reflects people’s psychological reactions and decision-making behavior when faced with uncertainty and potential risks. This concept expands the boundaries of the assumption of rational agency in traditional economics and also offers a new perspective for understanding individual behavior in complex social situations. In the response process of natural disasters or emergencies, the psychological risk perception of the affected population is not only directly related to the individual perception of the intensity and urgency of the demand for relief supplies, but also has a profound impact on the formulation of the distribution strategy of the entire relief supplies and optimization of the choice of transport routes11. Particularly after a disaster, disaster-affected people often experience high levels of anxiety, fear and insecurity, and these factors interact to produce non-linear and dynamic changes in their relief needs12. On the one hand, individuals with higher psychological risk perceptions may need basic living materials and psychological comfort more urgently. On the other hand, this difference in perception leads to an uneven distribution of demand, which increases the difficulty and complexity of material distribution. In order to improve the accuracy of emergency response and better understand the psychological reactions and demand changes of the affected population during disasters, scientists have tried to integrate psychological theories and methods into the emergency logistics path optimization model.

Therefore, in the emergency response phase after an earthquake, the rapid and accurate assessment of the severity of the disaster in each region and the effective integration of the psychological risk perception of disaster victims into the emergency logistics management system are the key links to optimize resource allocation and ensure efficient use of materials and personnel. Given the significant differences in disaster severity between affected regions, this paper proposes the development of a satisfaction-oriented optimization model that aims to determine the priority of material deployment and transportation through data analysis and aims to maximize the efficient allocation and precise placement of rescue resources to improve disaster response capability and recovery efficiency.

Literature review

Earthquakes are one of the extremely destructive natural disasters, whose suddenness and unpredictability have brought great threats to human society13,14; Earthquakes not only directly cause large losses of life and property, but also indirectly affect rescue and recovery work in the disaster area by destroying transportation infrastructure, communication system and supply chain15. After an earthquake disaster, emergency logistics quickly become the lifeline of rescue efforts.

Scientists at home and abroad have studied in detail how rescue materials can be organized efficiently and orderly. Ref.16 focus on building the emergency logistics system and researching the countermeasures for the coordinated development of its information technology. In researching relief stockpiling, Ref.17 comprehensively considers the uncertainty, diversity and equity characteristics of post-disaster materials demand, and, with the aim of minimizing the comprehensive risk, builds an optimization model for emergency materials stockpiling to make the optimal decision about the amount of material stockpiling; Ref.18 proposes a contractual approach with options to motivate a supplier to store supplies for its customers, taking into account low-carbon disposal costs, in order to derive the optimal stocking decision for emergency deliveries in different scenarios.

After determining the amount of material reserves, the ___location of emergency distribution centers becomes the next important step, and many scholars have conducted in-depth research and discussions from this perspective. Ref.19 created a model for the ___location of emergency distribution centers considering multiple modes of transportation and multi-time dynamics, aiming at the timeliness and distribution fairness of emergency materials. Ref.20 has developed a distributed robust optimization model (DROM) designed to optimize the ___location of distribution centers and standby warehouses by minimizing the expected total cost and delivery time, as well as the distribution of relief supplies in the emergency logistics network. For emergencies, Ref.21 develops a demand-weighted and hierarchical ___location model, which is combined with an algorithmic solution to obtain a ___location plan that provides decision support for the siting and categorization of reserve storage facilities.

After the rescue materials arrive at the distribution center, the question of how they can be distributed fairly and efficiently is also one of the important topics in emergency logistics research.The Vehicle Routing Problem (VRP) is a typical NP-hard problem, which was first proposed by Dantzig and Ramser in 195922. How to Reduce the complexity of paths and improve efficiency have been the main goals of study in this problem. In recent years, scholars carried out extensive research on emergency supply distribution and path optimization, and proposed a variety of models and methods.

Firstly, in terms of the emergency supply dispatching study, the current study focuses on how to distribute as many supplies as possible to the disaster sites at the lowest cost or minimum time. Ref.23,24 proposed the mean arrival time for emergency deliveries as a response objective to describe the effectiveness of vehicle route optimization for delivering various types of emergency supplies. Xiao Wei et al.25 constructed a multi-objective mathematical model with minimizing vehicle cost as the objective function and time window penalty coefficients to achieve time constraints by introducing the “emergency safety breakage cost”. In addition, some other scholars focused on the satisfaction of the victims of the disaster. M. Afshar-Bakeshloo et al.26 solved the problem by taking the maximum satisfaction as the objective function; Shiva Zokaee et al.27 implicitly increased the satisfaction level of people in disaster areas by imposing penalties for shortages of relief commodities to better measure the fairness objective. Some scholars explored the perspective of urgency/prioritization for supply demand at disaster sites. Royero et al.28 ranked the demand points according to their urgency and performed disaster relief emergency response according to priority. Min Chen et al.29 study the VRP problem of scheduling medical emergency supplies under demand urgency and design an algorithm to solve it. Jianjun Zhang et al.30 also paid attention to the differences in the importance of various emergency supplies as well as the subjective urgency needs of the disaster victims and established a multi-period integer planning model to minimize the total shortage of adjusted supplies.

Furthermore, the equity concern factor has attracted the attention of scholars in consideration of human-centered thinking after the disaster. For example, Shiva Zokaee et al.27 focused on the importance of humanitarianism in disaster relief operations, aiming to provide solutions for humanitarian logistics in an environment of uncertainty in demand, supply, and cost parameters, in order to reduce the level of suffering of disaster-affected people; Holguin et al.31 quantified the economic value of human suffering for the first time, and established a Deprivation Cost Function (DCF) to capture human suffering in the absence of relief services and argued that reducing deprivation costs may be a more effective strategic goal than reducing logistics costs; Li zhu et al.32 developed two models for better emergency relief by classifying disaster victims with the levels of injuries and using relative deprivation costs as a decision-making objective emphasizing fairness; By analysing psychosocial factors, Luis F. Macea et al.33 concludes that mass risk perception and confidence in the emergency response system play an important role in individual disaster preparedness and in capturing individual heterogeneity through further study, Wang Xihui et al.7 used a numerical rating scale to estimate the deprivation level function, and the results showed that the deprivation level can be expressed as a Logistic growth function with a typical S-shape to better quantify human suffering; compared to the deprivation cost, the main difference lies in the use of dimensionless pain level rating instead of economic indicators, which is also widely used34,35,36.

In summary, in recent years, scientists at home and abroad have devoted themselves to improving the efficiency and precision of emergency logistics systems, using diverse optimization methods and advanced technical means to cope with the complexity and dynamics of emergency logistics systems. The evaluation of emergency logistics systems by most scholars is mostly limited to quantitative and economic perspectives and focuses on improving economic efficiency, while rarely considering the deprivations, pain and negative emotions that disaster-affected people experience during disasters. However, in reality, the negative psychological suffering of disaster victims should be considered as one of the more critical and appropriate measures. Therefore, it is extremely urgent to further deepen the humanistic concerns of disasters, expand the research horizon, incorporate the psychological risk perception of disaster victims into the model, and develop comprehensive emergency logistics solutions that can efficiently deliver relief supplies and effectively alleviate the psychological trauma of disaster victims, in order to to meet the challenges of various disaster scenarios.

Gap analysis

In this study, satisfaction is considered an important factor in path optimization and incorporated into an integrated two-stage optimization framework. The priority of supply distribution is followed by vehicle path optimization in the context of insufficient total supply of supplies in the short term after the earthquake. A theoretical basis and practical operation method are provided for establishing a more scientific and comprehensive supply allocation model, which is of great significance for the rapid and reasonable rescue work after the earthquake.

The main work of this study is as follows. Firstly, In the aftermath of a disaster, historical data, and seismic monitoring information will be combined and used to quickly estimate the number of people affected by the disaster and to forecast emergency supply requirements, such as magnitude and population density. This helps precise deployment of relief supplies and flexible response to changes in the disaster situation, thus reducing the fault rate of relief distribution and improving the efficiency of relief and the survival and quality of life of the people in the disaster area. Secondly, this study introduces psychological risk perception to implement a resource allocation strategy based on pain perception by modifying the prospect theory framework. The gains and losses in prospect theory are replaced by the sufficiency and shortage of disaster victims’ demands. In the urgent context of resource undersupply, the weight of supply allocation in potentially severely affected areas is targeted to be increased to obtain maximum relief efficiency. Thirdly, this study introduces the concepts of optimal and minimal needs to represent the situation where supplies can fully satisfy the needs of the disaster site and only meet the basic needs. The differentiation describes the satisfaction of the needs of the disaster victims in different degrees of disaster areas. Fourthly, the distribution urgency weights of different disaster points are introduced into the traditional path optimization model to improve the objectivity and rationality of the time satisfaction function. This makes the model closer to the actual situation to correct the impact of the severity of the disaster on the time satisfaction of supply distribution.

Parameters/variables and definitions

The relevant parameters in the article are defined in Table 1.

Table 1 Parameter interpretation.
Full size table

Assumptions

  1. (1)

    The ___location of each disaster site is known;

  2. (2)

    Before the disaster, the emergency stockpile center has limited supplies, and at the beginning of the disaster, the demand for supplies increases sharply, resulting in insufficient supply and restricted resources, producing an oversupply;

  3. (3)

    Vehicles departed from the stockpile center and returned to the stockpile center after delivering supplies to the disaster site.

  4. (4)

    The supply distribution time does not take into account vehicle maintenance time and supply loading and unloading time;

  5. (5)

    Distribution vehicles are of the same model with the same fixed load capacity and average speed;

  6. (6)

    The combination of supplies has been completed in a certain proportion, i.e., a single supply type has been considered;

  7. (7)

    The minimum fulfillment rate of supplies indicates the ratio of the minimum demand to the optimum demand, and the minimum fulfillment rate reaches a certain percentage.

  8. (8)

    Each vehicle can serve more than one disaster site and each disaster site is served at least once.

  9. (9)

    The total amount of supplies in the emergency storage center was determined.

Model development

Description of the problem

Earthquakes are complex and destructive natural disasters that can cause damage to buildings, roads, and other structures. Secondary disasters such as building collapses, tsunamis, and fires caused by earthquakes may result in casualties. Moreover, when an earthquake occurs, society may be thrown into a state of chaos and panic, which may result in problems such as blocked roads and disrupted communications, further increasing the difficulty of rescue and emergency response. For the disaster site, whether the emergency supplies are reasonably distributed and quickly delivered has become an important indicator of the effectiveness of emergency logistics operations. In emergencies such as earthquakes, the rapid and effective delivery of emergency supplies is critical to minimizing the impact of disasters and protecting lives and property. Due to the suddenness of earthquake disasters, the total amount of emergency supplies at the beginning of a disaster often fails to meet all the needs of the disaster site, resulting in a situation where demand exceeds supply.

Given the various types of problems that may exist during earthquake disaster response, this study focuses on the VRP problem of emergency response and material distribution from the Emergency Material Reserve Center to multiple disaster sites. Assuming the existence of a single distribution Center, \(\:M\) affected sites, \(\:n\) delivery vehicles of the same model and an epicenter. The objective of the VRP is to quickly estimate the number of affected people and the demand for emergency supplies based on available historical data and earthquake monitoring information and to construct a two-stage model of allocation followed by optimization. An achievable algorithm is designed to solve the model, thus obtaining the optimal allocation scheme and distribution path, and achieving the goal of maximizing demand satisfaction and time satisfaction at the affected points.

Analysis of psychological risk perception of disaster victims

Prospect Theory is a psychological theory that describes the decision-making process proposed by psychologists Daniel Kahneman and Amos Tversky in 197937. The theory describes how people are more sensitive to losses than to gains of the same amount.

In this study, a supply allocation model is presented in terms of pain perception based on a modification of the traditional prospect theory, to reflect the level of psychological pain of individuals in disaster situations more accurately. In this model, the decision of supply allocation is based on the difference between the actual allocation and the demand, and the sense of sufficiency and shortage of the victims’ demand for relief supplies is regarded as the equivalent of gain and loss in the traditional prospect theory. Furthermore, the study examines how to minimize the psychological suffering and physical injuries of the affected groups by adjusting the supply distribution strategy to maximize relief efficiency in a resource-limited emergency setting.

The perception of risk by the affected population is closely related not only to the disaster itself but also to the amount of relief supplies it receives. Before the delivery of relief supplies, disaster victims develop psychological expectations about the amount of supplies they are about to receive for allocation, and perceive feelings of sufficiency and shortage as gains and losses, respectively. In the aftermath of a disaster, the public tends to overestimate the damage of the event and exaggerate the risks. At this point, the public’s psychologically perceived value\(\:<\)objective value\(\:<\)0; relatively, psychologically perceived risk\(\:>\)objective risk\(\:>\) 0.

According to the value function model of prospect theory, the psychological risk perception function of the affected people for the quantity of emergency supplies acquired is constructed, as shown in Eq. (1).

$$\:\begin{array}{c}{R}_{j}=\left\{\begin{array}{c}\lambda\:{\varDelta\:}_{j}^{\alpha\:}+{R}_{0},{x}_{j}\le\:{y}_{j}\\\:{-\varDelta\:}_{j}^{\beta\:}+{R}_{0},{x}_{j}>{y}_{j}\end{array}\right.\end{array}$$
(1)

Where \(\:{R}_{j}\) denotes the psychological risk perception of the affected population regarding the quantity of emergency supplies to be acquired, \(\:{y}_{j}\) denotes actual supply requirements at disaster sites, \(\:{x}_{j}\) denotes actual supply availability at disaster sites, and \(\:{\varDelta\:}_{j}\) denotes emergency supplies shortfall; \(\:\lambda\:>1,\) denotes loss aversion, i.e., describes the loss range steeper than the gain range; \(\:0<\alpha\:,\:\beta\:<1,\alpha\:\:\)is the gain sensitivity coefficient, \(\:\beta\:\:\)is a loss sensitivity coefficient; \(\:{R}_{0}\) denotes the psychological risk perception when the actual supply of goods is equal to the quantity demanded. To facilitate the description, the psychological risk perception image is plotted as shown in Fig. 1 when the critical value \(\:\alpha\:=\beta\:=1\) is taken.

Fig. 1
figure 1

Psychological risk perception image.

Full size image

When \(\:{\varDelta\:}_{j}<0\), i.e., the actual supply of supplies \(\:{x}_{j}\) is less than the demand \(\:{y}_{j}\), the victims are in a high perception state. At this time, the psychological risk perception decreases with the reduction of the discrepancy between the two, i.e., the left side of the y-axis; when \(\:{\varDelta\:}_{j}>0\), the disaster victims are in a low-perception state, and the psychological risk perception decreases with the enhancement of the discrepancy between the two and the rate of decline slows down gradually.

Definition of the urgency of requirement

In earthquake disaster management, the urgency of requirement generally refers to the degree of urgency of the demand for relief resources in the affected area or among the affected population. This concept is usually based on a combination of several factors, including the extent of the disaster, population density, the epicentral distance, and the vulnerability of the population, etc. By evaluating these factors, it is possible to determine which areas or populations are in more urgent need of relief support, which in turn guides the organization of relief operations and the deployment of resources. It helps disaster managers to make quick decisions during emergencies to minimize the life and economic losses caused by disasters. Thus this study proposes to assess the urgency of need in terms of both distance from the epicenter and population vulnerability coefficients.

The epicentral distance

In natural earthquakes, the place where the rupture of the rock layers inside the earth causes shaking is called the seismic source, while the vertical projection of the epicenter on the ground is called the epicenter, and the epicentral distance is the distance from any point on the ground to the epicenter. The seismic intensity attenuation relationship is defined as the decrease in damage to structures by seismic waves with increasing epicentral distance38. As a result, earthquake hazards exhibit unique characteristics: differences in the severity of the destruction due to the different epicentral distances between the affected sites. At the same time, differences in the degree of destruction of existing supplies will lead to changes in the degree of dependence on emergency supplies. The epicentral distance is one of the most important indicators of the magnitude of an earthquake’s effects, directly reflecting the impact on the ground surface and its surroundings caused by the release point of seismic energy. Areas closer to the epicenter usually suffer greater earthquake damage (e.g., building structural damage, infrastructure destruction, and human casualties), which leads to a significant increase in the urgency of supply needs in this area.

Correspondingly, the urgency of requirement \(\:{\partial\:}_{j}\) is proposed to be related to the epicentral distance. where \(\:\partial\:\in\:\left(\text{0,1}\right)\). When \(\:\partial\:\) tends to 0, i.e., when the epicentral distance exceeds a certain range, there is no damage to residential housing and the severity of the damage tends to 039; When \(\:\partial\:\) tends to 1, it indicates that the point is severely damaged and the need for emergency supplies is high and urgent.

The population vulnerability coefficient

The population vulnerability coefficient also plays a crucial role in assessing the urgency of requirements. In this study, the population vulnerability coefficient is defined from two aspects: population density and the proportion of vulnerable populations.

In the aftermath of a disaster, it is often difficult for the supply of relief goods to satisfy the requirements of all affected populations. A high population density usually means that there is a greater demand for food, water, and medical resources. Moreover, due to the concentration of population, the irrational distribution and untimely delivery of supplies may lead to the amplification of public dissatisfaction, and the public may express their dissatisfaction and criticisms against the government or relief agencies through various media platforms, thus aggravating the public opinion storm and causing unnecessary political impacts. In addition, the elderly and children are often considered one of the vulnerable groups in disasters40. They often face higher risks and greater challenges for physical and psychological reasons. Firstly, the elderly may find it difficult to timely escape from hazardous areas due to limited movement or poor physical condition, while children may not be able to make the right self-protection decisions due to lack of cognitive capacity. In addition, the elderly and children often require additional care and support as more human resources and specialized skills are needed to deal with the special needs of the elderly and children, which adds to the complexity and urgency of relief efforts41. Overall, population density and the percentage of people over 60 years old and children under 12 years old may affect the urgency of supply needs at each disaster site, as shown in Eq. (2).

$$\:\begin{array}{c}{D}_{j}={\rho\:}_{j}*{\sigma\:}_{j}={\rho\:}_{j}*\frac{{q}_{j}\left(0<A<12\right)+{q}_{j}^{{\prime\:}}\left(A>60\right)}{{Q}_{j}}\end{array}$$
(2)

Where \(\:{D}_{j}\) denotes the population vulnerability coefficient of the affected site, \(\:{\rho\:}_{j}\) denotes the population density of the affected site \(\:j\), \(\:{\sigma\:}_{j}\) denotes the proportion of the vulnerable population, i.e., children and the elderly, in the total population of the affected site \(\:j\), \(\:{q}_{j}\) denotes the number of children in the age group of 0–12 years in the affected site \(\:j\), \(\:{q}_{j}^{{\prime\:}}\) denotes the number of elderly people aged more than 60 in the affected site \(\:j\), \(\:A\) denotes the age of the population in the affected site, and \(\:{Q}_{j}\) denotes the total population of the affected area \(\:j\).

Demand satisfaction and time satisfaction

In the early stages of the disaster, victims were able to rescue themselves by using their stockpiles of undamaged supplies, further providing emergency relief to neighboring affected areas. However, due to the limited pre-stocking of relief supplies, it is difficult to meet the optimal needs of all affected sites. Optimal requirements represent supplies that can completely satisfy the needs of the affected site, while minimum requirements represent supplies that can only satisfy the basic survival needs of the affected site. Therefore, to satisfy the basic needs of disaster victims in the shortest possible time, the objective function of maximum demand satisfaction is constructed to portray the relationship between demand satisfaction and the amount of supplies demanded. Thus, the demand satisfaction function for supplies at the disaster site is set as shown in Eq. (3).

$$\:\begin{array}{c}{M}_{j}={R}_{j}*{\partial\:}_{j}{\text{*}D}_{j}\end{array}$$
(3)

Where \(\:{R}_{j}\) denotes the psychological risk perception of the affected population regarding the quantity of emergency supplies to be acquired, \(\:{\partial\:}_{j}\) denotes the dependence of the affected point \(\:j\) on emergency supplies, and \(\:{D}_{j}\) denotes the population vulnerability coefficient of the affected point \(\:j\).

In areas where the vulnerability of the population is high, the more severely affected, the greater the dependence on supplies and relief, and the more urgent the need for emergency supplies. Therefore, when distributing emergency supplies, priority should be given to areas of high urgency to maximize overall time satisfaction. In traditional VRP, the total distribution time is usually a linear function of distance and speed. In this article, the effect of the degree of damage and population vulnerability on the urgency of distribution is considered, i.e., the extent of the urgency of the distribution task at different disaster sites. Specifically, it is assumed that the linear relationship between time per journey and distance and speed no longer holds. Then, with the weighting factor introduced, the greater the weighting, the greater the dependence of the disaster victims on their supplies, the earlier they should be assisted, and the larger the corrected transport time; Whereas, the smaller the weight, the lower the degree of damage to the area, the less destruction of residents’ supplies, and the relatively low urgency of the need for emergency supplies. The practical significance of this objective function indicates that to make the corrected total transport time smaller, supplies will be more likely to be transported first to affected areas with high population vulnerability close to the epicenter, thus making the model more realistic. Therefore, the revised transport time function is shown in Eq. (4).

$$\:\begin{array}{c}{t}_{j}^{{\prime\:}}=\frac{{\partial\:}_{j}{\text{*}D}_{j}}{\sum\:{(\partial\:}_{j}{\text{*}D}_{j})}{t}_{j}\end{array}$$
(4)

where \(\:{t}_{j}\) denotes the transport time of emergency supplies at the affected point \(\:j\).

The two-stage model

Under the premise of considering the dependency level of the disaster site, a two-stage model for the optimization of the emergency logistics path is constructed as follows:

Stage I - emergency supply allocation model

Objective function:

$$\:\begin{array}{c}{maxW}_{1}=min\sum\:_{j\in\:D}{M}_{j}\end{array}$$
(5)

Subject to:

$$\:\begin{array}{c}{M}_{j}=\sum\:{R}_{j}*{\partial\:}_{j}{\text{*}D}_{j}\end{array}$$
(6)
$$\:\begin{array}{c}{R}_{j}=\left\{\begin{array}{c}\lambda\:{\left({y}_{j}-{x}_{j}\right)}^{\alpha\:}+{R}_{0},{x}_{j}\le\:{y}_{j}\\\:{-\left({x}_{j}-{y}_{j}\right)}^{\beta\:}+{R}_{0},{x}_{j}>{y}_{j}\end{array}\right.\end{array}$$
(7)
$$\:\begin{array}{c}{D}_{j}={\rho\:}_{j}*{\sigma\:}_{j}\end{array}$$
(8)
$$\:\begin{array}{c}{\sigma\:}_{j}=\frac{{q}_{j}\left(0<age<12\right)+{q}_{j}^{{\prime\:}}\left(age>60\right)}{{Q}_{j}}\end{array}$$
(9)
$$\:\begin{array}{c}\frac{{x}_{j}}{{y}_{j}}\ge\:\gamma\:,\forall\:j\in\:D\end{array}$$
(10)
$$\:\begin{array}{c}{x}_{j}\le\:{y}_{j},\forall\:j\in\:D\end{array}$$
(11)
$$\:\begin{array}{c}{x}_{j}\ge\:0,{y}_{j}\ge\:0,\forall\:j\in\:D\end{array}$$
(12)

Equation (5) is the objective function of the first-stage model, which represents the satisfaction function of the supply demand at the disaster site, and reflects the degree of satisfaction of the disaster victims in each region with the supply distribution program. The larger the function value, the more rational the distribution of supplies and the lower the perceived psychological risk at each disaster site.

Equation (6) reflects the satisfaction function of the demand for supplies at each disaster site; Eq. (7) describes the psychological risk perception function of the disaster victims; Eq. (8) describes the population vulnerability function at the affected site; Eq. (9) describes how to determine the proportion of vulnerable populations; Eq. (10) ensures that the actual supply at the affected site must be a certain proportion of the demand (i.e. the minimum demand), thus guaranteeing a minimum level of security at each affected site; Eq. (11) indicates that the demand at each disaster site cannot be fully met, i.e., the actual supply of emergency supplies is less than the demand; Eq. (12) defines the range of values for each variable.

Stage II - path optimization model

Objective function:

$$\:\begin{array}{c}{minW}_{2}=\sum\:_{k\in\:K}\sum\:_{i,j\in\:U}{t}_{ij}^{{\prime\:}}\text{*}{z}_{ij}^{k}\end{array}$$
(13)

Subject to:

$$\:\begin{array}{c}S=\sum\:_{j\in\:D}{x}_{j}\end{array}$$
(14)
$$\:\begin{array}{c}\sum\:_{i\in\:U}{z}_{ij}^{k}=\sum\:_{q\in\:U}{z}_{jq}^{k},\forall\:k\in\:K,\forall\:j\in\:U,i\ne\:j,j\ne\:q\end{array}$$
(15)
$$\:\begin{array}{c}\sum\:_{k\in\:K}{f}_{j}^{k}=1,\forall\:j\in\:Q\end{array}$$
(16)
$$\:\begin{array}{c}\sum\:_{j\in\:D}{z}_{ij}^{k}={f}_{j}^{k},\forall\:i\in\:U,\forall\:k\in\:K\end{array}$$
(17)
$$\:\begin{array}{c}\sum\:_{i\in\:D}{z}_{ij}^{k}={f}_{i}^{k},\forall\:j\in\:U,\forall\:k\in\:K\end{array}$$
(18)
$$\:\begin{array}{c}\sum\:_{j\in\:D}\sum\:_{k\in\:K}{f}_{j}^{k}=n\end{array}$$
(19)
$$\:\begin{array}{c}\sum\:_{j\in\:D}{h}_{j}^{k}\le\:m,\forall\:k\in\:K\end{array}$$
(20)
$$\:\begin{array}{c}\sum\:_{j\in\:D}\sum\:_{k\in\:K}{z}_{ij}^{k}\ge\:1\end{array}$$
(21)
$$\:\begin{array}{c}\sum\:_{j\in\:C}\sum\:_{j\in\:D}{z}_{ij}^{k}\le\:1\end{array}$$
(22)
$$\:\begin{array}{c}\sum\:_{j\in\:D}{f}_{j}^{k}{x}_{j}\le\:E\end{array}$$
(23)
$$\:\begin{array}{c}\sum\:_{j\in\:D}{z}_{ij}^{k}=\sum\:_{j\in\:D}{z}_{ji}^{k},\forall\:i\in\:C,\forall\:k\in\:K\end{array}$$
(24)
$$\:\begin{array}{c}{t}_{ij}^{{\prime\:}}=\frac{{\partial\:}_{j}{\text{*}D}_{j}}{\sum\:{(\partial\:}_{j}{\text{*}D}_{j})}{t}_{ij},\forall\:i,j\in\:N\end{array}$$
(25)
$$\:\begin{array}{c}{t}_{ij}=\frac{{d}_{ij}}{{v}_{ij}},\forall\:i,j\in\:N\end{array}$$
(26)
$$\:\begin{array}{c}\sum\:_{i\in\:U}\sum\:_{j\in\:U}{{d}_{ij}z}_{ij}^{k}\le\:L,\forall\:k\in\:K\end{array}$$
(27)
$$\:\begin{array}{c}{z}_{ij}^{k}=\left\{\begin{array}{c}1,vehicle\:k(k\in\:K)\:drives\:from\:node\:i(i\in\:U)\:to\:node\:j(j\in\:U)\\\:0,\:\:otherwise\end{array}\right.\end{array}$$
(28)
$$\:\begin{array}{c}{f}_{j}^{k}=\left\{\begin{array}{c}1,vehicle\:k(k\in\:K)\:serves\:the\:affected\:point\:j(j\in\:U)\\\:0,\:\:otherwise\end{array}\right.\end{array}$$
(29)
$$\:\begin{array}{c}{h}_{j}^{k}=\left\{\begin{array}{c}1,vehicle\:k(k\in\:K)\:travels\:from\:the\:distribution\:center\:to\:node\:j(j\in\:U)\\\:0,\:\:otherwise\end{array}\right.\end{array}$$
(30)

Equation (13) is the objective function of the second stage, which represents the time satisfaction function of the affected points, and reflects the degree of satisfaction of the victims of each affected point with the urgency of the distribution of this supply. This function is the weighted total time combined with the degree of dependency, the smaller the function value, the shorter the consumed total time and the greatest time satisfaction.

Equation (14) indicates that the total reserve of the stockpile center is equal to the sum of the actual supply of each affected point; Eq. (15) indicates the continuity constraint of the path; Eq. (16) indicates that each affected point is served by a vehicle; Eqs. (17) and (18) indicate that each affected point is served only once and can only be present in one path; Eq. (19) indicates that each affected point is served by a vehicle; Eq. (20) indicates that there are enough transport vehicles for scheduling; Eq. (21) indicates that at least one vehicle departs from the stockpile center; Eq. (22) indicates that each vehicle departs from the stockpile center only once; Eq. (23) is a limit on the vehicle’s capacity; Eq. (24) indicates the circuit limit, i.e., the vehicle starts from the supply reserve center and returns to the reserve center after the distribution is completed; Eq. (25) calculates the weighted corrected distribution time for each affected point; Eq. (26) calculates the pre-corrected distribution time for each affected point; Eq. (27) indicates the maximum mileage limitation of the transport vehicle; Eqs. (28), (29)and (30) indicate the type and range of variables.

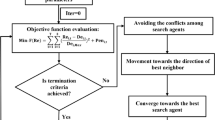
Algorithm design

Sparrow search algorithm

Sparrow Search Algorithm (SSA) is a heuristic optimization algorithm, whose design is inspired by the group behavior of sparrows while foraging and the information exchange between individuals. Each sparrow dynamically adjusts its search behavior according to its fitness value and the overall performance of the group. Highly adapted individuals are more likely to influence the direction and speed of movement of the whole group to find more optimal solutions faster.

Sparrow populations are divided into Discoverers, Followers, and Scouts, each corresponding to different behavioral strategies and roles. Discoverers dominate the sparrow population and typically represent 10–20% of the population. They are primarily responsible for global exploration and finding new potential solutions; Followers adjust their position to rapidly converge to a partially optimal solution by observing and learning from the actions of the Discoverers and other highly adaptive individuals; Scouts are primarily responsible for maintaining group diversity and avoiding premature convergence.

Discoverers position update formula is shown in Eq. (31):

$$\:\begin{array}{c}{x}_{i,d}^{t+1}=\left\{\begin{array}{c}{x}_{i,d}^{t}*exp\left\{\frac{-i}{\alpha\:*{iter}_{max}}\right\},if\:{R}_{2}<ST\\\:{x}_{i,d}^{t}+Q*L,if\:{R}_{2}\ge\:ST\end{array}\right.\end{array}$$
(31)

Followers position update formula is shown in Eq. (32):

$$\:\begin{array}{c}{x}_{i,d}^{t+1}=\left\{\begin{array}{c}Q*exp\left\{\frac{x{\omega\:}_{d}^{t}-{x}_{i,d}^{t}}{{t}^{2}}\right\},if\:i<\frac{N}{2}\\\:x{b}_{d}^{t}+\frac{1}{D}{\sum\:}_{d=1}^{D}\left(\left|{x}_{i,d}^{t}+x{b}_{d}^{t}\right|*rand\left\{-\text{1,1}\right\}\right),else\end{array}\right.\end{array}$$
(32)

Scouts position update formula is shown in Eq. (33):

$$\:\begin{array}{c}{x}_{i,d}^{t+1}=\left\{\begin{array}{c}x{b}_{d}^{t}+\beta\:*\left|{x}_{i,d}^{t}-x{b}_{d}^{t}\right|,if\:{f}_{i}\ne\:{f}_{g}\\\:{x}_{i,d}^{t}+K*\left\{\frac{\left|{x}_{i,d}^{t}-x{\omega\:}_{d}^{t}\right|}{\left|{f}_{i}-{f}_{\omega\:}\right|+\epsilon\:}\right\},if\:{f}_{i}={f}_{g}\end{array}\right.\end{array}$$
(33)

Particle swarm optimization

Particle Swarm Optimization (PSO) is mainly used to find the optimal solution by updating the velocity and position information of the particles and tracking the two “poles” (pbest, gbest). The PSO algorithm is adaptable to dynamic optimization problems and can perform dynamically in changing environments. The PSO updates the position and velocity of the particles through Eq. (34), (35).

$$\:\begin{array}{c}{v}_{i}={v}_{i}+{c}_{1}*rand\left(\right)*\left({pbest}_{i}-{x}_{i}\right)+{c}_{2}*rand\left(\right)*\left({gbest}_{i}-{x}_{i}\right)\end{array}$$
(34)
$$\:\begin{array}{c}{v}_{i}={x}_{i}+{v}_{i}\end{array}$$
(35)

In the above equation, \(\:i=\text{1,2},\cdots\:,N,\:\:N\) is the total number of particles in this swarm; \(\:{v}_{i}\) is the velocity of the particles; \(\:rand\left(\right)\) is a random number between \(\:\left(\text{0,1}\right)\); \(\:{x}_{i}\) is the current position of the particles; \(\:{c}_{1}\) and \(\:{c}_{2}\) are the learning factors, usually \(\:{c}_{1}={c}_{2}=2\); the maximum value of \(\:{v}_{i}\) is \(\:{V}_{max}\) (\(\:{V}_{max}>0)\), and if \(\:{v}_{i}>{V}_{max}\), then \(\:{v}_{i}={V}_{max}\).

Sparrow search algorithm improvement

Circle chaos mapping initializes the sparrow population

In optimal algorithms, chaotic mapping can be used as an alternative to traditional pseudo-random number generators for generating chaotic numbers that lie between 0 and 1. As a nonlinear mapping, the Circle chaotic mapping is highly random and chaotic in characteristics. It helps to significantly enhance the efficacy of the search algorithm in global search and further solve multimodal optimization problems. The Circle formulation is shown in Eq. (36).

$$\:\begin{array}{c}{x}_{i+1}=mod\left({x}_{i}+0.2-\left(\frac{0.5}{2\pi\:}\right)\text{sin}\left(2\pi\:{x}_{i}\right),1\right)\end{array}$$
(36)

In the above equation, \(\:mod\) is the residual function, \(\:{x}_{i}\) is the value of the chaotic variable for the current iteration.

Dynamic reverse learning

For meta-heuristic optimization algorithms, the population initialization is often generated randomly in the search space. Only the degree of dispersion of the population in the search space can be guaranteed, not the quality of the initial solution. However, it has been shown that the goodness of the initial solution will directly affect the speed of convergence and the accuracy of the algorithm. Based on this problem, scholars at home and abroad have introduced a variety of strategies into the initialization part (e.g. chaotic initialization, reverse learning, and Cauchy’s random generation, etc.) to improve the algorithm initialization performance. In this article, a dynamic reverse learning strategy is introduced to improve the quality of the initialized solution, which is calculated as in Eq. (37), (38), (39).

$$\:\begin{array}{c}{X}_{DOBL}={X}_{init}+{r}_{1}*\left({r}_{2}*\left(LB+UB-{X}_{init}\right)-{X}_{init}\right)\end{array}$$
(37)
$$\:\begin{array}{c}LB=min{X}_{init}\end{array}$$
(38)
$$\:\begin{array}{c}UB=max{X}_{init}\end{array}$$
(39)

\(\:{X}_{DOBL}\) denotes the new population obtained by the reverse learning strategy; \(\:{X}_{init}\) denotes the normal initial population obtained randomly; \(\:{r}_{1}\) and \(\:{r}_{2}\) denote a \(\:1*D\) matrix, respectively, with each element randomly assigned a random number of \(\:\left[0,1\right]\). Table 2 presents the SSA-PSO pseudo-codes.

Table 2 Pseudo-code of the proposed SSA-PSO method.
Full size table

Arithmetic example analysis

Arithmetic parameters

In this article, a two-stage model for emergency logistics path optimization considering the dependency of the affected points is established in the case of the Jishishan earthquake that occurred in Liugou Township, Gansu Province, on December 18, 2023. Both phases of the model are solved in Python using SSA-PSO, and the second phase is based on the results of the first phase to obtain the final allocation and distribution scheme.

In the Arithmetic Example, an emergency logistics network is constructed, which contains 23 nodes: an emergency supply allocation center and 22 disaster sites. The emergency supply allocation center is located in Linxia County, Gansu Province, and the affected points are measured in terms of townships, with statistics for townships with an earthquake intensity of VII. The node numbered 0 represents the emergency allocation center and the nodes numbered 1 to 22 represent the affected townships respectively. The coordinates of the nodes, the number of affected people, the population density and the number of vulnerable people are shown in Table 3. In the early stages of an earthquake, ready-made meals are considered the quickest and most effective food needed for survival. This usually includes instant noodles, cookies, bread and water. In order to facilitate modeling, this article selects instant noodles and water as an emergency supply package. According to the standard of basic daily survival requirements for ordinary people set in the Dietary Guidelines for Chinese Residents (2022), it is assumed that the per capita intake of 500 g food and 2,000 ml water per day results in a daily requirement of 2.5 kg per population unit. On this basis, a preliminary forecast of per capita demand for this category of consumer goods can be made.

In addition, it is anticipated that nine transport vehicles will be used. Due to the limited amount of supplies stored in the distribution center, it is assumed that the minimum demand satisfaction rate for this disaster site is 0.3 and that the amount of supplies that can be provided is 0.75 of the total demand at the disaster site; The magnitude of the earthquake is 6.2; All transport vehicles are of the same type, with a maximum loading capacity of 60t, a maximum mileage of 800 km and a speed of 50 km/h under normal conditions. \(\:\alpha\:=\beta\:=0.88,\lambda\:=2.25,{R}_{0}=16\).

Table 3 Information on supply allocation centers and disaster sites.
Full size table

Based on the raw data information in Table 3, the dependency and population vulnerability coefficients can be calculated for each affected site, as shown in Table 4.

Table 4 Calculation results.
Full size table

Solution results and analyses

Firstly, the SSA-PSO is used to solve the first stage, and the relevant parameters of this algorithm are as follows: the number of iterations is 400. the results of the supply allocation of each affected point are obtained as shown in Fig. 2.

Fig. 2
figure 2

Requirements and actual supplies at affected sites.

Full size image

Based on the supply allocation result of the first stage model, the second stage model solving is carried out for this result using SSA-PSO. The relevant parameters for the algorithm solution are as follows: the number of iterations is 400, the program is run 10 times in the Python platform, and the resulting emergency supply allocation routes are shown in Fig. 3, and the emergency distribution routes without considering the urgency of demand are shown in Fig. 4.

Fig. 3
figure 3

Optimal distribution routes for emergency supplies.

Full size image

The specific paths are as follows: 0→12→13→14→0; 0→7→3→0; 0→2→1→0;0→8→15→20→0; 0→11→9→10→0; 0→6→5→4→0; 0→19→21→0; 0→22→18→16→0; 0→17→0.

Taking route 1 as an example, the degree of urgency of demand 12 = 13 > 14; taking route 2 as an example, the degree of urgency of demand 7 > 3; route 3. the degree of urgency of demand 2 > 1; route 4 the degree of urgency of demand 8 > 15 > 20; route 5 the degree of urgency of demand 11 > 9 > 10; route 6 the degree of urgency of demand 6 > 5 > 4; route 7 the degree of urgency of demand 19 > 21; route 8 the degree of urgency of demand 22 > 18 > 16;

Fig. 4
figure 4

Optimal distribution routes for emergency supplies without considering the urgency of the requirement.

Full size image

The specific paths are as follows: 0→12→18→0; 0→3→7→0; 0→1→2→0; 0→9→10→8→0; 0→4→5→6→0; 0→19→16→15→0; 0→22→21→20→0; 0→14→11→13→0; 0→17→0.

By comparing the two, it can be seen that among the optimal distribution routes, taking into account the degree of urgency, the SSA-PSO algorithm follows a basic principle in arranging the distribution order: on the same distribution route, the affected points with higher urgency have When carrying out the material distribution The demand for distribution always takes precedence. In contrast, in the traditional model, the material distribution order is full of randomness. This result is fully consistent with the original purpose of introducing the urgency variable into the model, which is to ensure that with limited resources we can respond more quickly and efficiently to the points that need urgent assistance, thereby minimizing the losses and impacts of the disaster .

Sensitivity analysis

Validity analysis

Due to the limited storage of supplies in the distribution centers, the total amount of supplies they provided represented only 75% of the total requirements at the affected sites. According to the results of the supplies allocation in Fig. 2, the level of satisfaction with the needs of the first phase reached 82.61%. This indicates that the distribution program was more effective and less likely to raise questions about the fairness of the distribution of emergency supplies. Based on the distribution program for emergency supplies in the first phase, the distribution routes of the supplies have been further optimized. Comparison of Figs. 3 and 4 shows that, taking into account the degree of dependence, distribution is first concentrated in the severely damaged area at the epicenter of the earthquake, followed by distribution in the surrounding areas. In contrast, the distribution process in Fig. 4 exhibits randomness and is unable to prioritize the distribution according to the severity of the damage at the affected sites in an orderly manner.

Stability and sensitivity analysis

Solution results under different algorithms

The performance of the algorithm was tested by modifying the type of algorithm for the same problem size (1 distribution center, 22 demand points). For each of the above algorithms, 10 calculations were performed and their average values were calculated and the results of the runs are shown in Figs. 5 and 6.

Fig. 5
figure 5

Comparison of solution results under different algorithms.

Full size image
Fig. 6
figure 6

Iteration process under different algorithms.

Full size image

By observing and analyzing Fig. 5, it can be observed that the optimal solution derived from the SSA-PSO algorithm adopted in this study is of the highest quality: Both demand satisfaction and time satisfaction are maximized. By comparing the iterative process under different algorithms in Fig. 6, it can be observed that SSA-PSO has moderate convergence speed and optimal convergence speed; the SA algorithm’s convergence speed is too fast and it has fallen into the local optimum; SSA, PSO, and GA are not optimal in terms of convergence; and by comparing them, SSA-PSO achieves the optimal convergence effect.

Sensitivity analysis of total supply

In this study, it is assumed that the marginal increase in demand satisfaction is the percentage increase in demand satisfaction for every 10% increase in supply. In the context of responding to disasters and improving the efficiency of post-disaster response, determining the optimal range of total supply is critical. In general, the marginal increase in demand satisfaction decreases as the supply ratio increases. This is due to the stage where the supply of goods is much smaller than the demand for goods, and a small increase in the supply can significantly increase satisfaction, because at this point the supply has not yet been able to satisfy most of the demand. However, with increasing supply ratios, each additional unit of supply contributes progressively less to demand satisfaction. This study determines the optimal supply ratio by calculating the marginal growth rate of demand satisfaction at each supply ratio, as shown in Table 5. Based on the determined optimal supply ratios, appropriate quantities of emergency supplies are planned and stockpiled to enhance the efficiency and effectiveness of post-disaster emergency response.

Table 5 Rate of change of demand satisfaction.
Full size table

As can be seen from the data in Table 5, when the proportion of total supply is located at [0.55,0.65], satisfaction will increase by 10.72% for every 10% increase in the supply; when the proportion of total supply is located at [0.65,0.75], satisfaction will increase by 8.23% for every 10% increase in the supply; when the proportion of total supply is located at [0.75,0.85]. Satisfaction increases by 2.74% for every 10% increase in supplies, and the marginal growth rate of satisfaction gradually decreases. Therefore, to maximize the balance between the efficiency of resource utilization and the effect of demand satisfaction enhancement, to ensure that the supply can cope with most of the post-disaster needs, and to avoid inefficiencies caused by over-investment of resources, it is crucial to determine the ratio of the total amount of supplies.

Conclusion

Firstly, This study points out that due to the urgency of disasters, the total amount of supply stockpiles in the disaster areas usually cannot meet the total amount of needs of each disaster area, and proposes a two-stage model of allocation followed by optimization: The first stage proposes a resource allocation strategy based on pain perception. By introducing psychological risk perception and need urgency, it explores how to minimize the psychological pain and physical loss of the affected group by adjusting the resource allocation strategy; In the second stage, the dependence on the distribution time of emergency supplies is corrected, so that the supplies are more inclined to be transported to the disaster sites with high distance dependence. This not only reflects the guiding principle of “people-oriented”, but also enhances the practical significance of the model.

In the optimization phase, the model can ensure that the emergency supplies can quickly reach the most needed disaster sites. This significantly improves the practical effectiveness of optimizing emergency logistics paths, giving priority to the theoretically predicted severely affected areas. Secondly, the results of the examples in this study show that the proposed two-stage model results in a relatively balanced increase in satisfaction at the affected sites at the time of allocation. In addition, the optimal solution obtained by the SSA-PSO is of the highest quality, while avoiding the problem of local optimality caused by too fast convergence. This provides some reference for organizing post-disaster emergency response in reality. It is shown that the algorithm has practical feasibility and effectiveness in dealing with similar problems and can provide useful experience and methods for emergency logistics path planning.