Introduction

Extreme value analysis is a topic of significant interest for efficient prediction of rare but impactful events, prioritizing resource allocation, strengthening early warning systems, and supporting climate change adaptation. Modeling approaches include at-site and regional analysis. Regional frequency analysis mainly depends on the feasibility of regionalization and the availability of influential site characteristics. Moreover, the accuracy and reliability of estimated quantiles in at-site frequency analysis are affected by sample size, variable trends, shape characteristics, chosen probability distribution, parameter estimation methods, and sampling variability.

Another major concern in modeling extreme events is the choice of the variable for the analysis. The commonly utilized variables include the minimum and maximum values within a certain time interval, such as an hour, month, quarter, or year. Alternatively, peaks over a threshold value, i.e. peak over the threshold (POT) series have also been utilized in various studies. Few studies have indicated that the reliability of final estimates can be enhanced by utilizing yearly maximum or minimum data series relative to POT series1,2,3.

The modeling process of extreme values includes the choice of an appropriate model or probability distribution coupled with the method of estimation. Literature offers a variety of models, majorly having two to five parameters. However, three-parameter distributions suggested by Hosking and Wallis4are a popular choice, especially in regional frequency analysis. The procedure of regional frequency analysis includes simulations based on four-parameter KAPD. The preference of KAPD for the simulations is mainly because it can mimic the shape of various three-parameter distributions in extreme value analysis4.

KAPD introduced by Hosking5has unique characteristics and advantages for applying L-moments-based regional frequency analysis4. It has also been used for at-site flood frequency analysis, drought analysis, wet-day precipitation modeling, and climate model rainfall bias correction6,7,8,9. KAPD suits extreme values and skewed distributions in various data formats because of its four parameters and offers greater flexibility in fitting diverse data with varying tail behaviors. The application of KAPD is a preferred choice when three-parameter probability distributions are insufficient to capture the variability of the extreme observations10,11,12,13,14. Some applications illustrated that the KAPD is a better model than the three-parameter distributions in regional frequency analysis15,16. Therefore, this study focuses on the implications of various parameter estimation methods in the case of KAPD being the model for extreme value analysis considering variations in the sample size and measures of shape associated with the observed data.

In terms of the methods of estimation for the probability distributions, common choices include the method of moments, maximum likelihood, and L-moments. Studies revealed that the estimators based on L-moments consistently yield reliable and efficient results, especially in the case of modeling extreme values17,18,19. Some useful facts and practical implementation of maximum likelihood and L-moments as estimation methods for modeling extreme events are available20. However, a relatively newer, uncommon but effective estimation method exists, namely the maximum product of spacing (MPS). It is a useful method for estimating the parameters of a distribution especially when dealing with small samples. The results of Wong and Li21and Soukissian and Tsalis22 showed that the method of MPS exhibits more stability relative to maximum likelihood and probability-weighted moments (PWM) for the Generalized Extreme Value Distribution. Asquith et al.23 demonstrated a close similarity between the quantile estimates derived from MPS and L-moments in the context of PE3 distribution. Another study by Khan et al.24 illustrated similar findings, indicating that for the intermediate size of samples, the MPS method has better reliability in comparison to L-moments.

Existing literature reveals a multitude of research that provides choices for accurate and reliable estimates of the parameters of KAPD. For instance, the studies by Dupuis25, Dupuis and Winchester26, Singh and Deng27, Park and Kim28, Murshed et al.29, Seenoi et al.30, Papukdee et al.31, and Shin and Park32. However, there is a clear gap in the literature regarding a comprehensive analysis of the implications of MPS with other commonly used estimation methods on parameter estimation and the estimated quantiles for the KAPD. Therefore, this study is designed to analyze the choice of estimation method in at-site frequency analysis for KAPD considering various sizes of the sample and associated shape distribution.

Materials and methods

Kappa distribution

The four-parameter KAPD was first introduced by Hosking5. For a continuous random variable Y, the probability density function (PDF) of the KAPD is defined as follows.

$$\:f\left(y\right)={\theta\:}^{-1}{\left[1-\frac{k\left(y-\epsilon\:\right)}{\theta\:}\right]}^{1/k-1}{\left[F\left(y\right)\right]}^{1-h}$$
(1)

Here \(\:\theta\:\) is scale, \(\:\epsilon\:\) is ___location and \(\:k\) and \(\:h\) are shape parameters. The range of Y for the values of shape parameters \(\:k\) and \(\:h\) is:

$$\:\epsilon\:+\frac{\theta\:\left(1-{h}^{-k}\right)}{k}\le\:y\le\:\epsilon\:+\frac{\theta\:}{k}\:\text{i}\text{f}\:h>0,\:k>0$$
$$\:\epsilon\:+\theta\:\text{l}\text{o}\text{g}\left(h\right)\le\:y<\infty\:\:\text{i}\text{f}\:h>0,\:k=0$$
$$\:\epsilon\:+\frac{\theta\:\left(1-{h}^{-k}\right)}{k}\le\:y\le\:\infty\:\:\text{i}\text{f}\:h>0,\:k<0$$
$$\:-\infty\:\le\:y\le\:\epsilon\:+\frac{\theta\:}{k}\:\text{i}\text{f}\:h\le\:0,\:k>0$$
$$\:-\infty\:\le\:y\le\:\infty\:\:\text{i}\text{f}\:h\le\:0,\:k=0$$
$$\:\epsilon\:+\frac{\theta\:}{k}\le\:y\le\:\infty\:\:\text{i}\text{f}\:h\le\:0,\:\:k<0$$

The distribution function of KAPD is

$$\:F\left(y\right)={\left\{1-h{\left[1-\frac{k\left(y-\epsilon\:\right)}{\theta\:}\right]}^{\frac{1}{k}}\right\}}^{\frac{1}{h}}$$
(2)

The quantile function is defined as

$$\:y\left(F\right)=\epsilon\:+\frac{\theta\:}{k}\left[1-{\left(\frac{1-{F}^{h}}{h}\right)}^{k}\right]$$
(3)

Relationships of KAPD with other extreme value distributions and more details are provided in30,33.

Maximum likelihood estimation

Maximum Likelihood estimation (MLE) is a common parameter estimation method in parametric modeling. Suppose that \(\:Y=\left({y}_{1},{y}_{2},\:{y}_{3}\dots\:\dots\:.{y}_{n}\right)\) is a sample of size \(\:n\) derived from KAPD having a PDF \(\:f\left(y\right)\) given in Eq. 1, and then the log-likelihood function of the parameters is given as follows.

$$\:L\left[\raisebox{1ex}{$\left(\epsilon\:,\theta\:,k,h\right)$}\!\left/\:\!\raisebox{-1ex}{$y$}\right.\right]=n\text{log}\left(\theta\:\right)-(1-h)\sum\:_{i=1}^{n}\text{log}\left[F\left({y}_{i}\right)\right]-\frac{1-k}{k}\sum\:_{i=1}^{n}\text{log}[1-\frac{k({y}_{i}-\epsilon\:)}{\theta\:}]$$
(4)

For the maximum likelihood estimates of the parameters, take the first partial derivatives of Eq. 4with respect to the parameters and put them equal to zero. Resultantly, four equations are obtained but no explicit minimizer is possible, a numeric algorithm quasi-newton method available in the R-program developed by Team34 has been used for the MLEs of the parameters of KAPD.

L-moments

L-moments (LM) is a widely used method for the estimation of parameters of probability distributions in extreme value analysis35. The LM estimators of the KAPD parameters are given in4.

If \(\:h<0\) and \(\:-1<k<\frac{-1}{h}\) or if \(\:h\ge\:0\) and \(\:k>-1\), then the first two L-moments and L-moments ratios of Kappa distribution are given below.

$$\:{\lambda\:}_{1}=\epsilon\:+\frac{\alpha\:\left(1-{z}_{1}\right)}{k}$$
(5)
$$\:{\lambda\:}_{2}=\frac{\alpha\:\left({z}_{1}-{z}_{2}\right)}{k}$$
(6)
$$\:{\tau\:}_{3}=\frac{\left({-{z}_{1}+3z}_{2}-{2z}_{3}\right)}{\left({z}_{1}-{z}_{2}\right)}$$
(7)
$$\:{\tau\:}_{4}=\frac{\left({-{z}_{1}+6z}_{2}-{10z}_{3}+5{z}_{4}\right)}{\left({z}_{1}-{z}_{2}\right)}$$
(8)

Where

$$\:{z}_{s}=\left\{\begin{array}{c}\frac{s{\Gamma\:}\left(1+k\right){\Gamma\:}\left(\raisebox{1ex}{$s$}\!\left/\:\!\raisebox{-1ex}{$h$}\right.\right)}{{h}^{1+k}{\Gamma\:}\left(1+k+\raisebox{1ex}{$s$}\!\left/\:\!\raisebox{-1ex}{$h$}\right.\right)}\:,\:\:h>0\\\:\frac{s{\Gamma\:}\left(1+k\right){\Gamma\:}\left(-k-\raisebox{1ex}{$s$}\!\left/\:\!\raisebox{-1ex}{$h$}\right.\right)}{{\left(-h\right)}^{1+k}{\Gamma\:}\left(1-\raisebox{1ex}{$s$}\!\left/\:\!\raisebox{-1ex}{$h$}\right.\right)}\:,\:\:h<0\end{array}\right.$$

Few studies using LM for the estimation of parameters of KAPD include the work of Parida10, , Kjeldsen et al.16,, and Moses and Parida36. Dupuis and Winchester26provided a comparison of LM and MLE for the application of KAPD and found that the performance of LM is better than MLE. The R package, namely “lmomco” has been used in this study to obtain the parametric values of the KAPD, as Asquith37 explained.

Maximum product of spacing

The MPS is an order statistics-based parameter estimation approach, which serves as an alternative to MLE38. Literature showed that the MPS method demonstrates asymptotic efficiency and consistency in situations where MLE is unsuccessful39. Additionally, MPS exhibits all the features of MLE. A few details of MPS method are provided below:

Suppose \(^{\prime\prime}\text{Y}^{\prime\prime}\) is any continuous random variable having CDF F(y, θ) and pdf f(y, θ). Let \(\:{Y}_{1:n}\le\:{Y}_{2:n}\le\:{Y}_{3:n}\dots\:\dots\:.\le\:{Y}_{n:n}\) be the ordered sequence of the random variable \(^{\prime\prime}\text{Y}^{\prime\prime}\). The space between two CDFs of the consecutive points can be defined as.

$$\:{Z}_{i}\left(\omega\:\right)=F\left({y}_{i:n},\omega\:\right)-F\left({y}_{i-1:n},\omega\:\right)=\underset{{y}_{i-1:n}}{\overset{{y}_{i:n}}{\int\:}}\text{f}(\text{y},\omega\:)\text{d}\text{y}\:i=\text{1,2},3\dots\:\dots\:.n+1$$
(9)

The optimum value of the parameter \(\:\omega\:\) is obtained through MPS by maximizing the log of the geometric mean of \(\:{Z}_{i}\left(\omega\:\right)\).

$$\:g\left(\omega\:\right)=\frac{1}{n+1}\sum\:_{i=1}^{n+1}log\left[{Z}_{i}\left(\omega\:\right)\right]$$
(10)

The MPS estimator of \(\:\omega\:\) is given as.

$$\:{g}_{opt}\left(\omega\:\right)=log\left(\frac{1}{n+1}\right)$$
(11)

We can use Eq. 5, by replacing the pdf in Eq. 1, for the MPS estimates of KAPD.

$$\:{g}_{opt}\left(\epsilon\:,\theta\:,k,h\right)=\frac{1}{n+1}\sum\:_{i=1}^{n+1}log\left[\underset{{y}_{i-1:n}}{\overset{{y}_{i:n}}{\int\:}}{\theta\:}^{-1}{\left[1-\frac{k\left(y-\epsilon\:\right)}{\theta\:}\right]}^{1/k-1}{\left[F\left(y\right)\right]}^{1-h}\text{d}\text{y}\right]$$
(12)

The MPS estimates of the parameters (ε, θ, k, h) are produced by maximizing Eq. 12 for each parameter. The closed-form solutions for estimating the parameters are not yet accessible. Therefore, the estimation of parameters has been obtained by the numerical solution of Eq. 12. The utilization of a nonlinear optimization approach is employed in the estimation of parameters by MPS. Further details are available in37.

Simulation analysis

The study is executed in two steps. The first step consists of Monte Carlo Simulations, while the second step includes the analysis of the adopted methodology considering the Annual Maximum Peak Flows (AMPF) of a site in Khyber Pakhtunkhwa (KPK), Pakistan. For the simulation experiments, KAPD has been fitted using three estimation methods: LM, MLE, and MPS. Various sample sizes, including 20, 40, 75, 100, and 200 have been used to cover the small, moderate, and large sample sizes. The simulations have employed the standardized version of the KPAD, as suggested by Jan and Shabri40 and Khan et al.24. The accuracy of the estimations has been assessed using standard measures like RMSE and bias. Further specifications of the simulations are provided below:

  1. 1)

    Random samples of varying sizes (20, 40, 75, 100, and 200) have been used with 1000 replications. The ___location parameter (ε) and scale parameter (θ) have been fixed at 0 and 1 respectively. However, variations in the shape parameter (k) have been introduced systematically varying between 0.1 and 0.3, while the other parameter (h) has been varied between 0.4 and 1.2. The introduction of linear variations in the parameter values helps analyze the performance of the three estimating methods across different levels of skewness.

  2. 2)

    The parameters of the KAPD have been estimated using the three stated methods, in each of the 1000 sample instances. Nevertheless, it is important to acknowledge that in certain scenarios of simulations, MLE and MPS were unable to generate accurate estimates of the distribution parameters. The problem may be linked to the difficulties associated with the convergence of the optimization algorithm, which may impede the precise estimation of parameters using these methodologies.

  3. 3)

    The estimated parameters obtained through simulations have been arranged into vectors. This set of vectors consisting of 1000 estimations has been employed subsequently to compute the root mean square error (RMSE) and bias for each parameter. The RMSE and bias have been computed using the mathematical equations outlined in the following equations, Eq. (13) and Eq. (14), designed to assess the precision and deviance of the calculated values. The indicators offer significant insights into the efficacy and dependability of the parameter estimation process, as determined by the simulation outcomes.

$$\:bias\left(\phi\:\right)=E\left(\widehat{\phi\:}\right)-\phi\:$$
(13)
$$\:RMSE\left(\phi\:\right)=\sqrt{Var\left(\widehat{\phi\:}\right)-{\left(bias\left(\phi\:\right)\right)}^{2}}$$
(14)

Here \(\:\phi\:\) is the true value of the parameter and \(\:E\left(\widehat{\phi\:}\right)\) is the expected value of the parameter estimated through simulations. The simulation results obtained using various combinations of shape parameters are given in Tables 1, 2, 3, 4, 5 and 6.

Table 1 Simulations results for values of k = 0.1 and h = 0.4.
Full size table
Table 2 Simulations results for values of k = 0.1 and h = 0.8.
Full size table
Table 3 Simulations results for values of k = 0.1 and h = 1.2.
Full size table
Table 4 Simulations results for values of k = 0.3 and h = 0.4.
Full size table
Table 5 Simulations results for values of k = 0.3 and h = 0.8.
Full size table
Table 6 Simulations results for values of k = 0.3 and h = 1.2.
Full size table

Tables 1, 2, 3, 4, 5 and 6 illustrate the values of RMSE and bias for the six combinations of the values of “k” and “h”, i.e., “k” has been varied as 0.1 and 0.3 while the parameter “h” changes linearly between 0.4 and 1.2. These variations have been introduced in the samples to generate different shape characteristics for the analysis of the implications of three estimating methods (LM, MLE, and MPS) on the parametric estimates of KAPD. The lowest values of RMSE and bias for the parameters “k” and “h” regarding various sample values and estimation methods have been highlighted in Tables 1, 2, 3, 4, 5 and 6. The summaries of the choice of estimation methods in multiple scenarios considering RMSE and bias have been illustrated in Tables 7 and 8 respectively. 3.1 For RMSE.

The results of Table 7 illustrate that the method of MPS is a preferred choice and has the lowest RMSE values in most of the generated scenarios. Their performance is particularly superior in the presence of a heavy tail and significant positive skewness with small to very large sample sizes. The methods of LM and MLE have the lowest RMSE in the case of moderately heavy tail and slight positive skewness with a small sample size.

Table 7 Choice of estimation method based on the sample size and shape characteristics for KAPD considering RMSE.
Full size table

For bias

The results of Table 8 are in favor of the LM method in most of the generated scenarios and it can be concluded that the method of LM exhibits the smallest bias. However, in the case of moderately heavy tail and significant positive skewness, the performance of the MPS method is the best for small to very large sample sizes, especially the cases of h = 1.2.

Table 8 Choice of estimation method based on sample size and shape characteristics for KAPD considering BIAS.
Full size table

The results of simulation experiments reveal that the shape of the data distribution, sample size, and choice of method for the estimation of parameters play a vital role in the accuracy and efficiency of the parametric estimates in the case of KAPD as a choice of model. Special attention may be required in cases where a distribution has a more flexible form that is dependent on multiple parameters. In situations where more generalized distributions are employed to fit real data, particularly in the context of forecasting extreme events, the significance of the distribution’s shape with other aspects becomes crucial. Moreover, the accuracy and reliability of the predicted quantiles are contingent upon the quality of the parametric estimates of the chosen distribution. An empirical analysis of the implications of three methods of estimation of parameters on predicted quantiles using KAPD, a practical illustration has been shown in the subsequent section.

Estimation of flood quantiles and accuracy measures

This section deals with the analysis of the effects of LM, MLE, and MPS methods considering AMPF of a particular site namely “Shahi Bala” located in the KPK, Pakistan. The geographical coordinates of the site in degrees are given as latitude 34.1858 (N) and longitude 71.7661 (E). Secondary data of AMPF measured in unit cubic feet per second (\(\:{f}^{3}/s\)) has been provided by the Flood Section, Provincial Irrigation Department of KPK, Pakistan. The dataset comprises a 25-year observed record spanning from 1987 to 2011. However, values for the years 2000 to 2004 were missing. These missing values were replaced by the average value of the AMPF of the site. The time series plot of the observed data is illustrated in Fig. 1.

Fig. 1
figure 1

Time series plot of annual maximum peak flows of Shahi Bala, KPK, Pakistan.

Full size image
Table 9 Descriptive measures of AMPF of Shahi Bala.
Full size table
Table 10 Estimated values of KAPD parameters.
Full size table

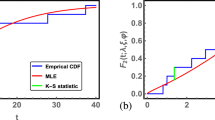
A few descriptive measures of the observed data at Shahi Bala are provided in Table 9. These measures indicate that the values of observed data lie between 30 \(\:{f}^{3}/s\) to 8911 \(\:{f}^{3}/s\) with an average value of 2792.4 \(\:{f}^{3}/s\:\)and a standard deviation of 2583.84 \(\:{f}^{3}/s\). The high dispersion is an indicator of the heterogeneous nature of the data series with outliers, which can also be observed in Fig. 1. The shape characteristics show that the data series has slight positive skewness and Platy-Kurtic behavior. The estimated parameters of the KAPD using three estimation methods are given in Table 10. Diagnostic measures such as quantile-quantile (Q-Q plots) and CDF plots have been used to evaluate how well the data set aligns with the KAPD. The KAPD fitted via LM, MLE, and MPS display comparable behavior, according to the Q-Q plots shown in Fig. 2. However, there is a closer similarity between the LM and MPS estimates for KAPD. The high outlier in the data set is the data point that departs most from the diagonal line. However, when analyzing yearly maximum series, the high outliers provide valuable information. As a result, these outliers are included in the study. Similar findings were observed in CDF plots given in Fig. 3.

Fig. 2
figure 2

Q-Q plots for the Kappa distribution were obtained using MLE, MPS, and LM methods.

Full size image
Fig. 3
figure 3

CDF plots for the Kappa distribution were obtained using MLE, MPS, and LM methods.

Full size image

For T-year quantile estimation, the estimates of Table 10 have been used for the estimation of at-site flood quantiles for various return periods (5, 10, 20, 30, 50, 75 and 100 years), for which the quantile function given in the Eq. (3) has been used. Here the Monte Carlo Simulations have been used to analyze the effect of the methods of parameter estimation. For which the details include the following: Two distinct sample sizes have been utilized: i.e. the first sample has 25 observations (actual data), while the second sample has 50 observations (simulated data). The quality of each computed quantile has been estimated using accuracy metrics, including quantile standard error (QSE), quantile L-scale (QL-scale), and 90% confidence limits (CL). A complete set of flood quantiles, i.e. 5000, have been generated for each case considering various return periods of 5, 10, 20, 30, 50, 75, and 100 years using the estimated parameters by the three methods. The QSE provides information on the efficiency of the estimates, whereas the L-scale assesses the inherent sampling variability of the estimates for the T-year’s quantile.

The confidence intervals for each estimated flood quantile with a significance level of 90% have been computed using simulated data for both sample sizes. An important point in the error analysis is the examination of error distribution, for which, the normal distribution is the most prominent and frequently employed. However, if the data deviates from normality, the Generalized Normal Distribution (GNO) can be employed because of its ability to provide more reliable and consistent estimates compared to other distributions37. Hence, we have used the GNO as a distribution of errors in the analysis of the simulation output. The estimated quantiles and their corresponding accuracy measures are given in Table 11. The findings indicate that the QSE and QL-scale values of the estimated quantiles corresponding to the return periods of 5, 10, 20, and 30 using the LM method are comparatively lower than those obtained using the MPS and MLE methods. However, in the case of longer return periods, i.e. for return periods of 50, 75, and 100 years, the estimates considering MPS method have lower QSE and QL-scale values relative to the LM and MLE methods. A similar trend has been observed in the 90% CL for the quantiles. The 90% CL obtained at sample sizes of 25 and 50 are depicted in Figs. 4 and 5, respectively, alongside empirical and theoretical quantiles. In both figures, the theoretical and empirical quantiles of the data fall within the 90% confidence limits. Furthermore, Fig. 5 illustrates that at a sample size of 50, which is double the actual size of the data, the 90% confidence limits become narrower compared to those obtained at the actual sample size of 25 shown in Fig. 4. Therefore, Fig. 5 clarifies that as the sample size increases, the distribution of quantiles becomes more stable, resulting in smaller standard errors of the estimated quantiles.

Consequently, it can be concluded that the quantile estimates for shorter return periods derived from the LM method exhibit greater efficiency and reduced sampling variation compared to those obtained through the MPS and MLE methods. However, the quantile estimates for moderate to high return periods derived from the MPS method demonstrate greater efficiency and reduced sampling variation in comparison to the LM and MLE methods.

dfgh.

Table 11 Estimated flood quantiles with their 90% confidence limits (lower bound (LB) and upper bound (UB)), quantiles standard error (QSE), quantile mean (QM) and quantiles L-scale (QL-scale).
Full size table
Fig. 4
figure 4

Growth curves of estimated flood quantiles with 90% CL and empirical quantiles.

Full size image
Fig. 5
figure 5

Growth curves of estimated flood quantiles with 90% CL and empirical quantiles.

Full size image

Conclusion

The following are the major conclusions of the study:

  1. 1)

    MPS is a preferred method of estimation for KAPD, i.e. having the lowest RMSE values, especially in the presence of heavier tail and significant positive skewness for small to very large sample sizes.

  2. 2)

    In general, the method of LM provides the estimates having the lowest bias for all sample sizes with the distribution of shape parameters having a slightly heavier tail and slight positive skewness. However, for heavier tails and significant positive skewness, the method of MPS has comparable performance with LM.

  3. 3)

    The real-life applications demonstrate that the use of LM yielded accurate flood quantiles throughout the temporal range of the dataset, accompanied by the shortest 90% CL. Additionally, LM showed decreased sampling variability in these estimates. The estimates of flood quantiles using the method of MPS have an elevated degree of stability, with minimal sampling variability when extrapolated outside the available data range with the shortest 90% CL.

The study provides useful guidelines for the choice of estimation method in the application of KAPD for various sample sizes and the shape of the distribution associated with the data. Future studies can include more real-life applications to analyze the proposed scheme and the quality of the resultant estimates of quantiles.