Introduction

In the area of scientific inquiry, scientists are increasingly intrigued by the subtle dynamics of natural occurrences. Leveraging cutting-edge approaches and procedures, they attempt to decode these complexities with more accuracy and insight. An important tool in this effort is the use of partial differential equations (PDEs) to create models that correctly capture these events. The expanding capacity of 3D visualization plays a crucial role in boosting researchers’ knowledge and analysis of such occurrences. By applying PDEs, scientists are able to reveal the complicated patterns controlling physical processes and give greater insights into their behavior.

A soliton is an isolated solitary wave that propagates over a material without wasting energy or altering its shape due to contact with other waves. Solitons are distinct from regular wave occurrences due to their strong localization and remarkable stability and endurance. Soliton plays a crucial role in several disciplines of study such as nonlinear optics1,2, mechanics3, plasma physics4, engineering5, hydrodynamics6, communication systems7, optical fiber8, biology9, fluid dynamics10,11.

Nonlinear partial differential equations (NLPDEs) grow as exceptionally crucial assets in this scientific pursuit. NLPDEs provide sophisticated insights into a wide range of fields, including optics, acoustics, plasma dynamics, and condensed matter physics. They not only increase our comprehension of the researched events but also allow scientists to make precise estimates about their future proliferation. As a result, many academics have committed to analyzing diverse NLPDEs, seeking to expand their comprehension of the exhibited behavior in the examined natural occurrences. Recent assessments have involved inquiries into the Batman–Burger equation12,13, Schrodinger equation14,15,16,17,18, Date–Jimbo–Kashiwara–Miwa equation19,20,21, thin film ferroelectric material equation22,23,24,25, Benjamin–Bona–Mahony equation26,27,28, Boussinesq equation29,30,31,32, generalized Calogero-Bogoyavlenskii-schiff equation33,34, Buckmaster equation35, non-linear non classical Sobolev-type wave model36, and different other37,38,39,40,41,42,43,44,45,46,47,48,49.

The study of the single-wave solutions of NLPDEs is significant for giving better views and understanding of the underlying process and useful uses. Therefore, numerous researchers have created new ways to study these NLPDEs answers. Plenty of strong techniques such as,exp \((-\chi (\Theta ))\) expansion method50, extend mapping method51, homotopy perturbation method52, Darboux transformation53, exp-function method54, generalized Kudryashov method55, extended trial equation method56, Hirota bilinear method57, extended jacobian method58, extended direct algebric method59, improved extended fan-sub equation method60, modified extended tanh method, Backlund transform method61, Novel \((\frac{G'}{G})\) expansion method62, extended auxiliary equation mapping method63, extended simple equation method64 and many more methods65,66,67,68,69,70,71.

In this work, we shall analyze the AE

$$\begin{aligned} & I \mathcal {U}_{t}+ a\hspace{0.1cm} \mathcal {U}_{xx}+ b\hspace{0.1cm} \mathcal {U}_{x,t} +\gamma S\mathcal {U} = 0,\nonumber \\ & {S}_{x}-2\epsilon (a {|\mathcal {U}|_{x}}^2 + b{|\mathcal {U}|_{t}}^2) = 0, \epsilon = \pm {1} \end{aligned}$$
(1)

here S = S(x,t) is a real-valued function and \(\mathcal {U}\) = \(\mathcal {U} (x,t)\) is a complex function and a,b and \(\gamma\) are arbitrary constants. The AE represents a generalized form of the two additional equations that can be derived from it:

\(\bullet\) When a equals zero, AE becomes the Kuralay equation.

\(\bullet\) When b equals zero, AE becomes the Schrodinger equation.

The Darboux transformation approach yields many wave solutions, including breather, rogue wave, and semi-rational solutions to the AE, as shown by Kong and Guo72. Sagidullayeva et al.73 derive the Lax representations and their gauge equivalent substitutes for AE. The New Extended Auxiliary Equation (NEAE) approach (Mathanaranjan et al.74; Zayed and Alurrfi75) is used to get the soliton solutions of the auxiliary equation. Zhao Li and Shan Zhao researched the dynamical behavior and soliton solutions of the AE based on the analytical approach of the planar dynamic system76. The AE is characterized as a Heisenberg ferromagnet-type equation, playing a significant role in the study of nonlinear dynamics in magnetism, the differential geometry of surfaces and curves, and optics. Analytical solutions serve as crucial instruments in scientific research as well as technical applications. Not only do they increase our knowledge of natural processes, but they also offer a robust framework for theoretical growth, allowing accurate control and prediction of systems. Due to its extensive application across multiple scientific areas, getting analytical answers is important to unlocking the full potential of the AE model. These solutions give a clear and straightforward picture of the interactions between parameters and variables, making it easy to fully appreciate the underlying behavior of the systems the equations describe. They also give a more thorough knowledge of the fundamental principles controlling these complicated structures.

This paper investigates solutions of soliton waves of the understudied model using the Kumar-Malik method Riccati equation method and the new Kudryashov method. Particularly, research on this specific question has not been done in the existing literature. The utilization of such processes gives a broad variety of options, such as incorporating bright, dark, and kink solitons. The usefulness of these strategies has been shown in solving various models in the accessible research.

The full article is summarized as follows: “Reduction of proposed model into ODE” explains the mathematical analysis needed to convert the nonlinear partial differential problem to an ordinary differential equation. “Description of Kumar–Malik method” discusses the mathematical processes of the Kumar–Malik method, and its application, and gives graphical representations. “The new Kudryashov method” describes the new Kudryashov method and its application. “Riccati equation method” discusses the mathematical processes of the Riccati Equation method and its application. “Graphical representation and discussion” discusses the graphical representation and discussion of the obtained results. Finally, “Conclusion” closes the work.

Reduction of proposed model into ODE

Consider general NLPDEs have the following form:

$$\begin{aligned} Y(\mathcal {U},\mathcal {U}_{t}, \mathcal {U}_{x}, \mathcal {U}_{t,t}, \mathcal {U}_{x,x},... )=0. \end{aligned}$$
(2)

Its non linear ordinary differential equations (NLODEs) will be

$$\begin{aligned} {P(\Phi , \Phi ', \Phi '',...)=0.} \end{aligned}$$
(3)

Consider the traveling ansatz solution to simplify the NLPDEs into NLODEs.

$$\begin{aligned} \mathcal {U}(x,t) = {\Phi }(\xi )e^{i(k x -\omega t)} \hspace{0.1cm},\hspace{1cm} \mathcal {S}(x,t) = g(\xi ) \hspace{0.1cm}; \hspace{1cm} \xi = x- \eta t. \end{aligned}$$
(4)

here \(\omega\), k and \(\eta\) are the constants. Inserting Eq. (4) into Eq. (1) and separating the real and Imaginary parts we obtained the following equation:

$$\begin{aligned} \left( -n^2 \delta - \omega + n \theta \omega + \gamma {g(\xi )}\right) \Phi (\xi ) + (\delta - \theta \eta ) \Phi ''(\xi ) = 0. \end{aligned}$$
(5)
$$\begin{aligned} \left( -2n\delta - \eta + n\theta \eta + \theta \omega \right) \Phi '(\xi ) = 0. \end{aligned}$$
(6)
$$\begin{aligned} 4\epsilon (\delta - \theta \eta ) \Phi (\xi ) \Phi '(\xi ) + g'(\xi ) = 0. \end{aligned}$$
(7)

From Eq. (6), we get

$$\begin{aligned} \omega = \frac{2n\delta + \eta - n\theta \eta }{\theta }. \end{aligned}$$
(8)

Integrating Eq. (7) w.r.t \(\xi\) and assuming the integration constant zero, we get:

$$\begin{aligned} g(\xi ) = 2\epsilon (\delta - \theta \eta ) \Phi (\xi )^2. \end{aligned}$$
(9)

By substituting Eqs. (8,9) into Eq. (5), we attain:

$$\begin{aligned} \left( -\eta + n \left( -2 + n \theta \right) \left( \delta - \theta \eta \right) \right) \Phi (\xi ) + 2 \theta \gamma \epsilon \left( \delta - \theta \eta \right) \Phi (\xi )^3 + \theta \left( \delta - \theta \eta \right) \Phi ''(\xi ) = 0. \end{aligned}$$
(10)

here \((\delta - \theta \eta ) \ne 0\) .

Description of Kumar–Malik method

Following are the major steps of the Kumar–Malik method.

Step 01: The Kumar-Malik method provides the solution of Eq. (10) as:

$$\begin{aligned} \Phi (\xi )= B_0 + \sum _{i=1}^{N} B_i\hspace{0.1cm} f(\xi )^i. \end{aligned}$$
(11)

where the coefficients \(B_{i}'s\) (i = 1,2,..., N) are constants, and the first-order differential equation is accomplished by the function \(f(\xi )\) as :

$$\begin{aligned} f(\xi )' = \sqrt{\sigma _1 f(\xi )^4 + \sigma _2 f(\xi )^3 + \sigma _3 f(\xi )^2 + \sigma _4 f(\xi ) + \sigma _5} \end{aligned}$$
(12)

where \(\sigma _{i}'s\), for (i = 1,2,...., N) are constants. The solution to the Eq. (12) as follows:

Case 01: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=0\) then Eq. (12) has the following Jacobi elliptic solutions:

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}>0\),

$$\begin{aligned} f_{01}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiCN}\left[ \frac{\sqrt{-\sigma _1 k_1}}{4 \sigma _1} \xi , \frac{\sigma _2}{2 \sqrt{k_1}}\right] }. \end{aligned}$$
(13)
$$\begin{aligned} f_{02}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm {\frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiDN}\left[ \frac{\sigma _2 }{4 \sqrt{-\sigma _1}}\xi , \frac{2 \sqrt{k_1}}{\sigma _2}\right] }. \end{aligned}$$
(14)

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}<0\), \(k_{2}<0\),

$$\begin{aligned} f_{03}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiCN}\left[ \frac{\sqrt{\sigma _1 k_1} }{4 \sigma _1}\xi , \frac{\sqrt{k_2 k_1}}{2 k_1}\right] }. \end{aligned}$$
(15)
$$\begin{aligned} f_{04}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiDN}\left[ \frac{\sqrt{\sigma _1 k_1}}{4 \sigma _1}\xi , \frac{2 \sqrt{k_2 k_1}}{k_2}\right] }. \end{aligned}$$
(16)

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}>0\), \(k_{2}<0\),

$$\begin{aligned} f_{05}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiNC}\left[ \frac{\sqrt{-\sigma _1 k_1}}{2 \sigma _1}\xi , \frac{\sigma _2}{2 \sqrt{k_2}}\right] }. \end{aligned}$$
(17)
$$\begin{aligned} f_{06}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiND}\left[ \frac{\sqrt{-\sigma _1 k_1}}{2 \sigma _1}\xi , \frac{\sigma _2}{2 \sqrt{k_2}}\right] }. \end{aligned}$$
(18)

\(\bullet\) If \(\sigma _{1} k_{1}>0\), \(k_{1} k_{2}>0\),

$$\begin{aligned} f_{07}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiNC}\left[ \frac{\sqrt{\sigma _1 k_1}}{2 \sigma _1}\xi , \frac{\sqrt{k_1 k_2}}{2 k_1}\right] }. \end{aligned}$$
(19)
$$\begin{aligned} f_{08}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiND}\left[ \frac{\sqrt{\sigma _1 k_2} \cdot \xi }{2 \sigma _1}, \frac{2 \sqrt{k_1 k_2}}{k_2}\right] }. \end{aligned}$$
(20)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{2}<0\),

$$\begin{aligned} f_{09}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiNS}\left[ \frac{\sigma _2}{2 \sqrt{\sigma _1}}\xi , \frac{\sqrt{-k_2}}{\sigma _2}\right] }. \end{aligned}$$
(21)
$$\begin{aligned} f_{10}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiNS}\left[ \frac{\sqrt{-\sigma _1 k_2} \cdot }{4 \sigma _1}\xi , \frac{\sigma _2}{\sqrt{-k_2}}\right] }. \end{aligned}$$
(22)
$$\begin{aligned} f_{11}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_2}}{4 \sigma _1} \cdot \text {JacobiSN}\left[ \frac{\sigma _2}{2 \sqrt{\sigma _1}}\xi , \frac{\sqrt{-k_2}}{\sigma _2}\right] }. \end{aligned}$$
(23)
$$\begin{aligned} f_{12}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sigma _2}{4 \sigma _1} \cdot \text {JacobiSN}\left[ \frac{\sqrt{-\sigma _1 k_2}}{4 \sigma _1}\xi , \frac{\sigma _2}{\sqrt{-k_2}}\right] }. \end{aligned}$$
(24)

Case 02: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=\frac{k_1^2}{64 \sigma _1^3}\) then Eq. (12) has the following hyperbolic and trigonometric solutions:

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}<0\),

$$\begin{aligned} f_{13}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_3}}{4 \sigma _1} \tanh \left[ \frac{\sqrt{-\sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(25)
$$\begin{aligned} f_{14}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-k_3}}{4 \sigma _1} \coth \left[ \frac{\sqrt{-\sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(26)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}>0\),

$$\begin{aligned} f_{15}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{k_3}}{4 \sigma _1} \tan \left[ \frac{\sqrt{\sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(27)
$$\begin{aligned} f_{16}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{k_3}}{4 \sigma _1} \cot \left[ \frac{\sqrt{\sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(28)

Case 03: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=\frac{\sigma _2^2 k_2}{256 \sigma _1^3}\) then we get the solution Eq. (12) has the following form:

\(\bullet\) If \(\sigma _{1}<0\), \(k_{3}<0\),

$$\begin{aligned} f_{17}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-2 k_3}}{4 \sigma _1} \, \text {sech} \left[ \frac{\sqrt{2 \sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(29)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}>0\),

$$\begin{aligned} f_{18}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{2 k_3}}{4 \sigma _1} \, \text {csch} \left[ \frac{\sqrt{2 \sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(30)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}<0\),

$$\begin{aligned} f_{19}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-2 k_3}}{4 \sigma _1} \, \text {sec} \left[ \frac{\sqrt{-2 \sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(31)
$$\begin{aligned} f_{20}(\xi ) = -\frac{\sigma _2}{4 \sigma _1} \pm { \frac{\sqrt{-2 k_3}}{4 \sigma _1} \, \text {csc} \left[ \frac{\sqrt{-2 \sigma _1 k_3}}{4 \sigma _1}\xi \right] }. \end{aligned}$$
(32)

Case 04: when \(\sigma _{2} = \sigma _{4} = \sigma _{5} = 0\), \(\sigma _{3}>0\) then we find out the solution Eq. (12) as:

$$\begin{aligned} f_{21}(\xi ) = \frac{4 \zeta \sigma _3}{4 \zeta \exp \left( \sqrt{\sigma _3 \xi }\right) - \sigma _1 \sigma _3 \exp \left( -\sqrt{\sigma _3 \xi }\right) }. \end{aligned}$$
(33)

where

$$\begin{aligned} k_1 = 4\sigma _1\sigma _3 - \sigma _2^2,\hspace{0.3cm} k_2 = 16\sigma _1\sigma _3 - 5\sigma _2^2,\hspace{0.3cm} k_3 = 8\sigma _1\sigma _3 - 3\sigma _2^2. \end{aligned}$$
(34)

Step 02: The value of N may readily be calculated by following the homogeneous balancing principle on Eq. (10).

Step 03: After putting the Eq. (11) and its derivatives according to the Eq. (12) in Eq. (10) the polynomials of \(f(\xi )\) is obtained. After collecting all the coefficients of the different powers of \(f(\xi )\) and equating to zero provides the system in the unknown parameters \(B_{i}'s\) (i = 1,2,3,..., N), \(\sigma _{i}'s\) (i = 1,2,3,..., N). Solving this set of algebraic equations yields the precise solution of Equation (1).

Solution by Kumar–Malik method

To obtain the solution of Eq. (10), find the value of positive integer N =1 and put it in Eq. (11), then Eq. (11) will become:

$$\begin{aligned} \Phi (\xi ) = B_0 + B_1 f(\xi ). \end{aligned}$$
(35)

By inserting Eqs. (35) and (12) in Eq. (10) we obtained the set of algebraic equations by equating the different powers of \(f(\xi )\) and then solving these equations for unknowns.

Set 1:

$$\begin{aligned} \delta = \eta \frac{8n^2\theta ^2\sigma _1 + 8\theta ^2\sigma _1\sigma _3 - 3\theta ^2\sigma _2^2 - 16n\theta \sigma _1 + 8\sigma _1}{8n^2\theta \sigma _1 + 8\theta \sigma _1\sigma _3 - 3\theta \sigma _2^2 - 16n\sigma _1}, \hspace{0.3cm} B_0 = -\frac{\sigma _2}{4\rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}}, \hspace{0.3cm} B_1 = \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \end{aligned}$$
(36)

By putting set 1 in Eq.(35) we obtained the exact solution as follows:

Case 01: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=0\) then Eq. (12) has the following Jacobi elliptic solutions:

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}>0\),

$$\begin{aligned} \mathcal {U}_{01}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \text {JacobiCN}\left( \frac{\sqrt{-\sigma _1 k_1}}{4 \sigma _1}\xi , \frac{\sigma _2}{2 \sqrt{k_1}}\right) }{4 \sigma _1} \right] . \end{aligned}$$
(37)
$$\begin{aligned} \mathcal {U}_{02}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \text {JacobiDN}\left( \frac{\sigma _2}{4 \sqrt{-\sigma _1}}\xi , \frac{2 \sqrt{k_1}}{\sigma _2}\right) }{4 \sigma _1} \right] . \end{aligned}$$
(38)

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}<0\), \(k_{2}<0\),

$$\begin{aligned} \mathcal {U}_{03}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-k_2} \cdot \text {JacobiCN}\left( \frac{\sqrt{\sigma _1 k_1}}{4 \sigma _1}\xi , \frac{\sqrt{k_2 k_1}}{2 k_1}\right) }{4 \sigma _1} \right] . \end{aligned}$$
(39)
$$\begin{aligned} \mathcal {U}_{04}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \sqrt{-k_2} \cdot \textrm{JacobiDN} \left( \frac{\sqrt{\sigma _1 k_1}}{4 \sigma _1}\xi , \frac{2 \sqrt{k_2 k_1}}{k_2} \right) \bigg / (4 \sigma _1) \right] . \end{aligned}$$
(40)

\(\bullet\) If \(\sigma _{1}<0\), \(k_{1}>0\), \(k_{2}<0\),

$$\begin{aligned} \mathcal {U}_{05}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \sqrt{-k_2} \cdot \textrm{JacobiNC} \left( \frac{\sqrt{-\sigma _1 k_1}}{2 \sigma _1}\xi , \frac{\sigma _2}{2 \sqrt{k_2}} \right) \bigg / (4 \sigma _1) \right] . \end{aligned}$$
(41)
$$\begin{aligned} \mathcal {U}_{06}(\xi ) =-\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \sqrt{-k_2} \cdot \textrm{JacobiND} \left( \frac{\sqrt{-\sigma _1 k_1}i}{2 \sigma _1}\xi , \frac{\sigma _2}{2 \sqrt{k_2}} \right) \bigg / (4 \sigma _1) \right] . \end{aligned}$$
(42)

\(\bullet\) If \(\sigma _{1} k_{1}>0\), \(k_{1} k_{2}>0\),

$$\begin{aligned} \mathcal {U}_{07}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \textrm{JacobiNC} \left( \frac{\sqrt{\sigma _1 k_1}}{2 \sigma _1}\xi , \frac{\sqrt{k_1 k_2}}{2 k_1} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(43)
$$\begin{aligned} \mathcal {U}_{08}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \textrm{JacobiND} \left( \frac{\sqrt{\sigma _1 k_2}}{2 \sigma _1}\xi , \frac{2 \sqrt{k_1 k_2}}{k_2} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(44)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{2}<0\),

$$\begin{aligned} \mathcal {U}_{09}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \textrm{JacobiNS} \left( \frac{\sigma _2}{2 \sqrt{\sigma _1}}\xi , \frac{\sqrt{-k_2}}{\sigma _2} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(45)
$$\begin{aligned} \mathcal {U}_{10}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-k_2} \cdot \textrm{JacobiNS} \left( \frac{\sqrt{-\sigma _1 k_2}}{4 \sigma _1}\xi , \frac{\sigma _2}{\sqrt{-k_2}} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(46)
$$\begin{aligned} \mathcal {U}_{11}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-k_2} \cdot \textrm{JacobiSN} \left( \frac{\sigma _2}{2 \sqrt{\sigma _1}}\xi , \frac{\sqrt{-k_2}}{\sigma _2} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(47)
$$\begin{aligned} \mathcal {U}_{12}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sigma _2 \cdot \textrm{JacobiSN} \left( \frac{\sqrt{-\sigma _1 k_2}}{4 \sigma _1}\xi , \frac{\sigma _2}{\sqrt{-k_2}} \right) }{4 \sigma _1} \right] . \end{aligned}$$
(48)

Case 02: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=\frac{k_1^2}{64 \sigma _1^3}\) then Eq. (12) has the following hyperbolic and trigonometric solutions:

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}<0\),

$$\begin{aligned} \mathcal {U}_{13}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-k_3} \cdot \tanh \left( \frac{\sqrt{-\sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(49)
$$\begin{aligned} \mathcal {U}_{14}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-k_3} \cdot \coth \left( \frac{\sqrt{-\sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(50)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}>0\),

$$\begin{aligned} \mathcal {U}_{15}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{k_3} \cdot \tan \left( \frac{\sqrt{\sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(51)
$$\begin{aligned} \mathcal {U}_{16}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{k_3} \cdot \cot \left( \frac{\sqrt{\sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(52)

Case 03: when \(\sigma _4:= \frac{\sigma _2 k_1}{8 \sigma _1^2}\), \(\sigma _5=\frac{\sigma _2^2 k_2}{256 \sigma _1^3}\) then we get the solution Eq. (12) has the following form:

\(\bullet\) If \(\sigma _{1}<0\), \(k_{3}<0\),

$$\begin{aligned} \mathcal {U}_{17}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-2 k_3} \cdot \text {sech} \left( \frac{\sqrt{2} \sqrt{\sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(53)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}>0\),

$$\begin{aligned} \mathcal {U}_{18}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{2} \sqrt{k_3} \cdot \text {csch} \left( \frac{\sqrt{2} \sqrt{\sigma _1 k_3}}{4 \sigma _1}\xi \right) }{4 \sigma _1} \right] . \end{aligned}$$
(54)

\(\bullet\) If \(\sigma _{1}>0\), \(k_{3}<0\),

$$\begin{aligned} \mathcal {U}_{19}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-2 k_3} \cdot \sec \left( \frac{\sqrt{-2 \sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(55)
$$\begin{aligned} \mathcal {U}_{20}(\xi ) = -\frac{\sigma _2}{4 \rho \epsilon \sqrt{-\frac{\sigma _1}{\epsilon \rho }}} + \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \left[ -\frac{\sigma _2}{4 \sigma _1} + \frac{\sqrt{-2 k_3} \cdot \csc \left( \frac{\sqrt{-2 \sigma _1 k_3}}{4 \sigma _1} \right) }{4 \sigma _1}\xi \right] . \end{aligned}$$
(56)

Case 04: when \(\sigma _{2} = \sigma _{4} = \sigma _{5} = 0\), \(\sigma _{3}>0\) then we find out the solution of Eq. (12) as:

$$\begin{aligned} \mathcal {U}_{21}(\xi ) = \frac{4 \sqrt{-\frac{\sigma _1}{\epsilon \rho }} \cdot \zeta \cdot \sigma _3}{4 \zeta \exp \left( \sqrt{\sigma _3 \xi } \right) - \sigma _1 \sigma _3 \exp \left( -\sqrt{\sigma _3}\xi \right) }. \end{aligned}$$
(57)

The new Kudryashov method

Here are the main steps of the new Kudryashov method (NK)77.

Step 01:  The NK method provides the solution of Eq. (10) as:

$$\begin{aligned} \Phi (\xi )=c_{0}+\sum _{j=1}^{N}\left( b_{i} f^{i}(\xi )\right) . \end{aligned}$$
(58)

where the coefficients \(b_{i}\) for (i = 0,1,2,...,N) are constants to be determined such that \(b_{N} \ne 0\), and \(f(\xi ) = \frac{1}{a B^{\sigma \xi } + b B^{-\sigma \xi }}\) is the solution of the following non-linear ODE:

$$\begin{aligned} f'(\xi )^{2} = (\sigma \ln (B) f(\xi ))^2 (1 - 4ab f^2(\xi )). \end{aligned}$$
(59)
$$\begin{aligned} f''(\xi ) = (\sigma ^{2} \ln (B)^{2} f(\xi )) (1 - 8ab f^{2}(\xi )). \end{aligned}$$
(60)

here constants a, b, \(\sigma\), and B are all non-zero, with \(B > 0\) and \(B \ne 1\).

Step 02:  Using the homogeneous balance principle, we may get the positive integer N by balancing the highest-order derivative and nonlinear variables in Eq. (10).

Step 03:  After inserting Eq. (58) into Eq. (10) and recognizing that \(f(\xi ) \ne 0\) we set all coefficients of \(f^{i}(\xi )\) to zero. After that, we get particular values for a, b, and the \(c'_{i}\)s by solving the resultant non-linear algebraic system. By plugging the values back into Eq. (61) and applying the transformation of Eq. (4), we may get a solution for Eq. (1).

Solutions by NK method

The exact solution of Eq. (10), by plugging value of N=1 in to Eq. (58) then Eq. (58) will become as follows:

$$\begin{aligned} \Phi (\xi ) := b_{0} + b_{1} f(\xi ). \end{aligned}$$
(61)

By putting the value of Eq. (61) and Eq. (59,60) in Eq. (10) we obtain the following set of algebraic equations by equating the coefficients of different powers of \(f(\xi )\) equal to zero. Then values of unknown constants are obtained by solving the system of algebraic equations simultaneously.

Set 01: 

$$\begin{aligned} \eta = \frac{\delta \left( \sigma ^2 \theta \ln (B)^2 + \theta n^2 - 2n \right) }{\sigma ^2 \theta ^2 \ln (B)^2 + n^2 \theta ^2 - 2 n \theta + 1} ,\hspace{0.3cm} \theta = \theta , \hspace{0.3cm} b_0 = 0, \hspace{0.3cm}, \hspace{0.3cm} b_1 = 2 \sqrt{\frac{a b}{\gamma \epsilon }} \ln (B) \sigma . \end{aligned}$$
(62)

Set 02: 

$$\begin{aligned} \eta = -2 \delta n, \hspace{0.3cm} \theta = 0 , \hspace{0.3cm}, \hspace{0.3cm}b_0 = b_0, \hspace{0.3cm}b_1 = b_1. \end{aligned}$$
(63)

By inserting Set 1 in Eq. (61), we find out the solution as follows:

$$\begin{aligned} \mathcal {U}_{1}(x,t)= \frac{2 \sqrt{\frac{a b}{\gamma \epsilon }} \ln (B) \sigma }{a B^{\sigma \xi } + b B^{-\sigma \xi }}. \end{aligned}$$
(64)

By inserting Set 2 in Eq. (61), we find out the solution as follows:

$$\begin{aligned} \mathcal {U}_{2}(x, t)= b_0 + \frac{b_1}{a B^{\sigma \xi } + b B^{-\sigma \xi }}. \end{aligned}$$
(65)

Riccati equation method

The following are the fundamental steps of the Riccati equation method(RE)78.

Step:01  The RE method provides the solution of Eq. (10) as:

$$\begin{aligned} \Phi (\xi )= b_0 + \sum _{j=1}^{N} b_j\hspace{0.1cm} f(\xi )^j. \end{aligned}$$
(66)

where \(f(\xi )\) satisfies the ODE, and the constants \(b_{j}\) for (j= 1,2,...,N) will be obtained subsequently such that \(b_{N} \ne 0\) and \(f(\xi )\) holds the RE.

$$\begin{aligned} f'(\xi ) = \sigma _{0} + \sigma _{1} f(\xi ) + \sigma _{2} f(\xi )^{2} \hspace{0.3cm},\sigma _{2}\ne 0. \end{aligned}$$
(67)

with \(\sigma _{0}, \sigma _{1}\) and \(\sigma _{2}\) are arbitrary constants. The answers to Eq. (67) are as follows.

  • If \(\mu >0\), then,

    $$\begin{aligned} f(\xi )=-\frac{\sigma _{1}}{2\sigma _{2}} - \frac{\sqrt{\mu }}{2\sigma _{2}} \tanh \left[ \frac{\sqrt{\mu }}{2} \xi + \xi _{0} \right] . \end{aligned}$$
    (68)

  • If \(\mu >0\), then,

    $$\begin{aligned} f(\xi )= -\frac{\sigma _{1}}{2\sigma _{2}} - \frac{\sqrt{\mu }}{2\sigma _{2}} \coth \left[ \frac{\sqrt{\mu }}{2} \xi + \xi _{0} \right] . \end{aligned}$$
    (69)

  • If \(\mu < 0\), then,

    $$\begin{aligned} f(\xi )= -\frac{\sigma _{1}}{2\sigma _{2}} - \frac{\sqrt{-\mu }}{2\sigma _{2}} \tan \left[ \frac{\sqrt{-\mu }}{2} \xi + \xi _{0} \right] . \end{aligned}$$
    (70)

  • If \(\mu < 0\), then,

    $$\begin{aligned} f(\xi )= -\frac{\sigma _{1}}{2\sigma _{2}} - \frac{\sqrt{-\mu }}{2\sigma _{2}} \cot \left[ \frac{\sqrt{-\mu }}{2} \xi + \xi _{0} \right] . \end{aligned}$$
    (71)

  • If \(\mu = 0\), then,

    $$\begin{aligned} f(\xi )= -\frac{\sigma _{1}}{2\sigma _{2}} -\left[ \frac{1}{\xi \sigma _{2} + \xi _{0}}\right] . \end{aligned}$$
    (72)

    Where, \(\mu =\sigma _{1}^{2}-4\sigma _{0}\sigma _{2}\).

Step:02  By using the highest order derivative and non-linear term present in Eq. (10) and deriving the value of N with the help of the Homogeneous balance principal.

Step:03  After plugging Eqs. (66,67) in Eq. (10) and taking into account that \(G(\xi )\ne 0\) we put all the constants of \(f^{i}(\xi )\) = 0. Next, we get particular values for a, b, and the \(b'_{j}\)s by solving the resultant non-linear algebraic system. By inserting values in Eq. (73) and utilizing transformation Eq. (4), we can get the solutions of Eq. (1).

Solution by Riccati equation method

The precise solution of Eq. (10) can find out by plugging N = 1 in to Eq. (66) then Eq. (66) will become as follows:

$$\begin{aligned} \Phi (\xi )= b_{0} + b_{1} f(\xi ). \end{aligned}$$
(73)

By putting the value of Eqs. (73) and (67) in Eq. (10) we obtain the following set of algebraic equations by equating the coefficients of different powers of \(f(\xi )\) is equal to zero. Then values of unknown constants are obtained by solving the system of algebraic equations simultaneously.

Set 1: 

$$\begin{aligned} \eta = \frac{(2 n^2 \theta + 4 \theta \sigma _0 \sigma _2 - \theta \sigma _1^2 - 4n) \delta }{2 n^2 \theta ^2 + 4 \theta ^2 \sigma _0 \sigma _2 - \theta ^2 \sigma _1^2 - 4n \theta + 2}, \hspace{0.2cm} \theta = \theta , \hspace{00.2cm} b_0 = -\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}}, \hspace{0.2cm} b_1 = \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2. \end{aligned}$$
(74)

Family 01:   Solutions corresponding to Set 1 are given below:

Case 01. 

\(\bullet\) when \(\mu >0\) then,

$$\begin{aligned} \mathcal {U}_{1}(x,t)=-\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}} + \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2 \left[ -\frac{\sigma _1}{2 \sigma _2} - \frac{\sqrt{-4 \sigma _0 \sigma _2 + \sigma _1^2} \tanh \left( \frac{\sqrt{-4 \sigma _0 \sigma _2 + \sigma _1^2} \xi }{2} + d \right) }{2 \sigma _2} \right] . \end{aligned}$$
(75)

Case 02: 

\(\bullet\) when \(\mu >0\) then,

$$\begin{aligned} \mathcal {U}_{2}(x,t)=-\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}} + \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2 \left[ -\frac{\sigma _1}{2 \sigma _2} - \frac{\sqrt{-4 \sigma _0 \sigma _2 + \sigma _1^2} \coth \left( \frac{\sqrt{-4 \sigma _0 \sigma _2 + \sigma _1^2} \xi }{2} + d \right) }{2 \sigma _2} \right] . \end{aligned}$$
(76)

Case 03: 

\(\bullet\) when \(\mu <0\) then,

$$\begin{aligned} \mathcal {U}_{3}(x,t)=-\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}} + \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2 \left[ -\frac{\sigma _1}{2 \sigma _2} - \frac{\sqrt{4 \sigma _0 \sigma _2 - \sigma _1^2} \tan \left( \frac{\sqrt{4 \sigma _0 \sigma _2 - \sigma _1^2} \xi }{2} + d \right) }{2 \sigma _2} \right] . \end{aligned}$$
(77)

Case 04: 

\(\bullet\) when \(\mu <0\) then,

$$\begin{aligned} \mathcal {U}_{4}(x,t)=-\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}} + \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2 \left[ -\frac{\sigma _1}{2 \sigma _2} - \frac{\sqrt{4 \sigma _0 \sigma _2 - \sigma _1^2} \cot \left( \frac{\sqrt{4 \sigma _0 \sigma _2 - \sigma _1^2} \xi }{2} + d \right) }{2 \sigma _2} \right] . \end{aligned}$$
(78)

Case 05: 

\(\bullet\) when \(\mu = 0\) then,

$$\begin{aligned} \mathcal {U}_{5}(x,t)= -\frac{\sigma _1}{2 \epsilon \gamma \sqrt{\frac{-1}{\epsilon \gamma }}} + \sqrt{\frac{-1}{\epsilon \gamma }} \sigma _2 \left[ -\frac{\sigma _1}{2 \sigma _2} - \frac{1}{\xi \sigma _2 + d} \right] . \end{aligned}$$
(79)

Graphical representation and discussion

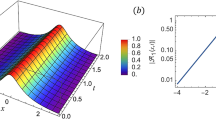
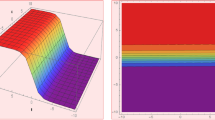
The pictorial appearance of the solutions produced is investigated in this section. Specific values are supplied to the unknown constants to construct 3D and 2D graphs of the resulting solutions. The figures depicted in part (a) reflect a 3D plot, while part (b) represents the 2D line graph of the solutions, part (c) displays the Contour graph, and part (d) depicts the density plot. Figure 1 illustrates periodic solitary wave with varying values of constants \(\mathcal {U}_{01}(x,t): \sigma _{1} = -2, \sigma _{2} = 1, \sigma _{3} = -1,\) \(k{1} = 7, n = 1, \eta = 1, \theta = 0.3, \epsilon = 4, \rho = 0.01, \delta = 0.78, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 2 represents dark solitary wave with varing values of constants \(\mathcal {U}_{02}(x,t): \sigma _{1} = -0.2, \sigma _{2} = 0.8, \sigma _{3} = -1,\) \(k{1} = 0.16, n = 1, \eta = 2, \theta = 0.3, \epsilon = 5, \rho = 2, \delta = 1.44, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 3 represents periodic solitary wave with \(\mathcal {U}_{03}(x,t): \sigma _{1} = -0.1, \sigma _{2} = 0.6, \sigma _{3} = 0.1,\) \(k_{1} = -0.40, k_{2} = -1.96, n = -1, \eta = 2, \theta = 0.3, \epsilon = 5, \rho = 2, \delta = 1.33, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 4 represents periodic solitary wave with varying values of constants \(\mathcal {U}_{04}(x,t): \sigma _{1} = -0.1, \sigma _{2} = 0.4, \sigma _{3} = 0.1,\) \(k_{1} = -0.20, k_{2} = -0.96, n = -1, \eta = 1, \theta = 0.3, \epsilon = 5, \rho = 2, \delta = 0.69, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 5 represents bright solitary wave with different values of constants \(\mathcal {U}_{05}(x,t): \sigma _{1} = -0.2, \sigma _{2} = 0.28, \sigma _{3} = -0.1,\) \(k_{1} = -0.0016, k_{2} = -0.0720, n = -1, \eta = 0.5, \theta = 0.3, \epsilon = 2, \rho = 0.36, \delta = 0.69, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 6 indicates kink solitary wave with specific values of constants \(\mathcal {U}_{13}(x,t): \sigma _{1} = 0.2, \sigma _{2} = -0.4, \sigma _{3} = 0.1,\) \(k_{3} = -0.32, n = -2, \eta = -1, \theta = 0.3, \epsilon = -2, \rho = 1, \delta = 0.49, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 7 indicates dark solitary wave with \(\mathcal {U}_{15}(x,t): \sigma _{1} = 0.01, \sigma _{2} = 0.02, \sigma _{3} = 0.03,\) \(k_{3} = -0.0012, n = -2, \eta = 0.2, \theta = 0.3, \epsilon = 4, \rho = 0.2, \delta = 0.09, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 8 depicts dark solitary wave with \(\mathcal {U}_{17}(x,t): \sigma _{1} = -0.02, \sigma _{2} = 0.03, \sigma _{3} = 0.04,\) \(k_{3} = -0.91, n = 1, \eta = 6.5, \theta = 3, \epsilon = 2, \rho = 2, \delta = 21.90, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 9 depicts bright solitary wave with varing values of constants \(\mathcal {U}_{1}(x,t): a = 1, b = 3, B = 0.5, \sigma = -1, \gamma = 1, \theta = 0.4, \delta = 1.5, n = 0.5, \epsilon = 1, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 10 represents dark solitary wave with \(\mathcal {U}_{2}(x,t): a = 1, b = 1, B = 0.5, \sigma = 1, \gamma = 1, \theta = 0.01,\) \(\delta = -1.5, n = 0.5, \epsilon = 1, b_{0} = 1, b_{1}, \eta = 1.5, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 11 indicates kink solitary wave with varying values of constants \(\mathcal {U}_{1}(x,t): \delta = -1, \sigma _0 = -1, \sigma _1 =0.5, \sigma _2 = 0.5, \gamma = -1,\) \(n = 0.5, m = 1.5, \theta = 0.1, \eta = 1.2, d = 0.4, \epsilon = 1, \mu = 2.2, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 12 indicates singular bright solitary wave with \(\mathcal {U}_{2}(x,t): \sigma _0 = -0.1,\delta = 0.3, \sigma _1 =0.5,, \gamma = -0.1, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 1, \epsilon = -0.1, \mu = 0.33, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 13 represents singular kink solitary wave with varying values of constants \(\mathcal {U}_{3}(x,t): \sigma _0 = 0.2,\delta = 0.3, \sigma _1 =0.01, \gamma = -1.5, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 0.9, \epsilon = 0.01, \mu = -0.159, \xi = x - \eta t\), for line graph t = -1,0,1. Figure 14 indicates singular kink solitary wave with varying values of constants \(\mathcal {U}_{4}(x,t): \sigma _0 = 0.2, \delta = 0.3, \sigma _1 =0.01, \gamma = -1.5, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 1, \epsilon = 0.01, \mu = -0.159, \xi = x - \eta t\), for line graph t = -1,0,1.

Figure 1
figure 1

The visual representation of the obtained solution of Eq. (37) represented as \(\mathcal {U}_{01}(x,t): \sigma _{1} = -2, \, \sigma _{2} = 1, \, \sigma _{3} = -1, \, {k_{1} = 7}, \,\) \(n = 1, \, \eta = 1, \, \theta = 0.3, \, \epsilon = 4, \, \rho = 0.01, \, \delta = 0.78\).

Full size image
Figure 2
figure 2

The visual representation of the obtained solution of Eq. (38) represented as \(\mathcal {U}_{02}(x,t): \sigma _{1} = -0.2, \, \sigma _{2} = 0.8, \, \sigma _{3} = -1, \, {k_{1} = 0.16}, \,\) \(n = 1, \, \eta = 2, \, \theta = 0.3, \, \epsilon = 5, \, \rho = 2, \, \delta = 1.44\).

Full size image
Figure 3
figure 3

The visual representation of the obtained solution of Eq. (39) represented as \(\mathcal {U}_{03}(x,t): \sigma _{1} = -0.1, \, \sigma _{2} = 0.6, \, \sigma _{3} = 0.1, \, k_{1} = -0.40, \, k_{2} = -1.96, \,\) \(n = -1, \, \eta = 2, \, \theta = 0.3, \, \epsilon = 5, \, \rho = 2, \, \delta = 1.33\).

Full size image
Figure 4
figure 4

The visual representation of the obtained solution of Eq. (40) represented as \(\mathcal {U}_{04}(x,t): \sigma _{1} = -0.1, \, \sigma _{2} = 0.4, \, \sigma _{3} = 0.1, \, k_{1} = -0.20, \, k_{2} = -0.96, \,\) \(n = -1, \, \eta = 1, \, \theta = 0.3, \, \epsilon = 5, \, \rho = 2, \, \delta = 0.69\).

Full size image
Figure 5
figure 5

The visual representation of the obtained solution of Eq. (41) represented as \(\mathcal {U}_{05}(x,t): \sigma _{1} = -0.2, \, \sigma _{2} = 0.28, \, \sigma _{3} = -0.1, \, {k_{1} = 1.006}, \, k_{2} = -0.0720, \,\) \(n = -1, \, \eta = 0.5, \, \theta = 0.3, \, \epsilon = 2, \, \rho = 0.36, \, \delta = 0.69\).

Full size image
Figure 6
figure 6

The visual representation of the obtained solution of Eq. (49) represented as \(\mathcal {U}_{13}(x,t): \sigma _{1} = 0.2, \, \sigma _{2} = -0.4, \, \sigma _{3} = 0.1, \, k_{3} = -0.32, \,\) \(n = -2, \, \eta = -1, \, \theta = 0.3, \, \epsilon = -2, \, \rho = 1, \, \delta = 0.49\).

Full size image
Figure 7
figure 7

The visual representation of the obtained solution of Eq. (51) represented as \(\mathcal {U}_{15}(x,t): \sigma _{1} = 0.01, \, \sigma _{2} = 0.02, \, \sigma _{3} = 0.03, \, {k_{3} = 0.0012}, \,\) \(n = -2, \, \eta = 0.2, \, \theta = 0.3, \, \epsilon = 4, \, \rho = 0.2, \, \delta = 0.09\).

Full size image
Figure 8
figure 8

The visual representation of the obtained solution of Eq. (53) represented as \(\mathcal {U}_{17}(x,t): \sigma _{1} = -0.02, \sigma _{2} = 0.03, \sigma _{3} = 0.04, k_{3} = -0.91, \,\) \(n = 1, \, \eta = 6.5, \, \theta = 3, \, \epsilon = 2, \, \rho = 2, \, \delta = 21.90\).

Full size image
Figure 9
figure 9

The visual representation of the obtained solution of Eq. (64) represented as \(\mathcal {U}_{1}(x,t): a = 1, b = 3, B = 0.5, \sigma = -1, \gamma = 1, \,\) \(\theta = 0.4, \delta = 1.5, n = 0.5, \epsilon = 1\).

Full size image
Figure 10
figure 10

The visual representation of the obtained solution of Eq. (65) represented as \(\mathcal {U}_{2}(x,t): a = 1, b = 1, B = 0.5, \sigma = 1, \gamma = 1,\) \(\theta = 0.01, \delta = -1.5, n = 0.5, \epsilon = 1, b_{0} = 1, b_{1}, \eta = 1.5\).

Full size image
Figure 11
figure 11

The visual representation of the obtained solution of Eq. (75) represented as \(\mathcal {U}_{1}(x,t): \sigma _0 = -1, \delta = -1, \sigma _1 =0.5, \gamma = -1,\) \(\sigma _2 = 0.5, n = 0.5, m = 1.5, \theta = 0.1, \eta = 1.2, d = 0.4, \epsilon = 1, \mu = 2.25\).

Full size image
Figure 12
figure 12

The visual representation of the obtained solution of Eq. (76) represented as \(\mathcal {U}_{2}(x,t): \sigma _0 = -0.1, \delta = 0.3, \sigma _1 =0.5, \gamma = -0.1, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 1, \epsilon = -0.1, \mu = 0.33\).

Full size image
Figure 13
figure 13

The visual representation of the obtained solution of Eq. (77) represented as \(\mathcal {U}_{3}(x,t): \sigma _0 = 0.2, \delta = 0.3, \sigma _1 =0.01, \gamma = -1.5, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 0.9, \epsilon = 0.01, \mu = -0.159\).

Full size image
Figure 14
figure 14

The visual representation of the obtained solution of Eq. (78) represented as \(\mathcal {U}_{4}(x,t): \sigma _0 = 0.2, \delta = 0.3, \sigma _1 =0.01, \sigma _2 = 0.2, \gamma = -1.5, \sigma _2 = 0.2,\) \(n = 0.01, m = 0.01, \theta = 0.01, \eta = -0.006, d = 1, \epsilon = 0.01, \mu = -0.159\).

Full size image

Conclusion

This work used the Kumar-Malik method, and the new Kudryashov and Riccati equation approaches to get precise solutions for the AE, a Heisenberg ferromagnet equation. AE is an essential instrument for examining nonlinear manifestation in optics, magnetism, and the differential geometry of curves and surfaces. It is often used to depict optical solitons in nonlinear optical fibers, which are essential for fiber-optic communication because of their ability to preserve shape over long distances. To achieve this purpose, it was crucial to use a particular wave transformation technique to turn the original NLPDEs into a NODEs. Notably, these approaches provided a wide range of soliton solutions, spanning periodic, bright, dark, Kink, trigonometric, rational, and exponential solitons. For a thorough comprehension of the physical processes inherent in the integrable AE, we graphically portrayed chosen solutions by assigning parameter values in 3D-surface graphs, 2D-line graphs, and contour and density plots, according to particular limitations. These graphical representations aid in deepening our knowledge of the various soliton structures originating from the equation. Additionally, we underlined the usefulness and potency of the Kumar-Malik method, and new Kudryashov, and Riccati equation strategies in discovering soliton solutions for NLPDEs. The discovered solutions contribute greatly to expanding our grasp of the nonlinear dynamics regulating the propagation of photonic solitons. This paper tries to give helpful insights for scientists and researchers aiming to enhance their experimental activities. Moreover, there exists a possibility for widening the extent of our work include issues related to lump interactions, researching multi-soliton situations, and analyzing the dynamics of rouge wave breathers. Such additions might improve the practical application and relevance of the research.