Introduction

Detector research is advancing rapidly to meet the growing demands of applications like remote sensing, quantum communication, and 3D LiDAR, which require low-noise, high-sensitivity devices1,2,3,4. These requirements include low noise and high sensitivity. Barrier photodetectors and ultra-sensitive devices with internal or intrinsic gain are thought to yield better sensitivity5. Avalanche photodiodes (APDs) are a well-established internal gain device that provide a practical means of achieving enhanced sensitivity performance. Over the past few decades, Si, GeSi and InGaAs APDs have been used in cutting-edge applications in the visible and short-wavelengths infrared, respectively, particularly for single-photon detection systems6,7,8. Long- wavelength infrared (LWIR) detectors especially with cutoff wavelength longer than 10 \(\mu\) m are employed in a number of fields, including astronomical observation, space remote sensing, meteorological detection and defense. For instance, certain astronomical observations necessitate high-gain characteristics to discern exceedingly faint incident fluxes from exceedingly distant stars9. However, the sensitivity of LWIR APD is still limited by the simultaneous action of high dark current and low gain.

HgCdTe and Type-II superlattices (T2SLs) are prominent materials for long-wavelength infrared (LWIR) detectors. The current state-of-the-art HgCdTe LWIR avalanche photodiodes exhibit a dark current density of approximately 100 A/cm2, a maximum gain below 60, and a responsivity lower than 3 A/W9,10. In comparison, short-wave and mid-wave infrared APDs can achieve gains exceeding 1000 and responsivities greater than 100 A/W, respectively. The advantages of T2SLs over HgCdTe include superior energy band engineering capabilities, reduced Auger recombination rates, and a broader range of material system options. While T2SLs have demonstrated extensive performance improvements in mid-wave infrared APDs11,12,13,14,15, achieving comparable performance in T2SLs LWIR APDs remains challenging due to issues such as high dark current and low responsivity. Recently, researchers have designed InAsSb/InAs T2SLs LWIR APD incorporating AlAsSb wide-bandgap multiplication layers, which have achieved a responsivity of 650 A/W at 8.4 μm wavelengths 16. Furthermore, the integration of T2SLs detectors with heterojunction bipolar transistors has resulted in LWIR detectors with responsivities exceeding 1000 A/W and a specific detectivity (D*) of 2.34 \(\times\) 1013 cmHz1/2W-1 at 6.8 \(\mu\) m.

Recent studies on LWIR APDs have shown that band-to-band tunneling (BBT) at low temperatures in these narrow bandgap materials may be the main source of dark currents10,17,18. They strongly depend on the magnitude of the built-in electric field values. With increasing response wavelength BBT is even worse. A potential choice for longer wavelength infrared APDs is separating the absorption region (low electric field to minimize tunneling current) from the multiplication region (high electric field to improve photocurrent gain) using energy band engineering (SAM structure). It has been demonstrated to be highly efficient on InGaAs APDs and directly led to the invention of single-photon avalanche diodes for short-wave infrared (SWIR)19,20,21. This structure has recently been implemented in medium-wave infrared T2SLs APDs, with results showing that using a wide-band gap material as a multiplier layer can effectively suppress APD tunneling dark current11,14. This solution effectively addresses the issue of high tunneling dark current while improving the gain.

In this work, we introduce an innovative T2SLs LWIR APD with 12 \(\mu\) m cutoff wavelength that incorporates an AlxGa1-xSb multiplication layer. This design is aimed at significantly enhancing the detector’s responsivity. Compared to standard LWIR detectors, our device demonstrates a more than 100-fold increase in responsivity at a temperature of 77 K. These improvements can be attributed to the effectiveness of the SAM structure in confining the majority of electric fields to the wide bandgap multiplication material AlxGa1-xSb. In addition, we present a detailed discussion of the structural parameters’ influence on device performance. Our research offers a framework for the development of high-performance LWIR avalanche optoelectronic devices and has the potential to be applied in the emerging and promising LWIR field with internal gain.

Modeling of T2SLS LWIR APD

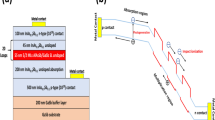
As an infrared material system with significant potential22, InAs/GaSb T2SLs allow continuous tuning of absorption wavelengths from SWIR to LWIR, a family of 6.1 Å lattice constants, and outstanding growth uniformity. GaSb, AlSb, InAs, and their related compounds form a nearly lattice-matched semiconductor family23. Figure 1(b) shows a cross-section diagram of T2SLs LWIR APD. The device is designed for LWIR based on the InAs/GaSb T2SLs absorption layer and AlxGa1-xSb multiplication layer. When the molar fraction of Al in AlxGa1-xSb is less than 0.2, the lattice strain between AlxGa1-xSb and both InAs and GaSb is maintained at less than 1%24. The material AlxGa1-xSb has demonstrated superior impact ionization characteristics (Fig. 2(b)), boasting hole (\(\beta\)) and electron (\(\alpha\)) impact ionization coefficients that significantly exceed those of InP by two to three orders of magnitude across a broad spectrum of electric field intensities25,26,27,28,29,30. Furthermore, the hole-electron ionization coefficient ratio (\(\beta /\alpha\)) of AlxGa1-xSb is notably superior to that of InP (\(\beta /\alpha <2\) and classically used in SWIR APDs). Through meticulous adjustment of the Al composition (0.04 ~ 0.06), the ratio can not only comfortably surpass a value of 5 but also potentially achieve magnitudes exceeding 2026. According to the classical and practical McIntyre excess noise model31, higher β/α result in higher gain bandwidth product32.

Fig. 1
figure 1

Avalanche photodiode schematic and energy band structure. (a) Schematic diagram of photocurrent amplification principle (hole dominant); (b) Three-dimensional view of the T2SLs LWIR-APD; (c) The band structures at low and high reverse bias.

Full size image
Fig. 2
figure 2

(a) The band structures at 0 V, 77 K. Inset zooms in on the details of the valence band interface of the T2SLs and AlxGa1-xSb, (b) The impact ionization coefficients of AlxGa1-xSb and InP as a function of the magnitude of the electric field (1/E). The x being incrementally varied from a value of 0.0 to 0.06. Solid lines and solid markers: Hole impact ionization coefficient \(\beta\). Dashed lines and open markers: Electron impact ionization coefficient \(\alpha\). Conduction band minimum (CBM), Valence Band Maximum (VBM).

Full size image

Impact ionization is defined through the following expression for generation rate G:

$$\text{G}=\alpha \overrightarrow{{\text{J}}_{\text{n}}}/\text{q}+\beta \overrightarrow{{\text{J}}_{\text{p}}}/\text{q}$$
(1)

\(\overrightarrow{{\text{J}}_{\text{n}}}\) and \(\overrightarrow{{\text{J}}_{\text{p}}}\) the electron and hole current density. \(\text{q}\) the electronic charge. A commonly used expression for \(\beta\) was first proposed by Chynoweth33:

$$\beta ={\beta }^{\infty }{\text{e}}^{-\frac{{\text{F}}_{\text{cn}}}{\text{F}}}$$
(2)

where \({\text{F}}_{\text{cn}}\) is the critical field and \({\beta }^{\infty }\) is the inverse of the mean free path between impacts when \(\text{F}=\infty\). A similar expression can be written for the electrons. The relationship between impact ionization coefficient and electric field comes from references25,26,27,28. For Al0.08Ga0.92Sb, \({\upbeta }^{\infty }=3.3\times {10}^{6}\text{ c}{\text{m}}^{-1}\) and \({\text{F}}_{\text{cn}}=1.29\times {10}^{6}\text{ V}/\text{cm}\) in range of \(2.2\times {10}^{5}<\text{F}<3.4\times {10}^{5}\text{ V}/\text{cm}\).

The active area size for all outcomes has been configured to be 40 μm2, in alignment with typical real-world design parameters. Monochromatic light with a wavelength of 12 \(\mu \text{m}\) and an optical power per unit area of 2826 Wm-2 (600 K blackbody radiation) is directed vertically from the top onto the active area. In this APD, incoming photons generate electron–hole pairs in the absorption layer. The built-in electric field, resulting from the reverse bias voltage, drives the electrons toward the N pole of the device. Simultaneously, the holes migrate into the multiplication material, triggering impact ionization gain (refer to Fig. 1(a)) (Tables 1 and 2).

The top layer is an N-type (1 × 1018 cm-3) T2SLs contact layer. The active region of LWIR is composed of InAs/GaSb 21 ML/8 ML with a thickness of 2.0 \(\mu \text{m}\) (N-type, 2 × 1016 cm-3). This configuration has been experimentally demonstrated to exhibit a cutoff wavelength of over 12 \(\mu \text{m}\)34. The band structure and absorption coefficient of T2Sls are achieved by solving the 6 × 6 Hamiltonian of the Luttinger-Kohn type 35 and Fermi’s golden rule36. The absorption coefficient at a wavelength of 12 \(\mu \text{m}\) is 1458 cm-1, which is consistent with previously documented results in literature37. The material parameters used in the numerical calculations are shown in Table 3 of the Methods.

Table 1 Performance comparison of long-wave infrared avalanche diodes.
Full size table

A hole-type multiplication with weak P-type doping AlxGa1-xSb (Background doping is set to a 1 × 1015 cm-3 because there is no inherent AlxGa1-xSb). A charge layer is inserted between the absorption layer and the multiplication. And finally, a P-type (1 × 1018 cm-3) AlxGa1-xSb contact layer.

Different current physical models of the device are simulated by the commercial software Crosslight APSYS. Detailed information can be found in the Methods. All simulations are constructed at a temperature of 77 K, which is the typical temperature for the actual operation of such devices.

Results and discussion

Figure 1(c) illustrates that, under the influence of the reverse low bias voltage, AlxGa1-xSb does not impede the transport of photogenerated electrons. When the Al component x is between 0.0 and 0.06, the band interface of T2SLs and AlGaSb forms a type III band alignment (Fig. 2 (a) illustration), which would lead to significant tunneling leak current. Considering the transport direction of the hole carriers with low energy from T2SLs to AlGaSb, the Type II contact formed by Al0.08Ga0.92Sb can avoid the tunneling current and make no barrier to block the hole transport. This band design helps the device generate punch-throug at very low bias voltages (Fig. 3(a) Black arrow). Another rationale for selecting Al0.08Ga0.92Sb is the absence of an expression for impact ionization at higher Al component in academic literature. The impact ionization capacity of AlxGa1-xSb at different x values is shown in Fig. 2(b). It not only delineates the superior ionization coefficient of AlxGa1-xSb in comparison to InP, but also elucidates the rationale behind the elevated β/α of Al0.04Ga0.06Sb: a low \(\alpha\)28.

Fig. 3
figure 3

(a) The total current Itol (solid line), dark current Id (dash line) and gain curves are derived from simulations at 77 K. Color differentiation of multiplication thickness. (b) Responsivity R and Quantum efficiency \(\upeta\) increases with the bias voltage. (c) The electric field at the breakdown voltage Vbd (Id = 10–5 A).

Full size image

The full gain potential of the multiplication layer is unleashed following its total depletion (see Fig. 1(c) High Bias). This leads to a rapid increase in current as the bias voltage increases. Figure 3(a) demonstrates that the device gain can exceed 103. The initial current reference point (gain = 1) was set at 2.0 V for this calculation to ensure that all examples punch-through current is fully established. Responsivity is fully gain controlled and exceeds 200 A/W (see Fig. 3(b)). The relationship between quantum efficiency and responsivity follows:

$${\text{R}} = \frac{{\lambda {\text{q}}}}{{{\text{hc}}}}\eta$$
(3)

where \(\text{h}\) is the Planck constant, c is the speed of light, \(\text{q}\) is the electron charge and \(\uplambda\) is the wavelength of the incident light (12 \(\mu \text{m}\)).

The initial quantum efficiency \(\upeta\) of our device, as depicted in Fig. 3(b), is approximately 1%. This value is attributed to the combined effects of the intentionally non-depleted absorption layer and the heavily doped charge layer. The excellent gain can be attributed to two primary factors: The superiority of the AlxGa1-xSb material in this design. The β exceeds 105 cm-1 in the range of electric fields involved (1.7 \(\times\) 105 V/cm ~ 2.2 \(\times\) 105 V/cm, from Fig. 2(b)), which ensures rapid carrier multiplication (see Fig. 3(a)); The SAM structure was effective in confining the electric field to the multiplication of the wide bandgap (see Fig. 3(c)). Because the device is deliberately not fully depleted, a multiplication of more than 2.0 \(\times\) 105 V/cm and absorption with almost no electric field exist simultaneously at avalanche breakdown. The heavy N-type doped charge layer (light green in Fig. 3(c)) prevents the depletion from spreading further into the absorption, so that depletion occurs only in the middle of the n-i-p junction composed of the charge layer, multiplication and P-type contact layer. As the thickness of the multiplication increases linearly, the magnitude of electric field enhancement at elevated bias diminishes , leading to a relatively low electric field value in thicker gain layers at the onset of avalanche breakdown (The dark current reaches 10–5 A). This effect, governed by thickness-controlled depletion rates, reduces both gain and responsiveness prior to avalanche breakdown while also slightly mitigating dark current.

In order to fully release the advantages of structural design, the charge layer parameters must be carefully designed. Figure 4(a) shows changes in band alignment as a result of changes in charge layer doping concentration. Throughout the linear increase in charge layer doping concentration from \(5.0\times {10}^{16}\text{ c}{\text{m}}^{-3}\) to \(1.5\times {10}^{17}\text{ c}{\text{m}}^{-3}\), the pre-avalanche responsivity exhibited a reduction of two orders of magnitude (Fig. 4(d)). The decrease of responsivity R and the quantum efficiency η are due to the hole barrier caused by charge layer doping. Upon reaching a doping concentration of \(1.5\times {10}^{17}\text{ c}{\text{m}}^{-3}\) the hole barrier at the interface between the charge layer and the absorption elevates to approximately 0.05 eV. This increase in barrier height impedes carrier transport to the multiplication, particularly for the intentionally non-depleted absorption. Figure 4(b) reveals the inhibition of doping concentration on the diffusion of the depletion electric field to the absorption, and \(1.0\times {10}^{17}\text{ c}{\text{m}}^{-3}\) can just limit the electric field to the multiplier layer. Continuing to increase the doping concentration will cause the quantum efficiency η loss to exceed the benefit of dark current suppression, resulting in a decrease in the max responsivity at post-avalanche (see Fig. 4(c) and Fig. 4(d)).

Fig. 4
figure 4

(a) The increase of the doping concentration of the charge layer leads to the increase of the potential barrier relative to the absorption layer. Color differentiation of charge layer doping concentration. (b) The electric field at the breakdown voltage Vbd. (c) Change in quantum efficiency \(\upeta\) of the device due to charge layer doping concentration (at gain = 1). (d) The change of charge layer doping concentration mainly affects the minimum responsivity of the device.

Full size image

The performance of long-wave infrared avalanche diodes reported in the last three years is listed in Table 1. The LWIR SAM-APD achieves a maximum gain while maintaining a relatively low dark current density, attributed to the electric field strength exceeding 2.0 \(\times\) 105 V/cm within the AlGaSb multiplication layer. Compared to LWIR detectors with similar cutoff wavelengths without internal gain, LWIR SAM-APDs can significantly enhance responsivity, increasing from approximately 2 A/W to over 200 A/W34,40,41,42,43,44.

In summary, this study successfully constructed LWIR SAM-APDs by combining T2SLs energy band engineering with a separate absorption and multiplication layer design. A dedicated Al0.08Ga0.92Sb layer was used to generate impact ionization gain, achieving a gain of over 3000. The electric field analysis indicates that we were able to create a sufficiently large electric field in the Al0.08Ga0.92Sb multiplication layer while maintaining almost no depletion in the absorption layer. By optimizing the doping of the charge layer, we achieved the best detection performance, realizing a responsivity of over 200 A/W for 12 \(\mu \text{m}\) wavelength light. Overall, the T2SLs APDs presented in this paper offer an opportunity to develop high-performance LWIR photodetectors with low dark current and high avalanche gain. We anticipate that this will significantly contribute to the advancement of gain-type ultrasensitive detectors and find applications in the field of LWIR weak photon detection.

Methods

The numerical simulation process utilizes the following current transport model. The continuity equation of charge conservation is used to solve carrier drift diffusion transport. Numerical calculations include the Shockley–Read–Hall (SRH) recombination, Auger recombination, Trap-Assisted Tunneling (TAT), and avalanche generation models. All equations listed in Table 2 are based on a temperature setting of 77 K. The corresponding parameters are as follow: \(\overrightarrow{{\text{J}}_{\text{n}}}\) and \(\overrightarrow{{\text{J}}_{\text{p}}}\) the electron and hole current density. \(\text{n}\) and \(\text{p}\) are the electron and hole density. \({\text{R}}_{\text{n}}^{\text{tj}}\) and \({\text{R}}_{\text{p}}^{\text{tj}}\) are the electron (n) and hole (p) recombination rates per unit volume through the j th deep trap. \({\text{R}}_{\text{au}}\) the Auger recombination rate per unit volume. \({\text{G}}_{\text{opt}}(\text{t})\) the photogenerated carrier generation rate. \({\text{N}}_{\text{D}}\) and \({\text{N}}_{\text{A}}\) the doping density of shallow donors (\(\text{D}\)) and shallow acceptors (\(\text{A}\)). \({\text{f}}_{\text{D}}\) and \({\text{f}}_{\text{A}}\) . \({\text{c}}_{\text{nj}}\) and \({\text{c}}_{\text{pj}}\) the electron (\(\text{n}\)), hole (\(\text{p}\)) capture coefficients of the j th deep trap. \({\text{N}}_{\text{tj}}\) the density of the j th deep trap. \({\text{f}}_{\text{tj}}\) the occupancy of the j th deep trap level. \(\text{G}\) the impact ionization generation rate. \({\alpha }_{\text{n}}\) the electron ionization rate defined as the number of electron–hole pairs generated by an electron per unit distance traveled; \({\alpha }_{\text{p}}\) is similarly defined for holes. \({\alpha }^{\infty }\) the inverse of the mean free path between impacts of electrons or holes when electric field \(\text{E}\) = \(\infty\). \({\text{E}}_{\text{c}}\) the critical field. \(\text{q}\) the electronic charge. \({\text{C}}_{\text{n}}\) and \({\text{C}}_{\text{p}}\) the Auger recombination coefficients, for electrons (\(\text{n}\)) and holes (\(\text{p}\)). \({\text{n}}_{\text{i}}\) the intrinsic carrier density.

Table 2 Current transport models.
Full size table
Table 3 Input material parameters for the simulation method.
Full size table

The parameters for AlxGa1-xSb alloys were calculated using a linear interpolation method: AlSb*x + GaSb*(1-x). All parameters were obtained from the literature (P.-F. Qiao, S. Mou, and S. L. Chuang, “Electronic band structures and optical properties of type-ii superlattice photodetectors with interfacial effect,” Optics express 20, 2319–2334 (2012).).

Even when the device has breakdown and reached 31 V, the electric field in the multiplication layer, which is close to 200 kV/cm, is only partially diffused into the absorption layer. At this point, the absorption layer maintains an electric field of only ~ 40 V/cm. The numerical computational validation of band-to-band tunneling (BBT) demonstrates the superiority of this electric field modulation. The generation rate GBBT of BBT tunneling is described as12. For materials with a band gap of approximately 0.1 eV, GBBT tends to zero when the electric field is less than 103 V/cm. Therefore, the BBT current in the absorption layer can be disregarded.