Introduction

With the rise of the global electric vehicle industry, lithium-ion batteries (LIBs) have gained widespread adoption due to their high reliability, long cycle life, and other advantages1. However, current lithium-ion batteries face several challenges, including limited capacity, low cost-effectiveness, safety concerns, insufficient global lithium resources, and significant price fluctuations, which hinder their ability to fully meet the growing demand for energy storage2,3,4,5,6. Consequently, the search for more economical, safer, and sustainable alternatives has become a key direction in battery development. In contrast to lithium, sodium is more abundant, offers higher safety, superior energy density, and excellent high-temperature performance, making Sodium-ion batteries (NIBs) one of the most promising alternatives to LIBs7,8. Developing high-performance advanced electrode materials has thus become a major research focus in this field9.

In recent years, significant efforts have been dedicated to the development of electrode materials suitable for LIBs/NIBs10,11,12,13. Among these materials, two-dimensional (2D) materials have garnered considerable attention due to their high surface area and unique physicochemical properties, such as graphene, carbides, and phosphides14,15,16. However, most of the 2D anode materials studied to date have failed to address critical issues, such as the structural stability of the material and the formation of Li/Na dendrites during the energy storage process, which in turn leads to a significant reduction in energy storage capacity. Therefore, the development of high-performance 2D anode materials for NIBs, with excellent energy storage capability, electrochemical performance, mechanical properties, and thermal stability, remains a major challenge17,18,19,20.

Previous studies have shown that doping 2D materials with elements such as P, B, and Ta can enhance their energy storage performance21,22,23. In this context, we propose a novel 2D material, termed k-B2C3, and predict its structural properties through first-principles calculations. The results indicate that k-B2C3 possesses stable mechanical properties and thermal stability, exhibits high electrical conductivity, and demonstrates excellent energy storage capability. Both sodium and lithium atoms experience low diffusion barriers and high specific capacities within this material. Therefore, the 2D material based on k-B2C3 holds great potential as a high-performance electrode material. We believe that k-B2C3 based 2D materials can serve as an excellent candidate for high-performance anode materials in batteries.

Computational details

The first-principles calculations were performed using the Vienna Ab Initio Simulation Package (VASP)24, based on density functional theory (DFT). The interaction between valence and core electrons was treated using the projector augmented wave (PAW) method, and the exchange–correlation energy was approximated using the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA)25,26. To minimize interactions between adjacent layers, a 20 Å vacuum layer was introduced along the perpendicular direction. To ensure the reliability of the calculated values, we performed a k-point convergence test. Figure S1 shows that the total energy converges with increasing k-point sampling density. Therefore, we employed a 5 × 5 × 1 Monkhorst–Pack grid27 and a plane-wave basis set with a cutoff energy of 500 eV to ensure the self-consistent convergence of the total energy and atomic forces. The convergence criteria for total energy and forces were set to 10⁻⁶ eV and 0.01 eV·Å⁻1, respectively. The diffusion barriers for Li/Na ions were calculated using the climbing-image nudged elastic band (CI-NEB) method28, employing a 3 × 2 × 1 supercell. The phonon dispersion was calculated using the PHONOPY code29. To assess the thermal stability of k-B2C3, ab initio molecular dynamics (AIMD) simulations30 were performed at 300 K under standard NVT conditions. For energy storage calculations in adsorption structures, Li/Na atoms were randomly distributed on both sides of the k-B2C3 monolayer at different atomic concentrations to determine the maximum storage capacity, Mn k-B2C3 (M = Li, Na)22. Additionally, the electronic band structure was precisely calculated using the Heyd–Scuseria–Ernzerhof (HSE06) functional31.

Results and discussion

Structural stability and electronic properties of k-C2B3

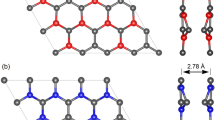
As shown in Fig. 1, the crystal structure of k-B2C3 is a two-dimensional configuration composed of hexagonal and octagonal rings formed by carbon (C) and boron (B) atoms, with adjacent octagonal chains covalently bonded by C = C bonds. In the figure, blue represents C atoms and brown represents B atoms. The unit cell of k-B2C3 belongs to the space group with PMMM symmetry. After full structural optimization, the lattice constants were obtained as a = 2.73 Å, b = 5.87 Å, with three distinct bond lengths. The longest B-B bond is 1.692 Å, followed by the C-B bond at 1.566 Å, and the shortest C = C bond at 1.322 Å, corresponding to the bonds labeled l1–l3 in Fig. 1. Moreover, the bond angles within the hexagonal and octagonal rings in k-B2C3 are 121.4° and 119.3°, respectively, indicating that k-B2C3 possesses unique electronic properties and adsorption activity.

Fig. 1
figure 1

Crystal structure of the k-B2C3.

Full size image

To investigate the dynamic and thermodynamic stability as well as the conductivity of k-B2C3, we performed calculations on its phonon spectrum, AIMD simulations, total energy, and electronic band structure. As shown in Fig. 2a, the phonon band structure of k-B2C3 does not exhibit any imaginary frequencies throughout the entire Brillouin zone, indicating that k-B2C3 is a dynamically stable structure. To further examine the thermal stability of k-B2C3, AIMD simulations were conducted using a 3 × 2 × 1 supercell at 300 K for 3 ps, with a time step of 1 fs32. The results, shown in Fig. 2b, reveal that the average potential energy remains constant throughout the heating process, and no structural reconstruction was observed, indicating that k-B2C3 maintains thermal stability at least up to 300 K.

Fig. 2
figure 2

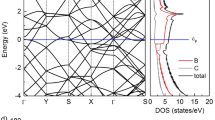
(a) Phonon band structure of k-B2C3, showing no imaginary frequencies, indicating dynamic stability. (b) Potential energy fluctuations of k-B2C3 during AIMD simulations at 300 K, confirming thermal stability. (c) Total energy comparison of k-B2C3 with other 2D materials33,34,35, showing its relative stability. (d) Electronic band structure of k-B2C3, calculated with PBE and HSE06, revealing metallic behavior with no band gap.

Full size image

In Fig. 2c, the total energy of k-B2C3 was compared with that of graphyne, Bi2Te2Se, Bi2Te2S, kust-α, and penta-graphene33,34,35. The results indicate that k-B2C3 is more stable than all materials except for kust-α. To further confirm the conductivity of k-B2C3 as a potential electrode material, we analyzed its electronic band structure and density of states. As shown in Fig. 2d, both PBE and HSE06 calculations reveal no band gap, with the occupied states crossing the Fermi level, indicating its metallic behavior. Moreover, k-B2C3 exhibits a density of states at the Fermi level of 0.18 states/eV, further supporting its excellent electrical conductivity, which is crucial for efficient charge transport in electrode applications.

In the lattice system of k-B2C3, there are four independent elastic constants, and the strain energy and elastic constants can be calculated using the following Eq. (1):36

$${E}_{strain}=\frac{1}{2}\left({C}_{11}{\varepsilon }_{a}^{2}+{C}_{22}{\varepsilon }_{b}^{2}\right)+{C}_{12}{\varepsilon }_{a}{\varepsilon }_{b}+2{C}_{44}{\varepsilon }_{ab}^{2}$$
(1)

Here, \({E}_{strain}\) represents the strain energy per unit area, \({C}_{11}\), \({C}_{12}\), \({C}_{22}\), and \({C}_{44}\) are the four independent elastic constants, and \({\varepsilon }_{a}\), \({\varepsilon }_{a}\), and \({\varepsilon }_{ab}\) represent the strains along the a, b, and shear directions, respectively. By fitting the curves related to uniaxial, biaxial, and shear strains, the following elastic constants were obtained: \({C}_{11}=239.07GPa\cdot mm\), \({C}_{12}=34.86GPa\cdot mm\), \({C}_{22}=217.51GPa\cdot mm\), and \({C}_{44}=94.61GPa\cdot mm\). Since \({C}_{11}{C}_{22}-{C}_{12}^{2}>0\), \({C}_{44}>0\), the Born-Huang criterion is satisfied, indicating that the mechanical structure of k-B2C3 is stable.

To further assess whether the material may undergo volumetric deformation during the charge–discharge process, we calculated the Young’s modulus (C) and Poisson’s ratio (v) of k-B2C3, which were obtained from Eqs. (2) and (3), respectively.

$$C\left(\theta \right)=\frac{{C}_{11}{C}_{22}-{C}_{12}^{2}}{{C}_{11}{a}^{4}+{C}_{22}{\beta }^{4}+\left(\frac{{C}_{11}{C}_{22}-{C}_{12}^{2}}{{C}_{44}}-2{C}_{12}\right){\alpha }^{4}{\beta }^{4}}$$
(2)
$$v\left(\theta \right)=\frac{\left({C}_{11}+{C}_{22}-\frac{{C}_{11}{C}_{22}-{C}_{12}^{2}}{{C}_{44}}\right){\alpha }^{2}{\beta }^{2}-{C}_{12}\left({\alpha }^{4}+{\beta }^{4}\right)}{{C}_{11}{\alpha }^{4}+{C}_{22}{\beta }^{4}+\left(\frac{{C}_{11}{C}_{22}-{C}_{12}^{2}}{{C}_{44}}-2{C}_{12}\right){\alpha }^{2}{\beta }^{2}}$$
(3)

In the equation, \(\alpha = \cos \theta\) and \(\beta = \sin \theta\), where θ is the angle along the a-direction. \(C\left(\theta \right)\) and \(v\left(\theta \right)\) represent the Young’s modulus and Poisson’s ratio, respectively, for the plane at angle θ. As shown in Fig. 3a, b, the Young’s modulus and Poisson’s ratio of k-B2C3 are presented in polar coordinates. From Fig. 3a, it can be seen that the material exhibits orthogonal symmetry, indicating anisotropic mechanical properties. The Young’s moduli of k-B2C3 along the a-axis and b-axis are 145.17 GPa·mm and 274.43 GPa·mm, respectively, both lower than that of graphene, suggesting that k-B2C3 is softer than graphene. The Poisson’s ratios of k-B2C3 along the a-axis and b-axis are 0.1 and 0.4, respectively. Combined with the Young’s modulus, this indicates that the material is more ductile along the a-direction and more resistant to deformation along the b-direction37. Therefore, k-B2C3 can effectively prevent deformation during charge–discharge cycles, making it more suitable for use as an electrode material in batteries.

Fig. 3
figure 3

Mechanical properties of k-B2C3. (a) Polar diagram for in-plane Young’s modulus. (b) Polar diagram for Poisson’s ratio.

Full size image

Adsorption and diffusion of single Li/Na atom on k-B2C3

To more accurately determine the optimal adsorption sites in the k-B2C3 structure, we calculated the adsorption energies at eight possible adsorption points (\({C}_{1}\), \({C}_{2}\), \({B}_{1}\), \({H}_{1}\), \({H}_{2}\), \({L}_{1}\), \({L}_{2}\), \({L}_{3}\)) shown in Fig. 4a. Specifically, \({C}_{1}\) and \({C}_{2}\) correspond to the top sites of different C atoms, \({B}_{1}\) corresponds to the top site of a B atom, \({L}_{1}\), \({L}_{2}\), and \({L}_{3}\) represent the bridge sites between B-B, B-C, and C = C bonds, respectively, and \({H}_{1}\) and \({H}_{2}\) are the hollow sites of the hexagonal and octagonal rings, respectively. To account for the interaction between adjacent adsorbed atoms, we constructed a 3 × 2 × 1 supercell for the adsorption of a single Li/Na atom. The optimization results showed that when Li/Na adsorbs at \({C}_{1}\), \({B}_{1}\), or \({L}_{2}\), it spontaneously moves to the \({H}_{1}\) site, while adsorption at \({C}_{2}\) or \({L}_{3}\) leads to movement to the \({H}_{2}\) site. The adsorption energy can be accurately calculated using the following Eq. (4):

Fig. 4
figure 4

(a) The inequivalent adsorption sites in k-B2C3, labeled as C, B, H, and l. (b) Adsorption energies of a single Li/Na atom at the sites \({l}_{1}\),\({l}_{2}\), \({l}_{3},\) \({H}_{1}\), \({H}_{2},\) \({C}_{1}\), \({C}_{2}\), and \({B}_{1}\) on the k-B2C3 structure.

Full size image
$${E}_{ads}={E}_{Li/Na+k-{B}_{2}{C}_{3}}-{E}_{k-{B}_{2}{C}_{3}}-{E}_{Li/Na}$$
(4)

In the equation, \({E}_{Li/Na+k-{B}_{2}{C}_{3}}\) represents the adsorption energy, \({E}_{k-{B}_{2}{C}_{3}}\)​ and \({E}_{Li/Na}\) refer to the energies of the system before and after the adsorption of Li/Na atoms, respectively, while \({E}_{Li/Na}\) represents the energy of a single Li/Na atom. A negative value of adsorption energy indicates that the adsorption process is spontaneous, and the more negative the value, the greater the released energy and the more stable the system after adsorption38. As shown in Fig. 4b, the adsorption energies of Li and Na atoms at the eight possible adsorption sites are presented. The lowest adsorption energies for both Li and Na occur at the \({H}_{1}\) site, with adsorption energies of −0.873 eV and −0.753 eV, respectively. Therefore, \({H}_{1}\) is the most stable adsorption site.

To gain deeper insights into the interaction mechanism of k-B2C3 with Li and Na atoms, we calculated the charge density difference for a single atom adsorbed at the \({H}_{1}\) site using Eq. (5):

$$\Delta \rho ={\rho }_{Li/Na+k-{B}_{2}{C}_{3}}-{\rho }_{k-{B}_{2}{C}_{3}}-{\rho }_{Li/Na}$$
(5)

In the equation, \(\Delta \rho\) represents the charge density difference, \({\rho }_{Li/Na+k-{B}_{2}{C}_{3}}\) and \({\rho }_{k-{B}_{2}{C}_{3}}\) refer to the charge densities of the system before and after the adsorption of the Li/Na atom, respectively, and \({\rho }_{Li/Na}\) represents the charge density of a single Li/Na atom. The calculation results are shown in Fig. 5, where the yellow region represents electron transfer to the surface, and the cyan region represents electron transfer from the surface. It is clearly observed that electrons transfer from the Li/Na atom to the k-B2C3 surface. Bader analysis further indicates that at the \({H}_{1}\) site, Li and Na atoms transfer 0.89 |e| and 0.86 |e|, respectively, to the k-B2C3 surface. Since Li has a smaller radius and higher reactivity compared to Na, Li is more readily adsorbed closer to the k-B2C3 surface39, as shown in Fig. 5c, d. The electron transfer between the Li/Na atoms and the k-B2C3 surface is indicative of chemisorption, where the formation of chemical bonds is driven by the electron redistribution.

Fig. 5
figure 5

(a) and (b) Top views of the differential charge density distribution for a single Li and Na atom adsorbed at the \({H}_{1}\) site on k-B2C3, respectively, highlighting the electron transfer from the Li/Na atom t the k-B2C3 surface. (c) and (d) Side views corresponding to (a) and (b), showing the electron redistribution across the surface.

Full size image

The diffusion rate of Li/Na ions directly influences the charge and discharge rates of batteries. To explore this, we considered two potential diffusion pathways from \({H}_{1}\) to adjacent \({H}_{1}\) positions in the k-B2C3 structure (Fig. 6a, Path 1 and Path 2). Based on these pathways, the diffusion barriers for Li and Na ions were calculated using the CI-NEB method, with the results shown in Fig. 6b. Along Path 2, two barrier peaks are observed, as Li/Na ions need to traverse two C-B bonds to reach the equivalent position. In contrast, along Path 1, only one B-B bond needs to be crossed. The lowest diffusion barriers for Li and Na ions are 0.55 eV and 0.17 eV, corresponding to Path 2 and Path 1, respectively. Therefore, Li ions are more likely to diffuse along Path 2, while Na ions preferentially diffuse along Path 1. For Li ion diffusion, Path 2 has a lower diffusion barrier than Path 1, due to the more stable \({H}_{2}\) position along Path 2, with a diffusion barrier of 0.55 eV, which is superior to typical 2D materials such as phosphorene (0.76 eV)40, borophene (0.60 eV)41, and silicon (0.57 eV)33. In contrast to Li ion diffusion, Na ions, due to the higher stability of the B1 position, more readily diffuse along Path 1, with a diffusion barrier of 0.17 eV, which is lower than the diffusion barrier of B2C3 (0.23 eV)22. These results demonstrate that k-B2C3 exhibits excellent diffusion capabilities, which can enhance the charge and discharge rates of battery materials.

Fig. 6
figure 6

Li/Na ion diffusion behavior on the k-B2C3 monolayer. (a) Diffusion paths of Li/Na ions (Path 1 and Path 2). (b) Corresponding energy barriers for Li and Na ions along the diffusion paths.

Full size image

Theoretical capacity and open-circuit voltage of Li/Na on k-B2C3

As the core component of lithium/sodium-ion batteries, the performance of the anode material is not only influenced by the adsorption and diffusion of Li/Na ions but also by the Li ion storage capacity and the average insertion potential, both of which are critical indicators of battery performance. A low and stable insertion potential helps ensure a high output voltage, while a higher specific capacity improves the battery’s energy density. To investigate the theoretical specific capacity and average open-circuit voltage, we used a 3 × 2 × 1 k-B2C3 monolayer as the substrate. Li/Na atoms were randomly placed on both sides of the k-B2C3 monolayer, and all possible atomic configurations were optimized. The adsorption configurations were further optimized to determine the most stable adsorption sites, continuing until the maximum adsorption capacity and the most stable structure were achieved This resulted in a series of configurations with stoichiometries of Mn k-B2C3 (M = Li, Na, n = 1/3, 2/3, 1, 4/3, 5/3, 2). By calculating the average energy of Li/Na adsorption on the k-B2C3 monolayer, we obtained the maximum possible adsorption number. The average adsorption energy (\({E}_{ads}\)) is calculated using the following formula (6):

$${E}_{ads}=\frac{{E}_{{M}_{n}\left(k-{\text{B}}_{2}{C}_{3}\right)}-{E}_{k-{\text{B}}_{2}{\text{C}}_{3}}-n{E}_{M}}{n}$$
(6)

The total energy \({E}_{{M}_{n}\left(k-{B}_{2}{C}_{3}\right)}\) corresponds to the energy of the k-B2C3 monolayer with n lithium/sodium atoms adsorbed on both sides, while \({E}_{k-{B}_{2}{C}_{3}}\) represents the energy of the bare k-B2C3 monolayer and \({E}_{{M}_{n}}\) is the energy of a single metal (Li/Na) atom. According to our definition, a negative adsorption energy indicates an exothermic adsorption process42. The structures and average adsorption energies for the \({E}_{ads}\) configurations are shown in Fig. 7a, b. For both Li and Na, we found that the average adsorption energies were negative when n = 1/3, 2/3, 1, 4/3, 5/3, and 2, indicating stable intermediate phases for the \({M}_{n\left(k-{B}_{2}{C}_{3}\right)}\) configurations (M = Li, Na, and n = 1/3, 2/3, 1, 4/3, 5/3, 2), with a maximum of 12 Li/Na atoms adsorbed.

Fig. 7
figure 7

(a) and (b) Show the adsorption energies of Mn k-B2C3 (M = Li, Na) at different concentrations. The triangles and pentagons represent the positions of Li and Na atoms, respectively, which were randomly and uniformly placed, centered at \({H}_{1}\). (c) and (d) Display the AIMD simulations for the 3 × 2 × 1 supercell of the k-B2C3 monolayer with 12 atoms adsorbed, illustrating the stability of the system.

Full size image

To further investigate the stability of Li2 k-B2C3 and Na2 k-B2C3, we performed a 3 ps AIMD simulation at 300 K. The structures of all Li2 k-B2C3 and Na2 k-B2C3 configurations remained stable during the simulation, as shown in Fig. 7c, d. The energy variation trends were relatively stable, indicating that the materials possess good thermodynamic stability.

The theoretical specific capacity (C) for the maximum adsorption configuration of Mn k-B2C3 can be evaluated using the following formula (7):

$$C=\frac{qnF}{{M}_{k-{B}_{2}{C}_{3}}}$$
(7)

where q represents the charge number of Li/Na adsorbed on each unit of the k-B2C3 monolayer, and n represents the number of Li or Na atoms adsorbed on each unit of the k-B2C3 monolayer. F is Faraday’s constant (26,801 mAh mol−1), and \({M}_{k-{B}_{2}{C}_{3}}\) is the molar mass of k-B2C3. The calculated maximum theoretical capacities of k-B2C3 for Li and Na are 930 mAhg−1. As shown in Fig. 8, the energy storage capacity of k-B2C3 is compared with several other 2D anode materials43,44,45,46. The maximum capacity of k-B2C3 is lower than that of B2C (1596/1596 mAhg−1)22,47, β12-borophene (1984/1984 mAhg−1)48, and k-C6B4 (1395/1395 mAhg−1)49, but higher than most other anode materials50,51,52.

Fig. 8
figure 8

Maximum LIB/NIB capacity of k-B2C3 monolayer compared to other 2D anode materials.

Full size image

The formula for calculating the average open-circuit voltage (OCV) is as follows (8):

$$OCV=\frac{-{E}_{{M}_{{n}_{2}}\left(k-{\text{B}}_{2}{\text{C}}_{3}\right)}+{E}_{{M}_{{n}_{1}}\left(k-{\text{B}}_{2}{\text{C}}_{3}\right)}+\left({n}_{2}-{n}_{1}\right){E}_{M}}{\left({n}_{2}-{n}_{1}\right)e}$$
(8)

where \({E}_{{M}_{{n}_{2}}\left(k-{\text{B}}_{2}{\text{C}}_{3}\right)}\) and \({E}_{{M}_{{n}_{1}}\left(k-{\text{B}}_{2}{\text{C}}_{3}\right)}\) represent the total energies of the k-B2C3 monolayer with \({n}_{2}\) and \({n}_{1}\) Li/Na atoms adsorbed, respectively. \({E}_{M}\) is the energy of a single atom in bulk metallic lithium or sodium. As shown in Fig. 9, the open-circuit voltage (OCV) decreases with the increasing number of adsorbed Li/Na atoms. The average OCV of Li decreases from 1.297 V to 0.542 V, and the average OCV of Na decreases from 1.174 V to 0.341 V. These low voltage values are comparable to those of other materials, such as B2C (Li average voltage = 0.57 V, Na average voltage = 0.43 V), β12-borophene (Li: 0.89–0.53 V, Na: 0.60–0.27 V), and k-C6B4 (Li: 0.86–0.59 V, Na: 0.76–0.34 V). The relatively low average voltage values of k-B2C3 indicate its potential to effectively prevent the formation of Li/Na dendrites, thus ensuring the high safety and stability of Lithium/Sodium-ion batteries, making it a promising candidate as a potential electrode material for Li/Na batteries.

Fig. 9
figure 9

(a) The average voltage and specific capacity of the k-B2C3 monolayer at different concentrations of Li. (b) The average voltage and specific capacity of the k-B2C3 monolayer at different concentrations of Na.

Full size image

Conclusions

In this study, we investigated the electrochemical properties and performance of k-B2C3 as a potential electrode material for lithium and sodium-ion batteries. Our results show that k-B2C3 exhibits excellent stability and conductivity for both Li and Na ions. The diffusion barriers calculated for Li and Na ions along different paths demonstrate that k-B2C3 offers efficient ion diffusion. Specifically, the diffusion energy barriers for Li and Na ions were found to be 0.55 eV and 0.17 eV, respectively, with Li favoring path 2 and Na preferring path 1. These low barriers indicate that k-B2C3 could effectively facilitate fast charging and discharging processes in batteries. The maximum theoretical capacity of k-B2C3 was calculated to be 930 mAhg−1 for both Li and Na ions, which is competitive with other 2D materials, although slightly lower than materials such as B2C and β12-borophene. Furthermore, the average open-circuit voltage (OCV) of k-B2C3 was calculated to be 1.297 V for Li and 1.174 V for Na, showing a decreasing trend with increasing ion concentration. These voltage values are comparable to other materials, such as B2C and β12-borophene, indicating that k-B2C3 could offer stable energy output over multiple cycles. The study also highlights that k-B2C3 prevents dendrite formation, enhancing the safety and stability of Li/Na batteries. Overall, k-B2C3 demonstrates promising potential as a high-performance electrode material for future energy storage systems.