Introduction

This work aims to approximate \(\sqrt{x^2+y^2}\) aka Euclidean distance or \(L_2\)-norm. One needs this when one converts Cartesian coordinates into polar coordinates, and it has many applications1. But computing a square root is expensive. tasks.

Since the applicability of Moore’s Law is nearing its end, scientists have been looking for other computing paradigms for the last few decades2,3,4,5. As such, we are looking at bio/neuro-inspired computing6,7,8,9,10 with membrane computing (also so-called P systems) as a new paradigm11,12. A class of membrane computing13 called spiking neural P systems14 is inspired by neural cells, and can be implemented both as electronic devices, as well as other systems, such as micro-fluidic devices.

The present study is based on the work introduced by Xu et al.15, which proposes the implementation of arbitrary SN P systems using two basic neuron types HP (HP stands for High-Pass) and LP (LP stands for Low-Pass).

We don’t have any device that computes the square root using HP/LP-neurons in membrane computing. However, we have the MUST-Adder (MUST stands for Mongolian University of Science and Technology) composed of HP/LP-neurons introduced in16 and can be used to compute the tasks of \(L_2\) norm.

This paper also presents an implementation of these neurons in CMOS logic. However, the approach appears to be more general and is suitable for implementation in a wide range of different substrates, such as bio-nanotechnology17, microfluidic biochip technology18, and electronic substrates19.

Spiking neural (SN) P systems

Spiking neural P systems is a class of membrane systems11,13 and are based on the neuro-physiological behavior of neurons14,20. In SN P systems, the processing elements are neurons, which are connected by a directed graph–the synapse graph. The SN P systems work only with spikes, and all the spikes it deals with are identical but a powerful21,22,23 and an effective computing framework to solve computationally hard problems24,25, combinatorial optimization problems26, arithmetic operations27,28,29, and various other applications30,31,32.

This section explains the basic rules of SN P neurons in a mathematical way.

In SN P systems the neural cells (also called neurons) are placed in the nodes of a directed graph. The contents of each neuron consist of several copies of a single object, called spike, and a number of firing and forgetting rules.

Firing rules allow a neuron to send information to other neurons in the form of spikes (electrical impulses), which are accumulated in the target cells. The applicability of each rule is determined by checking the contents of the neuron against a regular set associated with the rule. In each time unit, if a neuron can use multiple rules, then one such rule must be selected. The rule to be applied is non-deterministically chosen. The rules are used sequentially within each neuron, but the many neurons function in parallel with each other.

If no firing rule can be applied in a neuron, it may be possible to apply a forgetting rule that removes a predefined number of spikes from the neuron.

Formally, a spiking neural P System (SN P system, for short) of degree \(m\ge 1\), as defined in33 in the computing version (i.e., able to take an input and provide an output) is a construct of the form

$$\begin{aligned} {\Pi }=(O,\sigma _1,\sigma _2,\cdots ,\sigma , syn, in, out) \end{aligned}$$

where:

  1. 1.

    \(O = \{a\}\) is the singleton alphabet (a is called a spike);

  2. 2.

    \(\sigma _1,\sigma _2,\dots ,\sigma\) are neurons, of the form \(\sigma _i = (n_i, R_i), 1 \le i \le m\); where

    1. (a)

      \(n_i \ge\) 0 is the initial number of spikes contained in \(\sigma _i\);

    2. (b)

      \(R_i\) is a finite set of rules of the following two forms:

      1. i.

        firing (also spiking) rules \(E/a^c\rightarrow a; d\), where E is a regular expression over a, and \(c\ge 1, d\ge 0\) are integer numbers; if \(E = a^c\), then it is usually written in the simplified form: \(a^c\rightarrow a; d;\) similarly, if \(d = 0\) then it can be omitted when writing the rule;

      2. ii.

        forgetting rules \(a^s \rightarrow \lambda ,\) for \(s \ge 1\), with the restriction that for each rule \(E/a^c\rightarrow a; d\) of type (1) from \(R_i\), we have \(a^s \notin L(E)\) (the regular language defined by E);

  3. 3.

    \(syn\subseteq \{1,2,\dots ,m\}\times \{1,2,\dots ,m\},\) with \((i,i) \notin syn\) for \(1\le i \le m,\) is the directed graph of synapses between neurons;

  4. 4.

    \(in,out \in \{1,2,\dots ,m\}\) indicate the input and the output neurons of \(\mathtt {\Pi }\), respectively.

A firing rule \(E/a^c\rightarrow a; d \in R_i\) can be applied at neuron \(\sigma _i\) if it contains \(k\ge c\) spikes, and \(a^k \in L(E)\). The execution of this rule removes c spikes from \(\sigma _i\) (thus leaving \(k {-} c\) spikes), and prepares one spike to be delivered to all the neurons \(\sigma _j\) such that \((i,j) \in syn\). If \(d = 0\) then the spike is immediately emitted, otherwise, it is emitted after d computation steps of the system. As stated above, during these d computation steps the neuron is closed and it cannot receive new spikes (if a neuron has a synapse to a closed neuron and tries to send a spike along it, then that particular spike is lost), and cannot fire (and even select) rules.

A forgetting rule \(a^s \rightarrow \lambda ,\) can be applied in neuron \(\sigma _i\) if it contains exactly s spikes; the execution of this rule simply removes all the s spikes from \(\sigma _i\).

For more information on SN P systems, the reader is referred to20,34,35,36,37,38.

Basic type of neurons HP/LP

We have the basic information on SN P systems from the previous sections. Since there is no restriction on the expression E, the combination of different rules in a neuron is infinite, which would complicate the fabrication of neuron circuit design.

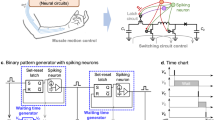
A general SN P neuron may contain several rules36,39. In this paper, two basic types of SN P neurons, introduced and elaborated in15,16, are used, shown in Figure 1: High-Pass (HP) neuron and Low-Pass (LP) neuron, defined with complementary spiking rules (so-called firing rules). They can receive an unlimited number of inputs and produce only one output.

The threshold in their firing rules is set to be 2. This means that HP neurons fire when receiving two or more input spikes, while LP neurons fire when there is only one input spike. In this case, because of the specific type of neurons, we prefer to use an explicit (threshold-like) syntax instead of the usual and more general regular expression36.

For simplicity, the HP and LP neurons are represented by their shapes shown in Figure 1.

Fig. 1
figure 1

HP and LP are the basic neurons. HP neuron will fire a spike out if it receives more than two spikes and otherwise will forget input spikes. LP neuron works oppositely.

Full size image

During the implementation of an SN P system, the role of these simple neurons is similar to those of a NAND gate in Boolean logic. They may not provide the most compact design, but they are sufficient to be the basis for more generic implementations. HP and LP neurons could be used to build more complicated neurons in the following manner. A neuron with several rules can operate in two consecutive steps: counting the input spikes received and then deciding which rule to apply. (We will call these two stages as the counting and decision steps.) To implement a more complex neuron using HP and LP neurons, we can start by considering these two steps separately.

Methods

One major difference between standard CMOS logic and neural systems is the property that CMOS logic processes stable signal values of 0 and 1, while neural networks use transient spikes. These spikes might occasionally be delayed or lost. The implementation described by Xu et al. 15 is related to domino logic in digital systems40,41. Domino logic is typically implemented using dual-rail logic42.

A binary full-adder using the HP and LP primitives based on Xu et al. 15 has been implemented in16. Where an HP neuron with 2 inputs is an AND, an LP neuron with 2 inputs is an XOR, and an LP with one input is a delay. Then ({0,1}, XOR, AND) is a finite field. We adopted an approach in which we evaluate the signals in dual-rail logic in domino logic. In this way, we can easily detect spike losses, which were identified as the main error model in Xu et al.15.

The unary number representation in the previous work has two drawbacks: due to the specific implementation properties of the adder of Xu et al., it can only add numbers, such that one of the numbers is one; we envision applications in cryptology, and as such, the unary representation of a 2048-bit RSA key is impractical. Therefore, we chose a binary number representation.

Fig. 2
figure 2

Signal Representation. If the logic value of signal X is 1, then there is a spike on signal X and no spike on signal \(\overline{X}\); if the logic value of signal X is 0, then there is a spike on \(\overline{X}\), and no spike on X.

Full size image

Figure 2 shows the representation of logic values in SN P systems. We have a logic value X, which we represent using two signals X and \(\overline{X}\). If the logic value of signal X is 1, then there is a spike on signal X and no spike on signal \(\overline{X}\). On the other hand, if the logic value of signal X is 0, then there is a spike on \(\overline{X}\), and no spike on X.

Implementation of the Euclidean distance

Implementation concept

We perform the approximation with 4 bits. According to43, we have to represent the parameters a and b in 4 bits in Table 1.

Table 1 4-bit implementation concept
Full size table

With the simulation of all possible input values for x and y, we have determined that the worth relative error \(\varepsilon = 7.19\%\), which gives us 3.80 bits precision in the result. The input values that produce this worst possible error are x=0x1 and y=0x1.

Our task is to compute \(a\cdot x+b\cdot y\). x and y can be any deliberate value with \(x \ge y \ge 0\). a is 1111 in binary, while b is 0110 in binary. Both a and b are constants. The format of the inputs and parameters is shown in Figure 3.

Fig. 3
figure 3

Inputs and Parameters. Binary numbers are represented from the most significant bit (MSB) on the right to the least significant bit (LSB) on the left.

Full size image

Let’s consider our test case, x=0x1 and y=0x1: We want to compute the length of the vector

$$\begin{aligned} \left[ \begin{array}{c}x\\ y\end{array}\right] = w = \sqrt{x^2+y^2} \end{aligned}$$

Let’s check our worst-case test case: The exact result is

$$\begin{aligned} \left[ \begin{array}{c}x\\ y\end{array}\right] = \left[ \begin{array}{c}1\\ 1\end{array}\right] = \sqrt{2} \approx 1.4142\dots \end{aligned}$$

If we perform the approximation, we obtain:

$$\begin{aligned} a\cdot x+b\cdot y = \text{0xf }\cdot \text{0x1 } + \text{0x6 }\cdot \text{0x1 } = \text{0x15 } = 1.3125 \end{aligned}$$

Please note how we obtain the result. The resulting value 0x15 is a fixed point value with a binary point at bit position four. So, the real value is 0x1.5 or \(\frac{\text{0x15 }}{2^4}\). This is in decimal: \(1 + \frac{5}{16} = 1.3125\).

From this, we can calculate the error, i.e. the relative error \(\varepsilon\). It is:

$$\begin{aligned} \varepsilon = \left| \frac{1.3125-1.4142}{1.4142} \right| = 7.1922\% \end{aligned}$$

Our exhaustive simulation with all possible input values has shown that this is the worst-case error.

Block diagram

Figure 4 represents the new design. We call it MUST-Euclidean with 4-bits, in short musteucl4 as MUST stands for Mongolian University of Science and Technology. We can see the dual-rail logic, as each logic value X has a signal of X and \(\overline{X}\) in its implementation. For example, the input bits A and B are input as A, \(\overline{A}\) and B, \(\overline{B}\), respectively.

Fig. 4
figure 4

MUST-Euclidean: Netlist.

Full size image

The arrow under \(x_4\) needs to point in the other direction. The middle MUST-Adder (leftmost) has to be a subtractor.

Implementation strategy

The following paragraph describes the concept of the implementation of the calculation.

Multiplication by ‘a’. We have to multiply the input x by the constant parameter a. Since a multiplier is expensive44, we use a combination of shifts and additions instead. We shift x by 4 bits to the left. This is multiplication by 16. Then we subtract x. The result is multiplication by 15.

$$\begin{aligned} 15\cdot x = (16-1)\cdot x = 16\cdot x - x = (x\ll 4) - x \end{aligned}$$
(1)

How do we subtract using MUST-Adder? We use the identity that: \(-x = \overline{x} + 1\). We produce a negative x by inverting all bits and adding one. Inverting the bits is easy since we are working with dual-rail logic. We just switched all the bit lines with the inverse bit lines.

But adding one is a little tricky. We accomplish this by setting the initial carry bit to one. But due to the design of the MUST-Adder, the carry flag is an internal signal that cannot be controlled directly. As discussed for the MUST-Adder16, we input two zeros just before the actual addition, so the carry flag is certainly zero at the beginning of the addition.

For the subtraction, we have to input two ones at the beginning, so the carry flag is certainly one. But we cannot control the two inputs of the MUST-Subtractor ADDx independently. The second input, the inverted input of the number that is being subtracted, is the same input number x, just delayed by four cycles and inverted. We will have to plan the sequence of bits carefully to achieve the desired result.

The multiplication of the second input y with the parameter a is easier: a is 0x6. We shift y by two and y by one, adding these intermediate results; no subtraction is required.

$$\begin{aligned} \text{0x6 }\cdot y = (4+2) \cdot y = (y\ll 2) + (y\ll 1) \end{aligned}$$

The timing of the input signals is as follows:

  •  [cycle 1] input \(x_0\), \(y_0\) on the right hand side,

  •  [cycle 2] input \(x_1\), \(y_1\) on the right hand side,

  •  [cycle 3] input \(x_2\), \(y_2\) on the right hand side,

  •  [cycle 4] input \(x_3\), \(y_3\) on the right hand side,

  •  [cycle 5] input \(x_4\), \(y_4\) on the right hand side.

Then, we have \(x_0\) in \(x_0\) (right signal) and \(x_4\) in \(x_4\) (left signal). Now we have to calculate \(x_0 - x_4\). This calculation is being performed in ADDx. At the same time, we calculate \(y_2 + y_3\). This calculation is being performed in ADDy.

  •  [cycle 6] input \(x_5\), \(y_5\) on the right hand side.

Then, we have \(x_1\) in \(x_0\) (right signal) and \(x_5\) in \(x_4\) (left signal). Now we have to calculate \(x_1 - x_5\). This calculation is being performed in ADDx. At the same time, we calculate \(y_3 + y_4\). This calculation is being performed in ADDy. We have \(x_0 - x_4\) and \(y_2 + y_3\) from the previous cycle. In this cycle, we add these two, and we get the first bit of the result \(w_0 = x_0 - x_4 + y_2 + y_3\). This calculation is being performed in ADDz.

Timing and signal initialization

In the design, we have three MUST-Adders, named ADDx, ADDy, and ADDz. Please note that ADDx is actually doing a subtraction. They perform the following calculations: (see Table 2).

Table 2 Combined operation by MUST-Adders.
Full size table

For MUST-Adder to function properly, we have to feed ‘0’ before the actual number to add in order to reset the internal carry signal. Please see the MUST-Adder paper for details16.

The ‘y’ input is easy. We just feed in a number of ‘0’ at the beginning of the calculation. However, with ADDx, it is very tricky. Since we subtract, and do not add, we need to set the carry to ‘1’ in the beginning. In a stand alone MUST-Subtractor, i.e., a MUST-Adder performing subtraction, we would have to feed ‘1’ before the calculation, instead of ‘0’.

Additionally, to subtract, we need to logically invert the number that is negative. Since we have dual rail logic (see MUST-Adder16), this is very easy: we just switch the x and \(\overline{x}\) signals, and thus we have inverted the signal.

However, it is tricky to produce the ‘1’ in the carry flag at the beginning of the subtraction operation, since we do not control both inputs of ADDx independently. There is only one input signal x. x is fed into ADDx twice: once inverted, and a second time delayed by 4 cycles. So, we have to very carefully design a leading input sequence that produces the desired result. Additionally, to start up ADDz properly (i.e., clear its internal carry signal), ADDx and ADDy both have to produce a ‘0’ output before they give out the actual payload numbers. So, at the start of the calculation, ADDx has to produce a ‘1’ internal carry flag, and at the same time a ‘0’ sum output to ‘ADDz’. This critical time is marked with the double lines in Table 3.

Table 3 Timing of input signals. Time progresses from left to right.
Full size table

In Table 3, the upper half shows the computation of ‘ADDx’, while the lower half shows the computation of ‘ADDy’. In the lower half, we feed enough ‘0’s at the beginning of ‘y’. This is the easy part. In the upper half of Table 3, we have to feed four ‘0’s before ‘x’, such that the shifted ‘x’ is padded with zeros for the subtraction. However, this means we will get four initial ‘1’s at the second input of ‘ADDx’ because everything is time shifted and inverted.

In the clock cycle before the number ‘x’ starts, we have to produce a ‘0’ in the sum, and a ‘1’ in the carry. So, we set the x signal at the dotted line to ‘1’, which means that we will get a ‘0’ at the inverted input 4 cycles earlier. Then we have to make sure that the carry signal is ‘0’ one cycle earlier. However, since all the inputs at input ‘B’ are ‘1’, all the inputs at input ‘A’ have to be zero. And then, the carry from the previous cycle is being propagated to the next cycle. The only occasion to break this propagation is right to the four ‘1’s at ‘B’, when the ‘1’ at ’A’ turns into a ‘0’ at ‘B’. At this point, we add another ‘0’. This ‘0’, together with the ‘1’ four clock cycles later, produces the desired ‘0’ in the internal carry flag. In total, we have to prefix the input ‘x’ with ‘000010000’, and the input ‘y’ with ‘000000000’.

Simulations implemented in System-C have been presented in Figure 5 and test cases of x=0x0, y=0x0 in Figure 6, x=0x1, y=0x0 in Figure 7, and the test case of x=0x1, y=0x1 in Figure 8, respectively.

Fig. 5
figure 5

MUST-Euclidean. Simulation in System-C.

Full size image
Fig. 6
figure 6

MUST-Euclidean. Test Case: x=0x0, y=0x0.

Full size image
Fig. 7
figure 7

MUST-Euclidean. Test Case: x=0x1, y=0x0.

Full size image
Fig. 8
figure 8

MUST-Euclidean. Test Case: x=0x1, y=0x1.

Full size image

We have approximated \(\sqrt{x^2+y^2}\) by \(a\cdot x+b\cdot y\) or \(a\cdot y+b\cdot x\),43. such that the larger of the two numbers x, y is multiplied by a, and the smaller is multiplied by b. Before that, we took the absolute value of both numbers. Furthermore, a and b are constants with just a few bits, so we replaced the multiplication with shifts and additions.

This computation is implemented in the environment of SN P systems using HP / LP neurons16 based on the MUST-Adder. Simulation models in the System-C programming language are available on request.

Discussion and future work

The experiments presented in this paper only validate 4-bit inputs. As presented, this method already reduces the relative error from 41% to only 4% and demonstrates that only two Newton-Raphson iterations are required for 16-bit precision instead of four. This is also very useful in applications in embedded systems or resource-constrained environments.

To demonstrate practical utility in other application domains, the work should be extended to higher bit-widths (e.g., 8/16-bit) in the future. Additional tests with diverse input cases (e.g., random vectors, varying bit-widths) and comparisons with traditional methods (e.g., CORDIC) in terms of accuracy and efficiency remain to be conducted.

It is well-known how to use a binary adder for both addition and subtraction, by adjusting the inputs and the initial carry flag.

Even though the discussion of the fixed initialization sequence constitutes a rigorous mathematical proof of its properties, there might be errors in the mathematical argument performed by humans. It would be better to verify the mathematical proof by an automated system. This issue of performing formal verification using such an automated system, e.g., Coq, is to be investigated. This will ensure the accuracy in all scenarios, provided that there are no errors in the formal verification tool.

The mathematical background of the underlying algorithm, which shows that the relative error is bounded and does not increase significantly when inputs ‘xx’ or ‘yy’ approach zero, is worth exploring in more detail in the future. In the future study, performing both Lagrange remainder analysis, as well as Monte Carlo simulations to verify global stability to be considered.

The parallelism advantage of SN P systems is underexplored. The plan is to develop a parallel MUST-Adder in the future that has the potential to further improve computational efficiency.

The current paper presents the implementation of the Euclidean Distance in the context of HP/LP systems and biochips. The authors plan to explore about the methodology in other contexts, e.g., embedded systems. This will further demonstrate practical implications, e.g., latency/power metrics in embedded systems, and strengthen the case for real-world applicability.

Conclusion

We have introduced an algorithm that eliminates square root computation and improves the precision of an approximation from 41% to just 4%. As successive Newtonian iterations double the number of bits, this eliminates the need for two initial iterations. For example, a result with 16-bit precision can be obtained by just two iterations instead of four iterations. We implement the computation using HP/LP-neurons in P systems using System-C. Furthermore, a performance-optimized version of the approximation algorithm could be produced and also used in some applications such as automated driving assistance (ADA) systems and RSA (Rivest-Shamir-Adleman) cryptanalysis.