Introduction

CVD is a significant disease that mainly affects the blood and heart vessels. The death of mortal lives can be connected primarily to a deficiency of initial disease diagnostics, and a preventive CVD risk prediction will significantly alleviate the disorder1. Generally, medical data can be accessible through digital health records collected from patients. This can provide data to support healthcare experts, identify mistakes or acute conditions, and make the medical experts subsequently aware. Related to cardiac system disease, CVD can be affected by numerous causes such as high blood pressure, lack of exercise, diabetes, and smoking2. CVD is an alternative term for heart disease and is the most predominant cause of mortality globally. Doctors may have difficulty effectively and quickly identifying some cardiac illnesses. Consequently, there is a progressive need for cost-effective healthcare services to be delivered to everybody, everywhere, and at any time universally to assist and observe patients and evade exclusive hospital-based treatment3. PH is a novel discipline using global computation technology to deliver preventive and emergency healthcare services to patients4. It is a developing field with an extensive surplus of health sensors, transmission protocols, and smart context-aware applications. PH methods aim to recognize important patient vitals, assuring prevention care and constant monitoring solutions, thus increasing system efficiency or reliability5.

There is increasing evidence that the importance and benefits of PH have been value the effort and are above reason. The main advantages include its prevalent and helpful technology nature, remote monitoring, self-management of circumstances, medical service, higher quality health evaluation, and an essential decrease in healthcare costs6. Traditional methods are often the most important for incorrect analysis and take longer because of human errors7. Also, it is a costly and exhaustive calculation method for disease study and ensues time in the evaluation. To overwhelm the difficulties in classical invasive-based techniques for identifying heart disease, many researchers have tried to develop various noninvasive intelligent healthcare methods based on analytical machine learning (ML) methods8. AI is frequently used in prediction to solve these difficulties, among other deep learning (DL) and ML taking the lead. This method studies an enormous number of healthcare data to describe whether the patient has the illness and achieves more accurate prediction results than physical diagnosing9. Among the techniques often created in clinical decision support systems is a diagnosing method based on ML, which can predict a patient’s disease’s survival depending upon the risk factors10. ML approach has recognized a possible space and is frequently utilized in circulatory medicine.

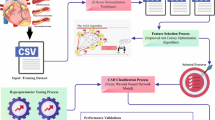
This manuscript presents a deep convolutional fuzzy neural networks with stork optimization on cardiovascular disease classification (DCFNN-SOCVDC) technique for PH services. The main goal of the DCFNN-SOCVDC method is to detect and classify CVD in the healthcare environment. At first, the presented DCFNN-SOCVDC model performs data preprocessing by utilizing Z-score normalization to preprocess the medical data. For the feature selection (FS) process, the presented DCFNN-SOCVDC technique utilizes an arithmetic optimization algorithm (AOA) model. Besides, the deep convolutional fuzzy neural network (DCFNN) method is employed to identify and classify CVD. Eventually, the presented DCFNN-SOCVDC approach employs a stork optimization algorithm (SOA) method for the hyperparameter tuning method involved in the DCFNN model. The performance of the DCFNN-SOCVDC approach is evaluated using a CVD dataset, and the results are assessed based on various metrics. The key contribution of the DCFNN-SOCVDC approach is listed below.

  • The DCFNN-SOCVDC model employs Z-score normalization to preprocess medical data, effectually standardizing all features to a standard scale. This step improves the accuracy of subsequent ML models by ensuring that each feature contributes equally during training. It also assists in mitigating the impact of outliers, resulting in more reliable predictions.

  • The DCFNN-SOCVDC technique employs the AOA method for FS, efficiently detecting the most relevant features from the medical dataset. AOA improves the model’s classification performance by choosing key features, mitigating complexity and improving prediction accuracy. This approach assists in focusing on the most influential data aspects for improved model outcomes.

  • The DCFNN-SOCVDC approach utilized the DCFNN method for precise identification and classification of CVD, integrating spatial processing with fuzzy logic to improve decision-making. This approach enhances the model’s capability to learn from complex, uncertain data. DCFNN effectively addresses the challenges of CVD diagnosis by incorporating convolutional and fuzzy logic capabilities.

  • The DCFNN-SOCVDC methodology implements the SOA model to fine-tune the hyperparameters of the DCFNN model, ensuring optimal performance and reducing the risk of overfitting. By improving parameter selection, SOA enhances the accuracy and robustness of the model. This technique allows the DCFNN model to attain enhanced generalization on unseen data, optimizing its predictive capabilities.

  • Integrating Z-score normalization, AOA-based FS, DCFNN for classification, and SOA for hyperparameter optimization creates a novel hybrid approach that improves CVD prediction accuracy. This method uniquely incorporates advanced ML techniques with optimization strategies to optimize each process step. DCFNN allows for robust classification, while AOA and SOA contribute to improved FS and model tuning, improving overall model performance.

The article is structured as follows: “Literature works” section presents the literature review, “Proposed methodology” section outlines the proposed method, “Experimental results and analysis” section details the results evaluation, and “Conclusion” section concludes the study.

Literature works

Baseer et al.11 propose a new coronary artery disease prediction method, which easily unites the Internet of Medical Things (IoMT) and AI in responding to the development of a universal cardiovascular problem. The method utilizes innovative methods, especially TabNet in combination with catBoost, to increase heart disease prediction precision and efficacy. The IoMT is a significant module because it allows continuous data collection from various healthcare devices. In CVDs, the method utilizes innovative techniques, especially TabNet in combination with catBoost, to increase heart disease prediction precision and efficacy. Husnain et al.12 propose an extensive accuracy health service intended for health prevention and promotion of chronic illnesses. It contains constant real-time lifestyle monitoring and environmental features incorporating wearing devices and internal air quality sensors. The AI-supported telehealth platform provides comprehensive visions into patients’ environmental, clinical, and lifestyle data, enabling consistent predictions of upcoming severe worsening actions. ML and DL methods advance extensible chronic disease-predicting methods that endured outside confirmation. Sheela and Krishnamurthy13 proposed a new Inception v3 with a VGG16 for predicting cardiovascular risk rates by noninvasive fundus and freely accessible images. This technique exploits innovative image analyzing methods containing noise reduction and contrast enhancement. The significant features of optic disc detection and blood vessel segmentation have been detached from the fundus images. In such cases, the Inception-v3 structure can be primarily used to capture the complicated hierarchical patterns. By incorporating these features with medical data, the method can be trained to forecast cardiovascular risk rates. Kaur et al.14 proposed to study the application of DL-based techniques to create an automatic method for hypertension recognition. A database containing demographic information, lifestyle factors, blood pressure measurements, and medical history has been used. Various DL methods were utilized to create a prediction method for detecting hypertension with stroke and heart-illness prediction. Preprocessing can be completed on the utilized dataset with several dissimilar characteristics for hypertension prediction, handling misplaced values, dealing with class imbalance, and normalizing features. Methods for FS were used to regulate which variables are most beneficial for hypertension prediction.

Rajkumar et al.15 present an improved DL-based structure for forecasting heart illness. The common freely accessible Hungarian heart illness dataset, which contains heart illness-associated data gathered from patients over IoT sensor devices, has been used for execution. The input dataset has been preprocessed utilizing a medium studentized outstanding technique for solving missing values and error data. The alteration in LSTM output can be enhanced by using an ISHO method. Zhang et al.16 propose physics-guided DL networks to effectively evaluate CVD in an IoT-based method. The author specially initiates an attending system to identify the effectual features by studying the significance of coronary artery dissection features and artery sections. Physical knowledge of blood movement should be incorporated into the loss function to attain the evaluation with explainability. Mandava17 introduced a hybrid DL smart system. Assessments and tests are performed utilizing the five benchmark datasets for cardiac illness. Three data processing methods are initially used in the preprocessing phase to enhance the dataset quality by averting undesirable falsifications: replacing missing values, solving data imbalance difficulties, and outlier removals. Afterwards, DL-based MDenseNet201 extracts the illness’s interrelated features. Least Absolute Shrinkage and Selection Operator (LASSO) and Relief methodologies have been utilized to choose the suitable features. Lastly, a DL-based IDRSNet can be used to predict CVD. Ramesh and Lakshmanna18 presented an Optimum Scrutiny Boosted Graph Convolutional LSTM (O-SBGC-LSTM), SBGC-LSTM improved by Eurygaster Optimizer Algorithm (EOA) for fine-tuning the hyperparameter for initial detection and inhibition of diabetes illness. This technique takes the discriminatory features in temporal and spatial dynamics and explores the co-occurrence relationships among temporal and spatial areas. This technique also proposes a temporal hierarchical structure to upsurge the topmost SBGC-LSTM layer temporal fields, increasing the capability to study higher-level semantic representations and substantially reducing the computational cost. Geetha et al.19 propose the HEART SAVIOUR model for real-time heart disease analysis using DL and Transformer methods. Patient data undergo preprocessing and encryption at the edge gateway before being sent to the cloud for analysis using the Dense Nested Four Way Transformer Network (DNFW-Net) model. Liao et al.20 explore the use of artificial neural networks (ANNs), integrated with genetic algorithms (GAs) and error-back propagation, to enhance predictive models, optimizing resources in smart electronic health systems through the analysis of large-scale patient data.

Verma et al.21 present a framework for predicting zoonotic virus infections using AI and IoT. It integrates IoT devices, fog-layer user authentication, and an ensemble model for user classification with cloud computing for data analysis. Malviya et al.22 aim to improve heart disease diagnosis by optimizing a convolutional neural network (CNN) with Galactic Swarm Optimisation (GSO) models for improved performance. Alturki et al.23 explore the IoMT, focusing on its role in healthcare for remote patient monitoring and disease detection. Alrowais et al.24 develop reliable stroke prediction models using adaptive neuro-fuzzy inference and CNNs, addressing class imbalance and improving accuracy through AI and fuzzy logic. Wei and Yi25 propose an ML-based approach integrating Naive Bayes (NB) classifier, Jellyfish Search Optimizer (JSO), and Flying Foxes Optimization (FFO) to predict the effects of yoga on Chronic Venous Insufficiency (CVI). Lu et al.26 present an effective method for the early detection of cardiorespiratory complications during pandemics using wearable ECG sensors and CNNs. Rajeshkumar et al.27 introduce the UTO-LAB framework using a blood pressure meter and RGB-D camera. Heart rate and blood pressure data are captured and processed to extract significant features for analyzing respiratory patterns. Advanced techniques like UMFCC and PCA extract relevant features, which are then analyzed using Aquila-optimized OMSVM to classify breathing activities. Yogeesh and William28 explore integrating fuzzy logic and DL in BDSS for improved CVD prediction, enhancing accuracy and diagnosis using sensor data. Mohanty et al.29 present an ML methodology for chronic kidney disease (CKD) risk prediction by integrating neutrosophic logic with classification algorithms. Neutrosophic logic handles uncertainty in medical data, improving accuracy and stability. Mani et al.30 integrate IoT with cloud and DL to enable accurate, proactive healthcare predictions by utilizing electronic medical records and IoT data, improving early intervention and preventive care. Sahni and Shukla31 discuss how precision medicine and AI can personalize healthcare. It emphasizes the requirement for collaboration and robust infrastructure for effectual implementation. Mansoor and Subramaniam32 propose a Healthcare Monitoring-based IoT (HM-IoT) framework by using IoT devices, securely encrypting data, and using an ANN model to classify data and alert healthcare professionals to abnormalities. Desai et al.33 discuss how ML models can assist in predicting diseases based on symptoms.

Despite the advancements in predictive models for CVD and chronic illnesses, various limitations remain. Many existing methods face difficulty handling class imbalances and uncertain data, affecting prediction accuracy. While AI, IoT, and ML methods have shown promise, challenges like data privacy, real-time processing, and integrating heterogeneous healthcare data (e.g., IoT, clinical, and lifestyle data) remain unresolved. Furthermore, most models lack scalability, are limited by available patient data, or fail to present explainability in predictions. There is also a requirement for more personalized models that account for individual patient variations and contextual factors. Further research is required to improve model generalization, improve computational efficiency, and address data accessibility issues in real-world applications.

Proposed methodology

This manuscript emphasizes the design and progress of the DCFNN-SOCVDC technique for PH services. The main goal of the DCFNN-SOCVDC method is to detect and classify CVD in the healthcare environment. It contains four processes: data normalization, AOA-based feature selection, classification, and parameter tuning. Figure 1 defines the workflow of the DCFNN-SOCVDC technique.

Fig. 1
figure 1

Workflow of DCFNN-SOCVDC technique.

Full size image

Data normalization: Z-score

At first, the presented DCFNN-SOCVDC model performs data preprocessing by using Z-score normalization to preprocess the medical data34. This model is chosen due to its capability to standardize data effectually by transforming it to have a mean of zero and a standard deviation of one. This confirms that all features contribute equally to the model, preventing any specific feature from disproportionately influencing the results. It is instrumental in medical datasets, where feature scales can vary significantly. Unlike other normalization techniques, such as min–max scaling, Z-score normalization is less sensitive to outliers, making it more robust for datasets with extreme values, which are usual in CVD prediction. Additionally, it improves the performance of ML models, particularly those based on distance metrics, ensuring more accurate and reliable predictions.

Z-score normalization is an essential preprocessing method in identifying chronic CVD for PH services. It regulates data by converting features to hold a standard deviation of one and a mean of zero, enabling superior contrast and model performance. This normalization model aids in managing various data scales and expanding the accuracy of predictive techniques. By moderating the effect of fluctuating feature scales, Z-score normalization improves the model’s capability to discover patterns indicative of cardiovascular states. Finally, it aids in more consistent and reliable classification outcomes in PH applications.

FS: AOA model

For the FS process, the presented DCFNN-SOCVDC technique employs the AOA model35. This model is selected for FS due to its efficiency in solving complex optimization problems by replicating arithmetic operations. AOA has effectively chosen the most relevant features by balancing exploration and exploitation during the search process. This is valuable in high-dimensional datasets, such as those in medical applications, where irrelevant or redundant features can affect the model’s performance. Unlike conventional methods like recursive feature elimination or correlation-based FS, AOA can handle continuous and discrete features and is less prone to overfitting. Its capability to find global optima ensures that the most influential features are chosen, ultimately improving classification accuracy. Additionally, AOA is computationally effectual and easy to implement, making it ideal for large-scale medical datasets. Figure 2 illustrates the structure of the AOA model.

Fig. 2
figure 2

Structure of the AOA model.

Full size image

AOA is a population‐based stochastic model based on a mathematical basis. The AOA typically comprises two searching stages related to exploitation and exploration, which are patterned after mathematical operations. The stage of exploration uses multiplication (×) and division (\(\div\)) operators, whereas the stage of exploitation employs addition (+) and subtraction (−) operators. The AOA initially produces searching agents at random. Everyone has a solution to a problem. The finest solution can be defined by computing every solution’s fitness function (FF).

The Math Accelerated Function (MAF) value is further applied to define whether AOA must perform exploitation or exploration processes. At the same time, the MAF is a tool utilized to guide decision-making in exploitation and exploration processes. Its importance lies in its ability to offer a quantitative degree that notifies the system of the more suitable strategies at an assumed time. Lastly, the value of MAF can be applied using the subsequent Eq. (1):

$$MAF\left( {Citr} \right) = {\text{min}} + Citr\left( {\frac{{{\text{max}} - {\text{min}}}}{{total_{ - } Itr}}} \right)$$
(1)

whereas \(total_{ - } Itr\) indicates the total iteration counts. The minimum–maximum values of the accelerating function are stated as Min and Max, respectively. As is perceived in the succeeding stage of AOA’s exploration, it mainly uses multiplication (×) and division (\(\div\)).

$$P_{i,j} \left( {Citr + 1} \right) = \left\{ {\begin{array}{*{20}l} {bst_{j} \div \left( {Opt + \varepsilon } \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right)} \hfill & {\quad r < 05} \hfill \\ {bst_{j} \times Opt \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right)} \hfill & {\quad otherwise} \hfill \\ \end{array} } \right.$$
(2)

Here, \(bst_{j}\) signifies reduction j of the best solution ever, r denotes randomly generated numbers between 0 and 1, the ___domain of search lower and upper limits is represented by \(UB_{j}\) and \(LB_{j}\), now ε represents a smaller integer value in the jth dimension, and μ denotes the controller function. Furthermore, the Optimizer (Opt) can be signified in

$$Opt\left( {Citr} \right) = 1 - \frac{{Citr^{{\frac{1}{\alpha }}} }}{{total_{ - } Itr^{{\frac{1}{\alpha }}} }}$$
(3)

The α parameter controls the performance of the stage of exploitation where the addition (+) and subtraction (−) are applied in the stage of exploitation using Eq. (4).

$$P_{i,j} \left( {Citr + 1} \right) = \left\{ {\begin{array}{*{20}l} {bst_{j} - \left( {Opt + \varepsilon } \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right)}&\quad { r < 05} \hfill \\ {bst_{j} + Opt \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right)} &\quad {otherwise} \hfill \\ \end{array} } \right. \left( 4 \right)$$
(4)

FS is a binary problem, whereas the solution lists ones and zeros, 0 for the extracted selected features, and 1 for the chosen features. Hence, a binary model must be applied for solving the FS problem. In AOA, the transfer function (TransFunc) is used to gain the binary solutions and later calculate the original solution. AOA was initially offered in constant problem space; then, a TransFunc was established for AOA named an S‐shaped TransFunc to address the binary problem space as exposed in Eq. (5).

$$TransFunc\left( {P_{ij} \left( {Citr} \right)} \right) = \frac{1}{{1 + \exp \left( { - P_{ij} \left( {Citr} \right)} \right)}}$$
(5)

Now, Citr signifies iteration counts presently being performed. \(\partial\) are applied to upgrade the solution in AOA for S‐shaped TransFunc to make the feature subsets.

$$P_{ij} \left( {Citr + 1} \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad r > TransFunc\left( {P_{ij} \left( {Citr} \right)} \right)} \hfill \\ {1,} \hfill & {\quad r \le TransFunc\left( {P_{ij} \left( {Citr} \right)} \right)} \hfill \\ \end{array} } \right.$$
(6)

The minimization of the selected feature counts and classification error rate are two opposite objectives in the multi‐objective optimizer problem. Every solution can be evaluated after the proposed FF, which depends on the classifier to define the classifier rate of error along with the feature counts of the solution, which are precisely selected for the solution. The new type of AOA and the upgraded AOA (AOA_NBH) models measure the solution qualities with the FF in

$$fitnessFun = \partial \times et + \left( {1 - \partial } \right) \times \frac{SelectedFeatures}{{TotalFeatures}}$$
(7)

Here, \(fitnessFun\) denotes FF to be minimalized, \(\partial\) representing a parameter among 0 and 1, which symbolizes the weight of the error rate and the feature counts elected in the function, and et stands for the error rate provided by the classifier. The complete AOA for FS is demonstrated in Algorithm 1.

Algorithm 1
figure a

AOA for FS pseudocode.

Full size image

Classification: DCFNN model

Besides, the DCFNN method is utilized to identify and classify CVD36. This method is chosen due to its ability to effectively integrate the advantages of DL and fuzzy logic. The convolutional layers enable the model to automatically extract hierarchical features from raw medical data. At the same time, the fuzzy logic component assists in interpreting uncertainty and handling imprecise data, often present in medical records. Unlike conventional ML methods, DCFNN can capture spatial patterns and non-linear relationships within complex datasets. Additionally, its capability to provide human-readable fuzzy rules makes the model more interpretable, which is significant in the medical field for decision-making. The DL aspect confirms high accuracy, while the fuzzy logic improves robustness, making DCFNN a powerful tool for CVD classification. Its adaptability to varying data types strengthens its suitability for complex medical applications. In DL, CNN is extensively applied in computer vision tasks, image classification, speech recognition, etc. Using the human brain-inspired structure, CNN is comprised of layers, such as pooling, batch normalization (BN), convolutional, loss layer, and fully connected (FC) layers. The FS and extraction are very reliant on the layered framework. Figure 3 specifies the architecture of the DCFNN model.

Fig. 3
figure 3

Structure of the DCFNN model.

Full size image

Backward and forward propagation

The Forward run is also named the advance run, which an input can approximate to the output layer. Assume Xk exists as the kth layer input for CNN and wk as a parameter set for every layer. The output and input are equal to loss error function estimation. The backward propagation (BP) transfers the output to an input layer. It utilizes a learning model such as stochastically gradient descent Eq. (8) for adjusting the training parameters of CNN.

$$\left( {w^{k} } \right)^{i + 1} = \left( {w^{k} } \right)^{j} - \eta \frac{\partial z}{{\partial \left( {w^{k} } \right)^{{i^{\prime}}} }}$$
(8)

Here, η characterizes the learning speed of a model, and i for the ith training iteration, the learning rate η denotes hyper‐parameter type, the improper selection of which may offer sub-optimal results.

Convolution layer

Convolution layers are vital for principles of classification. These layers present the dot product of the dual matrices, while one comprises parameters over the kernel, whereas the other denotes the receptacle field’s limited part. It comprises numerous kernels, all of which are trainable and are adapted with every iteration. Let \(X^{k} \in\) \({\mathbb{R}}^{{M^{k} \times N^{k} \times D^{k} }}\) and \(F \in {\mathbb{R}}^{{m\times n\times d^{k} \times S}}\) remain input for the kth convolutional layer and rank four tensors for these layers with the span m × n. The result from the layer Eq. (9) represents third order tensor for \(Y^{k} \left( {orX^{k + 1} } \right) \in {\mathbb{R}}^{{M^{k} - m + 1\times N^{k} - n + 1\times S}}\)

$$y_{{i^{k} ,j^{k} ,s}} = \mathop \sum \limits_{i = 0}^{m} \mathop \sum \limits_{j = 0}^{n} \mathop \sum \limits_{l = 0}^{{d^{k} }} F_{{i,j,d^{k} ,s}} \times x_{{i^{k} i^{k} ,l}}^{k}$$
(9)

Equation (9) can be solved for every \(0 \le s \le S\) and for each position \(0 \le i^{k} \le M^{k} - m + 1\) and \(0 \le j^{k} \le\) \(N^{k} - n + 1.\)

Pooling layer

This layer aids in saving the computation of statistics. It declines the spatial dimensions of the output by gathering the close outputs’ summaries statistics while maintaining the significant identified patterns. Therefore, pooling can be performed on each slice separately. There are some pooling functions; among them, the max pooling is symbolized in Eq. (10). The function has been applied now as it yields maximal output from the neighbourhood.

$$y_{{i^{k} ,j^{k} ,d}} = \mathop {\max }\limits_{{0 \le {\text{i}} \le {\text{m}},0, \le {\text{j}} \le {\text{n}}}} x_{{i^{k} \times m + i,j^{k} \times n + j,d}}^{k}$$
(10)

where \(0 \le i^{k} \le M^{k} ,0 \le j^{k} \le N^{k} ,0 \le d \le D^{k} .\)

Let the input be characterized as \(X^{k} \in {\mathbb{R}}^{{M^{k} \times N^{k} \times D^{k} }}\) inside the \(m\times n\) spatial span for the kth layer. Previously, it can be determined that \(m\varepsilon M\) and \(n\varepsilon N\), then a single stride denotes the pooling span. The gained outcome is the rank three tensor \(Y^{k} \in {\mathbb{R}}^{{M^{k + 1} \times N^{k + 1} \times D^{k + 1} }}\), whereas \(M^{k + 1}\) is considered as in Eq. (11).

$$M^{k + 1} = \frac{{M^{k} }}{m},\;N^{k + 1} = \frac{{N^{k} }}{n},\;D^{k + 1} = D^{k} ,$$
(11)

FC layer

The FC layer works in combination with the first layer of CNN. This result of the fattening process represents input for the first FC layer. The outcomes of the final FC layer were subjected to classifier functions, namely sigmoid, tanh, and softmax. Depending on the function of loss, the real outcome (\(Yj\)) is offered to compare with the projected output (say \(\hat{y}j\)). The sigmoid activation function is used.

$$\hat{y}_{{\text{j}}} = \left( {\frac{{e^{{x_{j} }} }}{{1 + e^{{x_{j} }} }}} \right)x_{j} \in {\mathbb{R}}$$
(12)

Describing the over‐fitting problem and raising the learning process’s influence, they added a dropout layer that rearranges the node-specific parameter to 0. ReLU Eq. (13) and BN are added in the final method to steady the neural networks. BN can be obtained by recentring and rescaling the input to the layers at every iteration, \(0 \le i \le M^{k} ,\;0 \le j \le N^{k}\), and \(0 \le d \le D^{k}\), to recollect one of the necessary and significant features, which could help classification.

$$y_{i,j,k} = {\text{max}}\left( {0,l_{i,j,d} } \right)$$
(13)

Loss function layer

This layer describes the drawback of the deviance between the projected output and the real labelled data. If a loss function displays significant deviance and makes an error, zz, BP comes into action. Fuzzy NNs inform the NNs through the capacity to manage noise in data. This method of including a fuzzy layer is termed Fuzzification. These layers transform an input matrix to the fuzzy area, and the demonstration gained was complicated for the higher‐dimensional extraction of features. This diffusion method was termed defuzzification; it adds a defuzzy layer to the CNN method. When X denotes the input matrix, the fuzzy set \(\ddot{X}\) is formerly approximated in each Eqs. (14) and (15). These equations discover the possibility that the features lie in the fuzzy ___domain numbers \(MF_{i,j}\).

$$\ddot{X} = fuzzification\left( {x_{i,j} {|}cx_{i,j} } \right)$$
(14)

whereas

$$x_{ij} = possibility\left( {x_{i,j} {|}MF_{i,j} } \right) = {\text{max}}MF_{i,j} \delta \left( {x - x_{i,j} } \right)$$
(15)

Here, \(\delta \left( {x - x_{i,j} } \right)\) is the Kronecker delta function.

The crispy value \(v_{i}\) can be assessed from the defuzzification process in Eq. (16). FC takes the crispy value of output from the defuzzification method and performs as the last classifier in Eq. (17).

$$v_{i} = defuzz\left( {x_{i} } \right) = \frac{{\sum C_{y} x_{i} }}{{\sum x_{i} }}$$
(16)

Here, \(C_{y}\) denotes the middle of the defuzzifcation membership function.

$$y_{i} = W_{fc} v_{i}$$
(17)

Now, \(W_{fc}\) is the weight selected for an FC layer.

CNN decreases the higher dimension with no loss of information, whereas fuzzy logic assists in combining the data by removing the noise. This grouping aids in taking the significant features within the data and manages the higher difference of the present data owing to various loads, speeds, and additional aspects on the test rig by the data acquisition time.

Parameter optimizer: SOA technique

Finally, the presented DCFNN-SOCVDC approach employs SOA for the hyperparameter tuning process involved in the DCFNN model37. This model was chosen due to its effectiveness in optimizing complex objective functions and ability to handle high-dimensional search spaces. SOA is appropriate for non-linear optimization problems like hyperparameter tuning, where conventional gradient-based methods may face difficulty with local minima or sparse gradients. Unlike other optimization techniques, SOA is less prone to getting stuck in suboptimal solutions due to its exploration–exploitation balance. Its population-based approach allows it to explore the search space more effectually, improving the chances of finding the global optimum for model hyperparameters. Additionally, the ability of the SOA to adapt to the dynamic nature of the data confirms that the DCFNN method can attain optimal performance across diverse datasets. This makes SOA an ideal choice for fine-tuning the hyperparameters in the DCFNN framework, ensuring high classification accuracy and robustness. Figure 4 portrays the structure of the SOA model.

Fig. 4
figure 4

Steps involved in the SOA technique.

Full size image

The presented SOA method is a meta-heuristic algorithm initiated in population dynamics, with storks establishing its members of individuals. Every member of SOA represents specific values for decision variables, defined by its spatial position within the searching space. Therefore, each SOA member aids as a potential solution to the issue, and its features can be precisely signified in the mathematical form through a vector. The initial locating of storks within the searching space is attained using a randomly generated initialization method.

$$X = \left[ {\begin{array}{*{20}c} {X_{1} } \\ \vdots \\ {X_{i} } \\ \vdots \\ {X_{N} } \\ \end{array} } \right]_{N \times m} = \left[ {\begin{array}{*{20}c} {x_{1,1} } & \cdots & {x_{1,d} } & \cdots & {x_{1,m} } \\ \vdots & \ddots & \vdots & & \vdots \\ {x_{i,1} } & \cdots & {x_{i,d} } & \cdots & {x_{i,m} } \\ \vdots & & \vdots & \ddots & \vdots \\ {x_{N,1} } & \cdots & {x_{N,d} } & \cdots & {x_{N,m} } \\ \end{array} } \right]_{N \times m}$$
(18)
$$x_{i,d} = lb_{d} + r \cdot \left( {ub_{d} - lb} \right)$$
(19)

Here, X signifies the matrix demonstrating the population of SOA, \(X_{i}\) defines the ith stork, the element \(x_{i,d}\) in this matrix signifies the stork’s ___location in the dth dimension, the parameters N and m denote the number of storks, and the sum of decision variables, respectively. The variable r takes a generated value randomly within the range of \(\left[ {0,1} \right]\), while \(lb_{d}\) and \(ub_{d}\) denote the lower and upper limits of the dth decision variable. An evaluation is led to evaluate the problem’s objective function, which depends upon the developed decision variable values for every stork. The mathematical formulae are presented as follows:

$$F = \left[ {\begin{array}{*{20}c} {F_{1} } \\ \vdots \\ {F_{i} } \\ \vdots \\ {F_{N} } \\ \end{array} } \right]_{N \times 1} = \left[ {\begin{array}{*{20}c} {F\left( {X_{1} } \right)} \\ \vdots \\ {F\left( {X_{i} } \right)} \\ \vdots \\ {F\left( {X_{N} } \right)} \\ \end{array} } \right]_{N \times 1}$$
(20)

In the equation above, F signifies the vector compressing the assessed objective function, and \(F_{i}\) denotes the exact evaluation of the objective function, depending on the ith stork. Throughout every iteration of the SOA, the locations of the storks within the searching space are upgraded, consequently influencing the values of the objective function. This iterative procedure needs constantly upgrading the finest‐performing member by equating the newly attained values of the objective function in every iteration. Throughout this procedure, the technique certifies that the optimum solution is gradually superior.

The proposed SOA functions as an iterative procedure intended to upgrade the locations of population members over dual main stages such as exploration and exploitation. In the exploration phase, the algorithm pretends the migrant patterns of storks, supporting a wide search across the solution space to recognize various probable solutions. In contrast, the exploitation phase simulates the hunting tactics of storks, concentrating on enhancing and refining the present solutions to attain optimum outcomes. This dual‐phase approach permits SOA to efficiently balance exploring novel areas with exploiting recognized high‐quality regions, improving its global performance and sturdiness in discovering optimum solutions.

Phase 1: migration strategy (exploration)

One of the significant behaviours detected in storks is their yearly migration throughout the winter, where they navigate to more auspicious habitats. This migration strategy, simulated in the SOA, creates the basis of the algorithm’s first stage for upgrading population members in the search space. In the SOA structure, every member recognizes latent migration objectives depending upon the higher values of the objective function. This method permits SOA to influence the collective intellect of the population, raising effectual exploration of the solution space and improving the algorithm’s capability to find optimum solutions.

$$CD_{j} = \{ X_{k} :F_{k} < F_{j} \;and\;k \ne i\} ,\quad i = 1,2, \ldots ,N\;\;and\;\;k \in \left\{ {1,2, \ldots , N} \right\}$$
(21)

Here, \(CD_{i}\) denotes a set of candidate destinations of the ith stork, \(X_{k}\) refers to a stork with a superior objective function value than the ith stork, and \(F_{k}\) denotes an objective function value.

Within the structure of SOA, the technique imagines that each stork separately picks a destination of migration in a random mode before boarding its journey near the selected destination. Drawing inspiration from the complex movements of storks throughout the migration, the technique calculates a new ___location for every stork as it improves near its elected migration target, as definite by Eq. (22). Then, depending upon reaching the novel ___location, the method estimates the value of an objective function. Must this estimation develop an objective function’s value, the novel ___location efficiently replaces the preceding area of the separate stork, as defined in Eq. (23).

$$x_{i,d}^{P1} = x_{i,d} + \left( {1 - 2r} \right) \cdot \left( {SCD_{i,d} - I \cdot x_{i,d} } \right), \quad i = 1,2, \ldots ,N, \;and\;d = 1,2, \ldots ,m$$
(22)
$$X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P1} ,} \hfill & {\quad F_{i}^{P1} < F_{i} } \hfill \\ {X_{i} , } \hfill & {\quad else} \hfill \\ \end{array} } \right.$$
(23)

Here, \(X_{i}^{P1}\) denotes a novel recommended ___location of an ith stork, \(x_{i,d}^{P1}\) refers to dth dimension, \(F_{i}^{P1}\) denotes a value of objective function, r is a randomly generated number with a usual distribution in the interval of \(\left[ {0,1} \right],\) \(SCD_{i,d}\) specifies dth dimension of nominated candidate destination for migration of ith stork, I is a random value from set {1, 2}, N and m indicates storks and decision variables counts, respectively.

Phase 2: hunting strategy (exploitation)

One unique characteristic of storks is their hunting tactic, which is described as an accurate method to chase and capture victims. Storks use a combination of pursuit, surveillance, and stealth models to shoot and grab their prey. Leveraging the pretend dynamics of the stork’s predatory attack on the victim, the technique calculates a new ___location for the stork using Eq. (24). Then, depending upon assessing the value of the objective function related to the novel ___location, the algorithm establishes if a performance improvement was achieved. Development in the value of an objective function must be separated; then, the stork is repositioned to the novel ___location according to Eq. (25). This iterative procedure of upgrading stork locations depends upon pretend hunting tricks. It raises localized alteration and exploitation of the searching space.

$$x_{i,d}^{P2} = \left( {1 + \frac{1 - 2r}{{t + 1}}} \right) \cdot x_{i,d} , \quad i = 1,2, \ldots , N,\; d = 1,2, \ldots , m, \;and\;t = 1,2, \ldots , T$$
(24)
$$X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P2} ,} \hfill & {\quad F_{i}^{P2} < F_{i} } \hfill \\ {X_{i} , } \hfill & {\quad else} \hfill \\ \end{array} } \right.$$
(25)

Here, \(X_{i}^{P2}\) is the novel ___location of an ith stork, \(x_{i,d}^{P2}\) is a dth dimension, \(F_{i}^{P2}\) denotes a value of an objective function, t represents an iteration count, and T refers to the maximum number of iterations.

The SOA derives an FF to achieve heightened classification performance. It describes many factors that suggest improved efficiency of the candidate solution. In this paper, the reduction of the classifier rate of error was considered as FF, as set in Eq. (26).

$$\begin{aligned} fitness\left( {x_{i} } \right) & = ClassifierErrorRate\left( {x_{i} } \right) \\ & = \frac{no. \;of\;misclassified\;instances}{{Total\;no.\;of\;instances}} \times 100 \\ \end{aligned}$$
(26)

Experimental results and analysis

The DCFNN-SOCVDC technique’s performance is examined using a CVD dataset38. The dataset contains 60,000 instances under dual-class labels, as denoted in Table 1. The total number of features is 12, such as height, id, age, gender, ap_lo, weight, cholesterol, gluc, smoke, alco, ap_hi, active. Among these, only six features are selected: age, id, height, gender, cholesterol, and weight. The suggested technique is simulated using the Python 3.6.5 tool on PC i5-8600k, 250 GB SSD, GeForce 1050Ti 4 GB, 16 GB RAM, and 1 TB HDD. The parameter settings are provided: learning rate: 0.01, activation: ReLU, epoch count: 50, dropout: 0.5, and batch size: 5.

Table 1 Details of dataset.
Full size table

Figure 5 displays a set of confusion matrices produced by the DCFNN-SOCVDC technique on several epochs. The results state that the DCFNN-SOCVDC model efficiently detects and identifies all classes precisely.

Fig. 5
figure 5

Confusion matrices of DCFNN-SOCVDC method (a–f) Epochs 500–3000.

Full size image

Table 2 and Fig. 6 indicate the classifier outcomes of the DCFNN-SOCVDC technique under various epochs. The outcomes denote that the DCFNN-SOCVDC model appropriately identified and classified all the samples. On 500 epochs, the DCFNN-SOCVDC model offers an average \(accu_{y}\) of 99.05%, \(prec_{n}\) of 99.05%, \(reca_{l}\) of 99.05%, \(F1_{score}\) of 99.04%, and \(G_{Measure}\) of 99.05%. Likewise, on 1000 epochs, the DCFNN-SOCVDC model provides an average \(accu_{y}\) of 97.40%, \(prec_{n}\) of 97.40%, \(reca_{l}\) of 97.40%, \(F1_{score}\) of 97.40%, and \(G_{Measure}\) of 97.40%. Furthermore, on 2000 epochs, the DCFNN-SOCVDC methodology offers an average \(accu_{y}\) of 97.02%, \(prec_{n}\) of 97.02%, \(reca_{l}\) of 97.02%, \(F1_{score}\) of 97.02%, and \(G_{Measure}\) of 97.02%. Also, on 3000 epochs, the DCFNN-SOCVDC methodology provides an average \(accu_{y}\) of 98.04%, \(prec_{n}\) of 98.04%, \(reca_{l}\) of 98.04%, \(F1_{score}\) of 98.04%, and \(G_{Measure}\) of 98.04%.

Table 2 Classifier outcome of DCFNN-SOCVDC model under dissimilar epochs.
Full size table
Fig. 6
figure 6

Average outcome of DCFNN-SOCVDC model (a–f) Epochs 500–3000.

Full size image

Figure 7 indicates the training (TRA) and validation (VLA) accuracy outcomes of the DCFNN-SOCVDC methodology under various epochs. The accuracy values are computed for 0–3000 epochs. The figure emphasized that the TRA and VLA accuracy values are increasing, indicating the DCFNN-SOCVDC method’s capability to perform better over various iterations. In addition, the TRA and VLA accuracy rests closer over the epochs, which shows the lowest minimum overfitting and displays improved efficiency of the DCFNN-SOCVDC technique, guaranteeing consistent prediction on hidden samples.

Fig. 7
figure 7

\(Accu_{y}\) curve of DCFNN-SOCVDC model (a–f) Epochs 500–3000.

Full size image

Figure 8 demonstrates the TRA and VLA loss graph of the DCFNN-SOCVDC method under various epochs. The loss values are computed for 0–3000 epochs. It is denoted that the TRA and VLA accuracy values display a lower tendency, notifying the ability of the DCFNN-SOCVDC approach to balance a trade-off between generalization and data fitting. The continual decrease in loss values ensures the DCFNN-SOCVDC approach’s heightened performance and tunes the forecast outcomes over time.

Fig. 8
figure 8

Loss curve of DCFNN-SOCVDC technique (a–f) Epochs 500–3000.

Full size image

In Fig. 9, the precision–recall (PR) curve study of the DCFNN-SOCVDC model under different epochs interprets its performance by mapping Precision against Recall for the class. The outcome exhibits that the DCFNN-SOCVDC method continuously accomplishes enhanced PR values across various class labels, representing its capability to uphold an essential part of true positive predictions among each positive prediction (precision) while taking many actual positives (recall). The sturdy increase in PR results among every class depicts the efficiency of the DCFNN-SOCVDC methodology in the classification process.

Fig. 9
figure 9

PR curve of DCFNN-SOCVDC method (a–f) Epochs 500–3000.

Full size image

In Fig. 10, the ROC curve of the DCFNN-SOCVDC model is analyzed. The outcomes indicate that the DCFNN-SOCVDC technique obtains more excellent ROC results over each class under various epochs, representing the vital ability to discriminate the classes. This dependable tendency of enhanced ROC values over different classes shows the efficient performance of the DCFNN-SOCVDC approach in predicting classes, emphasizing the robust nature of the classification process.

Fig. 10
figure 10

ROC curve of DCFNN-SOCVDC technique (a-f) Epochs 500–3000.

Full size image

Table 3 and Fig. 11 demonstrate the comparative study of the DCFNN-SOCVDC technique with current approaches39,40,41,42. The simulation result indicated that the DCFNN-SOCVDC technique outperformed superior outcomes. Based on \(accu_{y}\), the DCFNN-SOCVDC technique has a higher \(accu_{y}\) of 99.05% while the SMO, SVM, RF, K-Nearest, EDLACNN, Bagging, and ACVD-HBOMDL models have lower \(accu_{y}\) of 84.16%, 96.72%, 94.25%, 80.65%, 94.10%, 97.47%, and 98.81%, correspondingly. Likewise, based on \(prec_{n}\), the DCFNN-SOCVDC methodology has greater \(prec_{n}\) of 99.05% while the SMO, SVM, RF, K-Nearest, EDLACNN, Bagging, and ACVD-HBOMDL methods have lowest \(prec_{n}\) of 81.95%, 97.22%, 96.39%, 94.28%, 89.30%, 94.20%, and 97.32%, respectively. Eventually, based on \(F1_{score}\), the DCFNN-SOCVDC model has a superior \(F1_{score}\) of 99.04% while the SMO, SVM, RF, K-Nearest, EDLACNN, Bagging, and ACVD-HBOMDL techniques have reduced the \(F1_{score}\) of 87.06%, 89.74%, 92.29%, 93.98%, 93.28%, 89.57%, and 97.70%, respectively.

Table 3 Comparative analysis of DCFNN-SOCVDC approach with existing methods39,40,41,42.
Full size table
Fig. 11
figure 11

Comparative analysis of DCFNN-SOCVDC technique with existing models.

Full size image

Table 4 and Fig. 12 compare the DCFNN-SOCVDC methods for execution time (ET). The outcomes suggest that the DCFNN-SOCVDC model gets improved results compared to other recent methods. Based on ET, the SMO, SVM, RF, K-Nearest, EDLACNN, Bagging, and ACVD-HBOMDL models have attained greater ET values of 5.87 s, 8.27 s, 7.98 s, 7.48 s, 7.34 s, 6.97 s, and 5.88 s, correspondingly, where the DCFNN-SOCVDC technique has gotten least ET of 2.13 s.

Table 4 ET outcome of DCFNN-SOCVDC technique with recent models.
Full size table
Fig. 12
figure 12

ET outcome of DCFNN-SOCVDC technique with recent models.

Full size image

Conclusion

This manuscript concentrates on designing and expanding the DCFNN-SOCVDC method for PH services. The main goal of the DCFNN-SOCVDC method is to detect and classify CVD in the healthcare environment. It contains four processes involving data normalization, AOA-based selection of features, classification process, and parameter tuning. At first, the presented DCFNN-SOCVDC technique applies data preprocessing using Z-score normalization to preprocess the medical data. For the FS process, the presented DCFNN-SOCVDC technique performs AOA can be exploited. Besides, the DCFNN method can be deployed to identify and classify CVD. Eventually, the presented DCFNN-SOCVDC approach employs SOA for the hyperparameter tuning method involved in the DCFNN model. The performance of the DCFNN-SOCVDC approach is evaluated using a CVD dataset, and the results are assessed based on various metrics. The performance validation of the DCFNN-SOCVDC approach portrayed a superior accuracy value of 99.05% over recent models.