A novel interval valued bipolar fuzzy hypersoft topological structures for multi-attribute decision making in the renewable energy sector

Exponential growth of innovation and changing technologies has profoundly impacted human life in various ways. As the human race moves forward, it is essential to strike a balance between embracing progress and addressing the challenges that arise, to create a future that benefits all of humanity. It’s essential to understand that the choice of a mathematical model depends on the nature of the problem at hand, the available data, and the specific requirements of the application. In some cases, a combination of classical and alternative approaches might be necessary to achieve the most robust and accurate results. Fuzzy set theory (\(\mathbb {FST}\)), introduced by Zadeh¹, allows for gradual membership degrees instead of strict membership in sets. It is particularly useful in dealing with vague or uncertain data, where elements can belong to sets to a certain degree rather than a crisp binary classification. The concept of vague set (\(\mathbb{V}\mathbb{S}\)) presented Gau and Buehrer² is a mathematical concept that extends the idea of classical sets by introducing the notion of ”vagueness” or ”imprecision” in the membership of elements. In a \(\mathbb{V}\mathbb{S}\), each element is associated with a grade of membership, represented as a continuous subinterval of the unit interval [0, 1].

Soft sets (\(\mathbb{S}\mathbb{S}\)) introduced by Molodtsov³ provide a valuable mathematical tool for dealing with complex and uncertain scenarios, where strict boundaries and crisp membership functions may not be appropriate. The parameterized nature of soft sets enables a more adaptable representation, making them useful in a wide range of real-world problems. However, it is essential to carefully define the parameters and their effects on the sets to ensure the meaningful interpretation and application of \(\mathbb{S}\mathbb{S}\) theory in practice. Maji et al.⁴ developed operations for \(\mathbb{S}\mathbb{S}\) and established a decision-making (\(\mathbb{D}\mathbb{M}\)) technique based on these operations. This \(\mathbb{D}\mathbb{M}\) technique likely involves using soft sets to represent uncertain or imprecise information in decision-making processes. Maji et al.⁵ merged \(\mathbb{F}\mathbb{S}\) and \(\mathbb{S}\mathbb{S}\), leading to the concept of fuzzy soft sets (\(\mathbb {FSS}\)). \(\mathbb {FSS}\) combine the notions of gradual membership from \(\mathbb{F}\mathbb{S}\) and parameterized family of sets from \(\mathbb{S}\mathbb{S}\), providing a more flexible approach to modeling uncertainty. Maji et al.⁶ further extended the concept of \(\mathbb {FSS}\) to intuitionistic fuzzy soft sets (\(\mathbb {IFSS}\)). \(\mathbb {IFSS}\) combines these ideas with \(\mathbb{S}\mathbb{S}\), adding an extra level of flexibility for representing complex and uncertain information.

Shabir and Naz⁷ independently introduced the concept of bipolar soft sets (\(\mathbb {BSS}\)) as a hybrid framework that combines bipolarity and \(\mathbb{S}\mathbb{S}\) theory. This extension aims to address situations where uncertainty is represented by both positive and negative aspects, allowing for a more comprehensive modeling of complex decision-making scenarios. Shabir has contributed to the investigation of various aspects of \(\mathbb {BSS}\), including notions, properties, operations, and their application in decision-making problems. Naz and Shabir⁸ has made further contributions by introducing the concept of fuzzy bipolar soft sets (\(\mathbb {FBSS}\)) and investigating their algebraic structures and applications. This extension likely combines the notions of \(\mathbb{F}\mathbb{S}\), bipolarity, and \(\mathbb{S}\mathbb{S}\). Abdullah et al..⁹ extends the ideas of \(\mathbb{F}\mathbb{S}\)s, bipolarity, and \(\mathbb{S}\mathbb{S}\)s to create a novel framework bipolar fuzzy soft set (\(\mathbb {BFSS}\)) that addresses uncertainty and conflicting information in decision-making problems. Karaaslan and Cagman¹⁰ introduced the concept of bipolar soft rough sets, which is likely an extension that combines the notions of bipolarity, \(\mathbb{S}\mathbb{S}\)s, and rough sets. This combination allows for handling uncertain and rough information in decision-making problems. Shabir and Gul¹¹ made modifications of rough bipolar soft sets, which might further enhance the representation and handling of uncertainty and bipolarity in rough set theory.

Karaaslan and Karatas¹² reintroduced a \(\mathbb {BSS}\) by using a bijective map between a set of parameters and its negative. This approach likely provides a novel way to represent bipolarity and uncertainty in decision-making scenarios. Karaaslan et el.¹³ contributed to the construction of bipolar soft groups and investigated some of their properties. Bipolar soft groups are likely an extension of the concept of bipolar soft sets, offering more advanced tools for handling uncertainty in group decision-making. Samarandache¹⁴ introduced the concept of hypersoft sets (\(\mathbb {HSS}\)) with the aim of extending the idea of SS to handle multiple subattributes. The key feature of \(\mathbb {HSS}\) is that it involve the Cartesian product with n attributes, allowing for a more comprehensive representation of uncertain information. Saeed et al..¹⁵ contributions to the development and presentation of the basics of \(\mathbb {HSS}\) have likely played a significant role in advancing the field and making it more accessible for researchers and practitioners alike. Saeed and Harl¹⁶ presented the idea of picture fuzzy hypersoft sets (\(\mathbb {PFHSS}\)) with its fundamental operations and application. Picture fuzzy hypersoft graph with application is a revolutionary concept developed by Saeed et al.¹⁷. The introduction of bipolar hypersoft sets (\(\mathbb {BHSS}\)) by Musa and Asaad¹⁸ represents a significant advancement in the field of soft computing, as it combines the concepts of bipolarity and \(\mathbb {HSS}\). This hybrid framework allows for the representation of uncertain information with both positive and negative aspects, making it well-suited for handling complex decision-making problems. The concept of an interval-valued fuzzy set (\(\mathbb {IVFS}\)) was introduced by Zadeh¹⁹. In \(\mathbb {IVFS}\), instead of a single crisp membership value, each element is associated with an interval representing the range of possible membership degrees. This interval can be expressed in terms of lower and upper bounds.

The introduction of Interval-Valued Bipolar Fuzzy Sets (\(\mathbb {IVBFS}\)s) by Zhang²⁰ has enriched the field of \(\mathbb {FST}\), providing researchers and practitioners with a powerful tool for handling diverse forms of uncertainty. \(\mathbb {IVBFS}\)s continues to be an active area of research and finds applications in various domains where dealing with contradictory or ambiguous information is essential. The fundamental characteristic of \(\mathbb {IVBFS}\)s is that the values of both the positive membership degree function and the negative membership degree function are represented as intervals rather than precise values. Wei et al.²¹ focuses on investigating Multiple Attribute Decision Making (MADM) problems with \(\mathbb {IVBFS}\)s. When dealing with uncertain and imprecise information, \(\mathbb {IVBFS}\)s can be a valuable tool for conducting MADM, as they allow for handling both bipolarity and uncertainty through interval representations. Chang²² introduced the concept of a fuzzy topological space, where basic topological concepts like continuity, compactness, open sets, and closed sets were extended to handle fuzzy membership degrees. Coker²³ introduced the idea of an intuitionistic fuzzy topological space, extending fuzzy topological spaces to handle both membership and non-membership degrees. Results on continuity, compactness, and connectedness in intuitionistic fuzzy topological spaces were further explored by²⁴ Coker and Haydar. Olgun et al.²⁵ proposed the concept of Pythagorean fuzzy topological space, which combines the concepts of fuzzy sets and Pythagorean fuzzy sets with topological spaces. Kiruthika and Thangavelu²⁶ discussed the relationship between topology and soft topology, which deals with uncertainty and vagueness using soft sets. Taskopru and Altinta²⁷ introduced the concept of elementary soft topology using elementary operations over a universal set with a set of parameters.

Tanay and Kandemir²⁸ defined the idea of fuzzy soft topology and introduced concepts such as fuzzy soft neighborhood, fuzzy soft basis, fuzzy soft interior, and fuzzy soft subspace topology. Osmanoglu and Tokat²⁹ proposed the subspace, compactness, connectedness, and separation axioms for intuitionistic fuzzy soft topological spaces, further exploring their properties. Riaz et al..³⁰ proposed the concept of Pythagorean fuzzy soft topology based on Pythagorean fuzzy soft sets, which combines the principles of Pythagorean fuzzy sets and soft sets to handle uncertainty and imprecision. Additionally, they demonstrated the application of Pythagorean fuzzy soft topology in medical diagnosis using the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) method. Ozturk³¹ defined the concept of ”bipolar soft topological spaces” and investigated their properties. This work likely involves extending the notions of soft sets and bipolarity to the realm of topological spaces, providing a framework to handle uncertainty and bipolar evaluations in the context of topology. Fadel et al..³² provided further exploration of bipolar soft topological spaces. They likely presented additional properties and results, expanding the understanding of the structure and characteristics of these spaces. Malik and Shabir³³ applied rough fuzzy bipolar soft sets in the context of decision-making problems. Rough fuzzy bipolar soft sets combine rough sets, fuzzy sets, and bipolarity, making them suitable for handling uncertainty, vagueness, and conflicting information in decision-making scenarios.

Musa and Asaad³⁴ defined hypersoft topology as a collection of hypersoft sets over the universe set. It represents a significant milestone in the field of hypersoft topological spaces, introducing and defining fundamental concepts related to this novel framework. Hypersoft topology is a natural extension of soft topology, allowing for a more flexible and expressive representation of uncertainty and vagueness in topological contexts. Musa et al..³⁵ represents a further extension and integration of concepts from soft computing and topology. The introduction of \(\mathbb {BHST}\) involves combining the notions of bipolarity, \(\mathbb {HSS}\), and topological spaces, providing a more versatile and comprehensive framework to represent uncertain and complex data.

Numerous instances of fuzzy set-based methodologies can be found in the literature, showcasing their applicability across diverse multi-attribute decision-making scenarios. Puska et al.. pioneered a green supplier selection model, employing fuzzy Multiple Criteria Decision Making (MCDM) methods, to analyze agricultural food companies³⁶. Similarly, Stevic et al.. utilized analogous MCDM techniques to assess safety parameters in different sections of constructed roads³⁷. Jana et al.. introduced linguistic Dombi operators based on interval-valued picture fuzzy soft sets, employing them for the optimal distribution of funds within an industry³⁸. In the realm of smart technology, Chakraborty et al.. developed similarity measures using intuitionistic fuzzy sets to address smartphone selection challenges³⁹. Ge et al.. used an fuzzy neural network under uncertain environment for the development of an adaptive inventory control system to track in real-time the target inventory while also showing how the system can be used using three experiments⁴⁰. Riaz et al.. contributed to the field by creating specialized fuzzy soft-max aggregation operators based on linear Diophantine sets. This innovation proved instrumental in developing an efficient algorithm for addressing green supply chain issues⁴¹. Another fuzzy linear diophantine hybrid titled Spherical Linear Diophantine Fuzzy Rough Aggregation Operators was developed by Qiyas et al..⁴² to access emergency systems using a specialized EDAS decision-making method. In a similar study by Abdullah et al..⁴³, Pythagorean Cubic fuzzy Hamacher aggregation operators were used for the analysis of green suppliers for green supplier selection.

When it comes to modelling uncertainty in decision-making scenarios, fundamental fuzzy and soft set structures fall short when it comes to capturing complex interdependencies and multidimensional uncertainty which are inherent in real-world problems. Currently, available frameworks like intuitionistic fuzzy set, picture fuzzy set, and bipolar fuzzy sets, these extensions are valuable, but these fall short in handling higher-order uncertainty, multiple attribute dependencies, and decision-making scenarios involving conflicting opinions. Now, to address these challenges, this article introduces Interval-Valued Bipolar Fuzzy Hypersoft Topological Structure which is formed by a combination of interval-valued representation, bipolarity, and hypersoft sets allowing for decision-making problems to be addressed up to a sub-attributive level while also having the ability to represent the bipolar behavior of the attribute allowing for flexible representation of uncertainty, particularly in scenarios where the expert opinions exhibit both positive and negative inclinations simultaneously. With that said, the article focuses on the following work:

• The principal aim of this paper is to introduce the concept of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) into the field of \(\mathbb {IVBFS}\) settings. \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) functions as an extension to the established topological concept known as \(\mathbb {BHST}\).

• In numerous practical MADM scenarios, \(\mathbb{D}\mathbb{M}\) often grapple with a dearth of complete and precise information. Instead of quantifying their assessments with crisp numerical values, \(\mathbb{D}\mathbb{M}\)s may find themselves limited to expressing their opinions or preferences as intervals within the [0, 1] range. This interval-based representation aptly captures the inherent uncertainty and imprecision in their evaluations. In such circumstances, the concept of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) assumes paramount importance. \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) extends the traditional \(\mathbb {BHST}\) framework to adeptly handle interval-valued membership degrees, encompassing both positive and negative aspects within a given set.

• Using the designed data structure, an algorithm has been crafted to facilitate access to the most optimal renewable energy technologies for sustainable clean energy production in the foreseeable future. This innovative system integrates expert knowledge-based data encompassing diverse factors such as financial considerations, environmental impact, technical complexity, and energy output. It processes this data using advanced operators developed for the purpose of computing the ideal alternative from a given set of options.

• A comprehensive mathematical structural comparative analysis is presented demonstrating the superior capabilities of the designed structure in expressing and managing human intuitionistic data for decision-making purposes, outperforming existing structures found in the literature.

The study is organized in the following manner: Some primary notions that might be relevant to the context of the discussion in Section 3. In Section 4, the concept of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) is introduced and its properties through illustrative examples are explored. \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) are proposed as a decision-making tool in Section 5. A comparison between \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) and other topological spaces is found in Section 6. The key findings are outlined in Section 7, and recommendations for additional research are included.

Let’s recall some basic terminologies regarding bipolar hypersoft topological spaces that will be helpful for introducing novel concept of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\).

Definition 1

³ Let \(\mathbb {O}\) be a universe of discourse, \(\mathbb {P}(\mathbb {O})\) the power set of \(\mathbb {O}\) and E a set of attributes. Then, the pair \((\mathbb {F}, E),\) where \(\mathbb {F}: E \longrightarrow \mathbb {P}(\mathbb {O})\) is called a \(\mathbb{S}\mathbb{S}\) over \(\mathbb {O}\).

Definition 2

¹⁴. Let \(\mathbb {O}\) be a universe of discourse, \(\mathbb {P}(\mathbb {O})\) the power set of \(\mathbb {O}\). Let \(E =\{ \textbf{f}_1, \textbf{f}_2, \textbf{f}_3, \textbf{f}_4 \ldots \textbf{f}_n\}\) be n disjoint parameters set whose corresponding attribute values are \(\textbf{G}_1, \textbf{G}_2, \textbf{G}_3, \textbf{G}_4 \ldots \textbf{G}_n\). Suppose \(\mathbb {G}= \textbf{G}_1 \times \textbf{G}_2 \times \textbf{G}_3 \times \ldots \times \textbf{G}_n\), with \(\textbf{G}_t \cap \textbf{G}_s = \phi\), \(t \ne s\), and t, s \(\in\) \(\{1, 2, \ldots , n\}\). The pair \((\mathbb {F}, \mathbb {G})\), where \(\mathbb {F}\): \(\mathbb {G}\) \(\rightarrow\) \(\mathbb {P}(\mathbb {O})\) is called a \(\mathbb {HSS}\) over \(\mathbb {O}\).

Definition 3

²¹. Let \(\mathbb {O}\) be a universe of discourse, a \(\mathbb {IVBFS}\) is defined as follows:

\(\mathbb {B}^{\textbf{f}} = \{\langle {\varvec{j}_{\varsigma }^{\kappa }}, {\varvec{K}_{\varsigma }^{\kappa }}({\varvec{j}_{\varsigma }^{\kappa }}), {\varvec{X}_{\varsigma }^{\kappa }}({\varvec{j}_{\varsigma }^{\kappa }}) \rangle |{\varvec{j}_{\varsigma }^{\kappa }} \in \mathbb {O} \}\) \(= \{\langle {\varvec{j}_{\varsigma }^{\kappa }}, [{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}({\varvec{j}_{\varsigma }^{\kappa }}), {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}({\varvec{j}_{\varsigma }^{\kappa }})], [{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{-}}({\varvec{j}_{\varsigma }^{\kappa }}), {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{-}}({\varvec{j}_{\varsigma }^{\kappa }})] \rangle | {\varvec{j}_{\varsigma }^{\kappa }} \in \mathbb {O} \}\) where degree of positive membership function \({\varvec{K}_{\varsigma }^{\kappa }}({\varvec{j}_{\varsigma }^{\kappa }})\ \subset \ [0, 1]\) and degree of negative membership function \({\varvec{X}_{\varsigma }^{\kappa }}({\varvec{j}_{\varsigma }^{\kappa }})\ \subset \ [-1, 0]\), and \(\textbf{b}^{\textbf{f}} = \{[{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}, {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}], [{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{-}}, {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{-}}]\}\) be an \(\mathbb {IVBF}\) number.

Some basic operations on \(\mathbb {IVBFS}\) are expressed as follows:

Definition 4

²¹. Let \(\textbf{b}^{\textbf{f}} _{1}\) and \(\textbf{b}^{\textbf{f}} _{2}\) be two IVBF numbers. Then:

• \(\textbf{b}^{\textbf{f}} _{1} \subseteq \textbf{b}^{\textbf{f}} _{2}\) iff \({\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_1 \le {\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_2\), \({\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_1 \le {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_2\), and \({\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1 \ge {\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\), \({\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1 \ge {\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\);

• \(\textbf{b}^{\textbf{f}} _{1} \cup \textbf{b}^{\textbf{f}} _{2}\) = \(([\ max \ \{{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_1, {\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_2\}\), \(\ max \{{\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_1, {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_2\}]\), \([ min\ \{{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1,{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\}\), \(min \ \{{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1, {\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\)}]);

• \(\textbf{b}^{\textbf{f}} _{1} \cap \textbf{b}^{\textbf{f}} _{2}\) = \(([\ min \ \{{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_1, {\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}_2\}\), \(\ min \{{\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_1, {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}_2\}]\), \([ max\ \{{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1,{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\}\), \(max \ \{{\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_1, {\varvec{X}_{\varsigma }^{\kappa }}^{{L}^{-}}_2\)}]);

• \(({\textbf{b}^{\textbf{f}}})^{'} = \{[1 - {\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{+}}, 1- {\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{+}}], [|{\varvec{K}_{\varsigma }^{\kappa }}^{{R}^{-}}| -1, |{\varvec{K}_{\varsigma }^{\kappa }}^{{L}^{-}}| -1]\}\)

Definition 5

¹⁸ Suppose \(\mathbb {O}\) is universal set and \(\mathbb {P}(\mathbb {O})\) be power set of \(\mathbb {O}\). Let \(E =\{ \textbf{f}_1, \textbf{f}_2, \textbf{f}_3, \textbf{f}_4........\textbf{f}_n\}\) be n disjoint parameters set whose corresponding attribute values are \(\textbf{G}_1, \textbf{G}_2, \textbf{G}_3, \textbf{G}_4........\textbf{G}_n\). Suppose \(\mathbb {G}= \textbf{G}_1 \times \textbf{G}_2 \times \textbf{G}_3 \times .......\times \textbf{G}_n\). The triple \(({\varvec{K}_{\varsigma }^{\kappa }}, {\varvec{X}_{\varsigma }^{\kappa }},\mathbb {G})\) is said to be \(\mathbb {BHSS}\) over \(\mathbb {O}\), where \({\varvec{K}_{\varsigma }^{\kappa }}\) and \({\varvec{X}_{\varsigma }^{\kappa }}\) are functions given by \({\varvec{K}_{\varsigma }^{\kappa }}: \mathbb {G} \rightarrow \mathbb {P}(\mathbb {O})\) and \({\varvec{X}_{\varsigma }^{\kappa }}: \mathbb {G} \rightarrow \mathbb {P}(\mathbb {O})\) such that \({\varvec{K}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) \cap {\varvec{X}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) = \phi\) for all \({{\varvec{q}_{\varsigma }^{\kappa }}_{s}} \in \mathbb {G}\). A \(\mathbb {BHSS}\) can be represented as following:

\(({\varvec{K}_{\varsigma }^{\kappa }}, {\varvec{X}_{\varsigma }^{\kappa }},\mathbb {G}) = \{({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}, {\varvec{K}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}), {\varvec{X}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}})): {{\varvec{q}_{\varsigma }^{\kappa }}_{s}} \in \mathbb {G} \wedge {\varvec{K}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) \cap {\varvec{X}_{\varsigma }^{\kappa }}({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) = \phi \}\).

Definition 6

¹⁸ Suppose \(({\varvec{K}_{\varsigma }^{\kappa }}_1,{\varvec{X}_{\varsigma }^{\kappa }}_1,\mathbb {G}_1)\) and \(({\varvec{K}_{\varsigma }^{\kappa }}_2, {\varvec{X}_{\varsigma }^{\kappa }}_2,\mathbb {G}_2)\) are two \(\mathbb {BHSS}\)s. \(({\varvec{K}_{\varsigma }^{\kappa }}_1, {\varvec{X}_{\varsigma }^{\kappa }}_1,\mathbb {G}_1)\) is subset of \(({\varvec{K}_{\varsigma }^{\kappa }}_2, {\varvec{X}_{\varsigma }^{\kappa }}_2,\mathbb {G}_2)\) if

1. (i)

   \(\mathbb {G}_1 \subseteq \mathbb {G}_2\)

2. (ii)

   \({\varvec{K}_{\varsigma }^{\kappa }}_1({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) \subseteq {\varvec{K}_{\varsigma }^{\kappa }}_2({{\varvec{q}_{\varsigma }^{\kappa }}_{s}})\) and \({\varvec{X}_{\varsigma }^{\kappa }}_2({{\varvec{q}_{\varsigma }^{\kappa }}_{s}}) \subseteq {\varvec{X}_{\varsigma }^{\kappa }}_1({{\varvec{q}_{\varsigma }^{\kappa }}_{s}})\) for all \({{\varvec{q}_{\varsigma }^{\kappa }}_{s}} \in \mathbb {G}_1, \mathbb {G}_2.\)

Definition 7

¹⁸ The union of two \(\mathbb {BHSS}\)s, \(({\varvec{K}_{\varsigma }^{\kappa }}_1, {\varvec{X}_{\varsigma }^{\kappa }}_1,\mathbb {G}_1)\) and \(({\varvec{K}_{\varsigma }^{\kappa }}_2, {\varvec{X}_{\varsigma }^{\kappa }}_2,\mathbb {G}_2)\) is \(({\varvec{K}_{\varsigma }^{\kappa }}_3, {\varvec{X}_{\varsigma }^{\kappa }}_3, \mathbb {G}_3)\), where \(\mathbb {G}_3 = \mathbb {G}_1 \cap \mathbb {G}_2\) and, for all \({{\varvec{q}_{\varsigma }^{\kappa }}_{s}} \in \mathbb {G}_3\),

Definition 8

¹⁸ The intersection of two \(\mathbb {BHSS}\)s \(({\varvec{K}_{\varsigma }^{\kappa }}_1, {\varvec{X}_{\varsigma }^{\kappa }}_1,\mathbb {G}_1)\) and \(({\varvec{K}_{\varsigma }^{\kappa }}_2, {\varvec{X}_{\varsigma }^{\kappa }}_2,\mathbb {G}_2)\) is a \(\mathbb {BHSS}\) \(({\varvec{K}_{\varsigma }^{\kappa }}_3, {\varvec{X}_{\varsigma }^{\kappa }}_3, \mathbb {G}_3)\), where \(\mathbb {G}_3 = \mathbb {G}_1 \cap \mathbb {G}_2\) and for all \({{\varvec{q}_{\varsigma }^{\kappa }}_{s}} \in \mathbb {G}_3\),

Definition 9

³⁵ If \(T_{BH }\) is a collection of \(\mathbb {BHSS}\) over \(\mathbb {O}\), then \(T_{BH }\) is a \(\mathbb {BHST}\) on \(\mathbb {O}\) if:

• \((\Phi , \Psi , \mathbb {G}\)), \((\Psi , \Phi , \mathbb {G})\) belong to \(T_{BH }\).

• The intersection of any two \(\mathbb {BHSS}\)s in \(T_{BH }\) belongs to \(T_{BH }\).

• The union of any number of \(\mathbb {BHSS}\)s in \(T_{BH }\) belongs to \(T_{BH }\). Then, (\(\mathbb {O}\), \(T_{BH }\), \(\mathbb {G}\), -\(\mathbb {G}\)) is called a bipolar hypersoft topological space over \(\mathbb {O}\).

Definition 10

⁴⁴ In the comparison table, columns and rows have the same amount of elements and are identified by members of the universal set. The number of decision variables for which the membership degree of \(m_i \ge m_j\) is present is represented by the symbol \(m _{ij}\), which is used to denote the entries.

In this section, the concept of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) is introduced and its relationship with other topological spaces are explored.

Definition 11

Let \(\mathbb {O}\) be a universal set, \((\mathbb {P}(\mathbb {O}))^{D[0,1]}\) be the collection of all degree of positive membership \(\mathbb {IVBF}\) subsets of \(\mathbb {O}\) and \((\mathbb {P}(\mathbb {O}))^{D[-1,0]}\) be the collection of all degree of negative membership \(\mathbb {IVBF}\) subsets of \(\mathbb {O}\). Let \(E =\{ \textbf{f}_1, \textbf{f}_2, \textbf{f}_3, \textbf{f}_4 \ldots \textbf{f}_n\}\) be n disjoint parameters set whose corresponding attribute values are \(\textbf{G}_1, \textbf{G}_2, \textbf{G}_3, \textbf{G}_4 \ldots \textbf{G}_n\). Suppose \(\mathbb {G}= \textbf{G}_1 \times \textbf{G}_2 \times \textbf{G}_3 \times \cdots \times \textbf{G}_n\). The triple \(({\varvec{K}_{\varsigma }^{\kappa }}_{t}, {\varvec{X}_{\varsigma }^{\kappa }}_{t}, \mathbb {G})\) is called a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\), where the functions are defined as \({\varvec{K}_{\varsigma }^{\kappa }}_{t}: \mathbb {G} \rightarrow (\mathbb {P}(\mathbb {O}))^{D[0,1]}\) and \({\varvec{X}_{\varsigma }^{\kappa }}_{t}: \mathbb {G} \rightarrow (\mathbb {P}(\mathbb {O}))^{D[-1,0]}\).

It can be defined as follows:

\(({\varvec{K}_{\varsigma }^{\kappa }}_{t}, {\varvec{X}_{\varsigma }^{\kappa }}_{t}, \mathbb {G}) = ({\varvec{K}_{\varsigma }^{\kappa }}_{t}, {\varvec{X}_{\varsigma }^{\kappa }}_{t})({\varvec{q}_{\varsigma }^{\kappa }}_{s}) = \{\langle {\varvec{j}_{\varsigma }^{\kappa }}_{i}, \ \ {\varvec{K}_{\varsigma }^{\kappa }}_{t}({\varvec{j}_{\varsigma }^{\kappa }}_{i}), \ \ {\varvec{X}_{\varsigma }^{\kappa }}_{t}({\varvec{j}_{\varsigma }^{\kappa }}_{i}) \rangle : \forall \ \ {\varvec{j}_{\varsigma }^{\kappa }}_{i} \in \mathbb {O},\ \wedge \ {\varvec{K}_{\varsigma }^{\kappa }}_{t}({\varvec{j}_{\varsigma }^{\kappa }}_{i})\ \ \cap \ \ {\varvec{X}_{\varsigma }^{\kappa }}_{t}({\varvec{j}_{\varsigma }^{\kappa }}_{i}) = \phi \},\) where \({\varvec{q}_{\varsigma }^{\kappa }}_{s} \ \in \ \mathbb {G}\) and \((t, s, i) \in \{1, 2, 3, \ldots , n\}\).

Definition 12

A \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) over \(\mathbb {O}\) is said to be a relative null \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) denoted by \((\Phi , \Psi , \mathbb {G})\) if for all \(q_i\) \(\in\) \(\mathbb {G}\), \(\Phi (q_i) = \phi\)

Definition 13

A \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) over \(\mathbb {O}\) is said to be a relative whole \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) denoted by \((\Psi , \Phi , \mathbb {G})\) if for all \(q_i\) \(\in\) \(\mathbb {G}\), \(\Psi (q_i) = \mathbb {O}\)

Definition 14

If \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) is a collection of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) over \(\mathbb {O}\), then \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) if:

• \((\Phi , \Psi , \mathbb {G})\), \((\Psi , \Phi , \mathbb {G})\) belong to \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\).

• The intersection of any two \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) in \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) belongs to \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\).

• The union of any number of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) in \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) belongs to \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\).

Then, \((\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\)is called a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) over \(\mathbb {O}\).

Example 1

Consider \(\mathscr {U} = \{{\varepsilon ^{a}_{b}}_1, {\varepsilon ^{a}_{b}}_2, {\varepsilon ^{a}_{b}}_3 \}\) be three construction companies.

Let \(E = \{ e_1, e_2\}\) stand skilled team and equipment whose corresponding attribute values are \(\{A_1, A_2\}\), respectively. let \(A_1 = \{ b_{11}\) = Credentials , \(b_{12}\) = Experience , \(b_{13}\) = Goodwill and Reputation ,\(b_{14} = \{b_{11}, b_{12}, b_{13}\} \}\)

\(A_2 = \{ b_{21}\) = New construction , \(b_{22}\) = Repair , \(b_{23}\) = demolition , \(b_{24} = \{b_{21}, b_{22}, b_{23}\} \}\)

\(\mathbb {G} = A_1 \times A_2\) (There are sixteen possibles outcomes, but only two are considered for the example.)

Then, it can be seen that \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) = \(\{(\Phi , \Psi , \mathbb {G}), (\Psi , \Phi , \mathbb {G}), (\Psi , \Re , \mathbb {G})^{1}, (\Psi , \Re , \mathbb {G})^{2}, (\Psi , \Re , \mathbb {G})^{3}, (\Psi , \Re , \mathbb {G})^{4}\}\) is an \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) on \(\mathbb {O}\).

Definition 15

The pair \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) = \(\{(\Phi , \Psi , \mathbb {G}), (\Psi , \Phi , \mathbb {G})\}\) is \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) on \(\mathbb {O}\) and it is called indiscrete \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) on \(\mathbb {O}\). It is denoted by [\(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{indscrt}\).

Definition 16

If \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) is a collection of all \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) over \(\mathbb {O}\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) on \(\mathbb {O}\) is called discrete \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\). It is denoted by \([\Gamma _{IVF }]^{dscrt}\).

Definition 17

Consider (\(\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}\) then the members of \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) are said to be \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) open sets in \(\mathbb {O}\).

Definition 18

Suppose that \((\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}\). A \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) is closed in \(\mathbb {O}\), if \((\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}})^{c}\) belongs to \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\).

Definition 19

Suppose that \((\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}\) then:

• \((\Phi , \Psi , \mathbb {G})\), \((\Psi , \Phi , \mathbb {G})\) are \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed set over \(\mathbb {O}\).

• The union of any two \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\)closed sets is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed set over \(\mathbb {O}\).

• The intersection of any number of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed sets is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed set over \(\mathbb {O}\).

Proposition 1

The intersection of two \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topologies \(\Gamma ^{\textbf{IVB}}_{\textbf{HS1}}\) and \(\Gamma ^{\textbf{IVB}}_{\textbf{HS2}}\) is also \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space.

Proof

• Suppose \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}} \cap \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) then \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}}\) this implies \(\cap _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}}\) also \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) and \(\cap _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) hence \(\cap _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}} \cap \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\)

• Let \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}} \cap \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) then \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}}\) this implies \(\cup _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}}\) also \((\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) and \(\cup _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\) hence \(\cup _{t =1}^{k} (\Psi , \Re , \mathbb {G})_{t}^{z} \in \Gamma ^{\textbf{IVB}1}_{\textbf{HS}} \cap \Gamma ^{\textbf{IVB}2}_{\textbf{HS}}\)

\(\square\)

Remark 1

The Union of two \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topologies \(\Gamma ^{\textbf{IVB}}_{\textbf{HS1}}\) and \(\Gamma ^{\textbf{IVB}}_{\textbf{HS2}}\) need not to be \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space.

Theorem 1

Consider a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space (\(\mathbb {O}\), \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\), \(\mathbb {G}, -\mathbb {G}\)) over \(\mathbb {O}_{\mathbb {G}}\), then

• \((\Phi , \Psi , \mathbb {G})\) and \((\Psi , \Phi , \mathbb {G})\) both are \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed.

• The arbitrary intersection of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed sets is \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed.

• The finite union of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed sets is \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed.

Proof

• Since \((\Phi , \Psi , \mathbb {G})^{c} = (\Psi , \Phi , \mathbb {G})\) and \((\Psi , \Phi , \mathbb {G})^{c} = (\Phi , \Psi , \mathbb {G})\) so both are \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed.

• \((\Psi , \Re , \mathbb {G})_{t}^{z}\) is closed \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) so \((((\Psi , \Re , \mathbb {G})_{t}^{z})^{c})^{c} \in \Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) Thus, we have \(\cup ((\Psi , \Re , \mathbb {G})_{t}^{z})^{c} \in \Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) therefore \(\cup (((\Psi , \Re , \mathbb {G})_{t}^{z})^{c}))^{c} = \cap (\Psi , \Re , \mathbb {G})_{t}^{z}\)

• For each \((\Psi , \Re , \mathbb {G})_{t}^{z}\) is closed \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) therefore \(((\Psi , \Re , \mathbb {G})_{t}^{z})^{c} \in \Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) this implies \(\cap ((\Psi , \Re , \mathbb {G})_{t}^{z})^{c} \in \Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) hence \(\cap (((\Psi , \Re , \mathbb {G})_{t}^{z})^{c}))^{c} = \cup (\Psi , \Re , \mathbb {G})_{t}^{z}\) is closed in \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\).

\(\square\)

Definition 20

Suppose that \((\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}_{\mathbb {G}}\) then closure of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) is denoted by \([\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{clr}\) and defined as the intersection of all \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closed supersets of \(\mathbb {O}\). It is seen that closure of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) is the smallest subset of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) collection.

Example 2

It is clear from Example 1\([\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{c} = \{(\Phi , \Psi , \mathbb {G})^{c}, (\Psi , \Phi , \mathbb {G})^{c}, ((\Psi , \Re , \mathbb {G})^{1})^{c}, (((\Psi , \Re , \mathbb {G})^{2})^{c}, ((\Psi , \Re , \mathbb {G})^{3})^{c}, ((\Psi , \Re , \mathbb {G})^{4})^{c}\}\)

Let \(\widetilde{(\Psi , \Re , \mathbb {G})}\) be \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\), then:

\(\widetilde{(\Psi , \Re , \mathbb {G})} = \left\{ \begin{array}{l}\ (\Psi _3, \Re _3)(q_1)=\{ ([0.5, 0.7] / {\varepsilon ^{a}_{b}}_1, [0.7, 0.8]/ {\varepsilon ^{a}_{b}}_2, [0.5, 0.6]/ {\varepsilon ^{a}_{b}}_3, [0.2, 0.5]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.4, -0.3] / {\varepsilon ^{a}_{b}}_1, [-0.8, -0.7] / {\varepsilon ^{a}_{b}}_2, [-0.6, -0.5]/ {\varepsilon ^{a}_{b}}_3, [-0.7, -0.6]/ {\varepsilon ^{a}_{b}}_4)\},\\ (\Psi _3, \Re _3)(q_2)=\{([0.4, 0.5]/ {\varepsilon ^{a}_{b}}_1, [0.1, 0.4]/ {\varepsilon ^{a}_{b}}_2, [0.2, 0.5]/ {\varepsilon ^{a}_{b}}_3 , [0.4, 0.6]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.6, -0.5] / {\varepsilon ^{a}_{b}}_1, [-0.7, -0.6]/ {\varepsilon ^{a}_{b}}_2, [-0.7, -0.5]/ {\varepsilon ^{a}_{b}}_3, [-0.3, -0.2]/{\varepsilon ^{a}_{b}}_4)\}, \end{array}\right\}\)

Then \({\widetilde{(\Psi , \Re , \mathbb {G})}}^{clr}\) = \(((\Psi , \Re , \mathbb {G})^{4})^{c}\).

Definition 21

Suppose that (\(\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, -\mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}\) then interior of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) is denoted by \([\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{intr}\) and defined as the union of all \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) open subsets of \(\mathbb {O}\).

Example 3

It is clear from example 1 that:

Let \(\widehat{(\Psi , \Re , \mathbb {G})} = \left\{ \begin{array}{l}\ (\Psi _3, \Re _3)(q_1)=\{ ([0.5, 0.8] / {\varepsilon ^{a}_{b}}_1, [0.2, 0.35]/ {\varepsilon ^{a}_{b}}_2, [0.3, 0.55]/ {\varepsilon ^{a}_{b}}_3, [0.2, 0.5]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.9, -0.3] / {\varepsilon ^{a}_{b}}_1, [-0.7, -0.2] / {\varepsilon ^{a}_{b}}_2, [-0.6, -0.5]/ {\varepsilon ^{a}_{b}}_3, [-0.8, -0.3]/ {\varepsilon ^{a}_{b}}_4)\},\\ (\Psi _3, \Re _3)(q_2)=\{([0.1, 0.5]/ {\varepsilon ^{a}_{b}}_1, [0.3, 0.45]/ {\varepsilon ^{a}_{b}}_2, [0.2, 0.8]/ {\varepsilon ^{a}_{b}}_3 , [0.1, 1.0]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.4, -0.3] / {\varepsilon ^{a}_{b}}_1, [-0.9, -0.6]/ {\varepsilon ^{a}_{b}}_2, [-0.7, -0.5]/ {\varepsilon ^{a}_{b}}_3, [-0.6, -0.2]/{\varepsilon ^{a}_{b}}_4)\}, \end{array}\right\}\) \({\widehat{(\Psi , \Re , \mathbb {G})}}^{intr}\) = \((\Psi , \Re , \mathbb {G})^{1}\).

Definition 22

Suppose that (\(\mathbb {O}, \Gamma ^{\textbf{IVB}}_{\textbf{HS}}, \mathbb {G}, - \mathbb {G})\) is a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) topological space over \(\mathbb {O}\) then exterior of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) is denoted by \([\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{ext}\) and defined as \([\Gamma ^{\textbf{IVB}}_{\textbf{HS}}]^{ext}\) = \((\Gamma ^{c}_{IVF })^{intr}\).

Example 4

Using Examples 1 and 3, let:

\(\overbrace{(\Psi , \Re , \mathbb {G})}= \left\{ \begin{array}{l}\ (\Psi _3, \Re _3)(q_1)=\{ ([0.2, 0.8] / {\varepsilon ^{a}_{b}}_1, [0.1, 0.25]/ {\varepsilon ^{a}_{b}}_2, [0.3, 0.35]/ {\varepsilon ^{a}_{b}}_3, [0.2, 0.3]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.7, -0.3] / {\varepsilon ^{a}_{b}}_1, [-0.9, -0.5] / {\varepsilon ^{a}_{b}}_2, [-0.8, -0.5]/ {\varepsilon ^{a}_{b}}_3, [-0.9, -0.5]/ {\varepsilon ^{a}_{b}}_4)\},\\ (\Psi _3, \Re _3)(q_2)=\{([0.4, 0.9]/ {\varepsilon ^{a}_{b}}_1, [0, 0.35]/ {\varepsilon ^{a}_{b}}_2, [0.2, 0.5]/ {\varepsilon ^{a}_{b}}_3 , [0.4, 0.6]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.4, -0.3] / {\varepsilon ^{a}_{b}}_1, [-0.7, -0.6]/ {\varepsilon ^{a}_{b}}_2, [-0.7, -0.4]/ {\varepsilon ^{a}_{b}}_3, [-0.7, -0.1]/{\varepsilon ^{a}_{b}}_4)\} \end{array} \right\}\)

Also,

\(\overbrace{(\Psi , \Re , \mathbb {G})^{c}}= \left\{ \begin{array}{l}\ (\Psi _3, \Re _3)(q_1)=\{ ([0.3, 0.7] / {\varepsilon ^{a}_{b}}_1, [0.1, 0.5] / {\varepsilon ^{a}_{b}}_2, [0.2, 0.5]/ {\varepsilon ^{a}_{b}}_3, [0.1, 0.5]/ {\varepsilon ^{a}_{b}}_4),\\ ([-0.8, -0.2] / {\varepsilon ^{a}_{b}}_1, [-0.9, -0.75]/ {\varepsilon ^{a}_{b}}_2, [-0.7, -0.65]/ {\varepsilon ^{a}_{b}}_3, [-0.8, -0.7]/ {\varepsilon ^{a}_{b}}_4)\},\\ (\Psi _3, \Re _3)(q_2)=\{([0.6, 0.7] / {\varepsilon ^{a}_{b}}_1, [0.3, 0.4]/ {\varepsilon ^{a}_{b}}_2, [0.3, 0.6]/ {\varepsilon ^{a}_{b}}_3, [0.3, 0.9]/{\varepsilon ^{a}_{b}}_4),\\ ([-0.6, -0.1]/ {\varepsilon ^{a}_{b}}_1, [-1, -0.65]/ {\varepsilon ^{a}_{b}}_2, [-0.8, -0.5]/ {\varepsilon ^{a}_{b}}_3 , [-0.6, -0.4]/ {\varepsilon ^{a}_{b}}_4)\}, \end{array}\right\}\) \({\overbrace{(\Psi , \Re , \mathbb {G})}}^{extr}\) = \((\Psi , \Re , \mathbb {G})^{1}\).

Selection of a particular technology for a particular region for installation is a complex process that involves the consideration of numerous factors and variables. Fuzzy logic-based systems have been increasingly used to support this process due to their ability to handle uncertainty and imprecision in environmental data. Fuzzy logic-based systems are particularly useful in situations where there is incomplete or uncertain information available, making them a valuable tool in designing effective environmental policy measures. This approach can help policymakers to make better-informed decisions and design more effective policies that consider a wide range of factors. One of the key advantages of fuzzy logic-based systems is their ability to handle complex data sets that are typical of environmental policy design. These systems can be used to analyze data from multiple sources and evaluate the potential impact of different policy options. This approach can help to identify the most effective policies for achieving environmental objectives, while also considering the potential trade-offs between different policy options. The use of fuzzy logic-based systems for environmental policy design is an area of active research and development. There are numerous studies in literature that demonstrate the effectiveness of these systems in environmental policy design.

The MAGDM is a process that allows a group to unanimously decide between a range of options. The decision cannot be further linked to a specific group member. Because the integral panel and related social factors are subsidised to the ultimate choice in the aforementioned procedure, this is the case. The panel’s results are more reliable and accurate than those of an individual. For decisions involving ambiguities and uncertainties, this method is helpful.

Flowchart of algorithm.

Full size image

The management of ambiguous data that might classify the positive and negative ways for a given problem has benefited from the application of the \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\)s. Because it is crucial to provide provisions for human decision-making, which contains various decision variables or requirements with membership values, the concepts of bipolarity, \(\mathbb {IVFS}\), and \(\mathbb {HSS}\) are combined in this article. The suggested \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\)s based technique’s numerical example is illustrated in Fig. 1.

One potential application for the designed structure is the performance analysis of renewable energy power generation facilities installed throughout a region. The decision-making process involved in selecting renewable energy technologies often involves multiple criteria, such as cost, efficiency, environmental impact, and social acceptance. Fuzzy multi-criteria decision making analysis can be used to evaluate the different renewable energy technologies based on their performance on each of these criteria. The fuzzy logic-based approach allows for the consideration of uncertain or imprecise data, which is often the case when evaluating the performance of renewable energy technologies. This approach also allows for the consideration of multiple criteria simultaneously, which is important when selecting renewable energy technologies that meet a variety of different objectives. Suppose that an environmental agency is planning to develop a renewable energy based power generating project at a certain ___location. As a number of options are available each having there pros and cons, they rely on the expertise of two selected experts that analyse the data and decide of the hypothetical performance they can achieve when a power plant is deployed and functional while considering multiple factors. The team of experts \(L_1\) and \(L_2\) first decide on a set of parameters for the decision making process that is to be processed by the devised algorithm. The set of parameters is given as: Let E= \(\{l_1\) = Financials, \(l_2\)= Power Output, \(l_3\) = Environmental Impact\(\}\) be the set of decision variables whose corresponding attribute values are \(\{A_1, A_2, A_3\}\) respectively. Let \(A_1 = \{ b_{11}\) = Running Cost, \(b_{12}\) = Initial Cost \(\}\), \(A_2 = \{ b_{21}\) = Power output per year , \(b_{22}\) = Deteriration in Performance per year\(\}\), and \(A_3 = \{ b_{31}\) = Change in AQI, \(b_{32}\) = Sound Pollution, \(b_{33}\) = Carbon Footprint per kWh of power produced \(\}\). There are twelve possible outcomes but for simplicity, only four outcomes have been used for the computational process. Now,

where the experts team choose subset \(E_1 = \{q_1, q_2\}\), and \(E_2 = \{q_1, q_2, q_4 \}\) of \(D\) respectively. Let \(\mathbb {O} = \{{\complement ^{k}_{l}}_1, {\complement ^{k}_{l}}_2, {\complement ^{k}_{l}}_3, {\complement ^{k}_{l}}_4\}\) be a set of the four alternatives out of which one has to be selected as the final vendor of the equipment. The structured approach to vendor selection incorporating both linguistic terms and numerical ranges, is a method commonly used in decision-making and evaluation processes, particularly in fields like environmental compliance and sustainability. This approach helps ensure that vendor selection is not only based on quantitative data but also takes into account qualitative factors that can play a significant role in achieving environmental goals.

The linguistic weight values allow for a qualitative representation of the relative significance of each parameter. This approach ensures that the evaluation process considers both quantitative data and the experts’ subjective judgments about the importance of different parameters in achieving positive grades for vendor selection. Table 1 shows the linguistic weights of parameters for positive grades, as determined by experts. The linguistic terms presented in Tables 1 and 2 are used for qualitative assessment of the criteria used in the example problem. These values are mapped to interval-values for computational processing and have the following significance:

• Positive Linguistic Weights are used to present the degree of agreement, satisfaction, and positive inclination of an expert towards a criterion.

• Negative Linguistic Weights capture the degree of disagreement and negative inclination of an expert allowing for bipolar behavior of the criterion to be addressed.

• As for the use of interval-valued fuzzy numbers, the expert opinions have some degree of uncertainty which can now be presented in the range of confidence rather than a single crisp value.

The linguistic weight values provide a qualitative representation of the experts’ judgment on the relative importance of each parameter for assigning negative grades in the vendor evaluation process. The linguistic weight of parameters for negative grades might be represented in Table 2.

For instance, if a company’s products fall short on the criterion of energy conservation, its products would be given a weight of [0.01, 0.02] \(\le q_i \le\) [0.02, 0.1]. Similarly, with negative weighting, if a company’s products have a very low level of the parameter energy saving, then it has weight \([-1.0, -0.9] \le q_i \le [-0.9, -0.7]\). The other levels can be justified using analogous justifications. Since the issue involves actual decision-making carried out by actual decision-makers.

As illustrated that \(\Gamma ^{\textbf{IVB}}_{\textbf{HS}}\) = \(\{(\Phi , \Psi , \mathbb {G}), (\Psi , \Phi , \mathbb {G}), (\Psi , \Re , \mathbb {G})^{1}_{E_1}, (\Psi , \Re , \mathbb {G})^{2}_{E_2}\}\) define a \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\). This demonstrates the harmony between the opinions of the decision-makers, which is necessary for a sound and accurate choice. Creating a table of positive membership degrees for \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) involve listing the intervals along with the corresponding membership degrees. The positive membership function informations is presented in Table 3.

A comparison table for positive membership degrees is shown in Table 4. For each parameter, compare the entity’s value to the membership functions’ intervals and assign a positive membership degree based on the linguistic terms. This involves applying the membership functions to convert numerical values to linguistic terms and degrees of positivity.

The aggregated score for each row \((\lambda )\) is calculated by summing up the numerical values of positive membership degrees for each row and the aggregated score for each column \((\chi )\) is calculated by summing up the numerical values of positive membership degrees for each column. The score of positive membership degrees is calculated by formula \(\lambda - \chi\) shown in Table 5.

The negative membership degrees of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) as evaluated by \({E_1}\) is shown in Table 6.

Comparison table of Negative membership degrees of \((\Psi , \Re , \mathbb {O})^{1}_{E_1}\) is shown in Table 7. Each row corresponds to an entity being evaluated, and each column represents a parameter or attribute.

The aggregated score for each row \((\lambda _1)\) is calculated by summing up the numerical values of positive membership degrees for each row and the aggregated score for each column \((\chi _1)\) is calculated by summing up the numerical values of positive membership degrees for each column. The score of positive membership degrees is calculated by formula \(\lambda _1 - \chi _1\) shown in Table 8.

Similarly for the the calculation of score value \((\Psi , \Re , \mathbb {G})^{2}_{E_2}\) procedures adopted are given in Tables 9, 10, 11, 12, 13, and 14.

The scores of positive membership degrees of all sets can be calculated by using the formula \(S_1 = (\lambda - \chi ) + (\lambda _1 - \chi _1)\). The result shown in Table 15.

The scores of negative membership degrees of all sets can be calculated by using the formula \(S_2 = (\lambda _2 - \chi _2) + (\lambda _3 - \chi _3)\). The result is shown in Table 16.

Now, the final score is obtained by formula \(S_1 - S_2\) and shown in Table 17 .

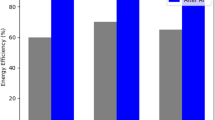
The selection of the optimal choice from Table 17 is determined by identifying the company with the highest score. In this case, \({\complement ^{k}_{l}}_2\) emerges as the superior option, having achieved the maximum score. Consequently, it is designated as the best alternative within the decision-making process. This approach adeptly applies the previously discussed concepts. By incorporating hypersoft topology and interval-valued bipolar fuzzy logic into the framework of fuzzy decision-making, as demonstrated in the example above, empowers decision-makers to make more enlightened and efficacious choices. The scores of the positive and negative membership degrees are presented in Fig. 2a,b, respectively, while the final rankings of the alternatives is presented in Fig. 2c.

Representation of scores computed using \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) algorithm.

Full size image

This approach’s clever fusion of the carefully considered ideas is what makes it truly unique. The astute integration of interval-valued bipolar fuzzy logic and hypersoft topology into the general framework of fuzzy decision-making, as flawlessly illustrated in the aforementioned illustration, not only improves the decision-making process but also equips decision-makers to set out on a path of more wise and effective decisions. This comprehensive integration improves evaluation accuracy while also facilitating a deep comprehension of the intricacies at play. As a result, decision-makers are better equipped to handle complexity with renewed assurance. Future directions for this work promise to yield even more paradigm-shifting revelations.There is a tempting opportunity to investigate the connections between these sophisticated approaches and cutting-edge technology, including machine learning and artificial intelligence, as the decision-making landscape continues to change. Exploring these unexplored areas may reveal new capacities for decision-making, where data-driven algorithms work in tandem with the subtlety of fuzzy logic to provide judgments that are not only well-informed but also flexible to changing circumstances. Similarly, some other future avenues that are opened by this study include programmed solutions of the designed \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) structure for advance decision making applications and the integration of machine learning, optimization techniques, and hybrid intelligent systems presents promising directions for further advancements. Also, the designed structure can be incorporated to design specialized decision-making algorithms (\(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) TOPSIS, \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) VIKOR, \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) MOORA etc.) for tailored scenario based decision making applications. In summary, the combination of these cutting-edge methodologies shows a paradigm change in approaches to making decisions. It fills the gap between theoretical ideas and real-world implementations, ushering in a time when decisions are no longer made haphazardly but rather are measured steps forward.

This section is primarily dedicated to conducting a comparative analysis, a crucial aspect for highlighting the superior qualities of the introduced structure. When examining \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\), its remarkable capability to comprehensively address each factor comes to the forefront, owing to the inherent attributes of \(\mathbb {HSS}\). In the context of \(\mathbb {IVBFS}\)s, the positive and negative membership degrees are represented as intervals, allowing for the inherent uncertainty and imprecision in decision-makers’ assessments. This interval-valued approach recognizes that \(\mathbb{D}\mathbb{M}\)s may not be able to provide exact crisp values but can express their preferences or opinions within a range. To provide a comprehensive overview of the comparative analysis, a detailed breakdown in Table 18 is provided. This table serves as a mathematical reference, offering a comprehensive examination of the presented structure’s strengths and capabilities in relation to the factors under consideration. To summarize the findinds in the table, fuzzy topology only has the ability to address aspects of the problem in the form of a membership function while soft topology allows for the decision-making problem’s parameterization. The hybrid of these 2 structures (Fuzzy Soft Topology) can address the parameterization issue while also allowing for the quantities to be presented in the form membership values between 0 and 1. The bipolar fuzzy topological hybrids allow for the quantities to be addressed using membership functions while also providing the ability to address the bipolar behavior of the available data. In the presented study, the hybridization of hypersoft topological spaces with bipolar fuzzy soft topology allows for the quantities to be parameterized and be divided into attributes and sub-attributes due to the hypersoft set aspect while also addressing the bipolarity in the data using interval-valued bipolar fuzzy set making it superior compared to the set-theoretic structures presented in Table 18.

In this study, a decision-support system based on novel \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) concept is presented that emerges on the foundational principals of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\). Also, the intricate relationships between the concepts of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) interior, \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) closure, and \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{S}}\) exterior are explored. The study underscores the necessity of expanding the repertoire of topological structures for practical applications. In addition to exploring the intricacies of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\), we emphasize the importance of incorporating additional topological concepts, such as compactness, connectedness, and separation axioms, to enrich the scope of the presented analytical framework. This expansion opens up new avenues for addressing complex real-world challenges. To demonstrate the structure’s application in the real world, we demonstrate the tangible impact of \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) through its application to a critical decision-making problem concerning the performance analysis of renewable energy systems. The presented system showcases its ability to effectively manage data predictability and navigate uncertainties, thus contributing significantly to the field of environmental policy development. As a part of this research, we present a comprehensive introduction to \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\), including an exploration of its fundamental operations. This knowledge serves as a valuable foundation for further investigations into \(\mathbb {BHST}\) and its application in diverse decision-making domains, marking a significant advancement in the realm of decision support systems. The future directions of the study include programmed solutions of the designed \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) structure for advance decision making applications and the integration of machine learning, optimization techniques, and hybrid intelligent systems presents promising directions for further advancements. Also, the designed structure can be incorporated to design specialized decision-making algorithms (\(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) TOPSIS, \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) VIKOR, \(\mathbb {BFH}^{\textbf{IV}}_{\textbf{ST}}\) MOORA etc.) for tailored scenario based decision making applications.