Introduction

When an aircraft engine operates, the high-speed intake airflow often draws foreign hard objects (sand, rivets, and stones et al.) into the engine, resulting in damage to the fan or compressor blades. This type of damage, caused by the impact of hard objects on the engine, is typically called foreign object damage (FOD)1,2,3,4,5. FOD can significantly reduce the fatigue limit of blades, leading to unforeseeable fatigue fractures and posing a serious risk to the flight safety6,7,8. Since the 1990s, numerous scholars have researched FOD with experimental simulation methods, numerical simulations and theoretical predictions for damaged blades. Mechanical processing methods are widely used in FOD research due to their simplicity, high repeatability, controllability and cost-effectiveness. Dunham et al.9 and Nicholas et al.10 investigated the impact of external material damage notches on fatigue limits during mechanical processing. Studies have revealed that the surface conditions of externally damaged areas created by high-speed impact methods are intricate and exhibit a significant variability in notch shape, size and surface properties. It is difficult to control and predict their influence on fatigue limits.

In contrast, notch machining method is straightforward, controllable and repeatable. Therefore, mechanical machining remains one of the pivotal prefabrication methods for addressing foreign object damage in engineering.

Numerous researchers have investigated the influence of Foreign Object Damage (FOD) on the fatigue limit of blades, providing extensive data for investigation of blade external damage and high-cycle fatigue tests6,11,12,13. It has been discerned that the fatigue limit is primarily governed by two factors14,15,16,17. The initial factor is the stress concentration induced by notches. H. Neuber18 introduced the average stress model to predict the notch fatigue strength and devised the Neuber formula for determining the notch fatigue coefficient. Peterson19 further refined the average stress model, proposing a simplified version of Peterson’s formula, which is widely adopted in engineering practices. Ruschau20 used the aforementioned empirical formula for fatigue notch coefficient to predict the high-cycle fatigue strength of damaged TC4 material specimens. It was found that the predicted results derived from the empirical formula were relatively high. Weibull21 developed the weakest cycle theory based on the statistical analysis. This theory posits that the underlying cause of component failure is the breakdown of specific geometric dimensions under the influence of internal material forces and external loads. Zhang H22,23 carried out laboratory simulated FOD tests by air gun. The effect of the initial stress state and impact position on FOD was investigated by numerical prediction. Additionally, FOD prediction models about impact velocity and impact energy were developed using the linear and power formulas, respectively. The predicted results could serve as the upper and lower bounds within the damage space to envelope the test results, providing a reference for fatigue life assessment of the aeroengine blades.

The second factor involves the influence of local stress/strain field within the notch. Taylor24 proposed the theory of critical distances (TCD) to predict notch fatigue limits. This theory assesses the average stress within a localized area of the cross-section at the notch root. Yamashita25 used the critical distance theory to predict the fatigue strength of micro-notched specimens. A good correlation exists between the critical distance stress and fatigue life of small-notched specimens if the critical distance is calibrated by the two notched fatigue failure curves of specimens with different notch root radii. Benedetti et al.26 used the line method of critical distance theory to predict the notch fatigue strength of shot-peened Al-7075-T651 material flat specimens. The TCD demonstrates relative accuracy when predicting the notch fatigue specimens under residual compressive stress fields. Hudak27 proposed a worst-case notch model to predict high-cycle fatigue in damaged components. This model posits that microcracks initiated at the damage root during the initial fatigue loading stage, enabling prediction of the high-cycle fatigue strength of damaged components based on the crack propagation boundary conditions. Nowell28 used a short crack arrest model which is akin to the worst-notch theory to predict the high-cycle fatigue strength of FOD notch specimens. The primary factor influencing the prediction accuracy is that the model neglected the influence of residual compressive stress at the damage root. Chaves et al.29 proposed a method based on the microstructure fracture mechanics model (Navarro, 198830) for predicting fatigue limits under remote loading via stress gradient and linear elastic analysis. The circular holes and V-shaped notches under I-type loads showed that the prediction errors are within 12%.

Based on the literature survey summarized above, it can be found that it’s a challenging but necessary work to build more accurate models for predicting the high cycle fatigue limit of foreign object damaged blades. In this paper, machining aerofoil specimens were manufactured to simulate the foreign object damaged blade, and the high cycle fatigue limit of machining foreign object damaged TC17 titanium aerofoil specimen were tested at 3 × 107 cycles, and a high cycle fatigue limit prediction model of machining foreign object damaged TC17 titanium aerofoil specimen was built based on the theory of critical distances, and compared with the Peterson model.

Experimental procedures

Material and specimen

The material used in the present work is TC17 titanium alloy, which is a typical α + β two phase titanium alloy with near β mutually. The nominal composition of the material is Ti-5Al-2Sn-2Zr-4Mo-4Cr. The material properties at room temperature are as follows: the density is 4680 kg/m3, the elastic modulus is 112.0GPa, the Poisson’s ratio is 0.301, the tensile strength is 1120 MPa and the bending fatigue strength of R = -1 is 440 MPa.

To simulate the characteristics of aero-engine compressor blades’ leading edge, the specimen is designed as an aerofoil specimen. The specimen dimension and specimen entity are shown in (Figs. 1, 2), respectively.

Fig. 1
figure 1

Specimen dimension (all dimensions are in millimeters).

Full size image
Fig. 2
figure 2

The manufactured specimen (a) front view (b) rear view (c) left view (d) vertical view.

Full size image

Machining of notches

To investigate the influence of machining notch size parameters on the fatigue performance, the specimens were mechanically machined. The shape and machining position of the notch are shown in (Figs. 3, 4), respectively. The normal line of the notch plane is perpendicular to the neutral surface of the leading edge of the specimen. The machining size of the notch is shown in (Table 1). The laser confocal scanning microscope (LEXT OLS5000) was used to measure the surface roughness of the machined notch.

Fig. 3
figure 3

The shape of notch.

Full size image
Fig. 4
figure 4

The position and type of notch (a) the notch position (b) notch type I (c) notch type II (d) notch type III.

Full size image
Table 1 The machining size of notch.
Full size table

To investigate the stress intensity factor of the notched blade, the first-order bending mode vibration was simulated with the complete blade and the notched blade. The model was meshed with tetrahedral grids by Altair Hypermesh 14.0. The mesh size of the whole structure is 0.3 mm, and the mesh size near the notch is 0.1 mm. The meshes of the complete specimen and the machined notch specimen are shown in (Fig. 5a,b), respectively. The constraints were imposed on both sides of the clamping end, limiting all degrees of freedom. The calculated results of stress distribution of the first-order bending mode are shown in (Fig. 6).

Fig. 5
figure 5

The mesh of aerofoil specimen (a) the complete specimen (b) the notched specimen.

Full size image
Fig. 6
figure 6

The mesh of aerofoil specimen (a) the complete specimen (b) the notched specimen of type I (c) the notched specimen of type II (d) the notched specimen of type III.

Full size image

The maximum stress around the notch (corresponding to the dangerous point) σmax of the notched specimen and the stress σ0 of the same position of complete specimen are extracted. The maximum displacement of the blade tip Smax (for notched specimen) and S0 (the same position for the complete specimen) are also extracted. Typically, the stress concentration factor Kt is calculated as the ratio of σmax and σ0, i.e. Kt = σmax/σ0. However, this equation derives from the prerequisite that the far-field displacement S0 (or stress σfar) of the complete specimen and the far-field displacement Smax (or stress σ’far) of the notched specimen are consistent. Otherwise, the influence of far-field stress or displacement inconsistency should be considered, and the Kt should be multiplied by the corresponding proportional coefficient S0/Smax or σfar/σ’far. This approach is typically used in the vibration fatigue experiment of notched blade31,32. Therefore, the stress concentration factor Kt of the notch is obtained by Eq. (1):

$$K_{{\text{t}}} = \frac{{\sigma_{\max } }}{{S_{\max } }} \times \frac{{S_{0} }}{{\sigma_{0} }}$$
(1)

The stress concentration factor Kt calculated by finite element method is shown in (Table 1).

High cycle fatigue tests

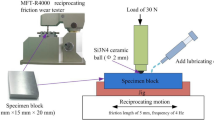
High cycle fatigue (HCF) tests of machined notched specimens were carried out on a vibration table with a dedicated fixture. The fixture is divided into three parts: the pressure block, the top block, and the base. The base is connected to the vibration table base via M12 bolts, while the pressure block is connected to the base using M14 bolts to clamp the holding section of the simulated blade. The fixture is made of 45# steel, which provides sufficient stiffness. Additionally, larger-sized bolts are used in the design to ensure adequate preload, preventing any changes in boundary conditions due to loosening during the test. The load of vibration table is feedback controlled by an accelerometer. The vibration status of specimen was real-time monitored through a strain gauge and the target strain amplitude was maintained by adjusting the load of vibration table. Figure 7 shows the clamping method of specimen and the position of strain gauge.

Fig. 7
figure 7

The HCF test (a) vibration test bench (b) the fixture (c) the strain gauge ___location (d) the strain gauge.

Full size image

Based on the stress calculation results in Part 2.2, the relationship between nominal stress and strain measurement positions of different notch depths was established. In the HCF test, the strain data was collected and saved in real-time using a strain gauge, and the nominal stress at the root of the notch is calculated. The fatigue limit of the specimen is determined at the time of fatigue failure33.

HCF tests were carried out by “step-loading method” (Maxwell and Nicholas34, 1999), and the fatigue limit at 3 × 10⁷ cycles was evaluated experimentally. In this method, if a given specimen survives at the initial stress level, the stress level should be increased by 10% of the initial value and then the test repeats. This process continued until the specimen failed in less than 3 × 107 cycles. The load spectrum for one of specimen in notch type I is shown in the Fig. 8 as an example. For specimens of different notch types, the initial stress level should be changed appropriately.

Fig. 8
figure 8

The load spectrum for HCF tests.

Full size image

Assume that the fatigue damage accumulates linearly in the last step of loading, the fatigue limit at 3 × 107 cycles can be calculated by the following equation33:

$$\sigma_{{\text{e}}} = \sigma_{{\text{p}}} + \frac{n}{{3 \times 10^{7} }} \times \left( {\sigma_{{\text{f}}} - \sigma_{{\text{p}}} } \right)$$
(2)

where σe is the fatigue strength of specimen at 3 × 107 cycles, σp is the stress level before fatigue failure occurs in specimen, σf is the stress level at which fatigue failure occurs in specimen, and n is the number of cycles when fatigue failure occurs. In the present work, 9 specimens of various dimensions were HCF tested, and the specimen number is shown in (Table 1). After the HCF tests, the scanning electron microscope (Zeiss Sigma 300) was used to characterize the fatigue fracture surface of the machined notch.

Experimental results

Surface roughness

Figure 9 showed the surface profile measurement results of three types of machined notches. The arithmetic mean deviation (Sa) of the contours of three machined notches with depths of 0.5, 1, and 1.5 mm are 23.908, 16.632, and 17.433 µm, respectively. The arithmetic mean deviations Sa of the contours of three machined notches with depth of 1 mm and width of 1.62 mm are 17.464um, 21.319um and 23.119um, respectively. The arithmetic mean deviations Sa of the contours of three machined notches with depth of 1.5 mm and width of 2.31 mm are 13.161um, 19.106um and 19.638um, respectively.

Fig. 9
figure 9

The surface roughness measurement results.

Full size image

Fatigue limit

In the high cycle fatigue test, the stress of notch root (the damaged position with maximum stress) is calculated according to the strain of the strain measurement point by the following equation33:

$$\sigma_{{{\text{B\_Test}}}} = {\text{E}}\varepsilon_{{{\text{A}}{\prime} }} \cdot \frac{{\sigma_{{{\text{B\_Simu}}}} }}{{\sigma_{{{\text{A\_Simu}}}} }}$$
(3)

where σA_Simu is the Mises stress of strain measurement point (point A) in finite element simulation results of first order bending mode analysis with un-notched aerofoil sample, σB_Simu is the Mises stress of notch root (the damaged position with maximum stress, point B) in finite element simulation results of first order bending mode analysis with un-notched aerofoil sample, εA′ is the strain measured at the strain measurement point in the test, E is the elastic modulus of TC17.

The HCF limit of the machined notch specimen at 3 × 107 cycles was shown in (Fig. 10). The high cycle fatigue limit of machined notch specimens with different sizes has a large dispersion. With the increase of stress concentration factor Kt, the HCF fatigue limit of the machined notch specimen was reduced significantly.

Fig. 10
figure 10

The HCF limit tested.

Full size image

Fatigue strength prediction model

TCD model

Model building process

According to the theory of critical distances (TCD), the fatigue strength can be predicted by the hot spot stresses within a certain range in front of crack tip. In our previous work35, a model based on the TCD method was built to predict the fatigue strength of FOD notched blades. Considering integrity of the paper, the model building process was presented here. The model construction process was shown in (Fig. 11).

Fig. 11
figure 11

Schematic diagram of fatigue limit prediction model based on TCD. (a) The overall morphology of the fracture surface. (b) Fatigue source. (c) Fatigue striation.

Full size image

According to the volume method of TCD, the average stress within the region near critical point B (i.e., the region within the hemispherical ___domain along the notch depth direction with point B as the hemisphere center and the critical distance rc as the hemisphere radius), σaver_0, is equal to the fatigue limit of smooth specimen σ-1, namely σaver_0 = σ-1. Similar first-order bending vibration mode analysis can also be carried out by numerical simulation. Therefore, the following relationship can be reached:

$$\frac{{\sigma_{{{\text{A}}{\prime} }} }}{{\sigma_{ - 1} }} = \frac{{\sigma_{{{\text{A}}{\prime} }} }}{{\sigma_{{{\text{aver}}\_0}} }} = \frac{{\sigma_{{{\text{A}}{\prime} \_{\text{Simu}}}} }}{{\sigma_{{{\text{aver}}\_{\text{Simu}}}} }}$$
(4)

where σAꞌ_Simu and σaver_Simu are the stresses of corresponding positions calculated by numerical simulation, respectively. Multiply both sides of Eq. (4) by σB_Simu/σA_Simu:

$$\frac{{\sigma_{{{\text{A}}{\prime} }} }}{{\sigma_{ - 1} }} \cdot \frac{{\sigma_{{{\text{B\_Simu}}}} }}{{\sigma_{{{\text{A\_Simu}}}} }} = \frac{{\sigma_{{{\text{A}}{\prime} \_{\text{Simu}}}} }}{{\sigma_{{{\text{aver\_Simu}}}} }} \cdot \frac{{\sigma_{{{\text{B\_Simu}}}} }}{{\sigma_{{{\text{A\_Simu}}}} }}$$
(5)

Substitute Eq. (3) into Eq. (5):

$$\frac{{\sigma_{{{\text{B\_Test}}}} }}{{\sigma_{ - 1} }} = \frac{{\sigma_{{{\text{A}}{\prime} {\text{\_Simu}}}} }}{{\sigma_{{{\text{aver\_Simu}}}} }}\frac{{\sigma_{{{\text{B\_Simu}}}} }}{{\sigma_{{{\text{A\_Simu}}}} }}$$
(6)

In Eq. (6), σB_Test is obtained from Eq. (3) with the first-order bending vibration fatigue experiment, σ-1 is the material parameter and can be obtained from the material manual, σAꞌ_Simu and σaver_Simu are obtained from the numerical simulation of first-order bending vibration mode analysis of notched sample, σA_Simu and σB_Simu are obtained from the numerical simulation of first-order bending vibration mode analysis of un-notched sample.

Model application

Equation (6) can be used for the critical distance calculation or bending vibration fatigue strength prediction with the following method:

  1. (I)

    To calculate the critical distance rc, the first-order bending vibration fatigue experiment and the numerical simulation of first-order bending vibration mode analysis was conducted on both the notched blade and the un-notched blade. With σB_Test, σ-1, σAꞌ_Simu, σA_Simu and σB_Simu already known, the critical distance rc which matches Eq. (6) can be calculated by numerical iteration.

  2. (II)

    To predict the bending vibration fatigue strength, the critical distance rc was already known, and the numerical simulation of first-order bending vibration mode analysis was conducted on both the notched blade and the un-notched blade. With σ-1, σAꞌ_Simu, σaver_Simu, σA_Simu and σB_Simu already known, the predicted σB_Test can be calculated as σB_Predicted with Eq. (6) and validated by comparison with the experimental result σB_Test.

Peterson model

Peterson model is one of the most widely used models for predicting the fatigue strength of notched components in engineering, which can be described by the following equation36:

$$K_{{\text{f}}} = 1 + \frac{{K_{{\text{t}}} - 1}}{{1{ + }{\raise0.7ex\hbox{${a_{{\text{p}}} }$} \!\mathord{\left/ {\vphantom {{a_{{\text{p}}} } \rho }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\rho $}}}}$$
(7)

where Kt is the stress concentration factor, ρ is the radius of the notch root, ap is the material constant influenced by tensile strength. In the present work, the stress concentration factor Kt is calculated by numerical simulation with the Eq. (1), and ap (Unit: MPa) is calculated with the following equation37:

$$a_{{\text{p}}} { = }0.0254\left( {\frac{{2070{\text{MP}}a}}{{\sigma_{{\text{u}}} }}} \right)^{1.8}$$
(8)

where σu is the tensile strength (Unit: MPa). In the present work, ap = 0.07673 mm. After getting the fatigue notch factor Kt by Eq. (8), the fatigue limit of notched sample σ-1/Kf can be calculated using σ-1 of TC17 at 3 × 107 cycles. In the present work, σ-1 = 440 MPa.

Fatigue strength prediction

Fatigue strength prediction based on the TCD method

First-order bending vibration fatigue experiments were carried out with 3 notched aerofoil specimens of various notch dimensions (specimen No. I-2/II-1/III-1). For details of the experiment procedure, please tend to Part 2 and Part 3 of this paper. The fatigue strength of notched aerofoil sample σB_Test was calculated with Eq. (6) for each specimen.

First-order bending vibration mode analysis of the un-notched aerofoil sample and 3 notched aerofoil sample of various notch dimensions (specimen No. I-2/II-1/III-1) were carried out by numerical simulation. For details of the numerical simulation procedure, please tend to Part 2 of this paper. FEM models of the un-notched and notched aerofoil specimen for bending vibration mode analysis were also shown in (Fig. 11). The Mises stress and the normal stress along the aerofoil specimen length direction at point A, the Mises stress at point B, and the node position coordinate, element volume and the principal stress of each node around the point B were calculated. Therefore, the σAꞌ_Simu, σA_Simu and σB_Simu in Eq. (6) can be obtained directly.

In Eq. (6), σaver_Simu is the average stress of the region near point B (i.e., the region within the hemispherical ___domain along the notch depth direction with point B as the hemisphere center and the critical distance rc as the hemisphere radius) in numerical simulation of the notched aerofoil specimen, and can be calculated as:

$$\sigma_{{{\text{aver\_Simu}}}} = \eta \frac{{\sum\limits_{i = 1}^{N} {\sigma_{i} \cdot V_{i} } }}{{\sum\limits_{i = 1}^{N} {V_{i} } }}$$
(9)

where N is the number of elements whose gravity center is within the proposed hemisphere ___domain, σi is the maximum absolute value of the principal stress of element, Vi is the volume of element, η is the correction factor for bending effect and η = 4 in the present work.

The σB_Test, σAꞌ_Simu, σA_Simu and σB_Simu have been obtained in Part 3.2, and σ-1 = 440 MPa of TC17 material was used here. Therefore, the critical distance rc can be calculated by numerical interaction with Eq. (6) for each notched blade specimen. For simplicity, the critical distance rc is supposed to be a constant material parameter in the present work. The average value of the critical distance rc for the 3 specimens is rc = 0.7075 mm. The critical distance rc of each specimen is shown in (Table 2).

Table 2 The critical distance rc of each specimen.
Full size table

Fatigue strength prediction results

To validate the accuracy of the TCD model, another 6 notched blades of various notch dimensions (specimen No. I-1/I-3/II-2/II-3/III-2/III-3) were HCF tested, and the predicted fatigue strength σB_Predicted were compared with the experimental test results σB_Test. The first-order bending vibration fatigue experiments were carried out and the fatigue strength σB_Test was calculated with Eq. (3) for each specimen. Numerical simulation of the first-order bending vibration mode analysis was carried out, and σAꞌ_Simu and σaver_Simu can be obtained with η = 4 and rc = 0.7075 mm. Un-notched blades were also used for numerical simulation of the first-order bending vibration mode analysis, and σA_Simu and σB_Simu can be obtained. Therefore, the predicted σB_Test can be calculated as σB_Predicted with Eq. (6), where σ-1 = 440 MPa.

Peterson model was also used to predict the fatigue limit of these 6 notched samples. Table 3 and Fig. 12 showed the comparison between the predicted fatigue strength σB_Predicted and the tested results σB_Test. The prediction error is 9.56% ± 6.78% for TCD model and 59.76% ± 16.93% for Peterson model (Fig. 13). The accuracy of fatigue limit prediction on notched samples using TCD model is much higher than that of Peterson model. It can be concluded that the TCD method model is more efficient to evaluate the fatigue strength of notched blade.

Table 3 Fatigue strength prediction results.
Full size table
Fig. 12
figure 12

Comparison of the predicted results with the test results for different models.

Full size image
Fig. 13
figure 13

Comparison of fatigue limit prediction results by TCD model and Peterson model

Full size image

Conclusion

In the present work, comprehensive investigation of machining foreign object damage effect on the fatigue limit of TC17 aerofoil specimen and high cycle fatigue limit prediction of machining foreign object damaged titanium aerofoil specimen were carried out. The following conclusions can be reached:

  1. (1)

    Machining notch can be used for foreign object damage analysis, and the machined notch dimension and surface roughness can influence the high cycle fatigue limit of the TC17 titanium aerofoil specimen. The high cycle fatigue limit of machined notch specimens with different sizes has a large dispersion. With the increase of stress concentration factor Kt, the HCF fatigue limit of the machined notch specimen reduced significantly.

  2. (2)

    The model based on the TCD method can be used for fatigue strength prediction of notched blades in first-order bending vibration mode. The prediction error is 9.56% ± 6.78% for TCD model and 59.76% ± 16.93% for Peterson model. The accuracy of fatigue limit prediction on notched samples using TCD model is much higher than that of Peterson model, and the TCD method model is more efficient to evaluate the fatigue strength of notched blade.