Introduction

In the emergence of quantum technologies, various quantum-secured protocols have been studied including quantum key distribution (QKD)1,2, blind quantum computation3,4,5, and quantum-secured sensing6,7,8. These protocols provides security based on the principles of quantum mechanics, such as the no-cloning theorem9 and nonlocality10, rather than the computational complexity.

In 1999, quantum secret sharing (QSS) was introduced by Hillery et al. Secret sharing is a scheme proposed for distrubuting a secret among participants11,12. In the scheme, one party, called a dealer, gives a part of the secret to participants, called players. Each player cannot access full information on the secret, since a player has only a share of the secret. The secret can be reconstructed only when the sufficient number of players cooperates by combining their shares. The scheme is called a (k, n)-threshold secret sharing, when the number of players is n and the sufficient number of players for reconstructing the secret is k. In QSS, a quantum secret or a classical secret can be shared by using a Greenberger–Horne–Zilinger (GHZ) type entangled state13 without an information leakage of the share not only to a potential eavesdropper, conventionally called Eve, but also to the other players. After its first proposal, the information-theoretic security of the QSS has been studied14,15,16,17, and experimental demonstrations of QSS protocols have been conducted as well18,19,20,21,22,23,24.

After the first proposal of QKD, significant efforts were made to improve efficiency of a secret key rate such as the protocol involving high-dimensional quantum states, called qudits. A qudit naturally carry more classical information than a qubit. QSS using qudits25,26,27,28,29 have been studied as well as a multiparty extension of QKD using qudits30,31. These results show that QSS based on qudits can achieve a higher secret key rate and a higher upper bound on the allowed error rate than the original protocols exploiting two-dimensional quantum states, called qubits, because of the structure of a qudit. From the results, it is known that a quantum communication protocol adopting qudit is noise robust compared to that with qubit. Moreover, there were the studies that fidelity of an optimal state estimation and the optimal fidelity of the \(1\rightarrow 2\) universal optimal quantum cloning machine decrease for increasing d, the dimension of a target quantum state32,33. Therefore, Eve can obtain less information when a qudit is exploited as an information carrier in QSS, i.e., qudits can make a quantum communication protocol more secure.

However, generation of a qudit GHZ state, which needs demanding technologies, is necessary to implement the QSS protocols using qudits. In 2018, there was the first generation of a tripartite three-dimensional GHZ state, called tripartite qutrit GHZ state, using orbital angular momentum (OAM) modes of a single photon34, but its generation efficiency and fidelity were not enough to implement a practical QSS protocol using qudits. Under the situation, it is natural to investigate a QSS protocol based on correlation measurement35,36. In QKD, Bell state measurement (BSM)37 based protocols have been widely studied rather than generation of entangled states38. Moreover, they provide measurement-device-independent (MDI) security, i.e., security loopholes from imperfection of measurement devices are closed, since BSM reveals only correlation between the two quantum state, not the exact key information. To enhance the efficiency, high-dimensional version of MDIQKD protocols have been studied39,40,41,42. However, there is an obstacle to implementing high-dimensional MDIQSS protocols that a high-dimensional BSM and a high-dimensional GHZ state analyzer cannot be implemented with linear optical elements43.

In this article, we investigate a possibility of QSS with a qutrit cyclic-entangled state (3d-CQSS). It is known that implementation of a qudit GHZ state analyzer is not possible with linear optics. However, high-dimensional correlation measurement projecting on the cyclic-entangled state is possible with linear optical elements41,44, especially based on a multiport interferometer45,46, and it was successfully implemented for qudit quantum teleportation47,48. With the correlation measurement setup, we propose an implementable 3d-CQSS protocol for (2, 2)-threshold QSS; there are a dealer, called Alice, and two Bobs who are authorized. The protocol would be generalized to d-dimensional CQSS (d-CQSS), and a class of the proposed protocol is \((d-1,d-1)\)-threshold QSS; there are a dealer, called Alice, and \((d-1)\) players, called \(\hbox {Bob}_{{1}}\) to \(\text {Bob}_{d-1}\). In this protocol, Charlie, an untrusted third party, is introduced, and only Charlie has the correlation measurement setup, which is performed on the three photons sent from the authorized parties. We analyze the security of d-CQSS and investigate conditions for security enhancement using qudits. We show the security of the protocol is not trivial like other high-dimensional quantum communication protocol, since the cyclic-entangled state has different properties to a GHZ-type entangled state. The conditions for the proposed protocol has higher secret sharing rate compared to two-dimensional QSS or entanglement-based d-CQSS are investigated as well.

Results

Three-dimensional correlation measurement with linear optical elements

In this section, an implementation of experimental elements to construct the three-dimensional correlation measurement with linear optical elements is introduced. For a qudit, it is impossible to construct a measurement setup with linear optical elements of which projector is a maximally entangled state or a GHZ-type state even if ancillary modes or systems are introduced43. Thus, a direct high-dimensional generalization of BSM or GHZ state analyzer is not implementable with linear optical elements. However, it is possible to construct a correlation measurement for a certain type of d-partite d-dimensional entangled state39,44. We investigate an entangled state exactly discriminated by the setup.

Here, we utilize the OAM mode of a single photon as an information carrier, but another mode could also be used. OAM modes, whose dimensionality can, in principle, be infinite, have been employed as high-dimensional information carriers not only in classical optical communication49, but also in quantum information processing50,51, including QKD52,53. Encoding information in OAM modes enhances both channel capacity and resilience to noise54,55. Despite these advantages, OAM-based systems face certain challenges, such as state-dependent diffraction56 and sensitivity to atmospheric turbulence in free-space links57. Various strategies have been proposed to improve the efficiency of OAM-encoded protocols, including the use of focusing techniques to address state-dependent diffraction58, and vortex-mode-division multiplexing to mitigate inter-mode crosstalk caused by turbulence59.

A single photon OAM state is written as follows:

$$\begin{aligned} |0\rangle =\hat{a}_{l=-1}^{\dagger }|\text {vac}\rangle ,\quad |1\rangle =\hat{a}_{l=0}^{\dagger }|\text {vac}\rangle ,\quad |2\rangle =\hat{a}_{l=1}^{\dagger }|\text {vac}\rangle , \end{aligned}$$
(1)

where \(\hat{a}_{l=x}^{\dagger }\) denotes the photon creation operator of which the OAM mode is x, and \(|\text {vac}\rangle\) is a vacuum state. Two mutually unbiased bases (MUBs), called ordinary basis and bar basis, will be exploited for QSS. The quantum states in the bar basis can be obtained from the three-dimensional Fourier transformation of the states in the ordinary basis as follows:

$$\begin{aligned} \begin{aligned} |\bar{0}\rangle&=\frac{1}{\sqrt{3}}\left( |0\rangle +|1\rangle +|2\rangle \right) ,\\ |\bar{1}\rangle&=\frac{1}{\sqrt{3}}\left( |0\rangle +\omega _{3}|1\rangle +\omega _{3}^{2}|2\rangle \right) ,\\ |\bar{2}\rangle&=\frac{1}{\sqrt{3}}\left( |0\rangle +\omega _{3}^{2}|1\rangle +\omega _{3}|2\rangle \right) , \end{aligned} \end{aligned}$$
(2)

where \(\omega _{d}=\exp (2 \pi i / d)\). These two bases are MUBs, since \(\left| \langle \bar{\alpha }|\beta \rangle \right| ^{2}=1/3\) is always satisfied for all \(\alpha , \beta \in \{0,1,2\}\), i.e., a quantum state from one MUB can be expressed as an equal-probability superposition of the quantum states forming another MUB.

Fig. 1
figure 1

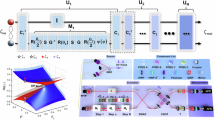
A schematic diagram of a tripartite three-dimensional correlation measurement setup. Three photons enter into a 3-port interferometer, called a tritter. After interference in the tritter constructed by Clements’ method46, an OAM value and a label of existing output port of the photons are measured by means of OAM discrimination elements and single photon detectors. The setup can discriminate a part of tripartite qutrit entangled states from a combination of clicked detectors. For the tritter operation in Eq. (4), the parameters are \(\theta _{A}=\arccos (1/\sqrt{3})\); \(\theta _{B}=\pi /4\); \(\theta _{C}=\pi /4\); \(\varphi _{A}=0\); \(\varphi _{B}=\pi\); \(\varphi _{C}=3\pi /2\); \(\varphi _{B'}=\pi /4\); and \(\varphi _{C'}=\pi /4\). \(D_{Xy}\) : a detector corresponding to the OAM state \(|y\rangle\) on the path X.

Full size image

An example of schematic setup of the three-dimensional correlation measurement is presented in Fig. 1. The three photons sent from three users, called Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), enter each input port of a three-port interferometer, called a tritter45,46,60. The tritter consists of linear optical elements including beam splitters, mirrors, and phase modulators46. In linear optics, the response of a material to incident light is directly proportional to the intensity of the light. In contrast, nonlinear optics involves more complex interactions, where the material’s response depends nonlinearly on the light intensity. As a result, linear optical systems are generally less sensitive to input power fluctuations and are simpler to align and maintain, making them more stable than their nonlinear counterparts. Owing to these advantages, linear optical quantum interferometers play a significant role in quantum information processing61. The tritter performs the three-dimensional Fourier transformation on path modes of the photons as described in the following equation:

$$\begin{aligned} \hat{U}_{3}|a,b_{1},b_{2}\rangle _{ABC}=\frac{1}{3\sqrt{3}}\left[ (|a\rangle +|b_{1}\rangle +|b_{2}\rangle )_{A'} \otimes (|a\rangle +\omega _{3}|b_{1}\rangle +\omega _{3}^{2}|b_{2}\rangle )_{B'} \otimes (|a\rangle +\omega _{3}^{2}|b_{1}\rangle +\omega _{3}|b_{2}\rangle )_{C'}\right] , \end{aligned}$$
(3)

where a, \(b_{1}\), and \(b_{2}\) are the encoded information of Alice, Bob1, and Bob2, respectively. The input ports and output ports are distinguished by the subscripts, A, B, and C for the input ports, and \(A'\), \(B'\), and \(C'\) for the output ports. Then the unitary operation on the path modes, \(\hat{U}_{3}\), performed by the tritter can be written as shown in the following equation:

$$\begin{aligned} \hat{U}_{3}=\frac{1}{\sqrt{3}} \begin{pmatrix} 1 & 1 & 1\\ 1 & \omega _{3} & \omega _{3}^{2}\\ 1 & \omega _{3}^{2} & \omega _{3} \end{pmatrix}. \end{aligned}$$
(4)
Fig. 2
figure 2

A schematic diagram for measuring an OAM value of a single photon. The OAM BSs change a direction of propagation of an incoming single photon according to its OAM value. OAM BS consists of a Mach-Zehnder interferometer with Dove prisms. The relative angle between the two Dove prisms in each arm of the Mach-Zehnder interferometer is denoted as \(\alpha /2\). In the setup, value one is added in the OAM value of an incoming photon by using an OAM hologram \((+1)\). Then the first OAM BS (\(\alpha /2=\pi /2\)) splits photons whose OAM value is odd and even, and the second OAM BS (\(\alpha /2=\pi /4\)) does photons whose OAM value is \(l=0\) and \(l=2\). Finally, the incoming photon enters into corresponding single photon detector.

Full size image

Subsequently, an OAM value of the photons is measured. Figure 2 shows a possible setup with linear optical elements that changes a direction of propagation of incoming photons according to their OAM value. The OAM hologram, which adds \((+1)\) to the OAM value of an incoming photon, and OAM beam splitters (OAM BSs) are exploited in the setup62. An OAM BS consists of a Mach-Zehnder interferometer and two Dove prisms in each arm. The relative angle between the two Dove prisms is \(\alpha /2\), and the relative phase between photons in the two arms is given by \(e^{il\alpha }\). The first OAM BS (\(\alpha =\pi\)) splits photons whose OAM value is even and odd, and the second OAM BS (\(\alpha =\pi /2\)) does photons whose OAM value is 0 and 2. Then there is one-to-one correspondence between the OAM value of an incoming single photon and the label of clicked detector. In our proposal, the OAM value discrimination setup should be able to measure an OAM value of the three incoming photons simultaneously, since there can be at most three photons on the same output port of the tritter. Direct measurements of an OAM value of a single photon are also considerable, such as the OAM value measurement by using refractive optical elements63,64, the measurement separating OAM modes spatially65,66, and the measurement using a single phase screen67.

To describe our protocol, we define 27 orthonormal tripartite qutrit entangled states \(|\Phi ^{3}\rangle\) as follows:

$$\begin{aligned} |\Phi ^{3}_{(2i+j,\sigma )}\rangle&=\frac{1}{\sqrt{6}}\sum _{k=0}^{2}\omega _{3}^{\sigma k}|k\rangle \left[ |k+i+1,k+i+2\rangle +(-1)^{j}|k+i+2,k+i+1\rangle \right] ,\end{aligned}$$
(5)
$$\begin{aligned} |\Phi ^{3}_{(6+m,\sigma )}\rangle&=\frac{1}{\sqrt{3}}\sum _{k=0}^{2}\omega _{3}^{\sigma k}|k,k+m,k+m\rangle , \end{aligned}$$
(6)

where \(\omega _{3}=\exp (2\pi /3)\), i, m, \(\sigma \in \{0,1,2\}\), and \(j\in \{0,1\}\). With these states, the relation between the three-photon quantum states that enter the tritter and its corresponding detector click events are investigated. The correlation measurement setup cannot discriminate all of the tripartite qutrit entangled state written in Eqs. (5) and (6). The only state that can be exactly discriminated and its click events are described as follows:

$$\begin{aligned} |\Phi ^{3}_{(0,0)}\rangle \rightarrow \left\{ \begin{matrix} D_{A'0},D_{B'1},D_{C'2}\quad \text {with probability }1/12\\ D_{A'0},D_{B'2},D_{C'1}\quad \text {with probability }1/12\\ D_{A'1},D_{B'2},D_{C'0}\quad \text {with probability }1/12\\ D_{A'1},D_{B'0},D_{C'2}\quad \text {with probability }1/12\\ D_{A'2},D_{B'0},D_{C'1}\quad \text {with probability }1/12\\ D_{A'2},D_{B'1},D_{C'0}\quad \text {with probability }1/12\\ D_{A'0},D_{A'1},D_{A'2}\quad \text {with probability }1/6\\ D_{B'0},D_{B'1},D_{B'2}\quad \text {with probability }1/6\\ D_{C'0},D_{C'1},D_{C'2}\quad \text {with probability }1/6 \end{matrix},\right. \end{aligned}$$
(7)

where \(D_{Xy}\) denotes a click event of the detector corresponding to the quantum state \(|y\rangle\) in the output port X. The three click events of which probability is 1/6 can be used in our protocol, since the other events are overlapped with the click events of \(|\Phi ^{3}_{(1,0)}\rangle\) as shown in the following equation:

$$\begin{aligned} |\Phi ^{3}_{(1,0)}\rangle \rightarrow \left\{ \begin{matrix} D_{A'0},D_{B'1},D_{C'2}\quad \text {with probability }1/6\\ D_{A'0},D_{B'2},D_{C'1}\quad \text {with probability }1/6\\ D_{A'1},D_{B'2},D_{C'0}\quad \text {with probability }1/6\\ D_{A'1},D_{B'0},D_{C'2}\quad \text {with probability }1/6\\ D_{A'2},D_{B'0},D_{C'1}\quad \text {with probability }1/6\\ D_{A'2},D_{B'1},D_{C'0}\quad \text {with probability }1/6 \end{matrix}.\right. \end{aligned}$$
(8)

There are always overlaps of click events for the other states, so only \(|\Phi ^{3}_{(0,0)}\rangle\)is exactly discriminated by using the correlation measurement setup. The details of calculation are drawn in the Methods section. We call this state as qutrit cyclic-entangled state68, since the state has the form of the following equation:

$$\begin{aligned} |\Phi ^{3}_{(0,0)}\rangle =\frac{1}{\sqrt{6}}\left[ |0\rangle (|1,2\rangle +|2,1\rangle )+|1\rangle (|2,0\rangle +|0,2\rangle )+|2\rangle (|0,1\rangle +|1,0\rangle )\right] . \end{aligned}$$
(9)

We expect that the existing setup41 also can be used for the 3d-CQSS protocol as well, which can exactly discriminate three tripartite qutrit entangled states, but it needs nondestructive photon number measurement setups that require demanding technologies.

This setup could be generalized to a d-dimensional correlation measurement which consists of a d-port interferometer and d-dimensional OAM mode discrimination elements. The d-port interferometer performs the d-dimensional Fourier transformation on the path modes, and its operator is shown in Eq. (10):

$$\begin{aligned} \hat{U}_{d}=\frac{1}{\sqrt{d}}\begin{pmatrix} 1 & 1 & 1 & 1 & \cdots & 1\\ 1 & \omega _{d} & \omega _{d}^{2} & \omega _{d}^{3} & \cdots & \omega _{d}^{d-1}\\ 1 & \omega _{d}^{2} & \omega _{d}^{4} & \omega _{d}^{6} & \cdots & \omega _{d}^{2(d-1)}\\ 1 & \omega _{d}^{3} & \omega _{d}^{6} & \omega _{d}^{9} & \cdots & \omega _{d}^{3(d-1)}\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega _{d}^{d-1} & \omega _{d}^{2(d-1)} & \omega _{d}^{3(d-1)} & \cdots & \omega _{d}^{(d-1)(d-1)} \end{pmatrix}, \end{aligned}$$
(10)

where \(\omega _{d}=\exp (2\pi i /d)\). In this case, a d-dimensional cyclic-entangled state, which is a d-partite d-dimensional entangled state, is written as follows:

$$\begin{aligned} |\Phi ^{d}_{(0,0)}\rangle =\frac{1}{\sqrt{d !}}\text {perm}(\Lambda )|\text {vac}\rangle , \end{aligned}$$
(11)

where perm(A) is the permanent of the matrix A. The matrix \(\Lambda\) is defined as shown in the following equation:

$$\begin{aligned} \Lambda =\begin{pmatrix} \hat{a}^{\dagger }_{00} & \hat{a}^{\dagger }_{01} & \cdots & \hat{a}^{\dagger }_{0(d-1)}\\ \hat{a}^{\dagger }_{10} & \hat{a}^{\dagger }_{11} & \cdots & \hat{a}^{\dagger }_{1(d-1)}\\ \vdots & \vdots & \ddots & \vdots \\ \hat{a}^{\dagger }_{(d-1)0} & \hat{a}^{\dagger }_{(d-1)1} & \cdots & \hat{a}^{\dagger }_{(d-1)(d-1)} \end{pmatrix}, \end{aligned}$$
(12)

where \(\hat{a}_{xy}^{\dagger }\) denotes the photon creation operator. The subscript x denotes an OAM value of the single photon. The subscript y means a label of the party who sent the photon to Charlie, where \(y=0\) means Alice, and \(y=n\) means \(\hbox {Bob}_{{n}}\) for \(n\in \{1,2,...,d-1\}\).

Schematic description of QSS with correlation measurement

In this section, a schematic description of 3d-CQSS is presented. In this protocol, three authorized parties, Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), participate in secret sharing, and an untrusted third party, Charlie, performs a measurement. Each authorized party has a single photon generator and a three-dimensional information encoder, such as a spatial light modulator (SLM) to encode in OAM modes of a single photon. Note that another degree-of-freedom of a single photon can be used in this protocol for three-dimensional encoding, such as multi time-bin modes. In QSS, it is necessary that one party cannot expect distributed secrets of the others. If the system of one party is traced out, the quantum states of the others are entangled for Eq. (5). Therefore, it is impossible to exactly predict the secret of the other party in this case. For the quantum state described in the form of Eq. (6), when the system of one party is traced out, the quantum states of the others are a fully mixed state.

Fig. 3
figure 3

A schematic diagram of our protocol. There are three authorized parties, Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), and one untrusted party, Charlie. Each of the authorized parties generates a single photon state according to their choice of an encoding basis and three-dimensional information. They send the quantum states to Charlie who measures a correlation among the OAM mode of the three photons by means of a tripartite three-dimensional correlation measurement. The three authorized parties can share a secret by using their encoded information and the result of the measurement.

Full size image
Table 1 Alice’s local operation when the result of the three-dimensional correlation measurement is \(|\Phi ^{3}_{(2i+j,\sigma )}\rangle\). To satisfy the condition, \(a+b_{1}+b_{2}=0\) (mod 3), a local operation is necessary, where a, \(b_{1}\), and \(b_{2}\) are encoded number of Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), respectively.
Full size table

The procedure of the 3d-CQSS protocol is as follows:

  1. 1.

    Alice (\(\hbox {Bob}_{{1}}\), \(\hbox {Bob}_{{2}}\)) randomly generates binary information to choose a basis, and three-dimensional information, a (\(b_{1}\), \(b_{2}\)).

  2. 2.

    Each authorized party generates a single photon state, \(|i\rangle\) or \(|\bar{i}\rangle\), according to his/her three-dimensional information, i.

  3. 3.

    The authorized parties send their single photon states to Charlie, who has a correlation measurement setup.

  4. 4.

    Charlie performs the correlation measurement onto the incoming photons, and he announces the result of the measurement.

  5. 5.

    The authorized parties compare their encoding bases through classical communication. They keep the encoded information if the encoding bases are the same. The trials that Alice’s and Bobs’ bases are not identical, are discarded.

  6. 6.

    If Charlie’s measurement result is one of the states described in Eq. (5), Alice performs a local operation to satisfy the following condition: \(a+b_{1}+b_{2}=0\) (mod 3). (See Table 1.)

  7. 7.

    After several repetition of steps 2.2–2.2, they estimate parameters for security analysis by revealing a part of data.

    • A portion of the data is revealed when all authorized parties choose the ordinary basis and Charlie’s measurement outcome corresponds to one of the states given in Eq. (5).

    • The entire dataset is revealed when all authorized parties choose the ordinary basis and Charlie’s measurement outcome corresponds to one of the states described in Eq. (6).

    • All of the data is revealed if all authorized parties used the bar basis.

  8. 8.

    At this point, Alice and the Bobs are prepared to share a classical secret based on their measurement outcomes and proceed with the analysis of security parameters.

The parameters for security analysis will be described in the Security Analysis section. Measurement statistics from both the ordinary and bar bases are required for security analysis. However, outcomes obtained in the bar basis are used solely for parameter estimation, not for secret sharing, since a party could potentially infer the encoded values of the others when the encoding is done in the bar basis. For example, the 3d-cyclic-entangled state is written in the bar basis as follows:

$$\begin{aligned} |\Phi ^{3}_{(0,0)}\rangle =&\frac{1}{3\sqrt{2}}\sum _{k=0}^{2}\left( 2|\bar{k},\bar{k},\bar{k}\rangle -|\bar{k},\overline{k+1},\overline{k+2}\rangle +|\bar{k},\overline{k+2},\overline{k+1}\rangle \right) . \end{aligned}$$
(13)

If Alice sent \(|\bar{0}\rangle\) to Charlie, the number of possible cases is three. The two cases are that \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\) sent \(|\bar{1}\rangle\) and \(|\bar{2}\rangle\), or \(|\bar{2}\rangle\) and \(|\bar{1}\rangle\) to Charlie, respectively, and the probability of each case is one fourth. The other case is that both \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\) sent \(|\bar{0}\rangle\) to Charlie, and its probability is one half. Since these three cases are not equally probable, the encoded number of the other parties is not random for one party. Therefore, the bar basis cannot be used to share a secret. In conclusion, measurement results obtained in the ordinary basis are used for both QSS and its security analysis, whereas those obtained in the bar basis are used exclusively for security analysis.

In step 5 of the protocol, the probability that all players choose the same basis is \((1/2)^2\), since each player independently selects between two bases with equal probability, and there are two players involved. Therefore, only a fraction \((1/2)^2\) of the trials is retained after basis sifting. In step 7, although there are 27 orthonormal entangled states in total, secret sharing is performed only using the quantum states defined in Eq. (5). As a result, only one-third of the sifted trials contribute to secret sharing, while the remaining two-thirds are used solely for security analysis under the assumption of ideal correlation measurements. When using the practical correlation measurement introduced in Fig. 1, it can successfully distinguish only one entangled state with probability 1/2. Thus, the success probability of this measurement is \((1/27) \times (1/2)\), and the total sifting probability becomes the product of the basis-sifting probability from step 5 and the success probability of the correlation measurement, yielding \((1/2)^2 \times (1/54)\).

When Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\) distributed three-dimensional classical information, a, \(b_{1}\), and \(b_{2}\), then the procedure of sharing a three-dimensional classical number is as follows:

  1. 1.

    The dealer, Alice, chooses a classical secret, S, where \(S\in \{0,1,2\}\).

  2. 2.

    Alice announces the message, M, through classical communication. M is defined from the equation: \(M=S+a\) (mod 3).

  3. 3.

    Players, \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\), can decode the classical secret by sharing their encoded numbers, but cannot without collaboration. The decoding is shown in the following equation:

    \(M+b_{1}+b_{2}\) (mod 3) \(=S+a+b_{1}+b_{2}\) (mod 3) \(=S\).

The protocol can be extended to d-dimensional CQSS (d-CQSS) among a dealer, Alice, and players, \(\hbox {Bob}_{{1}}\) to \(\text {Bob}_{d-1}\). In the d-CQSS protocol, each of the authorized parties send a d-dimensionally encoded photon to Charlie who has a d-dimensional correlation measurement setup. They use two different bases, the ordinary basis \(\{|0\rangle ,|1\rangle ,...,|d-1\rangle \}\) and the bar basis \(\{|\bar{0},|\bar{1}\rangle ,...,|\overline{d-1}\rangle \rangle \}\). Similarly with the three-dimensional case, the relation between the two bases is the d-dimensional Fourier transformation. They can distribute a d-dimensional classical secret with the d-partite d-dimensional quantum state written in Eq. (11). If the result of the d-partite d-dimensional correlation measurement is \(|\Phi ^{d}_{(0,0)}\rangle\), a sum on (mod d) of the encoded numbers of all the quantum state always becomes zero. A participant cannot predict the encoded number of the others, since if k photons in \(|\Phi ^{d}_{(0,0)}\rangle\) are traced out, for \(k<d-1\), the rest of the photons are entangled with the same probabilities. Therefore, the authorized parties can employ \((d-1,d-1)\)-threshold QSS by using this quantum state.

Security analysis of our QSS protocol

Strategy for security analysis

Before we analyze security of the 3d-CQSS protocol, we should define constraints to construct a secure QSS protocol: (i) The single photon generators and the OAM encoders, which the authorized parties have, should be characterized and not be influenced by Eve. (ii) The authorized parties hold trusted random number generators to select an encoding basis and encoding information. (iii) Successive rounds of the protocol must be completely independent, i.e., we assume an independent and identically distributed (i.i.d.) attack of Eve. (iv) The laboratory of each authorized party must be isolated from the outside to prevent unintended information leakage or inflow. Under these assumptions, we analyze security of the 3d-CQSS protocol in the asymptotic limit.

Here, we introduce the security analysis for 3d-CQSS. To analyze the security, we exploit the entanglement distillation process (EDP)69,70,71 of an equivalent protocol of the 3d-CQSS protocol, which the authorized parties share a tripartite qutrit entangled state \(|\Phi _{(0,0)}^{3}\rangle\). The equivalent protocol can be constructed by replacing the qutrit generation setups of the authorized parties to bipartite qutrit maximally entangled state generation setups and qutrit discrimination measurement setups. Each authorized party generates the bipartite three-dimensional maximally entangled state described in the following equation:

$$\begin{aligned} |\Theta \rangle =\frac{1}{\sqrt{3}}\left( |0,0\rangle +|1,1\rangle +|2,2\rangle \right) , \end{aligned}$$
(14)

and send one photon to Charlie. Subsequently, Charlie performs the three-dimensional correlation measurement and announces the result. The six-photon quantum state is described as follows:

$$\begin{aligned} \begin{aligned} |\Xi \rangle _{AA'B_{1}B_{1}'B_{2}B_{2}'}&=|\Theta \rangle _{AA'}\otimes |\Theta \rangle _{B_{1}B_{1}'}\otimes |\Theta \rangle _{B_{2}B_{2}'}\\&=\sum _{\sigma =0}^{2}\sum _{j=0}^{8}\left[ |\Phi ^{3}_{(j,\sigma )}\rangle _{A'B_{1}'B_{2}'}\otimes |\Phi ^{3}_{(j,3-\sigma )}\rangle _{AB_{1}B_{2}}\right] , \end{aligned} \end{aligned}$$
(15)

where the subscripts A, \(B_{1}\), and \(B_{2}\) denote the photons that Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\) keep, and \(A'\), \(B_{1}'\), and \(B_{2}'\) are the photons sent from Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\) to Charlie, respectively. If Charlie’s result is \(|\Phi ^{3}_{(j,\sigma )}\rangle\) where j is an even number and \(j<6\), the authorized parties can share \(|\Phi ^{3}_{(0,0)}\rangle _{AB_{1}B_{2}}\) by means of local operations and classical communication (LOCC). Finally, the authorized parties choose a measurement basis and measure their photon. If the measurement bases are the same, \(a+b_{1}+b_{2}=0\) (mod 3) is always satisfied where a, \(b_{1}\), and \(b_{2}\) are the outcome of Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), respectively.

In order to assure the information-theoretic security, the authorized parties analyze their security under the assumption that Eve can exploit everything allowed by the quantum mechanics for an attack. The worst case is that Eve has full control over the shared quantum state. This attack can be realized by means of purification of the total quantum system, including Eve’s ancillary system. The total system can be described in the form of a pure state as shown in Eq. (16):

$$\begin{aligned} \sum _{\sigma =0}^{2}\sum _{j=0}^{8}\sqrt{\lambda _{(j,\sigma )}}|\Phi ^{3}_{(j,\sigma )}\rangle _{AB_{1}B_{2}}\otimes |e_{(j,\sigma )}\rangle _{E}, \end{aligned}$$
(16)

where \(\{|e_{(j,\sigma )}\rangle \}\) is Eve’s orthonormal basis. Then the quantum system of the authorized parties can be obtained by tracing out Eve’s system as described in the following equation:

$$\begin{aligned} \hat{\rho }_{AB_{1}B_{2}}=\sum _{\sigma =0}^{2}\sum _{j=0}^{8}\lambda _{(j,\sigma )}|\Phi ^{3}_{(j,\sigma )}\rangle \langle \Phi ^{3}_{(j,\sigma )}|. \end{aligned}$$
(17)

Now, we analyze the amount of a shared classical secret through a single sifted pulse in the asymptotic limit, which we refer a secret key rate for simplicity from now on. A sifted pulse means that a pulse can be used for generating a secret key. In the 3d-CQSS protocol, the sifted pulse is obtained when all the authorized parties use the ordinary basis, and the result of the three-dimensional correlation measurement is \(|\Phi ^{3}_{(0,0)}\rangle\). The asymptotic secret key rate of the 3d-CQSS protocol can be calculated from the Devetak–Winter formula71, which is used in various QSS protocols72,73,74, shown in Eq. (18):

$$\begin{aligned} r_{\text {min}}=I(A,\overline{B})-\chi (A;E)=I(A,3-B_{1}-B_{2})-\chi (A;E), \end{aligned}$$
(18)

where \(\overline{B}\) denotes joint measurement result of Bobs and (mod 3) is omitted in the bracket of the mutual information. Hereafter, we omit min in the subscript of the secret key rate r. The first term of the right-hand side in Eq. (18) is defined as the mutual information between Alice’s encoded information, A, and joint measurement result of players, which is a modular sum of \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\)’s encoded information, \(3-B_{1}-B_{2}\) (mod 3). In a multiparty QKD, all the authorized parties share a symmetric secret key, so the smallest mutual information between two parties is necessary to obtain a secret key rate75,76. Unlike multiparty QKD, in QSS, it is necessary to consider the mutual information between Alice’s information and the modular sum of the others to evaluate a secret key rate since a classical secret is shared by using Alice’s encoded information and the modular sum of the others. The second term is the Holevo information which is defined as an upper bound to the amount of information that Eve can know about a quantum state transmitted through the quantum channel77. By subtracting the Holevo information from the mutual information, we can obtain the amount of information that the authorized parties can share securely by using the quantum state.

There is another case that one of the authorized players is malicious. For instance, \(\hbox {Bob}_{{1}}\) can collaborate with Eve to obtain Alice’s information without \(\hbox {Bob}_{{2}}\)’s information. In this case, the security of the proposed protocol becomes more vulnerable compared with a QSS protocol using a tripartite qutrit GHZ state shown in the following equations:

$$\begin{aligned} \begin{aligned} |3d\text {-GHZ}_{3}\rangle =&\frac{1}{\sqrt{3}}\left( |0,0,0\rangle +|1,1,1\rangle +|2,2,2\rangle \right) \\ =&\frac{1}{3}\sum _{k=0}^{2}\left( |\bar{k},\overline{k+1},\overline{k+2}\rangle +|\bar{k},\overline{k+2},\overline{k+1}\rangle +|\bar{k},\bar{k},\bar{k}\rangle \right) . \end{aligned} \end{aligned}$$
(19)

In a QSS protocol using the GHZ state, if \(\hbox {Bob}_{{1}}\)’s measurement outcome is \(\bar{0}\), then there are three possible outcomes of Alice and \(\hbox {Bob}_{{2}}\), \(\{\bar{0},\bar{0}\}\), \(\{\bar{1},\bar{2}\}\), and \(\{\bar{2},\bar{1}\}\). However, in the proposed protocol, only the two cases, \(\{1,2\}\) and \(\{2,1\}\), are possible from Eq. (5) when \(\hbox {Bob}_{{1}}\)’s measurement outcome is 0. Therefore, intuitively, a secret key rate of the proposed protocol with a malicious player could be low compared with that of a QSS protocol using the GHZ state with a malicious player. To analyze the security of the proposed protocol with the malicious \(\hbox {Bob}_{{1}}\), the Devetak–Winter formula is shown in Eq. (20) can be used:

$$\begin{aligned} r=I(A,3-B_{1}-B_{2})-\chi (A;EB_{1}), \end{aligned}$$
(20)

where (mod 3) is omitted in the bracket of the mutual information.

Like the case of 3d-CQSS, a secret key rate of d-CQSS can be obtained from the Devetak–Winter formula as shown in Eq. (21):

$$\begin{aligned} r=I\left( A,d-\sum _{n=1}^{d-1}B_{n}\right) -\chi (A;E), \end{aligned}$$
(21)

when all the authorized parties are trusted. The secret key rate is changed to the following equation:

$$\begin{aligned} r=I\left( A,d-\sum _{n=1}^{d-1}B_{n}\right) -\chi \left( A;E\prod _{n=1}^{k}B_{n}\right) , \end{aligned}$$
(22)

when \(\hbox {Bob}_{{1}}\) to \(\hbox {Bob}_{{k}}\) are malicious players who collaborate with Eve.

Error parameters

We define three groups of the tripartite qutrit entangled states, \(\{|\Phi ^{3}_{(2i,\sigma )}\rangle \}\), \(\{|\Phi ^{3}_{(2i+1,\sigma )}\rangle \}\), and \(\{|\Phi ^{3}_{(6+i,\sigma )}\rangle \}\), where \(i,\sigma \in \{0,1,2\}\). A state can be transformed to another state in the same group by means of LOCC but cannot be transformed to a state in another group. To simplify the analysis, the density matrix described in Eq. (17) is transferred to the depolarized state written in Eq. (23):

$$\begin{aligned} \begin{aligned} \hat{\rho }_{\text {dp}}=\sum _{\sigma =0}^{2}&\left( \lambda _{(0,\sigma )}|\Phi ^{3}_{(0,\sigma )}\rangle \langle \Phi ^{3}_{(0,\sigma )}|+\sum _{i=1}^{2}\lambda _{-}|\Phi ^{3}_{(2i,\sigma )}\rangle \langle \Phi ^{3}_{(2i,\sigma )}|\right. \\&\left. +\sum _{j=0}^{2}\lambda _{+}|\Phi ^{3}_{(2j+1,\sigma )}\rangle \langle \Phi ^{3}_{(2j+1,\sigma )}|+\sum _{k=6}^{8}\lambda _{=}|\Phi ^{3}_{(k,\sigma )}\rangle \langle \Phi ^{3}_{(k,\sigma )}|\right) , \end{aligned} \end{aligned}$$
(23)

by means of LOCC like the multipartite qubit description78under the assumption that Eve performs a symmetric attack to obtain encoded information in the both bases well79. The coefficients, \(\lambda _{-}\), \(\lambda _{+}\), and \(\lambda _{=}\), can be obtained from the following equations:

$$\begin{aligned} \lambda _{-}&=\frac{1}{6}\sum _{\sigma =0}^{2}\sum _{j=1}^{2}\lambda _{(2j,\sigma )},\end{aligned}$$
(24)
$$\begin{aligned} \lambda _{+}&=\frac{1}{9}\sum _{\sigma =0}^{2}\sum _{j=0}^{2}\lambda _{(2j+1,\sigma )},\end{aligned}$$
(25)
$$\begin{aligned} \lambda _{=}&=\frac{1}{9}\sum _{\sigma =0}^{2}\sum _{j=6}^{8}\lambda _{(j,\sigma )}. \end{aligned}$$
(26)

To evaluate a secret key rate, it is necessary to define parameters which can be obtained from the revealed data. The four different error rates are defined as shown in the following equations:

$$\begin{aligned}&Q_{s}=\sum _{j=2}^{8}\lambda _{(j,0)}=2\lambda _{+}+2\lambda _{-}+3\lambda _{=},\end{aligned}$$
(27)
$$\begin{aligned}&Q_{\omega }=\sum _{\sigma =1}^{2}\sum _{j=0}^{8}\lambda _{(j,\sigma )}=\lambda _{(0,1)}+\lambda _{(0,2)} +6\lambda _{+}+4\lambda _{-}+6\lambda _{=},\end{aligned}$$
(28)
$$\begin{aligned}&Q_{\pm }=\lambda _{(1,0)}=\lambda _{+},\end{aligned}$$
(29)
$$\begin{aligned}&Q_{u}=\frac{1}{9}\sum _{k,\sigma =0}^{2}\lambda _{(k+6,\sigma )}=\lambda _{=}. \end{aligned}$$
(30)

The \(Q_{s}\) is called a state error rate, which is defined as the probability that the result state does not have a \(\omega _{3}\) phase change; however, it is not the wanted state. The \(Q_{\omega }\) is a three-dimensional phase error rate, the probability that the result state has a phase of \(\omega _{3}\). The \(Q_{\pm }\) is a two-dimensional phase error rate, the probability that the \((+)\) sign in \(|\Phi ^{3}_{(0,0)}\rangle\) is changed to \((-)\). Finally, the \(Q_{u}\) is called a user error rate, the probability of a state for which the two players, \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\), have the same encoded information. The parameters can be obtained from the statistics of the authorized parties as shown in the following equations:

$$\begin{aligned}&Q_{s}=p(a+b_{1}+b_{2}\ne 0 \; \& \; b_{1}\ne b_{2})-p(\bar{a}+\bar{b}_{1}+\bar{b}_{2}\ne 0)\nonumber \\&\quad +\frac{1}{3}\left[ 2p(a+b_{1}+b_{2}=0 \; \& \; b_{1}\ne b_{2})-(\langle \hat{X}\hat{X}\hat{X}\rangle +\text {c.c.})\right] ,\end{aligned}$$
(31)
$$\begin{aligned}&Q_{\omega }=p(\bar{a}+\bar{b}_{1}+\bar{b}_{2}\ne 0),\end{aligned}$$
(32)
$$\begin{aligned}&Q_{\pm }=\left| 1-2p(\bar{a}=\bar{b}_{1}=\bar{b}_{2}\;|\;\bar{a}+\bar{b}_{1}+\bar{b}_{2}=0)\right| ,\end{aligned}$$
(33)
$$\begin{aligned}&Q_{u}=\frac{1}{9}p(b_{1}=b_{2}), \end{aligned}$$
(34)

where p(x) can be obtained from (the number of pulses for which x is true)/(the number of sifted pulses for which the basis including x is used), and (mod 3) is omitted in all the brackets. In Eq. (31), c.c. denotes complex conjugate of \(\langle \hat{X}\hat{X}\hat{X}\rangle\). The operator \(\hat{X}\) is defined as the following equation:

$$\begin{aligned} \hat{X}=\begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{pmatrix}, \end{aligned}$$
(35)

where the bases of the matrix are the OAM modes.

Secret key rate

In this section, the secret key rate for 3d-CQSS is evaluated using Eqs. (17) and (18) under the assumption that all authorized parties are trusted, as shown in Eq. (36):

$$\begin{aligned} \begin{aligned} r=&\log 3+\sum _{j=0}^{8}\sum _{\sigma =0}^{2}\left( \lambda _{(j,\sigma )}\log \lambda _{(j,\sigma )}\right) -\sum _{j=0}^{8}\left[ \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \log \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \right] +\sum _{i=0}^{2}\Lambda _{i}\log \Lambda _{i}. \end{aligned} \end{aligned}$$
(36)

In the absence of isotropy, the secret key rate can be determined through numerical analysis based on the measurement outcomes from the authorized parties. This analysis seeks to identify a shared quantum state that minimizes the secret key rate80.

To compare our protocol with others, we consider a depolarizing channel, which has been commonly used in the literature for such comparisons81,82. With the depolarized state in Eq. (23), an analytic secret key rate of 3d-CQSS can be evaluated by using the Eqs. (23–30), as shown in Eq. (37):

$$\begin{aligned} \begin{aligned} r=&(1-3Q_{u}-3Q_{\pm })\log 3 -(Q_{\omega }+Q_{s}-2Q_{\pm }-3Q_{u})\\&+(1-Q_{\omega }-Q_{s}-Q_{\pm })\log (1-Q_{\omega }-Q_{s}-Q_{\pm })+3(Q_{s}-Q_{u})\log (Q_{s}-Q_{u})\\&+(Q_{\omega }-2Q_{s}-2Q_{\pm })\log (Q_{\omega }-2Q_{s}-2Q_{\pm })-(1-3Q_{s}-3Q_{\pm })\log (1-3Q_{s}-3Q_{\pm }). \end{aligned} \end{aligned}$$
(37)

The unit of the secret key rate is (bits)/(sifted pulse). This equation can be used to evaluate not only the secret key rate of the 3d-CQSS protocol, but also that of an entanglement-based 3d-QSS protocol that exploits the tripartite qutrit cyclic-entangled state, \(|\Phi ^{3}_{(0,0)}\rangle\). By using the same method, a secret key rate of d-CQSS can be calculated as well. Calculation details are drawn in the Methods section.

Now, let us compare the secret key rate of QSS using qudit. To compare the secret key rates, we consider a depolarizing channel with white noise. The depolarized state for d-CQSS is shown in Eq. (38):

$$\begin{aligned} \hat{\rho }_{d,\text {dp}}=(1-p)|\Phi ^{d}_{(0,0)}\rangle \langle \Phi ^{d}_{(0,0)}|+\frac{p}{d^{d}}\mathbbm {1}_{d^{d}}, \end{aligned}$$
(38)

where \(\mathbbm {1}_{x}\) is the \(x\times x\) identity operator. For 2d-QSS, we calculate the secret key rate evaluated by using the Devetak–Winter formula and a N-partite qubit GHZ state under a depolarizing channel is described in the following equation:

$$\begin{aligned} \hat{\rho }_{2,\text {dp}}=(1-p)|2d\text {-GHZ}_{N}\rangle \langle 2d\text {-GHZ}_{N}|+\frac{p}{2^{N}}\mathbbm {1}_{2^{N}}. \end{aligned}$$
(39)

where the N-partite qubit GHZ state is defined as shown in the following equation:

$$\begin{aligned} |2d\text {-GHZ}_{N}\rangle =\frac{1}{\sqrt{2}}(|0\rangle ^{\otimes N}+|1\rangle ^{\otimes N}). \end{aligned}$$
(40)
Fig. 4
figure 4

Secret key rates per sifted pulse under a depolarizing channel. The secret key rate of the three-party QSS protocol using qubits (black, dashed line) and that of the 3d-CQSS protocol (red, solid line) are drawn. p is the ratio of white noise. (a) The secret key rates when all the authorized parties are trusted. (b) The secret key rates when \(\hbox {Bob}_{{1}}\) cooperates with Eve.

Full size image

Figure 4(a) shows the secret key rate of 3d-CQSS (red solid line) and that of three-party 2d-QSS (black dashed line) evaluated under a depolarizing channel when all the parties are trusted. 3d-CQSS has a higher secret key rate than 2d-QSS since d-dimensional information is transferred by a single quantum, rather than binary information. The plots show 3d-CQSS has noise robustness compared with 2d-QSS as well. Figure 4(b) shows the secret key rate of 3d-CQSS (red solid line) and that of 2d-QSS (black dashed line) when \(\hbox {Bob}_{{1}}\) cooperates with Eve. Since \(\hbox {Bob}_{{1}}\) can expect values of the others from his number, the security becomes more vulnerable against a dishonest authorized party compared with three-party 2d-QSS. The secret key rate of 3d-CQSS is slightly higher only when the noise factor is smaller than approximately \(7\%\), and then 2d-QSS becomes more efficient when the noise factor is larger than the value.

Fig. 5
figure 5

Secret key rates per sifted pulse under a depolarizing channel. The secret key rate of the four-party QSS protocol using qubits (black, dashed line) and that of the 4d-CQSS protocol (blue, solid line) are drawn. p is the ratio of white noise. (a) The secret key rates when all the authorized parties are trusted. (b) The secret key rates when \(\hbox {Bob}_{{1}}\) cooperates with Eve. (c) The secret key rates when \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\) cooperate with Eve.

Full size image

Figure 5 shows the secret key rate of 4d-CQSS (blue solid line) and that of four-party 2d-QSS (black dashed line) evaluated under a depolarizing channel. Figure 5(a) shows the secret key rates when all players are trusted. Similarly with three-dimensional case, 4d-CQSS has the higher secret key rate and the protocol can be accomplished when the noise is larger compared with four-party 2d-QSS. Figure 5(b) shows the secret key rates when \(\hbox {Bob}_{{1}}\) collaborates with Eve to obtain Alice’s encoded number without encoded numbers of \(\hbox {Bob}_{{2}}\) and \(\hbox {Bob}_{{3}}\). Since the mutual information between Alice and \(\hbox {Bob}_{{1}}\) is \(2-\log 3\) for the ideal situation, i.e., the authorized parties share \(|\Phi ^{4}_{(0,0)}\rangle\), the maximum secret key rate of the protocol can be obtained the mutual information among the authorized parties subtracted by the mutual information between Alice and \(\hbox {Bob}_{{1}}\), \(\log 3\). Therefore, 4d-CQSS has the higher secret key rate compared with four-party 2d-QSS even when there is one malicious player. If there are two malicious players, \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\), the secret key rate becomes almost similar with that of four-party 2d-QSS as shown in Fig. 5(c) since the mutual information between Alice’s number and the numbers of \(\text {Bob}_1\) and \(\text {Bob}_2\) becomes one for the ideal situation.

For d-CQSS, the maximum secret key rate per sifted pulse can be obtained as \(\log (d-m)\) where m is the number of malicious players for \(0\le m\le d-2\). This value comes from the mutual information among the authorized parties, \(\log d\), and the mutual information among Alice and malicious players, \(\log d -\log (d-m)\), for the ideal situation, i.e., the authorized parties share the quantum state \(|\Phi ^{d}_{(0,0)}\rangle\). Because of the structure of the quantum state, d-CQSS cannot guarantee the same security with d-party QSS using d-dimensional GHZ state when there are malicious players. However, if there are more than two trusted players in d-CQSS, the protocol can be more efficient compared with d-party 2d-QSS.

Fig. 6
figure 6

The secret key rates per sifted pulse with experimental factors when all players are trusted. The secret key rates of the 2d-MDIQSS protocol (black dashed line), the entangled state based 3d-CQSS (3d-ECQSS) protocol (blue dotted line), the correlation measurement based 3d-CQSS protocol (red solid line), and single photon based 3d-QSS (3d-SQSS) protocol (Purple dotted line) are plotted. Experimental factors, transmission loss \(\eta\) and a dark count rate of a single photon detector, are considered in the plots. The dark count rate is assumed as \(10^{-5}\) per pulse.

Full size image

In Fig. 6, the secret key rates of the 2d-MDIQSS protocol35 (black dashed line), the entangled state based 3d-CQSS (3d-ECQSS) protocol (blue dotted line), the correlation measurement based 3d-CQSS protocol (red solid line), and single photon based 3d-QSS (3d-SQSS) protocol83 (Purple dotted line) are compared under the consideration of experimental factors, transmission loss of a photon and a dark count rate of a single photon detector. The other conditions are assumed as the ideal, for instance, there is no Eve, state preparation is perfect, and the all authorized parties are trusted. In the plot, it is shown that the secret key rate of the 3d-CQSS protocol is higher than that of the 2d-MDIQSS protocol, when the transmission loss is lower than approximately 39 dB. This effect also can be seen in QKD, as it was known that a high-dimensional QKD protocol is vulnerable to the transmission loss compared with the same type of QKD protocol using qubits84,85.

As shown in the plot, the 3d-CQSS with the correlation measurement has an advantage compared with the entanglement-based 3d-CQSS (3d-ECQSS) protocol regarding resistance to the transmission loss when all authorized parties are trusted. Note that this advantage appears even when the preparation efficiency of an entangled state is not considered. This effect come from the number of errors which occur when two or more photons are lost. For example, let us consider the case that \(\hbox {Bob}_{{1}}\)’s and \(\hbox {Bob}_{{2}}\)’s photons are lost. In the correlation measurement based 3d-CQSS protocol, if Alice’s photon clicks the detector \(D_{A'0}\), then the three-dimensional correlation measurement succeeds only when \(D_{A'1}\) and \(D_{A'2}\) are clicked due to the dark count. In this situation, if \(\hbox {Bob}_{{1}}\) and \(\hbox {Bob}_{{2}}\) did not send quantum states having an OAM mode of 1 and 2, the trial introduces an error. In the 3d-ECQSS protocol, if one photon clicks Alice’s detector \(D_{0}\), where \(D_{x}\) is the detector corresponding to the OAM mode x, there are two cases that an error does not occur. The first case is that \(\hbox {Bob}_{{1}}\)’s detector \(D_{1}\) and \(\hbox {Bob}_{{2}}\)’s detector \(D_{2}\) are clicked, and the other is that \(\hbox {Bob}_{{1}}\)’s detector \(D_{2}\) and \(\hbox {Bob}_{{2}}\)’s detector \(D_{1}\) are clicked. Errors are introduced for the other cases, for which \(\hbox {Bob}_{{1}}\)’s one detector and \(\hbox {Bob}_{{2}}\)’s one detector are clicked due to the dark count. Therefore, the transmission loss and the dark count introduce more errors in the 3d-ECQSS. In conclusion, the 3d-CQSS protocol has the advantage of its practicality compared with the 3d-ECQSS even though the state generation rate is not considered. A QSS protocol based on a 3-dimensional GHZ state would yield similar results, as the measurement setup for the 3-dimensional GHZ state QSS protocol is identical to that of the 3d-ECQSS protocol. Details of the calculation are described in the Methods section.

We compare the performance of our protocol with that of another high-dimensional QSS protocol. As an example, we consider the single-photon-based d-QSS (d-SQSS) protocol29,83. In this protocol, a dealer generates a single-photon quantum state and sends it to the players. The players then sequentially perform unitary operations chosen from a predefined set and return the results to the dealer. The dealer selects a measurement basis from the players’ broadcasts to obtain a deterministic outcome. Therefore, the protocol relies on just a single photon, and with active basis choice, only three detectors are needed. The mutual information for 3d-SQSS is shown in Fig. 6 for performance comparison. Since 3d-SQSS uses only three detectors, it is less susceptible to photon loss and detector dark counts compared to other protocols. Although SQSS appears to be the best QSS protocol in this comparison, our protocol offers certain advantages.

Transmission loss can be translated into communication distance. For instance, a typical single-mode fiber (SMF) has a loss of about 0.25 dB/km at a 1550 nm wavelength signal. Thus, the maximum distance for QSS protocols can be obtained from Fig. 6. However, due to the differences in protocol constructions, some corrections are needed in the conversion. In the case of 3d-SQSS, since the dealer generates the single photon and the photon must return to the dealer, the communication distance is effectively half of the photon transmission distance. For CQSS and MDIQSS, an untrusted third party with the correlation measurement setup can serve as an intermediary between the authorized parties, meaning the communication distances in these protocols can be doubled in the conversion of the plots in Fig. 6. In the case of 3d-ECQSS, due to the trusted device assumption, Alice must possess the entangled state generator, so the plot in Fig. 6 can be directly translated into the communication distance. With these conditions in mind, we conclude that QSS protocols with correlation measurement capabilities can achieve longer-distance quantum communication compared to other QSS protocols.

Discussion

In this article, the \((d-1,d-1)\)-threshold d-CQSS was investigated. It was shown that the d-CQSS protocol can be implemented with the current state-of-the-art technologies and is more practical compared with the entanglement-based d-QSS protocol since generation of qudit GHZ state is not necessary. By employing correlation measurement, our protocol inherently ensures MDI security35,36,38,39, meaning that all types of potential side-channel attacks exploiting detector imperfections are mitigated, especially when such imperfections pose significant security risks86. Even if an untrusted party attempts to deceive the authorized parties, the deception will influence their measurement statistics, making the attempt detectable.

The security of the d-CQSS protocol was analyzed, showing improvement on the secret key rate compared with 2d-QSS. The security when there are malicious players was investigated as well. Due to the properties of the entangled state discriminated by the correlation measurement, the advantage of high-dimensional system decreases with malicious players. However, it was shown that there is enhancement on the secret key rate compared with the 2d-QSS when there are more than two trusted players. Even when there is only one trusted player, the enhancement exists at low error regime. It was also shown that the 3d-CQSS protocol with the correlation measurement would have robustness against transmission loss compared with the entanglement-based 3d-CQSS protocol. A single-photon-based 3d-QSS protocol29,83 offers a higher secret key rate for the same transmission loss compared to our protocol. However, when translated into communication distance, our protocol outperforms in terms of the maximum achievable communication distance due to its design.

We have analyzed the security of our protocol under certain assumptions to highlight its characteristics through a simple comparison. However, in practical scenarios, these assumptions may not always hold. Several studies have focused on relaxing these assumptions, such as finite key analysis82,87,88,89 as opposed to asymptotic key rates, and analysis against coherent attacks without the i.i.d. assumption90,91. Additionally, device-independent (DI) security analysis, based on nonlocality tests, can eliminate most of the assumptions74,92,93,94,95. In DI analysis, only two assumptions are required: first, that quantum physics is correct; and second, that there is no unintended information leakage in the laboratories of each authorized party. Nonlocality tests, often referred to as Bell-type inequalities10,96, reveal correlations that cannot be explained by classical means based on measurement statistics. In other words, quantum correlations are confirmed when measurement statistics violate the Bell inequality, without assuming any specific device. For DI analysis, an appropriate Bell inequality is necessary. While the Clauser–Horne–Shimony–Holt (CHSH) inequality96 satisfies tightness and maximal violation with maximal entanglement (MVME) conditions, no such inequality exists for high-dimensional systems. The Collins–Gisin–Linden–Massar–Popescu (CGLMP) inequality97 is known as the unique tight inequality for 3-dimensional bipartite quantum systems98, but its maximal violation occurs with a partially entangled state. A nonlocality test for high-dimensional bipartite quantum systems that satisfies MVME has been proposed99. However, since our protocol relies on cyclic-entangled states for security analysis, the GHZ-type generalization cannot be applied. Therefore, it is crucial to construct a suitable nonlocality test for cyclic-entangled states to ensure the DI security of our protocol.

Methods

Three-dimensional correlation measurement

Here, click events of the three-dimensional correlation measurement are investigated. The interference among the three photons sent from the authorized parties is performed by using the tritter described in Eq. (3) and Eq. (4). The tripartite quantum states, \(|\Phi ^{3}_{(0,\sigma )}\rangle\) and \(|\Phi ^{3}_{(1,\sigma )}\rangle\) are considered where \(\sigma \in \{0,1,2\}\). In the other states, there are photons whose OAM mode is identical. This causes the two photons to enter the same detector. These states cannot be discriminated, since photon number resolving detectors are not involved in the setup.

With the tritter operation shown in Eq. (4), the detector click events can be calculated. A quantum state \(|0,1,2\rangle _{ABC}\) is transformed with the tritter operation as follows:

$$\begin{aligned} \begin{aligned} |0,1,2\rangle _{ABC} \xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left[ (|0\rangle _{A'}+|0\rangle _{B'}+|0\rangle _{C'})(|1\rangle _{A'}+\omega _{3}|1\rangle _{B'}+\omega _{3}^{2}|1\rangle _{C}')(|2\rangle _{A'}+\omega _{3}^{2}|2\rangle _{B'}+\omega _{3}|2\rangle _{C'}) \right] \\&=\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}^{2}|0,1,2\rangle _{A'B'C'}+\omega _{3}|0,2,1\rangle _{A'B'C'}\right. \\&\quad \left. +\omega _{3}^{2}|1,2,0\rangle _{A'B'C'}+\omega _{3}|1,0,2\rangle _{A'B'C'}+\omega _{3}^{2}|2,0,1\rangle _{A'B'C'}+\omega _{3}|2,1,0\rangle _{A'B'C'}+\cdots \right) . \end{aligned} \end{aligned}$$
(41)

Similarly, quantum states after tritter operation can be obtained as follows:

$$\begin{aligned} \begin{aligned} |0,2,1\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}|0,1,2\rangle _{A'B'C'}+\omega _{3}^{2}|0,2,1\rangle _{A'B'C'}\right. \\&\left. +\omega _{3}|1,2,0\rangle _{A'B'C'}+\omega _{3}^{2}|1,0,2\rangle _{A'B'C'}+\omega _{3}|2,0,1\rangle _{A'B'C'}+\omega _{3}^{2}|2,1,0\rangle _{A'B'C'}+\cdots \right) , \end{aligned}\end{aligned}$$
(42)
$$\begin{aligned} \begin{aligned} |1,2,0\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}^{2}|0,1,2\rangle _{A'B'C'}+\omega _{3}|0,2,1\rangle _{A'B'C'}\right. \\&\left. +\omega _{3}^{2}|1,2,0\rangle _{A'B'C'}+\omega _{3}|1,0,2\rangle _{A'B'C'}+\omega _{3}^{2}|2,0,1\rangle _{A'B'C'}+\omega _{3}|2,1,0\rangle _{A'B'C'}+\cdots \right) , \end{aligned}\end{aligned}$$
(43)
$$\begin{aligned} \begin{aligned} |1,0,2\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}|0,1,2\rangle _{A'B'C'}+\omega _{3}^{2}|0,2,1\rangle _{A'B'C'}\right. \\&\left. +\omega _{3}|1,2,0\rangle _{A'B'C'}+\omega _{3}^{2}|1,0,2\rangle _{A'B'C'}+\omega _{3}|2,0,1\rangle _{A'B'C'}+\omega _{3}^{2}|2,1,0\rangle _{A'B'C'}+\cdots \right) , \end{aligned}\end{aligned}$$
(44)
$$\begin{aligned} \begin{aligned} |2,0,1\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}^{2}|0,1,2\rangle _{A'B'C'}+\omega _{3}|0,2,1\rangle _{A'B'C'}\right. \\&\left. +\omega _{3}^{2}|1,2,0\rangle _{A'B'C'}+\omega _{3}|1,0,2\rangle _{A'B'C'}+\omega _{3}^{2}|2,0,1\rangle _{A'B'C'}+\omega _{3}|2,1,0\rangle _{A'B'C'}+\cdots \right) , \end{aligned}\end{aligned}$$
(45)
$$\begin{aligned} \begin{aligned} |2,1,0\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{3}}\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}+\omega _{3}|0,1,2\rangle _{A'B'C'}+\omega _{3}^{2}|0,2,1\rangle _{A'B'C'}\right. \\&\left. +\omega _{3}|1,2,0\rangle _{A'B'C'}+\omega _{3}^{2}|1,0,2\rangle _{A'B'C'}+\omega _{3}|2,0,1\rangle _{A'B'C'}+\omega _{3}^{2}|2,1,0\rangle _{A'B'C'}+\cdots \right) . \end{aligned} \end{aligned}$$
(46)

Then, the quantum states after tritter operation with \(|\Phi ^{3}_{(0,0)}\rangle _{ABC}\) and \(|\Phi ^{3}_{(1,0)}\rangle _{ABC}\) can be calculated as follows:

$$\begin{aligned} \begin{aligned} |\Phi ^{3}_{(0,0)}\rangle _{ABC}\xrightarrow {tritter}&\frac{1}{3\sqrt{2}}\left[ 2\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}\right) +(\omega _{3}+\omega _{3}^{2})\left( |0,1,2\rangle _{A'B'C'}+|0,2,1\rangle _{A'B'C'}\right. \right. \\&\left. \left. +|1,2,0\rangle _{A'B'C'}+|1,0,2\rangle _{A'B'C'}+|2,0,1\rangle _{A'B'C'}+|2,1,0\rangle _{A'B'C'}\right) \right] \\ =&\frac{1}{3\sqrt{2}}\left[ 2\left( |0,1,2\rangle _{A'A'A'}+|0,1,2\rangle _{B'B'B'}+|0,1,2\rangle _{C'C'C'}\right) -|0,1,2\rangle _{A'B'C'}-|0,2,1\rangle _{A'B'C'}\right. \\&\left. -|1,2,0\rangle _{A'B'C'}-|1,0,2\rangle _{A'B'C'}-|2,0,1\rangle _{A'B'C'}-|2,1,0\rangle _{A'B'C'}\right] , \end{aligned}\end{aligned}$$
(47)
$$\begin{aligned} \begin{aligned} |\Phi ^{3}_{(1,0)}\rangle _{ABC}\xrightarrow {tritter}&\frac{\omega _{3}^{2}-\omega _{3}}{\sqrt{6}}\left( |0,1,2\rangle _{A'B'C'}-|0,2,1\rangle _{A'B'C'}+|1,2,0\rangle _{A'B'C'}-|1,0,2\rangle _{A'B'C'}\right. \\&\left. +|2,0,1\rangle _{A'B'C'}-|2,1,0\rangle _{A'B'C'}\right) . \end{aligned} \end{aligned}$$
(48)

As shown in the above equations, the rest terms, denoted as \(\cdots\) in Eqs. (41–46), are canceled with the definitions, \(\omega _{3}^{2}+\omega _{3}+1=0\) and \(\omega _{3}^{3}=1\). From the equations, we can obtain the detector click events and their probabilities written in Eqs. (7) and (8).

The other detector click events of the quantum states exploited in the protocol are described in the following equation:

$$\begin{aligned} |\Phi ^{3}_{(0,1)}\rangle , |\Phi ^{3}_{(0,2)}\rangle ,|\Phi ^{3}_{(1,1)}\rangle ,|\Phi ^{3}_{(1,2)}\rangle \rightarrow \left\{ \begin{matrix} D_{A'0},D_{A'2},D_{B'1}\quad \text {with probability } 1/18\\ D_{A'0},D_{A'1},D_{C'2}\quad \text {with probability } 1/18\\ D_{A'0},D_{A'2},D_{B'1}\quad \text {with probability } 1/18\\ D_{A'0},D_{A'2},D_{C'1}\quad \text {with probability } 1/18\\ D_{A'0},D_{B'1},D_{B'2}\quad \text {with probability } 1/18\\ D_{A'0},D_{C'1},D_{C'2}\quad \text {with probability } 1/18\\ D_{A'1},D_{A'2},D_{B'0}\quad \text {with probability } 1/18\\ D_{A'1},D_{A'2},D_{C'0}\quad \text {with probability } 1/18\\ D_{A'1},D_{B'0},D_{B'2}\quad \text {with probability } 1/18\\ D_{A'1},D_{C'0},D_{C'2}\quad \text {with probability } 1/18\\ D_{A'2},D_{B'0},D_{B'1}\quad \text {with probability } 1/18\\ D_{A'2},D_{C'0},D_{C'1}\quad \text {with probability } 1/18\\ D_{B'0},D_{B'1},D_{C'2}\quad \text {with probability } 1/18\\ D_{B'1},D_{B'2},D_{C'1}\quad \text {with probability } 1/18\\ D_{B'0},D_{C'1},D_{C'2}\quad \text {with probability } 1/18\\ D_{B'1},D_{B'2},D_{C'0}\quad \text {with probability } 1/18\\ D_{B'1},D_{C'0},D_{C'2}\quad \text {with probability } 1/18\\ D_{B'2},D_{C'0},D_{C'1}\quad \text {with probability } 1/18 \end{matrix},\right. \end{aligned}$$
(49)

where \(D_{Xy}\) denotes a click event of the detector corresponding to the state \(|y\rangle\), the photon exists in the output port X, and the fractional numbers denote the probability of the click events. The click events of \(|\Phi _{(0,0)}^{3}\rangle\) and \(|\Phi _{(1,0)}^{3}\rangle\) are described in the maintext.

Even if photon number resolving detectors are involved, the other states cannot be discriminated. An example is described in the following equation:

$$\begin{aligned} |\Phi ^{3}_{(2,0)}\rangle ,|\Phi ^{3}_{(2,1)}\rangle ,|\Phi ^{3}_{(2,2)}\rangle ,|\Phi ^{3}_{(3,0)}\rangle ,|\Phi ^{3}_{(3,1)}\rangle ,|\Phi ^{3}_{(3,2)}\rangle \rightarrow \left\{ \begin{matrix} D_{A'2},D_{B'0}^{2}\\ D_{B'0}^{2},D_{B'2}\\ D_{B'0},D_{B'1}^{2}\\ \vdots \end{matrix}\right. , \end{aligned}$$
(50)

where the superscripts 2 in the right-hand side mean that two photons enter the detector. In conclusion, only \(|\Phi ^{3}_{(0,0)}\rangle\) is exactly discriminated by using the three-dimensional correlation measurement.

Calculations for a secret key rate of 3d-CQSS

Main results

In this section, calculation details of the secret key rate written in Eq. (37) are described. To calculate the secret key rate, it is necessary to obtain the mutual information and the Holevo information written in Eq. (18). The mutual information can be obtained from the following equation:

$$\begin{aligned} I(A,3-B_{1}-B_{2})=H(A)+H(3-B_{1}-B_{2})-H(A,3-B_{1}-B_{2}), \end{aligned}$$
(51)

where (mod 3) is omitted in the all brackets, A, \(B_{1}\), and \(B_{2}\) are encoded information of Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\), respectively, H(x) is the Shannon entropy, and H(x, y) is the joint entropy. The entropies can be evaluated by using the tripartite quantum state written in Eq. (17) and they are shown in Eqs. (52–54):

$$\begin{aligned}&H(A)=\log 3,\end{aligned}$$
(52)
$$\begin{aligned}&H(3-B_{1}-B_{2})=\log 3,\end{aligned}$$
(53)
$$\begin{aligned}&H(A,3-B_{1}-B_{2})=\log 3-\sum _{i=0}^{2}\Lambda _{i}\log \Lambda _{i}, \end{aligned}$$
(54)

where

$$\begin{aligned} \Lambda _{i}=\sum _{\sigma =0}^{2}\left[ \lambda _{(2i,\sigma )}+\lambda _{(2i+1,\sigma )}+\lambda _{(6+i,\sigma )}\right] , \end{aligned}$$
(55)

and the base 2 of all the logarithms is omitted.

The definition of the Holevo information is given as

$$\begin{aligned} \chi (A;E)=S(\hat{\rho }_{AE})-\sum _{a=0}^{2}p(a)S(\hat{\rho }_{E|A=a}), \end{aligned}$$

where \(S(\hat{\rho })\) is the von Neumann entropy. The Holevo information means that the maximum information that Eve can obtain through the quantum state. Since Alice will encrypt a classical secret by using her encoded information, a, Eve’s attack strategy is obtaining the maximum information about Alice’s encoded number. The reduced density matrix between Alice and Eve is obtained by tracing out \(\hbox {Bob}_{{1}}\)’s and \(\hbox {Bob}_{{2}}\)’s systems from the full quantum state written in Eq. (16). Eve’s conditional density matrix, \(\hat{\rho }_{E|A=a}\), can be obtained by performing projection of Alice’s system onto \(|a\rangle \langle a|\). Then the two terms in the Holevo information can be calculated as shown in Eq. (56) and Eq. (57):

$$\begin{aligned}&S(\hat{\rho }_{AE})=-\sum _{j=0}^{8}\sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\log \lambda _{(j,\sigma )},\end{aligned}$$
(56)
$$\begin{aligned}&\sum _{a=0}^{2}p(a)S(\hat{\rho }_{E|A=a})=-\sum _{j=0}^{8}\left[ \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \log \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \right] . \end{aligned}$$
(57)

From the equations, the secret key rate is obtained as shown in Eq. (58):

$$\begin{aligned} \begin{aligned} r=&\log 3+\sum _{j=0}^{8}\sum _{\sigma =0}^{2}\left( \lambda _{(j,\sigma )}\log \lambda _{(j,\sigma )}\right) -\sum _{j=0}^{8}\left[ \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \log \left( \sum _{\sigma =0}^{2}\lambda _{(j,\sigma )}\right) \right] +\sum _{i=0}^{2}\Lambda _{i}\log \Lambda _{i}. \end{aligned} \end{aligned}$$
(58)

When the depolarized state written in Eq. (23) is considered, the secret key rate becomes the equation shown in Eq. (59):

$$\begin{aligned} \begin{aligned} r=&(<span class='convertEndash'>1-3</span>\lambda _{+}-3\lambda _{=})\log 3\\&+\left[ \left( \sum _{\sigma =0}^{2}\lambda _{(0,\sigma )}\right) +3\lambda _{+}+3\lambda _{=}\right] \log \left[ \left( \sum _{\sigma =0}^{2}\lambda _{(0,\sigma )}\right) +3\lambda _{+}+3\lambda _{=}\right] \\&+\sum _{\sigma =0}^{2}\left( \lambda _{(0,\sigma )}\log \lambda _{(0,\sigma )}\right) -\left( \sum _{\sigma =0}^{2}\lambda _{(0,\sigma )}\right) \log \left( \sum _{\sigma =0}^{2}\lambda _{(0,\sigma )}\right) +6\left( \lambda _{+}+\lambda _{-}+\lambda _{=}\right) \log \left( \lambda _{+}+\lambda _{-}+\lambda _{=}\right) . \end{aligned} \end{aligned}$$
(59)

Finally, the secret key rate becomes the form described in Eq. (37) by substituting the \(\lambda\)s to the error rates defined in Eqs. (27–30).

$$\begin{aligned} \begin{aligned} r=&(1-3Q_{u}-3Q_{\pm })\log 3 -(Q_{\omega }+Q_{s}-2Q_{\pm }-3Q_{u})\\&+(1-Q_{\omega }-Q_{s}-Q_{\pm })\log (1-Q_{\omega }-Q_{s}-Q_{\pm })+3(Q_{s}-Q_{u})\log (Q_{s}-Q_{u})\\&+(Q_{\omega }-2Q_{s}-2Q_{\pm })\log (Q_{\omega }-2Q_{s}-2Q_{\pm })-(1-3Q_{s}-3Q_{\pm })\log (1-3Q_{s}-3Q_{\pm }). \end{aligned} \end{aligned}$$
(60)

Error parameters

Here, we describe how the error rates written in Eqs. (27–30) can be calculated in the 3d-CQSS protocol. First, \(Q_{p}\) is the most simple error rate to calculate. As it is shown in Eq. (28), the 3d-phase error rate is a sum of the probabilities of the tripartite quantum states which have \(\omega\) and \(\omega ^{2}\) phases. The 3d-phase error rate can be calculated from the statistics of the bar basis, since \(\bar{a}+\bar{b}+\bar{c}=0\) (mod 3) is satisfied only when there are no \(\omega\) and \(\omega ^{2}\) phases in the state. Therefore, the 3d-phase error rate can be calculated as shown in Eq. (61):

$$\begin{aligned} p(\bar{a}+\bar{b}_{1}+\bar{b}_{2}\ne 0)=\sum _{\sigma =1}^{2}\sum _{j=0}^{8}\lambda _{(j,\sigma )}=\lambda _{(0,1)}+\lambda _{(0,2)} +6\lambda _{+}+4\lambda _{-}+6\lambda _{=}=Q_{\omega }, \end{aligned}$$
(61)

where p(x) is defined as (the number of signals that x is true)/(the number of sifted signals of which bases including x are used), and (mod 3) is omitted in the bracket in the left-hand side of the equation.

The state error rate is defined as a sum of the probabilities of the states \(|\Phi _{j}^{0}\rangle\), where \(j\in \{0,1,2,...,8\}\) as shown in Eq. (27). To evaluate the state error rate written in Eq. (27), we use the equations shown in Eq. (62):

$$\begin{aligned} \begin{aligned}&p(a+b_{1}+b_{2}\ne 0 \; \& \; b_{1}\ne b_{2})=\sum _{\sigma =0}^{2}\sum _{j=2}^{5}\lambda _{(j,\sigma )}=6\lambda _{+}+6\lambda _{-},\\&p(a+b_{1}+b_{2}=0\; \& \; b_{1}\ne b_{2})=\sum _{\sigma =0}^{2}\left( \lambda _{(0,\sigma )}+\lambda _{(1,\sigma )}\right) =\left( \sum _{\sigma =0}^{2}\lambda _{(0,\sigma )}\right) +3\lambda _{+}, \end{aligned} \end{aligned}$$
(62)

and an expectation value of the operator \(\hat{X}\), which is defined in Eq. (35). The expectation value of one party, for example Alice’s, can be obtained from the following equation:

$$\begin{aligned} \langle \hat{X}\rangle _{A}=p(a=0)+\omega p(a=1)+\omega ^{2} p(a=2). \end{aligned}$$

By using the depolarized state in Eq. (23), we can obtain the value shown in Eq. (63):

$$\begin{aligned} \langle \hat{X}\hat{X}\hat{X}\rangle +\text {c.c.}=\sum _{j=0}^{8}\left( 2\lambda _{(j,0)}-\lambda _{(j,1)}-\lambda _{(j,2)}\right) =2\lambda _{(0,0)}-\lambda _{(0,1)}-\lambda _{(0,2)}. \end{aligned}$$
(63)

Then the state error rate can be obtained by using the probabilities described in Eqs. (62) and (63) as shown in Eq. (64):

$$\begin{aligned} \begin{aligned} Q_{s}=&2\lambda _{+}+2\lambda _{-}+3\lambda _{=}\\ =&p(a+b_{1}+b_{2}\ne 0 \; \& \; b_{1}\ne b_{2})-p(\bar{a}+\bar{b}_{1}+\bar{b}_{2}\ne 0)+\frac{1}{3}\left[ 2p(a+b_{1}+b_{2}=0 \; \& \; b_{1}\ne b_{2})- (\langle \hat{X}\hat{X}\hat{X}\rangle +\text {c.c})\right] . \end{aligned} \end{aligned}$$
(64)

The user error rate is easily obtained when the depolarized state is considered as shown in Eq. (30) and Eq. (34), but the 2d-phase error rate is difficult to be exactly evaluated. Therefore, the error rate is approximated by using the probability shown in Eq. (65):

$$\begin{aligned} p(\bar{a}=\bar{b}_{1}=\bar{b}_{2}\;|\; \bar{a}+\bar{b}_{1}+\bar{b}_{2}=0). \end{aligned}$$
(65)

This probability is 1/2 for the states \(\{|\Phi _{(2j,0)}^{3}\rangle \}\), zero for the states \(\{|\Phi ^{3}_{(2j+1,0)}\rangle \}\), and 1/3 for the states \(\{|\Phi ^{3}_{(6+j,0)}\rangle \}\), where \(j\in \{0,1,2\}\). From these probabilities, we define the 2d-phase error rate as Eq. (34) of which value is zero for the ideal state, \(|\Phi _{(0,0)}^{3}\rangle\), and one for the state \(|\Phi _{(1,0)}^{3}\rangle\). The 2d-phase error rate is not always the same as \(\lambda _{(1,0)}\), since the probability is affected by other states as well.

Secret key rate with experimental factors

Here, the secret key rate is evaluated by using the experimental factors, transmission loss, \(\eta\), and a dark count of single photon detectors, \(\mu\). The situation is the ideal case, where there is no Eve, and there is no state error. In the 3d-CQSS protocol, there are nine single photon detectors and three photons propagate through quantum channels. A success probability of the 3d-CQSS protocol, \(p_{3\text {MDI}}(x,y,z)\), is defined as the probability that when Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\) send the quantum states, \(|x\rangle\), \(|y\rangle\), and \(|z\rangle\) to Charlie, respectively, the result of the three-dimensional correlation measurement is \(|\Phi _{(0,0)}^{3}\rangle\). Then the success probability can be calculated from the experimental factors as shown in Eq. (66):

$$\begin{aligned} p_{3\text {CM}}(a,b_{1},b_{2})=(1-\mu )^{6}(1-\eta )^{3}+3(1-\mu )^{6}\mu (1-\eta )^{2}\eta +3(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +3(1-\mu )^{6}\mu ^{3}\eta ^{3}, \end{aligned}$$
(66)

when \(a+b_{1}+b_{2}=0\) (mod 3) and \(a\ne b_{1}\ne b_{2}\ne a\) are satisfied. The subscript 3 CM denotes the three-dimensional correlation measurement based protocol. The first term means the three photons sent from the authorized parties arrive at the measurement setup successfully, and there is no dark count. The second term is the case that one photon is lost, and the others arrive, but it is considered to be a successful trial, since one detector is clicked due to the dark count. The coefficient 3 comes from the number of possibilities that one photon is lost among the three photons. The success probability when two photons and when all the photons are lost are described in the third term and the final term, respectively. The coefficient 3 of the final term comes from the fact that there are three different click combinations considered for the successful trial, as shown in Eq. (7).

The case is considered when \(a+b_{1}+b_{2}=0\) (mod 3) and \(a\ne b_{1}\ne b_{2}\ne a\) are not satisfied. If \(a=b_{1}=b_{2}\) is true, the success probability becomes as shown in Eq. (67):

$$\begin{aligned} p_{3\text {CM}}(a,b_{1},b_{2})=3(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +3(1-\mu )^{6}\mu ^{3}\eta ^{3}. \end{aligned}$$
(67)

In this case, at least two photons should be lost, and two detectors are clicked due to the dark count for a successful trial. Therefore, the success probability has only two terms which are the cases that two photons are lost, and all the photons are lost.

If two photons have the same OAM mode, then the success probability can be obtained from Eq. (68):

$$\begin{aligned} p_{3\text {CM}}(a,b_{1},b_{2})=(1-\mu )^{6}\mu (1-\eta )^{2}\eta +3(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +3(1-\mu )^{6}\mu ^{3}\eta ^{3}. \end{aligned}$$
(68)

By using the equations, Eqs. (66–68), the error rates can be calculated as an example is shown in Eq. (69):

$$\begin{aligned} Q_{\omega }=\frac{\sum _{\bar{a}+\bar{b}_{1}+\bar{b}_{2}\ne 0}p_{3\text {CM}}(\bar{a},\bar{b}_{1},\bar{b}_{2})}{\sum _{\bar{a},\bar{b}_{1},\bar{b}_{2}=0}^{2}p_{3\text {CM}}(\bar{a},\bar{b}_{1},\bar{b}_{2})}, \end{aligned}$$
(69)

where (mod 3) is omitted.

For the entanglement-based 3d-CQSS protocol, the probabilities are changed. Assume that each party has three SPDs to discriminate three different OAM modes. The \(p_{3\text {E}}(a,b_{1},b_{2})\) is defined as a probability that Alice’s a detector, \(\hbox {Bob}_{{1}}\)’s \(b_{1}\) detector, and \(\hbox {Bob}_{{2}}\)’s \(b_{2}\) detector are clicked, and an entangled state generator produces the \(|\Phi ^{3}_{(0,0)}\rangle\) state. When \(a+b_{1}+b_{2}=0\) (mod 3) and \(a\ne b_{1}\ne b_{2}\ne a\), the probability becomes as shown in Eq. (70):

$$\begin{aligned} p_{3\text {E}}(a,b_{1},b_{2})=(1-\mu )^{6}(1-\eta )^{3}+3(1-\mu )^{6}\mu (1-\eta )^{2}\eta +6(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +12(1-\mu )^{6}\mu ^{3}\eta ^{3}, \end{aligned}$$
(70)

where the subscript 3E denotes three-dimensional entanglement-based protocol. As in Eq. (66), n-th term is defined as the probability that \((n-1)\) photons are lost, but the measured values of Alice, \(\hbox {Bob}_{{1}}\), and \(\hbox {Bob}_{{2}}\) are a, \(b_{1}\), and \(b_{2}\), respectively, due to the dark count. The first term and the second term are the same with those of Eq. (66), but there are differences in the third term and the fourth term. In the correlation measurement based 3d-CQSS protocol, if one photon arrives at the corresponding detector, the other two detectors for the successful trial is determined as shown in Eq. (7). The other detector click events are not considered, since they are discarded in the correlation-measurement based 3d-CQSS protocol. However, in the entanglement-based 3d-CQSS protocol, if one photon arrives at the detector of one party, there are only two different cases for a successful trial. If Alice’s detector \(D_{0}\) is clicked by an arriving photon, the successful trial can occur when \(\hbox {Bob}_{{1}}\)’s \(D_{1}\) and \(\hbox {Bob}_{{2}}\)’s \(D_{2}\) are clicked, or when \(\hbox {Bob}_{{1}}\)’s \(D_{2}\) and \(\hbox {Bob}_{{2}}\)’s \(D_{1}\) are clicked. Therefore, the coefficient of the third term and that of the fourth term are different from Eq. (66), and this difference enlarges the error rates of the entanglement-based 3d-CQSS protocol.

The probability can be calculated when OAM value of all the authorized parties is the same, \(a=b_{1}=b_{2}\), as shown in Eq. (71):

$$\begin{aligned} p_{3\text {E}}(a,b_{1},b_{2})=6(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +3(1-\mu )^{6}\mu ^{3}\eta ^{3}. \end{aligned}$$
(71)

The probability of two of the parties having the same results of the OAM mode detection is written in Eq. (72):

$$\begin{aligned} p_{3\text {E}}(a,b_{1},b_{2})=6(1-\mu )^{6}\mu (1-\eta )^{2}\eta +4(1-\mu )^{6}\mu ^{2}(1-\eta )\eta ^{2} +12(1-\mu )^{6}\mu ^{3}\eta ^{3}. \end{aligned}$$
(72)

By using the probabilities, the error rates can be calculated with Eq. (69), as well. Since the coefficient of the terms in Eq. (71) and Eq. (72) is greater than those in Eq. (67) and Eq. (68), the error rates of an entanglement-based 3d-CQSS protocol are greater than those of the correlation measurement based 3d-CQSS protocol.