Introduction

Brain tumors account for roughly one in four cancer-related deaths. The task of brain tumor segmentation is particularly challenging, as different tumor types require distinct segmentation approaches. Currently, manual brain tumor segmentation by experienced physicians remains the predominant method for identifying lesion locations, a tedious and time-consuming process. The development of automated and reliable brain tumor segmentation algorithms could greatly enhance tumor detection and therapy by minimizing the need for manual segmentation and expert neuroradiologist analysis.

Deep learning is currently the leading approach for brain tumor segmentation1. Most tasks can be automated using artificial neural networks, reducing the need for human intervention. AI-based tumor detection systems require large datasets that encompass diverse anatomical, pathological, and input data sequences to function effectively. Medical brain imaging data is inherently sensitive and contains personally identifiable information (PII). Strict regulations govern the sharing of medical data, enforced by frameworks such as the General Data Protection Regulation (GDPR) in Europe2 and the Health Insurance Portability and Accountability Act (HIPAA) in the United States3. Healthcare organizations often exhibit reluctance to share patient data with external parties due to concerns about data ownership. Many healthcare organizations, particularly smaller clinics and hospitals, may encounter limitations in accessing comprehensive datasets. Federated Learning (FL) addresses this challenge by enabling collaborative learning of shared machine learning models while preserving localized data4. FL is a privacy-preserving distributed machine learning approach that enables training without direct access to participant data. FL systems employ client-server communication to update the global model, where a central server initializes a machine learning model and distributes it to participating devices or servers. Each client trains the model locally on its own data and sends its computed updates to the global model after training. The central server aggregates these updates from participating clients to refine the global model, which is then redistributed for further training. By repeating this cycle of local training and global aggregation over multiple rounds, the global model improves iteratively until convergence is reached. Thus, FL not only complies with ethical and legal requirements, but also safeguards privacy, fosters inter-institutional collaboration, addresses data scarcity, and improves model generalization. Furthermore, FL minimizes the need for costly and resource-intensive data centralization efforts.

However, some hospitals and institutions may have limited annotated brain imaging data. Additionally, institutions may present imbalanced distributions of brain imaging data, with some possessing larger datasets and greater case diversity. In practical settings, data across institutions frequently exhibits non-IID (non-independent and non-identically distributed) characteristics, leading to reduced accuracy and slower convergence rates. The federated learning algorithm forms the foundation, and developing an effective client model for image segmentation in this context is critical.

Developing effective client models is essential for advancing federated training algorithms in brain tumor image segmentation. Due to the scarcity of data from multiple sources, the datasets available to each client often lack the diversity necessary to train models with robust generalization capabilities. As a result, models designed for traditional centralized training often underperform when applied across distributed clients in federated learning environments. Moreover, brain data across multiple clients often exhibits non-IID (non-independent and non-identically distributed) characteristics. The non-IID nature of the data can introduce biases that hinder model convergence and reduce accuracy. Effectively addressing the feature shift is critical to improving model generalizability in federated contexts, ensuring their durability and effectiveness across multiple data sources.

This paper addresses significant challenges in the federated learning environment, including limited annotated brain imaging data, imbalanced distributions of brain imaging data across medical institutions, and the frequent presence of non-IID data between institutions. These challenges necessitate the development of an effective client model for brain image segmentation. To address these challenges, this paper presents a Federated High-Generalization (FedHG) algorithm for brain tumor image segmentation. The main contributions of this work are highlighted as follows:

• This paper proposes a client-side brain tumor image segmentation model utilizing Virtual Adversarial Training (VAT) integrated into a 3D U-Net to improve model performance under conditions of limited datasets, effectively addressing data scarcity and imbalance within the federated learning environment by optimizing the use of brain tumor image data held by each client.

• We introduce a novel federated model aggregation mechanism in FedHG, which presents an innovative method for constructing a public validation dataset and deriving model weights from it. This approach generates more effective and balanced federated weights for model aggregation, thereby addressing performance disparities across models trained on different clients.

• FedHG addresses performance degradation due to feature shifts by preserving the instance normalization parameters within client models throughout training, thereby improving the generalizability of the federated model.

This paper is organized as follows: Sect. "Related works" presents an overview of current research and relevant studies. Section "Method" provides a detailed description of the methodology, outlining the principles and techniques used in the experiments. Section "Experiments & results" outlines the training scheme and evaluation metrics of the proposed model. Research on training, validation, and test datasets supports the results. A thorough analysis and explanation of the results is provided, along with a performance comparison of different models. Finally, Sect. "Discussion" discusses the results, while Sect. 6 concludes with a summary and implications of the results.

Related works

Image segmentation algorithms have continuously improved with advancements in deep neural networks. The application of a fully convolutional network to image segmentation, introduced in5, revolutionized the traditional approach by replacing the combining a Convolutional Neural Network (CNN) with a fully connected layer. The U-net model6 has garnered considerable attention due to its incorporation of skip connections and a U-shaped architecture, effectively exploiting spatial and contextual information to significantly improve image quality. U-net + + improves the performance of U-net by incorporating redesigned skip connections and deep supervision7. An attention gate introduced in8 improves predictive performance and accelerates training. The V-Net model extends U-net to 3D data, making it suitable for 3D image segmentation9. U-net and its variants are extensively employed for brain tumor image segmentation.

The federated learning algorithm is fundamental, as it directly determines the effectiveness of the resulting model. The pioneering aggregation algorithm, Federated Averaging (FedAvg)10, aggregates client parameters to improve model performance. Building on FedAvg, the Federated Proximal (FedProx) algorithm11 introduces a generalized approach that addresses both system and statistical heterogeneity in participant data, leading to significant improvements. Federated Learning with Local Batch Normalization (FedBN) integrates local batch normalization to mitigate feature shifts before model averaging, demonstrating superior performance over FedAvg and FedProx12. FedSR incorporates Domain Generalization (DG) to enhance model generalization and applies regularization techniques to emphasize critical information13. Federated cross-correlation and continuous learning were introduced to address both heterogeneity and catastrophic forgetting14. Robust Heterogeneous Federated Learning was proposed to mitigate the impact of both internal and external noise on model performance15. An efficient adaptive algorithm for cross-silo federated learning was developed to tackle convergence and adaptivity challenges in non-convex distributed problems, offering theoretical guarantees and improving sampling complexity for identifying epsilon-stationary points16. Federated learning was also adaptively extended to adjust aggregation weights based on dataset discrepancies, outperforming existing methods and providing a modular solution for handling heterogeneous data distributions17. Another extension of federated learning introduced learnable aggregation weights, enhanced generalization through global weight regularization, and improved client coherence, achieving superior performance across diverse datasets and models18. A server-side federated learning algorithm was proposed to enhance group fairness without compromising local data privacy, effectively addressing bias and data heterogeneity in distributed data scenarios19. To tackle data heterogeneity, the harmonization of local and global drifts in federated learning was proposed20, where images were converted into the frequency ___domain to create a unified image frame, mitigating the problem of feature drift. Additionally, improvements were made in calculating the loss function for local models, allowing the participant server model to more closely approximate the local optimum. A novel federated learning approach was introduced to mitigate performance degradation due to data heterogeneity across institutions while maintaining accuracy and mean absolute error comparable to centralized training in diverse medical imaging tasks21. Lastly, a federated learning framework tailored for COVID-19 detection in CXR images was developed, focusing on model accuracy and stability by dynamically adjusting parameter aggregation weights based on training loss22.

The efficacy of a federated learning algorithm for image segmentation can be assessed through the evaluation of the learned models. Federated learning was initially applied to brain tumor image segmentation23. Subsequently24, demonstrated its broad applicability in the medical industry by employing the federated learning system in real-world scenarios involving multiple hospitals. In the ___domain of brain pathology segmentation25, introduced the Federated Disentanglement algorithm, which assumes uniform anatomical structure information across all images. Incremental Transfer Learning (ITL), presented in26, offers a novel multi-site segmentation approach by capitalizing on the informative properties of combined embedding features across datasets, enabling sequential training of a model in an end-to-end manner27. introduced a class-aware transformer module designed to enhance the learning of discriminative object regions through pyramid and semantic structures. This module employs a transformer-based discriminator that captures both low-level anatomical features and high-level semantically related content through adversarial training, thereby improving segmentation accuracy28. utilized knowledge distillation (KD) within a multi-head U-Net architecture to develop models that learn a shared embedding space for segmenting various organs. Finally29, introduced a multi-encoding U-Net that employs different encoding subnetworks to extract organ-specific features, with each subnetwork functioning as an expert specialized in a particular organ.

The challenge of insufficient datasets continues to be a significant issue. In30, synthetic anonymous brain vascular images are generated for medical imaging. These advancements underscore the significant evolution of Generative Adversarial Networks (GANs), broadening their applications in medical imaging segmentation. However, this approach may be susceptible to model collapse. In31, the self-supervised Federated Learning (FL) framework is proposed, which enhances medical image analysis by pre-training Transformer-based models on decentralized datasets to improve robustness and generalization. In32, the Inside-Outside Personalization framework for Federated medical image segmentation is introduced to advance federated learning in medical image processing by personalizing models for individual clients and previously unseen data distributions33. presents a straightforward yet effective framework for contrastive distillation, which predicts signed distance maps of object boundaries from dual perspectives within a contrastive framework34. introduces a contrastive voxel-wise representation learning technique that effectively captures both low-level and high-level features35. presents an anatomy-aware discriminative framework that selectively samples a sparse set of challenging negative pixels, capturing semantically related features, which results in smoother segmentation boundaries and improved prediction accuracy. Finally36, presents an enhanced contrastive learning framework that employs a dynamic scheduling approach to achieve improved separation, along with an adaptive anatomical contrast method for semi-supervised medical segmentation.

This paper proposes a client-side brain tumor image segmentation model utilizing Virtual Adversarial Training (VAT) integrated into a 3D U-Net to improve model performance under conditions of limited datasets. The model seeks to optimize the use of brain tumor image data possessed by each client. Furthermore, it constructs a public validation dataset to derive representative weights and incorporates instance normalization parameters into client models during training to enhance the generalizability of the federated model.

Method

Overall architecture

This paper proposes a client-side brain tumor image segmentation model based on Virtual Adversarial Training (VAT), which is incorporated into a 3D U-net to enhance model performance under limited dataset conditions. The model aims to optimize the utilization of brain tumor image data owned by each client while improving the generalizability and robustness of the model through the VAT technique. This approach addresses the challenge of insufficient client data and facilitates more accurate image segmentation results in a collaborative environment.

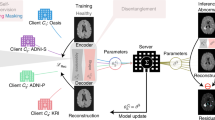
The structure of the client-side brain tumor image segmentation model utilizing VAT is depicted in Fig. 1. Both modules integrate loss functions with back-propagation to update the parameters of the image segmentation model. The U-Net framework is detailed in the section "Client-side brain tumor image segmentation model". ② implement federal model update based on the weights of public validation datasets, is discussed in the section "Weighted federated model update based on the public validation set". ④ accomplishes client model updates based on local IN, which is discussed in the section "Client-side model update based on local instance normalization".

Fig. 1
figure 1

Overall Diagram of Brain Tumor Image Segmentation.

Full size image

The VAT module enhances the model’s robustness against input perturbations. By introducing adversarial perturbations to the original image, VAT facilitates improved generalization to new data. This improvement is quantified by measuring the divergence between the model’s output distribution under perturbation and the original data’s labeling distribution using Kullback-Leibler (KL) divergence. Incorporating VAT effectively improves the generalization of the federated model and enhances the overall efficacy of federated learning.

The federated training environment for brain tumor image segmentation involves \(\:n\:(where\:n\ge\:2)\) hospitals, with the set of all clients denoted as \(\:C=\{{C}_{i},i\in\:[1,n\left]\right\}\). Each client \(\:{C}_{i}\) possesses a dataset \(\:{D}_{c}=\{{X}_{i},{Y}_{i}\}\), consisting of \(\:{J}_{i}\:(where\:i\in\:[1,n\left]\right)\) labeled images, which is kept locally. Here, \(\:{X}_{i}=\{{x}_{i}^{j},j\in\:[1,{J}_{i}\left]\right\}\) represents the raw brain tumor images of client \(\:i\), and \(\:{Y}_{i}=\{{y}_{i}^{j},j\in\:[1,{J}_{i}\left]\right\}\) represents the corresponding labels. All clients aim to engage in federated training while maintaining local data storage to develop an effective brain tumor image segmentation model \(\:{M}_{s}\), thereby ensuring data privacy. The server S facilitates the training of the federated model by minimizing the objective function \(\:F\left({M}_{s}\right)\), as shown in Eq. (1). In this context, \(\:l(x,y,w)\) denotes the loss value computed for input \(\:x\) and label \(\:y\) using model parameters \(\:w\).

$$\:\begin{array}{c}\begin{array}{c}min\\\:{M}_{s}\in\:{\mathcal{R}}^{d}\end{array}\left\{F\left({M}_{s}\right)={\sum\:}_{i=1}^{n}\frac{1}{{J}_{i}}\text{*}l\left({x}_{i},{y}_{i},\:{M}_{g}\right),\:{x}_{i}\in\:{X}_{i},{y}_{i}\in\:{Y}_{i}\right\}\:\:\end{array}$$
(1)

The Federated High-Generalization algorithm (FedHG) for brain tumor image segmentation training is a client-side model that incorporates virtual adversarial training to mitigate the limitations posed by small datasets from individual sources. It also integrates a federated model updating algorithm that leverages weights from a public validation set to effectively evaluate and balance client inputs for more accurate model aggregation. Furthermore, FedHG introduces a client-side model updating technique that applies local instance normalization to address feature shift challenges.

Client-side brain tumor image segmentation model

The client-side brain tumor image segmentation model consists of two modules: the image segmentation module and the Virtual Adversarial Training (VAT) module. These modules work together to update the parameters of the image segmentation model using a combined loss function, as shown in Eq. (2), where \({L}\) denotes the loss function for the model.

$$\:\begin{array}{c}L={{\lambda\:}_{seg}\text{*}L}_{seg}+{{\lambda\:}_{vat}\text{*}L}_{vat}\end{array}$$
(2)

Where \(\:{L}_{seg}\)​ and \(\:{L}_{vat}\) represent the loss values of the image segmentation module and VAT modules, respectively, where \(\:{\lambda\:}_{seg}\)​ and \(\:{\lambda\:}_{vat}\) represents their respective weights.

The image segmentation module plays a crucial role in the client-side brain tumor image segmentation system, utilizing the 3D U-net architecture depicted in Fig. 2.

Fig. 2
figure 2

The Image Segmentation Module of FedHG.

Full size image

This architecture represents a convolutional neural network (CNN) tailored for 3D medical imaging. The 3D U-net adopts an encoder-decoder architecture. The encoder compresses spatial data, extracting features through 3D convolution and pooling operations. The decoder utilizes 3D transposed convolution to enhance spatial resolution and integrates the encoder’s feature maps through skip connections to reconstruct detailed spatial information. The network architecture incorporates a normalization layer and applies the Rectified Linear Unit (ReLU) activation function after each convolutional operation. This configuration is designed to improve training stability, convergence speed, and the model’s generalization capabilities. The segmentation loss, \(\:{{L}}_{{seg}}\), employs the Dice Loss function to measure the similarity between the model’s predictions and the true labels. The Dice Similarity Coefficient (DSC) forms the basis of the Dice Loss by quantifying the overlap between segmentation predictions and ground truth labels. The DSC ranges from 0 to 1, with 0 indicating no overlap and 1 representing perfect overlap. A higher DSC indicates greater segmentation accuracy. Equation (3) provides the formal definition for calculating the DSC.

$$\begin{array}{*{20}c} {DSC\left( {\hat{Y},Y} \right) = ~\frac{{2 \times \left| {\hat{Y} \cap ~Y} \right| + \varepsilon }}{{\left| {\hat{Y}} \right| + \left| Y \right| + \varepsilon }}} \\ \end{array}$$
(3)

Here, Ŷ represents the predicted output of the image segmentation module, Y is the annotated true label, and ϵ is the smoothing factor, typically set to 1. The Dice loss complements Dice Similarity Coefficient (DSC), as depicted in Eq. (8).

The Virtual Adversarial Training (VAT) module significantly enhances a model’s robustness to input perturbations, thereby augmenting its capacity to generalize to new data. It achieves this by introducing minor adversarial perturbations to the original images and measuring the divergence between the Kullback-Leibler (KL) divergence between the model’s output distribution with perturbed inputs and the label distribution of the original data. This characteristic of the VAT module is particularly beneficial for federated learning client models that require robustness to diverse data sources. Integrating the VAT module can substantially enhance the federated model’s generalization capabilities, thus increasing the effectiveness of federated training. Furthermore, the loss function associated with the VAT module, denoted as \(\:{L}_{vat}\) and also referred to as Local Distributional Smoothness (LDS), quantifies the smoothness and consistency of the model output within a small neighborhood surrounding the input data points. This ensures that the model output remains consistent despite slight changes in the input data. Equation (4) presents the formulation for \(\:{L}_{vat}\).

$$\:\begin{array}{c}\:{L}_{vat}\left(X,Y,\theta\:\right)=\:{D}_{KL}(Y\left|\theta\:\left(X+{r}_{adv}\right)\right)\:\end{array}$$
(4)

Where X and Y represent the data and labels of the dataset, and θ represents the client’s image segmentation model. \(\:{r}_{adv}\) is the adversarial perturbation applied to the image, which reveals the most sensitive perturbation direction in the model’s input space and is used to generate adversarial samples, thereby increasing the model’s robustness. Equation (5) indicates that the initial value of\(\:{r}_{adv}\) follows a standard normal distribution with a mean of zero and a variance of one.

$$\:\begin{array}{*{20}c} {r_{{adv}} \sim {\text{N}}(x\:|\:\mu \: = 0,\:\sigma \:^{2} = 1)\:} \\ \end{array}$$
(5)

The VAT (Virtual Adversarial Training) module adds minute adversarial perturbations to the original image. It then measures the divergence between the model’s output distribution, when presented with the perturbed input, and the original data’s label distribution, using the Kullback-Leibler (KL) divergence. This process enables the model to become more resilient to input variations, ultimately leading to improved generalization performance on unseen data.

Equation (6) provides the formal definition of KL divergence.

$$\:\begin{array}{c}{D}_{KL}\left(P|Q\right)=\:\sum\:P\left(x\right)*\:log\left(\frac{P\left(x\right)}{Q\left(x\right)}\right)\:\end{array}$$
(6)

During the computation of \(\:{L}_{vat}\), the adversarial perturbation \(\:{r}_{adv}\) is updated iteratively. At each iteration, the gradient is updated by evaluating the Kullback-Leibler (KL) divergence loss between the model output modified by the perturbation applied to the current dataset and the original labels, using backpropagation. At each step, \(\:{r}_{adv}\) is refined to maximize the KL divergence. After a specified number of iterations, the final perturbation \(\:{r}_{adv}\) is obtained.

Weighted federated model update based on the public validation set

The federated model updating approach employs weights derived from the public validation set, involving all federated clients and the central server. This approach incorporates a client-side validation module, enabling the assessment of each client’s model performance after a predetermined number of training rounds. Objective performance metrics are evaluated and then sent to the central server. After receiving the model weights and performance evaluations from all participating clients, the central server aggregates the model updates using a specialized algorithm.

Initially, the central server owns a common validation set \(\:{D}_{t}\). This set, \(\:{D}_{t}\), comprises representative data while maintaining user privacy. This public validation set provides a consistent and unbiased evaluation standard for models across various clients. Typically, the public validation set is derived from extensive public datasets.

Next, client \(\:i\) uses its local data to train the model \(\:{M}_{i}\) and subsequently calculates the segmentation performance \(\:{s}_{i}\) of the model on the public validation set \(\:{D}_{t}\). \(\:{s}_{i}\) is computed using the Dice coefficient. Given that the client-side brain tumor image segmentation model may produce results across multiple modalities, an average is computed. The calculation method for \(\:{s}_{i}\) is detailed in Eq. (7).

$$\:\begin{array}{c}{s}_{i}=\underset{a\_regions}{\mu\:}\left(DSC\left({M}_{i}\left({X}_{t}\right),{Y}_{t}\right)\right)\end{array}$$
(7)

After all clients have completed the training and validation modules, the calculated \(\:{s}_{i}\) values, denoted as \(\:S=\:\left\{{s}_{i}\right|i\in\:\:[1,\:N]\}\), are uploaded to the central server to calculate the weights for the federated model updates. Next, the weights for updating the federated model are computed, which consisting of two parts: the base weight and the validation weight, as detailed in Eq. (8).

$$\:\begin{array}{c}W={\lambda\:}_{base}\times\:{W}_{base}+{\lambda\:}_{pv}\times\:{W}_{pv}\end{array}\:\:$$
(8)

Here, \(\:{W}_{base}\) and \(\:{W}_{pv}\) represent the base weight and the validation weights, respectively. \(\:{\lambda\:}_{base}\) and \(\:{\lambda\:}_{pv}\) represent the proportions of the two components, where their sum is one. The base weight, analogous to the weights used in FedAvg, is calculated as the reciprocal of the total number of clients. Equation (9) defines how the base weight ensures each client contributes to the federated model in every communication round.

$$\:\begin{array}{c}{W}_{base}=\frac{1}{N}\:\end{array}$$
(9)

The validation weight is determined using the segmentation effects, denoted as \(\:S\), computed by the clients, as shown in Eqs. (10) and (11).

$$\:\begin{array}{c}{W}_{pv}=\frac{{max}\left(s-{\mu\:}_{s},0\right)}{\sum\:_{s}{max}\left(s-{\mu\:}_{s},0\right)}\end{array}$$
(10)
$\mu_s=\frac{\underset {k \in [1, N]_k} {\sum}s }{|C_1|}$
(11)

The validation weight \(\:{W}_{pv}\) is computed as the non-negative normalized result of \(\:s\:-\:{\mu\:}_{s}\), where \(\:{\mu\:}_{s}\) is the average value of \(\:S\). This ensures that client models that perform better on the public validation set have a greater influence on the federated model. This weighting technique accounts for performance variations among client models by assigning more weight to those with better results, thereby enhancing their contribution to the federated model updates. Finally, the central server updates the federated model for the current round by integrating the received client model parameters. Each client contributes the product of its model parameters and the corresponding update weights.

Client-side model update based on local instance normalization

FedBN12 addresses feature shift in federated learning by introducing client-specific Batch Normalization (BN), which allows each client to maintain distinct mean and variance parameters derived from its local data distribution. This approach mitigates the degradation in global model performance caused by feature shift. However, in brain tumor image segmentation, the large model and image sizes necessitate small batch sizes, which lead to inaccurate BN statistical estimates. Therefore, directly applying local BN in this scenario becomes impractical.

Instance Normalization (IN), which emphasizes stylistic features and reduces contrast, effectively mitigates feature shift across clients, regardless of batch size, making it well suited for brain tumor segmentation. Building on the FedBN approach to addressing feature shift and considering the characteristics of alternative normalization techniques, this study proposes a client model updating algorithm that leverages localized Instance Normalization (IN). This novel approach removes the IN layer from client-side model updates, while preserving the distinct normalization parameters for each model. Consequently, this method enhances the model’s adaptability to varying data distributions across individual clients, thereby strengthening the generalization capabilities of the federated model across diverse datasets.

Algorithm 1
figure a

Client Model Update Algorithm Based on Local IN.

Full size image

Experiments & results

Setups environment preparation

A series of experiments were conducted using an Intel(R) Core (TM) i5-10600KF 4.10 GHz CPU, 32.0 GB of RAM, and a GeForce GTX 4070Ti GPU. The experiments were performed using Python 3.8.0 and PyTorch 2.2.2.

Datasets

The Brain Tumor Segmentation (BraTS) dataset is a widely recognized and frequently utilized benchmark in medical image analysis, especially for brain tumor segmentation tasks. This dataset was employed to evaluate the performance of our proposed model. The BraTS 2021 dataset consists of over 1000 patients, with each patient’s data comprising five components: (a) native T1-weighted (T1), (b) post-contrast T1-enhanced (T1ce), (c) T2-weighted (T2), (d) T2 Fluid-Attenuated Inversion Recovery (T2-FLAIR) volumes, and (e) manually segmented ground truth. The ground truth is divided into four regions: GD-enhancing tumor (ET, labeled as 4), peritumoral edematous/infiltrated tissue (ED, labeled as 2), necrotic tumor core (NCR, labeled as 1), and the background (labeled as 0). The objective of segmentation is to accurately delineate three distinct subregions based on these components. These subregions are: (1) ET, which includes only the enhancing tumor portion (pixels labeled as 4); (2) TC, which includes both the enhancing and non-enhancing tumor portions (pixels labeled as 1 and 4); and (3) WT, which contains all three tumor portions (with non-zero pixel values).

Preprocessing of the datasets

The dataset consists of over 1000 images. 85% of the images are distributed across multiple clients for model training, forming the training dataset. Each client uses 20% of the images as the test dataset, while the remaining 80% are used for training. The remaining 15% of the images comprise the validation set. For the validation set, 60% is designated for generating weights for the client models, while the remaining 40% is used to evaluate the federated learning model’s performance. The original images have dimensions of 240 × 240 × 155 pixels. Each image is resized to 155 × 240 × 240 pixels and subsequently used as input for the model on each client.

Evaluating metrics

Segmentation performance in this study is evaluated using the Dice Similarity Coefficient (DSC), as presented in Eq. (3). The models segment the ET, TC, and WT regions by calculating and reporting DSC values for each region independently. The average DSC across these regions, referred to as the MEAN, serves as the primary metric for evaluating the overall model performance. This metric reflects the average DSC across the three target regions, providing a reliable measure of the federated model’s test accuracy variability across multiple training rounds.

$$\:\begin{array}{c}Dic{e}_{coef}\left({Y}_{p},Y\right)\:=\:1-Dice\left({Y}_{p},Y\right)\:\end{array}$$
(12)

Experimental results

Controlled experiment

This controlled experiment aims to evaluate the effectiveness of the FedHG algorithm. FedHG is compared against the baseline federated learning algorithm, fedavg, to highlight performance differences. The baseline segmentation model is independently deployed on 20 clients for brain tumor image segmentation, illustrating the segmentation effectiveness when clients train exclusively on their local datasets. In addition, a centralized training model aggregates all client datasets to provide a comprehensive comparison. In the simulation, 20 hospital clients participate in federated training for brain tumor image segmentation, utilizing both FedHG and fedavg. To simulate a realistic federated learning environment, examples from the training dataset are randomly distributed among the 20 clients. Due to differences in algorithmic design, fedavg.does not require a public validation set. In the simulation, the hyperparameter settings for both federated learning algorithms are kept consistent.

The client training round is set to 1; the learning rate is set to \(\:2\times\:{10}^{-4}\), the width of the U-net model is 32, the optimizer algorithm is adam, and the number of federated training rounds is 50. The base weight \(\:\left({{\lambda\:}}_{{base}}\right)\) and the validation weight \(\:\left({{\lambda\:}}_{{pv}}\right)\) for the federated weight calculation are both set to 0.5. The dropout rate is set to 0 in this experiment to enable the federated model to learn as many features as possible from the client data. In the local client experiments, the dataset allocation adheres to the FedAvg experiment’s scheme, with each client allocated 56 cases. In the centralized dataset training, the training set consists of the combined data from all clients. Other experimental conditions are consistent with those of the federated environment experiment.

Table 1; Fig. 3 compare the performance of the four training approaches—FedHG, fedavg, client-side local training, and centralized dataset training—over 50 rounds of federated training, evaluating the dice similarity coefficient (DSC) in the ET, TC, WT, and mean regions. The line plots illustrate the variation in DSC values across federated training rounds.

In a comparison between the FedHG and FedAvg federated learning algorithms, FedHG outperforms FedAvg in the ET, TC, WT, and mean regions by margins of 3.7%, 1.1%, 0.8%, and 2.2%, respectively. Figure 3 shows that FedHG converges more rapidly than fedavg, achieving optimal performance by the 33rd round, whereas FedAvg only reaches this threshold after 50 rounds of federated training.

Table 1 Performance comparison of different methods across different rounds.
Full size table
Table 2 Performance comparison on non-IID distribution cases.
Full size table

Partitioning the BraTS 2021 dataset into a non-IID distribution entails distributing data across multiple clients, where each client receives a distinct subset that does not necessarily represent the overall distribution. The BraTS 2021 dataset comprises glioma images, annotated for distinct tumor regions: Enhancing Tumor (ET), Tumor Core (TC), and Whole Tumor (WT). Each patient’s data typically includes multiple MRI modalities, such as T1, T1Gd, T2, and FLAIR. Labels were redistributed among clients to establish non-IID federations, thereby diversifying data distribution in accordance with the methodology outlined in37.

Case 1

Partitioning by Tumor Type:

  • Client 1 is allocated predominantly High-Grade Glioma (HGG) cases (80%).

  • Client 2 receives a majority (80%) of Low-Grade Glioma (LGG) cases.

  • Client 3 receives a randomized selection of cases or a mix of tumor types from the remaining data.

  • Client 4 follows the same strategy, receiving a randomized selection or a mix of tumor types.

Case 2

Partitioning by Tumor Sub-Region:

Images are assigned based on tumor sub-regions (ET, TC, WT). Client 1 predominantly receives ET images (80%), Client 2 receives mainly TC images (80%), Client 3 primarily receives WT images (80%), while Client 4 is assigned the remaining data.

Case 3

Partitioning by Tumor Size:

The dataset was partitioned into four subsets according to tumor core volume: Client 1 was allocated data with tumor volumes of 3 cm³ or less, Client 2 received data with tumor volumes greater than 3 cm³ but less than or equal to 6 cm³, Client 3 was allocated data with tumor volumes greater than 6 cm³ but less than or equal to 9 cm³, and Client 4 was assigned data with tumor volumes exceeding 9 cm³.

By following the steps outlined above, the BraTS 2021 dataset can be efficiently partitioned into a non-IID distribution, making it suitable for federated learning experiments. Table 2 shows that FedHG outperforms FedAvg in the ET, TC, and WT categories, respectively.

Fig. 3
figure 3

DSC Comparison for Different Methods on Different Rounds.

Full size image

The FedHG algorithm demonstrates significant improvements over client-side local training, showing notable performance gains after only two rounds of federated training. These results underscore the substantial advantages of federated learning algorithms compared to client-side local training. Furthermore, when compared to the centralized training strategy, the DSC for FedHG is only 3% lower, highlighting its strong practicality.

Fig. 4
figure 4

The Actual Segmentation Effects for Different Methods.

Full size image

Figure 4 presents the segmentation results of FedHG, FedAvg, centralized training, and client-side local training. Clients numbered 5 and 15 were randomly selected to exemplify the performance of client-side local training. The segmentation performance of FedHG is comparable to that of centralized training, aligning more closely with the true labels than FedAvg, thereby demonstrating superior segmentation capabilities.

Stability testing

In federated learning environments, client dropouts—whether temporary or permanent—are inevitable due to device or network-related issues. Stability testing was conducted to evaluate the FedHG algorithm’s ability to address this challenge.

The experiment assumes that each client has a probability of failing to upload its local model during a federated training round. Clients that fail to upload their local models will not participate in the current federated training round and will not contribute to updating the federated or local models. However, local training will proceed as usual.

The simulation assumes that the probability of client dropouts across training rounds is independent. Let \({d}\) denote the probability of a client dropout. This experiment evaluates the impact of \({d}\) on the performance of the federated model using fedhg, with \({d}\) ranging from 0 to 0.6 in increments of 0.2.

Table 3; Fig. 5 present the highest dice similarity coefficients (DSC) achieved by the FedHG algorithm in the ET, TC, WT, and mean regions after 50 rounds of federated training under varying client dropout probabilities (\({d}\)). Additionally, Fig. 4 illustrates the fluctuation of DSC values over the course of the federated training rounds.

Table 3 DSC performance of FedHG in various regions under different value image.
Full size table
Fig. 5
figure 5

DSC Performance of FedHG in Various Regions under Different Value Dropout Rate.

Full size image

At a dropout rate of \({d}\)=0.2, the peak and variability of the Dice Similarity Coefficient (DSC) during training are similar to those observed at \({d}\)=0, demonstrating the FedHG algorithm’s robustness against minor client dropout events. As \({d}\) increases to 0.4, FedHG experiences a moderate degradation in DSC, with an average decrease of 1.3% and a slight reduction in convergence speed. Nevertheless, FedHG’s performance under these conditions continues to surpass that of the FedAvg algorithm. At a dropout rate of \({d}\)=0.6, the DSC in the Enhancing Tumor (ET) region experiences a notable decline, accompanied by significant fluctuations during training. Nevertheless, FedHG maintains a high training effectiveness despite these challenges.

In practical federated settings, particularly where client devices are prone to instability yet maintain a dropout rate below \({d}\)=0.5, client selection processes in brain tumor image segmentation within federated learning typically prioritize stability, underscoring the practicality of the FedHG approach.

Ablation experiment

FedHG introduces three significant enhancements over the traditional FedAvg federated learning approach: virtual adversarial training, a weighted aggregation mechanism utilizing a public validation set, and localized Instance Normalization (IN) during client model updates.

The ablation experiment involves the individually removing each of the three enhancements: virtual adversarial training, weighting based on a public validation set, and localized Instance Normalization (IN).

In the experiment excluding weighting based on a public validation set, the base weight \(\:{{\lambda\:}}_{{base}}\) for the federated weight calculation is set to 1, and the validation weight \(\:{{\lambda\:}}_{{pv}}\) is set to 0. The experiment excluding localized Instance Normalization involves only the omission of maintaining the IN layer parameters on the client side, while the model structure for brain tumor image segmentation remains unchanged. Aside from these modifications, all other experimental parameters remain consistent with those employed in the comparative experiment for FedHG.

Table 4 The DSC performance of FedHG for different regions during ablation experiment.
Full size table
Fig. 6
figure 6

The DSC Changes in FedHG during Ablation Experiment.

Full size image

Table 4; Fig. 6 present the Dice Similarity Coefficient (DSC) results for FedHG across the ET, TC, WT, and mean regions after 50 rounds of federated training. They include line graphs illustrating the DSC variations throughout federated training rounds. Figure 6 shows that omitting the weighted public validation set leads to a slight decrease in the final DSC score and a significant reduction in the convergence rate. This finding suggests that incorporating the federated aggregation technique with a weighted public validation set accelerates convergence, reducing the number of iterations required to achieve optimal results. Omitting the other two enhancements does not substantially impact convergence but causes a slight decrease in the DSC score, ranging between 1.1% and 1.5%. These findings confirm that the three enhancements proposed in this study significantly improve brain tumor segmentation performance.

Discussion

Federated learning for medical image segmentation presents unique challenges compared to conventional methods. Key challenges associated with federated learning in medical image segmentation include: Data Privacy: Federated learning adheres to stringent privacy constraints, ensuring data remains decentralized on client devices. Data Imbalance: Variability in data distribution across different clients can introduce bias into the federated model, resulting in non-IID (independent and identically distributed) data that impacts segmentation accuracy and generalizability. Adaptability to Local Data: Federated learning models must adjust to local data characteristics while preserving overall performance, requiring robust adaptation mechanisms. Computational and Infrastructural Requirements: Training complex models for brain image segmentation necessitates significant computational resources. Not all participating institutions possess the necessary infrastructure to support such intensive computations. Solutions such as federated edge computing, which utilizes edge devices to distribute the computational burden, and resource-efficient algorithms are crucial to addressing this issue. Validation and Evaluation: Assessing and validating federated learning models across multiple institutions, while ensuring clinical relevance and safety, remains a significant challenge.

To the best of our knowledge, this study is the first to provide a quantitative assessment of generalization using the BRATS2021 dataset within the framework of federated learning (FL). We integrate Virtual Adversarial Training (VAT) to address data limitations at each client by generating synthetic data that closely mimics authentic medical images. This approach augments the limited local datasets at each client, thereby improving the robustness and generalizability of the federated model. Additionally, it balances class distributions and mitigates data skew, further enhancing the model’s overall performance and fairness.

The Federated High-Generalization algorithm (FedHG) effectively aggregates models by evaluating them with a unified public validation set across all clients, significantly enhancing training results. This method ensures that model performance metrics are comparable and reflective of the overall efficacy of the federated learning system. This approach facilitates equitable comparisons among different federated learning methods and implementations. Validation frameworks in federated learning help ensure adherence to regulatory requirements and standards.

Moreover, the innovative approach of Federated Batch Normalization (FedBN) has significantly impacted our research. FedHG tackles the feature shift problem across various clients by utilizing FedBN’s method to replace batch normalization layers with instance normalization layers. This method allows for adaptation to client-specific data distributions without necessitating raw data sharing, thereby improving the convergence and generalization of federated models. FedBN’s client-specific normalization allows models to adapt more efficiently to the local data characteristics of each client.

Empirical experiments substantiate the efficacy of the proposed algorithm, demonstrating a 2.2% improvement in the Dice coefficient for brain tumor image segmentation compared to the baseline federated learning algorithm. The algorithm demonstrates substantial stability, with its Dice Similarity Coefficient (DSC) in the enhancing tumor (ET), tumor core (TC), whole tumor (WT), and mean regions exceeding that reported in32 by 5%. It also surpasses DResU-Net and AD-Unet by 2–4%38. Additionally, the DSC for FedHG is only 3% lower than that of the centralized training strategy, highlighting its considerable effectiveness.

Conclusion

This paper addresses critical challenges in brain tumor image segmentation within a federated framework and introduces the FedHG algorithm. FedHG effectively addresses key challenges, including data scarcity at individual clients, variations in local model training, and feature discrepancies across the federated network. The algorithm improves the generalizability and robustness of segmentation models by integrating Virtual Adversarial Training (VAT) with a 3D U-net architecture, addressing data scarcity and imbalance in the federated learning environment. The adoption of a model aggregation technique using weights derived from the public validation set helps to reduce performance disparities among models. FedHG also mitigates the adverse effects of feature shift by preserving instance normalization parameters within client models. Comprehensive evaluations, including comparative assessments, stability tests, and ablation experiments, demonstrate the effectiveness and robustness of the FedHG architecture in brain tumor image segmentation within a federated environment. Future research may explore adaptive model training techniques and efficient, secure communication methods for federated learning (FL) frameworks.