Abstract
To address the issue of controlling the deformation of adjacent tunnels after excavation of the foundation pit, a method combining servo steel strut and capsule grouting for controlling the deformation of adjacent tunnels is proposed. First, the scaled model tests were conducted to determine the influence of the number of servo loading and their arrangement on the stress and deformation of the tunnel and diaphragm wall under the same capsule grouting conditions. This led to the identification of the optimal servo loading mode. Subsequently, numerical simulations were performed to analyze the effects of different double-row capsule grouting spacings on the tunnel and diaphragm wall under the optimal servo loading mode. The research results indicate that in the model tests, both servo loading and capsule grouting reduce the horizontal deformation and horizontal convergence of the tunnel but increase the tunnel settlement and pressure at the right hance. The greater the number of servo loading struts, the more effective the control of deformation in the diaphragm wall and tunnel. When the number of servo steel strut is constant, the closer the burial depth of the servo loading arrangement is to the burial depth of the tunnel axis, the greater the deformation of the tunnel. In the numerical simulations, the change in the horizontal spacing of the double-row capsule grouting has a greater impact on the deformation of the diaphragm wall and the right hance of the tunnel than changes in the tunnel clearance. The smaller the horizontal spacing, the greater the deformation of the diaphragm wall and the right hance of the tunnel.
Similar content being viewed by others
Introduction
Excavation of foundation pits can induce deformation of diaphragm walls, which may further exacerbate the deformation of adjacent tunnels. Excessive tunnel deformation can lead to safety hazards such as segment cracking, water seepage, localized fragmentation, and track bed separation, which seriously threaten the safety of subway operations1,2,3,4. These failures are further manifested in full-scale tests where shield tunnel segments exhibit circumferential cracking and joint dislocation under excavation-induced deformation5,6. Measures such as partitioned and block excavation of the foundation pit and the installation of isolation piles (walls) can control the impact of excavation on adjacent tunnels to a certain extent, Although passive measures like partitioned excavation can delay deformation development7, they cannot eliminate existing deformation, which further justifies the necessity of the combined active control technology proposed in this study. Therefore, effective active control measures are needed to reduce both diaphragm wall and tunnel deformations.
Currently, control methods for the impact of foundation pit construction on nearby existing tunnels are mainly divided into active and passive measures8,9. Active control methods primarily include grouting and servo-strut control technologies. Grouting involves injecting slurry to exert pressure on the soil, causing a certain degree of deformation in the existing tunnel, thereby controlling the tunnel’s deformation. Zhang et al.10 treated the volume expansion of the grouting area as a combination of multiple spherical grouting volume expansions and studied the effects of different grouting pressures on tunnel structural deformation and the additional stresses. Zhao et al.11 employed the Material Point Method (MPM) to investigate the effect of grouting in reducing excessive convergence deformation in metro shield tunnels in soft soil areas. They found that the height, volume, and relative position of grouting with respect to the tunnel are key factors influencing grouting efficiency. Cheng et al.12 proposed a novel grouting control method by combining vertical grouting with unloading hole technology, which can simultaneously control both horizontal and vertical tunnel deformations, effectively restoring tunnel deformation caused by excavation. In laboratory experiments, Zhu13 simulated the grouting correction process for shield tunnels and analyzed the stress and deformation of the tunnel structure under different grouting conditions.Huang et al.14 conducted model experiments to study the impact of lateral grouting on the stress and deformation of existing tunnels. The results showed that grouting leads to a localized increase in soil pressure, causing cross-sectional deformation of the tunnel, and clarified the mechanism of additional load formation due to slurry diffusion.
The servo-strut control technology primarily works by controlling the deformation of the retaining structure, thereby inducing deformation in the soil behind the wall, which ultimately controls the deformation of the tunnel. Currently, many engineering cases have demonstrated the effectiveness of servo-strut control in mitigating metro tunnel deformations15,16,17,18,19,20,21,22. Guo et al.23 utilized a modified Mohr–Coulomb soil model to establish a finite element model that does not consider the stress relaxation of steel struts on the servo-control system, and studied the deformation patterns surrounding tunnels near foundation pits. Zhang et al.24 conducted in-depth research on the deformation characteristics of metro tunnels in the granite residual soil layer in the Shenzhen area. The study found that an automatic axial force adjustment system for steel struts effectively reduced foundation pit displacement, with the maximum reduction reaching 75%, which plays an important role in protecting nearby metro tunnels. Tang et al.25 analyzed the stress characteristics of the adjacent tunnel and foundation pit during servo-loading through a scaled model experiment. They found that the simultaneous expansion and contraction of the three struts had the greatest impact on the tunnel’s bending moment. The expansion and contraction of the steel strut had a greater effect on the soil pressure at the left and right arch shoulders than on the soil pressure at the arch crown and arch bottom.
From the aforementioned studies, it can be observed that current research both domestically and internationally primarily analyzes the control of tunnel deformation using a single active control method, with no studies addressing the combined use of servo steel struts and grouting. To investigate the effect of different servo-strut arrangements on tunnel deformation under the same grouting conditions, this study conducted indoor model tests to explore the control mechanism of different servo-strut arrangements on the deformation of adjacent tunnels. Additionally, numerical simulations were used to investigate the impact of varying grouting spacing on tunnel deformation, with the aim of providing reference for similar engineering projects.
Model test plan
Project information
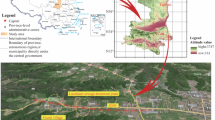
The project involves a subway station pit engineering that is parallel to the existing tunnel and station, as shown in Fig. 1. The depth of the experimental area pit is 17 m, the width is 24 m, and the length is 80 m. The thickness of the diaphragm wall on the side close to the tunnel is 0.8 m. A retaining scheme of 5 steel struts + 1 reinforced concrete strut is adopted. The diameter of the existing tunnel is 6.2 m, with a burial depth of 10.4 m, and a distance of 8.0 m from the pit. The strata it is located in are mainly ②42 sandy silt interbedded with silt sand and ③5 silt sand, as shown in Fig. 2. The Soil Parameters are shown in Table 1.
Plan view.
Geological profile (Unit: m).
Experimental setup design and material parameters
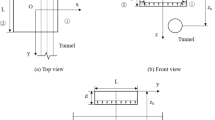
To avoid deviations in test results caused by boundary effects26, the dimensions of all models in the test need to be comprehensively considered. Therefore, a similarity ratio of 1:25 was chosen, and the model box dimensions are 2500 mm (length) × 2000 mm (width) × 1500 mm (height). The diaphragm wall is simulated using 6061 aluminum alloy plates, with dimensions designed based on the equivalent bending stiffness principle27: 2000 mm (length) × 1200 mm (height) × 5 mm (thickness). The capsule grouting, following the design of Zheng et al.28, has an expanded size of 250 mm (height) × 20 mm (diameter) according to the geometric similarity ratio. The tunnel is simulated using grooved PVC pipes to represent the actual longitudinal discontinuity of the tunnel29, and its dimensions are designed based on the bending stiffness similarity ratio: 2000 mm (length) × 250 mm (outer diameter) × 5 mm (wall thickness), with a burial depth of 416 mm and a clear distance from the foundation pit of 320 mm. The experimental setup is shown in Fig. 3.
Model test apparatus (Unit: mm).
The foundation pit adopts a symmetric semi-excavation simulation, with excavation dimensions of 2000 mm (length) × 480 mm (width) × 680 mm (depth). During the excavation process, steel struts are installed. In the horizontal direction, six internal struts are set with a spacing of 320 mm, while in the vertical direction, four layers of struts are arranged with a spacing of 170 mm, as shown in Fig. 4. The experimental design referenced findings on the influence of servo loading on foundation pit deformation30, where custom-made telescoping aluminum rods achieved precise simulation of servo steel struts. The first layer uses 6061 standard aluminum alloy rods, while layers 2–4 use custom-made telescoping aluminum rods to simulate servo steel struts. According to the equivalence principle of compressive stiffness, the cross-sectional outer diameter of these rods is designed as 10 mm, and the inner diameter as 7 mm. The soil is modeled using homogeneous sand, and its physical and mechanical properties, along with the test material parameters, are presented in Table 2.
Cross-section of the test apparatus (Unit: mm).
Test monitoring plan
As shown in Fig. 5a, his experiment establishes a total of 11 monitoring sections, namely Z1 to Z6 and M1 to M5. Specifically, the 6 sections (Z1 to Z6) are horizontally aligned with the 6 internal struts, whereas the 5 sections (M1 to M5) are situated between adjacent struts. Measurement points for all monitoring items are distributed across these sections. Figure 5b illustrates the monitoring layout for the M3 section. The deformation of the diaphragm wall is measured using laser sensors, with 5 measurement points placed along the section. Tunnel deformation is measured using displacement meters, with measurement points arranged at 90° intervals along the section. This setup allows for simultaneous monitoring of tunnel displacement and convergence. Tunnel surrounding pressure and the pressure of the surrounding soil are measured using miniature soil pressure cells with a range of 100 kPa and an accuracy of 0.05%. There are a total of four soil pressure cells. One of them is located at a horizontal distance of 40 mm from both the tunnel and the capsule grouting, with its depth consistent with the center of the capsule grouting. The other three measurement points are situated at a horizontal distance of 120 mm from both the capsule grouting and the diaphragm wall. Their depths are uniformly distributed along the length of the capsule grouting, with a spacing of 120 mm.
Model test setup diagram (Unit: mm); (a) Schematic plan view; (b) Schematic sectional view of section M3.
The experimental procedure and plan
The soil filling is carried out in layers with each layer being 10 cm thick. The diaphragm wall, tunnel, and capsule grouting are embedded at the corresponding depths. After the soil filling is completed, the model needs to remain undisturbed for 24 h. The data acquisition instrument is then activated to start the test. The excavation of the foundation pit is divided into four layers, each with a depth of 170 mm. After each layer is excavated, struts are installed. After the excavation reaches the bottom, the model needs to remain undisturbed for 12 h. Servo loading is then conducted, followed by another 12-h undisturbed period. Capsule grouting is then carried out at the M3 section, and the model is left undisturbed for 20 min after grouting is completed, marking the end of the test.
The elongation distance of each steel strut layer is determined by the maximum deformation of the diaphragm wall in that layer, as measured by a laser distance meter. Therefore, when servo loading is applied to a particular layer, the deformation of the diaphragm wall at the strut in that layer is controlled to the state it was in before excavation. Based on the experimental objectives, the test conditions are designed as shown in Table 3.
Analysis of test results
The M3 section is selected as the monitoring section to observe the changes in tunnel displacement, tunnel convergence, tunnel surrounding pressure, and diaphragm wall deformation before and after servo loading, as well as after grouting (data are not scaled according to the model ratio).
Tunnel horizontal and vertical displacements
Tunnel horizontal displacement
Figure 6 shows the impact of different servo methods on tunnel horizontal displacement under the same grouting conditions, where negative horizontal displacement indicates that the tunnel moves away from the foundation pit. From the Fig. 6, it can be seen that the combined control of capsule grouting and servo loading can cause the tunnel to experience horizontal displacement away from the foundation pit. However, there is a significant difference in the amount of horizontal displacement of the tunnel depending on the different servo arrangement patterns.
The variation in horizontal displacement of tunnels under different servo methods.
By observing the effect with and without servo loading, it can be seen that under the condition of servo loading, the effect of grouting is significantly enhanced. The horizontal displacement change of the tunnel in the non-servo grouting stage is only 0.025 mm, while under servo loading, the minimum horizontal displacement change of the tunnel after grouting is 0.065 mm.
From the perspective of the number of struts, the horizontal displacement change of the tunnel under three strut loading conditions can reach 0.12 mm, while under two strut loading conditions (3rd and 4th strut), the displacement is 0.105 mm, and under single strut loading, it is 0.065 mm. It can be observed that three strut loading provides the best control effect on grouting, followed by two strut loading, with single strut loading being the least effective. This is because three strut loading offers the best control over the deformation of the diaphragm wall. After three servo struts are applied, the displacement of the diaphragm wall is significantly reduced, the soil density between the tunnel and the foundation pit is increased, and it is higher than in the cases with two or single strut loading. Additionally, the expansion of the grout has a greater impact on the surrounding soil deformation, ultimately achieving the greatest control over tunnel horizontal displacement.
From the perspective of the strut arrangement, the horizontal displacement change of the tunnel under the 2nd and 4th strut loading is only 0.07 mm, while under the 3rd/4th strut loading, it can reach 0.105 mm. This indicates that the 2nd/4th strut loading has a smaller impact on the horizontal displacement of the tunnel compared to the 3rd/4th strut loading. This is because the burial depth of the 3rd/4th struts is closer to the tunnel depth than that of the 2nd/4th struts. During the servo loading process, the influence zone on the soil is more concentrated around the tunnel depth, which leads to a greater impact on the horizontal displacement of the tunnel.
Tunnel vertical displacement
Figure 7 illustrates the impact of different servo methods on tunnel vertical displacement under the same capsule grouting conditions. A negative vertical displacement indicates tunnel settlement, while a positive value represents heaving. As shown in Fig. 7, various factors such as the presence or absence of servo loading, the number of servo struts, and the strut arrangement result in different vertical displacement magnitudes.
The variation in vertical displacement of tunnels under different servo control methods.
An analysis based on the presence or absence of servo loading reveals that under servo loading conditions, the grouting effect increases the tunnel settlement. In the stage without servo loading, the tunnel settlement is only 0.01 mm, while under the combined action of servo and capsule grouting, the maximum tunnel settlement reaches 0.035 mm.
From the perspective of the number of strut loads, the vertical displacement pattern of the tunnel differs when three struts are used compared to other strut arrangements. With a single strut, the tunnel settlement is 0.02 mm, while with two struts, the settlement increases to 0.035 mm (using the 3rd and 4th struts). However, when three struts are used, the tunnel experiences heaving of 0.01 mm in the servo loading stage, followed by settlement of 0.045 mm in the grouting stage, resulting in a total settlement of 0.035 mm. From the above data, it is evident that both single and double strut loads increase the tunnel settlement in both the servo loading and grouting stage. In contrast, with three struts, the tunnel first heaves and then settles after grouting.
From the perspective of the strut arrangements, the 2nd and 4th strut loading results in a settlement of 0.015 mm, while the 3rd and 4th strut loading leads to a settlement of 0.03 mm. In both strut arrangements, the servo loading stage causes a vertical displacement of 0.005 mm in the tunnel, indicating that the strut mode has a relatively small impact on the tunnel’s vertical displacement in the servo loading stage. However, the strut arrangements have different effects on the subsequent vertical displacement caused by capsule grouting. Specifically, the strut arrangement where the average burial depth of the strut is closer to the tunnel’s burial depth has a greater impact on the tunnel’s vertical displacement. This observation is consistent with the pattern of horizontal displacement. In summary, while the strut modes have a minimal effect on the tunnel’s vertical displacement during the servo loading stage, they influence the vertical displacement during grouting differently. Strut arrangements with average burial depths closer to the tunnel depth exert a more significant effect on vertical displacement, which aligns with the behavior observed in horizontal displacements.
Tunnel horizontal convergence
Figure 8 shows the impact of different servo control methods on tunnel horizontal convergence under the same capsule grouting conditions, where a negative value in the horizontal convergence variation indicates a reduction in convergence. As shown in Fig. 8, the horizontal convergence of the tunnel caused by foundation pit excavation is reduced by servo loading and capsule grouting expansion, making the tunnel section more circular.
The variation in tunnel horizontal convergence under different servo control methods.
An analysis of the presence or absence of servo loading shows that under the condition of no servo loading, a horizontal convergence of 0.08 mm occurs, which is generally smaller than under other conditions. However, under the combined action of servo loading and capsule grouting, the maximum horizontal convergence variation of the tunnel can reach up to 0.25 mm.
An analysis of the number of strut loads shows that the horizontal convergence of the tunnel under single strut loading is 0.17 mm, while the maximum horizontal convergence under double strut loading is 0.23 mm (at the 3rd/4th strut). Under triple strut loading, the horizontal convergence variation reaches 0.25 mm. It can be seen that the horizontal convergence induced by triple strut loading is greater than that of the other loading arrangements.
From the observation of the strut arrangement, the tunnel experiences a horizontal convergence of 0.12 mm under the 2nd/4th strut loading, and a horizontal convergence of 0.23 mm under the 3rd/4th strut loading. The difference between these two values is as high as 0.11 mm. This is because the 3rd/4th strut arrangement has a stronger concentration effect on horizontal convergence compared to the 2nd/4th strut, resulting in better control of the tunnel’s horizontal convergence.
Tunnel right hance pressure
Figure 9 illustrates the variation in pressure at the right hance of the tunnel under different servo control methods with capsule grouting conditions. Positive values indicate an increase in pressure, suggesting exacerbated compression. When capsule grouting and servo control are applied in combination to control tunnel deformation, the pressure at the right hance increases.
The variation in pressure at the right hance of the tunnel under different servo control methods.
An analysis of the presence or absence of servo loading shows that the pressure at the right hance of the tunnel is 12.121 kPa without servo loading. However, under the condition of servo loading, the pressure at the right hance is higher than in the case without servo loading. Under the combined effect of servo control and capsule grouting, the maximum pressure variation at the right hance can reach up to 40.799 kPa.
An analysis of the number of strut loadings shows that the pressure variation at the right hance of the tunnel is 13.949 kPa with single strut loading. With two strut loadings, the pressure variation increases to 38.611 kPa, and with three strut loadings, the pressure variation reaches 40.799 kPa. It can be observed that under the same capsule grouting conditions, three strut loadings have the greatest impact on the pressure at the right hance of the tunnel.
An analysis of the strut arrangement modes shows that loading with the 2nd and 4th struts results in a pressure variation of 15.037 kPa at the tunnel. In contrast, loading with the 3rd and 4th struts leads to a pressure variation of 38.611 kPa. The difference between the two is 23.574 kPa, which is consistent with the reasoning behind the influence of strut arrangement modes on horizontal displacement. Specifically, different strut arrangements affect how the load is distributed, thereby influencing the tunnel’s deformation and pressure distribution.
Deformation of diaphragm walls
Figure 10 shows the deformation of the diaphragm wall under different servo control methods. Positive values indicate deformation of the diaphragm wall inward toward the excavation, while negative values indicate deformation outward away from the excavation. The “Grouting Stage” represents the deformation of the diaphragm wall caused by capsule grouting, and the “Loading Stage” represents the deformation caused by servo strut loading. The black strut indicates no servo loading, and the red strut indicates the activation of servo loading. From the Fig. 10, it can be seen that during the servo loading stage, the diaphragm wall moves outward toward the excavation, while during the grouting stage, the diaphragm wall moves inward toward the excavation within the grouting depth (− 41.6 cm to − 66.6 cm). At other depths, the diaphragm wall generally moves outward away from the excavation.
The deformation induced in diaphragm walls by different servo loading methods; (a) No loading; (b) 4th strut loading; (c) 2nd and 4th strut loading; (d) 3rd and 4th strut loading; (e) 2nd, 3rd and 4th strut loading.
Under the condition without servo loading, the deformation of the diaphragm wall increases within the grouting depth (− 41.6 cm to − 66.6 cm), while at other depths, the deformation decreases. The maximum deformation occurs at the 4th strut (at a depth of − 51 cm), where the deformation can reach 0.26 mm.
Under the loading condition at the 4th strut (buried depth of − 51 cm), the maximum deformation of the diaphragm wall in the servo stage is − 0.84 mm at the 4th strut. The deformation in the grouting stage at this position is 0.24 mm, resulting in a combined deformation of − 0.60 mm for the diaphragm wall. At the bottom of the excavation (depth of − 68 cm), the grouting stage has the greatest impact on the diaphragm wall, with a deformation of 0.56 mm. The deformation in the servo stage at this depth is − 0.27 mm, and the combined deformation of the diaphragm wall at this depth is 0.29 mm.
Under the loading condition at the 2nd and 4th struts, the maximum deformation of the diaphragm wall in the servo stage at the 2nd strut (depth of − 17 cm) is − 0.78 mm. The deformation in the grouting stage at this position is − 0.01 mm, resulting in a combined deformation of − 0.79 mm for the diaphragm wall. At the bottom of the excavation (depth of − 68 cm), the grouting stage has the greatest impact on the diaphragm wall, with a deformation of 0.21 mm. The deformation in the servo loading stage at this depth is 0.02 mm, and the combined deformation of the diaphragm wall at this depth is 0.23 mm.
Under the loading condition at the 3rd and 4th struts, the maximum deformation of the diaphragm wall in the servo stage at the 3rd strut (depth of − 34 cm) is − 1.06 mm. The deformation in the grouting stage at this position is 0.04 mm, resulting in a combined deformation of − 1.02 mm for the diaphragm wall. At the bottom of the excavation (depth of − 68 cm), the grouting stage has the greatest impact on the diaphragm wall, with a deformation of 0.10 mm. The deformation in the servo loading stage at this depth is − 0.06 mm, and the combined deformation of the diaphragm wall at this depth is 0.04 mm.
Under the loading condition at the 2nd, 3rd, and 4th strut, the maximum deformation of the diaphragm wall in the servo loading stage at the 3rd strut is − 1.16 mm. The deformation in the grouting stage at this position is 0.05 mm, resulting in a combined deformation of − 1.11 mm for the diaphragm wall. At the bottom of the excavation (depth of − 68 cm), the grouting stage has the greatest impact on the diaphragm wall, with a deformation of 0.31 mm. The deformation in the servo loading stage at this depth is − 0.33 mm, and the combined deformation of the diaphragm wall at this depth is − 0.02 mm.
From the above analysis, it can be observed that under the same conditions, the loading of the 2nd, 3rd, and 4th strut results in the maximum deformation of the diaphragm wall, followed by the 2nd and 4th strut loading, the 3rd and 4th strut loading, and the 4th strut loading. However, the depth at which the maximum deformation occurs differs. When a single strut is activated, the deformation at that position is greater than at other depths. In the case of two struts being loaded, the maximum deformation occurs at the position of the first activated servo strut. However, when three struts (2nd, 3rd, and 4th) are loaded, the maximum deformation occurs at the position of the 3rd strut. This is because, when one or two servo struts are activated, the deformation is largest at the first activated strut. In contrast, when three servo struts are loaded, the deformation at the middle position is influenced by the adjacent servo struts, which causes an accumulation of deformation, leading to the maximum deformation at the 3rd strut.
The deformation caused by capsule grouting in the diaphragm wall is mostly positive, meaning that capsule grouting tends to increase the deformation of the diaphragm wall. Except for the pit bottom position, the deformation induced by capsule grouting is generally smaller than that caused by the servo struts. This is because, at the pit bottom, the diaphragm wall is located within the grouting depth range and is not directly affected by the loading of the servo steel struts. As a result, the deformation caused by capsule grouting at this ___location exceeds that caused by the servo steel struts.
By superimposing the deformation caused by both capsule grouting and servo steel struts, it can be analyzed that at the depth where the servo steel struts are loaded, the deformation of the diaphragm wall will eventually move outward from the pit, while at the pit bottom, the deformation will move inward. Therefore, to prevent excessive deformation at the pit bottom due to the influence of capsule grouting, it is recommended to carry out capsule grouting control for the adjacent tunnel only after the base slab at the pit bottom has been poured.
Comparison of control effects
Control effects on tunnel horizontal displacement
Under the same capsule grouting conditions, the impact of different servo arrangement methods on the control of tunnel horizontal displacement varies. To evaluate the effectiveness of servo and capsule grouting in controlling tunnel horizontal displacement, a comparison is made based on the proportion of tunnel horizontal displacement control attributed to the servo and capsule grouting stage (as shown in Fig. 11). Negative values indicate displacement of the tunnel away from the excavation pit.
The proportion of influence of the servo stage and grouting stage on the tunnel horizontal displacement.
As can be seen from the figure, the proportion of total tunnel horizontal displacement control achieved by capsule grouting is consistently greater than that achieved by servo loading. This is because grouting is not only closer to the tunnel but also more targeted in its control of horizontal displacement, thus leading to better control effects. As the number of servo struts increases, the total control of tunnel horizontal displacement shows an increasing trend. At the same time, the proportion of control exerted by the servo and grouting stage becomes more similar. For instance, under a single strut, the control proportion of the grouting stage to the servo stage is 92.31% to 7.69%, whereas, under three struts, it decreases to 54.17% to 45.83%. From the above analysis, it can be concluded that under the same capsule grouting conditions, the greater the number of loaded struts, the larger the total control of tunnel horizontal displacement. Moreover, with an increase in the number of struts, the effectiveness of the servo strut in controlling tunnel displacement also improves.
From the Fig. 11, it can also be observed that different strut arrangement patterns have a certain impact on tunnel displacement control. Compared to the loading of the 2nd and 4th strut, the loading of the 3rd and 4th strut shows more significant control effects. This phenomenon can be attributed to the more concentrated loading effect of the 3rd and 4th strut, which provides more effective force transmission and distribution during the tunnel control process, thereby optimizing the control effect. In essence, the more concentrated loading pattern improves the efficiency of force application and enhances the overall stability and control of the tunnel’s horizontal displacement.
From the above data, it can be concluded that the loading of the 2nd, 3rd, and 4th strut provides the largest control over the tunnel’s horizontal displacement. The loading of the 3rd and 4th strut also offers a relatively good tunnel control effect. However, the control effects of the 4th strut and the 2nd and 4th strut loading are comparatively weaker in controlling tunnel displacement. This suggests that the combination of certain struts (such as 2nd/3rd/4th) is more effective in controlling horizontal displacement, likely due to better load distribution and force transfer, while other combinations (like 4th or 2nd/4th strut) do not provide as efficient control, possibly because the forces are not as well concentrated or distributed across the tunnel structure.
Control effects on diaphragm wall deformation
Since the servo loading was applied at the 4th strut, and the grouting depth is relatively close to the depth of the 4th strut, the study aims to observe the control effects of different servo methods on the displacement of the diaphragm wall under the same capsule grouting conditions. Therefore, the deformation of the diaphragm wall at the fourth strut (with a burial depth of − 51 cm) was selected as the observation parameter. The specific results are shown in Fig. 12.
Deformation and cumulative deformation of the diaphragm wall at different stages.
From the figure, it can be observed that at the burial depth of − 51 cm, the loading of the 4th strut has the greatest impact on the deformation of the diaphragm wall, with a maximum deformation of − 0.84 mm. The deformation is − 0.74 mm when the 3rd and 4th struts are loaded, − 0.54 mm when the 2nd, 3rd, and 4th struts are loaded, and the minimum deformation occurs when the 2nd and 4th struts are loaded, with a value of only − 0.2 mm. This shows that at a specific depth, the impact on diaphragm wall deformation is significantly related to the arrangement of the struts, and it is not necessarily the case that loading more struts results in better control.
The absolute deformation of the diaphragm wall in the grouting stage is generally smaller than that in the servo loading stage. Under the loading condition of the 4th strut, the maximum deformation is 0.24 mm. When the 3rd and 4th struts are loaded, the deformation has the smallest impact, with a value of only 0.06 mm. This indicates that under the same capsule grouting conditions, the grouting has different effects on diaphragm wall deformation depending on the arrangement of the servo struts and the number of loading struts.
By superimposing the effects of the two control methods on diaphragm wall deformation, it can be observed that under the loading condition of the 3rd and 4th struts, the diaphragm wall deformation is the largest at − 0.68 mm. The deformation is − 0.60 mm under the fourth strut loading condition, − 0.31 mm under the 2nd, 3rd, and 4th strut loading condition, and the smallest deformation of − 0.11 mm occurs when the 2nd and 4th struts are loaded. From the above data, it can be analyzed that both the arrangement of the servo struts and the number of loading struts have different effects on diaphragm wall deformation. However, after superimposition, the deformation of the diaphragm wall decreases in all cases. Therefore, combining the analysis from the previous section, when prioritizing the control of large horizontal tunnel displacements while ensuring that diaphragm wall deformation does not increase, the recommended servo strut arrangement is to load the 2nd, 3rd, and 4th strut.
Double-row capsule grouting simulation
Numerical model
Model development
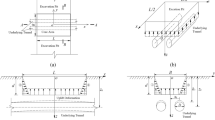
The numerical simulation was carried out using Plaxis 3D, and the specific model is shown in Fig. 13. Since the dimensions of the indoor model test are too small to be implemented in numerical simulations, the geometric dimensions have been scaled up according to a scaling ratio(1:25), while carefully considering boundary effects. The dimensions of the soil model are 200 m × 120 m × 70 m (length × width × depth), and the dimensions of the excavation pit are 82 m × 24 m × 17 m, with the depth of the diaphragm wall insertion being 30 m. In terms of strut, 10 horizontal struts are set, with the first and last strut positioned 5 m away from the edge of the excavation pit, and the horizontal spacing between each strut is 8 m, while the vertical spacing is 4.25 m. The tunnel has an external diameter of 6.2 m, a segment thickness of 0.35 m, and a length of 200 m. The tunnel is buried at a depth of 10.4 m, running parallel to the long side of the excavation pit, with a distance of 8 m between the tunnel and the excavation pit. To ensure computational accuracy, the initial diameter of the capsule grouting is set to 0.2 m.
Model Diagram (Unit: m). The model was established by Plaxis 3D (Version 2023.1.0.59; 2023; https://www.bentley.cn/software/plaxis-3d/).
The model boundaries are defined using standard constraint forms. Normal displacement constraints are applied to the lateral boundaries, full constraints are applied to the bottom surface, and the top surface of the model is allowed to deform freely.
Parameter selection
The model soil is consistent with the soil used in the physical model test, and overall sand is adopted as the soil. The constitutive model for the soil is the Mohr–Coulomb model, with soil parameters provided in Table 2. The contact relationship between the soil and the diaphragm wall is simulated using the interface elements embedded in PLAXIS 3D. Since there are no relevant test parameters in the geological investigation data, the strength and stiffness reduction factors of the interface are uniformly taken as the software system’s recommended value of 0.7. This value is an empirical value recommended by the software system based on a large number of engineering experiences and research statistics in the absence of specific test parameters, and it has certain universality for the contact interface between concrete and sandy soil.
The material properties of the structural components in the model are shown in Table 4. In the actual engineering project, due to the presence of other components, the stiffness of the steel struts in the project is much lower than the actual stiffness of the steel material. Lei et al.31 found through research that when simulating steel struts using beam elements, it is recommended to reduce their stiffness to 38% of the original value. Additionally, the actual tunnel segments of the shield tunnel are affected by the joints, which influence their elastic modulus. The elastic modulus of the tunnel segments is recommended to be reduced to 60% of the original value. The material properties of each structural component are listed in Table 4.
Simulation method
The construction sequence mirrors that of the model test: initially, the tunnel is constructed, succeeded by foundation pit excavation, servo loading, and capsule grouting expansion. The foundation pit is excavated in four layers, with each layer being 4.25 m. Struts are installed after each layer is excavated. The servo loading adopts the method of point load33. Based on the increase in axial force according to the scale ratio in the scaled model test, the deformation of the diaphragm wall is controlled by servo loading to achieve the required deformation. In the model test, capsule grouting is performed by inflating the grout bag, which undergoes constant volume expansion. Therefore, the capsule grouting simulation method in this study employs the volumetric strain control method, which has been proven feasible by previous researchers34,35.
Verification of numerical simulation results
The numerical simulation validation was carried out using the Group 2 in Table 3. The model test results were magnified 25 times and compared with the numerical simulation results, as shown in Fig. 14. This section corresponds to the M3 section in the model test, which is located at the center of the excavation in the numerical simulation. As can be seen from the figure, there is a slight discrepancy between the numerical simulation and the model test results, but the trends are consistent. Therefore, the model is in good agreement with the excavation, servo loading, and grouting stages of the foundation pit, confirming the feasibility of the model.
Comparison of model test results with numerical simulation results; (a) Comparison of horizontal deformation of diaphragm wall; (b) Tunnel horizontal deformation comparison chart.
The impact of double-row capsule grouting on tunnel deformation
Design of numerical simulation conditions
The arrangement of capsule grouting at different locations can have varying effects on the deformation of the diaphragm wall and tunnel. Based on previous model test studies, this research investigates the combinations of capsule grouting at different locations, with the primary control variables being the horizontal distance between the capsule grouting and the distance to the tunnel. Other capsule grouting parameters remain consistent with the standard conditions. The specific simulation conditions are shown in Table 5.
Taking Group 1 as an example, different horizontal spacing (S) and distance from the tunnel boundary (W) for the capsule grouting are arranged in the grouting area, as shown in Fig. 15. Before grouting, all capsule grouting points are located in sandy soil. During the grouting stage, the required capsule grouting are activated according to the working condition specifications. The A-A section is the primary observation section for the diaphragm wall, and the main observation data for the tunnel deformation are taken from the right hence deformation at the depth of the tunnel axis.
Schematic diagram of the plan layout of the capsule grouting.
Analysis of the impact of double-row capsule grouting spacing on diaphragm wall deformation
To facilitate the distinction between different spacings of the double-row capsule grouting combinations, the combinations are expressed in terms of the horizontal spacing (S) and the distance from the tunnel boundary (W). For example, the single-row spacing in working condition 1 is represented as (S4W4) and (S4W3), and the combined expression is (S4W4W3). Other combinations are expressed in a similar manner.
In order to investigate the impact of different capsule grouting spacings during the single and double-row capsule grouting stage on diaphragm wall deformation, the maximum deformation differences of the diaphragm wall for various spacings and grouting stage are summarized, as shown in Fig. 16. Positive values indicate that the diaphragm wall deforms inward toward the foundation pit. In the figure, the blank section represents the deformation change of the diaphragm wall during the first-row grouting stage, which is the difference between the diaphragm wall deformation after the first-row capsule grouting and the servo loading; the shaded section represents the deformation change during the second-row capsule grouting stage, which is the difference in diaphragm wall deformation between the first and second capsule grouting stage.
The effect of different double-row capsule grouting spacings on the maximum deformation value of the diaphragm wall.
As shown in the figure above, the impact of the first row of capsule grouting on the deformation of the diaphragm wall is greater than that of the second row. The proportion of the deformation caused by the second row of capsule grouting relative to the first row, in order of working conditions, is 81.73%, 75.91%, 75.27%, 77.15%, 70.78%, 78.29%, 79.31%, 71.86%, and 63.04%. From the proportion data, it can be observed that the effect of the second row of capsule grouting on the diaphragm wall is weaker than that of the first row. This is because after the first row of capsule grouting, a reinforced wall structure is formed within the grouting area. During the second row of capsule grouting, the soil squeezing effect between the first-row capsule grouting and the diaphragm wall is weakened, leading to a reduced influence of the second row of capsule grouting on the deformation of the diaphragm wall.
From the perspective of changes in capsule grouting spacing, whether it is the first or second row of capsule grouting, the variation in horizontal spacing has a significantly greater impact on the deformation of the diaphragm wall than changes in the grouting distance. Under the conditions of a 4 m and 3 m distance from the tunnel edge for the first row of capsule grouting, the impact of capsule grouting with a horizontal spacing of 4 m on the diaphragm wall deformation is 1.92 and 4.04 times greater than that of horizontal spacings of 8 m and 16 m, respectively. Under the condition of a 4 m and 2 m distance from the tunnel edge, the impact of a 4 m horizontal spacing is 1.81 times and 3.80 times greater than that of the other two spacing conditions. Under the condition of a 3 m and 2 m distance from the tunnel edge, this value is 1.82 times and 3.69 times greater, respectively.
For the second row of capsule grouting, these comparative data are 2.07 times and 4.38 times, 1.97 times and 3.74 times, and 2.01 times and 4.64 times, respectively. From the above comparative data, it can be observed that, under the same tunnel edge distance conditions, the sensitivity of the second row of capsule grouting to changes in horizontal spacing is similar to that of the first row. Among these, the first and second row capsule grouting effects in the S16W3W2 grouting group differ significantly, as the average distance from the tunnel edge is the furthest in this group, and the 16 m horizontal spacing further weakens the overlapping effect of the capsule grouting zones, resulting in the poorest effect for the second row of capsule grouting.
In summary, the influence of horizontal spacing on diaphragm wall deformation is clearly more significant than the change in grouting distance. Additionally, when the distance from the tunnel edge is relatively large, the effect of the second row of capsule grouting tends to be less effective due to the weakened overlapping effect of the grouting zones.
Analysis of the impact of double row capsule grouting spacing on tunnel deformation
In order to investigate the impact of different stages of double-row capsule grouting on the deformation of the tunnel’s right hance, the deformation variations at different grouting stages for various groups are compiled, as shown in Fig. 17. Positive values represent the deformation of the tunnel’s right hance away from the excavation pit. The blank section indicates the deformation change at the first row of capsule grouting stage, which is the difference in deformation of the tunnel’s right hance between the first row of capsule grouting and the servo-loading stage. The shaded section represents the impact of the second row of capsule grouting on the right hance deformation, which is the difference in deformation between the first and second rows of capsule grouting at the tunnel’s right hance.
The impact of different double-row capsule grouting spacings on the deformation of the tunnel’s right hance.
As shown in the figure above, the impact of the first row of capsule grouting on the deformation of the tunnel’s right hance is greater than that of the second row of capsule grouting. Specifically, the deformation caused by the second row of capsule grouting, in terms of the operating conditions, accounts for 87.66%, 75.22%, 87.91%, 96.46%, 78.12%, 96.59%, 89.12%, 73.24%, and 68.69% of the deformation caused by the first row of capsule grouting. From the proportional data, it can be observed that the effect of the second row of capsule grouting on the tunnel’s right hance deformation is weaker than that of the first row. This is because, after the first row of capsule grouting, the tunnel has already undergone some degree of deformation control. As a result, the second row of capsule grouting needs to exert a larger grouting effect to achieve the desired result, which leads to a slightly weaker effect compared to the first row of capsule grouting.
From the perspective of changes in grouting spacing, it can be observed that, regardless of whether it is the first or second row of capsule grouting, the effect of horizontal spacing on the deformation of the tunnel’s right hance is significantly greater than that of changes in grouting distance. Under the first-row capsule grouting conditions, when the distance from the tunnel’s edge is 4 m or 3 m, the capsule grouting with a horizontal spacing of 4 m causes deformations of the diaphragm wall that are 1.75 and 3.66 times greater than those for horizontal spacings of 8 m and 16 m, respectively. For the conditions with distances from the tunnel’s edge of 4 m and 2 m, the grouting with a horizontal spacing of 4 m causes deformations that are 1.64 times and 3.42 times greater than those for the other two conditions. Similarly, for the conditions with distances from the tunnel’s edge of 3 m and 2 m, the values are 1.67 times and 3.23 times greater, respectively.
For the second-row capsule grouting, these comparative data are 2.04 and 3.65 times, 2.00 and 3.42 times, and 2.03 and 4.18 times, respectively. From the above comparison, it is evident that, under the same distance from the tunnel’s edge, the second row of capsule grouting is more sensitive to changes in horizontal spacing than the first row of capsule grouting. Notably, the difference between the first and second rows of capsule grouting is more significant in the S16W3W2 grouting group. This is because the smaller the horizontal spacing, the more pronounced the superimposed effect of capsule grouting. At the same time, the average distance from the tunnel’s edge is closer to that of the other two groups, which explains why the difference in the effect on the tunnel’s right hance deformation is the greatest for the S4W3W2 and S16W3W2 groups.
Conclusion
This study conducted model tests to investigate the effects of different servo strut arrangements on controlling the deformation of adjacent tunnels under the same capsule grouting conditions. The study analyzed the impact of various servo strut arrangements on the tunnel and the diaphragm wall. Under the condition of full loading of the servo struts, the effects of different double-row capsule grouting spacing on the tunnel and diaphragm wall deformation were also analyzed. The main conclusions are as follows:
-
1.
Different servo strut arrangements have a controlling effect on the horizontal displacement of the tunnel, with a greater number of struts leading to a more significant impact on the tunnel’s horizontal displacement and a more pronounced grouting effect. In terms of vertical displacement, servo loading generally causes tunnel settlement. However, when the 2nd, 3rd, and 4th struts are applied, the tunnel experiences an uplift phenomenon. Capsule grouting tends to induce tunnel settlement, and the amount of settlement increases with the number of struts. After the application of servo strut and capsule grouting, the horizontal convergence of the tunnel is effectively controlled. Notably, when a full servo strut system is used, the reduction in convergence is most significant.
-
2.
Both servo strut and capsule grouting increase the pressure at the right crown of the tunnel. Among them, the pressure increase is most significant with the second, third, and fourth layers of struts. The pressure generated by the servo struts is much lower than that produced by capsule grouting. The second and fourth layers of struts have a weaker impact on the tunnel’s deformation, convergence, and stress compared to the third and fourth layers of struts. This is because the third and fourth layers of struts exert a more concentrated effect on the tunnel.
-
3.
Servo loading causes the diaphragm wall to deform outward, away from the excavation pit. The maximum deformation of the diaphragm wall occurs when the second, third, or fourth layer of struts are loaded. However, the depth at which the maximum deformation of the diaphragm wall occurs varies depending on the number of struts loaded. In cases with one or two struts, the maximum deformation of the diaphragm wall occurs at the depth of the first loaded strut. When three struts are applied, the maximum deformation occurs at the depth of the middle strut. Grouting, on the other hand, only causes inward deformation of the diaphragm wall within the grouting depth, and the deformation is smaller compared to the servo-loaded segment.
-
4.
The effects of servo strut and capsule grouting on the horizontal displacement of the tunnel are different. When only a single layer of strut is applied, capsule grouting has a much greater impact on the horizontal displacement of the tunnel than servo control. However, when the second, third, or fourth layers of struts are used, capsule grouting still provides better control over the horizontal displacement of the tunnel compared to servo control, although the difference between the two methods becomes smaller. Both the servo arrangement and the number of struts influence the deformation of the diaphragm wall in the servo and grouting stage. In the case where controlling the horizontal displacement of the tunnel is prioritized, while ensuring that the deformation of the diaphragm wall does not increase, it is recommended to use the second, third, or fourth layers of struts for the servo control arrangement.
-
5.
Under conditions of different spacing between the two rows of struts, the impact of horizontal spacing changes on the deformation of the diaphragm wall and the deformation of the right arch of the tunnel is greater than that of the distance to the tunnel side. As the horizontal spacing decreases, both the diaphragm wall deformation and the right arch deformation of the tunnel increase. When the horizontal spacing is 4 m, there is a risk of excessive control on the tunnel. When the horizontal spacing is equal, the capsule grouting combination W4W2 has the greatest impact on the deformation of the diaphragm wall. However, for the deformation of the tunnel’s right arch, the effects of capsule grouting combinations W4W2 and W3W2 are very similar and better than the combination W4W3.
Data availability
The datasets generated or analysed during the current study are not publicly available due to confidentiality agreements, but are available from the corresponding author on reasonable request.
References
Meng, F. et al. Characteristics of deformation and defect of shield tunnel in coastal structured soil in China[J]. Underground Space 21, 131–148 (2025).
Chang, C. T., Sun, C. W., Duann, S. W. & Hwang, R. N. Response of a taipei rapid transit system (TRTS) tunnel to adjacent excavation. Tunn. Undergr. Space Technol. 16, 151–158 (2001).
Yan, J. Y. & Wang, R. L. Cause analysis and typical characteristics of settlement and transverse convergence deformation of metro tunnel in soft ground in Shanghai. J. Nat. Disasters. 27, 178–187 (2018).
Yang, Y. B., Zhou, B. & Xie, X. Y. Study on transverse deformation and cracking property of shield-driven tunnel induced by adjacent excavation. Chin. J. Rock Mech. Eng. 35, 4082–4093 (2016).
Wei, G. et al. Full-scale loading test for shield tunnel segments：Load-bearing performance and failure patterns of lining structures[J]. Underground Space 20, 197–217 (2025).
Wei, G. et al. Research on the influence of foundation pit excavation on the lateral force and deformation of side shield tunnels based on full-scale experiments[J]. Tunnelling and Underground Space Technology 140, 105236 (2023).
Wei, G. et al. Deformation control of shield tunnels affected by staged foundation pit excavation: analytical method and case study[J]. Buildings 15(12), 2046 (2025).
Zheng, G. Method and application of deformation control of excavations in soft ground. Chin. J. Geotech. Eng. 44, 1–36 (2022).
Zheng, G., Zhu, H. H., Liu, X. R. & Yang, G. H. Control of safety of deep excavations and underground engineering and its impact on surrounding environment. Chin. Civ. Eng. J. 49, 1–24 (2016).
Zhang, M., Wang, X. H. & Wang, Y. Numerical evaluation of uplifting effect for upper structure by grouting. J. Cent. South Univ. 19, 553–561 (2012).
Zhao, T. C., Han, T. R., Wu, G., Gao, Y. & Lu, Y. Effects of grouting in reducing excessive tunnel lining deformation: Field experiment and numerical modelling using material point method. Tunn. Undergr. Space Technol. 116, 104114 (2021).
Cheng, X. S. et al. Grouting theory and strategy of simultaneous control of the horizontal and vertical deformations of tunnels. Int. J. Geomech. 24, 04023267 (2024).
Zhu, M. Studies on the Mechanism and Engineering Application for the Remediation of Excisting Shield Tunnel Using Grouting Technique Doctor thesis (Zhejiang University, 2019).
Huang, D. W. et al. Experimental study on influences of side grouting on deformation of shield tunnels under loads. Chin. J. Geotech. Eng. 46, 510–518 (2024).
Li, H., Tang, Y. J., Liao, S. M. & Shen, M. L. Structural response and preservation of historic buildings adjacent to oversized deep excavation. J. Perform. Constr. Facil. 35, 04021095 (2021).
Chen, B. G., Yan, T. F., Song, D. B., Luo, R. P. & Zhang, G. H. Experimental investigations on a deep excavation support system with adjustable strut length. Tunn. Undergr. Space Technol. 115, 104046 (2021).
Nangulama, H. K. & Jian, Z. Deformation control monitoring of basement excavation at field construction site: A case of hydraulic servo steel enhancement geotechnology. Adv. Civ. Eng. 2022, 6234581 (2022).
Nangulama, H. K., Jian, Z., Xiao, Z., Zhu, J. C. & Yuan, F.-F. Stage-by-stage control effect field analysis of steel material servo enhanced support system on lateral displacement and bending moment during deep basement excavation. Case Stud. Constr. Mater. 16, 01068 (2022).
Jia, J., Xie, X. L., Luo, F. Y. & Zhai, J. Q. Support axial force servo system in deep excavation deformation control. J. Shanghai Jiaotong Univ. (Chin. Ed.) 43, 1589–1594 (2009).
Liu, G. B., Ng, C. W. & Wang, Z. W. Observed performance of a deep multistrutted excavation in Shanghai soft clays. J. Geotech. Geoenviron. Eng. 131, 1004–1013 (2005).
Park, J. S., Joo, Y. S. & Kim, N. K. New earth retention system with prestressed wales in an urban excavation. J. Geotech. Geoenviron. Eng. 135, 1596–1604 (2009).
Zhao, G. Q., Meng, S. Y., Guan, C. L. & Yang, Y. Y. Test study on the stress and deformation behaviors of a shaft supported by a prefabricated prestressed structure. Appl. Sci. 9, 629 (2019).
Guo, X. H. & Zhai, J. Q. Study of deformation and displacement control of tunnels adjacent to deep foundation pit in soft clay. Sichuan Build. Sci. 45, 114–120 (2020).
Zhang, G. T., Su, D., Pang, X. H., Deng, B. & Tang, R. The influence of axial force servo system in excavation of foundation pit on the deformation of existing subway tunnel. Mod. Tunnel. Technol. S1, 521–527 (2020).
Tang, X. L., Zhang, L., Hu, Z. M. & Chen, B. G. Experimental study on the influence law of adjustable internal support pit suppport strcture on adjacent tunnel. Sci. Tech. Eng. 22, 15718–15726 (2022).
Kim, H., Kim, D., Lee, Y. & Kim, H. Effect of soil box boundary conditions on dynamic behavior of model soil in 1 g shaking table test. Appl. Sci. 10, 4642 (2020).
Liu, X. R. et al. Model tests on interaction between tunnel-type anchorage and underpass tunnel. Chin. J. Geotech. Eng. 44, 1978–1987 (2022).
Zheng, G. et al. Field measurements and analysis of real-time capsule grouting to protect existing tunnel adjacent to excavation. Tunn. Undergr. Space Technol. 122, 104350 (2022).
Sun, X. B., Hou, X. Y., Xu, Y., Ye, T. & Hao, Z. H. stress analysis of prefabricated steel structure primary lining of subway construction shaft. Chin. J. Undergr. Space Eng. 18, 281–289 (2022).
Wei, G. et al. Model Tests of the Influence of Excavation Unloading and Servo Loading on Subway Foundation Pits[J]. Buildings 15(12), 2054 (2025).
Lei, T., Ding, B. H., Zhang, R. X., Zhang, J. F. & Song, J. X. On stiffness values of finite element model in steel support structure. Found. Struct. Eng. 38, 220–223 (2020).
Zhou, Q. et al. Active control scheme of inclined grouting for settlement of adjacent important buildings caused by ultra-deep excavation in soft soil area: Taking a four floors underground station project. Sci. Tech. Eng. 23, 10049–10058 (2023).
Chen, J. M., Di, H. G., Xuan, W., Liang, H. Y. & Su, G. B. Optimization and analysis of the foundation pit support at haiyan north transfer station of ningbo rail transit. Urban Mass Transit. 24, 22–25 (2021).
Lin, X. F. et al. Research on mechanism and strategy for active grouting control of horizontal tunnel deformation. J. Beijing Jiaotong Univ. 46, 100–113 (2022).
Zhang, D. M., Zou, W. B. & Yan, J. Y. Effective control of large transverse deformation of shield tunnels using grouting in soft deposits. Chin. J. Geotech. Eng. 36, 2203–2212 (2014).
Author information
Authors and Affiliations
Contributions
G.W. and Z.W. primarily guided reviewing and revising. W.F. drafted the main manuscript. X.W. and H.L. were performed numerical simulations. P.W. and Z.Z. were responsible for model testing and data collection.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wei, G., Feng, W., Wu, X. et al. Research on the combined control of tunnel deformation adjacent to the foundation pit by servo steel strut and capsule grouting. Sci Rep 15, 23432 (2025). https://doi.org/10.1038/s41598-025-07678-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-07678-z
