Introduction

Rapid advancements in artificial intelligence and materials science have led to the widespread use of flexible structures in various industrial sectors, particularly in aerospace and intelligent manufacturing. The ubiquity of these flexible structures within the industrial milieu has yielded marked enhancements in operational efficiency and concomitant reductions in operational costs1,2.

Within the contemporary societal landscape, encompassing precision machineries such as aerospace technology, architectural design, robotics manufacturing, and basic mechanical manufacturing, the design and construction of structures within these domains have gravitated increasingly toward a paradigm characterized by heightened flexibility and diminished stiffness3,4,5. This trend towards structural lightweighting has the potential to improve operational efficiency, enhance precision, and reduce energy consumption.

Structures integral to aerospace systems, by virtue of their exacting specifications, necessitate meticulous attention to surface precision. The intrinsic susceptibility of flexible systems to excitations induced by external forces begets the inevitability of persistent, gradually attenuating, and vexatious flexible vibrations—an inherent attribute of mechanical structures. Except for a select cadre of specialized vibration testing apparatus and related products, the noise perturbations arising from vibrations can precipitate deleterious ramifications upon system performance. Consequently, mitigating vibration-induced effects on structures while maintaining their operational stability has become a critical focus for researchers in the aerospace, defense, and mechanical sectors6.

Piezoelectric-like materials, as a burgeoning class of smart materials, proffer distinct advantages such as compact structural profiles and rapid response times. These attributes furnish novel prospects for the active control of flexible structural vibrations. Therefore, the integration of piezoelectric materials into structural surfaces to engender sensors and actuators has become a commonplace approach within the ambit of structural vibration control. In the context of active control, the selection of sensors and actuators, serving as principal actuating components, wields direct influence over the efficacy of structural vibration mitigation7. Expedient and highly responsive sensors and actuators hold the potential to yield superior outcomes in the active control of structural vibrations. The active vibration control of flexible appendages, grounded in the utilization of piezoelectric sensors and actuators, represents a formidable scholarly pursuit that has garnered substantial attention from both domestic and international academic circles. Given that the performance of active vibration control within flexible structures hinges upon the configuration of sensors and actuators, the problem of optimizing their placement assumes paramount engineering significance. In recent years, scholars worldwide have focused their efforts on two main areas: developing appropriate optimization criteria for control and creating suitable optimization algorithms to solve this problem.

Cui et al.8 employed an energy-based criterion to ascertain the optimal positioning of piezoelectric actuators, with the initial few eigenmodes of the structural beam as the analytical focus. Pal et al.9 harnessed series quadratic programming techniques to optimize the distribution of piezoelectric layers vis-à-vis the transient vibration control of flexible plates, with transient vibration energy serving as the optimization objective. Mohommad & Ali10 cast the optimization of piezoelectric sensor and actuator locations as a binary optimization problem, using beam theory as a foundational framework. Thereafter, they leveraged the linear quadratic regulator (LQR) control system’s performance index function as the objective function for the optimization of the bidirectional discrete allocation of actuators and sensors across the flexible sheet. Gonçalves et al.11 adopted a system controllability perspective, employing the controllability index as the objective function in optimizing a pair of piezoelectric elements. Sun et al.12 proffered an optimal configuration strategy grounded in energy-based criteria for both sensors and actuators, predicated upon the equation of state characterizing the smart flexible plate. Once these optimization criteria are established, the next step is to solve constrained optimization problems with nonlinear functions. Traditional nonlinear solution methods often struggle in this area, as they can easily get stuck in local optima, leading to solution failures.

Wang et al.13 hinged their efforts on an experimental identification methodology for ascertaining the system transfer function. They subsequently adopted the pole configuration method to facilitate active control over the vibrations of piezoelectric flexible appendages. Li et al.14 employed a PID control strategy to effectuate control over piezoelectric smart structures. Xu et al.15 implemented negative velocity feedback within the context of modal control to suppress vibration in a cantilever beam. Ding et al.16 optimized the positions of sensors or actuators, leveraging the spatial H2 parametrization of the closed-loop transfer function concerning the interference and actuation output of the flexible structure as an optimization criterion. Argha et al.17 proposed a methodology encompassing the simultaneous design of H ∞ controllers and the optimization of sensor or actuator placement. Schlinquer et al.18 espoused the objective of maximizing actuator output force as the basis for actuator optimization. Bendine et al.19 advanced a modal controllability approach underpinned by the singular value analysis of the control vector for the optimization of actuator positions. In recent years, intelligent search algorithms, such as the simulated annealing algorithm, genetic algorithm, and particle swarm optimization method, have gained widespread adoption, yielding favorable results e20. Kouider et al.21 harnessed a genetic algorithm with decimal real number encoding to optimize the comprehensive and simultaneous allocation of actuators and sensors, with the objective of maximizing energy consumption within active control. Jia et al.22 optimized actuator and sensor placements via a particle swarm optimization algorithm, underpinned by the optimization criterion of singular values inherent to the controllable Gramian matrix.

Based on the existing research, this study proposes a new framework for optimally configuring piezoelectric sensors and actuators in the quintessential cantilever beam, a typical model of intelligent structural systems. The proposed methodology is founded upon the articulation of an optimization objective function contingent upon the controllability and observability criteria characterizing the system. A small habitat genetic algorithm is deployed to derive a preliminary configuration scheme for sensor and actuator optimization. The efficacy of this methodology is empirically validated through comparative simulations, affirming its commendable control performance. Furthermore, the framework is extended to encompass a vehicle suspension model, where its effectiveness and efficiency are corroborated through simulation-based comparisons with alternative control methodologies.

Related works

Definition of smart structure

A smart structure is a sophisticated composite structure created by integrating sensing elements, actuation components, and control systems within a matrix material. This integrated configuration endows the structure with the capability to perceive and autonomously respond to external stimuli, facilitating a range of functions encompassing self-detection, self-diagnosis, and self-adjustment. The genesis of smart structures can be traced back to the late 1970s and early 1980s when the United States military initially introduced the concept of “Smart Materials and Structures” with the aim of augmenting the performance of its vehicular assets. Subsequently, research endeavors pertaining to smart structures commenced in the 1980s, with the United States pioneering the conception and subsequent exploration of this ___domain. Simultaneously, various other developed nations and regions across the globe, including Japan, the United Kingdom, Germany, South Korea, Taiwan, and Hong Kong, embarked on research initiatives concerning intelligent materials and structures.

Smart structures are a modern and innovative concept with applications in various fields, including shape control, adaptive systems, and vibration mitigation, particularly in aerospace engineering. They exhibit remarkable proficiency in vibration suppression, yielding palpable advantages when juxtaposed with conventional passive vibration control methodologies. The key attribute of smart structures is their ability to sense changes in the external environment, identify the sources of these changes, and execute intelligent control actions. This “intelligence” emanates from their holistic integration of sensing, control, and actuation functions, thereby constituting a comprehensive adaptive control process. Consequently, a smart structure inherently comprises, at a minimum, three constituent elements: sensors, actuators, and a control system.

Vibration control methods

This discussion primarily focuses on the utilization of piezoelectric materials within the ___domain of structural vibration control. Within this context, three principal categories of control systems are delineated: active control, passive control, and hybrid active-passive control, commonly referred to as passive control. Passive control, as the nomenclature suggests, operates without necessitating external energy infusion. This mode of control achieves structural vibration mitigation by incorporating materials with energy dissipation or storage properties into the controlled structure, thereby enabling the absorption of energy generated during vibration.

Conversely, active control, often denoted as active control, entails a greater cost but offers superior control efficacy. This method leverages modern control theory as its theoretical foundation and embodies a control system imbued with robust adaptability to varying external environmental conditions and control objectives. In an Active Vibration Control (AVC) system, each component acts as an independent subsystem, seamlessly integrated into a closed feedback loop where the output of one component serves as the input for another. The application of active vibration control has found extensive adoption in metrology, photo-etching, the medical field, and the semiconductor industry. It has demonstrated commendable effectiveness and holds substantial potential for vibration control applications in mechanical and civil engineering contexts.

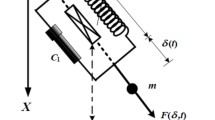
The piezoelectric active control methodology boasts adaptability for customization according to specific control targets, rendering it particularly suited for low-frequency range vibration control. A succinct overview of the active control process is depicted in Fig. 1.

Fig. 1
figure 1

Flow chart of active vibration control.

Full size image

Status of domestic and international research on intelligent active control

In consonance with the evolution of artificial intelligence, the ___domain of active vibration control technology has progressively shifted from conventional control methods towards a more intelligent paradigm. Notably, the efficacy of fuzzy control has stood out among various vibration attenuation techniques due to its aptitude for addressing nonlinear system characteristics and uncertainties in parameter values. Fuzzy controllers are widely used in active vibration control, especially in civil engineering structures, vehicle suspension systems for vibration damping, and robotic arms with flexible components.

Neuro-fuzzy control represents an amalgamation of a fuzzy logic system and artificial neural networks, harnessing the advantages of neural networks’ learning and optimization capabilities in tandem with the interpretability of fuzzy logic. A specialized variant of neuro-fuzzy systems is the neuro-fuzzy inference system, which draws from the Takagi-Sugeno fuzzy inference framework. This architecture, characterized by multilayered connectivity and supervised learning via unidirectional connections, each layer corresponding to a processing step, can be fine-tuned using a neuro-fuzzy inference system controller. Researchers such as Aela et al. (Reference23) have proposed adaptive radial basis neural networks coupled with quarter-car active suspension systems, effectively addressing model uncertainties and accommodating unknown smoothing functions. Awada et al. (Reference24) employed a neural network control algorithm to actively control intelligent cantilever beams featuring piezoelectric patches. Sahu et al. (Reference25) introduced a two-degree-of-freedom structure with electromagnetic actuators for vibration active control, deploying a differential evolution method for the identification of unknown stiffness and damping coefficients. The vibration active control was further optimized using fuzzy neural control theory.

In the context of structural vibration control, intelligent active vibration control research within domestic settings has been relatively nascent. Nevertheless, recent years have witnessed substantial advancements in this field, bolstered by the rapid growth of the mechanical, defense, aerospace, and communication industries. Researchers like He et al. (Reference26) pioneered the development of a comprehensive closed-loop damping controller for large flexible satellites, ensuring effective suppression of multiple vibration orders through the application of traditional closed-loop controllers, such as sliding-mode controllers. Furthermore, a dynamic optimal control assignment algorithm was introduced for a six-flywheel drive control system, accompanied by the formulation of a novel non-singular fast terminal sliding mode controller. Cao et al. (Reference27) projected the dynamic characteristics of intelligent composite plates using an effective model and subsequently implemented control mechanisms employing genetic algorithms. Zhai Xu and Luo Yajun (Reference28) delved into the active control of ring antenna vibrations under impulsive excitations. Zhan et al. (Reference29) devised an intelligent composite damper employing a fuzzy control strategy. This composite damper, endowed with an active control system, efficiently curtailed the dynamic response of engineered structures during seismic excitations, consisting of a shape memory alloy wire and a variable friction damper capable of modulating control forces by adjusting the voltage applied to the piezoelectric ceramic actuator.

Methodology

Establishing the optimization objective function

The partial differential equation for the epoxy resin flexible cantilever beam is as follows.

$$\:F(u,n)=W\left(u\right)\frac{{\partial\:}^{2}m(u,n)}{\partial\:{n}^{2}}+2\zeta\:\left[W\right(u)L{]}^{1/2}\frac{\partial\:m(u,n)}{\partial\:n}+L[m(u,n)]$$
(1)

Where: \(\:F(u,n)\) represents the external force distribution; \(\:\zeta\:\) represents the white noise signal of general intensity.

The principle of actuator distribution is to maximize its influence on structural disturbances. If the actuator energy is fixed, the energy transmitted to the structural modes should be maximized. Based on this principle, the optimization criterion of the actuator is as follows.

$$\:{opz}^{{\prime\:}}=2\left(\sum\:_{x=1}^{t}\:{E}_{x}\right)\sqrt[t]{\prod\:_{x=1}^{t}\:{E}_{x}}$$
(2)

Where \(\:{E}_{x}\) is the mathematical expectation of the total energy of the ith order of the mode. Based on the fact that the size of the diagonal elements of the sizable character Ram matrix is proportional to the steady state of the system, a criterion for optimal sensor configuration can be established as

$$\:{opz}^{{\prime\:}}=\left(\sum\:_{Y=1}^{2t}\:{\lambda\:}_{Y}\right)\sqrt[2t]{\prod\:_{Y=1}^{2t}\:\left({\lambda\:}_{Y}\right)}$$
(3)

Where \(\:{\lambda\:}_{Y}\) is the eigenvalue of the observable Gram matrix. Since the cantilever beam vibration control system has small damping system characteristics, the eigenvalues of the observable Gram matrix are approximately equal to the eigenvalues of the controllable Gram matrix. This leads to the conclusion that the same ___location and number of sensors and actuators is the best case.

The observable and controllable Gram matrices of the piezoelectric intelligent control system are closely related to the system model parameters, among which the sensor and actuator configurations are the most significant. The optimization of the configuration for sensors and actuators is also the process of seeking the optimal characteristics of controllability and observability Gram matrix. In this process, an objective function is needed as the basis and criterion.

Before establishing the optimization objective function, the controllability and viewability matrices of the system are first elicited based on the transformation relationship between the Gramian matrix and the modal energy expression of the system. The observable Gramian matrix \(\:{M}_{\text{obs\:}}\)and controllable Gramian matrix \(\:{M}_{\text{con\:}}\)are as follows.

$$\:{M}_{obs}=diag\left(\frac{{c}_{t}}{4{\xi\:}_{x}{m}_{x}},\frac{{c}_{t}}{4{\xi\:}_{x}{m}_{x}}\right),x=\text{1,2},\cdots\:,t$$
(4)
$$\:{M}_{\text{con\:}}=diag\left(\frac{{\beta\:}_{t}}{4{\zeta\:}_{x}{m}_{x}},\frac{{\beta\:}_{t}}{4{\zeta\:}_{x}{m}_{x}}\right),x=\text{1,2},\cdots\:,t$$
(5)

Where: m represents the disturbance function of the beam; \(\:\xi\:,\zeta\:\) represent the external disturbance signal, white noise signal; \(\:{\beta\:}_{t},{c}_{t}\) represent the corresponding matrix coefficients. If the inherent frequency distribution of the structural vibration system is good and the damping coefficient is relatively small, the following optimization objective function is established.

$$\:Obj=trace\left(M\right)\sqrt[2t]{den\left(M\right)}/\sigma\:\left({\lambda\:}_{x}\right)$$
(6)

Where: M is the Gramian matrix, which takes the values of \(\:{M}_{\text{obs\:}}\) or \(\:{M}_{\text{con\:}}\), and its physical meaning is the energy of the modes of each order. trace (M) represents the output energy of the actuator; \(\:\sqrt[2t]{\text{d}\text{e}\text{t}\left(M\right)}\) represents the geometric mean of the eigenvalues; t represents the degree of freedom coefficient, and its physical meaning is the product of the energy of the modes of each order. It is intended to actuate all its modalities of all orders (including higher-order modalities). \(\:\sigma\:\left({\lambda\:}_{x}\right)\) refers to the standard variance of the eigenvalues \(\:{\lambda\:}_{x}\) of the Gramian matrix M. The main purpose is to avoid positions with both very large and very small eigenvalues.

Sensor and actuator configuration optimization process

When optimizing the sensor and actuator parameters by the controllable/observable Gramian matrix, the Lyapunov equation needs to be solved several times, especially for multiple targets, and the computational effort increases exponentially. Therefore, in order to avoid the complicated calculation in the optimization process, this paper uses a genetic algorithm to optimize its objective function. The proposed algorithm is divided into three steps as follows: (1) To find the expressions of each order of the intrinsic frequency and each order of the modal strain of the piezoelectric cantilever beam. (2) Perform the modal analysis for the intelligent piezoelectric cantilever beam, and find out the basic parameters such as the inherent frequency, vibration pattern and stress distribution of each order. (3) The modal values and inherent frequencies are transformed into the form required by the optimized objective function and substituted into the optimized objective function; the position optimization is carried out according to the genetic algorithm, and the optimized arrangement of the piezoelectric sensors and actuators is finally derived.

Under the condition that all the piezoelectric cantilever beam units are ideal, the dynamic equations of the piezoelectric cantilever beam and its boundary conditions are derived as

$$\:\frac{EX}{\rho\:G}\frac{{\partial\:}^{4}j(i,n)}{\partial\:{i}^{4}}+2\zeta\:\sqrt{\frac{EX}{\rho\:G}}\left[\frac{{\partial\:}^{3}j(i,n)}{\partial\:{i}^{2}\partial\:n}\right]+\frac{{\partial\:}^{2}j(i,n)}{\partial\:{n}^{2}}=\frac{1}{\rho\:G}\sum\:_{l=1}^{U}\:\delta\:\left(i-{i}_{l}\right){f}_{l}\left(n\right)$$
(7)

Where: E represents the modal volume; \(\:\rho\:\) represents the density; G represents the cross-sectional area; X represents the cross-sectional quadratic distance. It can be transformed into the general solution form.

$$\:j\left(i\right)={C}_{1}sin\left(\beta\:i\right)+{C}_{2}cos\left(\beta\:i\right)+{C}_{3}sinh\left(\beta\:i\right)+{C}_{4}cosh\left(\beta\:i\right)$$
(8)
$$\:{\left.j(i,n)\right|}_{i=0}=0,{\left.\frac{\partial\:j(i,n)}{\partial\:i}\right|}_{i=0}=0$$
(9)
$$\:{\left.EX\frac{{\partial\:}^{2}j(i,n)}{\partial\:{i}^{2}}\right|}_{i=l}=0,{\left.EX\frac{{\partial\:}^{3}j(i,n)}{\partial\:{i}^{3}}\right|}_{i=l}=0$$
(10)

Equations (9) and (10) are the geometric boundary constraint at the fixed end and the force boundary constraint at the free end, respectively, which can be obtained from the two equations:

$$\:{C}_{1}=-{C}_{3},{C}_{2}=-{C}_{4}$$
(11)
$$\:\left\{\begin{array}{c}{C}_{1}[cos(\beta\:l)+cosh(\beta\:l\left)\right]+{C}_{2}[sin(\beta\:l)+sinh(\beta\:l\left)\right]=0\\\:-{C}_{1}[sin(\beta\:l)-sinh(\beta\:l\left)\right]+{C}_{2}[cos(\beta\:l)+cosh(\beta\:l\left)\right]=0\end{array}\right.$$
(12)

In Eq. (11), the conditions for C1 and C2 to be non-zero solutions is

$$\:\left|\begin{array}{cc}cos\left(\beta\:l\right)+cosh\left(\beta\:l\right)&\:sin\left(\beta\:l\right)+sinh\left(\beta\:l\right)\\\:-sin\left(\beta\:l\right)+sinh\left(\beta\:l\right)&\:cos\left(\beta\:l\right)+cosh\left(\beta\:l\right)\end{array}\right|=0$$
(13)

By expanding Eq. (13), the following results are derived:

$$\:cos\left(\beta\:l\right)cosh\left(\beta\:l\right)+1=0$$
(14)

The natural frequency equation for each mode is given by

$$\:{\omega\:}_{t}={\left({\beta\:}_{t}l\right)}^{2}\sqrt{\frac{EX}{\rho\:{l}^{4}}},t=\text{1,2},3,\cdots\:,t$$
(15)

From Eqs. (8), (14) and (15), the modal function of each order is as follows.

$$\:{\varphi\:}_{t}\left(i\right)=cos\left({\beta\:}_{t}i\right)-cosh\left({\beta\:}_{t}i\right)+{\xi\:}_{t}\left[sin\left({\beta\:}_{t}i\right)-sinh\left({\beta\:}_{t}i\right)\right]$$
(16)

In order to clearly describe the optimization method, a schematic diagram of the coordinate positions of the piezoelectric flexible cantilever beam is established as shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of coordinate establishment of a piezoelectric cantilever beam.

Full size image

The optimal configuration of piezoelectric sensors and actuators for the flexible cantilever beam intelligent control system is essentially a multi-objective optimization problem, which can be accomplished by using a small habitat genetic algorithm. In the process of the algorithm, the number of small habitats of each individual needs to be calculated, and the smaller habitat values give more chances to be inherited. It is calculated as follows.

$$w_{i} = \sum\limits_{{j \le t}} {\vartheta \left[ {d\left( {i,j} \right)} \right]}$$
(17)

Where: \(\:\vartheta\:\left[d\right]\) represents the sharing function; \(\:d(i,j)\) represents the Hemming distance between the two bodies i, j. The intrinsic frequencies and modal values are transformed into the form needed for the optimization objective function and substituted into the optimization objective function. Based on the genetic algorithm flow as shown in Fig. 3, the configuration optimization is carried out for the flexible cantilever beam.

Fig. 3
figure 3

Flow chart of the genetic algorithm based on the piezoelectric element position optimization.

Full size image

Figure 4 shows the average distance of individuals in the optimization process. The average distance is a decreasing process, indicating that the value of the number of individual habitats is decreasing, which indirectly indicates that the optimization algorithm is reasonable. Figure 5 shows the comparison between the best fitness and the average fitness. The best adaptation is significantly smaller than the average fitness, indicating that this optimal configuration is theoretically reasonable.

Fig. 4
figure 4

Average distance of individuals.

Full size image
Fig. 5
figure 5

Comparison between optimal fitness and average fitness.

Full size image

Result analysis and discussion

In this section, the control effect of the method is verified through two experiments, frequency ___domain simulation and time ___domain simulation. Additionally, the method is extended to a vehicle suspension model and compared with three existing control strategies: the sensor/actuator optimization method by Prakash et al.30, the H∞-observer-based disturbance rejection control by Zhang et al.31, and the finite element state-space control by Aktas & Esen32. These comparisons aim to demonstrate the superiority of the proposed method.

Frequency ___domain simulation experiments and analysis

In order to show the advantages of the proposed system, it is compared with three other control systems.

As seen in Fig. 6, the vibration control based on the small habitat genetic algorithm shows superior performance across a wide range of frequencies, including low, medium, and high frequencies. The system’s amplitude response converges close to zero in all resonance modes, demonstrating exceptional vibration suppression. This can be attributed to the precision of the genetic algorithm in minimizing amplitude fluctuations at multiple frequency bands, allowing for a more uniform and efficient control compared to other methods, which are more susceptible to frequency-specific resonances.

Fig. 6
figure 6

Amplitude response of the system output.

Full size image

A comparison of the amplitude response across different frequency ranges (low and medium frequencies) is presented in Table 1. This table provides a detailed comparison of the peak amplitude (dB) and resonance suppression efficiency (%) between the proposed method and the three baseline methods (Prakash et al.30, Zhang et al.31, and Aktas & Esen32).

Table 1 Frequency-___domain performance comparison.
Full size table

Table 1 demonstrates the proposed method’s superior ability to suppress vibrations across all frequency bands, achieving near-zero amplitude responses (e.g., -42.5 dB in low frequencies) and consistently higher suppression efficiency (> 90%) compared to other methods.

Time ___domain simulation experiments and analysis

Experiment 1: Random white noise signal using the Band-Limited White Noise module in MATLAB/SIMULINK as the excitation signal, the variance and rejection rate of the four control system amplitudes are shown in Table 2, and the time-___domain response is shown in Fig. 7.

Table 2 Performance under random excitation.
Full size table
Fig. 7
figure 7

Vibration amplitude under disturbance excitation of sinusoidal signal.

Full size image

As illustrated in Table 2, the proposed control method demonstrates superior performance in suppressing vibrations induced by random white noise interference. Specifically, the proposed method achieves the lowest amplitude variance (0.0018) and the highest rejection rate (1.2%), indicating its superior ability to maintain low vibration levels and effectively reject disturbances. Additionally, the proposed method exhibits the shortest settling time (1s) and the smallest peak amplitude (0.09 mm), further highlighting its effectiveness in disturbance rejection. As seen in Fig. 7, the time-___domain response also reveals that the proposed control method outperforms the other strategies in terms of maintaining lower vibration levels and more effectively rejecting disturbances. The improvement in control performance can be attributed to the adaptive nature of the proposed algorithm, which is capable of effectively addressing random fluctuations without excessive overshoot or steady-state error.

Experiment 2: Sine signal.

The time ___domain response of the four control systems is shown in Fig. 8.

Fig. 8
figure 8

Vibration amplitude under interference excitation of sinusoidal signal.

Full size image

As demonstrated in Fig. 8, the proposed control method yields significantly smaller vibration amplitudes compared to the other three methods. This superior performance indicates that the proposed system is more capable of handling periodic disturbances, which may excite specific resonant modes. This is consistent with the results from Experiment 1, where the proposed method exhibited superior disturbance rejection. The method’s ability to suppress vibrations in response to periodic excitation suggests that the algorithm is effective in mitigating vibrations across different excitation profiles.

Analysis of the extension application of the algorithm

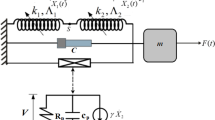
In order to verify the effectiveness of the method in this chapter for other controlled objects with modal characteristics, the method is extended to the field of active control of automotive suspension vibration.

Here, one of the output variables is studied first: the dynamic travel of the vehicle suspension. Here, the inverse model is used to treat the modal state at the second-order intrinsic frequency to suppress its amplitude response. The inverse model is calculated as

$$\:{A}_{inv}=o\frac{{s}^{2}+2{\xi\:}_{2p}{\omega\:}_{2p}+{\omega\:}_{2p}^{2}}{{s}^{2}+2{\xi\:}_{2z}{\omega\:}_{2z}+{\omega\:}_{2z}^{2}}$$
(18)

.

Where \(\:{\omega\:}_{2p}={f}_{2}=10.9\text{H}\text{z}\), \(\:{\omega\:}_{2z}=0.8{\omega\:}_{2p}\). Here the damping of the modes is generally smaller, \(\:{\xi\:}_{2p}=0.1\). And the damping \(\:{\xi\:}_{2z}\) is generally larger than the damping \(\:{\xi\:}_{2p}\), taken as \(\:{\xi\:}_{2z}=2\), \(\:o=0.64\). The corresponding three parameters of the controller are obtained by the trial-and-error method:\(\:{o}_{p}=1.2\), \(\:{o}_{d}=0.5\), \(\:{o}_{i}=0\).

Frequency ___domain simulation

In order to show the control effect of the proposed algorithm, the above three methods are also utilized as a comparison, and the output of its closed-loop system is shown in Fig. 9. As shown in Fig. 9, all three control strategies produced some level of suppression of the suspension dynamic travel. However, the proposed method demonstrated the most significant reduction in amplitude, bringing the output response closer to zero. This highlights the effectiveness of the small habitat genetic algorithm in controlling vehicle suspension vibrations, particularly in dynamic conditions where precise control is crucial to maintaining stability.

Fig. 9
figure 9

Amplitude response of suspension dynamic travel.

Full size image

Time ___domain simulation

When the road excitation is given as a step signal, the suspension dynamic travel of this control system and the other three control systems are shown in Fig. 10. Specifically, Fig. 10a shows the comparative results with other methods, while Fig. 10b shows the independent results of the proposed method to clearly demonstrate its near-zero dynamic travel.

Fig. 10
figure 10

Comparison graph of suspension dynamic travel.

Full size image

Figure 10 shows that the proposed system provides the best control performance, with the suspension dynamic travel essentially being reduced to zero, unlike the other methods that displayed larger displacement responses. The superior performance of the proposed system can be attributed to the optimal parameter tuning achieved through the genetic algorithm, which adapts better to the non-linear and time-varying dynamics of the suspension system. This demonstrates the method’s potential for real-world applications, particularly in active control systems for vehicles.

In order to verify the method’s applicability to real world systems, a comparison of suspension dynamic travel and settling time under step inputs was made in Table 3.

Table 3 Suspension dynamic travel comparison.
Full size table

As can be seen from Table 3, the proposed method shows significant advantages over the other methods in terms of suspension dynamic travel, settling time and peak amplitude. With a dynamic travel of only 0.02 mm, it achieves near - zero movement, which is far better than the 0.25 mm of Prakash et al.30, 0.20 mm of Zhang et al.31, and 0.15 mm of Aktas & Esen32. The settling time of 1.5 s also indicates a much faster stabilization process compared to the 3.0 s, 2.8 s and 2.5 s of the other three methods respectively. And the peak amplitude of 0.10 mm is the lowest among all, suggesting better control performance. These results demonstrate that the proposed method has outstanding performance and great practical value for automotive applications, as it can effectively reduce the suspension dynamic travel, shorten the settling time and control the peak amplitude, thus improving the overall stability and comfort of the vehicle.

Conclusion

Intelligent structural active vibration control systems are poised to offer significant contributions across various domains, including robotics, aerospace, and beyond. Central to the efficacy of these systems is the judicious arrangement of sensors and actuators. This study introduces an innovative method for the optimal placement of piezoelectric sensors and actuators, employing a small habitat genetic algorithm as the optimization tool. Extensive simulation experiments substantiate the method’s commendable control efficacy when compared to alternative techniques. Moreover, the method’s versatility is extended to encompass an automotive suspension model, where its effectiveness and efficiency are corroborated through supplementary simulation investigations. Notably, this proposed approach holds applicability beyond the automotive ___domain and can be readily extended to diverse flexible components, thereby offering valuable insights and a comprehensive exploration of optimal sensor and actuator configurations. While this study demonstrates the effectiveness of the proposed method, future research can further enhance the applicability and performance of intelligent vibration control systems by exploring multi-objective optimization techniques.