Introduction

Intelligent electric vehicle (IEV) is capable of handling complex transportation scenario and replacing people in extreme working conditions, so in many areas it possesses favorable application potential. Generally speaking, motion control is the most crucial component of a vehicle system. When the road curvature is relatively small, the motion control system can be decoupled into longitudinal control and lateral control1 and the latter occupies a central position in vehicle control technology, whose main task is to accomplish reference trajectory tracking. Although this research direction has attracted a crowd of researchers’ attentions in recent years, many excellent results have been obtained, for example, the widely used PID algorithm2,3, the mature linear quadratic regulator (LQR)4,5, and sliding mode control (SMC)6,7, as well as the fuzzy control8,9 and model predictive control (MPC)10,11, etc., the various challenges still remain. This paper focuses mainly on the resource-constrained lateral motion control problem for the IEV.

It is worth noting that the previously mentioned control methods are all based on time triggering mechanisms. Nevertheless, the IEV integrates sensing, communication, computation, complex controller, actuator and other modules12. If we would like to adapt the lateral motion control algorithm into its practical engineering applications, the resources (computing, communication and energy)-constrained problem must be considered seriously13,14. It is extremely possible that time-triggered control methods will lead to unnecessarily heavy workloads that consistently take up a large amount of computation and communication resources of various embedded systems15,16, nevertheless sometimes these valuable resources could be saved and more efficiently allocated to other tasks. On the other hand, in most current application scenarios, the communication among spatially distributed sensors, actuators and microprocessors for the IEV are networked and wireless17. Therefore, research on lateral motion control for the IEV has to create novel scheme to deal with limited network channel bandwidth and computing capability together with limited battery energy, otherwise these issues will most likely influence the overall performance of the IEV and the task scheduling18,19.

The introduction of event triggering mechanism (ETM) into the control system is an extremely promising solution to the above-mentioned problem, and it is extremely applicable, not only to intelligent electric vehicle systems, but also to the control problems of various systems, for which some excellent research results are available nowadays. For instance, for nonlinear multi-agent systems, a distributed adaptive event-triggered control scheme is proposed via command filter and backstepping technique by Li et al.20 to solve the consensus tracking problem. Furthermore, focusing on uncertain cyclic switched stochastic nonlinear systems, Yan et al.21 proposed a novel mode-dependent event-triggered optimized mechanism for the subsystem, which could effectively improve the overall performance of the system and lessen the communication workload. The control method with ETM determines the sampling instants at which the control system carries out a series of operations such as computation, communication, and updating the control input, according to some specific event triggering rules. This means that it is possible to alleviate the computation and communication loads of the networked/embedded control systems, to sharply reduce the number of the control updates, and to further lessen the mechanical wear and energy consumption. Therefore, this work aims to develop a control method based on ETM which allows to allocate system resources more rationally, thereby increasing resource utilization rate, saving energy, and improving the overall performance of the IEV.

Nonetheless, there are still various problems that need to be addressed in order to apply ETM to IEV platforms. Among them, the difficulty in designing and changing the triggering characteristics of event-triggered control system for the IEV is an extremely critical point, in which the triggering characteristics refer to the triggering threshold, the variable range and evolution rate of the triggering signals22, the event triggering frequency, and inter-event times, e.t.c. In existing ETM (such as the relative, absolute, and mixed ETM23), the triggering threshold in the triggering rule is fixed, with a small adjustable range, while the triggering number is on the high side. Subsequently, we noticed that some adaptive ETMs have been studied to break the fixed triggering rule. For example, Zhu et al.24 investigated a novel dynamically adaptive ETM for optimization tracking control of Stochastic nonlinear systems, which adjusts the triggering threshold online. Zhang et al.25 proposed an adaptive event-triggered dual-mode MPC algorithm for lateral reference trajectory tracking of unmanned vehicle.

Although some studies have tuned the triggering frequency by creating adaptive triggering thresholds, the variable range and evolution rate of adaptive variables may still be difficult to design or change. Besides, Zeno behavior is also noteworthy. Although most of the existing ETMs applied to actual systems can theoretically exclude the possibility of Zeno behavior, in real-world environments, it is inevitable to be affected by external disturbances26, which probably leads to the phenomenon of accumulation of events. Another side, in the presence of disturbances, it is extremely significant to prove whether they hold the event-separation property (RESP)27,28 and whether they can still exclude Zeno behaviour. However, at present, few studies have discussed and analyzed the RESP of the constructed event-triggered control systems.

On the basis of the above discussion, separate from existing event-triggered control methods29,30,31, our aim is to introduce a system-specific design and implementation of a dynamic ETM with designable triggering characteristics. Therein, a robust sliding mode controller (RSMC) is designed and RESP is analyzed for event-triggered lateral motion control dynamic system of IEV with bounded disturbances. The major contributions of this paper can be summarized as follows:

  • We design a new dynamic event-triggered RSMC (abbreviated as DET-RSMC) to address the lateral control issue of perturbed IEV. In contrast to the time-triggered control mechanism32,33, this dynamic ETM can effectively reduce computation and communication loads through decreasing the number of control input updates, thereby conserving constrained resources and minimising actuation hardware loss in IEV.

  • Different from the existing static ETMs34,35, the proposed triggering rule is dynamic, while its triggering characteristics are easy to design. This means that more or less triggering numbers can be generated by adjusting the maximum value and evolution rate of the triggering signals, and consequently the desired triggering characteristics can be obtained.

  • For the possible effects of disturbances during the movement of IEV in reality36, in the proposed control method, we not only design the time-triggered controller and extend it to the event-triggered RSMC, but also theoretically prove that the dynamic ETM allows the system to hold a semi-global RESP. This property could effectively suppress external disturbances and avoid potential Zeno behavior, as confirmed by our simulation results. It is worth mentioning that the above two aspects are not discussed or not considered simultaneously in the current research on dynamic ETMs with disturbances37,38.

The rest of this paper is organized as follows. Section "Problem formulation" presents the dynamics model of the vehicle and problem formulation. In Section "Main results", a RSMC is designed and a dynamic ETM with designable triggering characteristics is proposed. Stability proof and robust analysis are provided in section "Stability and feasibility analysis". The simulation results are shown in Section "Simulation results". Finally, Section "Conclusions" concludes the whole paper, with some remarks and prospects.

In this paper, the following notation is adopted: The set of real numbers is denoted as \(\mathbb {R}\), and then the set of positive real numbers and the set of non-negative real numbers are represented by \(\mathbb {R}_{\ge 0}\) and \(\mathbb {R}_{>0}\), respectively. \(\mathbb {R}^{n}\) indicates the n-dimensional Euclidean space. Next, \(|\cdot |\) expresses the absolute value. \(||\cdot ||\) denotes the 2-norm of a vector or the induced 2-norm of a matrix.

Problem formulation

Fig. 1
figure 1

Dynamic bicycle model.

Full size image

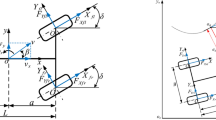
The target of lateral control for IEV is to minimize the lateral displacement of the vehicle vis-a-vis a specific reference path. To define the control problem and design the controller, we consider a widely dynamic bicycle model shown in Fig. 1.

Table 1 Parameters and nomenclature.
Full size table

Based on the dynamics of a vehicle’s lateral displacement error e relative to a reference path26:

$$\begin{aligned} \ddot{e}=V_x(\dot{\beta }+\dot{\psi })-{V_x}^2 \rho , \end{aligned}$$
(1)

and the dynamical equations for the side slip angle \(\beta\) and yaw rate \(\dot{\psi }\), system state variables can be denoted \(x=[\beta , \dot{\psi }, e, \dot{e}]^{\textrm{T}}\), and the control input is the steering wheel angle \(\delta\). The corresponding parameters and nomenclature are listed in Table 1.

Then, in order to eliminate the lateral displacement error, for a given road curvature \(\rho\) and \(V_x\), our control objective is to arrive at \(e=\dot{e}=0\). At the desired equilibrium point, it can be defined the desired reference state \(x^\star\) as

$$\begin{aligned} x^\star =\left[ \begin{array}{l} \beta ^\star \\ \dot{\psi }^\star \\ 0 \\ 0 \end{array}\right] =\left[ \begin{array}{cccc} L_{r}\rho -\dfrac{L_{f} m V_{x}^{2}\rho }{\mu C_{r}\left( L_{f}+L_{r}\right) } \\ V_{x} \rho \\ 0 \\ 0 \end{array}\right] , \end{aligned}$$
(2)

and the desired reference control input \(\delta ^\star\) as

$$\begin{aligned} \delta ^\star =\left( L_{f}+L_{r}\right) \rho +\dfrac{m V_{x}^{2}\rho \left( L_{r} C_{r}-L_{f} C_{f}\right) }{\mu C_{f} C_{r}\left( L_{f}+L_{r}\right) } , \end{aligned}$$
(3)

which are proved in39. Then, by constructing the error variable

$$\begin{aligned} \begin{aligned} \tilde{x}&=x-x^\star =\left[ \begin{array}{cccc} \beta -\beta ^\star \\ \dot{\psi } - \dot{\psi }^\star \\ e\\ \dot{e} \end{array} \right] =\left[ \begin{array}{cccc} \tilde{\beta } \\ \dot{\tilde{\psi }} \\ e\\ \dot{e} \end{array} \right] , \\ \tilde{\delta }&=\delta -\delta ^\star , \end{aligned} \end{aligned}$$
(4)

we can write the error dynamics as

$$\begin{aligned} \dot{\tilde{x}}(t)= A \tilde{x}(t)+B \tilde{\delta }(t), \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}\begin{array}{l} A=\left[ \begin{array}{cccc} -\frac{\mu \left( C_{f}+C_{r}\right) }{m V_{x}} & -1-\frac{\mu \left( L_{f} C_{f}-L_{r} C_{r}\right) }{m V_{x}^{2}} & 0 & 0 \\ -\frac{\mu \left( L_{f} C_{f}-L_{r} C_{r}\right) }{I_{z}} & -\frac{\mu \left( L_{f}^{2} C_{f}+L_{r}^{2} C_{r}\right) }{I_{z} V_{x}} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{\mu \left( C_{f}+C_{r}\right) }{m} & -\frac{\mu \left( L_{f} C_{f}-L_{r} C_{r}\right) }{m V_{x}} & 0 & 0 \end{array}\right] , \\ B=\left[ \begin{array}{cccc} \frac{\mu C_{f}}{m V_{x}} ;& \frac{\mu L_{f} C_{f}}{I_{z}};& 0;& \frac{\mu C_{f}}{m} \end{array}\right] ^{\textrm{T}}. \end{array}\end{aligned} \end{aligned}$$
(6)

Assumption 1

The derivative of road curvature \(\rho\) satisfies \(|\dot{\rho }| \le \lambda\), \(\lambda\) and vehicle longitudinal speed \(V_x\) are considered as continuous and bounded constants corresponding to the reality situation. Then, the reference side slip angle \(\beta ^{\star }\), yaw rate \(\dot{\psi }^{\star }\), and steering wheel angle \(\delta ^{\star }\) are bounded \(|\beta ^{\star }| \le \beta _{M}^{\star }\), \(|\dot{\psi }^{\star }| \le \dot{\psi }_{M}^{\star }\), and \(|\delta ^{\star }| \le \delta _{M}^{\star }\). Therefore, the error variable \(\tilde{x}\) always remains bounded, satisfying \(\tilde{x} \in \Omega \subset \mathbb {R}^4\).

More details of this section can be found in other papers using the same dynamic bicycle model26,39.

Main results

With respect to IEV, considering the limited resources of the embedded system, especially the scenarios of wireless communication application , it is necessary to design a class of control method that can accomplish the lateral control target under disturbances while reducing communication and computational loads. In this section, we will achieve the above goal through the following two steps: Firstly, design a continuous-time RSMC that can ensure the asymptotic stability of the error dynamics. Secondly, propose a DET-RSMC design and implementation method, which reduces the resource consumption of communication and computation. Furthermore, the triggering characteristics of the proposed ETM can be designable.

Continuous-time RSMC design

During the motion of IEV, it is inevitable to contemplate the effect of matched disturbances on the lateral control system. Hence, we rewrite the error dynamics of the system (5) as

$$\begin{aligned} \dot{\tilde{x}}(t)= A \tilde{x}(t)+B \left( \tilde{\delta }(t) + \xi (t)\right) , \end{aligned}$$
(7)

Assumption 2

\(\xi (t)\) denotes a bounded matched disturbance term, \(\sup _{t \ge 0}|\xi (t)| \le \bar{\xi }\) and \(\bar{\xi }>0\).

According to the lateral control objective of minimizing the lateral displacement e, constructing the sliding variable

$$\begin{aligned} s(t)=\dot{e}(t)+ve(t), \end{aligned}$$
(8)

where v is a positive constant. Then, the stable sliding manifold for the system (7) is defined as

$$\begin{aligned} S:=\{\tilde{x} \in \Omega \mid s=c \tilde{x}=0\}, \end{aligned}$$
(9)

where \(c=[0\quad 0 \quad v \quad 1]\). According to the dynamical expressions of \(\dot{e}\), \(\beta\) as well as \(\dot{\psi }\)26, the derivative of sliding variable s can be written as:

$$\begin{aligned} \begin{aligned} \dot{s}=&\ddot{e}+v\dot{e} \\ =&-\frac{\mu \left( C_{f}+C_{r}\right) }{m} \beta -\frac{\mu \left( L_{f} C_{f}-L_{r} C_{r}\right) }{m V_{x}} \dot{\psi } -V_{x}^{2} \rho +v \dot{e}+\frac{\mu C_{f}}{m}(\delta +\xi ). \end{aligned} \end{aligned}$$
(10)

Then, replacing with error variables (4), we can get

$$\begin{aligned} \dot{s}(t)=G \tilde{x}(t)+d(\tilde{\delta }(t)+\xi (t)) \end{aligned}$$
(11)

with

$$\begin{aligned} \begin{aligned} G&=\left[ -\frac{\mu \left( C_{f}+C_{r}\right) }{m},-\frac{\mu \left( L_{f} C_{f}-L_{r} C_{r}\right) }{m V_{x}}, 0, v\right] , \\ d&=\frac{\mu C_{f}}{m}, \\ F&=-\frac{G}{d}. \end{aligned} \end{aligned}$$
(12)

Next, depending on the improved exponential reaching law \(\dot{s}=-K_{1}|s|^{\alpha } \operatorname {sign}(s)-K_{2} \operatorname {sign}(s)\) that we derived, the continuous time RSMC can be obtained:

$$\begin{aligned} \tilde{\delta }(t)=F \tilde{x}(t)-\frac{1}{d}\left( K_{1}|s(t)|^{\alpha }+K_{2}\right) \operatorname {sign}(s(t))-\xi (t), \end{aligned}$$
(13)

where \(K_{1}>0\), \(K_{2}>0\), \(0<\alpha <1\), \(\operatorname {sign}(s(t))\) is a signum function described by

$$\begin{aligned} \operatorname {sign}(s(t)):=\left\{ \begin{array}{cl} 1 & \text{ if } s>0, \\ 0 & \text{ if } s=0, \\ -1 & \text{ if } s<0. \end{array}\right. \end{aligned}$$
(14)

Since the disturbance term \(\xi (t)\) is unknown in the continuous-time RSMC (13), let it be \(\xi _{d}(t)\). Additionally, according to the Assumption 2, there is always \(-\bar{\xi } \le \xi _{d}(t) \le \bar{\xi }\). Then, (13) is written as

$$\begin{aligned} \tilde{\delta }(t)=F \tilde{x}(t)-\frac{1}{d}\left( K_{1}|s(t)|^{\alpha }+K_{2}\right) \operatorname {sign}(s(t))-\xi _d(t). \end{aligned}$$
(15)

Theorem 1

The continuous-time RSMC (13) that fulfills \(K_1>0\), \(K_2>0\), \(0<\alpha <1\), and \(\xi _{d}(t)=\bar{\xi }\operatorname {sign}(s(t))\) can drive the sliding variable s to the sliding manifold (9) and asymptotically stabilize the disturbed error dynamics (7).

Proof

Substituting (15) into (11) gives

$$\begin{aligned} \dot{s}=-K_{1}|s|^{\alpha } \operatorname {sign}(s)-K_{2} \operatorname {sign}(s)-d\xi _{d}+ d\xi . \end{aligned}$$
(16)

Consider the Lyapunov candidate function as \(V_c=\frac{1}{2}s^{\textrm{T} }s\), differentiating for \(V_c\) and using (16),

$$\begin{aligned} \begin{aligned} \dot{V_c}&=s^\textrm{T} \dot{s} \\&=- s^\textrm{T} \left( K_{1}|s|^{\alpha }+K_{2}\right) \operatorname {sign}(s)- s^\textrm{T}d(\xi _{d}-\xi ). \end{aligned} \end{aligned}$$
(17)

Therefore, \(\xi _{d}(t)=\bar{\xi }\operatorname {sign}(s(t))\) is selected so that the disturbance term in the disturbed error dynamics (7) is effectively suppressed, always ensuring that \(\dot{V_c}<0\). Then, here is

$$\begin{aligned} \begin{aligned} \dot{V_c} \le&- \left( K_{1}|s|^{\alpha }+K_{2}\right) ||s|| -d(\bar{\xi }-\xi )||s|| \\ \le&- \left( K_{1}|s|^{\alpha }+K_{2}\right) ||s||. \end{aligned} \end{aligned}$$
(18)

The proof is complete. \(\square\)

As a result, we get the continuous time RSMC:

$$\begin{aligned} \begin{aligned} \tilde{\delta }(t)=&F \tilde{x}(t)-\frac{1}{d}\left( K_{1}|s(t)|^{\alpha }+K_{2}\right) \operatorname {sign}\left( \textrm{s}(t)\right) \\&-\bar{\xi } \operatorname {sign}\left( \textrm{s}(t)\right) . \end{aligned} \end{aligned}$$
(19)

Remark 1

The proposed RSMC requires the prior knowledge of the disturbance upper bound \(\bar{\xi }\). It has to be argued that this dependency may appear restrictive, but modern sensor technologies and data-driven estimation methods (e.g., real-time monitoring of vehicle dynamics, historical disturbance profiles, or worst-case scenario analysis) can provide conservative yet practical bounds for in many engineering applications. Therefore, we do not further explore adaptive mechanisms for \(\bar{\xi }\)-free designs. However, this simplification aligns with existing industrial practices where safety margins are often predefined based on prior system knowledge.

DET-RSMC With designable triggering characteristics

For almost all ETMs that exist, the triggering characteristics is fixed once designed, and the evolution rate of the triggering signal is difficult to be adjusted based on explicit theories, subsequently generating inter-event times or frequency that may not be desired. To overcome this problem, this subsection proposes a dynamic ETM, rendering the triggering characteristics designable and adjustable.

Before introducing the dynamic ETM, define the measurement error \(\eta (t)\) as

$$\begin{aligned} \begin{array}{l} \eta (t)=\tilde{x}\left( t_{k}\right) -\tilde{x}(t), \quad \forall t \in \left[ t_{k}, t_{k+1}\right) \\ \dot{\eta }(t)=-\dot{\tilde{x}}(t) . \end{array} \end{aligned}$$
(20)

Among them, \(k \in \mathbb {N}_{\ge 0}\), \(t_k\) represents the k-th triggering instant, and \(\left\{ t_k \right\}\) denotes the sequence of triggering moments generated by the ETM. It should be noted that at each triggering instant \(t_k\), the measurement error will be reset to 0, that is, \(\eta (t_k)=0\).

Now, we propose a dynamic triggering rule below:

$$\begin{aligned} \begin{array}{c} t_{0} =0, \\ t_{k+1} =\inf \left\{ t>t_{k}: \varepsilon \sigma +\Phi (\chi (t)) \le \Vert G\Vert \Vert \eta (t)\Vert \right\} , \end{array} \end{aligned}$$
(21)

where constant \(\varepsilon >0\), design parameter \(\sigma \in \left[ 0,1 \right)\), and \(\Phi (\chi (t))\) resembles a countdown variable with the following expression

$$\begin{aligned} \Phi (\chi (t))=\frac{1}{2 \theta } \chi (t)(1+\operatorname {sign}(\chi (t)-\varepsilon )), \end{aligned}$$
(22)

which has the other design parameter \(\theta \in \mathbb {R}_{\ge 0}\). The differential equation of the dynamic variable \(\chi (t)\) is formulated as

$$\begin{aligned} \begin{array}{c} \chi (0)=\bar{\chi }>\varepsilon , \\ \dot{\chi }(t)=-l(\chi (t))-\left( \chi (t)-\varepsilon \sigma +\Vert G\Vert || \eta (t) \Vert \right) |s(t)|, \end{array} \end{aligned}$$
(23)

where we set the initial value of the dynamic variable \(\chi (0)\) also its maximum value to be \(\bar{\chi } \in \mathbb {R}_{> 0}\), and \(l(\chi (t))\) is a locally Lipschitz-continuous function.

Based on the above dynamic triggering rule (21) and the continuous-time RSMC (19), design the event-triggered RSMC:

$$\begin{aligned} \begin{aligned} \tilde{\delta }(t)=&F \tilde{x}\left( t_{k}\right) -\frac{1}{d}\left( K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha }+K_{d 2}\right) \operatorname {sign}\left( s\left( t_{k}\right) \right) -\bar{\xi } \operatorname {sign}\left( \textrm{s}\left( t_{k}\right) \right) , \quad \forall t \in \left[ t_{k}, t_{k+1}\right) . \end{aligned} \end{aligned}$$
(24)

Noteworthy, F, d, \(\alpha\), etc. are the same as in (19), whereas the relevant descriptions of \(K_{d1}\) and \(K_{d2}\) are presented in the next section. Furthermore, with respect to \(\tilde{x}\left( t_{k}\right)\), there are

$$\begin{aligned} \begin{aligned} \dot{\tilde{x}}(t_k)&=0, \quad \forall t \in \left( t_{k}, t_{k+1}\right) , \\ \tilde{x}\left( t_{k}^{+}\right)&=\tilde{x}\left( t_{k}\right) , \end{aligned} \end{aligned}$$
(25)

which means that the event-triggering RSMC (24) will only be updated at each triggering moment \(t_k\) determined by the triggering rule (21). Specifically, during the time between two adjacent triggering moments, the error variable \(\tilde{x}\) communicated to the controller is no longer updated real-time, and consequently the control input \(\tilde{\delta }\) always held unchanged by \(\tilde{\delta }_{tk}\), which can be realized by a Zero-order-hold.

Remark 2

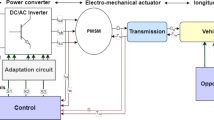
On the basis of dynamic triggering rule (21) and event-triggering RSMC (24), Fig. 2 presents the control architecture of this system. \(\Phi (\chi (t))\) dynamically varies depending on the values of the dynamic variable \(\chi (t)\), and the triggering threshold of triggering rule is no longer fixed. By selecting different \(\varepsilon\), \(\sigma\), \(\theta\) and \(l(\chi (t))\) the evolution rate of \(\Phi (\chi (t))\) can be designed in a certain degree, and then the evolution rate of the triggering signal can be changed, which leads to desired inter-event times and event-triggering frequency. Therefore, it is named that this dynamic ETM with designable triggering characteristics.

Fig. 2
figure 2

Architecture for the disturbed lateral control system of IEV under DET-RSMC (The blue line denotes transmission via local data exchange).

Full size image

Stability and feasibility analysis

In the proposed DET-RSMC which unlike the SMC under continuous time mechanism that realizes the ideal sliding motion, the trajectory of error variable \(\tilde{x}\) will be in the vicinity of the sliding manifold S, realizing practical sliding mode as defined below.

Definition 1

(Practical sliding mode40,41) For \(\forall r\in \mathbb {R}_{> 0}\), if exists a time \(t_r>0\) such that when \(t > t_r\) the sliding variable s always has \(|s(t)| \le r\), then the system is said to be in practical sliding mode.

For the purpose of proving the existence of practical sliding mode for the system (7), it is necessary to ensure that the DET-RSMC enables the sliding trajectory of \(\tilde{x}\) to be bounded within a desired range. First, it is required to prove the boundedness of dynamic variable \(\chi (t)\) in triggering rule (21).

Lemma 1

Considering the dynamic variable \(\chi (t)\) (23), given the following two sets:

$$\begin{aligned} \begin{array}{c} \Lambda _{\chi }:=\{\chi (t) \in \mathbb {R}: 0 \le \chi (t) \le \bar{\chi }\}, \\ \Lambda _{\varepsilon }:=\{\chi (t) \in \mathbb {R}: 0 \le \chi (t) \le \varepsilon \}, \end{array} \end{aligned}$$
(26)

there is always \(\chi (t) \in \Lambda _{\chi }\) and there exists a time \(t_\varepsilon >0\) such that \(\chi (t) \in \Lambda _{\varepsilon }\) when \(t \ge t_\varepsilon\).

Proof

Recalling the dynamic triggering rule (21), it is known that when \(t \ge 0\), we have

$$\begin{aligned} \varepsilon \sigma +\Phi (\chi (t))>\Vert G\Vert \Vert \eta (t)\Vert . \end{aligned}$$
(27)

Substituting (23) and (22) into the above inequality yields

$$\begin{aligned} \begin{aligned} \dot{\chi }(t)&\ge -l(\chi (t))-\chi (t)|s(t)|-\Phi (\chi (t))|s(t)| \\&\ge -l(\chi (t))-\chi (t)|s(t)| -\frac{1}{2 \theta }\chi (t)\left( 1+\operatorname {sign}(\chi (t)-\varepsilon )\right) |s(t)| \\&\ge -l(\chi (t))-\left( 1+\frac{1}{\theta }\right) \chi (t)|s(t)|, \end{aligned} \end{aligned}$$
(28)

where the equal sign holds if and only if \(|s(t)|=0\). Then, based on Comparison Lemma, one obtains that \(\chi (t) \ge 0\) when \(t\ge 0\). Choose the Lyapunov function with respect to the dynamic variable \(\chi\) as \(V_\chi =\frac{1}{2}\chi ^2\), and deriving it produce

$$\begin{aligned} \begin{aligned} \dot{V}_{\chi }&=-l(\chi ) \chi -\chi ^{2}|s|+\left( \varepsilon \sigma -\Vert G\Vert || \eta \Vert \right) \chi |s| \\&\le -l(\chi ) \chi -\chi ^{2}|s|+\chi \varepsilon |s| \\&\le -l(\chi ) \chi -\chi (\chi -\varepsilon )|s|. \end{aligned} \end{aligned}$$
(29)

Hence when \(\chi >\varepsilon\), that is, when \(\chi (t) \in \Lambda _{\chi } \setminus \Lambda _{\varepsilon }\), one gets

$$\begin{aligned} \dot{V}_{\chi } \le -l(\chi ) \chi . \end{aligned}$$
(30)

So, here is always \(0 \le \chi (t) \le \bar{\chi }\), and \(\dot{\chi }(t) \le 0\) would lead to \(\chi (t)\) converge to \(\Lambda _{\varepsilon }\) after \(t \ge t_\varepsilon\). \(\square\)

Next, we prove that under the DET-RSMC, there exists the practical sliding mode for the system (7), meaning that the stability can be guaranteed.

Theorem 2

Consider the system (7), the dynamic triggering rule (21) which determines the triggering instants \(t_k\) and the event-triggered RSMC (24) with parameters satisfying

$$\begin{aligned} K_{d1}>0,\quad K_{d2}\ge \varepsilon \sigma . \end{aligned}$$
(31)

For all \(t \ge 0\), the trajectory of sliding variable s(t) will reach and remain within the set \(\bar{\Gamma }\) in finite time, and be bounded in the set \(\Gamma\) after the finite time \(t_\varepsilon\), where

$$\begin{aligned} \begin{array}{l} \bar{\Gamma }:=\left\{ \tilde{x} \in \Omega :\Vert s(t)\Vert<\frac{\Vert \tilde{c}\Vert (\varepsilon +\Phi (\chi (t)))}{\Vert G\Vert }\right\} , \\ \Gamma :=\left\{ \tilde{x} \in \Omega :\Vert s(t)\Vert <\frac{\Vert \tilde{c}\Vert \varepsilon }{\Vert G\Vert }\right\} , \end{array} \end{aligned}$$
(32)

and the invariant set \(\Gamma \subset \bar{\Gamma }\).

Proof

Construct the Lyapunov candidate of the sliding variable s(t) as \(V_1=\frac{1}{2} s^\textrm{T}(t) s(t)\). Between two adjacent triggering moments, i.e., at \(t \in [t_k,t_{k+1})\), the time derivative of \(V_1\) is given by

$$\begin{aligned} \begin{aligned} \dot{V}_{1}(s) =&s(t) \dot{s}(t) \\ =&s(t)\left( G \tilde{x}(t)+d \tilde{\delta }\left( t_{k}\right) +d \xi (t)\right) \\ =&s(t)(G \eta (t)-K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha } \operatorname {sign}\left( s\left( t_{k}\right) \right) \\&-K_{d 2} \operatorname {sign}\left( s\left( t_{k}\right) \right) -d \bar{\xi } \operatorname {sign}\left( s\left( t_{k}\right) \right) +d \xi (t)) \\ \le&|s(t)|\Vert G\Vert \Vert \eta (t)\Vert -K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) \\&-K_{d 2} s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) -d \bar{\xi } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) +d|\xi (t) \Vert s(t)|. \end{aligned} \end{aligned}$$
(33)

In the following, the trajectory of the sliding variable and the existence of practical sliding mode will be analyzed step by step in two cases. \(\square\)

Case 1

When \(0\le t < t_\varepsilon\), by Theorem 1, it follows that \(\chi (t) \in \Lambda _{\chi } \setminus \Lambda _{\varepsilon }\). Based on Lyapunov function \(V_1\) and dynamic variable \(\chi\), consider the new Lyapunov function \(V_2(s,\chi )=V_1(s)+\chi\), and its derivative can be written as

$$\begin{aligned} \begin{aligned} \dot{V}_{2}(s, \chi )=&\dot{V}_{1}(s)+\dot{\chi } \\ \le&-K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) -K_{d 2} s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) \\&-d \bar{\xi } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) +d|\xi (t)||s(t)|\\&-l(\chi (t))-\chi (t)|s(t)|+\varepsilon \sigma |s(t)|. \end{aligned} \end{aligned}$$
(34)

For \(s(t) \notin \bar{\Gamma }\), where \(\bar{\Gamma }\) is the maximum deviation when \(t\in [t_k,t_{k+1})\) generated by the sliding variable s(t) after reaching the manifold S, it is clear that the trajectory of the s(t) moves towards the sliding mode surface from its initial position. And hence always \(\operatorname {sign}\left( s\left( t_{k}\right) \right) =\operatorname {sign}(s(t))\) with respect to any triggering moment \(t_k\), then (34) becomes

$$\begin{aligned} \begin{aligned} \dot{V}_{2}(s, \chi ) \le&-K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha }|s(t)|-K_{d 2}|s(t)|-d \bar{\xi } |s(t)|\\&+d|\xi (t)||s(t)| -l(\chi (t))-\chi (t)|s(t)|+\varepsilon \sigma |s(t)|, \\&\le -K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha }|s(t)|-\left( K_{d 2}-\varepsilon \sigma \right) |s(t)| \\&-d\left( \bar{\xi }-|\xi (t)|\right) |s(t)|-l(\chi (t))-\chi (t)|s(t)|, \end{aligned} \end{aligned}$$
(35)

where \(\sigma \in [0,1)\), the disturbance \(0\le |\xi (t)|\le \bar{\xi }\), and \(l(\cdot )\) is locally Lipchitz-continuous. Thus, further obtaining

$$\begin{aligned} \dot{V}_{2}(s, \chi ) \le -K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha }|s(t)|-\left( K_{d 2}-\varepsilon \sigma \right) |s(t)|, \end{aligned}$$
(36)

where \(K_{d1}>0\) and \(K_{d2} \ge \varepsilon \sigma\) ensure that

$$\begin{aligned} \dot{V}_{2}(s, \chi )<0 \end{aligned}$$
(37)

always holds when \(s(t) \notin \bar{\Gamma }\) and \(\chi (t) \in \Lambda _{\chi } \setminus \Lambda _{\varepsilon }\). Since \(V_{1}(s)= V_{2}(s,\chi )-\chi\), where both \(V_2(s,\chi )\) and \(\chi (t)\) are decreasing, it can be concluded that \(V_1(s)\) is also decreasing. Thus, the trajectory of s(t) will move to the \(\bar{\Gamma }\) within a finite time.

For \(s(t) \in \bar{\Gamma }\), if \(\operatorname {sign}\left( s\left( t_{k}\right) \right) =\operatorname {sign}(s(t))\), then there is also \(\dot{V}_{2}(s, \chi )<0\), which can ensure the reachability of the sliding surface, and the trajectory of s(t) will pass through the sliding mode surface. Afterwards, \(\operatorname {sign}\left( s\left( t_{k}\right) \right) \ne \operatorname {sign}(s(t))\), s(t) will move away from the sliding mode surface until the next triggering moment. After the next triggering moment, there will be \(\operatorname {sign}\left( s\left( t_{k}\right) \right) =\operatorname {sign}(s(t))\), which is the same as the above situation. In this way, s(t) moves in a zigzag path around the sliding manifold S, and when \(t\in [t_k,t_{k+1})\), the maximum deviation generated by s(t) can be calculated as follows

$$\begin{aligned} \begin{aligned} \left| s\left( t_{k}\right) -s(t)\right|&=\left| c \tilde{x}\left( t_{k}\right) -c \tilde{x}(t)\right| \\&\le \Vert c\Vert \Vert \eta (t)\Vert \\&<\frac{\Vert c\Vert \left( \varepsilon \sigma +\Phi (\chi (t))\right) }{\Vert G\Vert } \\&<\frac{\Vert c\Vert (\varepsilon +\Phi (\chi (t)))}{\Vert G\Vert }, \end{aligned} \end{aligned}$$
(38)

prove that the trajectory of s(t) will reach and always remain within the set \(\bar{\Gamma }\).

Case 2

When \(t\ge t_\varepsilon\), it follows that \(\chi (t) \in \Lambda _{\varepsilon }\). At this point, by (22), there is \(\Phi (\chi (t))=0\), and according to the dynamic triggering rule (21), the inequality \(\varepsilon \sigma >\Vert G\Vert \Vert \eta (t)\Vert\) always holds, so we can rewrite (33) as:

$$\begin{aligned} \begin{aligned} \dot{V}_{1}(s) \le&-K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) -K_{d 2} s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) +\varepsilon \sigma |s(t)|\\&-d \bar{\xi } s(t) \operatorname {sign}\left( s\left( t_{k}\right) \right) +d|\xi (t)||s(t)|. \end{aligned} \end{aligned}$$
(39)

Similar to Case 1, s(t) moves in a zigzag path. When \(\operatorname {sign}\left( s\left( t_{k}\right) \right) =\operatorname {sign}(s(t))\), we also get

$$\begin{aligned} \begin{aligned} \dot{V}_{1}(s) \le -K_{d 1}\left| s\left( t_{k}\right) \right| ^{\alpha }|s(t)|-\left( K_{d 2}-\varepsilon \sigma \right) |s(t)|, \end{aligned} \end{aligned}$$
(40)

which renders \(\dot{V}_{1}(s)<0\) on the basis of \(K_{d1}>0\) and \(K_{d2}\ge \varepsilon \sigma\). And if \(\operatorname {sign}\left( s\left( t_{k}\right) \right) \ne \operatorname {sign}(s(t))\), the maximum deviation generated by s(t) as \(t\in [t_k,t_{k+1})\) becomes

$$\begin{aligned} \left| s\left( t_{k}\right) -s(t)\right| <\frac{\Vert \tilde{c}\Vert \varepsilon }{\Vert G\Vert }. \end{aligned}$$
(41)

Therefore, it is proved that after the finite time \(t_\varepsilon\), the trajectory of s(t) converges to the set \(\Gamma\). This completes the proof.

\(\square\)

Finally, in the DET-RSMC designed above, we need to prove that the inter-event times are limited by a positive value to avoid potential Zeno behavior, which ensures the feasibility of execution on a hardware platform.

Theorem 3

Consider the system (7) with the event-triggered RSMC (24), in which the sequence of triggering instants \(t_k\) generated by the dynamic triggering rule (21), the inter-event times can be expressed as \(\tau _{\chi }:=t_{k+1}-t_{k}\). There always exists a minimum inter-event time \(\tau _{min}\), and \(\tau _{\chi }> \tau _{min}>0\), where

$$\begin{aligned} \tau _{\min }=\frac{1}{\Vert A\Vert } \ln \left( 1+\frac{\varepsilon \sigma +\Phi (\chi (t)) }{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }} \cdot \frac{\Vert A\Vert }{\Vert G\Vert }\right) . \end{aligned}$$
(42)

Proof

From the dynamic triggering rule (21), the minimum inter-event time can be obtained by calculating the time required for the value of \(\Vert \eta (t)\Vert\) to grow from 0 to \(\left( \varepsilon \sigma +\Phi (\chi (t))\right) /\Vert G\Vert\).

In view of (20), defining \(\textrm{T}_{k}:=\left\{ t \in \left( t_{k}, t_{k+1}\right] :\Vert \eta (t)\Vert =0\right\}\), for all \(t \in \left( t_{k}, t_{k+1}\right] \backslash \textrm{T}_{k}\), the time between all two adjacent event-triggering instants, deriving \(|\eta (t)\Vert\) yields

$$\begin{aligned} \begin{aligned} \frac{d}{d t}\Vert \eta (t)\Vert \le&\left\| \frac{d \tilde{x}(t)}{d t}\right\| \\ \le&\left\| A \tilde{x}(t)+B\left( \tilde{\delta }\left( t_{k}\right) +\xi (t)\right) \right\| \\ \le&\Vert A\Vert \Vert \eta (t)\Vert +\underbrace{\Vert A+B F\Vert \left\| \tilde{x}\left( t_{k}\right) \right\| }_{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) } +\underbrace{\Vert B\Vert \left( \frac{K_{d 1}\left( \frac{\Vert \tilde{c}\Vert \varepsilon }{\Vert G\Vert }\right) ^{\alpha }+K_{d2}}{d} +2\left\| \xi (t) \right\| \right) }_{\omega (\Vert \xi (t)\Vert )}, \end{aligned} \end{aligned}$$
(43)

where \(\omega (\Vert \xi (t)\Vert )\) is bounded, and it is easy to obtain \(\omega (\Vert \xi (t)\Vert ) \le \omega (\Vert \bar{\xi }\Vert )\). Then, defining \(\bar{\omega }=\omega (\Vert \bar{\xi }\Vert )\), we have

$$\begin{aligned} \begin{aligned} \frac{d}{d t}\Vert \eta (t)\Vert \le \Vert A\Vert \Vert \eta (t)\Vert +\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }. \end{aligned} \end{aligned}$$
(44)

For the above inequality and its initial condition \(\Vert \eta (t_k)\Vert =0\) by applying the comparison lemma, the solution is provided:

$$\begin{aligned} \begin{aligned} \Vert \eta (t)\Vert&\le \Vert A\Vert \Vert \eta (t)\Vert +\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }\\&\le \int _{t_{k}}^{t} \eta ^{\Vert A\Vert (t-v)}\left( \Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }\right) d v \\&=\frac{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }}{\Vert A\Vert }\left( \eta ^{\Vert A\Vert \left( t-t_{k}\right) }-1\right) , \end{aligned} \end{aligned}$$
(45)

where \(t \in \left( t_{k}, t_{k+1}\right] \backslash \textrm{T}_{k}\). Consequently, the time required for the value of \(\Vert \eta (t)\Vert\) to grow from 0 to \(\left( \varepsilon \sigma +\Phi (\chi (t))\right) /\Vert G\Vert\) can be calculated by

$$\begin{aligned} \begin{aligned} \frac{\varepsilon \sigma +\Phi (\chi (t))}{\Vert G\Vert }&=\left\| \eta \left( t_{k+1}\right) \right\| \\&\le \frac{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }}{\Vert A\Vert }\left( \eta ^{\Vert A\Vert \tau _{\chi }}-1\right) , \end{aligned} \end{aligned}$$
(46)

and hence the minimum inter-event time \(\tau _{\min }\) can be solved as

$$\begin{aligned} \tau _{\min }=\frac{1}{\Vert A\Vert } \ln \left( 1+\frac{\varepsilon \sigma +\Phi (\chi (t))}{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }} \cdot \frac{\Vert A\Vert }{\Vert G\Vert }\right) . \end{aligned}$$
(47)

In summary, there is always

$$\begin{aligned} \tau _{\chi } \ge \tau _{\min }>0 \end{aligned}$$
(48)

holds, with the result that potential Zeno behavior is excluded, and the proof is complete. \(\square\)

In addition, we further analyze the above dynamic triggering rule (21) and the minimum inter-event time \(\tau _{min}\).

Theorem 4

The proposed dynamic ETM are capable to generate larger inter-event times than the absolute ETM such as31. Meanwhile, the disturbed system (7) under DET-RSMC has semi-global RESP.

Proof

According to Lemma 1, there is always \(\dot{\chi }(t)<0\) and coupled with the expression (22) for the countdown variable, it can be known that \(\Phi (\chi (t))\) always decreases from a maximum (initial value). And after time \(t_\varepsilon\), \(\Phi (\chi (t)) = 0\) is kept invariant. Therefore, we can obtain \(\Phi (\chi (t)) \ge 0\). Besides, the dynamic triggering rule (21) will become the following absolute triggering rule

$$\begin{aligned} \begin{array}{c} t_{0} =0, \\ t_{k+1} =\inf \left\{ t>t_{k}: \varepsilon \sigma \le \Vert G\Vert \Vert \eta (t)\Vert \right\} , \end{array} \end{aligned}$$
(49)

and at this time, the minimum inter-event time \(\tau ^{\prime }_{min}\) can be derived

$$\begin{aligned} \tau ^{\prime }_{\min }=\frac{1}{\Vert A\Vert } \ln \left( 1+\frac{\varepsilon \sigma }{\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) +\bar{\omega }} \cdot \frac{\Vert A\Vert }{\Vert G\Vert }\right) . \end{aligned}$$
(50)

As a result, it is obvious that \(\tau _{\min } \ge \tau ^{\prime }_{\min }\), which means that when the same triggering threshold are selected in dynamic and absolute ETM, the inter-event times generated by the proposed dynamic ETM are enlarged.

The RESP is worth discussing for practical systems such as IEV. In accordance with Assumption 1, Assumption2 and (50), for all \(\tilde{x} \in \Omega\), \(\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right)\) is bounded, which we denote by \(\Upsilon \left( \Vert \tilde{x}(t_k)\Vert \right) \le \bar{\Upsilon }\). Then, defining \(\theta =\varepsilon \sigma \Vert A\Vert / \Vert G\Vert\) and \(p=\left( \bar{\Upsilon }+\bar{\omega }\right) /\theta\), we have

$$\begin{aligned} \tau _{\min } \ge \tau ^{\prime }_{\min } =\frac{1}{\Vert A\Vert } \ln \left( 1+ p\right) >0, \end{aligned}$$
(51)

which matches the results of semi-gobal RESP27. Therefore, it can be concluded that this event-triggered control system has semi-gobal RESP. \(\square\)

Remark 3

Event separation properties can be categorized into two types based on whether they are robust or not, and each has three more detailed divisions - local, semi-global and global. If the event-triggered control system does not even possess the local RESP, it implies when the system is subject to external disturbances, a high probability of event accumulation (extremely high triggering frequency in a short time) or even Zeno behavior.

Remark 4

The proposed DET-RSMC enables the disturbed system (7) to have a semi-global RESP, which is a property that effectively suppresses external disturbances and avoids Zeno behavior as well as event accumulation27. It is worth noting that if an event-triggered control system whose state variable is x, the external disturbance term is \(\xi\) and the inter-event time is \(\tau\), the system has a semi-global RESP but not a global RESP, then \(\text {limsup}_{||x||\rightarrow \infty } \tau (x,\xi ) =0\). However, this is not a problem for practical systems such as lateral control of intelligent electric vehicle, where the state variables are always bounded.

Remark 5

It is worth noting that in most of the existing static ETMs, the triggering threshold is fixed, and selecting a larger triggering threshold does result in larger event inter-event times, but behind it is the tolerance of larger measurement errors, which will most likely affect the control performance (larger lateral displacement errors). Should a large error not be desired, a large control gain is necessary. However, in a practical control system, the large control gain may lead to phenomena such as overshooting or input saturation. In proposed control method, the control gain \(K_{d1}\) and \(K_{d2}\), with only the latter depending on the triggering parameter, imply the capability to obtain longer inter-event times by increasing the thresholds \(\varepsilon\) and \(\sigma\) without the requirement for larger control gains.

Simulation results

The DET-RSMC designed for lateral control of IEV is demonstrated in experimental validation within this section. In simulation, the dynamic bicycle model parameter values are employed refer to the actual vehicle statistics as follows: \(m=1723\mathrm {~kg}\), \(I_{z}=4175\mathrm {~kg} \cdot \textrm{m}^{2}\), \(L_{f}=1.232 \mathrm {~m}\), \(L_{r}=1.468 \mathrm {~m}\), \(C_{f}=66900 \mathrm {~N}/\textrm{rad}\), and \(C_{r}=62700 \mathrm {~N}/\textrm{rad}\). Select \(\varepsilon =0.5\) and \(\sigma =0.3\) in the dynamic triggering rule (21). By Theorem 1 and Theorem 2, the gains of the event-triggered RSMC (24) are chosen as \(K_{d1}=1.5\), \(\alpha =0.7\) and \(K_{d2}=0.3\). Thus, on the basis of the above parameters, we can design the dynamic variable \(\chi (t)\) and \(\Phi (t)\) as follows

$$\begin{aligned} \begin{aligned} \chi (0)&=\bar{\chi }=10, \\ \dot{\chi }(t)&=-0.2\chi (t)-\chi (t)|s(t)|+\left( \varepsilon \sigma -\Vert G\Vert || \eta (t) \Vert \right) |s(t)|, \\ \Phi (\chi (t))&=\frac{1}{5}\chi (t)(1+\operatorname {sign}(\chi (t)-\varepsilon )). \end{aligned} \end{aligned}$$
(52)

Taking into account external disturbances, we introduce the disturbance term \(\xi (t)\) that directly affect the control input \(\delta (t)\) in the disturbed system (7). Therefore, we assume that the IEV is always subjected to a bounded disturbance of \(\bar{\xi }=0.005\) while in motion, which has exceeded 10% of the maximum value of the control input throughout this simulation. We believe that this is actually more than realistic enough for the disturbance to make a difference and demonstrate the robustness of the proposed scheme. And we design the sliding variable \(s=c\tilde{x}=\left[ 0,0,v,1\right] \tilde{x}=\left[ 0,0,0.5,1\right] \tilde{x}\). For the disturbed error dynamics system, setting the initial state \(\tilde{x}=[0;0;0;0]\), maintaining the longitudinal velocity \(V_x=15\textrm{m} / \textrm{s}\) and the road friction coefficient \(\mu =0.8\) throughout the simulation.

Fig. 3
figure 3

Two consecutive lane changing overtaking.

Full size image
Fig. 4
figure 4

Trajectory of IEV with different control method.

Full size image
Fig. 5
figure 5

Evolution of side slip angle \(\beta\), yaw rate \(\dot{\psi }\) and lateral displacement error e.

Full size image
Fig. 6
figure 6

Control input based the RSMC.

Full size image

Lane-changing overtaking is a representative scenario of the lateral control problem of a vehicle in real driving. We verify the effectiveness of the proposed method by two consecutive lane-changing overtaking in the simulation, as shown in Fig. 3. The entire simulation time is \(25\mathrm {~s}\) and the sampling period is \(0.01 \mathrm {~s}\). Based a lane-changing overtaking reference trajectory, which is satisfied Assumption 1, we firstly implement three different methods to achieve the lateral control target: the continuous time RSMC (19), DET-RSMC, and DET-RSMC with disturbances. Figure 4 presents the actual trajectories of three control methods. It can be seen that the trajectory of the continuous-time RSMC is almost the same as the other two methods, which further proves the effectiveness of the proposed solution. In order to show the simulation results of the proposed method more clearly, we omit the results based the continuous time in the later figures.

Table 2 Comparison of control update numbers.
Full size table
Fig. 7
figure 7

Cumulative number of control update.

Full size image

In the simulation, the variation curves of side slip angle \(\beta\), yaw rate \(\dot{\psi }\) and lateral displacement error e are illustrated in Fig. 5, and the control input \(\tilde{\delta }\) calculated by event-triggered RSMC (24) is provided in Fig. 6. The control input is step-shaped, i.e., between two adjacent triggering moments, the control input remains the same as the value at the previous triggering moment, which effectively reduces the number of control input update. For a comparison of control update numbers, we provide in Table 2 and Fig. 7. It can be clearly known that the proposed DET-RSMC achieves the desired lateral control target and leads to a reduction in control update numbers exceeding \(43\%\) in this simulation case, thus improving the resource utilization of embedded control system and alleviating the communication load in controller area network (CAN) or wireless network.

Concerning dynamic triggering rule (21) together with related expressions (22) and (23), we demonstrate the evolution of dynamic variable \(\chi (t)\) and \(\Phi (t)\) in Fig. 8. The dynamic variable \(\chi (t)\) decreases from its initial value \(\chi (0)=\bar{\chi }=10\), but is always larger than 0. And when \(\chi (t)<\varepsilon\), there is \(\Phi (t)=0\), as described in Lemma 1. Then, Fig. 9 presents the trajectory of s(t). Corroborating Theorem 2, s(t) reaches and remains within the set \(\bar{\Gamma }\) after finite time, which is not very obvious in the figure because the designed reference trajectory is in a lane change overtaking condition with a relatively high speed. However, it can be clearly seen that after time \(t_{\varepsilon }\), s(t) is bounded in set \(\Gamma\).

Fig. 8
figure 8

Dynamic variable \(\chi (t)\) and \(\Phi (t)\).

Full size image
Fig. 9
figure 9

Trajectory of s(t).

Full size image
Fig. 10
figure 10

Inter-event times.

Full size image

Besides, Fig. 10 shows the inter-event times generated by DET-RSMC With and without disturbances. And in conjunction with the above simulation results, we conclude that the designed DET-RSMC has the ability to suppress external disturbances. Next, the following simulations are carried out to further demonstrate the robustness of the proposed control method as well as the designability of the triggering characteristics. Keeping all the parameters and reference trajectory settings unchanged in the previous simulation, and ensuring that the lateral displacement error e generated during the motion process is within \(0.1\mathrm {~m}\), different \(\sigma\) (in the dynamic triggering rule (21)) and \(l(\chi (t))\) (in the dynamic variable dynamics equation (23)) are selected, and then the statistics of control update numbers are provided in Table 3.

Table 3 Statistics on control update numbers.
Full size table

According to Table 3, it is known that by designing the evolution rate and the effective range (the definition of the set \(\Lambda _{\varepsilon }\) (32)) of dynamic variable \(\chi\) can increase or decrease the triggering frequency, and thereby adjust the control update numbers and the generated inter-event times, which we suggest that it could be the most reasonable and effective adjustment. Certainly, it is also effective to change the settings of other parameters, such as \(\bar{\chi }\) (maximum value of dynamic variables), etc., but we consider it not intuitive or regular enough. In addition, we also present the case of the static triggering rule in Table 3, i.e., always keeping \(\Phi (\chi (t)) = 0\). As mentioned in Theorem 4, the control update numbers and the average inter-event times generated by the proposed DET-RSMC are always larger than the average inter-event times generated by the static triggering rule (49) similar to some previous work31,42, which implies that it is possible to reduce the control update numbers without necessarily choosing a larger triggered threshold to produce larger inter-event times. Besides, it is worth remarking that each simulation compares the two cases are compared for each simulation: without disturbances \(\xi (t)\) and with disturbances \(\xi (t)\). This confirms that for the system executing DET-RSMC, due to its semi-global RESP and the event-triggered RSMC (24), when subjected to disturbances, although there is a certain degree of floating in the control update numbers, it can still effectively reduce the computation and communication loads and also exclude Zeno behavior and event accumulation.

Remark 6

We need to have a brief discussion on the selection of some of the design parameters. In event-triggered RSMC (24), when \(K_{d1}\) and \(K_{d2}\) are selected with larger values, it makes the global convergence speed faster, but it should be noted that larger values will aggravate the chattering. Meanwhile, when \(\alpha \rightarrow 1\), the chattering is obvious, but when \(\alpha \rightarrow 0\), the convergence speed of the sliding variables will be slowed down. Regarding the effect of selecting the values of \(\varepsilon\) and \(l(\chi (t))\) towards the proposed DETM-RSMC, we can get it clearly from Table 3: \(\varepsilon\) acts as the static part of the dynamic triggering rule, and a larger \(\varepsilon\) implies a lower triggering frequency, but subsequently there is an increase in the lateral displacement error, which may affect the control performance. \(l(\chi (t))\) mainly contributes to regulating the evolution rate of the dynamic variables \(\chi\), and \(\bar{\chi }\) is the variable range of the triggering signal, which together affect the triggering frequency. Intuitively, the larger \(\bar{\chi }\), the fewer control update number, but after a longer inter-event time during trajectory tracking process, more controller update numbers may be required to compensate. In summary, the DET-RSMC proposed in this paper, when appropriately extended to different application scenarios, can effectively adjust the trigger frequency and inter-event times by designing the evolution rate and effective range of dynamic variable \(\chi\). However, in actual applications, it is definitely not advisable to have a lower triggering frequency and longer inter-event times. It is also necessary to comprehensively consider the required control performance, such as error and steady-state time.

Finally, we compare the proposed DET-RSMC in this paper with some typical control schemes based on ETM for and present it in Table 4, where the symbol \(\times\) denotes that it was not considered and the symbol \(\setminus\) denotes that it was not discussed, even having some kind of RESP. Dynamic triggering rule, robustness of controller and RESP, all three are extremely important in our opinion for the execution of ETM in practical systems. Among them, the dynamic triggering rule indicates whether there is an intrinsic dynamic variable to break the fixed triggering threshold. Moreover, disturbances are inevitable in reality, the practical system is highly susceptible to disturbances, and an arbitrarily small disturbance may lead to event accumulation or even Zeno behavior. However, in this paper, we not only consider the robustness of the controller, but also analyze the robustness of the inter-event times - an event-triggered RSMC is designed as well as the event-triggered control system with the semi-global RESP is proved. We believe that this is the first dual measure taken to block external disturbances such that the DET-RSMC may be a much more comprehensive solution to the actual lateral control problem.

Table 4 Comparison of ETMs.
Full size table

Conclusions

This paper focuses on the lateral motion control of IEV under bounded disturbances. The proposed RSMC, which can effectively suppress external disturbances, ensures the stability of the lateral control system. Then, the RSMC is redesigned with a dynamic ETM, whose triggering characteristics have a certain degree of designability, e.g., the evolution range and evolution rate of the dynamic variable can be designed, so that the triggering frequency and the inter-event times can be adjusted. Above all, the proposed DET-RSMC implementation scheme is able to fulfill the desired lateral control target as well as provide advantages over existing control systems based on static ETMs. Besides, in this paper, not only the effect of disturbances on stability but also the deterioration on the inter-event times are considered. We prove that the control system implementing this DET-RSMC has the semi-global RESP such that no Zeno behavior occurs due to external disturbances. We simultaneously consider the robustness of the control law and the robustness of the inter-event times, which is absent in current control systems based on dynamic ETMs. Future extensions will integrate online disturbance estimation to eliminate the reliance on prior knowledge of disturbances, thereby enhancing applicability in more scenarios. Meanwhile, higher-order SMC schemes based on dynamic ETM are considered to further reduce the chattering phenomenon.