Introduction

Acoustic black holes (ABH) were first proposed by Mironov1. When the thickness of the plate varies according to a power-law function, the bending wave velocity within the structure decreases, while the amplitude increases accordingly. Theoretically, this leads to an absence of wave reflection, resulting in an energy accumulation effect1,2. In practical applications, however, the plate’s thickness cannot be reduced to zero, leading to a truncation thickness that affects the vibration reduction efficacy. The application of damping within the ABH region can suppress bending waves and enhance the energy dissipation capacity of the structure3,4,5,6,7,8,9,10,11. Feurdado posits that applying damping throughout the tapered region of the ABH is effective in reducing modal frequencies and enhancing low-frequency performance12. Zhao used viscoelastic materials to effectively control the vibration of conical ABH13. Due to its excellent bending wave aggregation effect, ABH have been extensively studied in applications such as vibration reduction and noise reduction14,15,16,17,18,19, energy recovery20,21,22, etc. Park generalized the structure of ABH and designed a structure with an Archimedean spiral shape using the coalescence effect of ABH23. They found that this new structure has better coalescence effect than general wedge-shaped ABH and can more effectively dissipate vibration energy. Zhou designed a planar swirl-shaped ABH structure that can suppress vibration waves in any direction including bending torsional coupling vibration24. To address the potential reduction in structural strength associated with ABH structures, most researchers incorporate these structures as supplementary components to achieve vibration control in the primary structure. Zhou proposed a resonant damper for one-dimensional ABH, which has a significant suppression effect on the vibration of beam structures25. Souza applied one-dimensional ABH structures as resonators for vibration reduction in plate structures26. Jia improved the low-frequency vibration reduction effect of ABH structures by combining dynamic vibration absorbers in two-dimensional ABH structures27,28. Ji designed a two-dimensional ABH dynamic absorber attached to a plate structure and studied its influence on the vibration effect of the plate structure29,30.

The existing literature provides a thorough analysis of the principles of ABHs and their applications, with the majority of studies focusing on frequencies above the cut-off frequency. However, research on vibration suppression at lower frequencies remains limited. As a result, the study of vibration suppression across a broader frequency range becomes increasingly important. Building on previous research, this paper presents damping connectors and vibrator structures within the ABH region to create an acoustic black hole damping oscillator (ABH-DO) structure. By leveraging the high-frequency (above the cut-off frequency) vibration aggregation effect of the ABH and the low-frequency vibration absorption properties of the damping connector and oscillator, vibration suppression across a wide frequency range is achieved. Providing a new approach for vibration control below the cut-off frequency of ABH.

Vibration characteristics of a single ABH-DO structure

Describing the model

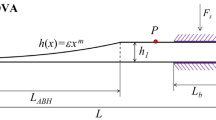
The function of the thickness change of ABH is \(\:h\left(x\right)=\epsilon\:{(x-{R}_{0})}^{m}(m\ge\:2)\) (depicted in Fig. 1a). However, in practical applications, taking into account the processing conditions and the mechanical properties of the structure, there exists a cut-off thickness (h0). The radius of ABH designed in this paper is 50 mm, and h0 is set to 0.5 mm. When the material properties and plate thickness are determined, the cut-off frequency of ABH depends on the ABH radius (RABH) and has nothing to do with the cut-off radius31. Therefore, the model does not include the cut-off thickness. ε represents the coefficient in the power function, while m is a constant. In the case of m = 2, the thickness variation of the ABH finite element model established in this study follows a power-law function, as described in Eq. (1). The specific parameters are shown in the Table 1.

$$h\left( x \right)=0.002{x^2}+0.5$$
(1)

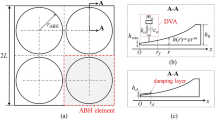
ABH-DO is a structure where a layer of damping material is placed at the center of an ABH, and oscillators are incorporated into this damping layer (depicted in Fig. 1b).

Fig. 1
figure 1

Schematic diagram of ABH and ABH-DO structures; (a) ABH structure; (b) ABH-DO structure.

Full size image
Table 1 The structural parameters of ABH-DO structure.
Full size table

The three-dimensional solid models of the structures were created using NX, and the models were subsequently imported into ANSYS for Harmonic Response analysis and others. The size of the uniform plate structure is 470 mm × 350 mm × 5.5 mm, and the ABH-DO structure is located at the center of the uniform plate. The mesh elements are implemented using tetrahedral elements. The mesh in the region of the ABH is refined to a maximum element size of 2.5 mm, while the maximum element size in other regions is set to 6 mm (depicted in Fig. 2). The material parameters are shown in Table 2. A simple support boundary condition was applied along the plate edge and a force of 1 N was applied at the excitation point. A frequency sweep from 200 Hz to 3200 Hz (with a cut-off frequency of 3088 Hz) was performed with a frequency step of 10 Hz. To more clearly demonstrate the vibration characteristics of the ABH-DO structure, this paper sets up two control groups. One control group is a uniform plate with the same size, and the other is an ABH structure. The locations of the points are listed in Table 3, which provides the coordinates for each point in the study. The maximum values of the normal acceleration (amax) at points 1, 2, and 3 are collected and processed using the function 2.

$$A=20{\log _{10}}({a_{\hbox{max} }})$$
(2)
Fig. 2
figure 2

Finite element model of ABH-DO; (a) Uniform plate; (b) Plate with ABH structure; (c) Plate with ABH-DO structure; (d) The ___location of the points in the simulation; (e) The mesh division of the plate with ABH-DO structure.

Full size image
Table 2 The material parameters of ABH-DO structure.
Full size table
Table 3 The coordinates of the points in the simulation.
Full size table

Results

The results are shown in the Fig. 3. The resonance peak in the wider frequency band is reduced to varying degrees. The first resonance peak at 320 Hz is reduced by 7 dB compared with the uniform plate. This demonstrates the ABH-DO structure’s effective performance in vibration characteristics. However, due to the limited functionality of a single ABH-DO structure, the peak values at certain frequencies exceed those of other structures. Therefore, it is necessary to investigate the impact of different parameters on its vibrational characteristics.

Fig. 3
figure 3

Vibration acceleration response of a single ABH-DO.

Full size image

To better understand the impact of adding damping connectors and vibrators on the vibration characteristics of the plate, a modal analysis was conducted on three different structures. The displacement nephograms of the natural frequencies for these structures under the same vibration mode were obtained. As shown in Fig. 4, compared to the uniform plate, the vibration amplitude of the plate with an ABH is predominantly localized within the ABH region. The inclusion of the damping connector and oscillator structure has resulted in these components exhibiting the highest relative vibration amplitudes. This indicates that the damping connector and oscillator structure are capable of absorbing vibrational energy.

Fig. 4
figure 4

The mode shapes of the uniform plate; (a) \(f_{4} = 888.6{\text{ Hz}}\); (b) \({f_7}=1366.7{\text{ Hz}}\); (c) \(f_{26} = 3786.8{\text{ Hz}}\). The mode shapes of ABH; (d) \(f_{4} = 855.7{\text{ Hz}}\); (e) \(f_{7} = 1299{\text{ Hz}}\); (f) \(f_{31} = 4311.5{\text{ Hz}}\). The mode shapes of ABH-DO; (h) \(f_{4} = 848.3{\text{ Hz}}\); (i) \({f_{10}}=1323.9{\text{ Hz}}\); (j) \({f_{36}}=4317.8{\text{ Hz}}\).

Full size image

In the frequency ___domain analysis, a significant reduction in the peak at 1300 Hz is observed. The vibration of the oscillator is clearly evident around 1300 Hz in the displacement nephograms of the modal analysis. In the time ___domain, a 1300 Hz excitation force is applied to the ABH-DO structure (depicted in Fig. 5), with the point of application is indicated in Fig. 2. The velocities of point 4 and 5, as well as the oscillator, are recorded, and the results in the time ___domain are presented in Fig. 6. The velocity of the point 4 decreases while the velocity of the oscillator increases (It should be noted that the velocities of the oscillator and those at points 4 and 5 differ in magnitude). Additionally, the vibration velocity of the oscillator differs from that of the point 4 and point 5 due to the oscillator’s absorption of energy from the plate, which is subsequently converted into the oscillator’s kinetic energy.

Fig. 5
figure 5

Excitation force in time ___domain analysis.

Full size image
Fig. 6
figure 6

Results of the time ___domain analysis for the ABH-DO structure.

Full size image

The influence of structural parameters of a single ABH-DO

The radius of the ABH determines the frequency range of its effect, while the damping connector and the oscillator functions as a dynamic absorber within the ABH system. The stiffness of the damping connector is analogous to that of a spring, and the oscillator is modeled as a mass block. The stiffness of the damping connector and the mass of the oscillator are particularly critical in ABH-DO structures. Therefore, this paper investigates the effects of the ABH radius, the damping material elastic modulus, and the oscillator mass on the overall vibration characteristics of the structure.

Radius of the ABH

As the radius of the ABH increases, it becomes more effective at capturing low-frequency vibrations and dissipating vibration energy through damping connector and oscillators. An increase in the radius of the ABH shifts the cut-off frequency to lower values, leading to improved vibration attenuation in the low-frequency range (depicted in Fig. 7).

Fig. 7
figure 7

Influence of ABH radius on ABH-DO vibration characteristics; (a) Span point response; (b) Driving point response.

Full size image

Elastic modulus of the damping connector

Additionally, a reduction in the elastic modulus of the damping layer results in varying degrees of peak reduction, with the magnitude of each resonance peak exhibiting a significant positive correlation with the elastic modulus of the damping material. However, decreasing the elastic modulus of the damping layer has a limited impact on enhancing vibration characteristics. For instance, at the third resonance peak, the peak value for a damping layer with an elastic modulus of 30 MPa is reduced by only approximately 5.28 dB compared to a damping material with an elastic modulus of 90 MPa (depicted in Fig. 8). Furthermore, a reduction in the elastic modulus of the damping layer can also influence the mechanical properties of the ABH-DO structure, thus the elastic modulus of the damping material should not be excessively diminished.

Fig. 8
figure 8

The influence of the damping connector elastic modulus on ABH-DO vibration characteristics.

Full size image

The mass of the oscillator

This paper examines how varying the mass of oscillators affects the vibration reduction characteristics of a system by modifying the thickness of the oscillator. As the mass of the oscillator increases, the amplitude of the first resonance peak decreases to varying extents (depicted in Fig. 9). While increasing the oscillator mass improves the low-frequency vibration characteristics of the ABH-DO structure, it does not significantly help in suppressing high-frequency vibrations. This is because increase the oscillator mass shifts the structure action frequency to lower frequencies. It is possible to adjust the vibration characteristics of the ABH-DO structure in different frequency bands by changing the oscillator mass appropriately.

Fig. 9
figure 9

Influence of oscillator mass on ABH-DO vibration characteristics.

Full size image

Periodic arrangement of ABH-DO structure

The research discussed thus far focuses on a single ABH-DO structure. However, in practical applications, a single structure’s frequency range and effectiveness may be limited. To gain a deeper understanding of vibration characteristics, this study explores the use of a periodic arrangement of multiple ABH-DO structures. Six periodic configuration methods are examined: 2 × 2, 2 × 3, 3 × 3, 4 × 4, and 5 × 5 arrays of ABH-DO structures distributed across a uniform plate. The radius of the ABH is 30 mm, and the spacing between adjacent ABHs is 10 mm. The size of the uniform plate structure is 470 mm × 350 mm × 5.5 mm. The thickness of these oscillators is 5 mm.The other material and structural parameters are consistent with those stated previously.

The effects of varying numbers of ABH-DO structures on the vibration characteristics of a plate differ significantly. The 2 × 2 arrangement significantly reduces the amplitude at the first peak and high-frequency regions; however, its effectiveness in the 500–1600 Hz range is suboptimal and may even be detrimental (depicted in Fig. 10a). The ABH-DO structures with 2 × 3 and 2 × 4 arrangements exhibit better vibration reduction performance compared to the 2 × 2 arrangement after 1600 Hz (depicted in Fig. 10b–d).

The 3 × 3 arrangement negatively impacts the third peak but demonstrates favorable vibration reduction characteristics at other frequencies (depicted in Fig. 11a). For the 4 × 4 and 5 × 5 arrangements, although a few peaks are comparable to those observed in the plate without ABH-DO structures, the overall performance is improved (depicted in Fig. 11b,c). This improvement is attributed to the increased number of ABH-DO structures, which enhances the absorption and dissipation of vibration energy within the plate. Consequently, increasing and periodically arranging ABH-DO structures is a feasible approach for reducing plate surface vibrations (depicted in Fig. 11d).

Fig. 10
figure 10

(a) 2 × 2 Vibration response of arrangement; (b) 2 × 3 Vibration response of arrangement; (c) 2 × 4 Vibration response of arrangement (d) Vibration acceleration under different arrangements.

Full size image
Fig. 11
figure 11

(a) 3 × 3 Vibration response of arrangement; (b) 4 × 4 Vibration response of arrangement; (c) 5 × 5 Vibration response of arrangement (d) Vibration acceleration under different arrangements.

Full size image

Experimental verification

Both single and multiple ABH-DO structures can effectively enhance the vibration characteristics of a plate. To validate this, three types of uniform plates were designed and experimentally tested. The ABH is fabricated on a standard panel using a machining center. The three types of plates are as follows:

  1. (1)

    Eight ABH-DO structurers are added onto a uniform plate of 800 × 500 × 8 mm. The diameter of the damping connectors and oscillators are 10 mm, the damping connectors are made of chloroprene rubber with a thickness of 4 mm, and the oscillator is made of copper alloy with a thickness of 6 mm. The material of the plate is structural steel, which is the most commonly used material in the mechanical industry. The diameter of the ABH is 143 mm. The ABH satisfy a power-law function (3). (Note that the power law m = 2.2 in the experiment, which is different from that in the numerical analysis. It is not necessary to consider the specific parameters of the ABH structure utilized in the experiment. The focus is solely on the impact of incorporating damping connectors and oscillators on the vibration response of the ABH.)

    $$h\left( x \right)=0.0006{x^{2.2}}+0.8$$
    (3)
  2. (2)

    Eight ABHs are evenly arranged on a uniform plate.

  3. (3)

    Uniform plates of the same size.

The experimental instruments include the following: Channel acquisition instrument, Signal acquisition device, Accelerometer, Hammer, Single arm crane, Elastic rope, Nylon rope and PC.

Fig. 12
figure 12

The experiment site and connections of the instruments.

Full size image
Fig. 13
figure 13

The ___location of the points in the experiment.

Full size image
Table 4 The coordinates of the points in the experiment.
Full size table

Due to the practical difficulty in achieving the ideal boundary condition of fully simply-supported edges, inappropriate boundary conditions may lead to significant discrepancies between experimental results and simulation analyses. Therefore, in this experiment, we have selected free boundary conditions as the experimental setup. The first plate is lifted using elastic and nylon ropes to simulate a free boundary condition. Three acceleration sensors are installed on the plate, and connected to a signal acquisition device, which is subsequently linked to a PC and a hammer for data collection (depicted in Fig. 12). The excitation force is applied to the plate using a hammer. In the experiment, a hammer was used to strike the plate 30 times. After discarding the data with poor correlation, the average value of the remaining data was taken as one set of results. Furthermore, the average of three sets of results was selected as the final experimental outcome. The vibration data of the point 6, 7 and 8 are collected by accelerometers and transmitted to the PC for processing (depicted in Fig. 13; Table 4). Used the function 4 to calculate the results.

$$A=10\lg {\left( {\frac{x}{{{x_0}}}} \right)^2}=20lg\left( {\frac{x}{{{x_0}}}} \right)$$
(4)

x is the measured value (Displacement, Velocity and acceleration etc.) and x0 is the reference value. In this paper x is the average value of the measurements obtained from three accelerometers. The acceleration reference value is taken to 1 × 10−6 m/s2.

Simultaneously with the experiment, a finite element analysis was conducted on the same model under free boundary conditions. The experimental and simulation results are shown in the Fig. 14. It can be observed that the experimental results are nearly identical to the simulation results, with some discrepancies at the peak values. This is primarily due to the difficulty in measuring the material loss factor in actual situations, leading to discrepancies between the two. But the overall trend of the experimental results and simulation results is the same, which can prove the accuracy of the experimental results.

Fig. 14
figure 14

Experimental and simulation results of ABH-DO.

Full size image

The same experiment was conducted on additional uniform plates, and the processed results are shown in Fig. 15. The experimental results show that the ABH-DO structure exhibits a significant vibration reduction effect in the 10–1000 Hz frequency range at all locations, compared to the ABH structure. At 330 Hz, 439 Hz and 606 Hz, there were decreases of 4.2 dB, 6.7 dB and 7.7 dB, respectively. The experimental results further confirmed that the ABH-DO structure has a good vibration reduction effect.

Fig. 15
figure 15

Experimental results for three types of plates.

Full size image

Orthogonal experimental method for optimizing structural parameters

The ABH-DO structure primarily concentrates energy via the ABH and dissipates it through the damping oscillator mechanism. Increasing the radius of the ABH shifts the cutoff frequency, allowing it to absorb vibrations over a broader range of mid to high frequencies. However, this increase in radius also reduces the overall stiffness of the structure, which is disadvantageous for low-frequency vibrations. The presence of multiple ABHs exacerbates this issue. The damping oscillator mechanism is effective in mitigating low-frequency vibrations, necessitating a complex matching mechanism between the ABHs and damping oscillators. Consequently, this study designed an orthogonal experiment to determine the optimal levels of the three factors and employed range analysis to identify which factor most significantly impacts the reduction of structural vibrations. The arrangement of the ABH-DO structure is 5 × 5, with other parameters shown in Table 2.

Three factors were selected: the diameter of the ABH, the elastic modulus of the damping connector, and the thickness of the oscillator. The diameter of the ABH was set at 50 mm, 55 mm, and 60 mm across three levels; the damping elastic modulus was 30 MPa, 40 MPa, and 50 MPa at three levels; and the thickness of the oscillator was 2 mm, 4 mm, and 6 mm at three levels. The orthogonal experiment table is shown in Table 5. The ABH-DO structure is uniformly arranged on a flat plate, maintaining the same excitation point as previously. The accelerations at three points on the opposite side of the excitation point are then extracted for analysis (depicted in Fig. 2). To study the effects of three factors on the entire frequency range, the average value of the extracted acceleration between 200 and 3200 Hz was calculated as the result.

Table 5 Orthogonal experimental design and results.
Full size table
Table 6 Range analysis table and the optimized results.
Full size table

The value K is the sum of the results for each factor and level, and Kavg is the average of the value K (Kavg = K/3). The optimal level is the level of a given factor at which the value K is minimized. The value R is defined as the difference between the maximum and minimum values of Kavg for each factor. A larger value of R indicates a greater influence of the corresponding factor on the system’s vibration reduction performance. As illustrated in Table 6, the factor corresponding to the thickness of the oscillator (which can be interpreted as the oscillator mass) exhibits the highest value of R, followed by factor A, which pertains to the diameter of the ABH, while factor B, associated with the elastic modulus of the damping connector, shows the smallest value of R, and factor C, which corresponds to the minimum value R of the damping connector’s elastic modulus.

The vibration characteristics of the ABH-DO structure improve to varying extents at the optimal factor levels compared to other combinations of factor levels, as shown in Fig. 16. Specifically, the variation in oscillator thickness has a far greater impact on the vibration reduction performance of a single ABH-DO structure than the variation in the damping connector’s elastic modulus. This relationship also exists in multiple periodically arranged ABH-DO structures, and oscillator mass has the greatest impact on the vibration reduction characteristics of multiple periodically arranged ABH-DO structures.

Fig. 16
figure 16

Results at different factor levels and the optimal results.

Full size image

Conclusions

This study investigates the vibration characteristics of both single and multiple array ABH-DO structures using the finite element method. It examines how various parameters of a single ABH-DO structure affect its vibration characteristics. For multiple ABH-DO structures, an orthogonal experimental approach is employed to determine the optimal parameters within specified levels and identify the most significant influencing parameter. The main conclusions of the research are as follows:

  1. (1)

    The single ABH-DO structure has better vibration reduction characteristics over a wide frequency range compared to the uniform plates and plates embedded with ABH.

  2. (2)

    The radius of the ABH, the elastic modulus of the damping connector, and the thickness of the oscillator all have an impact on a single ABH-DO. Increasing the radius of the ABH and the mass of the oscillator will improve the mid to low frequency vibration reduction performance of the structure. Reducing the elastic modulus of the damping connector can also improve vibration reduction performance, but its effect is limited.

  3. (3)

    For the array ABH-DO structure, increasing the number of structures enhances the vibration reduction effect on uniform plates. Orthogonal experiments indicate that the structural parameters of ABH-DOs influence the overall structure similarly to individual structures, with oscillator mass having the greatest impact, followed by the ABH radius, and the damping connector elastic modulus having the least impact.

In this paper, the spacing between periodically arranged ABH-DO structures and the size of individual structures are kept constant. Future research will explore ABH-DO structures with varying spacing arrangements and mixed sizes to identify more effective combinations for vibration reduction across a broader frequency range.