Given the increasing importance of safety and stability in engineered rock, the study of rock failure under compression is crucial for predicting the instability of structures such as buildings and mines1. In natural settings, rocks frequently contain micro or macro fissures, which reduce their bearing capacity. Furthermore, engineered rock bodies are influenced not only by their intrinsic fissures but also by external loads from construction activities and natural stress. These factors contribute to the progressive expansion of both existing and newly formed fissures, ultimately leading to macroscopic damage2. The interaction between construction activities and ground stress alters the loading rate experienced by the rock mass, complicating predictions of its damage process. During rock damage, internal damage mechanisms are accompanied by corresponding acoustic emission phenomena3. Therefore, utilizing an acoustic emission (AE) monitoring system effectively tracks the development of internal cracks in the rock body. This approach is practically significant for predicting rock damage and provides a theoretical foundation for enhancing the safety and stability of fissured rock masses.

In recent years, rock mechanics has become a central research area, prompting extensive studies on fissured rock bodies. Key findings include: Darcel, C. et al.4 employed the discrete fracture network (DFN) modeling approach to develop a model of fractured rock masses. They integrated the normal stresses of fractures with their permeabilities and accounted for both far-field and local stress variations induced by the fractures to compute the normal stresses of each fracture in the DFN using a semi-analytical method; Kamiński, P. et al.5 proposed a novel method to establish the Ground Reaction Curve (GRC) for an elastic–plastic-fractured rock mass model. They demonstrated this method’s applicability by analyzing a typical circular roadway under various rock mass conditions; Kota, V. K. et al.6 investigated the impact of seismic activities on fractured rock mass stability using a model that integrates the discrete element method (DEM) and the discrete fracture network (DFN). They analyzed how varying input wavelengths and amplitudes, along with fracture density and stiffness, affect tunnel behavior; Barkat, U. et al.7 predicted rock failure by analyzing acoustic emission (AE) signals and energy evolution during the uniaxial compression process. They further explored the impact of freeze–thaw weathering on rock strength and stability by examining micro-fracture evolution and rock failure modes; Y Guo et al.8 demonstrated that in prefabricated fissured marble, the damage mode transitions from tensile to shear with increased peripheral pressure, with crack penetration behavior categorized into four modes; Wang S et al.9 introduced a modified phase-field model to simulate multi-crack extension, validating its accuracy with compression and shear tests; Kytýř, D. et al.10 utilized acoustic emission (AE) and four-dimensional X-ray computed tomography (4D XCT) techniques to investigate the failure mechanisms of rocks. Their analysis of AE responses elucidated the dynamic changes in these mechanisms; Zhou, H.-Y et al.11 applied Hopkinson impact tests and developed a numerical RHT model, revealing inconsistent patterns in how fissure inclination affects mechanical properties; Matěj, P. et al.12 conducted studies on the fracture behavior of four distinct granites under uniaxial compression. Employing acoustic emission (AE) technology, he monitored and analyzed the rock fracture processes, offering detailed insights into the formation and propagation of micro-fractures; Chen W et al.13 used uniaxial compression, NMR, SEM, EDS, and XRD to analyze the effects of high humidity, finding increased structural looseness and accelerated damage with longer immersion times; Mohammadi, S. D. et al.14 performed mechanical tests on rocks containing bedding planes, utilizing acoustic emission (AE) monitoring to record events during the process of through-rock-bridge failure. He investigated how various bedding angles affect the mechanical properties and failure modes of these rocks.

While previous research predominantly focuses on how fracture-related parameters affect mechanical properties and damage modes, fewer studies address the impact of loading rate on damage evolution. This paper investigates prefabricated fractured rock materials with a 45° fracture inclination. Utilizing the RYL-600 shear rheometer and the AMSY-6 32-channel monitoring system, uniaxial compression acoustic emission tests were conducted at various loading rates. A damage constitutive model was constructed using Logistic functions based on acoustic emission parameters. This study aims to explore the mechanical properties, AE parameters, and damage evolution of fissured rock specimens under different loading rates, providing theoretical support for engineering disaster prevention and control.

Pilot program

Materials and specimen preparation

The tests utilized rock-like specimens fabricated from cement, fine sand, and water. These specimens were designed to closely mimic natural rock properties, ensuring the relevance of the test results. The material proportions were cement: fine sand: water = 3.9:3.7:1.515. The specific steps are as follows: 1. After the preparation materials were thoroughly mixed, they were placed into a steel mold with the inner groove dimensions of 150 mm × 150 mm × 50 mm. The specimen was fully vibrated on a vibration Table to remove the air inside it. 2. Due to the relatively strong fluidity of the material at this time, the vibrated specimen needed to be horizontally placed at room temperature for approximately 4 h. Only after the fluidity of the specimen decreased could the next step be carried out. 3. Two steel sheets with a thickness of 0.5 mm were inserted parallelly and vertically into the specified positions of the specimen, and then the specimen was horizontally placed for about another 4 h. 4.After it was determined that the specimen had initially solidified, the steel sheets were vertically pulled out, and the specimen was continuously placed horizontally for approximately 8 h. At this time, after confirming that the specimen had completely solidified, the specimen was removed from the mold. To ensure test accuracy, the specimens were inspected for fully penetrated prefabricated cracks, and any surface unevenness was polished to reduce the impact of surface flatness on the results. The specimens were then cured for 28 days to develop adequate strength. Prior to testing, the cured specimens were inspected for surface integrity and free of cracks or other defects. The specimens are depicted in Fig. 1:

Fig. 1
figure 1

Diagram of specimen.

Full size image

The parameters of two prefabricated parallel fissures include: the angle between the fissure and the horizontal boundary (α), fissure length (a), and fissure width (b). The fissure angle was set at α = 45°, with a length of 25.0 mm and a width of 0.5 mm. A reference group consisting of intact rock specimens without prefabricated fractures was also included. Specimens were numbered based on the format: UC (uniaxial compression)—loading rate—fissure angle. The specimen numbering is detailed in Table 1.

Table 1 Specimen number Table.
Full size table

Pilot program

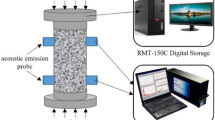
The tests were conducted using the RYL-600 rigidity testing machine (shear rheometer) located at the Hunan Provincial Key Laboratory of Coal Mine Safety Mining Technology, Hunan University of Science and Technology. Uniaxial compression tests were performed on specimens at various loading rates, employing a displacement-controlled loading method. The loading rate was set to four rates:0.5/1.0/3.0/5.0mm/min. To mitigate end effects due to friction between the specimen ends and the platen, lubricating oil was applied to both ends of the specimen. Acoustic emission (AE) characteristics were monitored during the loading process using the Vallen AMSY-6 32-channel system. Eight AE probes were strategically placed on the specimen surface to record AE parameters during specimen failure. The setup of the test equipment is illustrated in Fig. 2a, and the layout of the acoustic emission probes is shown in Fig. 2b:

Fig. 2
figure 2

Test Layout Diagram.

Full size image

Mechanical properties of rock samples

Mechanical properties of rock samples affected by loading rate law

The uniaxial compressive stress–strain curves of the specimens, as illustrated in Fig. 3, demonstrate that the loading rate significantly influences their mechanical properties. Specifically, an increase in the loading rate results in a steeper slope of the stress–strain curve. Figure 3a illustrates that as the loading rate gradually accelerates, the peak damage stage of the specimen transitions from plastic damage at lower loading rates to brittle damage at higher loading rates. Figure 3b shows that the effect of loading rate on the stress–strain curve of the prefabricated fissured specimen is comparable to that of the intact specimen. At a loading rate of v = 0.5mm/min, the specimen exhibits post-peak strength with a gradual decline in the stress–strain curve, indicative of plastic damage characteristics. As the loading rate gradually accelerates, the specimen reaches peak strength more quickly, and the stress–strain curve displays a sharp drop, signifying brittle damage characteristics.

Fig. 3
figure 3

Stress–strain curves of rock-like specimens under different loading rates.

Full size image

To visually assess the impact of loading rate on the mechanical properties of the specimen, the modulus of elasticity (E) was calculated using Eq. (1),The positions of each parameter in the stress—strain curve are shown in Fig. 4:

$$E = \frac{{\sigma_{2} - \sigma_{1} }}{{\varepsilon_{2} - \varepsilon_{1} }}$$
(1)

where: σ1 is the stress value at the beginning of the approximate straight line section of the stress–strain curve of the specimen, and σ2 is the stress value at the end of the section, in MPa; ε1 is the strain value at the beginning of the approximate straight line section of the stress–strain curve of the specimen, and ε2 is the strain value at the end of the section.

Fig. 4
figure 4

Schematic diagram of the positions of each parameter.

Full size image

The peak strength qc and the corresponding elastic modulus E of the specimens at different loading rates were recorded as shown in Table 2:

Table 2 Rock Sample Peak Stress/Modulus of Elasticity Record Sheet.
Full size table

Analysis of Table 2 reveals that prefabricated cracks adversely affect the mechanical properties of the specimens. Specifically, the peak strength of specimens with prefabricated cracks is lower than that of intact specimens at the same loading rate. The loading rate consistently impacts the mechanical properties of the specimens; as the loading rate increases, both the peak strength and modulus of elasticity of the specimens gradually rise.

For intact specimens, the peak strength qc increased by 63.14%, from 15.20 MPa at 0.5 mm/min to 24.80 MPa at 5.0 mm/min. Similarly, the modulus of elasticity E increased by 150.21%, from 1.18 GPa at 0.5 mm/min to 2.96 GPa at 5.0 mm/min, with increasing loading rates.

For prefabricated fissured specimens (α = 45°), the peak strength qc increased by 61.99%, from 9.12 MPa at 0.5 mm/min to 14.77 MPa at 5.0 mm/min. The modulus of elasticity E also increased by 117.45%, from 1.07 GPa at 0.5 mm/min to 2.32 GPa at 5.0 mm/min.

The relationships between specimen peak strength qc, modulus of elasticity E, and loading rate are illustrated in Fig. 5, with corresponding fitting curves presented in Eqs. (2) and (3). The analysis indicates a positive correlation between loading rate and both peak strength qc and modulus of elasticity E, with approximate linear growth patterns. Specifically, the slopes of the peak strength fitting curves σv are 1.529 for intact specimens and 9.899 for specimens with α = 45°. For the modulus of elasticity, the slopes are 2.823 for intact specimens and 2.088 for specimens with α = 45°. This data suggests that prefabricated cracks also weaken the elastic modulus of the specimens.

$$\sigma_{v} = \left\{ \begin{gathered} 1.529v - 16.203\;\;\;R^{2} = 0.9734\;\;{\text{Unslotted}} \hfill \\ 9.899v - 1.223\;\;\;R^{2} = 0.9684\;\;\;\;\alpha = 45^\circ \hfill \\ \end{gathered} \right.$$
(2)
$$E_{v} = \left\{ \begin{gathered} 2.823v - 1.596\;\;\;R^{2} = 0.9756\;\;\;{\text{Unslotted}} \hfill \\ 2.088v - 1.102\;\;\;R^{2} = 0.9651\;\;\;\;\alpha = 45^\circ \hfill \\ \end{gathered} \right.$$
(3)
Fig. 5
figure 5

Peak strength/modulus of elasticity evolution curve.

Full size image

The stress–strain rate curves of the specimens at different loading rates are plotted as shown in Fig. 6:

Fig. 6
figure 6

Stress stages in rock samples.

Full size image

Figure 6 illustrates that the stress–strain rate curves for both prefabricated crack specimens and intact specimens exhibit similar distribution patterns. These curves can be categorized into four distinct stages: (OA section) the initial compression and densification of cracks, (AB section) the transition from elastic deformation to the stable development of micro-elastic cracks, (BC section) the stage of unstable rupture development, and (CD section) the peak destruction stage16,17,18.

It is observed that as the loading rate increases, the duration of the initial crack compaction stage (OA section) shortens. This is because a higher loading rate reduces the time required for crack compaction within the specimen. Additionally, the OA section of the prefabricated crack specimens corresponds to a higher strain rate compared to intact specimens. This discrepancy arises because prefabricated cracks necessitate greater axial displacement to progress from crack compaction to the next stage.

During the elastic deformation stage leading to the stable development of micro-elastic cracks (AB section), internal crack compaction causes a rapid increase in specimen stress until new microcracks form. Figure 6b illustrates a notable stress drop at this stage, attributed to the increased propensity for cracking in prefabricated specimens. As the loading rate increases, the strain rate in this stage also increases.

In the unstable rupture development stage (BC section), the rate of stress increase diminishes as internal micro-cracks rapidly develop. Higher loading rates reduce the duration of this stage because they accelerate the development of internal micro-cracks, leading to a faster attainment of peak stress.

In the post-peak damage stage (CD section), following peak stress, the specimen loses its load-bearing capacity and ultimately fails. Figure 6a shows that at lower loading rates, this stage accounts for a larger proportion of strain rate and exhibits notable plastic damage characteristics, at higher loading rates, the strain rate proportion in this phase decreases.

In summary, as the loading rate increases, the proportion of the strain rate during the stage from the elastic deformation of the specimen to the stable development of micro-elastic cracks gradually increases, while the proportions of the strain rate during the initial crack compaction stage, the unstable fracture development stage and the post—peak failure stage gradually decrease.

Specimen progressive damage analysis

To examine the impact of loading rate on the progressive damage process in rocks, it is crucial to analyze the stress thresholds associated with each deformation stage19,20, These four key stress thresholds are: closing stress σCC, crack initiation stress σCi, peak stress σC, and penetration stress σCP. Closing stress refers to the stress at which the original crack within the specimen is fully closed under external load. Crack initiation stress is defined as the stress at which the first new crack forms within the specimen. Peak stress is the maximum stress attained by the specimen during the loading process, while penetration stress is the stress at which the two prefabricated cracks connect with each other. Figure 7 illustrates the distribution of these four stress thresholds within the stress–strain curve:

Fig. 7
figure 7

Stress threshold distribution.

Full size image

Figure 8 presents the individual stress thresholds for the specimens, illustrating that, with increasing loading rates, both the unopened seam specimen and the prefabricated fissured specimen exhibit a rising trend in their stress thresholds.

Fig. 8
figure 8

Stress threshold evolution curves for rock samples.

Full size image

In order to visualize and analyze how each stress threshold is affected by the loading rate, the values were recorded as Table 3:

Table 3 Stress threshold record sheet.
Full size table

Table 3 indicates that for unseamed specimens, stress thresholds increased with loading rate. Closing stress rose from 3.43 MPa at 0.5 mm/min to 4.81 MPa at 5.0 mm/min, an increase of 40.18%. Crack initiation stress increased from 12.61 MPa to 21.21 MPa, a rise of 68.29%. Peak stress increased from 15.20 MPa to 24.80 MPa, up by 63.16%. Penetration stress increased from 10.80 MPa to 23.80 MPa, a rise of 117.60%.

For the prefabricated fissure specimens, each stress threshold increased with loading rate. Closure stress rose from 1.95 MPa at 0.5 mm/min to 3.30 MPa at 5.0 mm/min, an increase of 69.24%. Crack initiation stress increased from 7.27 MPa to 12.40 MPa, up by 70.49%. Peak stress increased from 9.12 MPa to 14.77 MPa, a rise of 61.95%. Penetration stress increased from 8.07 MPa to 13.33 MPa, up by 65.15%.

It is evident that there is a positive correlation between the loading rate and the specimen’s stress thresholds; higher loading rates result in greater impacts on these thresholds. Moreover, comparison between intact and prefabricated fissured specimens reveals that prefabricated cracks significantly reduce stress thresholds, leading to an accelerated damage process.

An exploration of ringing and energy evolutionary patterns

AE ringing evolutionary pattern

The acoustic emission monitoring system records energy changes during the transition from micro-fractures to macro-destruction within rocks, converting these changes into acoustic emission signals through elastic waves. This capability makes acoustic emission technology widely employed for monitoring rock rupture states21,22. The Vallen AMSY-6 32-channel monitoring system was used to complete the acoustic emission testing required for this study, employing eight probes positioned on the specimen’s surface. To ensure the reliability and accuracy of the results, a coupling agent was applied to the probes before their installation to facilitate signal transmission. Following probe arrangement, the broken lead method was employed to verify the proper operation of each probe. The configuration of the acoustic emission probes is depicted in Fig. 9:

Fig. 9
figure 9

AE monitoring probe layout diagram.

Full size image

AE ring—down count refers to the number of oscillations in which a burst—type acoustic emission signal exceeds the threshold during acoustic emission signal processing. It can intuitively reflect the frequency of acoustic emission events. Because during the loading process, as the cracks in the specimen expand, new acoustic emission sources will be continuously generated inside the specimen, resulting in frequent acoustic emission events and an increase in the ring—down count. Therefore, analyzing the AE ring—down count can effectively judge the degree of internal damage of the specimen. The cumulative AE ring—down count refers to the sum of all ring—down counts within a certain period of time or loading history. It is a macroscopic indicator reflecting the cumulative internal damage of the material. During the long—term use or loading process of the material, as the damage continuously develops, the cumulative AE ring—down count will keep increasing. Analyzing the cumulative AE ring—down count can provide in-depth understanding of the laws of acoustic emission activities inside the material.

Use of AE monitoring equipment to record changes in the number of AE bells and the cumulative number of bells as a function of loading rate during uniaxial compression. This approach aimed to investigate the evolution of AE ringing counts in prefabricated fissure specimens under different loading rates. The characteristics of these AE ringing counts and cumulative ringing counts are presented in Fig. 10:

Fig. 10
figure 10

α = 45°Rock Sample AE Ring Count Monitoring Curve.

Full size image

Analysis of Fig. 10 reveals that during the loading process leading to specimen failure, a noticeable increase in AE ringing counts often correlates with corresponding changes in the stress–strain curve, such as those illustrated in Fig. 10b. When AE ringing counts show a marked increase accompanied by a stress drop in the stress–strain curve, it indicates a strong correlation between AE ringing counts and the stress–strain curve. Based on the characteristics of AE ringing counts, the process can be divided into three distinct stages:

Stage I: Calm Development Stage. This stage includes the initial compaction and linear elastic deformation phases of the stress–strain curve. During this phase, cracks and pores within the specimen are gradually compacted under external load, resulting in low AE ringing counts. As the specimen transitions to the linear elastic deformation stage, localized cracks form and expand, causing a no Table increase in AE ringing counts compared to the compaction stage. The abrupt increase in AE ringing counts during this stage, as illustrated in Fig. 10a and b, is attributed to the development and expansion of primary and localized cracks.

Stage II: Active Development Stage. This stage encompasses the unstable rupture phase leading up to the specimen’s peak compressive strength. During this period, cracks within the specimen expand and develop rapidly, causing irreversible plastic deformation. The development, penetration, and coalescence of these cracks result in increased AE ringing counts, which show a gradual upward trend as depicted in Fig. 10c. These counts are higher compared to those observed in Stage I.

Stage III: Surge Development Stage. This stage refers to the post-peak damage phase of the specimen. As the specimen progresses into this stage, macro-cracks continue to develop until the specimen fails completely. During this phase, AE ringing counts typically reach their maximum value, exhibiting a pronounced surge, as shown in Fig. 10d. After the specimen reaches peak strength, the stress–strain curve drops abruptly, coinciding with the surge in AE ringing counts.

The peak AE ringing counts as well as the cumulative ringing counts were recorded in Table 4 in order to explore the effect of loading rate on the AE ringing counts:

Table 4 Prefabricated Fractured Rock Sample AE Peak Ringing/Cumulative Ringing Record Sheet,
Full size table

Table 4 illustrates that as the loading rate increased, AE ringing counts rose progressively from 123.33 × 10–2 to 213.54 × 10–2, marking a 73.15% increase. Conversely, cumulative ringing counts decreased from 194.48 × 10–3 to 118.94 × 10–3, representing a 38.84% reduction. This phenomenon is attributed to the increased loading rate, which progressively enhances the specimen’s uniaxial compressive strength, thereby elevating the peak AE ringing counts observed during failure. Additionally, higher loading rates reduce the time available for microcracks to experience friction and sliding, leading to a decrease in cumulative AE ringing counts.

AE energy evolutionary pattern

The AE energy evolution curves during loading of the prefabricated fissure rock samples are plotted as shown in Fig. 11:

Fig. 11
figure 11

α = 45°Rock Sample AE Energy Monitoring Curve.

Full size image

Analysis of Fig. 11 reveals that the acoustic emission energy evolution during loading mirrors the three stages observed in ringing counts. In the initial calm development stage, energy release is minimal due to the compression of initial cracks. As the specimen transitions into the linear elastic deformation stage, localized cracks begin to form, causing a gradual increase in energy. During the active development stage, as the specimen undergoes plastic deformation and experiences extensive crack propagation and coalescence, acoustic emission energy rises significantly. In the surge stage, occurring during post-peak damage, AE energy reaches its peak. Additionally, a sudden increase in energy often coincides with the stress drop observed in the stress–strain curve23,24.

The specimen AE energy as well as the cumulative energy was recorded as shown in Table 5:

Table 5 Prefabricated Fractured Rock Sample AE Peak Energy/Cumulative Energy Record Sheet.
Full size table

The analysis shows that both the acoustic emission (AE) energy and the AE cumulative energy of the prefabricated crack specimens gradually increase with the increase of loading rate. Specifically, AE energy rises from 95.85 × 10−3 to 223.87 × 10−3, a 133.56% increase, while AE cumulative energy increases from 75.62 × 10−4 to 170.47 × 10−4, reflecting a 125.43% rise. This analysis demonstrates that AE energy and AE ringing counts follow a similar trend and are positively correlated with loading rate. In contrast, AE cumulative energy and cumulative ringing counts exhibit an inverse relationship, with AE cumulative energy positively correlated with loading rate. This is attributed to the fact that higher loading rates reduce the time required for microcracks to absorb unit energy, allowing them to absorb a larger amount of energy rapidly, which accelerates crack propagation and consequently increases the energy released during loading, leading to a higher cumulative AE energy.

Derivation and verification of damage constitutive model

Damage evolution law based on acoustic emission (AE) energy

To explore the damage evolution process of fissured rock samples, this chapter uses a rock specimen with a fissure inclination angle of 45° as a case study. The analysis is conducted from an energy perspective during uniaxial compression. Under uniaxial compression, persistent deformation phenomena—such as compaction, swelling, and the development of internal microfissures—result in increased energy dissipation. This progressive energy dissipation25,26,27. The damage variable for the rock is defined to be 0 at the initial stage and 1 at the final stage of damage, i.e., D ∈ 0,1. The expression for the rock damage variable, derived from the acoustic emission (AE) energy, is given by Eq. (4)28,29. This equation is based on the energy perspective, which directly links AE energy to the damage variable, providing a more comprehensive reflection of the complex damage process inside the rock.

$$D = \frac{N}{{N_{a} }}$$
(4)

where: D is the damage variable; N is the AE cumulative energy value of the rock sample at any moment, aJ; Na is the total AE cumulative energy value of the rock sample at the time of final damage, aJ.

According to Eq. (4) , the damage variable D is calculated and plotted against the strain curve at different loading rates, as shown in Fig. 12 . This approach not only demonstrates the relationship between damage and strain but also highlights the influence of loading rates on the damage evolution process, which is a key innovation of our model.

Fig. 12
figure 12

Relationship between damage variables and strain curves.

Full size image

As illustrated in Fig. 12, the relationship between the damage variable D and strain exhibits a similar pattern across different loading rates. Initially, as microfissures within the rock samples undergo continuous compaction, the stored elastic potential energy gradually increases. However, during this phase, the rock samples remain undamaged, resulting in a relatively slow increase in the damage variable D. Over time, as the microfissures expand and develop, the rock samples begin to exhibit damage under applied pressure. As time progresses, the internal microfissures in the rock samples continue to expand and develop, leading to increasing compressive damage. The stored elastic energy is progressively converted into dissipative energy, and as deformation and destruction intensify, the growth rate of the damage variable D accelerates.

Figure 12 also reveals that rock samples subjected to different loading rates exhibit varying damage behaviors: higher loading rates lead to rock damage occurring at smaller strains, indicating that rock samples exposed to greater loading rates sustain damage at lower strains. During external loading, damage initially develops in regions of lower internal strength and subsequently propagates outward until the cracks interconnect, ultimately resulting in the failure of the rock sample. This process mirrors the behavior described by the blocked growth model, specifically the Logistic function. To visually represent the damage evolution process of rocks under varying loading rates, the hysteresis growth model—specifically the Logistic growth model—is utilized. The Logistic growth model is expressed in Eq. (5).

$$D_{{\text{p}}} = \frac{1}{{1 + {\text{e}}^{\beta - \gamma \varepsilon } }}$$
(5)

Equation (5) can be obtained by varying Eq. (6):

$$\ln \left( {\frac{{1 - D_{{\text{p}}} }}{{D_{{\text{p}}} }}} \right) = 1 + {\text{e}}^{\beta - \gamma \varepsilon }$$
(6)

where: β and γ are test parameters.

The experimental data were fitted using Eq. (6), with the parameters β and γ detailed in Table 6. The fitting results show high R2 values (0.9663, 0.9884, 0.9712, and 0.9634), indicating that the logistic function effectively characterizes the rock’s damage evolution process. This method provides a reliable means for predicting damage under different loading rates.

Table 6 Damage parameters β, γ take values.
Full size table

Table 6 reveals that the damage model parameters β and γ exhibit a relationship that varies with different loading rates, suggesting a consistent connection in the damage evolution of the same rock under varying conditions. This finding highlights the versatility of our model in capturing the damage behavior under different loading rates. To elucidate this relationship, Fig. 13 presents the curve illustrating how the damage parameters β and γ vary with different loading rates.

Fig. 13
figure 13

Damage parameters β, γ evolution.

Full size image

Figure 13 shows that the damage parameter β exhibits an exponential correlation with the loading rate, while the damage parameter γ correlates linearly with the loading rate. The functional relationships between the damage parameters β and γ and the loading rate are derived from these fitted curves, as detailed in Eq. (7). This derivation process demonstrates the model’s ability to capture the complex interplay between loading rates and damage evolution.

$$\left\{ \begin{gathered} \beta = - 0.30352\exp \left( {\frac{ - v}{{1.13128}}} \right) + 5.73091\;\;R^{2} = 0.9998 \hfill \\ \gamma = 0.42633 + 0.07646v\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R^{2} = 0.9799 \hfill \\ \end{gathered} \right.$$
(7)

This leads to an improved relational equation for rock damage evolution based on the logistic function, as shown in Eq. (8):

$$D = \frac{1}{{1 + \exp \left\{ {\left[ {0.42633 + 0.07646v) - (5.73091 - - 0.30352\exp \left( {\frac{ - v}{{1.13128}}} \right)} \right]\varepsilon } \right\}}}$$
(8)

Loss ontology modeling

According to the Lemaitre strain equivalence hypothesis30,31, And combined with Eq. (8) can be obtained the damage constitutive model of rock under different loading rates as shown in Eq. (9):

$$\sigma = \left( {1 - D} \right)E_{c} \varepsilon = \left( {1 - \frac{1}{{1 + {\text{e}}^{{\left( {0.42633 + 0.07646v} \right) - \left( {5.73091 - - 0.30352\exp \left( {\frac{ - v}{{1.13128}}} \right)} \right)\varepsilon }} }}} \right)E_{c} \varepsilon$$
(9)

where: Ec is the modulus of elasticity of the unseamed specimen.

During the actual compression of rock samples, inherent cracks cause internal microfractures to gradually compact during the initial loading stages. The acoustic emission energy is minimal and nearly negligible compared to the overall loading process, leading to a damage variable D that approximates zero in the early stages. Consequently, it is necessary to adjust the constitutive equations for the compaction stage. According to effective medium theory, the axial strain ϵ\epsilonϵ in the compaction stage can be decomposed into two components: the elastic strain εm of the matrix and the strain εr resulting from the compaction of layered interfaces and cracks, as depicted in Eq. (10)32,33,34,35,36:

$$\varepsilon = \varepsilon_{{\text{m}}} + \varepsilon_{{\text{r}}}$$
(10)

During the initial loading phase, internal cracks in the rock gradually compact and close, with minimal crack expansion. Therefore, the rock can be approximated as a continuous solid material. According to generalized Hooke’s law, the relevant relationships can be expressed in Eq. (11):

$$\varepsilon_{m} = \frac{\sigma }{E}$$
(11)

Combining Eq. (10) with Eq. (11) leads to Eq. (12):

$$\varepsilon_{{\text{r}}} = \varepsilon - \frac{\sigma }{E}$$
(12)

Based on the theory of variable elasticity36, The microfracture compaction closure model of the rock during the initial compaction stage was established as in Eq. (13):

$$\varepsilon_{{\text{r}}} = \varepsilon_{{{\text{rr}}}} \left[ {1 - \exp \left( { - \frac{\sigma }{{E_{{{\text{rr}}}} }}} \right)} \right]$$
(13)

where: εrr is the strain during crack compaction, and Err is the equivalent modulus of elasticity at the crack closure stage.

In summary, by combining Eq. (9) with Eq. (13), the stress–strain relationship curve of the rock during the initial loading stage, when the fissures are compacted and closed, can be derived. Following the compaction stage, rock damage occurs; however, some deformation precedes this damage. Therefore, the strain associated with the damage stage must be adjusted by subtracting the strain from the compaction stage to obtain the rock constitutive model expression, as given in Eq. (14):

$$\left\{ \begin{gathered} \varepsilon_{{\text{r}}} = \varepsilon_{{{\text{rr}}}} \left[ {1 - \exp \left( { - \frac{\sigma }{{E_{{{\text{rr}}}} }}} \right)} \right] + \frac{\sigma }{E},0 < \varepsilon < \varepsilon_{m} \hfill \\ \sigma = \left\{ {1 - \frac{1}{{1 + \exp \left\{ {\left[ {\left( {0.42633 + 0.07646v} \right) - \left( {5.73091 - 0.30352\exp \left( {\frac{ - v}{{1.13128}}} \right)} \right)} \right]\varepsilon } \right\}}}} \right\}E\left( {\varepsilon - \varepsilon_{m} } \right),\varepsilon \ge \varepsilon_{m} \hfill \\ \end{gathered} \right.$$
(14)

Model correlation validation

To validate the reliability of the proposed model, four specimens with loading rates of 0.5 mm/min, 1.0 mm/min, 3.0 mm/min, and 5.0 mm/min were analyzed and compared against experimental data. Figure 14 illustrates the comparison between the measured data and the fitted data during the pore compacting stage of the rock samples.

Fig. 14
figure 14

Strain–stress curve in the compacting stage.

Full size image

Analysis of Fig. 14 reveals that, although there is some degree of dispersion in the fitting curve of the constitutive model during the compaction stage, the overall trend aligns well with the actual experimental curve. This suggests that the model effectively captures the strain–stress behavior during the rock’s compaction stage.

To derive the stress–strain curve for the rock during the damage stage, the data presented in Table 6 were substituted into the damage stage model. This model was then combined with the stress–strain curve from the compaction stage to generate the stress–strain curve for the specimen throughout the loading-to-destruction process, as illustrated in Fig. 15:

Fig. 15
figure 15

Theoretical/actual stress–strain curve.

Full size image

Figure 15 demonstrates that the overall trend of the theoretical model curve closely aligns with the actual data curve. Although there is some discrepancy in the peak value as shown in Fig. 15a, the theoretical curve generally reflects the peak strength effectively. The above analysis indicates that the theoretical model curve exhibits high accuracy and applicability in characterizing the uniaxial compression behavior of specimens under various loading rates.

Conclusions

  1. (1)

    Prefabricated cracks significantly impair the strength of the specimen, resulting in lower strength for specimens with prefabricated cracks compared to intact, unseamed specimens. Both the peak compressive strength and modulus of elasticity are positively correlated with the loading rate. Additionally, prefabricated cracks reduce the stress thresholds, making specimens more prone to damage; however, these stress thresholds increase progressively with the loading rate.

  2. (2)

    There is a strong correlation between the AE characteristic parameters and the stress–strain curve. The AE parameters are divided into three stages based on their behavior: the calm development stage, the active development stage, and the surge development stage. As the loading rate increases, AE ringing counts, AE energy, and AE cumulative energy rise progressively, while AE cumulative ringing counts show a negative correlation with the loading rate.

  3. (3)

    By utilizing AE energy data to investigate the damage evolution of the specimen, the Logistic function was employed to determine the damage parameters β and γ in relation to the loading rate, leading to the formulation of the specimen damage evolution equation.

  4. (4)

    Building on the specimen damage evolution relationship and Lemaitre’s strain equivalence hypothesis, a rock damage constitutive model was developed for varying loading rates. Verification results show that the theoretical curve closely aligns with the actual experimental data, demonstrating the model’s accuracy and applicability.