Introduction

Tight gas is a source of energy that is environmentally friendly and efficient. It has become an important source of natural gas development around the world. Tight gas reservoirs are characterized by low porosity, low seepage, and high water content. Their seepage characteristics are more complex than those of conventional gas reservoirs1,2,3,4,5,6,7.

Recent studies have shown that seepage mechanisms, including threshold pressure gradient, stress sensitivity and slip effect, coexist and cannot be overlooked in the depletion and development of tight water-bearing gas reservoirs8,9,10. The threshold pressure gradient(TPG) is defined as the pressure gradient at which the fluid begins to flow under the action of viscous forces between the solid gas, and it is an important parameter for characterizing nonlinear seepage in tight gas reservoirs11. B. A. Florin was the first to introduce the concept of the TPG12.Feng then presented the idea of non-Darcy low-velocity gas flow13. Li discovered that permeability is inversely related to the threshold pressure gradient through experimental methods14. Zeng used the steady-state ‘pressure-velocity’ method to analyze the influence of permeability and fluid composition on TPG, and found that the power function is a better TPG function15.Zhu et al. believed that TPG increased with the decrease of permeability or the increase of water saturation, but there was no clear correlation16. Ding et al. demonstrated that TPG is dependent on both pore pressure and water saturation. They observed that cores with high water saturation exhibited higher TPG values than those with low water saturation17. Cao et al. by fitting the relationship equation between the threshold pressure gradient and permeability and water saturation, concluded that the threshold pressure gradient increases when the water saturation increases or the permeability decreases during the development of a gas reservoir18. Atif Zafar used experimental methods to analyze the relationship between the starting pressure gradient and water saturation, pore pressure, and permeability. He believed that pore pressure also had an effect on TPG. The lower the pore pressure, the higher the TPG value19.

Stress sensitivity is a phenomenon in which permeability varies with effective stress. Fatt and Davis discovered that the envelope pressure exerted on the core significantly influences the permeability’s magnitude20. Thomas et al. concluded that the permeability of tight sandstone reservoirs decreases significantly with increasing overburden pressure21. Xue believes that tight sandstone gas reservoirs have strong stress sensitivity, and it increases with the increase of water production. Compared with the threshold pressure gradient, stress sensitivity has a greater impact on gas well productivity22.On the basis of analyzing the empirical and theoretical models of the relationship between permeability and effective stress, Xiao et al. summarized the expressions of three stress sensitivity coefficients ( S, α, β ). Further analysis shows that the stress sensitivity coefficient S is suitable for evaluating the stress sensitivity of tight reservoirs23. Zong et al. found through experiments that the permeability decreases with the increase of effective stress, and the downward trend gradually slows down. After the effective stress is restored, the permeability cannot be fully restored. The microscopic pore structure has an important influence on the stress sensitivity24.Fu et al. established the relationship between permeability and effective stress. They believe that the effective permeability decreases with the increase of effective pressure. The relationship between stress sensitivity and abandonment pressure of gas well is derived25.

The gas slip effect is a phenomenon of non-Darcy flow in porous media, which is mainly reflected in the fact that the gas relative permeability will deviate from the absolute permeability. Klinkenberg first proposed the theory of gas slippage and introduced the slippage coefficient to obtain the relationship between slippage coefficient, permeability, and average pressure26. Shi proposed an apparent gas permeability model that considers both the permeability and absolute permeability of low-permeability sandstone rock deformation, gas slip and water saturation, and analyzes the influence of these parameters on permeability27.Wang et al. found that when the pore pressure is low, the gas slip effect increases, resulting in a measured permeability higher than the absolute permeability28.

Fracturing technology is an important means to improve tight gas reservoirs. Many scholars have carried out a lot of research on the seepage model of fracturing wells in combination with the seepage law of tight water-bearing gas reservoirs. Yao established a gas-water two-phase seepage model for fractured wells considering water saturation, relative permeability and threshold pressure gradient, and analyzed the influence of seepage parameters such as threshold pressure gradient on productivity29. Zeng proposed a productivity model considering threshold pressure gradient, stress sensitivity and secondary fractures, and analyzed the influence of threshold pressure gradient, stress sensitivity and secondary fractures on gas production. The results show that threshold pressure gradient and stress sensitivity have an inhibitory effect on gas production. When the influence of secondary fractures is ignored, the predicted productivity is relatively low30. Wei et al. established a gas-water two-phase productivity model for fractured vertical wells considering threshold pressure gradient, stress sensitivity, and reservoir heterogeneity. The analysis shows that threshold pressure gradient, reservoir heterogeneity, and stress sensitivity are negatively correlated with gas well productivity, and fracture stress sensitivity has a greater impact on productivity31.

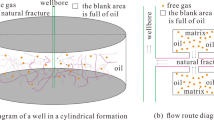
It is of great significance to the efficient production of a well to clarify the variation law of the supply boundary in the development process. Many scholars have studied this problem. PASCAL and Liu argued that the propagation of pressure perturbations in low-permeability reservoirs does not reach infinity instantaneously due to the presence of an initial pressure gradient, and that its seepage law is a moving boundary problem32,33. Li et al. used the steady state stepwise replacement method to solve the propagation law of oil supply radius in unsteady seepage flow, which provides a new method for determining the reasonable well spacing in low-permeability reservoirs34.Ma et al. demonstrated that the pressure propagation rate of ultra-low-permeability reservoirs is significantly lower than that of conventional reservoirs due to the influence of stress35. Wang et al. studied the pressure driven outflow problem of multi-component multiphase fluids under improved convective boundary and improved non-equilibrium rebound boundary conditions based on the lattice Boltzmann method. The results showed that the mCBC scheme is shown to be more capable to correctly treat such pressure specified boundary conditions36. Zhu et al. analyzed the unsteady seepage pressure characteristics of shale gas, and they concluded that the pressure propagation has the effect of a moving boundary, which propagates outward with time, and the propagation speed gradually slows down37,38. In summary, it can be observed that the supply boundary of wells in low-permeability gas reservoirs undergoes a temporal change due to the influence of seepage mechanisms, including the threshold pressure gradient and stress-sensitive effect. As shown in the Fig. 1, during tight reservoir development, the tight reservoir is opened up and the pressure gradually propagates outwards. At a specific point in time, t, the pressure propagates to R(t), at which time a pressure drop funnel is formed within R(t), and R(t) is the dynamic supply boundary of the seepage process. When the pressure propagates to the edge of the supply boundary, the pressure at the edge is equal to the original formation pressure.

Fig. 1
figure 1

Dynamic supply boundary diagram.

Full size image
Table 1 Summary of gas-water two-phase model of tight gas reservoir.
Full size table

As shown in Table 1, Currently, gas-water two-phase model of tight gas reservoirs considers various factors such as threshold pressure gradient, stress sensitivity, slip effect, and fracture interference. Despite numerous studies on the gas-water two-phase model for tight gas reservoirs, there are still some problems. Studies of gas-water two-phase supply boundaries in tight gas reservoirs that take into account multiple seepage mechanisms, such as threshold pressure gradient, stress sensitivity, and slip effect, have rarely been reported41,42.

The main purpose of this paper is to study the law of gas-water two-phase supply boundary in tight gas reservoirs. Firstly, based on the seepage theory of tight water-bearing gas reservoirs, considering the starting pressure gradient, stress sensitivity, and slippage effect, a gas-water two-phase two-zone coupling productivity model for fractured wells is established. Secondly, the dynamic supply boundary calculation model is established by using the material balance method and the steady-state substitution method. Finally, the model is solved to reveal the law of gas-water two-phase supply boundary of fractured wells, and the influence of starting pressure gradient, stress sensitivity, and production pressure difference on supply boundary and production is analyzed.

Methodology

Gas-water two-phase coupling model

Basic assumptions

According to the classification standards of China Petroleum and North America, gas reservoirs with matrix permeability of less than 1 mD and porosity of less than 12% are classified as tight gas reservoirs. Fracturing transformation is a crucial method for enhancing the productivity of these tight reservoirs7,43.

The establishment of a gas-water two-phase coupling model is based on the fracturing equivalent well diameter model and the seepage theory of tight water-bearing gas reservoirs. This model takes into account the threshold pressure gradient, stress sensitivity, and slip effects. The model is divided into two zones: the outer zone is defined as the matrix zone, while the inner zone is referred to as the fracture modification zone (see Fig. 2). In the fracturing transformation zone, both natural and hydraulic fractures are considered, and this area is treated as an equivalent circle with a radius of Rf. The underlying assumptions of the model are as follows:

(1) Reservoir homogeneous, equal thickness;

(2) Before the gas reservoir was developed, the formation pressure was equal everywhere.

(3) Gas reservoir is a two-phase flow of gas and water, there is no mixing of the phases, the gas flows under isothermal conditions40.

(4) The external matrix zone supplies gas to the fracture network zone, the fracture network zone supplies gas to the wellbore, and the fracture network zone does not consider the threshold pressure gradient.

Fig. 2
figure 2

Schematic diagram of two-zone coupled seepage model.

Full size image

Model formulation

(1) Fracturing transformation zone.

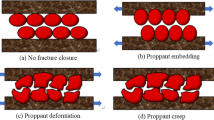
During the development of tight gas reservoirs, as the formation pressure decreases, fractures are affected by stress sensitivity and close, reducing gas flow channels and permeability, resulting in a decrease in gas well productivity. Research has demonstrated that the stress sensitivity of fractured rock cores is greater than that of matrix rock cores44,45,46. Therefore, in the fracture transformation zone, it is essential to account for the influence of fracture stress sensitivity. In this study, we use \(\alpha f\) to represent fracture stress sensitivity, which is derived from experimental fitting. Given the significant pressure drop in the fracture reconstruction area, seepage resistance is low. In this region, we do not consider the threshold pressure gradient, only consider the influence of fracture stress sensitivity and the slippage effect. The mathematical model is as follows:

① continuity equation.

$$\begin{gathered} - \nabla \cdot ({\rho _g}{\upnu _{f\_g}})=0 \hfill \\ - \nabla \cdot ({\rho _w}{\upnu _{f\_w}})=0 \hfill \\ \end{gathered}$$
(1)

② Equations of motion

$${\upnu _{f\_g}}= - \frac{{{k_f}{k_{rg}}{e^{ - \alpha f}}^{{({P_e} - {P_i})}}(1+\frac{b}{{\overline {p} }})}}{{{\mu _g}}}(\frac{{\partial {p_g}}}{{\partial r}})$$
(2)
$${\upnu _{f\_w}}= - \frac{{{k_f}{k_{rw}}{e^{ - \alpha f}}^{{({P_e} - {P_i})}}}}{{{\mu _w}}}(\frac{{\partial {p_w}}}{{\partial r}})$$
(3)

③ boundary condition

$$\begin{array}{*{20}{l}} {r={r_f},}&{p={p_f}} \\ {r={r_w}}&{p={p_w}} \end{array}$$
(4)

④ Special auxiliary Eq.

$$\begin{gathered} {p_g} - {p_w}={p_c} \hfill \\ {S_w}+{S_g}=1 \hfill \\ \end{gathered}$$
(5)

By solving the above model, the gas phase pressure at any point in the fracture network is obtained as:

$$p_{{fg}}^{2}=p_{w}^{2}+\frac{{p_{f}^{2} - p_{w}^{2}}}{{\ln \frac{{{r_f}}}{{{r_w}}}}} \cdot \ln \frac{r}{{{r_w}}}$$
(6)

The water phase pressure at any point is:

$${p_{fw}}={p_w}+\frac{{{p_{\text{f}}} - {p_w} - {p_c}}}{{\ln \frac{{{r_f}}}{{{r_w}}}}} \cdot \ln \frac{r}{{{r_w}}}$$
(7)

The gas phase production formula is:

$${q_{fg}}=\frac{{{T_{sc}}{Z_{sc}}}}{{{P_w}T}}\frac{{\pi h{k_i}{k_{rg}}{e^{ - \alpha f}}^{{({p_e} - \overline {p} )}}(1+\frac{b}{{\overline {p} }})}}{{{\mu _g}Z}}\frac{{p_{f}^{2} - p_{w}^{2}}}{{\ln \frac{{{r_f}}}{{{r_w}}}}}$$
(8)

The water phase production formula is:

$${q_{fw}}=\frac{{2\pi h{k_i}{k_{rw}}{e^{ - \alpha f}}^{{({p_e} - \overline {p} )}}}}{{{\mu _w}}}\frac{{{p_f} - {p_w} - {p_c}}}{{\ln \frac{{{r_f}}}{{{r_w}}}}}$$
(9)

where\({\upnu _{f\_g}}\)and\({\upnu _{f\_w}}\) are the gas phase and water phase velocities in the fracturing zone respectively,\({k_i}\) is absolute permeability,\({k_{rg}}\) is relative permeability of gas phase,\({k_{rw}}\) is relative permeability of water phase,\(\alpha f\) is Stress sensitivity coefficient of fracturing zone, b is slip factor,\({r_f}\) is fracture radius, \({r_w}\) is inner boundary radius \({p_f}\) is pressure at the junction of the fracturing transformation zone and the matrix zone,\({p_c}\) is capillary force, \(pfg\)is gas phase pressure at any point in the fracturing transformation zone, \({p_{fw}}\) is water phase pressure at any point in the fracturing transformation zone.

(2) Matrix zone.

Compared with the fracturing zone, the seepage characteristics of the reservoir in the matrix zone are more complex. It is necessary to consider the influence of threshold pressure gradient, stress sensitivity effect and slippage effect. The mathematical model is:

① continuity Eq.

$$\begin{gathered} - \nabla \cdot ({\rho _g}{\upnu _{m\_g}})=0 \hfill \\ - \nabla \cdot ({\rho _w}{\upnu _{m\_w}})=0 \hfill \\ \end{gathered}$$
(10)

② Equations of motion

$${\upnu _{m\_g}}= - \frac{{{k_m}{k_{rg}}{e^{ - \alpha m}}^{{({p_e} - {p_i})}}(1+\frac{b}{{\overline {p} }})}}{{{\mu _g}}}(\frac{{\partial {p_g}}}{{\partial r}} - G)$$
(11)
$${\upnu _{m\_w}}= - \frac{{{k_m}{k_{rw}}{e^{ - \alpha m}}^{{({p_e} - \overline {p} )}}}}{{{\mu _w}}}(\frac{{\partial {p_w}}}{{\partial r}} - G)$$
(12)

③ boundary condition

$$\begin{array}{*{20}{l}} {r={r_e},}&{p={p_e}} \\ {r={r_f}}&{p={p_f}} \end{array}$$
(13)

④ Special auxiliary Eq.

$$\begin{gathered} {p_g} - {p_w}={p_c} \hfill \\ {S_w}+{S_g}=1 \hfill \\ \end{gathered}$$
(14)

Define new pseudo pressure function: \(\psi =2\int_{{{\zeta _w}}}^{\zeta } {\frac{{\zeta +G(r - {r_w})}}{{\mu Z}}} d\zeta\), \(\zeta =p - G(r - {r_f})\)

A new quasi-pressure function is defined.

where\({\upnu _{m\_g}}\)and\({\upnu _{m\_w}}\) are the gas phase and water phase velocities in the matrix zone respectively, \(\alpha m\) is Stress sensitivity coefficient of matrix zone, b is slip factor, \({p_e}\) is supply pressure, \({r_e}\)is supply radius , G is threshold pressure gradient, z is deviation factor of natural gas.

Substituting the pseudo pressure function into the above mathematical model, the following can be obtained: The formation pressure at any point of the gas phase in the matrix zone is:

$$p_{{m\_g}}^{2}={({p_{fg}}+G(r - {r_f}))^2}+\frac{{p_{e}^{2} - {{({p_f}+G({r_e} - {r_f}))}^2}}}{{\ln \frac{{{r_e}}}{{{r_f}}}}} \cdot \ln \frac{r}{{{r_f}}}$$
(15)

The formation pressure at any point of the water phase in the matrix zone is:

$${p_{m\_w}}={p_{fw}}+G(r - {r_f})+\frac{{{p_e} - {p_{fw}} - G({r_e} - {r_f})}}{{\ln \frac{{{r_e}}}{{{r_f}}}}}\ln \frac{r}{{{r_f}}}$$
(16)

Combined with the equivalent seepage resistance method, the calculation formula of gas production in the matrix area can be obtained as follows:

$${q_{m\_g}}=\frac{{\pi h{T_{sc}}{Z_{sc}}}}{{{P_{sc}}T{\mu _g}Z}} \cdot {\text{ }}\frac{{p_{e}^{2} - p_{w}^{2} - {G^2}{{(r - {r_f})}^2} - 2{p_{fg}}G(r - {r_f}){\text{ }}}}{{\frac{1}{{{k_f}}}\ln \frac{{{r_f}}}{{{r_w}}}+\frac{1}{{{k_m}}}\ln \frac{r}{{{r_f}}}}}$$
(17)

The calculation formula of water phase production is:

$${q_{m\_w}}=\frac{{2\pi h}}{{{\mu _w}}} \cdot \frac{{({p_e} - {p_{fw}} - {p_w}) - G(r - {r_f})}}{{\frac{1}{{{k_f}}}\ln \frac{{{r_f}}}{{{r_w}}}+\frac{1}{{{k_m}}}\ln \frac{r}{{{r_f}}}}}$$
(18)

Dynamic supply boundary calculation

The material balance approach indicates that the change in pore volume over the effective range of a given tight reservoir is equal to the cumulative production.

$$\sum\limits_{{t=1}}^{n} {{Q_t}} =\int_{{{r_w}}}^{r} 2 \pi rh\left[ {{{({\rho _g}\phi )}_i} - ({\rho _g}\phi )} \right]dr$$
(19)

In the gas-water two-phase flow of tight gas reservoirs, the total output of gas phase and water phase is equal to the change of reservoir pore volume, that is:

$$Q=\pi h(R_{t}^{2} - r_{w}^{2})\left[ {{\phi _i} \cdot ({\rho _{gi}} \cdot {S_{gi}}+{\rho _{wi}} \cdot {S_{wi}}) - {\phi _f} \cdot ({\rho _g} \cdot {S_g}+{\rho _w} \cdot {S_w})} \right]$$
(20)

Furthermore, since the flow rate and pressure at the boundary of the matrix area and the transformation area are equal, we can obtain the gas phase interface pressure \({p_{fg}}\)through Eq. (8)(15), and then combine the special auxiliary equation to obtain \({p_{fw}}\), the average formation pressure is solved by using the following formula :

$$\bar {p}=\frac{1}{A}\int 2 \pi prdr$$
(21)

Based on the above analysis, as shown in Fig. 3, we first use (8) (9) (20) to solve the supply boundary value at the first-time step.

Then, the supply boundary value is substituted into Eq. (8) (9) (17) (18) (21) to calculate the pressure at the boundary of the transformation zone and the matrix zone and the average formation pressure, and the permeability value at the next time step is updated to calculate the production at the next time step. Repeat the above process and iteratively solve the production and dynamic supply boundary at each time step.

Fig. 3
figure 3

Solution process of seepage model.

Full size image

Model solution and verification

The tight sandstone core with a length of 5 cm and a diameter of 2.5 cm was selected from well X in the study area. The porosity and permeability of the core were 5% and 0.1 mD, respectively. In order to better compare with the results of the established model, core depletion experiments were carried out. Set the experimental temperature to 100℃.The experimental process is shown in Fig. 4. The main experimental steps are as follows :

(1) Core vacuum, saturated formation water.

(2) The saturated formation water core is put into the core holder, and CH4 is injected into the core with high pressure pump. The irreducible water saturation is established in the core to simulate the initial state in the actual gas reservoir.

(3) The high-pressure pump is used to pressurize the CH4 of the intermediate container to 30 MPa. After the pressure is stable, the inlet end is closed, and then the outlet valve is opened. The back pressure pump is used to control the constant pressure of 5 MPa, and the depletion development simulation experiment is carried out.

(4) Using gas flow to record gas flow data at different times.

Fig. 4
figure 4

Schematic diagram of depletion experiment. Components: (1) Methane cylinder, (2) High-pressure syringe pump, (3) Six-channel valve, (4) Valve, (5) Water, (6) Synthetic water, (7) Methane, (8) Thermotank (9) Pressure gauge, (10) Coreholder, (11) Confining pressure pump, (12) Back pressure pump, (13) Test tube (14) Gas flowmeter.

Full size image

Combined with the basic data of X well, the basic parameters are brought into the program for calculation. The basic parameters are shown in Fig. 5; Table 2. The results of the model calculation are compared with the experimental results to verify the accuracy of the model.As shown in Fig. 6, the comparison results show that the model prediction results are in good agreement with the experimental results, which verifies that the model is accurate and reliable. The constant pressure production mode adopted by the model decreases rapidly in the early stage of production due to the relatively fast pressure drop in the near-wellbore area. As the development progresses, the pressure gradually spreads outward, the pressure drop rate decreases, and the production gradually decreases and tends to be stable.

Table 2 Basic parameters of X well.
Full size table
Fig. 5
figure 5

X well relative permeability curve.

Full size image
Fig. 6
figure 6

The experimental results are compared with the model results.

Full size image

Results and discussions

In order to reveal the propagation law of gas-water two-phase supply boundary in tight gas reservoirs, we described the characteristics of supply boundary in different regions under the condition of two-zone coupling, and analyzed the influence of threshold pressure gradient, stress sensitivity, slippage effect and production pressure difference on the dynamic supply boundary and production of gas wells.

Dynamic supply boundary characteristics

As illustrated in Fig. 7, the gas well supply boundary exhibits a faster growth rate within the fracture modification zone, subsequently decelerating in the matrix zone. As a consequence of the considerable pressure reduction and minimal resistance to seepage within the fracture reforming zone, the supply boundary advances at a relatively rapid pace. The stress-sensitive effect is further amplified when the supply boundary extends to the matrix zone due to a decline in formation pressure, which also reduces permeability and amplifies the threshold pressure gradient, thereby delaying the supply boundary’s spread.

Fig. 7
figure 7

Dynamic supply boundary results.

Full size image

Effects of threshold pressure gradient on supply boundary

The threshold pressure gradient represents a crucial seepage characteristic of tight water-bearing gas reservoirs. During the 2000-day production development, the supply boundary is simulated and examined as well as the production characteristics for various threshold pressure gradient (0, 0.01, 0.02, and 0.03 MPa/m) (Figs. 8 and 9).

The Figure illustrates that the threshold pressure gradient increases from 0 to 0.03 MPa/m, the dynamic supply boundary propagation distance slows down by an average of 11.03 m, and the propagation speed slows down gradually with the increase of time.

The propagation velocity of the supply boundary is defined as the propagation distance per unit time. Without considering the threshold pressure gradient, the average propagation velocity of the supply boundary in the fracturing transformation zone is 1 m / d, and the average propagation velocity in the matrix zone is only 0.15 m / d.

Meanwhile, the cumulative gas production decreased by 141.14 × 104m3 during this process. During the development of tight water-bearing gas reservoirs, the threshold pressure gradient is enhanced and the seepage resistance is subsequently increased with the rise of water production and the fall of formation pressure, which slows down the propagation of the supply boundary and reduces the gas production.

Fig. 8
figure 8

Effect of the threshold pressure gradient on the supply boundary.

Full size image
Fig. 9
figure 9

Effect of threshold pressure gradient on gas production.

Full size image

Effects of stress sensitivity on supply boundary

In order to study the variation rule of supply boundary under the influence of stress sensitivity, the supply boundary and production conditions are simulated under different stress sensitivity coefficients during 2000 days of production. we simulated and analyzed the supply boundary as well as the production characteristics under different stress sensitivity coefficients (0, 0.02, 0.04, and 0.06) during the 2000-day development process(Figs. 10 and 11).

It can be seen from the figure that the stress sensitivity coefficient increases from 0 to 0.06, the dynamic supply boundary propagation speed is slowed down by 7.9 m on average, and the cumulative gas production is reduced by 93.83104 m3. Without considering the stress sensitivity, the average propagation velocity of the supply boundary in the fracturing transformation zone is 1.1 m / d, and the average propagation velocity of the supply boundary in the matrix area is only 0.08 m / d.

The larger the stress sensitivity coefficient, the smaller the propagation distance of the dynamic supply boundary, and the slower the gas production rate of the gas well. This is because as the development progresses, the formation pressure decreases, the stress sensitivity effect increases, the greater the degree of reservoir permeability damage, the greater the seepage resistance of gas flow, the smaller the propagation distance of the supply boundary, and the smaller the gas production of the gas well.

The propagation distance of the dynamic supply boundary is inversely correlated with the stress sensitivity coefficient, which also affects the gas well’s gas production rate. This is because as the formation pressure lowers, the stress sensitivity effect rises, the degree of reservoir permeability damage increases, the seepage resistance of gas flow increases, the supply boundary’s propagation distance decreases, and the gas well’s gas production decreases as development progresses.

Fig. 10
figure 10

Effects of stress sensitivity on supply boundary.

Full size image
Fig. 11
figure 11

Effect of stress sensitivity on gas production.

Full size image

Effects of production pressure difference on supply boundary

One effective method for overcoming seepage resistance is to increase the production pressure difference47,48.

The supply boundaries are simulated and analyzed as well as the production characteristics at different production pressure differences (5, 10, 15, and 20 MPa) during 2000 days of production development (Figs. 12 and 13). The figure shows that the dynamic supply boundary propagation velocity increases by 53.32 m on average, and that the production pressure difference increases from 5 to 20 MPa.

Under the condition that the production pressure difference is 5 MPa, the average supply boundary propagation velocity of the fracturing transformation zone is 0.67 m / d, and the supply boundary propagation velocity of the matrix zone is only 0.068 m / d. It also shows that the supply boundary propagation distance growth rate gradually decreases with increasing production pressure difference, and that a reasonable pressure difference is present for the development of gas wells.

Fig. 12
figure 12

Effect of production pressure difference on the supply boundary.

Full size image
Fig. 13
figure 13

Effect of production pressure difference on gas production.

Full size image

Conclusions

Based on the seepage theory of tight water-bearing gas reservoirs, this paper establishes a gas-water two-phase seepage model of fractured wells considering threshold pressure gradient, stress sensitivity and slippage effect. On this basis, the gas-water two-phase supply boundary model of tight gas reservoirs is established by material balance method and steady-state substitution method. Finally, the accuracy of the model is verified, the law of gas-water two-phase supply boundary of fractured vertical wells is revealed, and the influence of relevant influencing parameters on gas well supply boundary and production are carried out. The following conclusions are obtained.

(1) Because of the low seepage resistance, the supply boundary propagates more quickly in the fracturing area than in the matrix area. The supply boundary’s propagation speed in the matrix area progressively slows down as the process progresses.

(2) Reduced formation pressure and increased water production lead to an enhanced pressure gradient and stress sensitivity effect, which in turn increases seepage resistance and slows the supply boundary’s propagation. The threshold pressure gradient increases from 0 to 0.03 MPa/m, the dynamic supply boundary propagation distance slows down by an average of 11.03 m, and the stress sensitivity coefficient increases from 0 to 0.06, the dynamic supply boundary propagation speed is slowed down by 7.9 m on average.

(3) The threshold pressure gradient and stress sensitivity will decrease the gas production and a suitable production pressure difference can enhance the production of gas well. Thus, for the effective production of tight gas reservoirs, lowering water production and preserving formation pressure are essential.