Introduction

Physical activity (PA) plays a crucial role in adolescents’ holistic development and contributes significantly to their physical and mental health. Regular PA helps develop strong bones and muscles1,2, enhances cardiovascular fitness3, and reduces the risk of obesity and associated chronic diseases4,5. Furthermore, PA improves mental health by reducing symptoms of depression and anxiety6, boosting self-esteem7, and enhancing cognitive functions8. The social interaction and teamwork often involved in PA also foster better social skills and a sense of belonging9, which are vital during the formative years of adolescence. Therefore, promoting and facilitating regular PA is essential for adolescents’ well-being and healthy development.

However, insufficient PA and sedentary behaviour have become global epidemics among adolescents, exhibiting an upward trend10. Guthold et al.11 analysed 298 school-based surveys from 146 countries, encompassing 1.6 million students aged 11–17 years, to evaluate adherence to WHO’s PA recommendations12. Their study found a high global prevalence of insufficient PA with significant regional variations. The highest rates were observed in high-income Asia-Pacific countries (92.2%), whereas the lowest rates were observed in South Asia (75.2%). China is also affected by this trend. Despite the dramatic economic growth and improved living conditions, PA levels among Chinese children and adolescents are a concern13, with over 87% not meeting the recommended PA levels according to the WHO guidelines. Given the crucial role of PA in adolescents’ growth, development, and mental well-being14, there is an urgent need for effective interventions to increase PA levels among adolescents.

One method to promote PA is to enhance an individual’s exercise self-efficacy15. It refers to an individual’s confidence in their ability to succeed in challenging exercise contexts16, based on the concept of self-efficacy from social cognitive theory17. The self-efficacy concept is the confidence in one’s ability to perform a behaviour in a given situation, which is acknowledged as a crucial psychological construct in behaviour change18. It influences behaviour intention in the early stages of behaviour formation, motivation, and the maintenance of health behaviour changes, such as exercise habits and smoking cessation19,20,21. Adolescents with higher exercise self-efficacy are more likely to engage in exercise behaviour and demonstrate better adherence and sustainability in regular PA22,23,24. Therefore, enhancing exercise self-efficacy or preventing its decline is crucial for promoting and sustaining adolescents’ participation in PA. To effectively achieve this, researchers have emphasised the importance of reliable and valid instruments to identify and measure individual’s exercise self-efficacy25,26,27.

Several scales have been developed to evaluate individuals’ exercise self-efficacy. These include the Cardiac Exercise Self-Efficacy Scale28, the SCI Exercise Self-Efficacy Scale29, the Self-Efficacy for Exercise Scale30, and the Physical Activity Self-Efficacy Scale31. The first two scales are designed for specific populations: individuals with cardiovascular risks and those with spinal cord injuries, respectively. The last two scales are more general. However, the Self-Efficacy for Exercise Scale30 was specifically created for sedentary adults participating in outpatient programs. Furthermore, subsequent research has questioned the validity of the Physical Activity Self-Efficacy Scale due to concerns about its multidimensional structure32,33,34, suggesting it may not reliably assess exercise self-efficacy across different populations.

In contrast, Bandura’s25 Exercise Self-Efficacy Scale (ESES) was designed without targeting any specific sub-population. It assesses diverse exercise situations that might prevent individuals from maintaining their current exercise routines, making it a versatile and comprehensive tool. Comprising 18 items, the ESES evaluates a broad context of exercise-related challenges and has been extensively validated across various populations, showing consistent reliability and validity across different cultural contexts. Grounded in Bandura’s social cognitive theory35, a well-established psychological framework, the ESES is the most widely adopted and effective measure for assessing exercise self-efficacy, underscoring its robust theoretical foundation and broad applicability.

Some studies have also tested the structural effectiveness of ESES, with most proving the stability of the three-factor structure of ESES in different groups. Since then, several other versions of ESES have been created (Table 1) and translated into different languages.

Table 1 Different language versions of the ESES.
Full size table

Table 1 presents different factor structures across different populations and contexts. In unhealthy populations, such as patients undergoing cardiac rehabilitation or those with chronic diseases, both one- and three-factor models have been developed. For example, elderly Australian individuals in cardiac rehabilitation supported a unidimensional 18-item structure19, while Korean adults with chronic diseases exhibited a three-factor model with the same number of items43. In healthy adult populations, American undergraduate students demonstrated a two-factor structure with a reduced 15-item scale40, while Malaysian university students demonstrated a three-factor structure with only 18 items44. For the school-age population, a Malaysian study identified a three-factor structure comprising 13 items45.

To date, Yao et al.’s study38 is the only study that has validated the Chinese version of the ESES among 1,573 Chinese primary and secondary school students, with an average age of 12 years (SD = 1.68). Their findings supported a unidimensional model with 18 items using confirmatory factor analysis (CFA), demonstrating that the ESES is a valid instrument for assessing exercise self-efficacy in children and adolescents. However, Yao et al.’s38 study only employed CFA. Some researchers argue that CFA is less flexible when examining new factor structures47,48. This perceived inflexibility arises because CFA requires researchers to pre-specify the number of factors and their relationships with observed variables. Such a requirement can be limiting when the underlying factor structure has not been previously established or is not well understood47,48. Moreover, cultural and linguistic differences can significantly impact the psychometric properties of a scale49. Instruments validated in one cultural setting may not exhibit the same factorial structure in another. Notably, studies using both exploratory factor analysis (EFA) and CFA on the factor structure of the ESES have yielded different results across cultures. For example, Cornick40 identified a two-factor model with 15 items among U.S. university students. Hakim et al.42 found a three-factor model with 16 items among Indonesian university students. Similarly, Noroozi et al.46 reported a three-factor structure with 17 items among Iranian women with diabetes. Despite these studies, no research has examined or validated the ESES factor structure among Chinese secondary school students using both EFA and CFA. Therefore, without empirical validation, we could not assume that the existing factorial structure would apply to Chinese adolescents. Further, Yao et al.38 had only performed CFA in their study of primary and secondary school students, which does not conform to the standard procedure for exploratory factor structure50,51. Another important issue that requires investigation in relation to ESES is the measurement invariance across different populations. Achieving measurement invariance is crucial to make valid comparisons between groups such as those based on sex, ethnic backgrounds, and grades. This approach ensures that any significant differences observed truly reflect genuine distinctions, not psychometric inequalities, in the measuring instrument52. A construct can only be considered to have the same meaning across groups when it achieves invariance53. To the best of our knowledge, this aspect of ESES has not yet been examined, which reduces the reliability and validity of the conclusions drawn from future studies utilising the tool.

To address this gap, this study reports on secondary school students recruited from China. We used EFA and CFA approaches to explore and evaluate the factor structure within our study sample. Our objectives were to (1) explore the ESES factor structures in an independent sample of Chinese secondary school students, (2) evaluate the internal consistency reliability and convergent validity, and (3) measure invariance across different groups of students (e.g., sex, ethnic backgrounds, grades, and school locations) for the factor structure.

Methods

Translation

We translated ESES into Chinese using Brislin’s standard forward-backward translation procedure54. Two bilingual translators independently translated the scale into Chinese. We compared, contrasted, and merged the translations into a single version. Subsequently, two other bilingual translators, who had no contact with the first pair, back-translated the Chinese version into English. A lead translator compared these back-translations with the original scale to confirm the accuracy. Five native Chinese speakers reviewed the Chinese draft, addressed any ambiguities, and refined the final version. A pilot study with five native Chinese students confirmed the scale’s clarity and validity, thus finalising the translation process.

Participants

Exploratory results from EFA might influence confirmatory analyses and subsequent reliability and validity assessments, thereby increasing the risk of Type I errors55. Moreover, conducting both analyses on the same sample can artificially inflate model fit values56. Further, performing reliability and validity analyses on the independent sample helps avoid potential estimation biases that could arise from sample characteristic differences or data reuse57. To avoid these issues, we recruited 856 secondary school students from Chongqing, China, through random sampling between March and June 2024. In the first round, we recruited 510 students to perform the EFA. Comrey and Lee58 believe a sample size of 500 is considered very good for EFA. Following their guidelines, our sample size was appropriate for reliable factor analysis. In the second round, we recruited an additional 346 students to conduct the CFA. Kline59 suggests a sample size-to-item ratio of 10:1 to 20:1 for CFA. Given that the original ESES consists of 18 items, a sample within this range was necessary. These 346 participants were also tested for internal consistency, reliability, convergent validity, and measurement invariance. All participants met the following inclusion criteria: (1) currently enrolled as secondary school students, (2) willing to participate with parental consent, and (3) free from disabilities or illnesses. By conducting EFA and CFA on separate samples and adhering to recommended sample size standards, we aimed to enhance the validity and reliability of our study findings.

Measures

Demographic information form

We asked the participants to provide demographic information related to sex, ethnic backgrounds, grades, and school locations.

Exercise self-efficacy scale

The original ESES developed by Bandura consisted of 18 items25. Responses are provided on an 11-point scale ranging from 0 to 10, with higher scores reflecting greater confidence in one’s ability to exercise regularly. Kim60, Sabo44, and Yao38 employed a modified 18-item version of the ESES utilising a 5-point Likert scale ranging from 1 (not at all confident) to 5 (extremely confident). McDonald’s Omega of the revised scale was 0.910, and the test-retest reliability was 0.86060. Scales with fewer points are easier to understand and require less effort to complete for young participants61. Therefore, we used the revised 5-point version of the ESES.

Procedure

Our study involving human participants was performed in accordance with the Declaration of Helsinki. Ethical approval was obtained from the University Ethics Committee of the first author’s institution. Secondary school principals were informed of the study and secured permission to access their students. Written informed consent from parents and assent from students who agreed to participate were obtained. Students were informed that their participation was entirely voluntary and that they could withdraw without penalty. The students were told that the study’s objective was to assess their exercise self-efficacy, emphasising that the survey did not seek ‘right’ or ‘wrong’ answers. The ESES was completed in a quiet classroom setting supervised by a researcher, without teachers, to encourage honest responses. Anonymity was emphasised, and students were assured that their responses would remain confidential and inaccessible to their teachers, ensuring privacy and confidentiality.

Data analysis

Data analysis was conducted using IBM SPSS Statistics (Version 27) and IBM SPSS AMOS (Version 26). A bootstrap resampling procedure with 5,000 samples was implemented using AMOS. Bootstrapping is a robust technique that does not rely on the assumption of multivariate normality and can provide more accurate standard errors and confidence intervals under such conditions62.

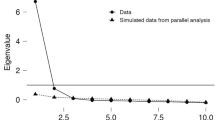
Our analysis included two steps to explore the factor structure. First, an EFA was conducted to identify the best-fitting factor model of the ESES among the students. The data’s appropriateness for the principal component analysis was assessed using the Kaiser-Meyer-Olkin (KMO) measure and Bartlett’s test of sphericity63. The extraction of factors was based on eigenvalues exceeding 1.0. According to Meyers et al.64, Promax rotation was applied to account for inter-factor correlations. Following the recommendation of Nunnally65, items exhibiting primary factor loadings below 0.50 or significant cross-loadings (secondary loadings above 0.40) were excluded.

Second, a CFA was performed. Model fit was assessed using various fit indices, including Chi-square with estimated degree of freedom, comparative fit index (CFI), Tucker-Lewis index (TLI), standardised root mean square residual (SRMR), and root mean square error of approximation (RMSEA). SRMR and RMSEA values at or below 0.08 and CFI and TLI > 0.90 indicated acceptable models50. Based on the factor structure from the above process, the internal consistency reliability of the ESES was estimated with McDonald’s Omega (cutoff value > 0.70)66. Composite reliability (CR) and average variance extracted (AVE) were calculated to determine the convergent validity of the ESES. Hair recommended that the CR meet or exceed the 0.70 cutoff point67. An AVE greater than 0.40 is accepted if the CR exceeds 0.6068.

After identifying the best-fitting model, measurement invariance tests were conducted across sex, ethnic backgrounds, grades, and school locations to assess the differences in intergroup comparisons. Here we implemented a model-testing approach that progressively introduced constraints. Initially, we established configural invariance by ensuring an identical factor structure across groups. Next, our study achieved metric invariance by requiring uniform factor loadings across the groups. Finally, our study attained scalar invariance by imposing uniform item intercepts across the groups. We did not enforce strict invariance (which involves equal error variances) as demonstrating metric and scalar invariance suffices for meaningful comparative group analyses50. Chen69 proposed the criteria for assessing measurement invariance, recommending a threshold of a 0.01 change in the CFI, coupled with RMSEA changes of up to 0.015. Moreover, Bollen70 demonstrated the degree of invariance is most frequently assessed by the likelihood ratio test (differences in χ2 between two nested models). If the p value between unconstrained and constrained models is less than 0.01, then the likelihood ratio test suggests that the null hypothesis of invariance should be rejected71.

Results

Demographic characteristics

A total of 856 secondary school students (431, male and 425, female) aged 11–16 years (M = 13.80, SD = 0.94) participated in this study. Most participants belonged to the Han Chinese ethnic group (80.8%), which was consistent with the demographic composition of most regions in China72. The distribution of participants across the grades was as follows: 36% from Secondary 1, 33.4% from Secondary 2, and 30.6% from Secondary 3. 43.9% of participants attended schools located in urban areas. The details of the participants are presented in Table 2.

Table 2 Descriptive statistics of demographic characteristics of participants (n = 856).
Full size table

Exploratory factor analysis

After completing the initial EFA, Bartlett’s test of sphericity (χ2 = 5527.214, p < 0.001) and the KMO value (0.935) suggested that correlations between indicators of the scale were significant enough to support principal component analysis73. This study identified two factors that accounted for 56.661% of the variance in the scale. To further refine our findings, we removed four items (items 9, 10, 14, and 15) from the pattern matrix using the criteria mentioned above (factor loadings less than 0.50). Another EFA was performed, resulting in Bartlett’s test of sphericity (χ2 = 4237.033, p < 0.001) and the KMO value (0.926), which yielded two factors accounting for 61.044% of the variance in the remaining 14 items (Table 3).

Table 3 Factor loadings from EFA of the ESES (n = 510).
Full size table

Confirmatory factor analysis

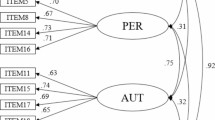
The initial ESES tests revealed poor overall fit indices (CFI = 0.888, TLI = 0.866, SRMR = 0.051, RMSEA [90% CI] = 0.112 [0.101 to 0.123]). To enhance the model’s fit, error covariances were added between items’ residuals, beginning with the pairs that had the highest modification index (MI) values. The MIs from the CFA indicated significant potential error covariances between Item 6 and Item 7 (MI = 103.476) and between Item 4 and Item 8 (MI = 42.258). Additional error covariances were sequentially added based on progressively lower MI values until an acceptable model fit was attained. These correlations were added within the same factor. This iterative process led to the final model, which demonstrated satisfactory goodness-of-fit indices: CFI = 0.950, TLI = 0.938, SRMR = 0.041, and RMSEA [90% CI] = 0.076 [0.065 to 0.088] (Fig. 1).

Fig. 1
figure 1

Confirmatory factor analysis model for the ESES.

Full size image

Internal consistency reliability and convergent validity

The overall McDonald’s Omega for the two-factor 14-item ESES was 0.928. Specifically, McDonald’s Omega for F1 and F2 were 0.921 and 0.843, respectively. To further verify the convergent validity of the ESES, CR and AVE were calculated, and the results showed that the CRs of the two factors were 0.917 (F1) and 0.845 (F2), and the AVEs of the two factors were 0.582 (F1) and 0.478 (F2).

Invariance test

Measurement invariance across sex

The configural invariance model across sex demonstrated good model fit: χ2 (346) = 326.382, df = 142, CFI = 0.937, RMSEA = 0.059, SRMR = 0.052, supporting for an equal number of factors between males and females. The metric invariance model was also strongly supported, showing minimal changes in model fit (ΔCFI = 0.004, ΔRMSEA = 0.003), with χ2 (346) = 329.073, df = 160, CFI = 0.941, RMSEA = 0.056, SRMR = 0.053. The χ2 difference test between baseline model and constrained model was not significant [∆χ2 (∆df) = 2.691 (12), p > 0.01], suggesting that factor loadings of both sex groups were invariant. Finally, the scalar invariance model showed good fit, χ2 (346) = 340.923, df = 163, CFI = 0.937, RMSEA = 0.056, SRMR = 0.058, with minimal changes in fit (ΔCFI = 0.004, ΔRMSEA = 0). Moreover, the χ2 difference test between the two constrained models was not significant [∆χ2 (∆df) = 14.541 (15), p > 0.01]. This suggested that, aside from the factor loadings, intercepts of each item were also invariant across sex (Table 4).

Table 4 Fit indices for the invariance testing of measurement model across sex (n = 346).
Full size table

Measurement invariance across ethnic backgrounds

The configural invariance model across ethnic backgrounds showed good model fit: χ2 (346) = 349.590, df = 148, CFI = 0.931, RMSEA = 0.063, SRMR = 0.045, supporting an equal number of factors between Han Chinese and the Minorites. The metric invariance model maintained good fit, χ2 (346) = 359.952, df = 160, CFI = 0.931, RMSEA = 0.060, SRMR = 0.044, with minimal changes in fit indices (ΔCFI = 0, ΔRMSEA = 0.003). The χ2 difference test between baseline model and constrained model was not significant [∆χ2 (∆df) = 10.362 (12), p > 0.01], suggesting that factor loadings of both ethnicity groups were invariant. The scalar invariance model also showed good fit, χ2 (346) = 362.823, df = 163, CFI = 0.931, RMSEA = 0.060, SRMR = 0.045, with no changes in fit (ΔCFI = 0, ΔRMSEA = 0). Moreover, the χ2 difference test between the two constrained models was not significant [∆χ2 (∆df) = 13.232 (15), p > 0.01]. This suggested that, aside from the factor loadings, intercepts of each item were also invariant across ethnicity (Table 5).

Table 5 Fit indices for the invariance testing of measurement model across ethnic backgrounds (n = 346).
Full size table

Measurement invariance across grades

The configural invariance model across grades demonstrated good model fit: χ2 (346) = 449.494, df = 222, CFI = 0.925, RMSEA = 0.055, SRMR = 0.057, supporting an equal number of factors across grades. The metric invariance model was well-supported, showing good fit, χ2 (346) = 460.114, df = 246, CFI = 0.929, RMSEA = 0.050, SRMR = 0.061, with minor changes in fit (ΔCFI = 0.004, ΔRMSEA = 0.005). The χ2 difference test between baseline model and constrained model was not significant [∆χ2 (∆df) = 3.540 (12), p > 0.01], suggesting that factor loadings of grades groups were invariant. The scalar invariance model also exhibited good fit, χ2 (346) = 488.349, df = 268, CFI = 0.927, RMSEA = 0.049, SRMR = 0.063, with minimal changes (ΔCFI = 0.001, ΔRMSEA = 0.001. Moreover, the χ2 difference test between the two constrained models was not significant [∆χ2 (∆df) = 6.863 (15), p > 0.01]. This suggested that, aside from the factor loadings, intercepts of each item were also invariant across grades (Table 6).

Table 6 Fit indices for the invariance testing of measurement model across grades (n = 346).
Full size table

Measurement invariance across school locations

The configural invariance model across school locations showed good model fit: χ2 (346) = 323.623, df = 148, CFI = 0.937, RMSEA = 0.059, SRMR = 0.052, supporting an equal number of factors across the urban and rural schools. The metric invariance model maintained good fit, χ2 (346) = 332.524, df = 160, CFI = 0.939, RMSEA = 0.056, SRMR = 0.053, with minor changes (ΔCFI = 0.002, ΔRMSEA = 0.003). The χ2 difference test between baseline model and constrained model was not significant [∆χ2 (∆df) = 8.901 (12), p > 0.01], suggesting that factor loadings of school locations were invariant. The scalar invariance model also showed a good fit, χ2 (346) = 333.454, df = 163, CFI = 0.939, RMSEA = 0.055, SRMR = 0.057, with minimal changes on RMSEA (ΔCFI = 0, ΔRMSEA = 0.001). Moreover, the χ2 difference test between the two constrained models was not significant [∆χ2 (∆df) = 9.831 (15), p > 0.01]. This suggested that, aside from the factor loadings, intercepts of each item were also invariant across school locations (Table 7).

Table 7 Fit indices for the invariance testing of measurement model across school locations (n = 346).
Full size table

Discussion

This study investigated the factor structure and measurement invariance of the ESES among secondary school students in China. First, we used EFA and CFA to explore the ESES factor structures among secondary school students. Second, we examined the structure’s internal consistency reliability and convergent validity. Third, we probed whether measurement invariance exists among secondary school students across different groups. Here, we briefly comment on our examination of the ESES factor structure, internal consistency reliability, convergent validity, and measurement invariance. Then, we focus on discussing the three main purposes.

The EFAs results revealed that four items had factor loadings below 0.50, leading to their removal. Consequently, a two-factor structure comprising 14 items was deemed appropriate for secondary school students, cumulatively explaining 61.044% of variance. CFA was conducted to validate the two-factor structure. The results confirmed that the two-factor structure (F1: individuals’ internal feelings and physical condition issues in exercise; F2: individuals’ situational issues in exercise) with 14 items fit well in the second sample of Chinese secondary school students (CFI = 0.950; TLI = 0.938; SRMR = 0.041; RMSEA [90% CI] = 0.076 [0.065 to 0.088]). Regarding internal consistency reliability, the scale and two factors achieved good values (total: 0.928, F1: 0.921, and F2: 0.843). The results showed that the CRs for the two factors were 0.917 (F1) and 0.845 (F2), while the AVEs were 0.582 (F1) and 0.478 (F2), indicating good convergent validity for each factor. Overall, the ESES demonstrated good internal consistency reliability and convergent validity. Model nesting results established scalar invariance, indicating that the scale is an effective and stable measurement tool that supports measurement invariance across sex, ethnic backgrounds, grades, and school locations among Chinese secondary school students.

The initial scale was unidimensional25. However, our findings align with previous Asian studies that have identified ESES as a multifaceted construct42,45,74. A widely used three-dimensional structure was introduced in a study by Shin et al.43, who used EFA based on patients with chronic diseases to divide the scale into three dimensions: Situational/Interpersonal (F1), which includes Items 11, 12, 13, 16, 17, and 18; Competing Demands (F2), which includes Items 4, 8, 10, 14, and 15; and Internal Feelings (F3), which includes Items 1, 2, 3, 5, 6, 7, and 9. This factor structure was validated in a study conducted in Iran by Noroozi et al.46, who recruited 348 women with diabetes and confirmed the same three-factor, 17-item structure, excluding Item 9. However, these studies focused on patients, and applying the three-dimensional structure with 18 items to other populations presents certain challenges. For example, in a study by Ting et al.41 on 562 undergraduate students, three items were retained for the Competing Demands (F2) factor after CFA analysis, but the standardised loading of Item 10 was only 0.317, which does not meet the retention criteria65. Similarly, in a study by Hakim et al. involving 379 university students42, Item 6 loaded onto the Situational/Interpersonal factor, Item 11 loaded onto the Competing Demands factor, and both Items 14 and 15 loaded onto the Situational/Interpersonal factor, complicating the interpretation of each factor.

In this study, factor analysis revealed a two-factor structure comprising 14 items, which differs from the factor structures and item compositions observed in scales developed for other populations19,36,39,40,41,42,43. There are two possible reasons for this finding. First, differences in psychological constructs between Eastern and Western cultures may have contributed to discrepancies in beliefs regarding exercise habits75. Second, the variation in the populations studied could play a significant role; as other studies focused on patients or university students19,36,39,40,41,42,43, we examined a younger and healthy demographic of secondary school students. These different age groups’ developmental and social contexts may influence their confidence and attitudes towards exercise. Adolescents’ developmental stage of physical growth and identity formation makes them more sensitive to social influences, which can significantly impact their confidence and attitudes toward exercise76. For example, their confidence in engaging in PA can increase with positive encouragement from teachers but may decline with discouragement from the same source77.

Specifically, owing to low loadings (less than 0.50), four items (Item 9: ‘When I feel physical discomfort when I exercise’, Item 10: ‘After a vacation’, Item 14: ‘If I do not reach my exercise goals’, and Item 15: ‘Without support from my family or friends’) were removed. Moreover, F1 comprised eight items (items 1 to 8), and F2 comprised six items (items 11 to 13 and 16 to 17). Based on the characteristics of each item, F1 demonstrated individuals’ internal feelings and physical condition issues in exercise. F2 demonstrated individuals’ situational issues in exercise.

Compared to previous studies, the factor loadings in our study on secondary school students indicated a better item representation within this population. Specifically, we found a mean factor loading of 0.746 (SD = 0.126, range = 0.502 to 0.902), which is higher than the factor loadings reported by Shin et al.43 (Mean = 0.678, SD = 0.084, range = 0.500 to 0.820) and Noroozi et al.46 (Mean = 0.683, SD = 0.076, range = 0.540 to 0.800), indicating that the items in our study are more effectively represented within the secondary school student population than among the patient samples used in the referenced studies.

In terms of internal consistency and reliability, our study achieved a strong value for the total scale, with a McDonald’s Omega of 0.928. This result is similar to that of a previous Chinese study on secondary school students, which reported a Cronbach’s alpha of .96838, suggesting that the two-factor model with 14 items of the ESES is a reliable measure. Moreover, most previous studies have not tested the convergent validity of the ESES19,39,40,41,42,43,45,46. Bagozzi (p. 375)78 described convergence in measurement, with convergent validity being a specific instance, as the expectation that ‘measures of the same construct should be highly intercorrelated among themselves and uniform in the pattern of intercorrelations’. Our study addresses this academic gap by demonstrating that both factors possess acceptable convergent validity (F1: CR = 0.917 and AVE = 0.582, F2: CR = 0.845 and AVE = 0.478), thereby reaffirming the validity of the two-factor structure with 14 items of the ESES.

Notably, MIs were introduced between items to improve the model fit (Item 4 and Item 8, Item 6 and Item 7). The correlation between Item 4 (After recovering from an injury that caused me to stop exercising) and Item 8 (After recovering from an illness that caused me to stop exercising) may be attributed to exercise self-efficacy related to resuming exercise after a health-related interruption. Both items involve regaining confidence to resume exercise after health setbacks. They require similar self-regulatory mechanisms. Specifically, overcoming physical or psychological barriers is crucial in both situations, leading to comparable challenges in restarting PA. Research indicates that confidence to resume exercise after disruptions like injury or illness often involves managing fears of recurrence and physical limitations79,80. The correlation between Item 6 (When I am feeling depressed) and Item 7 (When I am feeling anxious) may be attributed to the frequent co-occurrence of depression and anxiety, both of which negatively affect motivation and behaviours. These emotional states can create significant barriers to engaging in exercise81. Both items tap into emotional challenges that hinder exercise engagement. According to Kline59, potential error covariances can arise when items are worded similarly or involve related content that could influence responses independently of the latent construct. Therefore, introducing MIs between these items is theoretically justified and helps improve the model fit.

To assess two-factor structure of the ESES, we used several model fit indicators: CFI, TLI, RMSEA, and SRMR. Values for CFI and TLI exceeded 0.90, while the RMSEA and SRMR values were below 0.08, suggesting an adequate model fit50. The results of this study indicated that the two-factor structure demonstrated good fit indices, with CFI = 0.950, TLI = 0.938, SRMR = 0.041, and RMSEA (90% CI) = 0.076 (0.065–0.088). Additionally, this study employed ΔCFI and ΔRMSEA values, along with the likelihood ratio test, to compare the two-factor structure and assess measurement invariance. Significant differences were determined using the following criteria: changes in CFI and RMSEA up to 0.01 and .01569, respectively, and a p value < 0.01 in the likelihood ratio test71. We tested the measurement invariance of ESES using cohort CFA across different groups, including sex, ethnic backgrounds, grades, and school locations. The results supported the configural, metric, and scalar invariance of the ESES across these groups. Furthermore, comparisons between unconstrained and constrained models yielded p values > 0.01, indicating no significant differences between the models. Importantly, these findings highlight the value of the ESES, as the measurements provided by the instrument do not appear to be influenced by sex, ethnic backgrounds, grades, or school locations, thus enabling the comparison of scores obtained from different groups of secondary school students in China.

In the only prior study examining the psychometric properties of the ESES among secondary school students in China. Yao et al. used a CFA approach on a sample with a mean age of 12 years (SD = 1.68) to validate the Chinese version of the ESES among Chinese children and adolescents in Jiangxi, China38. They found 1-factor with 18 items on the ESES. In contrast, the present study employed the EFAs and CFA approaches to evaluate the factor structure and found two factors with 14 items. Consequently, differences in statistical methodologies explain the disparate patterns of results. Future research should test which factor model structure is more effective in assessing exercise self-efficacy among adolescents.

Strengths and limitations

This study had three strengths. First, the methodological advantage of this study lies in the combined use of EFAs and CFA to explore the suitability of ESES for Chinese secondary school students. This approach allowed for a comprehensive examination of the factor structure, ensuring that the identified model was theoretically sound and empirically validated within this population. Second, our study tested invariance across demographic groups, an aspect that has received limited attention in measurement studies until recently. This focus ensures that the ESES maintains its validity and reliability, irrespective of demographic variations in China, further supporting its robustness as a measurement tool for diverse populations. Finally, the two-factor approach with 14 ESES items could provide valuable insights for parents, teachers, and policymakers that will hopefully help them evaluate secondary school students’ exercise self-efficacy and potentially foster exercise adherence.

However, this study has several limitations. First, the sample primarily consisted of secondary school students from a single city in China. Future studies should include a nationally representative and diverse sample to enhance the applicability of the results. Additionally, this study focused solely on secondary school students, and it would be beneficial for future studies to consider including primary school and university students as well as adults, to provide a more comprehensive understanding of exercise self-efficacy across different age groups. Furthermore, the present study did not assess test-retest reliability or discriminant validity owing to time constraints, and the primary focus was on exploring the factor structure and measurement invariance of the scale within the sampled population. Addressing these psychometric properties in future studies will strengthen the robustness of our findings. Finally, since no studies in this field have implemented longitudinal designs, incorporating such designs into future research could provide valuable insights into the stability and development of exercise self-efficacy over time.

Conclusion

The primary aim of this study was to explore the factor structure of the ESES in a sample of Chinese secondary school students; evaluate its internal consistency, reliability, and convergent validity; and examine measurement invariance across different groups in Chongqing, China. A total of 856 students were recruited via random sampling. Using EFAs and CFA, this study examined the factor structure, internal consistency, reliability, convergent validity, and measurement invariance of a two-factor model with 14 items. The results support the validity and reliability of the 14-item, two-factor version of the ESES among secondary school students. Specifically, the findings demonstrate that this version of the ESES is a valid and reliable tool for assessing exercise self-efficacy in this population. Good internal consistency and support for measurement invariance across groups highlighted the scale’s applicability and robustness for use among Chinese secondary school students.