Introduction

Mathematics is one of the most dynamic and efficient tools that people use in daily life, especially researchers who use mathematical notion to derive and implement the equations and mechanism, respectively, for easy and effective estimation. Nowadays, most scholars would like to identify why they have to study numerous mathematics courses, although the core degree is not mathematics. To To answer this question, the scholar has to understand the importance of mathematics in our daily lives; therefore, when instructors try to convince their scholars that mathematics is valuable in many professions like engineering, technology, sciences, and many more some of the audience may have less interest in these occupations as some students love to become designers for computer games and some of They want to become sportsmen. Actually, they wrongly believe that the said professions did not involve mathematics.

Fuzzy logic (an important branch of mathematics) has exclusively used in the field of engineering for example aerospace, electrical, mechanical, civil, agricultural, bio-medical, chemical, environmental, computer, geological, industrial, and mechatronics as well as in the field of natural scientists like earth science, physics, chemistry, biology, medical research, computer software developers and social sciences like economics, management, political science, psychology, business, and public policy analysts for development of new algorithms in research areas. Fuzzy logic can also be efficiently used in advanced computing techniques for development of an intelligent system to identify, optimize, recognize the pattern and make an appropriate decision to solve the problem.

The theory of Fuzzy logic was conceived by Lotfi A. Zadeh2. Kaufmann 19733 gave the idea of a fuzzy graph first time through Zadeh’s4 fuzzy relations. Rosenfeld5,6 describe fuzzy graphs in 1975 later the renowned Zadeh’s article of4 of fuzzy Sets. Crisp graphs and fuzzy graphs have several similar properties therefore we can say that fuzzy graphs are the generalized form of the crisp graph having a \(one-to-one\) correspondence from \(f: E U V \rightarrow N.\) Bhattacharya7,8 introduced the notion of fuzzy bridges fuzzy nodes and cut. Various topological indicators are applied nowadays in chemistry for different purposes like, Randić communication index, hosoya index, Zagreb community index, etc. few are discussed in9,10. In chemistry and mathematics, the most popular and first distance-based topological index named the Wiener index, which relies on the distances of the atoms’ of the molecular structure, is discussed in J. Dinar, et al.11,12.

A revolutionary idea for magic labelling of cycle and star graphs in fuzzy instances was devised by Ameenal13,14. In a fuzzy instance, Vimala15,16 presented the energy of labelling a graph. In17,18, Nagoor forms several characteristics for labeling of the path and star graph in fuzzy case. Some basic concepts and definitions have been discussed in19,20,21. Fuzzy Zagreb indices of pizza graphs and linear and multicyclic hydrocarbons are discussed in22,23.

S.R. Islam and M. Pal are renowned researchers in the field of Fuzzy Graphs, with an impressive portfolio of publications26,27. Some of their notable research articles include: Hyper-Wiener index for fuzzy graph and its application in share market31,32, Second Zagreb index for fuzzy graphs and its application in mathematical chemistry33,34, Hyper-connectivity index for fuzzy graph with application35, Multiplicative Version of First Zagreb Index in Fuzzy Graph and its Application in Crime Analysis36,37, and An investigation of edge F-index on fuzzy graphs and application in molecular chemistry38,39. Their research contributions have significantly advanced the field of Fuzzy Graphs, shedding new insights into its applications and theoretical foundations.

S. Kosari, H. Rashmanlou, etal. are prolific researchers in the field of Fuzzy Graphs, with an extensive list of publications. Some of their notable research articles include: Investigation of the main energies of picture fuzzy graph and its applications40, Certain concepts of vague graphs with applications to medical diagnosis41, Notion of Complex Pythagorean Fuzzy Graph with Properties and Application42, Some Types of Domination in Vague Graphs with Application in Medicine43, New concepts of intuitionistic fuzzy trees with applications44, Properties of interval-valued quadripartitioned neutrosophic graphs with real-life application45. Their research has significantly contributed to the advancement of Fuzzy Graph theory and its applications.

Fuzzy Zagreb Index of the type first, second, harmonic, and Randić fuzzy of ladder graph and grid graph are discussed in this paper in detail.

Motivation

One cannot deny the importance of topological indices in recent days. Topological indices have several applications in various areas of applied sciences, engineering, and technology. In chemistry, biochemistry, chemical engineering, and many other fields degree-based, distance-based, and other indices are useful to study the properties and structure of various compounds. Applications of topological indices in these fields motivate researchers to explore more advanced work in these fields. In29,30, to investigate cybercrimes an innovative design of fuzzy molecular descriptors has been presented. The design, we developed in this paper can be very useful for the pharmaceutical industry to collect chemical data on the drug.

Fuzzy topological indices are crucial when dealing with systems and networks characterized by uncertainty, vagueness, or imprecision where traditional indices may fall short. Traditional topological indices typically rely on binary relationships between vertices and edges under crisp structure. However, real-world networks, such as social, biological, or communication networks, often involve uncertain or fuzzy relationships. In these cases, fuzzy topological indices provide several clear advantages.

Fuzzy indices effectively model uncertain or ambiguous relationships between entities. For instance, in social networks, the strength of relationships can vary and may not always be binary. Fuzzy indices capture nuances, providing a more realistic representation of such networks. In scenarios where decisions depend on uncertain data, such as in supply chain management or traffic flow analysis, fuzzy indices facilitate better prioritization and decision-making by incorporating the degree of connection or relevance.

Fuzzy indices are particularly useful in fields like biology, where protein-protein interactions are not always definitive, or in environmental science, where relationships between variables are influenced by uncertain factors like climate variability. While traditional indices may yield general insights, they fail to capture subtleties of gradation in connectivity or interaction strength. Fuzzy indices add this layer of complexity, allowing for more granular analysis. For example, comparing the fuzzy Zagreb index with the classical Zagreb index can reveal how uncertainty in edge weights impacts network properties.

Scenario based on crisp and fuzzy analysis of roads networks

Consider a transportation network where edge represent roads, and weight represent traffics intensity. In a crisp graph, a road is either congested or not congested, which oversimplifies the situation. Using fuzzy indices, we can assign degree of congestion to each road, leading to better route optimization and resource allocation. Fuzzy topological indices justify their inclusion by addressing the limitations of traditional indices in uncertain environments. They enrich the analytical toolkit of network theory, offering insights that both nuanced and practically relevant.

figure a

First Zagreb Index \(M_{1}(G)\):

$$\begin{aligned} M_1(G)= & \sum _{v \in V} d(v)^2\\ M_1(G)= & d(A)^2 + d(B)^2 + d(C)^2 + d(D)^2 = 4 + 4 + 4 + 4 = 16 \end{aligned}$$

Fuzzy First Zagreb Index \(FM_{1}(G)\):

$$\begin{aligned} FM_{1}(G)= & \sum _{v \in V} \mu (v) \cdot d(v)^2\\ FM_{1}(G)= & \mu (A) \cdot d(A)^2 + \mu (B) \cdot d(B)^2 + \mu (C) \cdot d(C)^2 + \mu (D) \cdot d(D)^2\\ FM_{1}(G)= & 0.9 \cdot 4 + 0.8 \cdot 4 + 0.7 \cdot 4 + 0.5 \cdot 4 = 2.4 + 3.2 + 2.8 + 2 = 10.4 \end{aligned}$$

The utilization of Zagreb and Fuzzy Zagreb indices in the analysis of road works shed lights on the adaptability of these tools in addressing both idealized and real-world conditions. The crisp indices serve as a theoretical baseline, while fuzzy indices bridge the gap between theoretical models and practical applications.

Basic elementary definitions

In this paper, we will use the following notations for the indices. The notations are given in Table 1.

Table 1 Crisp and fuzzy indices with their notations.
Full size table

Now, we describe the basic elements of graph theory.

Fuzzy Graph24

A simple graph G, is called a fuzzy graph with a finite vertex set V(G) and finite edge set E(G). Two mappings \(\sigma\) and \(\mu\), where \(\sigma :V(G) \rightarrow [0, 1]\) and \(\mu :V(G)\times V(G) \rightarrow [0, 1]\) such that \(\mu (v_{1}v_{2})\le \sigma (v_{1}) \wedge \sigma (v_{2})\) for every pair of vertices \(v_{1}, v_{2} \in V(G).\)

Fuzzy Graph’s Degree24,25

The degree of vertex q is denoted by d(q), in a fuzzy graph is defined as the sum of the weight of the edges connected to a vertex q

$$\begin{aligned} d(q)=\sum _{pq\in E} \mu (pq), \quad where \quad p \ne q \quad and \quad \mu (pq) \end{aligned}$$

is the weight of the edge pq.

Fuzzy Graph’s Order24

The order of a fuzzy graph denoted by O(G), is elaborated as;

$$\begin{aligned} O(G)=\sum _{p\in V} \sigma (p), \end{aligned}$$

where, \(\sigma (p)\) is the weight of the vertex p.

Fuzzy Graph’s Size 24

The size of a fuzzy graph is elaborated as,

$$\begin{aligned} S(G)=\sum \mu (pq), \end{aligned}$$

for all vertices \(p,q \in V(G)\) and \(p \ne q\) , where S(G) is called size for a fuzzy graph G. Kalathian et.al.9 introduce the fuzzy Zagreb indices of following types

FFZI(Fuzzy First Zagreb Index)

FFZI is denoted by \(FM_{1}(G)\) and is defined as

$$\begin{aligned} FM_{1}(G)= \sum _{p_{j}\in V(G)} \sigma (p_{j}) [dp_{j}]^{2} \end{aligned}$$

FSZI(Fuzzy Second Zagreb index)

FSZI is denoted by \(FSM ^{*}(G)\) and is defined as

$$\begin{aligned} FSM^{*}(G)= \frac{1}{2} \sum _{p_{j}q_{k} \in E(G)} [\sigma (p_{j})(dp_{j})\sigma (q_{k}) (dq_{k})] \end{aligned}$$

FRI(Fuzzy Randić index)

FRI is denoted by FR(G) and is described as

$$\begin{aligned} FR(G)= \frac{1}{2} \sum _{p_{j}q_{k} \in E(G)} [\sigma (p_{j})(dp_{j})\sigma (q_{k}) (dq_{k})]^{-1/2} \end{aligned}$$

FHI(Fuzzy Harmonic Index)

FHI is denoted by FH(G) and is defined as

$$\begin{aligned} FH(G)= \frac{1}{2} \sum _{p_{j}q_{k} \in E(G)} [\frac{1}{\sigma (p_{j})(dp_{j})+\sigma (q_{k}) (dq_{k})} ] \end{aligned}$$

Topological indices for crisp graph

In this section, we will discuss some classes of topological indices for crisp graphs.

FZI(First Zagreb Index)

FZI is denoted by \(M_{1}(G)\) and is defined as

$$\begin{aligned} M_{1}(G)= \sum _{j \in V(G)} d^{2}(j). \end{aligned}$$

SZI(Second Zagreb index)

SZI is denoted by \(M^{*}(G)\) and is defined as

$$\begin{aligned} M^{*}(G)= \sum _{jk \in E(G)}[ d(j) \times d(k)]. \end{aligned}$$

RI(Randić index)

RI is denoted by R(G) and is defined as

$$\begin{aligned} R(G)= \sum _{jk \in E(G)} [ d(j) \times d(k)]^{-1/2}. \end{aligned}$$

HI(Harmonic Index)

HI is denoted by H(G) and is defined as

$$\begin{aligned} H(G)= \sum _{jk \in E(G)} [\frac{2}{d(j)+ d(k)} ], \end{aligned}$$

where d(j) and d(k) are degrees of the vertices j and k, respectively.

Ladder graph (LG)

The selection of ladder and grid graph is the prime focus of study is grounded in their inherent structural properties, practical relevance in network theory, and their suitability for machine learning applications. Ladder graphs are widely used to model linear, constrained pathway in networks such as transportation system, electrical circuits, railway tracks, and communication channels. their symmetric and well-defined structure allows for precise mathematical modeling, making them a natural choice for testing new topological indices.

Grid graphs are commonly employed to model urban planning layout, traffic networks. The multi-pathway nature of grid graphs provides a robust frame work to study intricate relationships within networks, such as dependency and resource allocation. Ladder and grid graphs provide distinct and interpretable structure that can be encoded as features for machine learning. Their inherent regularity simplifies the development of graph-based algorithms, serving as benchmarks for testing machine learning techniques. These graphs offer scalability in complexity, from simple ladder graphs to more intricate grid graphs, enabling the progressive training of machine learning models.

Ladder Graph(LG) can be obtained through the Cartesian product of path graph \(P_{m}\) and path graph \(P_{2}.\) The ladder graph is a Cartesian product of two graphs, denoted by \(H_{1}\times H_{2}\), has a vertex set \(V(H_{1}\times H_{2})= V(H_{1})\times V(H_{2})\) and every vertex of \(H_{1}\times H_{2}\) is an ordered pair (x, y),  where \(x \in V(H_{1})\) and \(y \in V(H_{2}).\) Two distinct vertices \((x_{1},y_{1})\) and \((x_{2},y_{2})\) are adjacent in \(H_{1}\times H_{2}\) if either \(x_{1}=x_{2}\) and \(y_{1}y_{2} \in E(H_{2})\) or \(y_{1}=y_{2}\) and \(x_{1}x_{2} \in E(H_{1}).\) Ali and Hussain28 discussed magic and anti-magic labeling of subdivided Grid graphs and Ladder graphs.

Figure 1
figure 1

Ladder graph \(P_{5}\times P_{2}\).

Full size image

Molecular descriptor of ladder graph (LG)

Theorem 1

Let \(G=P_{m} \times P_{2}\) be a ladder graph, then the FZI of ladder graph \(G=P_{m} \times P_{2}\) is \(M_{1}(G)= (18m - 20),\) for \(m \ge 2.\)

Proof

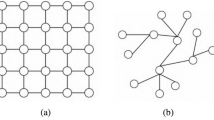
The representation of ladder graph \(G=P_{5} \times P_{2}\) is in Fig. 1. Ladder graph \(G=P_{m} \times P_{2}\) having total 2m vertices out of which 4 vertices have degree 2 while the remaining \(2m-4\) have degree 3. The total number of edges of Ladder graph \(G=P_{m} \times P_{2}\) are \(3m - 2\).

$$\begin{aligned} M_{1}(G)= & \sum _{v \in V(G)} d^{2}(v) \\= & 4[2^{2}]+ (2m-4)[3^{2}]\\= & 16 + 18m-36\\= & 18 m - 20, \end{aligned}$$

\(\square\)

Theorem 2

Let \(G=P_{m} \times P_{2}\) be a ladder graph,

(a):

then the SZI of the ladder graph is \(M^{*}(G)= 27m - 40,\) for \(m \ge 2.\)

(b):

then the RI of ladder graph is \(R(G)= m - 0.027,\) for \(m \ge 2.\)

(c):

then the HI of ladder graph is \(H(G)= (m - 0.06),\) for \(m \ge 2.\)

Proof of part (a)

The ladder graph \(G=P_{m} \times P_{2}\) has \(3m-2\) edges consisting of three types of partitions for the edges are as follows:

The first partition of edges (2, 2) has 2 edges, degree of both end vertices is 2. the second partition of edges (2, 3) has 4 edges, one vertex has degree 2 and other vertex has degree 3, and third partition of edges (3, 3) has \(3m-8\) edges, degree of both end vertices is 3.

$$\begin{aligned} M^{*}(G)= & \sum _{jk \in E(G)}[ d(j) \times d(k)] \\= & 2[2\times 2]+ 4[2 \times 3] + (3m-8)[3 \times 3]\\= & 8+24+27m-72\\= & 27 m - 40, \end{aligned}$$

\(\square\)

Proof of part (b)

By using the same edge partition of Part (a), we have

$$\begin{aligned} R(G)= & \sum _{jk \in E(G)} [ d(j) \times d(k)]^{-1/2}\\= & [2] [ 2 \times 2]^{-1/2} + [4] [ 2 \times 3]^{-1/2}+ [3m-8] [ 3 \times 3]^{-1/2}\\= & 1 + 1.633 + m -2.66\\= & m -0.027, \end{aligned}$$

\(\square\)

Proof of part (c)

By using the same edge partition of Part (a), we have

$$\begin{aligned} H(G)= & \sum _{jk \in E(G)} [\frac{2}{d(j)+ d(k)}]\\= & \frac{2\times 2}{2+2}+ \frac{4\times 2}{2+3} + \frac{2\times (3m-8)}{3+3}\\= & 1 + \frac{8}{5} + \frac{3m-8}{3} \\= & 1 + 1.6 + m -2.66\\= & m -0.06, \end{aligned}$$

After raising the values of m from 2 to 11 in the ladder graph \(G=P_{m} \times P_{2}\), we get the values of different indices shown in Table 2. \(\square\)

Table 2 Comparison of indices for \(H=P_{m} \times P_{2}\) Ladder graph.
Full size table

Jupyter notebook

Jupyter Notebook is a notebook authoring application, under the Project Jupyter umbrella. Built on the power of the computational notebook format, Jupyter Notebook offers fast, interactive new ways to prototype and explain your code, explore and visualize your data, and share your ideas with others. Notebooks extend the console-based approach to interactive computing in a qualitatively new direction, providing a web-based application suitable for capturing the whole computation process: developing, documenting, and executing code, as well as communicating the results. The Jupyter notebook combines two components:

A Web application: A browser-based editing program for interactive authoring of computational notebooks which provides a fast interactive environment for prototyping and explaining code, exploring and visualizing data, and sharing ideas with others

Computational Notebook documents: A shareable document that combines computer code, plain language descriptions, data, rich visualizations like 3D models, charts, mathematics, graphs and figures, and interactive controls.

Main features of the web application

In-browser editing for code, with automatic syntax highlighting, indentation, and tab completion/introspection.

The ability to execute code from the browser, with the results of computations attached to the code which generated them.

Displaying the result of computation using rich media representations, such as HTML, LaTeX, PNG, SVG, etc. For example, publication-quality figures rendered by the [matplotlib] library, can be included inline.

In-browser editing for rich text using the [Markdown] markup language, which can provide commentary for the code, is not limited to plain text.

The ability to easily include mathematical notation within markdown cells using LaTeX, and rendered natively by MathJax46.

Linear function derivation for ladder graphs via machine learning algorithms

Machine learning (ML) plays a vital role in different areas, particularly in data-related daily life applications. ML is a branch of artificial intelligence analysis that focuses on building systems capable of learning from data to make predictions or decisions without being explicitly programmed. Among the various techniques in machine learning, regression analysis is widely used to model and analyze relationships with variables.

Linear regression is a basic technique in ML. In linear regression, two variables are involved, one is independent and the other one is dependent. Linear regression builds a relationship between these variables to form a linear equation to observe the data. The equation of linear regression model is \(y = \alpha _{1} x + \alpha _{0}\), where, y is the dependent variable, x is the independent variable, and \(\alpha _{n}\),\(\alpha _{n-1}\), ..., \(\alpha _{1}\) ,and \(\alpha _{0}\) are the corresponding coefficients.

Multi-linear regression with multiple independent variables along with a single dependent variable. The multi-linear regression equation is \(y = \alpha _{n} x_{n} + \alpha _{n-1} x_{n-1}+ ... \alpha _{1} x + \alpha _{0}.\) Where, \(\alpha _{n}, \alpha _{n-1}, ..., \alpha _{1}, \alpha _{0}\) are the coefficients of \(x_{n}, x_{n-1}, ... , x_{1},\) respectively.

For this regression analysis, we will use Jupyter Notebook which is a very established server-client application that permits the code or editing in code. We will import our data after writing some code in a Jupyter Notebook. Afterward, we run our regression analysis code. The best-fit line equation is then obtained. We will also employ the coefficient of determination (R-squared), a statistical measure that will assist us in determining how near our data is to the best-fit line.

The regression analysis of the ladder graph between the vertices and FZI, SZI, RI, and HI. The equation of linear regression and their graph is presented in Table 3 below:

Table 3 Table showing the relationship between Vertex, FZI, SZI, RI, and HI.
Full size table

First Zagreb Index

The relationship between vertices and the FZI is represented by the equation and the graphical comparison shown in Fig. 2a and b.

$$\begin{aligned} FZI = 9.0167 \times Vertex -19.9778 \end{aligned}$$
Figure 2
figure 2

First Zagreb index vs vertices.

Full size image

Second Zagreb Index

The relationship between vertices and the SZI is represented by the equation and the graphical comparison shown in Fig. 3a and b.

$$\begin{aligned} SZI = 13.5000 \times Vertex -40.0000 \end{aligned}$$
Figure 3
figure 3

Second Zagreb index vs vertices.

Full size image

Randić Index

The relationship between vertices and RI is represented by the equation and the graphical comparison shown in Fig. 4a and b.

$$\begin{aligned} RI = 0.5000 \times Vertex -0.0270 \end{aligned}$$
Figure 4
figure 4

Randić index vs vertices.

Full size image

Harmonic Index

The relationship between vertices and HI is represented by the equation and the graphical comparison shown in Fig. 5a and b.

$$\begin{aligned} HI = 0.5000 \times Vertex -0.0600 \end{aligned}$$
Figure 5
figure 5

Randić index vs vertices.

Full size image

Zagreb indices of fuzzy ladder graph (FLG)

This section will discuss the fuzzy topological indices of the FLG \(P_{m}\times P_{2}.\) The FLG \(P_{4}\times P_{2}\) is shown in Fig. 6.

Figure 6
figure 6

Fuzzy ladder graph \(P_{4}\times P_{2}\).

Full size image

Theorem 3

Let \(G=P_{m} \times P_{2}\) be a FLG, then the FFZI of the LG \(G=P_{m} \times P_{2}\) is \(FM_{1}(G)= (0.321 m -0.424),\) for \(m \ge 2.\)

Proof

All vertices \(U_{i}'s\) have weight 0.4 having total count m,  in which \(m-2\) having weight 0.7 while the remaining 2 have 0.4. All vertices \(V_{i}'s\) have weight 0.5 having total count m,  in which \(m-2\) having weight 0.5 while the remaining 2 have 0.3.

$$\begin{aligned} FM_{1}(G)= & \sum _{k=1}^{q} \sigma (u_{k}) [du_{k}]^{2}, \\= & (0.4)[2(0.4)^{2}+(m-2)(0.7)^{2}]+ (0.5)[2(0.3)^{2}+(m-2)(0.5)^{2}]\\= & (0.4)[0.32 +(m-2)(0.49)]+ (0.5)[0.18 +(m-2)(0.25)]\\= & (0.4)[0.32 +0.49m-0.98]+ (0.5)[0.18 +0.25m-0.50]\\= & 0.196m + 0.125 m -0.264 -0.16 \\= & 0.321 m - 0.424, \end{aligned}$$

Theorem 4

Let \(G=P_{m} \times P_{2}\) be a FLG,

(a):

then the FSZI of the LG \(G=P_{m} \times P_{2}\) is \(FSM^{*}(G)= (0.1055m-0.1751),\) for \(m \ge 2.\)

(b):

then the FRI of LG \(G=P_{m} \times P_{2}\) is \(FR(G)= (5.6755 m + 1.2069),\) for \(m \ge 2.\)

(c):

then the FHI of a LG \(G=P_{m} \times P_{2}\) is \(FH(G)= (2.83625 m +0.4332),\) for \(m \ge 2.\)

\(\square\)

Proof of part (a)

Ladder graph \(G=P_{m} \times P_{2}\) in Figs. 1 and 6, has three edges consisting of three types of partitions for the edges which are as follows:

The first type of partition \(E_{1}=u_{i},u_{i+1}\) has \(m-1\) edges, from which 2 edges are of type- A, one vertex has degree 0.4 and other vertex has degree 0.7 i.e. (0.4, 0.7) and \(m-3\) edges are of type- B, degree of both end vertices is 0.7 i.e. (0.7, 0.7).

The second type of partition \(E_{2}=u_{i},v_{i}\) has m edges, from which 2 edges are of type- A, one vertex has degree 0.4 and other vertex has degree 0.3 i.e. (0.4, 0.3) and \(m-2\) edges are of type- B, one vertex has degree 0.7 and other vertex has degree 0.5 i.e. (0.7, 0.5).

The third type of partition \(E_{3}=v_{i},v_{i+1}\) has \(m-1\) edges, from which 2 edges are of type- A, one vertex has degree 0.3 and other vertex has degree 0.5 i.e. (0.3, 0.5) and \(m-3\) edges are of type- B, degree of both end vertices is 0.5 i.e. (0.5, 0.5).

Moreover, weight of \(u_{i}=0.4\) and weight of \(v_{i}=0.5.\)

$$\begin{aligned} FSM^{*}(G)= & (1/2)\sum _ {u_{k}v_{l} \in E(G)} [\sigma (u_{k})(du_{k})\sigma (v_{l}) (dv_{l}) ], \\= & (1/2)[(m-2)(0.4)(0.7)(0.5)(0.5)+ 2(0.4)(0.4)(0.5)(0.3)] \\&\quad +&(1/2)[(m-3)(0.4)(0.7)(0.5)(0.7)+ 2(0.4)(0.4)(0.4)(0.7)] \\&\quad +&(1/2)[(m-3)(0.5)(0.5)(0.5)(0.5)+ 2(0.5)(0.3)(0.5)(0.5)] \\= & (1/2)[0.048-0.14+0.07m+0.0896+0.0784m-0.2352+0.075\\&\quad +&0.0625m-0.1875]\\= & (1/2)[0.2109m -0.3501]\\= & 0.1055 m -0.1751 \end{aligned}$$

\(\square\)

Proof of part (b)

By using the same edge partition of Part (a), we have

$$\begin{aligned} FR(G)&= (1/2)\sum _{u_{k}u_{l} \in E(G)} [\sigma (u_{k})(du_{k})\sigma (v_{l}) (dv_{l}) ]^{-1/2}, \\&= (1/2)[(m-2)[(0.4)(0.7)(0.5)(0.5)]^{-1/2}+ 2 [(0.4)(0.4)(0.5)(0.3)]^{-1/2}\\&\quad +(1/2)[(m-3)[(0.4)(0.7)(0.4)(0.7)]^{-1/2}+ 2 [(0.4)(0.4)(0.4)(0.7)]^{-1/2}\\&\quad +(1/2)[(m-3)[(0.5)(0.5)(0.5)(0.5)]^{-1/2}+ 2 [(0.5)(0.3)(0.5)(0.5)]^{-1/2}\\&= (1/2)[11.351 m + 2.4138]\\&= 5.6755 m +1.2069 \end{aligned}$$

\(\square\)

Proof of part (c)

By using the same edge partition of Part (a), we have

$$\begin{aligned} FH(G)= & (1/2)\sum _{u_{k}u_{l} \in E(G)} [\frac{1}{\sigma (u_{k})(du_{k})+\sigma (v_{l}) (dv_{l})} ], \\= & (1/2)[\frac{m-2}{(0.4)(0.7)+(0.5)(0.5)}+ \frac{2}{(0.4)(0.4)+(0.5)(0.3)}\\ & \quad + \frac{m-3}{(0.4)(0.7)+(0.4)(0.7)}+ \frac{2}{(0.4)(0.4)+(0.4)(0.7)} \\ & \quad + \frac{(m-3)}{(0.5)(0.5)+(0.5)(0.5)}+ \frac{2}{(0.5)(0.3)+(0.5)(0.5)} ]\\= & (1/2)[5.6725m + 0.8664]\\= & 2.83625 m + 0.4332 \end{aligned}$$

After raising the values of m from 2 to 11 in the ladder graph \(G=P_{m} \times P_{2}\), we get the values of different indices shown in Table 4. \(\square\)

Table 4 Comparison of indices for \(H=P_{m} \times P_{2}\) Ladder graph.
Full size table

Linear regression model for fuzzy ladder graph

The regression analysis of the ladder graph between the vertices and FZI, SZI, RI, and HI. The equation of linear regression and their graph is presented in Table 5 below:

Table 5 Table showing the relationship between Vertex, FZI, SZI, RI, and HI.
Full size table

First Fuzzy Zagreb Index

The relationship between vertices and the first fuzzy Zagreb index(FFZI) is represented by the equation and the graphical comparison shown in Fig. 7a and b.

$$\begin{aligned} FFZI = 0.1605 \times Vertex - 0.1030 \end{aligned}$$
Figure 7
figure 7

FFZI vs vertices.

Full size image

Second Fuzzy Zagreb Index

The relationship between vertices and the second fuzzy Zagreb index(SFZI) is represented by the equation and the graphical comparison shown in Fig. 8a and b.

$$\begin{aligned} SFZI = 0.0528 \times Vertex - 0.0696 \end{aligned}$$
Figure 8
figure 8

SFZI vs vertices.

Full size image

Fuzzy Randić Index

The relationship between vertices and fuzzy Randić index(FRI) is represented by the equation and the graphical comparison shown in Fig. 9a and b.

$$\begin{aligned} FRI = 2.8378 \times Vertex + 6.8824 \end{aligned}$$
Figure 9
figure 9

FRI vs vertices.

Full size image

Fuzzy Harmonic Index

The relationship between vertices and the Fuzzy Harmonic Index (FHI) is represented by the equation and the graphical comparison shown in Fig. 10a and b.

$$\begin{aligned} FHI = 0.1605 \times Vertex - 0.1030 \end{aligned}$$
Figure 10
figure 10

Fuzzy harmonic index vs vertices.

Full size image

Statistical analysis for linear model of a ladder graph and fuzzy ladder graph

In this section, we observe the statistical analysis of the topological index(TI) of the ladder graph in crisp case. As we know with the increase of order of a graph, the topological index(TI) value also increases. This shows the strong correlation between the vertices and the TI’s. To determine the statistical measures. Firstly, we obtain the coefficient of determination (\(R^{2}\)), which lies between 0 and 1. 0 means this model does not explain the variance in the dependent variable (Topological Indices) with independent variables (Vertices) and 1 means this model is ideal. The standard error (SE) is the mean deviation between the expected and actual values. The lower error indicates a strong correlation as shown in Tables 6 and 7. The sum of squares (SS) quantifies the total variation in the data and is divided into component based on the sources of variability. The Mean Square (MS) is an average variation obtained by dividing the sum of squares (SS) by its respective degrees of freedom. Significance Factor (SF) represents the ratio of the variance between groups to the variance within groups, which is essentially the F-statistic.

Table 6 Statistical analysis of ladder graph.
Full size table
Table 7 Statistical analysis of fuzzy ladder graph.
Full size table

Exploring the relationship between ladder and fuzzy ladder graphs using machine learning model

The induction of machine learning techniques into the analysis of topological indices is intended to enhance the accuracy, efficiency, and predictive capabilities of the computation. The algorithm used particularly linear regression were chosen for their simplicity, interpretability, and efficiency in modeling relationships between topological indices and other graph properties. Linear regression effectively captures linear trends that are commonly observed in topological index computations. Linear regression algorithms are computationally efficient and can handle the dataset sizes typical in graph theoretical studies, making them an appropriate choice for initial modeling. We also apply some performance metrics such as significance factor (SF), standard error (SE), sum of squares (SS), and mean square (MS). This will not only enhance the credibility of the methodology but also establish a robust foundation for future research in this ___domain.

In this section, we will discuss how Fuzzy ladder graphs and ladder graphs behave alike. These graphs have a linear relationship with each other. These indices are related to each other by a linear equation along with 3D plot. There are four equations that are connected in such a way First Fuzzy Zagreb index is related to first Zagreb index, second fuzzy Zagreb index is related to second Zagreb index, Fuzzy Randić Index is related to Fuzzy Randić Index, and harmonic index is related to fuzzy harmonic index, respectively. The equations of different indices shown below and their graphical comparison is shown in Figs. 11 and 12 are given below:

$$\begin{aligned} FFZI= & 0.0178(FZI) - 0.0673\\ SFZI= & 255.92(SZI) - 22.188\\ FRI= & 0.1762(RI) - 1.2397\\ FHI= & 0.3526(HI) - 1.2127 \end{aligned}$$
Figure 11
figure 11

Analysis display.

Full size image
Figure 12
figure 12

Analysis display.

Full size image

Grid graph (GG)

Randić index, harmonic index, and fuzzy first and second Zagreb indices of grid graph have been discussed in this section. Grid graph can be obtained through the cartesian product of path \(P_{m}\) and \(P_{n}.\) A Cartesian product of two graphs, denoted by \(H_{1}\times H_{2}\), has a vertex set \(V(H_{1}\times H_{2})= V(H_{1})\times V(H_{2})\) and every vertex of \(H_{1}\times H_{2}\) is an ordered pair (x, y),  where \(x \in V(H_{1})\) and \(y \in V(H_{2}).\) Two distinct vertices \((x_{1},y_{1})\) and \((x_{2},y_{2})\) are adjacent in \(H_{1}\times H_{2}\) if either \(x_{1}=x_{2}\) and \(y_{1}y_{2} \in E(H_{2})\) or \(y_{1}=y_{2}\) and \(x_{1}x_{2} \in E(H_{1}).\)

Topological indices of grid graph

Theorem 5

Let \(G=P_{m} \times P_{n}\) be a grid graph, then the first Zagreb index of grid graph \(G=P_{m} \times P_{n}\) is \(M_{1}(G)= (16mn -14m- 14n + 8),\) for \(m,n \ge 2.\)

Proof

The representation of grid graph \(G=P_{m} \times P_{n}\) having mn vertices and \(2mn-(m+n)\) edges, is given below.

4 vertices have degree 2,  \(2(m+n-4)\) vertices have degree 3,  while the remaining \(mn-2(m+n)+4\) have 4.

$$\begin{aligned} M_{1}(G)= & \sum _{v \in V(G)} d^{2}(v) \\= & 4[2^{2}]+2(m+n-4)[3^{2}] +(mn-2(m+n)+4)[4^{2}]\\= & 16 mn-14m-14n+8, \end{aligned}$$

\(\square\)

Theorem 6

Let \(G=P_{m} \times P_{n}\) be a grid graph,

(a):

then the second Zagreb index of grid graph \(G=P_{m} \times P_{n}\) is \(M^{*}(G)= (32mn -38m-38n+36),\) for \(m,n \ge 2.\)

(b):

then the Randi’c index of grid graph \(G=P_{m} \times P_{n}\) is \(R(G)= (0.5mn-0.06m-0.06n-0.044),\) for \(m,n \ge 2.\)

(c):

then the harmonic index of grid graph \(G=P_{m} \times P_{n}\) is \(H(G)= (0.5mn - 0.012m- 0.012n - 0.084),\) for \(m,n \ge 2.\)

Proof of part (a)

The representation of ladder graph \(G=P_{m} \times P_{n}\) having mn vertices and \(2mn-(m+n)\) edges, is given below.

8 edges have end vertices degrees (2, 3),  \(2(m+n-6)\) edges have end vertices degrees (3, 3),  \(2(m+n-4)\) edges have end vertices degrees (3, 4),  while the remaining \(2mn-5(m+n)+12\) have end vertices degrees (4, 4).

$$\begin{aligned} M^{*}(G)= & \sum _{jk \in E(G)}[ d(j) \times d(k)] \\= & 8[2\times 3]+ 2(m+n-6)[3 \times 3] + 2(m+n-4)[3 \times 4]\\ & + 2mn-5(m+n+12)[4 \times 4]\\= & 48+18m+18n-108+24m+24n-96+32mn-80m-80n+192\\= & 32mn-38m-38n+36, \end{aligned}$$

\(\square\)

Proof of part (b)

By using the edge partition of part (a), we have

$$\begin{aligned} R(G)= & \sum _{jk \in E(G)} [ d(j) \times d(k)]^{-1/2}\\= & [8] [ 2 \times 3]^{-1/2} + 2[m+n-6] [ 3 \times 3]^{-1/2}+ 2[m+n-4] [ 3 \times 4]^{-1/2}\\ & \quad + [2mn-5(m+n)+12] [ 4 \times 4]^{-1/2}\\= & 8(0.408) +2[(0.333)(m+n-6)] +2[(0.289)(m+n-4)] + (0.25)[2mn-5(m+n)+12]\\= & 3.264+0.666m+0.666n-3.996+0.578m+0.578n-2.312\\ & \quad + 0.5mn-1.25m-1.25n+3\\= & 0.5 mn-0.06m-0.06n -0.044, \end{aligned}$$

Proof of part (c)

By using the edge partition of part (a), we have

$$\begin{aligned} H(G)= & \sum _{jk \in E(G)} [\frac{2}{d(j)+ d(k)}]\\= & \frac{8\times 2}{2+3}+ \frac{2\times 2(m+n-6)}{3+3} + \frac{2\times 2(m+n-4)}{3+4}\\ & + \frac{2\times (2mn-5(m+n)+12)}{4+4}\\= & 3.2+0.666m+0.666n-3.996+0.572m+0.572n-2.288+0.5mn \\- & 1.25m-1.25n+3\\= & 0.5 mn-0.012m-0.012n -0.084 \end{aligned}$$

The numerical comparison shown in Table 8. \(\square\)

Analysis of grid and fuzzy grid graph via machine learning techniques

After raising the values of m from 2 to 11 in the grid graph \(G=P_{m} \times P_{2}\), we get the values of different indices shown in Table 8.

Table 8 Table showing the relationship between Vertex, FZI, SZI, RI, and HI.
Full size table

The regression analysis of the grid graph between the vertices and FZI, SZI, RI, and HI. The equation of linear regression and their graph is presented below:

First Zagreb Index

The relationship between vertices and the first Zagreb index(FZI) is represented by the equation and the graphical comparison shown in Fig. 1a and b.

$$\begin{aligned} FZI = 11.3333 \times Vertex - 34.0000 \end{aligned}$$
Figure 13
figure 13

FZI vs vertices of grid graph.

Full size image

Second Zagreb Index

The relationship between vertices and the second Zagreb index(SZI) is represented by the equation and the graphical comparison shown in Figs. 13 and 14a and b.

$$\begin{aligned} SZI = 19.3333 \times Vertex - 78.0000 \end{aligned}$$
Figure 14
figure 14

SZI vs vertices.

Full size image

Randić Index

The relationship between vertices and Randić index(RI) is represented by the equation and the graphical comparison shown in Fig. 1a and b.

$$\begin{aligned} RI = 0.4800 \times Vertex - 0.2240 \end{aligned}$$
Figure 15
figure 15

RI vs vertices.

Full size image

Harmonic Index

The relationship between vertices and harmonic index (HI) is represented by the equation and the graphical comparison shown in Figs. 15 and 16a and b.

$$\begin{aligned} HI = 0.4960 \times Vertex - 0.1200 \end{aligned}$$
Figure 16
figure 16

HI vs vertices.

Full size image

Fuzzy molecular descriptors of fuzzy grid graph (FGG)

In this section, we will compute the fuzzy topological indices of the Fuzzy Grid Graph (FGG). We will use FGG for Fuzzy Grid Graph throughout this paper. The other notations will be used for fuzzy topological indices Such as the Fuzzy First Zagreb Index (FFZI), Fuzzy Second Zagreb Index (FSZI), Randić Index (RI), and Harmonic Index (HI). The total number of vertices of FGG is mn and the total edges are \(2(m\times n)-(n+m).\)

Figure 17
figure 17

Fuzzy grid graph \(P_{4}\times P_{4}\).

Full size image

Theorem 7

Let \(G=P_{m} \times P_{n}\) be a FGG, then the FFZI is \(FM_{1}(G)= (0.108 mn -0.12n -0.66m+0.048),\) for \(m,n \ge 2.\)

Proof

The Weight of the all vertices \(U_{i}'s\) is 0.3 and has a total count of \(m \times n\) where 4 vertices have weight 0.3,  \(2(n-2)\) vertices have weight 0.4,  \(2(m-2)\) vertices have weight 0.5 and remaining \(nm-(2m+2m-4)\) vertices have 0.6.

$$\begin{aligned} FM_{1}(G)= & \sum _{k=1}^{q} \sigma (u_{k}) [du_{k}]^{2}, \\= & 0.3[4(0.3)^{2}+2(n-2)(0.4)^{2} \\+ & 2(m-2)(0.5)^{2} +(mn-(2n+2m-4))(0.6)^{2}]\\= & (0.3)[0.36mn-0.40n-0.22m+0.16] \\= & 0.108 mn -0.12n -0.66m+0.048, \end{aligned}$$

\(\square\)

Theorem 8

Let \(G=P_{m} \times P_{n}\) be a FGG,

(a):

then the FSZI is \(FSM^{*}(G)= (0.0324 mn -0.0315 m-0.045 n+0.0351),\) for \(m,n \ge 2.\)

(b):

then the fuzzy FRI is \(FR(G)= (5.5556 mn -1.1365 m +1.2484n+ 21.512),\) for \(m,n \ge 2.\)

(c):

then the FHI is \(FH(G)= 2.7778 mn + 0.80805 m - 0.83335 n -1.2034,\) for \(m,n \ge 2.\)

Proof of part (a)

The weight of the all vertices \(U_{i}'s\) is 0.3 has a total count of \(m \times n\) and edges has a total count \(2(m \times n)-(n+m)\) where 4 have weight 0.3,  \(2(n-2)\) have weight 0.4,  \(2(m-2)\) have weight 0.5 and remaining \(nm-(2m+2m-4)\) have and have following type of representations. 2 have vertex degree (0.3, 0.5),  2 have vertex degree (0.5, 0.3),  \(2(m-3)\) have vertex degree (0.5, 0.5),  2 have vertex degree (0.3, 0.4),  2 have vertex degree (0.4, 0.3),  \((n-3)2\) have vertex degree (0.4, 0.4),  \(n-2\) have vertex degree (0.4, 0.6),  \(n-2\) have vertex degree (0.6, 0.4),  \((n-2)\times (m-3)\) have vertex degree (0.6, 0.6),  \(m-2\) have vertex degree (0.5, 0.6),  \(m-2\) have vertex degree (0.6, 0.5),  \((n-3)\times (m-2)\) have vertex degree (0.6, 0.6), 

$$\begin{aligned} FSM^{*}(G)= & (1/2)\sum _{u_{k}v_{l} \in E(G)} [\sigma (u_{k})(du_{k})\sigma (v_{l}) (dv_{l}) ], \\= & (1/2)[2(0.3)(0.3)(0.3)(0.3)+ 2(0.3)(0.5)(0.3)(0.3)\\ & + 2(m-3)(0.3)(0.5)(0.3)(0.5) + 2(0.3)(0.3)(0.3)(0.4)\\ & + 2(0.3)(0.4)(0.3)(0.3)+ 2(n-3)(0.3)(0.4)(0.3)(0.4)\\ & + (n-2)(0.3)(0.4)(0.3)(0.6)+ (n-2)(0.3)(0.6)(0.3)(0.4)\\ & + (n-2)(m-3)(0.3)(0.6)(0.3)(0.6)\\ & + (m-2)(0.3)(0.5)(0.3)(0.6)\\ & + (m-2)(0.3)(0.6)(0.3)(0.5)\\ & + (m-2)(n-3)(0.3)(0.6)(0.3)(0.6)]\\= & 0.0324 mn -0.0315m -0.045 n+0.0351 \end{aligned}$$

\(\square\)

Proof of part (b)

$$\begin{aligned} FR(G)= & (1/2)\sum _{u_{k}v_{l} \in E(G)} [\sigma (u_{k})(du_{k})\sigma (v_{l}) (dv_{l}) ]^{-1/2}, \\= & (1/2)[2[(0.3)(0.3)(0.3)(0.5)]^{-1/2}+ 2[(0.3)(0.5)(0.3)(0.3)]^{-1/2}\\ & \quad + 2(m-3)[(0.3)(0.5)(0.3)(0.5)]^{-1/2} + 2[(0.3)(0.3)(0.3)(0.4)]^{-1/2}\\ & \quad + 2[(0.3)(0.4)(0.3)(0.3)]^{-1/2}+ 2(n-3)[(0.3)(0.4)(0.3)(0.4)]^{-1/2}\\ & \quad + (n-2)[(0.3)(0.4)(0.3)(0.6)]^{-1/2}+ (n-2)[(0.3)(0.6)(0.3)(0.4)]^{-1/2}\\ & \quad + (n-2)(m-3)[(0.3)(0.6)(0.3)(0.6)]^{-1/2} \\ & \quad +(m-2)[(0.3)(0.5)(0.3)(0.6)]^{-1/2}\\ & \quad + (m-2)[(0.3)(0.6)(0.3)(0.5)]^{-1/2} \\ & \quad + (m-2)(n-3)[(0.3)(0.6)(0.3)(0.6)]^{-1/2}]\\= & 5.5556 mn -1.1365 m +1.2484 n+ 21.512 \end{aligned}$$

\(\square\)

Proof of part (c)

$$\begin{aligned} FH(G)= & (1/2)\sum _{u_{k}v_{l} \in E(G)} [\frac{1}{\sigma (u_{k})(du_{k})+\sigma (v_{l}) (dv_{l})} ], \\= & (1/2)[\frac{2}{(0.3)(0.3)+(0.3)(0.5)}+ \frac{2}{(0.3)(0.5)+(0.3)(0.3)}\\ & \quad + \frac{2(m-3)}{(0.3)(0.5)+(0.3)(0.5)}+ \frac{2}{(0.3)(0.3)+(0.3)(0.4)}\\ & \quad + \frac{2}{(0.3)(0.4)+(0.3)(0.3)}+ \frac{2(n-3)}{(0.3)(0.4)+(0.3)(0.4)}\\ & \quad + \frac{(n-2)}{(0.3)(0.4)+(0.3)(0.6)} + \frac{(n-2)}{(0.3)(0.6)+(0.3)(0.4)} \\ & \quad + \frac{(n-2)(m-3)}{(0.3)(0.6)+(0.3)(0.6)}+ \frac{(m-2)}{(0.3)(0.5)+(0.3)(0.6)}\\ & \quad + \frac{(m-2)}{(0.3)(0.6)+(0.3)(0.5)}+ \frac{(n-2)(m-3)}{(0.3)(0.6)+(0.3)(0.6)}\\= & 2.7778 mn + 0.80805 m - 0.83335 n -1.2034. \end{aligned}$$

\(\square\)

The numerical comparison shown in Table 9.

After raising the values of m from 2 to 11 in the grid graph \(G=P_{m} \times P_{2}\), we get the values of different indices shown in Table 9.

Table 9 Comparison of indices for \(H=P_{3} \times P_{n}\) Grid graph.
Full size table

Linear regression model for fuzzy ladder graph

The regression analysis of the ladder graph between the vertices and first Zagreb index, second Zagreb index, Randić index, and Harmonic index. The numerical comparison is shown in Table 10. The equation of linear regression and their graph is presented below:

Table 10 Table showing the relationship between Vertex, FZI, SZI, RI, and HI.
Full size table

First Fuzzy Zagreb Index

The relationship between vertices and the first fuzzy Zagreb index(FFZI) is represented by the equation and the graphical comparison shown in Figs. 17 and 18a and b.

$$\begin{aligned} FFZI = 0.1050 \times Vertices -2.5491 \end{aligned}$$
Figure 18
figure 18

FFZI vs vertices.

Full size image

Second Fuzzy Zagreb Index

The relationship between vertices and the second fuzzy Zagreb index(SFZI) is represented by the equation and the graphical comparison shown in Fig. 18a and b.

$$\begin{aligned} SFZI = 0.0234 \times Vertices -0.2299 \end{aligned}$$
Figure 19
figure 19

SFZI vs vertices.

Full size image

Fuzzy Randić Index

The relationship between vertices and fuzzy Randić index(FRI) is represented by the equation and the graphical comparison shown in Fig. 18a and b.

$$\begin{aligned} FRI = 5.9717 \times Vertices + 18.1025 \end{aligned}$$
Figure 20
figure 20

FRI vs vertices.

Full size image

Fuzzy Harmonic Index

The relationship between vertices and Fuzzy Harmonic Index(FHI) is represented by the equation and the graphical comparison shown in Figs. 19, 20, 21a and b.

$$\begin{aligned} FHI = 2.5000 \times Vertices + 1.2208 \end{aligned}$$
Figure 21
figure 21

FHI vs vertices.

Full size image

Exploring the relationship between grid and fuzzy grid graphs using machine learning model

In this section, we will discuss how Fuzzy grid graphs and grid graphs behave alike. These graphs have a linear and non-linear relationship with each other. These indices are related to each other by a linear equation and non-linear. There are four equations that are connected in such a way First Fuzzy Zagreb index is related to first Zagreb index, second fuzzy Zagreb index is related to second Zagreb index, Fuzzy Randić Index is related to Fuzzy Randić Index, and harmonic index is related to fuzzy harmonic index, respectively. The equations are given below:

$$\begin{aligned} FFZI= & -427.43(FZI)^{5} - 397.51(FZI)^{4} + 270(FZI)^{3} + 205.67(FZI)^{2} + 56.385(FZI) + 226.49\\ SFZI= & -1E+06(SZI)^{5} + 2E+06(SZI)^{4} - 872177(SZI)^{3} + 229612(SZI)^{2} - 27240(SZI) + 1384\\ FRI= & = 0.0804RI - 1.6791\\ FHI= & 0.1984HI - 0.3622 \end{aligned}$$

Discussion

The graphical results, including regression plots and 3D visualizations, offer crucial insights into the behavior of crisp and fuzzy topological indices. Crisp indices generally exhibit stable, linear patterns, reflecting their deterministic nature and suitability for analyzing well-defined networks. In contrast, fuzzy indices often show nonlinear trends, highlighting their ability to model uncertainty and adapt to imprecise data. For instance, fuzzy Zagreb indices in complex graphs display undulating behaviors influenced by membership values, capturing nuanced variations in network dynamics. While anomalies such as outliers in fuzzy indices may arise due to abrupt changes in membership functions, these deviations emphasize their sensitivity and robustness in handling uncertainty. Comparing the two, crisp indices excel in controlled environments, whereas fuzzy indices are indispensable for real-world applications involving ambiguity, such as traffic networks or communication systems. By interpreting trends, anomalies, and comparative behaviors, the graphical results underscore the versatility of fuzzy indices and their enhanced relevance for decision-making in complex, uncertain systems. This analysis not only validates the theoretical underpinnings but also demonstrates practical advantages, bridging the gap between theory and application.

Conclusion

This paper investigates the properties of fuzzy grid graphs and fuzzy ladder graphs, employing machine learning techniques and statistical analysis. Our study reveals strong correlations among these graphs, particularly between: Ladder graphs and fuzzy ladder graphs through machine learning, Grid graphs and fuzzy grid graphs through machine learning. We identify relationships governed by linear and polynomial regression models. Notably, our findings suggest that knowing one index in the crisp case allows for accurate prediction of the corresponding index in the fuzzy case. Key Contributions:

1. Comprehensive analysis of fuzzy grid and ladder graphs.

2. Identification of correlations and predictive relationships using machine learning and statistical methods.

3. Establishment of linear and polynomial regression models connecting crisp and fuzzy graph indices.

Open problems

Open Problem 1

Fuzzy Zagreb indices of subdivided grid graph and subdivided ladder graph is still an open problem.1